文章编号: 2096-3203(2024)04-0235-10 中图分类号: TM721
2. 许继电气股份有限公司, 河南 许昌 461000;
3. 西安许继电力电子技术有限公司, 陕西 西安 710075
为紧跟能源技术进步趋势并推动能源清洁低碳转型,建设以新能源为主体的新型电力系统、促进清洁能源高质量发展是关键[1-3]。然而,我国清洁能源与负荷中心总体上呈逆向分布格局[4-5],清洁能源生产的电能需要大规模、跨区域转移。目前,基于晶闸管的电网换相换流器型高压直流输电(line commutated converter-based high voltage direct current,LCC-HVDC)技术具有输电距离远、传输容量大、电能损耗小以及工程造价低等优点,是大规模新能源送出的主流方案之一[6-12]。
LCC-HVDC因采用半控型电力电子器件作为换流器的换流元件,当受端交流电网出现故障时,存在发生换相失败的风险,若逆变侧换相换流器(line commutated converter, LCC)发生换相失败,会造成系统直流电压跌落、传输功率中断,给整个送、受端交流电网带来冲击[13-15]。一般来说,LCC-HVDC系统第一次发生换相失败后,经一系列控制保护处理措施作用,在200 ms内可恢复至稳定状态,对送、受端交流电网冲击较小。但是,若系统在故障恢复过程中再次或多次发生换相失败(称之为后续换相失败),则可能引发系统停运、交流电网解列等严重后果,威胁电网安全[15]。
针对LCC-HVDC系统存在的后续换相失败问题,文献[16]和文献[17]分别提出在受端交流系统中加装基于半控型功率器件的静止无功补偿器以及基于全控型功率器件的静止同步补偿器,在系统换相失败恢复过程中,通过上述装置对发生故障的交流系统进行就地无功补偿,改善交流电压跌落程度,保证换相过程顺利实现,进而抑制后续换相失败,但附加无功补偿装置无疑会增加系统投资,经济性稍差。为了进一步释放控制保护系统调节能力,文献[18-19]对LCC-HVDC系统换相失败故障恢复过程进行了详细的理论分析,指出逆变侧LCC在电流偏差控制作用阶段发生后续换相失败风险较大,控制保护策略改进应围绕此阶段展开。文献[20]在电流偏差控制作用阶段通过配置预测模块增大逆变侧LCC触发超前角和换相裕度来抵御后续换相失败,且取得了积极效果,但未说明补偿系数的选择方法。文献[21]指出电流偏差控制环节的控制曲线斜率会对后续换相失败抑制能力产生影响,并借助仿真工具开展了影响分析,指出控制曲线斜率越大对恢复过程越有利。文献[22]通过对电流偏差控制中的控制曲线进行改造,由一阶函数变为二阶函数,增大了电流偏差控制作用初始阶段控制曲线斜率。文献[23]提出基于故障严重程度调整控制曲线斜率的改进方案,根据电压跌落程度对控制曲线斜率进行补偿,以达到增大斜率的目的,可以有效抑制后续换相失败,改善系统恢复特性。综上可知,现阶段电流偏差控制参数对于后续换相失败的影响分析多借助仿真工具,且控制曲线参数选取多依赖定性分析和大量仿真校核,数学分析较为空白,效率整体稍差,同时选取参数往往只适用于仿真校核系统,通用性不强。
文中首先基于以往研究,对电流偏差控制参数与换相失败之间的关系进行了理论分析,发现故障恢复过程中系统若不发生后续换相失败,逆变侧LCC直流电压和交流换相电压则存在一定的约束关系,而电流偏差控制曲线斜率对此约束关系有直接的影响。然后,在理论分析基础上,以抑制后续换相失败为目标,提出了一种电流偏差控制参数整定方法。该方法根据LCC-HVDC系统参数便可设计合理的电流偏差控制曲线参数,无须构造复杂控制曲线或关联其他电气量,同时可有效抑制后续换相失败,具有一定的优势。最后,利用PSCAD/EMTDC仿真平台,基于CIGRE标准测试模型对理论分析结果与参数整定方法开展了仿真验证工作。
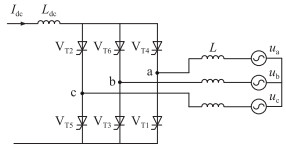
1 LCC-HVDC系统简介 1.1 LCC及换相失败逆变侧六脉动LCC拓扑如图 1所示,其中Idc为直流侧电流;Ldc为LCC直流平波电抗器的电感;VT1—VT6为半控型电力电子器件晶闸管,是换流器实现电能变换的核心元件;L为LCC交流端口的等效换相电感;ua、ub、uc为LCC接入交流系统的等效交流电压。
|
图 1 六脉动LCC拓扑 Fig. 1 Six-pulse LCC topology |
对于LCC来说,正常情况下一个交流电压周期内六脉动LCC共有6种工作状态,每个状态下均有2个晶闸管同时导通(VT1/VT2、VT2/VT3、VT3/VT4、VT4/VT5、VT5/VT6、VT6/VT1),其基本工作原理为通过晶闸管的交替导通将交流侧线电压按照一定时序引至直流侧,实现交流与直流之间的转换,晶闸管交替导通的过程也即是换相过程。
由于晶闸管自身开关特性,在换相过程中待关断晶闸管要承受一段时间的反压才能恢复正向阻断能力,该时间内对应的电角度为关断角γ[19]。若待关断晶闸管未恢复正向阻断能力,换相过程结束后该晶闸管两端承受正向电压将继续导通,接着待导通晶闸管两端长时间承受反压而关断,发生换相失败,随着其他晶闸管换相过程不断进行,后续会出现一个桥臂上下两晶闸管同时导通的情况,直流侧出现短路回路,直流电压迅速跌落,电流快速增大,对整个系统造成严重影响。
综上,换相过程中发生换相失败的最本质原因为晶闸管关断角γ不足,待关断晶闸管未能恢复正向阻断能力。当系统正常对称运行时,关断角γ[22]可表示为:
| $ \gamma=\arccos \left(\cos \beta+\sqrt{2} X I_{\mathrm{dc}} / U_{\mathrm{L}}\right) $ | (1) |
式中:β为逆变侧LCC的超前触发角;X为等值换相电抗;UL为交流换相电压的线电压有效值。
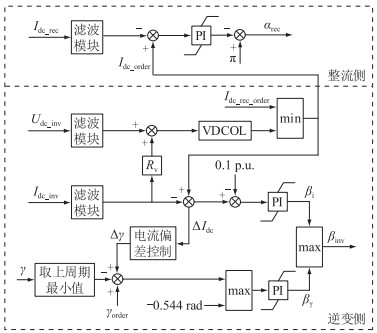
1.2 系统基本控制原理以CIGRE标准测试模型为例,LCC-HVDC系统的控制策略框图如图 2所示,其中Idc_rec、Idc_order分别为整流侧LCC直流电流和直流电流指令值;αrec为整流侧LCC触发延时角;Idc_rec_order为系统直流电流预期控制目标值;Udc_inv、Idc_inv分别为逆变侧LCC直流电压和直流电流;Rv为系统直流线路等效电阻;ΔIdc为直流电流指令值与实际值之间的偏差值;γorder为逆变侧LCC关断角指令值;Δγ为电流偏差控制环节输出的关断角补偿量;βi、βγ分别为逆变侧LCC定电流与定关断角控制器输出量;βinv为逆变侧LCC触发超前角;PI为比例积分控制器。
|
图 2 系统控制策略框图 Fig. 2 The block diagram of system control strategy |
从图 2中可以看出,整个系统中整流侧LCC主要配置定电流控制,逆变侧LCC主要配置定电流控制和定关断角控制。为了优化系统运行特性,整流侧和逆变侧LCC还额外附加了一些辅助控制策略,如低电压限流(voltage dependent current order limiter,VDCOL)策略和电流偏差控制策略。
电流偏差控制策略的作用是避免系统暂态过程中逆变侧LCC在定电流控制和定关断角控制之间出现频繁切换,达到两控制模式平稳转换的目的。电流偏差控制策略的控制曲线方程为:
| $ \Delta \gamma= \begin{cases}0 & \Delta I_{\mathrm{dc}} \leqslant 0 \\ k \Delta I_{\mathrm{dc}} & 0<\Delta I_{\mathrm{dc}} \leqslant \Delta I_{\mathrm{H}} \\ \Delta \gamma_{\max } & \Delta I_{\mathrm{dc}}>\Delta I_{\mathrm{H}}\end{cases} $ | (2) |
式中:k为控制曲线斜率参数;ΔIH为电流偏差量限制值;Δγmax为关断角补偿量限制值。
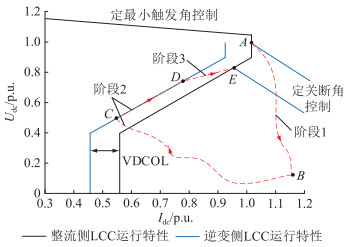
1.3 系统故障恢复过程根据图 2所示系统控制策略对LCC-HVDC系统进行控制,系统稳定运行时的稳态运行特性曲线如图 3所示,其中Udc为直流系统的直流电压。系统发生换相失败后,其故障恢复过程可以划分为3个阶段:故障初始阶段(阶段1)、VDCOL作用阶段(阶段2)和电流偏差控制作用阶段(阶段3)[18-19]。
|
图 3 系统稳态运行特性曲线 Fig. 3 Steady-state operating characteristic curves of the system |
阶段1:系统正常运行时工作在稳态运行点A,此时整流侧LCC工作在定电流控制模式,逆变侧LCC工作在定关断角控制模式。换相失败发生后,逆变侧LCC会出现同一相单元上下桥臂晶闸管同时导通的情况,直流侧出现短路回路,直流电压大幅度降低,直流电流迅速增大,系统运行点由A点移动至B点。
阶段2:直流电压大幅度降低后,VDCOL策略开始作用,对直流电流指令值进行限制,此时整流侧和逆变侧LCC均工作在定电流控制模式,力图将系统直流电流控制在一个较低的水平,两者争夺系统直流电流的控制权限。由于逆变侧LCC定电流控制模式下电流指令值与整流侧LCC相比存在0.1 p.u.裕度,因此电流指令值与实际值偏差更大,其控制器调节速度更快并起到主导作用,系统运行点由B点拉回至C点,并随着直流电压的恢复,按照VDCOL策略特性曲线逐渐向上移动。在系统运行点由C点向上移动的过程中,系统直流电流由逆变侧LCC进行控制,目标值和实际值相差不大,控制器调节速度逐渐趋于平稳。此时,整流侧LCC定电流控制的电流指令值与实际值存在一定的偏差值,经控制器不断调节,逐渐对系统电流控制起主导作用,接着系统故障恢复过程进入下一阶段。
阶段3:假设在系统运行点D处整流侧LCC接管了电流控制,逆变侧LCC将切换为电流偏差控制,随着系统不断恢复,电流偏差量会越来越小,关断角补偿量也越来越小,最终从D点过渡到E点,逆变侧LCC工作在定关断角控制模式,系统达到新的稳定运行状态。
文献[18]和文献[19]均指出系统在故障恢复过程(阶段3)中易发生换相失败,其主要原因是电流偏差控制曲线斜率选择不当,但未说明该斜率值与换相失败之间的具体关系以及斜率值的整定方法,因此有必要开展进一步研究。
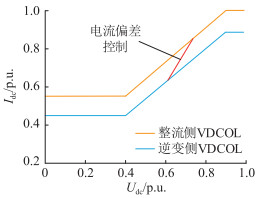
2 电流偏差控制曲线斜率对后续换相失败的影响分析及参数整定方法 2.1 影响分析参考图 3单独绘制VDCOL与电流偏差控制运行特性曲线,如图 4所示。
|
图 4 VDCOL和电流偏差控制运行特性曲线 Fig. 4 Operating characteristic curves of VDCOL and current deviation control |
在电流偏差控制策略的作用下,逆变侧LCC直流电流和直流电压之间的数学关系可以用一元一次函数进行描述:
| $ \frac{I_{\mathrm{dcr}}}{I_{\mathrm{dcn}}}=a \frac{U_{\mathrm{dcr}}}{U_{\mathrm{dcn}}}+b $ | (3) |
式中:a、b分别为一次函数斜率和截距,其数值与系统主回路参数和控制参数相关;Udcr为故障恢复过程中逆变侧LCC直流电压;Idcr为逆变侧LCC直流电流;Udcn、Idcn分别为系统额定直流电压和额定直流电流。
假设LCC-HVDC系统稳定运行过程中,逆变侧LCC关断角为γn,触发超前角为βn,交流换相电压有效值为ULn;故障恢复过程中,逆变侧LCC关断角为γr,触发超前角为βr,交流换相电压有效值为ULr。考虑系统故障恢复过程中若不再发生换相失败,系统电压、电流等电气量变化相对较为平稳,则根据LCC稳态运行特性方程可得:
| $ \left\{\begin{array}{l} U_{\mathrm{dcr}}=\frac{3 \sqrt{2}}{\mathsf{π}} U_{\mathrm{Lr}} \cos \gamma_{\mathrm{r}}-\frac{3}{\mathsf{π}} X I_{\mathrm{dcr}} \\ U_{\mathrm{dcn}}=\frac{3 \sqrt{2}}{\mathsf{π}} U_{\mathrm{Ln}} \cos \gamma_{\mathrm{n}}-\frac{3}{\mathsf{π}} X I_{\mathrm{dcn}} \end{array}\right. $ | (4) |
根据式(1),可得:
| $ \frac{U_{\mathrm{Lr}}}{U_{\mathrm{Ln}}}=\frac{I_{\mathrm{dcr}}}{I_{\mathrm{dcn}}} \times \frac{\cos \gamma_{\mathrm{n}}-\cos \beta_{\mathrm{n}}}{\cos \gamma_{\mathrm{r}}-\cos \beta_{\mathrm{r}}} $ | (5) |
假设系统在稳定运行与故障恢复过程中,逆变侧换相时的换相重叠角大小相同且为μ(实际上故障恢复阶段换相重叠角偏小,按式(6)计算得到的关断角偏大,因此判断是否会发生换相失败时可充分反映严重情况),则触发超前角和关断角之间存在关系如下:
| $ \left\{\begin{array}{l} \beta_{\mathrm{r}}=\gamma_{\mathrm{r}}+\mu \\ \beta_{\mathrm{n}}=\gamma_{\mathrm{n}}+\mu \end{array}\right. $ | (6) |
将式(4)中上下两式做商,再联立式(3)、式(5)和式(6),经整理可得:
| $ \begin{gathered} \frac{1-\cos \mu+\sin \mu \tan \gamma_{\mathrm{r}}}{1-\cos \mu+\sin \mu \tan \gamma_{\mathrm{n}}}= \\ \left\{U_{\mathrm{dcr}} I_{\mathrm{dcn}}+\frac{3}{\mathsf{π}} X I_{\mathrm{dcn}} I_{\mathrm{dcr}}+\left[b U_{\mathrm{dcn}}+(a-1) U_{\mathrm{dcr}}\right] I_{\mathrm{dcn}}\right\} / \\ \left(U_{\mathrm{dcr}} I_{\mathrm{dcn}}+\frac{3}{\mathsf{π}} X I_{\mathrm{dcn}} I_{\mathrm{dcr}}\right) \end{gathered} $ | (7) |
根据式(7)可知,bUdcn+(a-1)Udcr将直接影响γr、γn两者间大小。若bUdcn+(a-1)Udcr≥0,则γr≥γn,系统故障恢复过程中不会发生换相失败;若bUdcn+(a-1)Udcr<0,则γr<γn,系统故障恢复过程中存在发生换相失败的可能。
根据式(2)可知,在系统故障恢复过程中,关断角为γr为:
| $ \gamma_{\mathrm{r}}=\gamma_{\mathrm{n}}+k \Delta I_{\mathrm{dc}} $ | (8) |
式中:ΔIdc=(Idcn-Idcr)/Idcn。
将式(8)代入式(4)的上式中,可得:
| $ U_{\mathrm{dcr}}=\frac{3 \sqrt{2}}{\mathsf{π}} U_{\mathrm{Lr}} \cos \left(\gamma_{\mathrm{n}}+k \Delta I_{\mathrm{dc}}\right)-\frac{3}{\mathsf{π}} X I_{\mathrm{dcr}} $ | (9) |
由于后续换相失败一般发生在系统故障恢复过程末期,此时系统电流指令值与实际值偏差较小,关断角补偿量也较小,将式(9)中cos函数在γn处进行一阶泰勒展开可得:
| $ U_{\mathrm{dcr}}=\frac{3 \sqrt{2}}{\mathsf{π}} U_{\mathrm{Lr}}\left(\cos \gamma_{\mathrm{n}}-\frac{\sin \gamma_{\mathrm{n}}}{1!} k \Delta I_{\mathrm{dc}}\right)-\frac{3}{\mathsf{π}} X I_{\mathrm{dcr}} $ | (10) |
将式(10)按照式(3)进行形式转化,可得:
| $ \begin{aligned} & \frac{I_{\mathrm{dcr}}}{I_{\mathrm{dcn}}}=\underbrace{\frac{\mathsf{π} U_{\mathrm{dcn}}}{3 \sqrt{2} k U_{\mathrm{Lr}} \sin \gamma_{\mathrm{n}}-3 X I_{\mathrm{dcn}}}}_a \times \frac{U_{\mathrm{dcr}}}{U_{\mathrm{dcn}}}+ \\ & (\underbrace{-\frac{3 \sqrt{2} U_{\mathrm{Lr}} \cos \gamma_{\mathrm{n}}-3 \sqrt{2} k U_{\mathrm{Lr}} \sin \gamma_{\mathrm{n}}}{3 \sqrt{2} k U_{\mathrm{Lr}} \sin \gamma_{\mathrm{n}}-3 X I_{\mathrm{dcn}}}}_b) \\ & \end{aligned} $ | (11) |
为了保证系统在故障恢复过程中不会发生换相失败,将式(11)中变量a与b代入不等式bUdcn+(a-1)Udcr≥0,可得:
| $ \frac{U_{\mathrm{dcr}}}{U_{\mathrm{dcn}}} \geqslant \frac{3 \sqrt{2} U_{\mathrm{Lr}} \cos \gamma_{\mathrm{n}}-3 \sqrt{2} k U_{\mathrm{Lr}} \sin \gamma_{\mathrm{n}}}{\mathsf{π} U_{\mathrm{dcn}}-3 \sqrt{2} k U_{\mathrm{Lr}} \sin \gamma_{\mathrm{n}}+3 X I_{\mathrm{dcn}}} $ | (12) |
因此,在电流偏差控制曲线斜率k值保持不变的前提下,若系统故障恢复过程中不发生换相失败,则逆变侧LCC直流电压与交流换相电压须满足式(12)所示的约束关系。
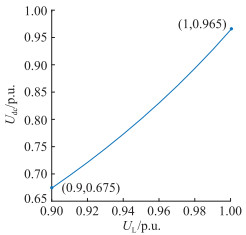
以CIGRE标准测试模型及其电流偏差控制参数为例,此时k值为2.793,将系统参数代入式(12)。系统故障恢复过程中逆变侧LCC若不发生换相失败,则其直流电压与交流换相电压间的约束关系曲线如图 5所示。为分析方便,图中电气量数值已进行标幺化处理。
|
图 5 直流电压与交流换相电压间约束关系曲线 Fig. 5 Constraint curve between DC voltage and AC commutation voltage |
从图 5中可以看出,当逆变侧LCC交流换相电压为额定值0.9 p.u.时,直流电压恢复至额定值0.675 p.u.便能保证系统不会发生换相失败;但交流换相电压为1 p.u.时,需要直流电压恢复至额定值0.965 p.u.才能保证系统不发生换相失败。从整个约束关系图来看,交流换相电压小范围改变需要直流电压恢复至较高的数值才能避免出现换相失败。考虑故障恢复过程中交流换相电压可能会出现一定波动,倘若直流电压恢复速度及恢复程度不能匹配相应波动,易导致后续换相失败的发生。
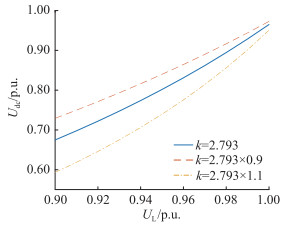
同样以CIGRE标准测试模型及其电流偏差控制参数为例,当k值分别取2.793×0.9、2.793和2.793×1.1时,可得不同k值下直流电压与交流换相电压的约束关系曲线,如图 6所示。
|
图 6 不同k值下约束关系曲线 Fig. 6 Constraint curves under different k values |
从图 6中可以看出,在故障恢复过程中,当交流换相电压出现相同范围的波动,电流偏差控制曲线斜率取值偏小时,对系统直流电压恢复程度要求高;而电流偏差控制曲线斜率取值偏大时,对直流电压恢复程度要求低。因此,电流偏差控制曲线斜率取值偏大能有效抑制故障恢复过程中因交流换相电压波动或直流电压恢复程度不足造成的后续换相失败,对抑制后续换相失败起积极效果,与文献[22-23]的分析吻合。
2.2 参数整定方法根据2.1节分析可知,电流偏差控制曲线斜率取值越大,当故障恢复过程中交流换相电压出现波动时,对直流电压恢复程度要求越低,系统抵御后续换相失败的能力越强。
但是,控制曲线斜率也不是越大越好,控制曲线斜率越大,相同电流偏差量下关断角补偿量也越大,逆变侧LCC吸收无功功率Q的计算公式如下:
| $ Q=P \tan \varphi $ | (13) |
| $ \cos \varphi=\frac{1}{2}(\cos \gamma+\cos (\gamma+\mu)) $ | (14) |
式中:Q为逆变侧LCC吸收无功功率;P为逆变侧LCC传输有功功率;φ为逆变侧LCC的功率因数角。
可见,关断角补偿量大会造成逆变侧LCC关断角γ变大,进一步导致吸收无功功率变大。因此,选取电流偏差控制曲线斜率时也不宜过大,过大不利于交流系统电压恢复,难以保证换相过程顺利进行。
假设系统稳定运行过程中逆变侧LCC传输有功功率额定值为Pn,配置无功补偿装置的容量为Qn;故障恢复过程中逆变侧LCC传输有功功率为Pr,吸收无功功率为Qr,功率因数角为φr。根据式(13)和式(14),为了避免故障恢复过程中逆变侧LCC吸收无功功率超过补偿装置配置容量,应满足:
| $ \left\{\begin{array}{l} Q_{\mathrm{r}}=P_{\mathrm{r}} \tan \varphi_{\mathrm{r}} \leqslant Q_{\mathrm{n}} \\ \cos \varphi_{\mathrm{r}}=\frac{1}{2}\left(\cos \gamma_{\mathrm{r}}+\cos \left(\gamma_{\mathrm{r}}+\mu\right)\right) \end{array}\right. $ | (15) |
将式(8)代入式(15),并将2个cos函数进行一阶泰勒展开,可得:
| $ \left\{\begin{array}{l} P_{\mathrm{r}} \tan \varphi_{\mathrm{r}} \leqslant Q_{\mathrm{n}} \\ \cos \varphi_{\mathrm{r}}=\left[\cos \gamma_{\mathrm{n}}+\cos \left(\gamma_{\mathrm{n}}+\mu\right)-\right. \\ \left.k\left(\sin \gamma_{\mathrm{n}}+\sin \left(\gamma_{\mathrm{n}}+\mu\right)\right) \Delta I_{\mathrm{dc}}\right] / 2 \end{array}\right. $ | (16) |
借助三角函数基本定理,联立式(16)上下两式,可得:
| $ k \leqslant \frac{\cos \gamma_{\mathrm{n}}+\cos \left(\gamma_{\mathrm{n}}+\mu\right)-2 / \sqrt{1+Q_{\mathrm{n}}^2 / P_{\mathrm{r}}^2}}{\left(\sin \gamma_{\mathrm{n}}+\sin \left(\gamma_{\mathrm{n}}+\mu\right)\right) \Delta I_{\mathrm{dc}}} $ | (17) |
考虑Pr最大值为Pn,Pr取最大值时式(17)分子中负数项数值最大,此时对k值约束最强。因此,为了确保系统故障恢复过程中满足无功功率约束条件,k值最大值kmax应满足:
| $ k_{\max } \leqslant \frac{\cos \gamma_{\mathrm{n}}+\cos \left(\gamma_{\mathrm{n}}+\mu\right)-2 / \sqrt{1+Q_{\mathrm{n}}^2 / P_{\mathrm{n}}^2}}{\left(\sin \gamma_{\mathrm{n}}+\sin \left(\gamma_{\mathrm{n}}+\mu\right)\right) \Delta I_{\mathrm{dc}}} $ | (18) |
在进行参数整定时, 文中电流偏差控制的首要目标为抑制对系统危害较大的后续换相失败。考虑经典控制理论中控制器在对系统进行控制时,将被控量控制到目标值90%的时间(上升时间)较短,同理,系统直流电压恢复至额定值90%所需时间也相对较短。因此,对于故障恢复过程中逆变侧直流电压和交流换相电压之间的约束关系,可以按交流换相电压为额定值时,直流电压恢复程度为额定值的90%进行设计,此时根据式(12)可得电流偏差控制曲线斜率k的整定值kcal的计算公式为:
| $ k_{\text {cal }}=\frac{3 \sqrt{2} U_{\mathrm{Ln}} \cos \gamma_{\mathrm{n}}-0.9 \mathsf{π} U_{\mathrm{dcn}}-2.7 X I_{\mathrm{dcn}}}{0.3 \sqrt{2} U_{\mathrm{Ln}} \sin \gamma_{\mathrm{n}}} $ | (19) |
以CIGRE标准测试模型为例进行参数整定,系统内逆变侧单个LCC交流换相电压额定有效值ULn=209.228 8 kV,额定直流电流Idcn=2 kA,额定直流电压Udcn=250 kV,额定关断角γn=15°,等值换相电抗X=13.315 2 Ω,代入式(19)可得到参数整定值为:
| $ k_{\mathrm{cal}}=3.424\;4 $ | (20) |
将Pn=1 000 MW、Qn=626 Mvar、μ=15°、ΔIdc=0.05 p.u.代入式(18)可得kmax≤3.603 4,参数整定结果满足无功约束条件。
3 仿真验证为了验证理论分析的正确性以及参数整定方法对抑制系统后续换相失败的有效性,利用PSCAD/EMTDC仿真平台中的CIGRE标准测试模型开展仿真工作,测试模型系统参数如表 1所示。
|
|
表 1 测试模型系统参数 Table 1 The system parameters of test model |
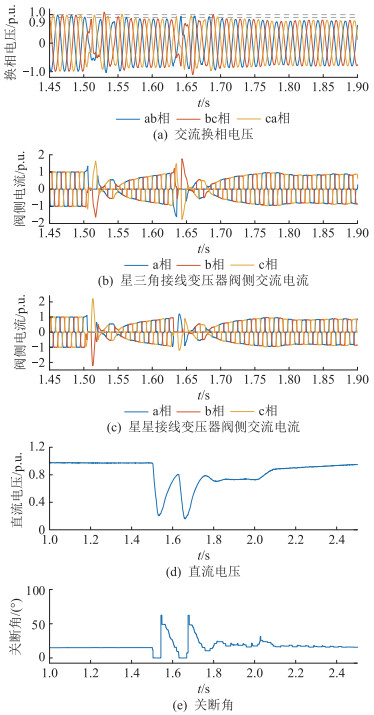
基于测试模型原有控制策略以及控制参数,故障设置方式参考文献[24-25],1.5 s时在逆变侧交流母线上设置三相经电感接地故障(接地电感值Lf=0.4 H),故障持续时间为0.5 s,逆变侧LCC交流换相电压、阀侧交流电流、直流电压以及关断角的变化情况如图 7所示。
|
图 7 三相故障Lf=0.4 H时系统运行特性 Fig. 7 System operation performance under three-phase fault with Lf=0.4 H |
由图 7可知,系统第一次发生换相失败的恢复过程后期,逆变侧LCC交流换相电压出现一定的波动,最大波动接近于额定值,此时直流电压恢复至额定值的0.8 p.u.,恢复程度相对较低,难以满足不发生换相失败时直流电压与交流换相电压间的约束关系,系统再次发生换相失败。而系统第二次发生换相失败的恢复过程后期,交流换相电压变化较为平稳,且幅值相对较低,对直流电压恢复程度要求也低,系统未再次发生换相失败,与理论分析一致。
为验证文中所提电流偏差控制参数整定方法的有效性,对下述不同算例进行仿真。
算例1:电流偏差控制参数不做任何更改,此时k=2.793;
算例2.1:对电流偏差控制参数进行优化,按照一般经验可将控制参数提高1.1倍,以提高换相过程中关断角大小,此时k=3.072 3;
算例2.2:对电流偏差控制参数进行优化,考虑足够关断角补偿量可将控制参数提高1.3倍,以提高换相过程中关断角大小,此时k=3.630 9;
算例3:对电流偏差控制参数进行优化,根据系统参数和式(19)进行计算,获取理论计算值,此时k=3.424 4。
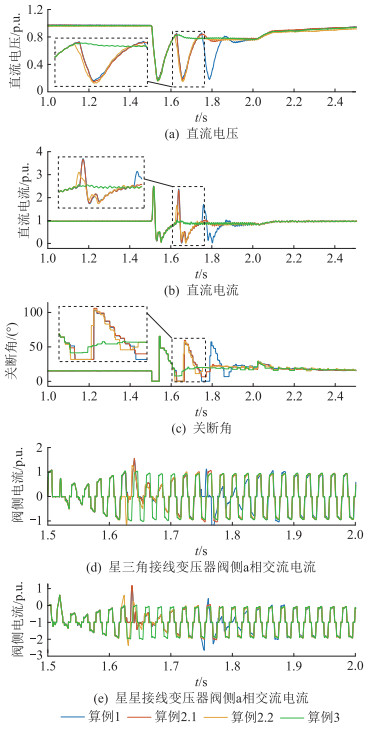
故障设置方式同样参考文献[24-25],故障工况为1.5 s时在逆变侧交流母线上设置单相经电感接地故障(Lf=0.4 H),故障恢复过程中不同算例下系统相关电气量的变化情况如图 8所示。
|
图 8 单相故障下参数更改前后系统运行特性 Fig. 8 System operation performance before and after parameter change under single-phase fault |
为验证文中所提参数整定方法同样适用于三相接地故障工况,同步开展了三相接地故障的仿真工作。故障工况为1.5 s时在逆变侧交流母线上设置三相经电感接地故障(Lf=0.4 H),故障持续时间为0.5 s,故障恢复过程中不同算例下系统相关电气量的变化情况如图 9所示。
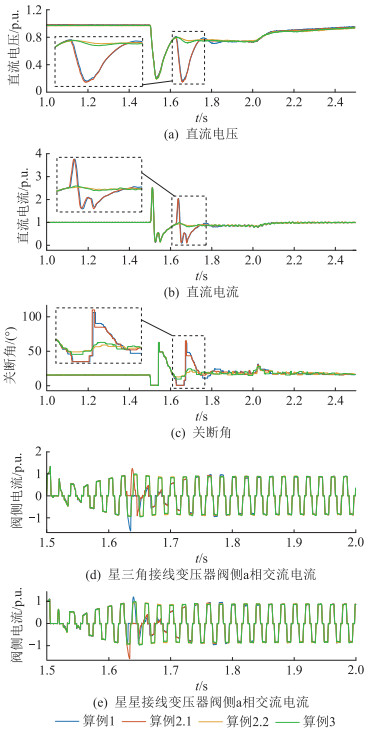
|
图 9 三相故障下参数更改前后系统运行特性 Fig. 9 System operation performance before and after parameter change under three-phase fault |
由图 9可知,算例1和算例2.1下系统故障恢复过程中发生了后续换相失败,而算例2.2和算例3下系统故障恢复过程中未发生后续换相失败,表明电流偏差控制参数按照经验提高1.1倍相对保守,关断角补偿量不足,未能完全抵御换相失败。
但是,电流偏差控制参数也并非越大越好。由图 8可以看出,算例1、算例2.1和算例2.2下系统故障恢复过程中均发生了后续换相失败,而算例3下系统故障恢复过程中未发生后续换相失败,表明部分工况下电流偏差控制参数若考虑足够关断角补偿量而提高过大,同样不利于系统故障恢复。
综上可知,电流偏差控制参数在进行优化时,不宜过小也不宜过大,过小会出现补偿量不足,过大则存在矫枉过正问题。文中所提控制参数整定方法,经数学分析推导获得,在一定程度上可以减少参数反复优化迭代的仿真工作量,提高系统控制参数整定效率,对工程实际控制参数设计也具有一定的指导价值。
进一步地,为验证所提电流偏差控制参数整定方法在不同严重程度的故障下均有效,按照研究LCC-HVDC系统换相失败的常用测试方法,通过改变接地电感值大小和接入系统方式来模拟故障严重程度及类型,对所提方法进行适应性测试。故障水平[26-27]定义为:
| $ f_{\mathrm{L}}=\frac{U_{\mathrm{L}}^2}{\omega L_{\mathrm{f}} P} \times 100 \% $ | (21) |
式中:fL为故障水平,数值越高表示故障越严重;ω为交流系统工作频率。
表 2为换相失败累计次数统计。由表 2可知,与原系统参数相比,绝大多故障工况下电流偏差控制参数按照文中所提整定方法优化后,LCC-HVDC系统累计发生换相失败的次数减少,表明文中所提电流偏差控制参数整定方法可以有效抑制系统故障恢复过程中的换相失败问题,验证了所提方法的有效性和适应性。
|
|
表 2 换相失败累计次数 Table 2 Cumulative number of commutation failure |
根据表 2还可以看出,文中所提电流偏差控制参数整定方法在三相故障工况下的换相失败抑制效果要优于单相故障工况。这是由于文中基于LCC稳态运行特性方程对电流偏差控制参数与换相失败之间的关系进行数学推导分析,但单相故障工况下系统不对称运行,交流换相电压会出现过零点偏移。以稳态运行方程分析换相失败约束关系时,在一定程度上忽略了角度偏移影响,造成单相故障下抑制效果未显示出良好的一致性。但是,由于分析推导方法符合系统运行一般规律,因此所提控制参数整定方法在抑制单相故障工况下后续换相失败方面仍取得了积极效果。从表 2不同算例的数据对比可以看出,控制参数优化后不会恶化系统故障恢复特性,且在大多数故障水平下换相失败问题均得到了改善。
4 结论文中针对电流偏差控制曲线斜率与后续换相失败之间的具体关系进行了理论分析,并在此基础上提出了一种电流偏差控制参数整定方法,将理论分析与仿真验证相结合,得出结论如下:
(1) LCC-HVDC系统换相失败恢复过程中,在逆变侧LCC的电流偏差控制作用阶段,若系统不发生换相失败,其直流电压与交流换相电压则存在一定的约束关系,且该约束关系受电流偏差控制曲线斜率直接影响;
(2) 当电流偏差控制曲线斜率取值较小时,系统故障恢复过程中对直流电压恢复程度要求高,在交流电压出现小范围波动时,为避免换相失败发生,需要直流电压快速调整或已恢复至较高水平,因此为提高系统抑制后续换相失败能力,电流偏差控制曲线斜率应在合理范围内取大一些;
(3) 提出一种根据系统自身参数对电流偏差控制曲线斜率进行参数整定的方法,所提方法计算简便,无须构造复杂的控制曲线即可实现对后续换相失败的抑制,对工程控制参数设计具有一定指导价值。
| [1] |
丁剑, 方晓松, 宋云亭, 等. 碳中和背景下西部新能源传输的电氢综合能源网构想[J]. 电力系统自动化, 2021, 45(24): 1-9. DING Jian, FANG Xiaosong, SONG Yunting, et al. Conception of electricity and hydrogen integrated energy network for renewable energy transmission in Western China under background of carbon neutralization[J]. Automation of Electric Power Systems, 2021, 45(24): 1-9. DOI:10.7500/AEPS20210211002 (  0) 0) |
| [2] |
姜红丽, 刘羽茜, 冯一铭, 等. 碳达峰、碳中和背景下"十四五"时期发电技术趋势分析[J]. 发电技术, 2022, 43(1): 54-64. JIANG Hongli, LIU Yuxi, FENG Yiming, et al. Analysis of power generation technology trend in 14th five-year plan under the background of carbon peak and carbon neutrality[J]. Power Generation Technology, 2022, 43(1): 54-64. (  0) 0) |
| [3] |
魏泓屹, 卓振宇, 张宁, 等. 中国电力系统碳达峰·碳中和转型路径优化与影响因素分析[J]. 电力系统自动化, 2022, 46(19): 1-12. WEI Hongyi, ZHUO Zhenyu, ZHANG Ning, et al. Transition path optimization and influencing factor analysis of carbon emission peak and carbon neutrality for power system of China[J]. Automation of Electric Power Systems, 2022, 46(19): 1-12. (  0) 0) |
| [4] |
李惠玲, 王曦, 高剑, 等. 新型电力系统背景下西部送端直流电网方案构建[J]. 中国电力, 2023, 56(5): 12-21. LI Huiling, WANG Xi, GAO Jian, et al. Scheme construction for sending end DC grids in Western China under the background of new power system[J]. Electric Power, 2023, 56(5): 12-21. (  0) 0) |
| [5] |
金楚, 李作红, 葛景, 等. 交直流混联受端电网动态无功规划研究[J]. 电力电容器与无功补偿, 2022, 43(1): 12-17. JIN Chu, LI Zuohong, GE Jing, et al. Research on dynamic reactive power planning of hybrid AC/DC receiving-end power grid[J]. Power Capacitor & Reactive Power Compensation, 2022, 43(1): 12-17. (  0) 0) |
| [6] |
辛保安, 郭铭群, 王绍武, 等. 适应大规模新能源友好送出的直流输电技术与工程实践[J]. 电力系统自动化, 2021, 45(22): 1-8. XIN Baoan, GUO Mingqun, WANG Shaowu, et al. Friendly HVDC transmission technologies for large-scale renewable energy and their engineering practice[J]. Automation of Electric Power Systems, 2021, 45(22): 1-8. DOI:10.7500/AEPS20210302001 (  0) 0) |
| [7] |
饶宏, 黄伟煌, 郭知非, 等. 柔性直流输电技术在大电网中的应用与实践[J]. 高电压技术, 2022, 48(9): 3347-3355. RAO Hong, HUANG Weihuang, GUO Zhifei, et al. Practical experience of VSC-HVDC transmission in large grid[J]. High Voltage Engineering, 2022, 48(9): 3347-3355. (  0) 0) |
| [8] |
李大虎, 李佳, 周悦, 等. 常规直流送端近区电网中调相机和柔性直流的无功协调控制[J]. 电力建设, 2023, 44(12): 148-160. LI Dahu, LI Jia, ZHOU Yue, et al. Reactive power-coordinated control of a synchronous condenser and VSC-HVDC in the sending-side near region power grid of an LCC-HVDC[J]. Electric Power Construction, 2023, 44(12): 148-160. DOI:10.12204/j.issn.1000-7229.2023.12.013 (  0) 0) |
| [9] |
李昊, 仝义, 赵成勇, 等. 大规模风电接入的特高压混合级联直流系统送端无功协调控制策略[J]. 现代电力, 2023, 40(2): 210-218. LI Hao, TONG Yi, ZHAO Chengyong, et al. A reactive power coordinated control strategy for sending-end of hybrid cascaded UHVDC system with grid-connected large-scale wind power[J]. Modern Electric Power, 2023, 40(2): 210-218. (  0) 0) |
| [10] |
孟沛彧, 向往, 潘尔生, 等. 分址建设直流输电系统拓扑方案与运行特性研究[J]. 电工技术学报, 2022, 37(19): 4808-4822. MENG Peiyu, XIANG Wang, PAN Ersheng, et al. Research on topology and operation characteristics of HVDC transmission system based on site-division construction[J]. Transactions of China Electrotechnical Society, 2022, 37(19): 4808-4822. (  0) 0) |
| [11] |
蔡旭, 杨仁炘, 周剑桥, 等. 海上风电直流送出与并网技术综述[J]. 电力系统自动化, 2021, 45(21): 2-22. CAI Xu, YANG Renxin, ZHOU Jianqiao, et al. Review on offshore wind power integration via DC transmission[J]. Automation of Electric Power Systems, 2021, 45(21): 2-22. (  0) 0) |
| [12] |
王秋楠, 晋宏杨, 刘东, 等. LCC-HVDC换流站无功电压控制问题综述[J]. 电力电容器与无功补偿, 2023, 44(2): 10-17. WANG Qiunan, JIN Hongyang, LIU Dong, et al. Review on reactive voltage control of LCC-HVDC converter station[J]. Power Capacitor & Reactive Power Compensation, 2023, 44(2): 10-17. (  0) 0) |
| [13] |
汤奕, 郑晨一. 高压直流输电系统换相失败影响因素研究综述[J]. 中国电机工程学报, 2019, 39(2): 499-513, 647. TANG Yi, ZHENG Chenyi. Review on influencing factors of commutation failure in HVDC systems[J]. Proceedings of the CSEE, 2019, 39(2): 499-513, 647. (  0) 0) |
| [14] |
高凯, 屈海涛, 任茂鑫, 等. 基于可控电压源的高压直流输电换相失败抑制技术[J]. 高压电器, 2023, 59(1): 49-57. GAO Kai, QU Haitao, REN Maoxin, et al. Commutation failure suppression technology for HVDC transmission based on controlled voltage source[J]. High Voltage Apparatus, 2023, 59(1): 49-57. (  0) 0) |
| [15] |
景柳铭, 王宾, 董新洲, 等. 高压直流输电系统连续换相失败研究综述[J]. 电力自动化设备, 2019, 39(9): 116-123. JING Liuming, WANG Bin, DONG Xinzhou, et al. Review of consecutive commutation failure research for HVDC transmission system[J]. Electric Power Automation Equipment, 2019, 39(9): 116-123. (  0) 0) |
| [16] |
金吉良, 刘瑶, 白菁, 等. 风电直流送出系统换相失败特性分析及其抑制措施[J]. 电网与清洁能源, 2023, 39(3): 74-82, 92. JIN Jiliang, LIU Yao, BAI Jing, et al. Characteristics analysis of the commutation failure and its suppression measures of the wind power DC transmission system[J]. Power System and Clean Energy, 2023, 39(3): 74-82, 92. (  0) 0) |
| [17] |
李宁, 高本锋, 张建坡, 等. 基于关断角偏差量的背靠背直流系统换相失败抑制研究[J]. 智慧电力, 2023, 51(2): 91-97, 123. LI Ning, GAO Benfeng, ZHANG Jianpo, et al. Commutation failure suppression for back to back DC system based on turn-off angle deviation[J]. Smart Power, 2023, 51(2): 91-97, 123. (  0) 0) |
| [18] |
刘席洋, 王增平, 郑博文, 等. LCC-HVDC故障恢复型连续换相失败机理分析与抑制措施[J]. 中国电机工程学报, 2020, 40(10): 3163-3172. LIU Xiyang, WANG Zengping, ZHENG Bowen, et al. Mechanism analysis and mitigation measures for continuous commutation failure during the restoration of LCC-HVDC[J]. Proceedings of the CSEE, 2020, 40(10): 3163-3172. (  0) 0) |
| [19] |
朱龙臻, 牛翀, 王志冰, 等. 一种抑制连续换相失败的关断角动态补偿控制方法[J]. 中国电机工程学报, 2021, 41(22): 7621-7631. ZHU Longzhen, NIU Chong, WANG Zhibing, et al. An extinction angle dynamic compensation control method for suppressing continuous commutation failure[J]. Proceedings of the CSEE, 2021, 41(22): 7621-7631. (  0) 0) |
| [20] |
赵晓龙, 陈卓, 田霄, 等. 高压直流输电系统抑制连续换相失败的策略研究[J]. 电测与仪表, 2022, 59(4): 185-190. ZHAO Xiaolong, CHEN Zhuo, TIAN Xiao, et al. Research on the strategy of mitigate consecutive commutation failure for HVDC transmission system[J]. Electrical Measurement & Instrumentation, 2022, 59(4): 185-190. (  0) 0) |
| [21] |
宋新甫, 陈伟伟, 周博昊, 等. 电流偏差控制对换相失败及其恢复过程的影响分析[J]. 电力工程技术, 2022, 41(2): 37-44. SONG Xinfu, CHEN Weiwei, ZHOU Bohao, et al. Influence of current error controller on commutation failures and system recovery[J]. Electric Power Engineering Technology, 2022, 41(2): 37-44. (  0) 0) |
| [22] |
高贵亮, 辛超山, 余中平, 等. 基于变斜率动态电流偏差控制的后续换相失败抑制方法[J]. 现代电子技术, 2023, 46(9): 148-154. GAO Guiliang, XIN Chaoshan, YU Zhongping, et al. Method of subsequent commutation failure suppression based on variable slope dynamic current deviation control[J]. Modern Electronics Technique, 2023, 46(9): 148-154. (  0) 0) |
| [23] |
晁武杰, 邓超平, 黄均纬, 等. 一种抑制后续换相失败的变斜率电流偏差控制方法[J]. 电力建设, 2023, 44(1): 73-81. CHAO Wujie, DENG Chaoping, HUANG Junwei, et al. A variable-slope current deviation control method to suppress subsequent commutation failure[J]. Electric Power Construction, 2023, 44(1): 73-81. (  0) 0) |
| [24] |
郭春义, 李春华, 刘羽超, 等. 一种抑制传统直流输电连续换相失败的虚拟电阻电流限制控制方法[J]. 中国电机工程学报, 2016, 36(18): 4930-4937, 5117. GUO Chunyi, LI Chunhua, LIU Yuchao, et al. A DC current limitation control method based on virtual-resistance to mitigate the continuous commutation failure for conventional HVDC[J]. Proceedings of the CSEE, 2016, 36(18): 4930-4937, 5117. (  0) 0) |
| [25] |
孟庆强, 刘泽洪, 洪乐荣, 等. 一种抑制连续换相失败的非线性VDCOL控制策略[J]. 电力系统保护与控制, 2019, 47(7): 119-127. MENG Qingqiang, LIU Zehong, HONG Lerong, et al. A sup-pression method based on nonlinear VDCOL to mitigate the continuous commutation failure[J]. Power System Protection and Control, 2019, 47(7): 119-127. (  0) 0) |
| [26] |
夏海涛, 周小平, 洪乐荣, 等. 一种抑制后续换相失败的自适应电流偏差控制方法[J]. 中国电机工程学报, 2019, 39(15): 4345-4355. XIA Haitao, ZHOU Xiaoping, HONG Lerong, et al. An adaptive current deviation control method for suppressing following commutation failures[J]. Proceedings of the CSEE, 2019, 39(15): 4345-4355. (  0) 0) |
| [27] |
袁博, 王颖, 邵华, 等. 抑制特高压直流系统连续换相失败的非线性动态电流偏差控制[J]. 中国电力, 2021, 54(8): 75-82. YUAN Bo, WANG Ying, SHAO Hua, et al. A nonlinear dynamic current deviation control method for suppressing continuous commutation failures in UHVDC systems[J]. Electric Power, 2021, 54(8): 75-82. (  0) 0) |
2. XJ Electric Co., Ltd., Xuchang 461000, China;
3. Xi'an XJ Power Electronics Technology Co., Ltd., Xi'an 710075, China
 2024, Vol. 43
2024, Vol. 43


 李娟(1982), 女, 硕士, 工程师, 从事特高压直流输电产品测试技术工作(E-mail:
李娟(1982), 女, 硕士, 工程师, 从事特高压直流输电产品测试技术工作(E-mail: