文章编号: 2096-3203(2024)04-0208-09 中图分类号: TM31
在同步发电机运行过程中,定子铁心作为能量转换的主要载体会产生损耗,其中涡流损耗、磁滞损耗占主要部分,附加损耗相对较小。铁心会随着损耗的积累而逐渐升温,而过高的温度会导致定子铁心变形和定子绕组绝缘磨损,最终影响发电机的稳定运行。另一方面,在气隙磁场中,定子铁心会受到磁拉力作用产生振动与机械变形。因此,分析磁-热-固耦合作用下的定子铁心温度变化和机械结构响应,可为研究发电机失效预防提供理论依据。
关于电机内部温度,文献[1]基于热损耗载荷构建了电机的磁-热耦合模型,模拟分析了电机在额定工况运行下的温度场分布规律。文献[2]采用流-热耦合模型优化设计方法,研制了一种模块化分数槽集中绕组发电机。文献[3]提出了一种通过温度分析来检测满载运行状态下发电机定子匝间短路故障的方法,并通过温度传感器将其应用到发电机的状态监测中。文献[4]为发电机的热分析和优化提供了很好的思路。文献[5]提出了热变形的理论计算模型和三维有限元模型,并进一步分析了不同温度分布条件下热变形对定子、转子和气隙长度的影响。文献[6]研究了电励磁发电机热网络建模和热特性,结果发现:相比于分布式励磁电机,集中式励磁电机的效率更高并且温升更低。文献[7]分析了发电机在实际运行过程中定子温度的变化情况,然后根据发电机内部传热过程,对定子温度进行建模。文献[8]研究了大型同步调相机在发生转子故障后的温度、热应力变化规律。
关于发电机电磁场分析,文献[9-10]推导了定子铁心磁拉力的公式,全面分析了同步发电机不同气隙静偏心情况下的定子振动特性,得到了铁心的危险位置。文献[11]对电磁场进行有限元分析,得到了气隙磁密的表达式和影响因素,进一步对转子不平衡磁拉力进行了解析计算和实验验证。文献[12]基于发电机组振动频谱特征,开发了一套智能监控系统用于发电机的状态监测和故障诊断。文献[13-14]提出了一种新颖的电磁力波计算方法。文献[15]对发电机定子系统进行了模态分析,以研究电磁力导致电机振动与噪声的问题。文献[16]构建了磁场预测模型,综合考虑了定子齿尖效应。文献[17-18]通过建立场路耦合模型,结合Maxwell应力法计算得到了齿部动态电磁力。
上述文献虽然在研究发电机内部温度和定子所受磁拉力方面奠定了较好的理论基础,但大都仅考虑温度场和电磁场等单一因素影响下的定子温度变化或机械结构响应。为此,文中对同步发电机定子铁心在磁-热-固耦合作用下的温升特性和磁-热耦合激励下的机械结构响应进行理论推导、仿真分析和实验验证,得到了定子铁心的温度分布规律及变形危险部位,对发电机失效预防和逆向优化设计有极其重要的现实意义。
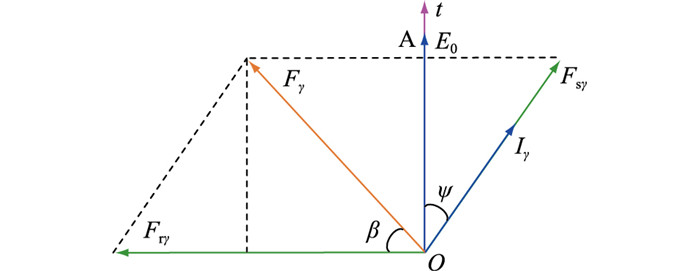
1 定子受载理论分析 1.1 电磁场 1.1.1 单位面积磁拉力正常运行时同步发电机气隙分布均匀,如图 1所示,其中g0为径向气隙长度;αm为周向角度。气隙磁密B(αm, t)等于气隙磁势f(αm, t)与气隙磁导Λ(αm)的乘积。如图 2所示,气隙磁势f(αm, t)可根据矢量法由定子磁势和转子磁势合成得到:
| $ \begin{gathered} f_\gamma\left(\alpha_{\mathrm{m}}, t\right)=F_{\mathrm{s} \gamma} \cos \left(\gamma \omega t-p \alpha_{\mathrm{m}}\right)+ \\ F_{\mathrm{r} \gamma} \cos \left(\gamma \omega t-p \alpha_{\mathrm{m}}+\psi+0.5 \pi\right)= \\ F_\gamma \cos \left(\gamma \omega t-p \alpha_{\mathrm{m}}-\beta\right) \end{gathered} $ | (1) |

|
图 1 同步发电机气隙 Fig. 1 Air gap of synchronous generators |
|
图 2 同步发电机气隙磁势 Fig. 2 Air gap magnetic potential of synchronous generators |
式中:γ为谐波次数,取奇数;fγ(αm, t)为γ次谐波的气隙磁势;Fsγ为γ次谐波的定子磁势幅值;Frγ为γ次谐波的转子磁势幅值;Fγ为γ次谐波的合成磁势幅值;ω为电角频率;p为极对数;ψ为内功角;β为合成磁势与转子磁势的夹角。
图 2中,E0为电枢电动势;Iγ为γ次谐波的电枢电流;t为时间轴;A表示发电机的A相。
则γ次谐波的气隙磁密可表示为:
| $ \begin{gathered} B_\gamma\left(\alpha_{\mathrm{m}}, t\right)=f_\gamma\left(\alpha_{\mathrm{m}}, t\right) \varLambda\left(\alpha_{\mathrm{m}}\right)= \\ \frac{\mu_0 F_\gamma}{g_0} \cos \left(\gamma \omega t-p \alpha_{\mathrm{m}}-\beta\right) \end{gathered} $ | (2) |
式中:μ0为真空磁导率。
由Maxwell张量法可得定子单位面积磁拉力q(αm, t)为:
| $ \begin{gathered} q\left(\alpha_{\mathrm{m}}, t\right)=\frac{B_\gamma^2\left(\alpha_{\mathrm{m}}, t\right)}{2 \mu_0}=\mu_0\left(\sum\limits_{\gamma=1}^{\infty} F_\gamma^2 \cos (2 \gamma \omega t-\right. \\ \left.\left.2 p \alpha_{\mathrm{m}}-2 \beta\right)+\sum\limits_{\gamma=1}^{\infty} F_\gamma^2\right) /\left(4 g_0^2\right) \end{gathered} $ | (3) |
由式(3)可知,定子磁拉力主要为直流分量与偶次谐波。根据同频响应,直流分量不引起定子铁心振动,偶次谐波成分引起定子偶次倍频振动,但二者作为激励,均可在定子铁心上产生机械结构响应。
1.1.2 发热机理(1) 定子铁心损耗。在发电机运行过程中,定子铁心中存在交变的磁场,因此会产生铁心损耗,引起定子铁心温升。根据Bertotti提出的经典三项式铁损耗模型,可得铁心总损耗PFe[19-23]为:
| $ \left\{\begin{array}{l} P_{\mathrm{Fe}}=P_{\mathrm{H}}+P_{\mathrm{E}}+P_{\mathrm{A}} \\ P_{\mathrm{H}}=k_{\mathrm{h}} f B^2 \\ P_{\mathrm{E}}=k_{\mathrm{e}} f^2 B^2 \\ P_{\mathrm{A}}=k_{\mathrm{a}} f^{1.5} B^{1.5} \end{array}\right. $ | (4) |
式中:PH为磁滞损耗;PE为涡流损耗;PA为由Buckhausen效应引起的附加损耗;kh为磁滞损耗系数;ke为涡流损耗系数;ka为附加损耗系数;f为频率;B为发电机气隙磁密幅值。
相较而言,定子铁心附加损耗的幅值远小于磁滞损耗和涡流损耗。鉴于此,后续分析定子铁心损耗主要为磁滞损耗和涡流损耗。
(2) 定子绕组铜损耗。定子绕组铜损耗主要表现为焦耳损耗,由电流的热效应产生[24]。定子绕组电流主要为基频和高次谐波,但高次谐波的幅值非常小;同时,考虑到集肤效应依赖于高频电流,因此文中忽略集肤效应。定子绕组的铜损耗PCu可表示为:
| $ P_{\mathrm{Cu}}=3 \sum\limits_{\gamma=1}^N I_{\mathrm{pm} \gamma}^2 R_{\mathrm{p}} $ | (5) |
式中:Ipmγ为γ次谐波的定子绕组电流均方根值;Rp为相电阻;N为电流谐波次数。
1.2 温度场损耗作为热源引起定子铁心的温升。铁心中的传热方式主要为热传导与热对流,热辐射的传热量相对较小,可忽略不计。定子铁心的传热方程和边界条件[25-28]可表示为:
| $ \left\{\begin{array}{l} \frac{\partial}{\partial x}\left(\varepsilon_x \frac{\partial T}{\partial x}\right)+\frac{\partial}{\partial y}\left(\varepsilon_y \frac{\partial T}{\partial y}\right)+\frac{\partial}{\partial z}\left(\varepsilon_z \frac{\partial T}{\partial z}\right)+q_\mathrm{v}=\rho c \frac{\partial T}{\partial t} \\ -S_n \frac{\partial T}{\partial n}=\alpha\left(T-T_{\mathrm{f}}\right) \end{array}\right. $ | (6) |
式中:εx、εy、εz、Sn分别为定子铁心在x、y、z、n方向上的导热系数;T为定子铁心的温度;Tf为定子铁心周围介质的温度;qv为热源密度;ρ为定子铁心的密度;c为定子铁心的比热容;α为定子铁心的散热系数。
定子铁心内圆表面和端面均与空气通过对流换热,其经验公式如下:
| $ \left\{\begin{array}{l} h_{\mathrm{n}}=25+12.5 v_{\mathrm{r}}^{0.5} \\ h_{\mathrm{e}}=15+6.5 v_{\mathrm{r}}^{0.7} \end{array}\right. $ | (7) |
式中:hn、he分别为内圆表面和端面的换热系数;vr为转子表面线速度。
发电机定子外圆表面直接与机壳接触,机壳表面的换热系数计算采用经验公式:
| $ h_{\mathrm{c}}=9.73+14 v_{\mathrm{k}}^{0.62} $ | (8) |
式中:hc为机壳表面的换热系数;vk为机壳表面流体介质的流速。
定子铁心与机壳接触面施加的等效热阻[29]为:
| $ R_\delta=\frac{\delta_0}{\lambda_0 A_0} $ | (9) |
式中:δ0为等效间隙;λ0为静止薄空气层的热导率;A0为导热面积。
1.3 机械结构响应定子铁心机械结构响应由2种激励引发,第一种是定子铁心受磁场作用产生的磁拉力激励,第二种是在温度场中定子铁心受非均匀热载荷而产生的热响应。
以瞬态温度场和瞬态电磁场运算结果为激励载荷,对定子铁心机械结构响应结果进行分析,其有限元方程可表示为:
| $ \left\{\begin{array}{l} \boldsymbol{K} \boldsymbol{u}=\boldsymbol{F}^{\mathrm{th}} \\ \boldsymbol{K}=\sum \int\limits_{\boldsymbol{V}} \boldsymbol{B}^{\mathrm{T}} \boldsymbol{D} \boldsymbol{B} \mathrm{d} \boldsymbol{V} \\ \boldsymbol{F}^{\mathrm{th}}=\sum \int\limits_{\boldsymbol{V}} \boldsymbol{B}^{\mathrm{T}} \boldsymbol{D} \boldsymbol{\varepsilon}^{\mathrm{th}} \mathrm{d} \boldsymbol{V} \\ \boldsymbol{\varepsilon}^{\mathrm{th}}=\Delta T\left[\begin{array}{ccc} a_x & a_y & a_z \\ 0 & 0 & 0 \end{array}\right]^{\mathrm{T}} \\ \Delta T=T-T_{\text {ref }} \\ \boldsymbol{\sigma}=\boldsymbol{D}\left(\boldsymbol{\varepsilon}-\boldsymbol{\varepsilon}^{\mathrm{th}}\right) \\ \boldsymbol{\varepsilon}=\boldsymbol{B} \boldsymbol{u} \end{array}\right. $ | (10) |
式中:K为单元刚度矩阵;u为节点位移矢量;Fth为温度节点载荷矩阵;B为单元应变-位移矩阵;D为弹性刚度矩阵;V为单元体积矩阵;εth为热应变矢量;ΔT为温升;ax、ay、az分别为x、y、z轴的材料热膨胀系数;Tref为参考温度值;σ为应力矢量;ε为全应变矢量[30]。
2 磁-热-固耦合仿真分析 2.1 有限元仿真设置文中以CS-5型同步发电机为研究对象,建立了三维有限元物理模型并进行了多物理场耦合仿真计算。发电机相关参数如表 1所示。
|
|
表 1 CS-5型发电机基本参数 Table 1 Primary parameters of CS-5 generator |
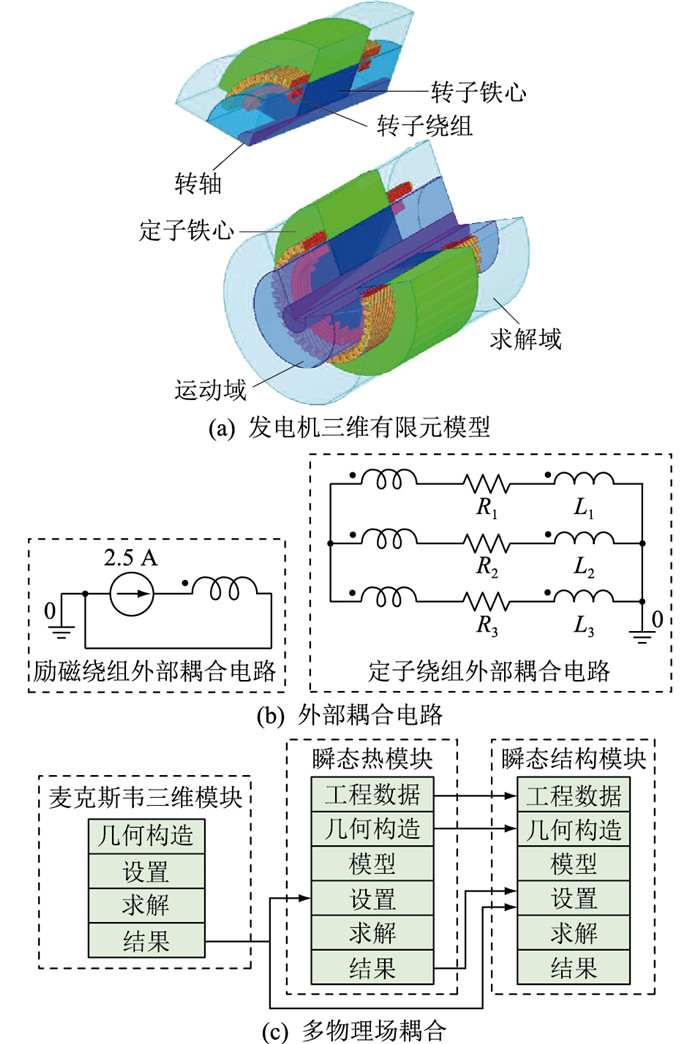
在电磁场仿真模块Maxwell 3D中,对发电机的定子铁心、定子绕组、转子铁心和转子绕组进行建模,图 3(a)为发电机的有限元物理模型。为降低仿真运算量,忽略对电磁影响较小的机壳、机座等部件。与物理模型耦合的外部电路如图 3(b)所示,其中励磁电流为2.5 A,每相负载为100 Ω电阻和0.238 H电感,对应表 1中发电机的功率因数为0.8。图 3(c)为多物理场耦合模块连接示意。耦合分析步骤如下:第一步,在麦克斯韦模块中进行电磁场仿真,求解得到损耗结果和单位面积磁拉力;第二步,在瞬态热模块中对发电机进行瞬态热分析,将损耗结果导入其中,求解定子铁心温度场分布结果;第三步,在瞬态结构模块中进行瞬态力学分析,将定子铁心单位面积磁拉力和热应力作为耦合激励导入其中,计算定子铁心的力学响应。软件根据铁心材料在50 Hz时的铁耗曲线(即B-P曲线)自动拟合得到系数kh、ke和ka,分别为309、0.822和0.000 03。针对文中所研究的实际情况,包括导热系数在内的定子材料属性如表 2所示。
|
图 3 有限元仿真 Fig. 3 Finite element simulation |
|
|
表 2 定子材料属性 Table 2 Material property of stators |
为便于有限元计算,文中对仿真作以下假设:
(1) 发电机磁场沿轴向均匀分布;
(2) 定子铁心材料各向同性,且端面循环空气的各点温度相同;
(3) 温度变化不影响材料的磁导率。
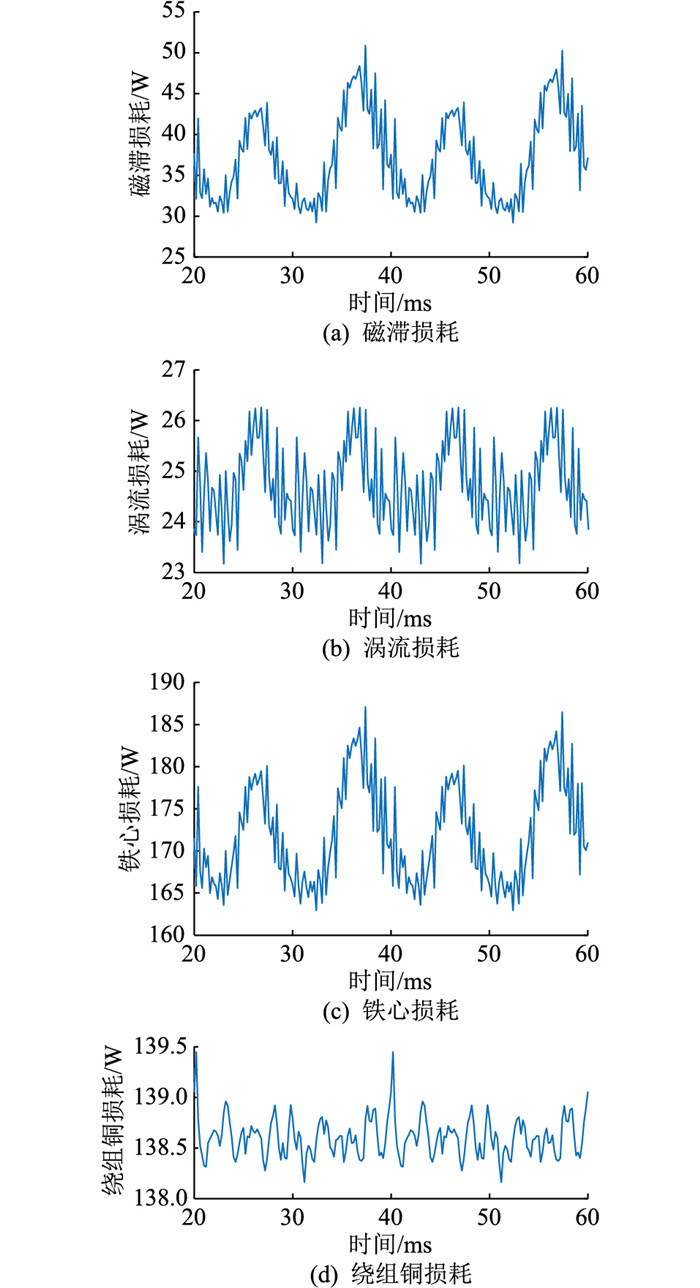
2.2 多物理场仿真结果分析 2.2.1 电磁场仿真图 4为发电机稳定运行后定子铁心损耗和定子绕组铜损耗曲线。由于磁场与转子同步转动,发电机中的损耗呈现周期性变化。
|
图 4 损耗有限元分析结果 Fig. 4 Finite element analysis results of loss |
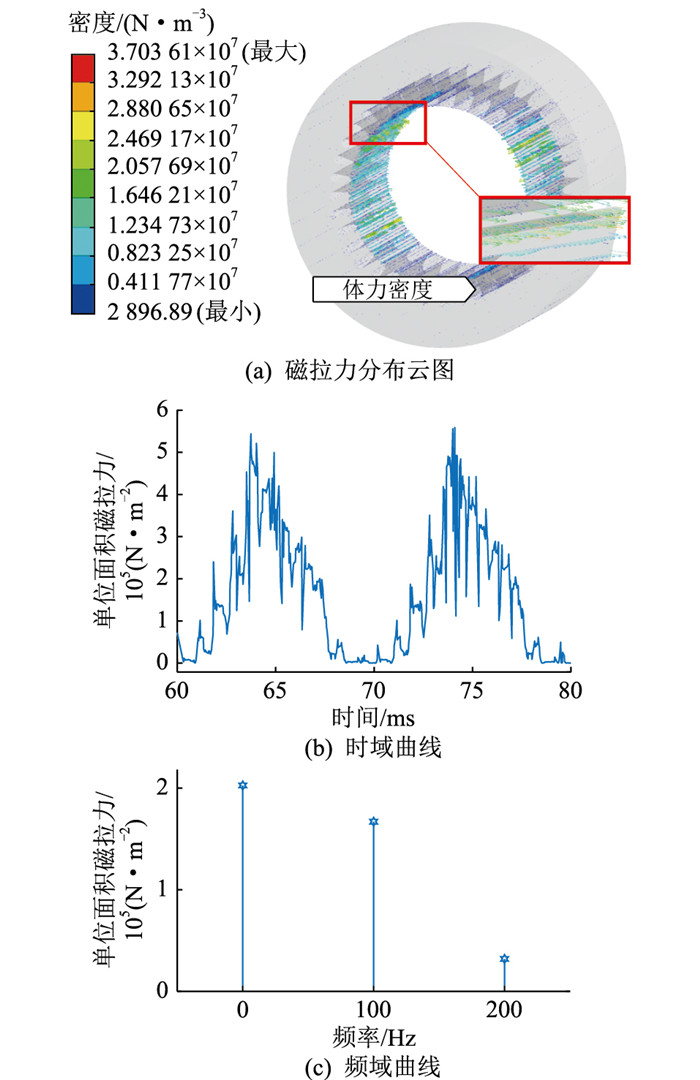
定子单位面积磁拉力如图 5所示。磁拉力集中在齿槽中,其时域波形随时间呈周期变化,频域主要成分为直流与二倍频,与理论分析部分的式(3)一致。
|
图 5 单位面积磁拉力有限元分析结果 Fig. 5 Finite element analysis results of magnetic tension per unit area |
(1) 单向耦合。将发电机损耗作为热源,导入瞬态热模块,可得定子铁心的三维温度场分布,初始温度设为20 ℃。
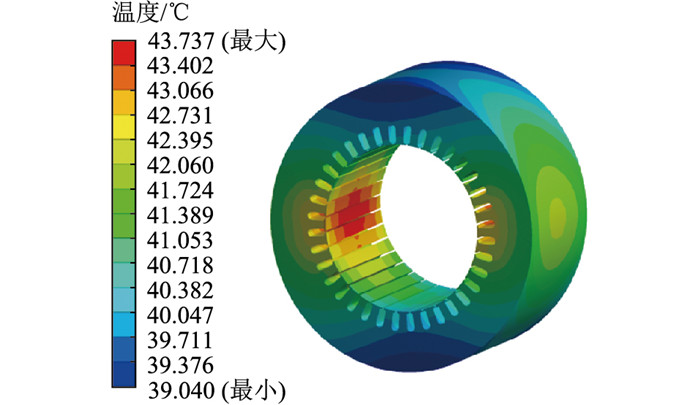
单向耦合温度场仿真结果如图 6所示,在定子铁心齿槽处温度最高,达到43.737 ℃;在外表面处温度最低,为39.040 ℃。定子铁心在齿根部位损耗密度较大,且外表面与外部空气直接进行对流换热,散热性能较好,因此最高温度出现在定子齿槽。由此分析可知,发电机正常运行时定子铁心应重点监测的温升部位为齿槽。
|
图 6 单向耦合温度场仿真结果 Fig. 6 Simulation results of temperature field under unidirectional coupling |
从图 6可以看出温度对称分布,分布规律与理论分析结果一致,因此仿真结果有效。
(2) 双向耦合。通常情况下,绕组电阻率随温度的变化而改变,电阻率的改变又反向影响绕组的电流和损耗从而影响温度,温度与电阻率是一个复杂的双向影响的关系。文中考虑绕组材料受工作温度的影响,采用磁-热双向耦合求解定子铁心的温升,分析定子铁心温度分布规律。
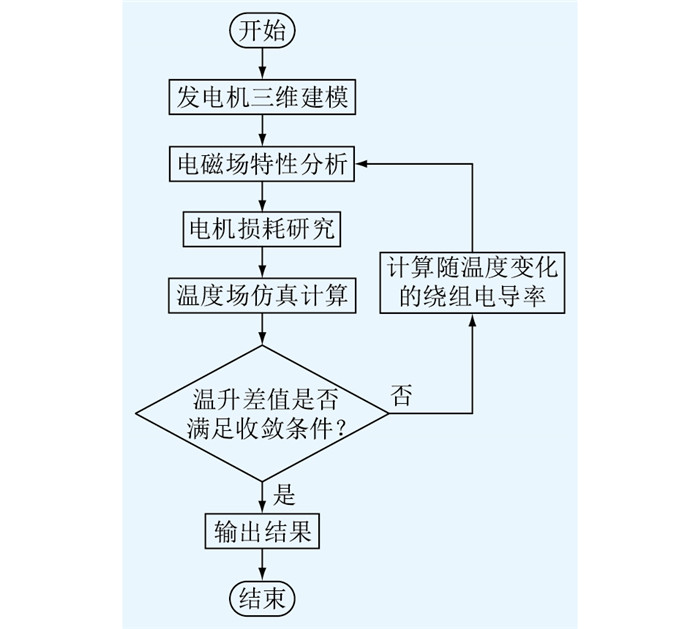
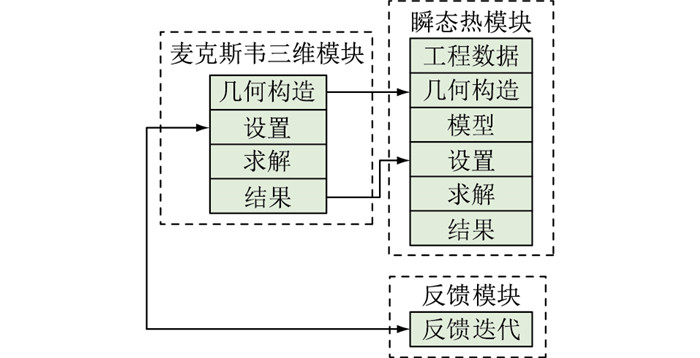
磁-热双向耦合流程如图 7所示,相对应的磁-热双向耦合Workbench模块连接如图 8所示。与单向耦合不同的是,双向耦合增加了反馈模块。
|
图 7 磁-热双向耦合流程 Fig. 7 Flow chart of magnetic-thermal bidirectional coupling |
|
图 8 磁-热双向耦合Workbench模块连接 Fig. 8 Magnetic-thermal bidirectional coupling Workbench module connection |
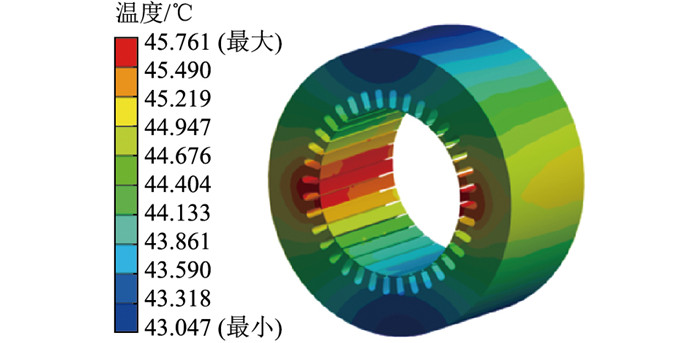
双向耦合温度场的仿真结果如图 9所示,定子铁心齿槽处温度最高,达到45.761 ℃,与单向耦合温度场仿真结果相比,最高温度增加了4.6%。实际工作过程中,电机整体温度升高会对内部具有温度特性的材料产生影响。绕组电阻会随着温度升高而增大,导致损耗进一步增加,整体温升持续增大。因此采用磁-热双向耦合计算方式,定子铁心最高温度较高,双向耦合的仿真结果精度更高。
|
图 9 双向耦合温度场仿真结果 Fig. 9 Simulation results of temperature field under bidirectional coupling |
在电磁场和温度场分析的基础上,对定子铁心机械结构响应进行分析。在非均匀磁载荷和非均匀热载荷的耦合激励下,铁心机械结构响应如图 10所示。
|
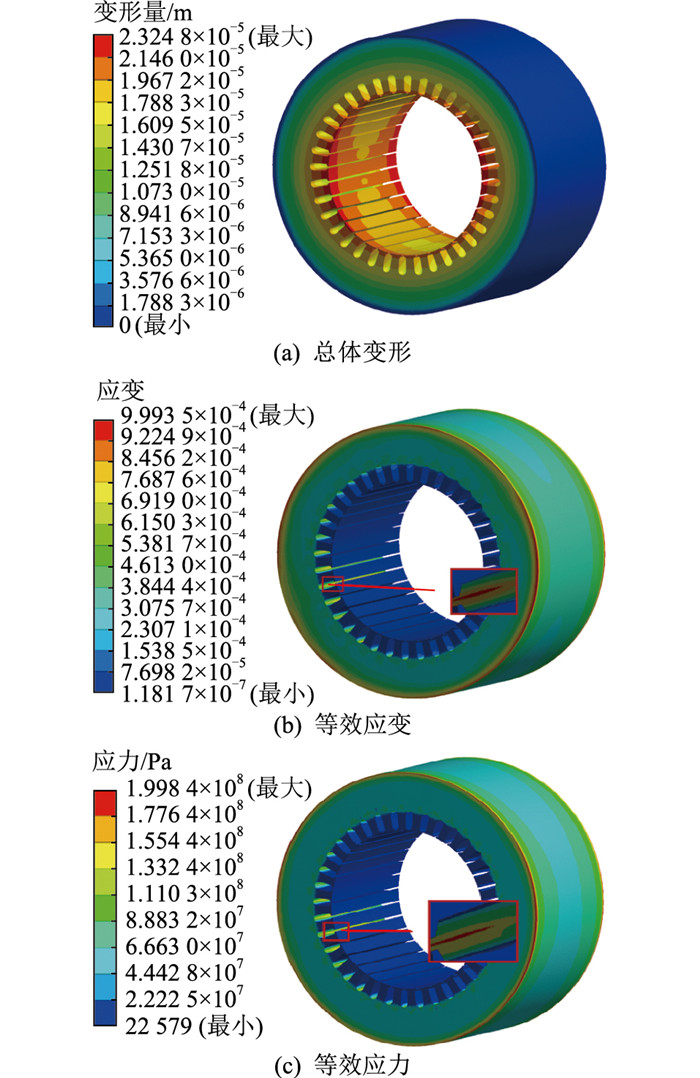
图 10 机械结构响应 Fig. 10 Mechanical structural response |
在2种激励的共同作用下,铁心整体变形最大处位于齿槽边缘,最大应力和应变出现在齿槽底部和铁心外边线上。这是由于在齿槽内部的磁载荷密度和热载荷密度较大,且端面处无约束,会产生较大的变形;此外,在外边线上结构突变会出现应力集中现象,因此也会存在较大的应力和应变。
定子槽部位存在较大的总体变形、应变以及应力,因此,在发电机的运行中应重点对定子槽部位进行监测。
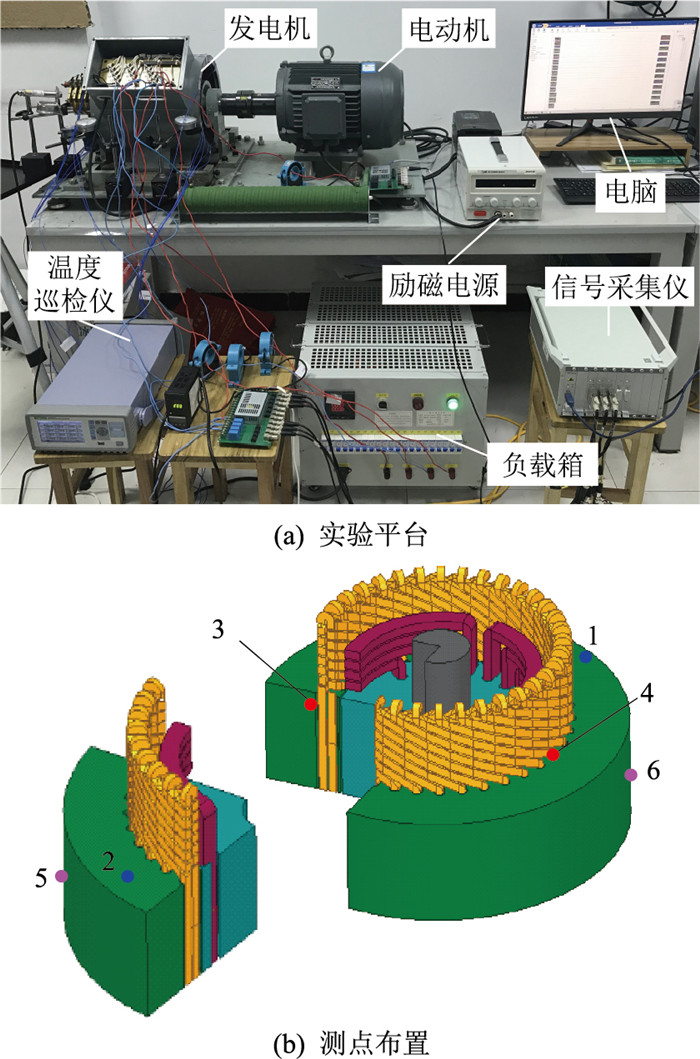
3 定子温度场实验测试与结果分析 3.1 实验设置文中实验以CS-5同步发电机为实验样机,实验平台如图 11(a)所示。整个实验机组主要由CS-5同步发电机、拖动电机、励磁电源、负载箱、温度巡检仪、信号采集仪、电脑构成。拖动电机通过弹性联轴器带动同步发电机转动,直流励磁电源提供绕线式转子励磁绕组中的直流电。发电机输出相电压为220 V,频率为50 Hz。其中发电机励磁电流、各项负载和初始温度等参数与仿真一致,励磁电流设置为2.5 A,每相负载为100 Ω电阻和0.238 H电感(功率因数为0.8)。
|
图 11 实验设置示意 Fig. 11 Schematic diagram of experiment setting |
实验温度测量装置采用普美DC5516G型16通道温度巡检仪,其测温范围为-100~1 200 ℃,传感器采用K型热电偶,通过特性传感器胶水固定在定子铁心上。为了分析定子铁心的温度分布,文中埋置了6组热电偶传感器对定子铁心不同部位进行温度测量。测点布置位置如图 11(b)所示,其中测点1、2位于定子铁心端面,测点3、4为定子铁心槽内预埋测点,测点5、6位于定子铁心外圆表面。在实验过程中,采用温度巡检仪对定子铁心温度进行实时监测。
3.2 实验结果分析在发电机稳定运行后,对温度巡检仪各通道温度信号进行多组别、多时段截取处理,分别对定子铁心端面、槽内、外圆表面3处得到的温度取均值,得到最终的温度变化曲线,如图 12所示。
|
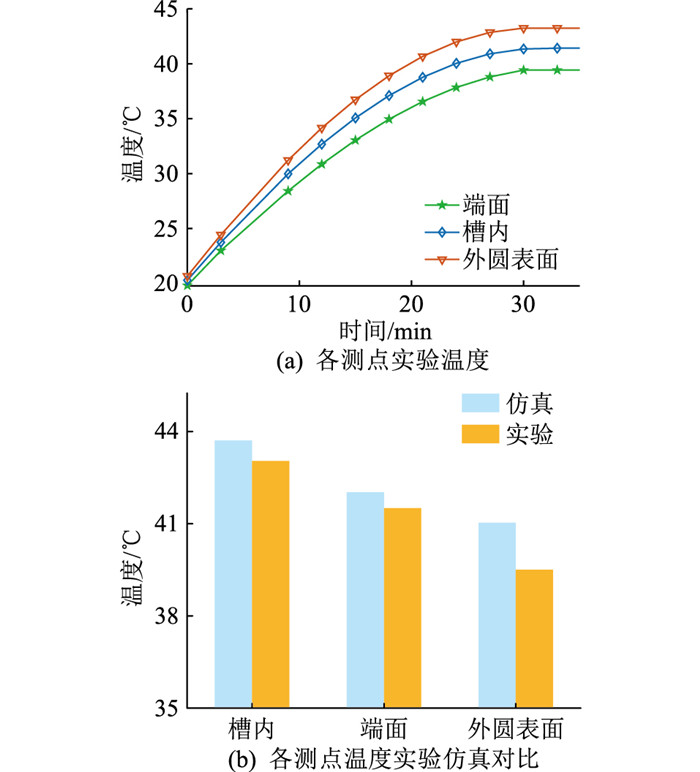
图 12 实验结果 Fig. 12 Experimental results |
由图 12(a)可知,随着发电机的运行时间增长,各测点位置的温度逐渐升高,并在运行30 min后基本趋于稳定。其中定子铁心端面温度最低,槽内温度最高,外圆表面温度介于两者之间。因此,发电机正常运行时,定子铁心应重点监测的温升部位为齿槽。图 12(b)为各测点温度仿真计算与实验的对比,铁心温度的实验结果略低于仿真计算结果。经分析,原因有以下2点:一是测量精度;二是有限元计算中边界设定及运行工况均为理想设定。总体上实验结果和仿真分析结果之间的误差在允许范围内。
4 结论文中以CS-5同步发电机为例,采用磁-热-固和磁-固单向单元耦合方式对同步发电机电磁场、温度场和机械结构响应进行了理论推导与数值计算,得到了定子铁心的损耗、温度与机械结构响应分布规律,并与实验数据进行了对比。定子铁心温度计算结果与实验结果吻合,验证了文中所建立的多物理场耦合下的三维模型的合理性,以及求解方法和计算结果的正确性,并得到如下结论:
(1) 定子铁心在发电机运行过程中产生涡流损耗和磁滞损耗,使定子铁心温度升高,并随着时间增长最终达到稳态。
(2) 发电机在稳定运行后,定子齿槽温度最高,槽口处变形最大,槽底应力较高。在温度场及结构响应的联合作用下,定子绕组在直线段与端面连接部位以及紧密接触槽底处的绝缘较别处更易造成损伤,实际制造中可在此处绕组表面涂一层耐热层。
致谢
本文得到河北省第三批青年拔尖人才支持计划([2018]-27)资助,谨此致谢!
| [1] |
杨晋强, 陈凤, 郑恩来, 等. 基于磁-热双向耦合的电动拖拉机轮边电机电磁性能分析与结构优化[J]. 农业工程学报, 2023, 39(6): 73-82. YANG Jinqiang, CHEN Feng, ZHENG Enlai, et al. Electromagnetic performance analysis and structural optimization of the wheel-side motors for electric tractors based on magneto-thermal bidirectional coupling[J]. Transactions of the Chinese Society of Agricultural Engineering, 2023, 39(6): 73-82. (  0) 0) |
| [2] |
XIA J, TIAN D, LIU J W, et al. Coupled airflow-thermal network model for large-scale offshore wind generators with modular fractional-slot concentrated winding[J]. IEEE Transactions on Energy Conversion, 2023, 38(2): 899-913. DOI:10.1109/TEC.2022.3229352 (  0) 0) |
| [3] |
BARRETT M. Analysis of temperature change in a permanent magnet synchronous generator under load due to stator winding inter-turn short circuit[C]//2021 International Conference on Electrical Drives & Power Electronics (EDPE). Dubrovnik, Croatia. IEEE, 2021: 56-61.
(  0) 0) |
| [4] |
WANG H H, CHEN J Q, JIANG Y P, et al. Coupled electromagnetic and thermal analysis of permanent magnet rectifier generator based on LPTN[J]. IEEE Transactions on Magnetics, 2022, 58(2): 8201705. (  0) 0) |
| [5] |
ZHANG J, ZHANG Z R, YU L. Thermal deformation analysis of water cooling doubly salient brushless DC generator with stator field winding[J]. IEEE Transactions on Industrial Electronics, 2020, 67(4): 2700-2710. DOI:10.1109/TIE.2019.2910032 (  0) 0) |
| [6] |
张健, 朱锡庆, 张卓然, 等. 电励磁双凸极无刷直流发电机热网络建模与热特性研究[J]. 中国电机工程学报, 2023, 43(1): 318-329. ZHANG Jian, ZHU Xiqing, ZHANG Zhuoran, et al. Thermal network modeling and thermal characteristics analysis of doubly salient brushless DC generator with stator field winding[J]. Proceedings of the CSEE, 2023, 43(1): 318-329. (  0) 0) |
| [7] |
杨明岱, 王宪, 赵前程, 等. 永磁同步风电机组发电机定子温度建模方法[J]. 太阳能学报, 2022, 43(5): 319-326. YANG Mingdai, WANG Xian, ZHAO Qiancheng, et al. Modeling method of stator temperature of PMSG wind turbine[J]. Acta Energiae Solaris Sinica, 2022, 43(5): 319-326. (  0) 0) |
| [8] |
陈浈斐, 李呈营, 马宏忠, 等. 大型同步调相机转子故障温度场分析[J]. 电力工程技术, 2022, 41(4): 192-198. CHEN Zhenfei, LI Chengying, MA Hongzhong, et al. Temperature field analysis of rotor fault in large synchronous condenser[J]. Electric Power Engineering Technology, 2022, 41(4): 192-198. DOI:10.12158/j.2096-3203.2022.04.025 (  0) 0) |
| [9] |
ZHANG W, HE Y L, XU M X, et al. A comprehensive study on stator vibrations in synchronous generators considering both single and combined SAGE cases[J]. International Journal of Electrical Power and Energy Systems, 2022, 143: 108490. DOI:10.1016/j.ijepes.2022.108490 (  0) 0) |
| [10] |
HE Y L, LI Y, ZHANG W, et al. Analysis of stator vibration characteristics in synchronous generators considering inclined static air gap eccentricity[J]. IEEE Access, 2023, 11: 7794-7807. DOI:10.1109/ACCESS.2022.3230907 (  0) 0) |
| [11] |
HE Y L, SUN Y X, XU M X, et al. Rotor UMP characteristics and vibration properties in synchronous generator due to 3D static air-gap eccentricity faults[J]. IET Electric Power Applications, 2020, 14(6): 961-971. DOI:10.1049/iet-epa.2019.0844 (  0) 0) |
| [12] |
PAVELEV S A, MAGOMEDOV S. Approach to the development of intelligent systems for controlling the vibration state of turbo-generators based on harmonic wavelet transformation and neural network analysis[J]. IFAC-PapersOnLine, 2018, 51: 418-423. (  0) 0) |
| [13] |
邢泽智, 王秀和, 赵文良, 等. 表贴式永磁同步电机电磁激振力波计算与定子振动特性分析[J]. 中国电机工程学报, 2021, 41(14): 5004-5013. XING Zezhi, WANG Xiuhe, ZHAO Wenliang, et al. Calculation of electromagnetic force waves and analysis of stator vibration characteristics of surface mount permanent magnet synchronous motor[J]. Proceedings of the CSEE, 2021, 41(14): 5004-5013. (  0) 0) |
| [14] |
苏武, 王东, 魏锟, 等. 交错磁极混合励磁同步发电机径向电磁力波分析[J]. 中国电机工程学报, 2020, 40(24): 7869-7879, 8224. SU Wu, WANG Dong, WEI Kun, et al. Analysis of radial electromagnetic force wave of consequent-pole hybrid excitation synchronous generator[J]. Proceedings of the CSEE, 2020, 40(24): 7869-7879, 8224. (  0) 0) |
| [15] |
路文开, 张卫, 唐杨. 永磁同步电机定子振动特性分析[J]. 机械设计与制造, 2020(8): 232-234, 238. LU Wenkai, ZHANG Wei, TANG Yang. Analysis of stator vibration characteristics of permanent magnet synchronous motor[J]. Machinery Design & Manufacture, 2020(8): 232-234, 238. (  0) 0) |
| [16] |
李瑞, 王强, 林棻, 等. 磁固耦合效应下集成式永磁电动轮定子振动响应与结构优化研究[J]. 重庆理工大学学报(自然科学), 2022, 36(9): 15-24, 7. LI Rui, WANG Qiang, LIN Fen, et al. Vibration response and structural optimization for the stator of integrated permanent magnet in-wheel motor under magnetism and solid coupling effect[J]. Journal of Chongqing University of Technology (Natural Science), 2022, 36(9): 15-24, 7. (  0) 0) |
| [17] |
戈宝军, 姜超, 吕品, 等. 大型核电汽轮发电机非全相运行转子动态电磁力分析[J]. 电机与控制学报, 2021, 25(5): 26-35. GE Baojun, JIANG Chao, LÜ Pin, et al. Analysis of rotor dynamic electromagnetic force in large nuclear turbines under open-phase operation condition[J]. Electric Machines and Control, 2021, 25(5): 26-35. (  0) 0) |
| [18] |
肖士勇, 王云阳, 戈宝军. 中性点侧小匝数相间短路下水轮发电机铁心动态电磁力[J]. 哈尔滨理工大学学报, 2021, 26(6): 73-80. XIAO Shiyong, WANG Yunyang, GE Baojun. Dynamic electromagnetic force of stator core for hydro-generators under phase to phase short circuit with two fault points close to the neutral point[J]. Journal of Harbin University of Science and Technology, 2021, 26(6): 73-80. (  0) 0) |
| [19] |
汤蕴璆. 电机学[M]. 5版. 北京: 机械工业出版社, 2014. TANG Yunqiu. Electric machinery[M]. 5th ed. Beijing: China Machine Press, 2014. (  0) 0) |
| [20] |
王艾萌, 李大双, 李小双. 改变定子铁芯面积对分数槽集中绕组永磁同步电机铁耗的影响[J]. 电测与仪表, 2022, 59(1): 45-50. WANG Aimeng, LI Dashuang, LI Xiaoshuang. Influence of changing core area of stator on iron loss of FSCW permanent magnet synchronous machine[J]. Electrical Measurement & Instrumentation, 2022, 59(1): 45-50. (  0) 0) |
| [21] |
LI Z N, HAN W J, XIN Z, et al. A review of magnetic core materials, core loss modeling and measurements in high-power high-frequency transformers[J]. CPSS Transactions on Power Electronics and Applications, 2022, 7(4): 359-373. DOI:10.24295/CPSSTPEA.2022.00033 (  0) 0) |
| [22] |
卓亮, 孙鲁, 施道龙, 等. 考虑温度变化的高温高速永磁电机转子涡流损耗半解析模型及实验验证[J]. 中国电机工程学报, 2021, 41(24): 8305-8315. ZHUO Liang, SUN Lu, SHI Daolong, et al. Semi-analytical model and experimental verification of rotor eddy current loss of high temperature high speed permanent magnet machine considering temperature change[J]. Proceedings of the CSEE, 2021, 41(24): 8305-8315. (  0) 0) |
| [23] |
胡蔡飞, 童力, 范学良, 等. 基于绝热温升方法的饱和铁心损耗分布分析[J]. 电力电容器与无功补偿, 2022, 43(2): 41-48. HU Caifei, TONG Li, FAN Xueliang, et al. Saturated laminated-core loss distribution analysis based on adiabatic temperature rise method[J]. Power Capacitor & Reactive Power Compensation, 2022, 43(2): 41-48. (  0) 0) |
| [24] |
徐钰航, 赵峰, 高锋阳. 基于博弈论的电动汽车轮毂电机热源损耗优化[J]. 电测与仪表, 2023, 60(4): 34-40. XU Yuhang, ZHAO Feng, GAO Fengyang. Optimal design of in-wheel motor loss based on game theory[J]. Electrical Measurement & Instrumentation, 2023, 60(4): 34-40. (  0) 0) |
| [25] |
DE SILVA GURUWATTA VIDANALAGE B, TOULABI M S, STACHL T, et al. Winding function-based analytical modeling of core loss in an induction machine considering slotting effects and the frequency-dependent B-H curve characteristics[J]. IEEE Transactions on Magnetics, 2022, 58(8): 8105906. (  0) 0) |
| [26] |
BARG S, BERTILSSON K. Core loss modeling and calculation for trapezoidal magnetic flux density waveform[J]. IEEE Transactions on Industrial Electronics, 2021, 68(9): 7975-7984. DOI:10.1109/TIE.2020.3013750 (  0) 0) |
| [27] |
ZHANG J, ZHANG Z R, XIA Y W, et al. Thermal analysis and management for doubly salient brushless DC generator with flat wire winding[J]. IEEE Transactions on Energy Conversion, 2020, 35(2): 1110-1119. DOI:10.1109/TEC.2020.2966046 (  0) 0) |
| [28] |
韩孟媛, 赵仲勇, 于跃强, 等. 同步电机定子绕组匝间短路前后的温度及力学响应仿真分析[J]. 电测与仪表, 2023, 60(4): 48-56. HAN Mengyuan, ZHAO Zhongyong, YU Yueqiang, et al. Simulation analysis of temperature and mechanical response of synchronous machine stator winding before and after inter turn short circuit[J]. Electrical Measurement & Instrumentation, 2023, 60(4): 48-56. (  0) 0) |
| [29] |
谢颖, 王泽, 单雪婷, 等. 基于多场量的笼型感应电机三维瞬态磁热固耦合计算分析[J]. 中国电机工程学报, 2016, 36(11): 3076-3084. XIE Ying, WANG Ze, SHAN Xueting, et al. The calculations and analysis of 3D transient magnetic-thermal-solid coupling for squirrel-cage induction motors based on multi fields[J]. Proceedings of the CSEE, 2016, 36(11): 3076-3084. (  0) 0) |
| [30] |
何玉灵, 武钰, 王烁, 等. 磁热固耦合作用下的同步发电机转子铁芯损耗及温升特性分析[J]. 华北电力大学学报(自然科学版), 2021, 48(6): 55-62. HE Yuling, WU Yu, WANG Shuo, et al. Rotor core loss & temperature rise properties in synchronous generators under magnet-heat-solid coupling action[J]. Journal of North China Electric Power University (Natural Science Edition), 2021, 48(6): 55-62. (  0) 0) |
 2024, Vol. 43
2024, Vol. 43


 何玉灵(1984),男,博士,教授,研究方向为发电机状态监测与故障诊断(E-mail:
何玉灵(1984),男,博士,教授,研究方向为发电机状态监测与故障诊断(E-mail: