文章编号: 2096-3203(2024)04-0045-11 中图分类号: TM73
2. 北方工业大学电气与控制工程学院, 北京 100144;
3. 国网浙江省电力有限公司杭州供电公司, 浙江 杭州 311400
微电网(microgrid, MG)是一种将分布式电源(distributed generation, DG)、用电负荷、储能设备及输配电装置搭配整合的小型“源-荷-储”系统[1],可以通过能源的互联互补促进可再生能源的就地消纳,其因较低的污染排放和较高的资源利用率得到了快速发展。新能源出力以及负荷波动性、随机性和间歇性等多元不确定性,给微电网的安全、经济调度发展带来了一系列挑战[2-5]。如何在尽可能利用清洁能源的同时,保证系统的安全经济运行具有十分重要的研究价值和意义[6]。
目前,处理源荷多元不确定性的方法主要有4种:随机优化(stochastic optimization, SO)[7-8]、机会约束规划(chance constrained programming, CCP)[9]、鲁棒优化(robust optimization, RO)[10-12]和分布鲁棒优化(distributionally robust optimization, DRO)[13]。其中,SO假设不确定变量的概率分布是准确的,每一个场景都是一个确定性问题, 但精确模型选取的离散场景数目将过于庞大; CCP则采用具有一定置信水平的约束条件,其主要问题是如何掌握不确定量的概率分布规律,且置信度的选取具有经验性,模型决策结果风险较大[14]; RO的不确定性主要通过随机变量边界来表征,这经常会使决策结果的保守性过强,而在实际工程中最恶劣的场景很少发生,对于部分可用概率信息也未考虑。
DRO考虑了随机变量的统计概率信息并采取具有不确定性的最恶劣分布代替确定的分布,综合了RO的保守性和SO的经济性,主要包括基于矩信息[15]、基于Wasserstein距离[16]、基于KL(Kullback-Leibler)散度[17]和基于多离散场景数据驱动[18]等类型,基于多离散场景的DRO方法离散化处理不确定变量的概率密度,并基于范数约束构建各离散场景的概率分布集合,其模型的保守度和经济性与离散场景的数目和置信度有关,避免了实际工程调度时出现片面或极端的情形,因此得到了广泛研究。文献[19]将基于多离散场景的分布鲁棒优化方法应用到主动配电网的无功优化模型中,但是单独以1-范数或者∞ -范数作为约束条件构造不确定集合,会造成优化调度结果并不准确。为此,文献[20]在建立不确定性概率分布置信集合时考虑了2类范数约束,使结果同时具备经济性和保守性,但未能处理好其计算复杂性。
此外,由于DG出力的不确定性会随着时间尺度的缩短逐步减小,只应用单阶段方法既不能抵抗微电网短时间内偶发性的干扰,也不能最小化系统的总调度成本[21],因此逐级细化调度时间尺度,考虑日前和日内调度等尺度不同组合策略的滚动优化是必要的,同时考虑到系统实时状态对当前优化调度模型的反馈校正问题,需要引入模型预测控制(model predictive control, MPC)理论来实现状态参数和预测数据的更新[22]。文献[23]在MPC滚动优化中考虑了微电网系统的运行/调度成本,对微电网单元进行控制,一定程度上处理了DG输出波动和负荷预测误差,但其只在有限的时域内对相关变量进行预测和优化,很难处理优化周期长的复杂约束。文献[24]提出一种基于MPC的微电网能量管理方法,通过协调微/配电网的电力交互作用来降低微电网的运行成本,但模型中的一些参数是固定的,难以解决微电网中的突发干扰。
现有研究在制定微电网优化调度方案时未能兼顾可靠性和经济性,并且难以协调不确定性分析方法与不同时间尺度之间的配合关系。
针对上述不足,首先,文中区别于传统单独以1-范数和∞-范数为约束条件的不确定集合,综合考虑两类范数约束,基于数据驱动的多离散场景DRO方法提出微电网两阶段优化调度模型,符合实际微电网工程中对系统运行安全性和经济性的双重要求,并使用改进列和约束生成(column-and-constraint generation, C&CG)算法进行求解,避免了启发式算法容易陷入局部最优解和对初值高依赖性的问题。然后,结合多时间尺度调度策略和MPC理论,协调不确定性分析方法与各时间尺度之间的配合关系,通过逐级细化调度时间尺度和预测周期长度来提高精度,以最小化发电及调节成本等为目标建立了日前-日内多时间尺度滚动优化调度模型,较大程度上抵抗了实际微电网内源荷的强不确定性因素的影响。最后,结合某示范微电网仿真结果,进一步验证了模型和算法的有效性。
1 基于数据驱动的两阶段分布鲁棒日前优化调度模型典型的微电网结构如图 1所示,由可控分布式电源[12]、风力发电机[25]、光伏发电机[26]、储能设备[27]及用户负荷组成,并通过公共连接点(point of common coupling, PCC)接入配电网。
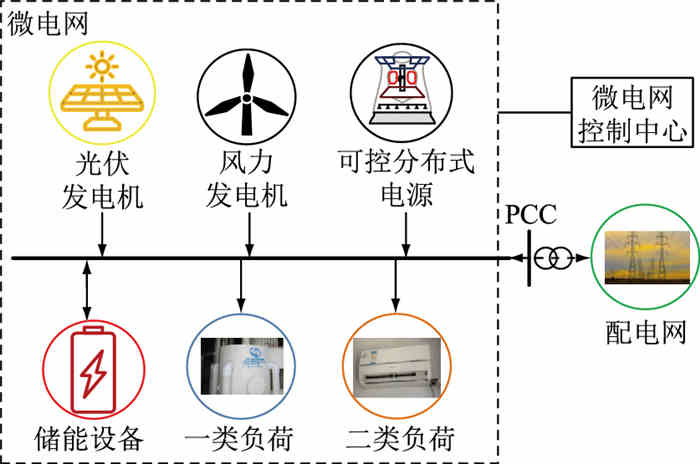
|
图 1 微电网架构 Fig. 1 Microgrid architecture |
确定性调度模型中新能源出力及负荷用电情况取值为其预测值,并假设预测误差为0。实际上预测信息ξ存在较大的不确定性,这将对优化调度造成不可忽视的影响。因此,文中构造基于数据驱动的两阶段DRO优化调度模型,并将M个历史数据聚类为多个典型的离散场景ξ1, ξ2, …, ξNA,NA为总场景个数,并求得每个场景对应的概率值。
1.1.1 目标函数数据驱动下的多离散场景DRO模型表达为:
| $ \left\{\begin{array}{l} \min\limits_{x \in X}\left(\sum\limits_{t=1}^T \sum\limits_{i=1}^N C_{\mathrm{S}, t, i}\left(u_{\mathrm{G}, t, i}, u_{\mathrm{G}, t-1, i}\right)+\right. \\ \max\limits_{P_s \in \varOmega} \sum\limits_{s=1}^{N_{\mathrm{A}}} p_s \min\limits_{y_s \in Y\left(x, \xi_s\right)}\left(\sum\limits_ {t = 1} ^ {T} \sum\limits_ {i = 1} ^ {N} \left(C_{\mathrm{G}, t, i} P_{\mathrm{G}, t, i}+\right.\right. \\ \quad C_{\mathrm{W}, t, i} P_{\mathrm{W}, t, i}+C_{\mathrm{P}, t, i} P_{\mathrm{p}, t, i}+ \\ \left.\left.\left.C_{\mathrm{E}, t, i} P_{\mathrm{E}, t, i}^{\mathrm{ch}}, P_{\mathrm{E}, t, i}^{\mathrm{dis}}+C_{M, t} P_{\mathrm{PCC}, t}\right)\right)\right) \\ C_{\mathrm{S}, t, i}=\max \left\{0, u_{\mathrm{G}, t, i}-u_{\mathrm{G}, t-1, i}\right\} S_{\mathrm{G}, t} \Delta t \\ C_{\mathrm{G}, t, i}=\left(a P_{\mathrm{G}, t, i}+b\right) \Delta t \\ C_{\mathrm{W}, t, i}=\left[\lambda_{\mathrm{W}} P_{\mathrm{W}, t, i}+c_{\mathrm{W}}\left(P_{\mathrm{w}, t, i}^*-P_{\mathrm{w}, t, i}\right)\right] \Delta t \\ C_{\mathrm{P}, t, i}=\left[\lambda_{\mathrm{P}} P_{\mathrm{p}, t, i}+c_{\mathrm{p}}\left(P_{\mathrm{p}, t, i}^*-P_{\mathrm{p}, t, i}\right)\right] \Delta t \\ C_{\mathrm{E}, t, i}=K_{\mathrm{E}}\left(\frac{1}{\eta_{\mathrm{E}, \mathrm{dis}}} P_{\mathrm{E}, t, i}^{\mathrm{dis}}+\eta_{\mathrm{E}, \mathrm{ch}} P_{\mathrm{Eh}, t, i}^{\mathrm{ch}}\right) \Delta t \\ C_{\mathrm{M}, t}=\lambda_{\mathrm{M}, t} P_{\mathrm{PCC}, t} \Delta t \end{array}\right. $ | (1) |
式中:x为第一阶段变量;X为x的可行域集合;T为总调度时段;N为总机组数量;CS, t, i(·)为第i台可控分布式电源在t时刻的启停成本;uG, t, i为第i台可控分布式电源在t时刻的启停状态,为0-1变量;ps为第s个场景的发生概率;Ω为不确定概率集合;ys为第s个场景下的第二阶段变量;ξs为场景s的预测信息;Y为ys的可行域集合;CG, t, i(·)、PG, t, i分别为第i台可控分布式电源在t时刻的运行成本及有功出力;CW, t, i(·)、CP, t, i(·)、CE, t, i(·)分别为第i台风机、光伏、储能设备在t时刻的运行成本;Pw, t, i、Pp, t, i分别为第i台风机和光伏在t时刻的输出功率;PE, t, ich、PE, t, idis分别为第i台储能设备在t时刻的充、放电功率;CM, t(·)为微/配电网的交互成本;PPCC, t为微/配电网的交互功率;SG, t为启停成本系数;Δt为调度步长;a、b为可控分布式电源运行成本系数;λW、λP分别为风电和光伏机组的单位发电成本;cw、cp分别为弃风和弃光的惩罚成本系数;Pw, t, i*、Pp, t, i*分别为第i台风电和光伏机组在t时刻的预测功率;KE为储能的充放电成本系数;ηE, ch、ηE, dis分别为储能设备的充、放电效率;λM, t为配电网的分时电价。
1.1.2 约束条件求解DRO模型还须满足以下约束条件(均为在场景s下的运行约束)。
(1) 功率平衡约束。
| $ \sum\limits_{i=1}^{N}\left(P_{\mathrm{G}, t, i}+P_{\mathrm{w}, t, i}+P_{\mathrm{p}, t, i}+P_{\mathrm{E}, t, i}^{\mathrm{dis}}\right)+P_{\mathrm{PCC}, t}= \\ \quad \quad \quad \quad \quad \sum\limits_{i=1}^{N} P_{\mathrm{E}, t, i}^{\mathrm{ch}}+P_{1, t} $ | (2) |
式中:Pl, t为t时刻系统负荷需求总功率。
(2) 可控分布式电源出力上下限约束。
| $ u_{\mathrm{G}, t} P_{\mathrm{G}}^{\min} \leqslant P_{\mathrm{G}, t} \leqslant u_{\mathrm{G}, t} P_{\mathrm{G}}^{\max} $ | (3) |
式中:PGmax、PGmin分别为可控发电机组输出功率的上限和下限。
(3) 可控分布式电源爬坡约束。
| $ \left\{\begin{array}{l} P_{\mathrm{G}, t}-P_{\mathrm{G}, t-1} \leqslant R^{\mathrm{up}} \Delta t \\ P_{\mathrm{G}, t-1}-P_{\mathrm{G}, t} \leqslant R^{\mathrm{down}} \Delta t \end{array}\right. $ | (4) |
式中:Rup、Rdown分别为爬坡速率的上、下限。
(4) 储能设备约束。
储能设备的充、放电功率PE, tch和PE, tdis需要满足的上、下限约束如式(5)所示。
| $ \left\{\begin{array}{l} u_{\mathrm{E}, t}^{\mathrm{ch}} P_{\mathrm{E}}^{\min , \mathrm{ch}} \leqslant P_{\mathrm{E}, t}^{\mathrm{ch}} \leqslant u_{\mathrm{E}, t}^{\mathrm{ch}} P_{\mathrm{E}}^{\max , \mathrm{ch}} \\ u_{\mathrm{E}, t}^{\mathrm{dis}} P_{\mathrm{E}}^{\mathrm{min}, \mathrm{dis}} \leqslant P_{\mathrm{E}, t}^{\mathrm{dis}} \leqslant u_{\mathrm{E}, t}^{\mathrm{dis}} P_{\mathrm{E}}^{\mathrm{max}, \mathrm{dis}} \end{array}\right. $ | (5) |
式中:uE, tch、uE, tdis分别为储能设备的充、放电状态,为0-1变量;PEmax, ch、PEmin, ch分别为储能设备充电功率的上、下限;PEmax, dis、PEmin, dis分别为储能设备放电功率的上、下限。
式(6)表示储能设备在t时刻只能处于1种状态,不能同时出现2种状态,即:
| $ u_{\mathrm{E}, t}^{\mathrm{ch}}+u_{\mathrm{E}, t}^{\mathrm{dis}} \leqslant 1 $ | (6) |
对充放电状态的转换次数进行约束。
| $ \sum\limits_{t=1}^{T}\left|u_{\mathrm{E}, t}^{\mathrm{dis}}-u_{\mathrm{E}, t-1}^{\mathrm{dis}}\right| \leqslant N_{\mathrm{E}}^{\mathrm{Lim}} $ | (7) |
式中:NELim为储能的最大充放电状态转换次数。
储能的荷电状态(state of charge,SOC)具体表示如下:
| $ \left\{\begin{array}{l} E_{\mathrm{E}, t}^{\mathrm{SOC}}=E_{\mathrm{E}, t-1}^{\mathrm{SOC}}-\frac{1}{\eta_{\mathrm{E}, \mathrm{dis}}} P_{\mathrm{E}, t}^{\mathrm{dis}} \Delta t+\eta_{\mathrm{E}, \mathrm{ch}} P_{\mathrm{E}, t}^{\mathrm{ch}} \Delta t \\ E_{\mathrm{E}}^{\mathrm{SOC}, \min} \leqslant E_{\mathrm{E}, t}^{\mathrm{SOC}} \leqslant E_{\mathrm{E}}^{\mathrm{SOC}, \max} \\ t=1, 2, \cdots, T \end{array}\right. $ | (8) |
式中:EE, tSOC为储能装置在t时刻所储存的电量;EESOC, min、EESOC, max分别为储能装置在t时刻所能够储存电量的下限和上限。式(8)的约束是防止储能装置过充或过放,从而延长其寿命。
储能在调度的始末时刻容量相等,即:
| $ \begin{equation*} \eta_{\mathrm{E}, \text {ch}} \sum\limits_{t=1}^{T} P_{\mathrm{E}, t}^{\mathrm{ch}} \Delta t-\frac{1}{\eta_{\mathrm{E}, \text {dis}}} \sum\limits_{t=1}^{T} P_{\mathrm{E}, t}^{\mathrm{dis}} \Delta t=0 \end{equation*} $ | (9) |
(5) 微/配电网交互约束。
| $ \left\{\begin{array}{l} 0 \leqslant P_{\mathrm{PCC}, t}^{\mathrm{buy}} \leqslant v_{\mathrm{M}, t} u_{\mathrm{PCC}, t} P_{\mathrm{PCC}}^{\max} \\ 0 \leqslant P_{\mathrm{PCC}, t}^{\mathrm{sell}} \leqslant v_{\mathrm{M}, t}\left(1-u_{\mathrm{PCC}, t}\right) P_{\mathrm{PCC}}^{\max} \end{array}\right. $ | (10) |
式中:PPCC, tbuy、PPCC, tsell分别为微网向配电网购电、售电时的联络线功率;vM, t为微网群并/离网的运行模式;uPCC, t为在并网运行模式下微网购售电状态,购电状态下取值为1;PPCCmax为最大允许交互功率。
(6) 潮流约束。整个系统还需要考虑支路功率约束、相角约束和节点电压约束等网络潮流约束,以考虑线性化后节点k与节点j之间的支路有功功率Pkj和无功功率Qkj关系式为例。
| $ \left\{\begin{array}{l} P_{k j}=g_{k j}\left(U_{k}-U_{j}\right)-b_{k j} \theta_{k j}\\ Q_{k j}=-b_{k j}\left(U_{k}-U_{j}\right)-g_{k j} \theta_{k j} \end{array}\right. $ | (11) |
式中:gkj、bkj分别为节点k与节点j之间的支路电导和电纳;Uk、Uj分别为节点k与节点j的电压幅值;θk、θj分别为节点k和节点j的相角;θkj为节点k与节点j之间的相角差,θkj=θk-θj。
1.2 不确定集合在DRO日前调度模型中,将风电、光伏这些新能源机组出力的预测误差和负荷节点的功率预测误差的概率分布定义为不确定集合,单独考虑1-范数和∞-范数对概率分布进行限制,可能会出现片面或者极端的情况,因此同时考虑2种范数,形成综合范数约束下的不确定概率置信集合Ω。
| $ \varOmega=\left\{p_{s} \mid p_{s} \geqslant 0, s=1, 2, \cdots, N_{A}, \sum\limits_{s=1}^{N_{A}} p_{s}=1\right. \\ \left.\sum\limits_{s=1}^{N_{A}}\left|p_{s}-p_{s, 0}\right| \leqslant \theta_{1}, \max\limits_{1 \leqslant s \leqslant N_{A}}\left\{\left|p_{s}-p_{s, 0}\right|\right\} \leqslant \theta_{\infty}\right\} $ | (12) |
式中:ps, 0为第s个场景的初始概率。1-范数限制所有场景概率分布允许偏差总和为上限θ1,∞-范数限制每个场景概率分布允许偏差为上限θ∞。
根据给定的历史数据量和置信水平来构造不同θ取值下的置信度约束[28]。
| $ \left\{\begin{array}{l} \operatorname{Pr}\left\{\sum\limits_{s=1}^{N_{\mathrm{A}}}\left|p_{s}-p_{s, 0}\right| \leqslant \theta_{1}\right\} \geqslant 1-2 N_{\mathrm{A}} \mathrm{e}^{-\frac{2 M \theta_{1}}{N_{\mathrm{A}}}} \\ \operatorname{Pr}\left\{\max\limits_{1 \leqslant s \leqslant N_{\mathrm{A}}}\left|p_{s}-p_{s, 0}\right| \leqslant \theta_{\infty}\right\} \geqslant 1-2 N_{\mathrm{A}} \mathrm{e}^{-2 M \theta_{\infty}} \end{array}\right. $ | (13) |
将式(13)的右边分别令为不确定性概率置信度α1和α∞可得到:
| $ \left\{\begin{array}{l} \theta_{1}=\frac{N_{\mathrm{A}}}{2 M} \ln \frac{2 N_{\mathrm{A}}}{1-\alpha_{1}}\\ \theta_{\infty}=\frac{1}{2 M} \ln \frac{2 N_{\mathrm{A}}}{1-\alpha_{\infty}} \end{array}\right. $ | (14) |
可以发现不确定集合Ω中含有绝对值项,在1-范数约束引入二进制辅助变量zs+、zs-,在∞-范数约束中引入二进制辅助变量ys+、ys-进行线性化,分别如式(15)、式(16)所示。
| $ \left\{\begin{array}{l} \sum\limits_{s=1}^{N_{\mathrm{A}}}\left(p_{s}^{+}+p_{s}^{-}\right) \leqslant \theta_{1} \\ p_{s}=p_{s, 0}+p_{s}^{+}-p_{s}^{-} \\ z_{s}^{+}+z_{s}^{-} \leqslant 1 \\ 0 \leqslant p_{s}^{+} \leqslant z_{s}^{+} \theta_{1} \\ 0 \leqslant p_{s}^{-} \leqslant z_{s}^{-} \theta_{1} \end{array}\right. $ | (15) |
| $ \left\{\begin{array}{l} p_{s}^{+}+p_{s}^{-} \leqslant \theta_{\infty} \\ p_{s}=p_{s, 0}+p_{s}^{+}-p_{s}^{-} \\ y_{s}^{+}+y_{s}^{-} \leqslant 1 \\ 0 \leqslant p_{s}^{+} \leqslant y_{s}^{+} \theta_{\infty} \\ 0 \leqslant p_{s}^{-} \leqslant y_{s}^{-} \theta_{\infty} \end{array}\right. $ | (16) |
式中:ps+、ps-分别为概率值ps相对原始概率ps, 0的正、负偏移量。
1.3 求解算法DRO模型可以表示为“min-max-min”两阶段三层的优化模型形式如下:
| $ \left\{\begin{array}{l} \min\limits_{x \in X} \boldsymbol{a}^{\mathrm{T}} x+\max\limits_{p_{s} \in \varOmega} \sum\limits_{s=1}^{N_{\mathrm{A}}} p_{s} \min\limits_{y_{s} \in Y\left(x, \xi_{s}\right)} \boldsymbol{b}^{\mathrm{T}} y_{\mathrm{s}} \\ \text {s.t.} \;\;\boldsymbol{A}^{\prime} x+\boldsymbol{B}^{\prime} y_{s}+\boldsymbol{C}^{\prime} \xi_{s} \leqslant \boldsymbol{D}^{\prime} \end{array}\right. $ | (17) |
式中:aT、bT分别为第一阶段决策变量x和第二阶段决策变量ys的成本系数矩阵;aTx、bTys分别为可控机组的启停成本和运行成本;x∈{uG, t, i, uG, t-1, i}; ys∈{PG, t, i, Pw, t, i, Pp, t, i, PE, t, ich, PE, t, idis, PPCC, t}; A′、B′、C′为与x、ys、ξs相对应的系数矩阵;D′为常数矩阵。
为便于求解式(17),采用C&CG算法将模型分解为主问题和子问题进行迭代计算,直到二者差值满足设置的收敛精度,迭代停止[18]。
(1) 主问题。主问题在已知的最恶劣概率分布情况下进行微网的日前优化调度,主问题求得的优化目标值给式(17)提供下界值。
| $ \left\{\begin{array}{l} \min\limits_{x \in X} \boldsymbol{a}^{\mathrm{T}} x+\max\limits_{p_{s, m} \in \varOmega} \sum\limits_{s=1}^{N_{\mathrm{A}}} p_{s, m} \min\limits_{y_{s, m} \in Y\left(x, \xi_{s}\right)} \boldsymbol{b}^{\mathrm{T}} y_{s, m} \\ \text {s.t.}\;\;\boldsymbol{A}^{\prime} x+\boldsymbol{B}^{\prime} y_{s, m}+\boldsymbol{C}^{\prime} \xi_{s} \leqslant \boldsymbol{D}^{\prime} \quad m=1, 2, \cdots, N_{\mathrm{B}} \end{array}\right. $ | (18) |
式中:m为C&CG算法的迭代次数;NB为迭代总次数。
(2) 子问题。子问题在已知第一阶段离散决策变量x*的情况下,寻找不确定集合内的最恶劣概率分布,并将最恶劣概率分布传递给主问题进行迭代,为式(17)提供上界值。
| $ f\left(x^{*}\right)=\max\limits_{p_{s, m} \in \varOmega} \sum\limits_{s=1}^{N_{\mathrm{A}}} p_{s, m} \min\limits_{y_{s, m} \in Y\left(x, \xi_{s}\right)} \boldsymbol{b}^{\mathrm{T}} y_{s, m} \\ \;\;\;\;\;\;\;\;m=1, 2, \cdots, N_{\mathrm{B}} $ | (19) |
子问题是一个双层优化问题,可以分为两步求解,先求内层最小值问题,再求解外层最大值。
设
| $ \left\{\begin{array}{l} f\left(x^{*}\right)=\max\limits_{p_{s, m} \in \varOmega} \sum\limits_{s=1}^{N_{\mathrm{A}}} p_{s, m} \eta_{s} \\ \text {s.t.} \;\;\;\eta_{s}=\operatorname{argmin} \boldsymbol{b}^{\mathrm{T}} y_{s, m} \end{array}\right. $ | (20) |
双层子问题首先求解各离散场景下的最优第二阶段目标值,如式(21)所示。
| $ \eta_{s}=\min\limits_{y_{s, m} \in Y\left(x, \xi_{s}\right)} \boldsymbol{b}^{\mathrm{T}} y_{s, m} $ | (21) |
其次,得到场景s下的ηs,根据式(22)求取最差期望下最恶劣场景概率{p1, m, p2, m, …, pNA, m}。
| $ f\left(x^{*}\right)=\max\limits_{p_{s, m} \in \varOmega} \sum\limits_{s=1}^{N_{\mathrm{A}}} p_{s, m} \eta_{s} $ | (22) |
在实际工程系统中,子问题的可行性受系统规模大小、模型线性化松弛程度等因素的影响,可行性难以保证。若子问题不可行, 则引入新的决策变量ys, m,并在主问题中增加如下“可行割约束”:
| $ \left\{\begin{array}{l} \eta \geqslant \sum\limits_{s=1}^{N_{A}} p_{s, m}^{*}\left(\boldsymbol{b}^{\mathrm{T}} y_{s, m}\right) \\ \boldsymbol{A}^{\prime} x+\boldsymbol{B}^{\prime} y_{s, m}+\boldsymbol{C}^{\prime} \xi_{s} \leqslant \boldsymbol{D}^{\prime} \end{array}\right. $ | (23) |
式中:ps, m*为第s个场景在第m次迭代时的已知概率;η为引入的连续辅助变量。
模型具体求解步骤如下。
步骤一: 设定下界LB=-∞,上界UB=+∞,迭代次数m=1,应用初始概率分布ps, 0。
步骤二: 求解C&CG算法主问题,获得最优解(x*, η*),更新下边界LB=max(LB, aTx*+η*)。
步骤三: 固定第一阶段离散变量x*,求解C&CG算法子问题,获得最恶劣的场景概率分布ps*,目标函数值f(x*),更新上界值UB=min(UB, aTx*+f(x*))。
步骤四: 如果
步骤五: 更新m=m+1,返回步骤二。
2 基于MPC的日内滚动优化调度模型 2.1 多时间尺度优化调度方案为了减小可再生能源出力及负荷预测误差对调度结果的影响,文中综合考虑实时阶段与日内阶段,建立日前-日内两阶段模型,取日前阶段的调度范围为24 h,时间间隔为1 h;日内阶段取较短的调度范围,设定为2 h,时间间隔为15 min[29-30]。
(1) 日前调度模型。微电网的日前调度模型以整个微电网系统的日运行成本最小化为目标,决策各个可控分布式电源在未来24 h的启停状态和计划出力,并在日内优化调度中保持此启停状态不发生改变,同时决策微电网向配电网的售电/购电功率、储能装置充放电功率的日前调度最优值。
(2) 日内调度模型。日内调度阶段采用MPC策略进行滚动优化调度。利用未来2 h的预测数据与当前的系统状态测量值,制定未来2 h的调度方案,但仅执行第一个15 min的调度结果,当第二个调度时段来临时,再重复上述过程。日内调度方案以日前调度结果为基值,在最小化系统运行成本的基础上,设置日内阶段中微/配电网交互功率、储能装置SOC等变量跟踪日前结果[31],以此为目标函数决策出最佳日内调度结果。文中所建立的日前-日内多时间尺度调度模型方案如图 2所示。
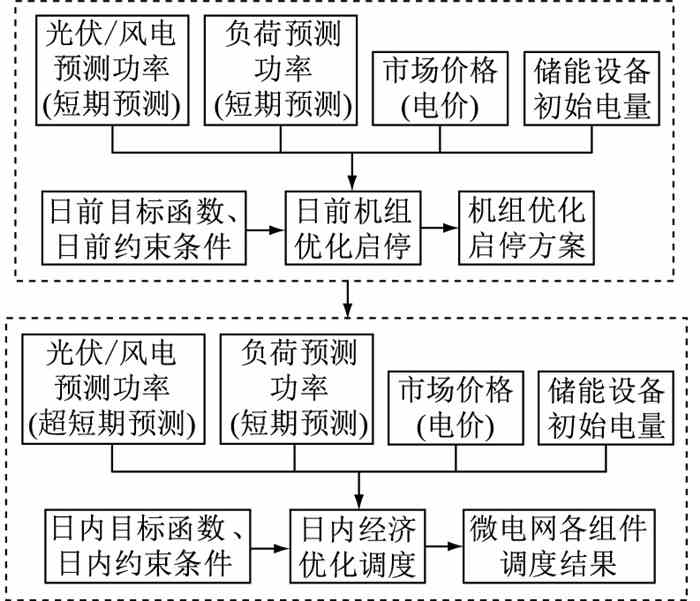
|
图 2 多时间尺度调度模型方案 Fig. 2 Multi-time scale scheduling model scheme |
微电网通过历史数据预测下一时刻的源/荷数值,这与实际状态存在一定误差,做出的优化调度决策会在一定程度上偏离实际,故而需要对日前阶段进行修正与滚动优化。MPC作为一种具有约束性的反馈控制优化策略,主要由预测模型、滚动优化和反馈校正三部分组成[32-34]。日内优化调度主要结合MPC理论,建立混合整数线性规划模型如下:
| $ \begin{aligned} & \min f^{\text {intra}}\left(x^{\text {intra}}\right)=\min \sum\limits_{t=1}^{N_{\mathrm{T}}}\left(C_{\mathrm{G}, t}^{\text {intra}}+C_{\mathrm{W}, t}^{\text {intra}}+\right. \\ &\quad \quad \quad \left.C_{\mathrm{P}, t}^{\text {inta}}+C_{\mathrm{E}, t}^{\text {inta}}+C_{\mathrm{M}, t}^{\text {inta}}\right) \end{aligned} $ | (24) |
式中:NT为日内调度周期;CG, tintra为微电网中可控发电机组在t时刻的成本,因为其启停状态不变,故只含有运行成本;CW, tintra、CP, tintra分别为日内弃风和弃光成本;CE, tintra为日内调度时储能的调度成本;CM, tintra为日内调度时微/配电网的购/售电成本。
储能的充放电功率尽量跟随日前调度结果,其日内调度成本表示为:
| $ C_{\mathrm{E}, t}^{\mathrm{intra}}=K_{\mathrm{E}}\left(\frac{1}{\eta_{\mathrm{E}, \mathrm{dis}}} P_{\mathrm{E}, t}^{\mathrm{dis}}+\eta_{\mathrm{E}, \mathrm{ch}} P_{\mathrm{E}, t}^{\mathrm{ch}}+\right. \\ \quad \quad \quad \left.\lambda_{\mathrm{E}}^{\mathrm{intra}}\left|E_{\mathrm{E}, t}^{\mathrm{SOC}, \text {intra}}-E_{\mathrm{E}, t}^{\mathrm{SOC}}\right|\right) \Delta t $ | (25) |
式中:λEintra为日内调度时储能调整量的权重系数;EE, tSOC, intra为日内阶段t时刻储能设备的SOC。式(25)含有绝对值项,引入辅助变量SE, tau来进行线性化处理,并且可控分布式电源出力和微/配电网交互功率也尽量跟随日前调度结果,具体形式与式(26)类似。
| $ \left\{\begin{align*} & C_{\mathrm{E}, t}^{i\text {ntra}}= K_{\mathrm{E}}\left(\frac{1}{\eta_{\mathrm{E}, \text {dis}}} P_{\mathrm{E}, t}^{\mathrm{dis}}+\eta_{\mathrm{E}, \mathrm{ch}} P_{\mathrm{E}, t}^{\mathrm{ch}}+\lambda_{\mathrm{E}}^{i\text {ntra}} S_{\mathrm{E}, t}^{\mathrm{au}}\right) \Delta t \\ & \text {s.t.} \;\;S_{\mathrm{E}, t}^{\mathrm{au}} \geqslant E_{\mathrm{E}, t}^{\mathrm{SC}, \text {intra}}-E_{\mathrm{E}, t}^{\text {ahead}} \\ & \quad \quad S_{\mathrm{E}, t}^{\mathrm{au}} \geqslant-\left(E_{\mathrm{E}, t}^{\mathrm{soc}, \text {intra}}-E_{\mathrm{E}, t}^{\text {ahead}}\right) \end{align*}\right. $ | (26) |
式中:EE, tahead为日前可调度每小时末的SOC。
日内阶段的约束条件包括:
(1) 与日前阶段相似的功率平衡等潮流约束,充、放电功率上、下限等储能约束以及可控分布式电源约束和微/配电网传输功率约束。
(2) 在日内调度时,储能的充放电功率为了更好地追踪日前调度结果,应满足如下约束。
| $ E_{\mathrm{E}, 4 t}^{\text {intra}}=E_{\mathrm{E}, t}^{\text {ahead}} \quad t=1, 2, \cdots, 24 $ | (27) |
式中:EE, 4tintra为日内调度每小时末的SOC。
3 算例分析选取实际微电网工程29节点算例,具体拓扑见图 3,除DG外还接入3台储能系统(energy storage system, ESS)。文中分析实验基于Intel Core i5-1135G7@2.40 GHz、16 GB操作系统,基于MATLAB R2018b结合Yalmip+Gurobi工具箱进行计算。
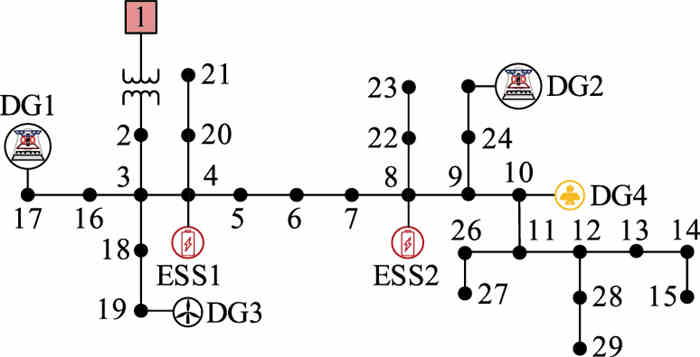
|
图 3 算例拓扑 Fig. 3 Example topology |
依托实际感知设备,选取36°5.8′N、103°46.1′E所在地区的风速和光照强度数据,并分别假定二者在各时间尺度内风光出力和负荷数据均不变化,处理得到光伏机组、风电机组和用户负荷的日前-日内有功功率预测值如图 4所示。
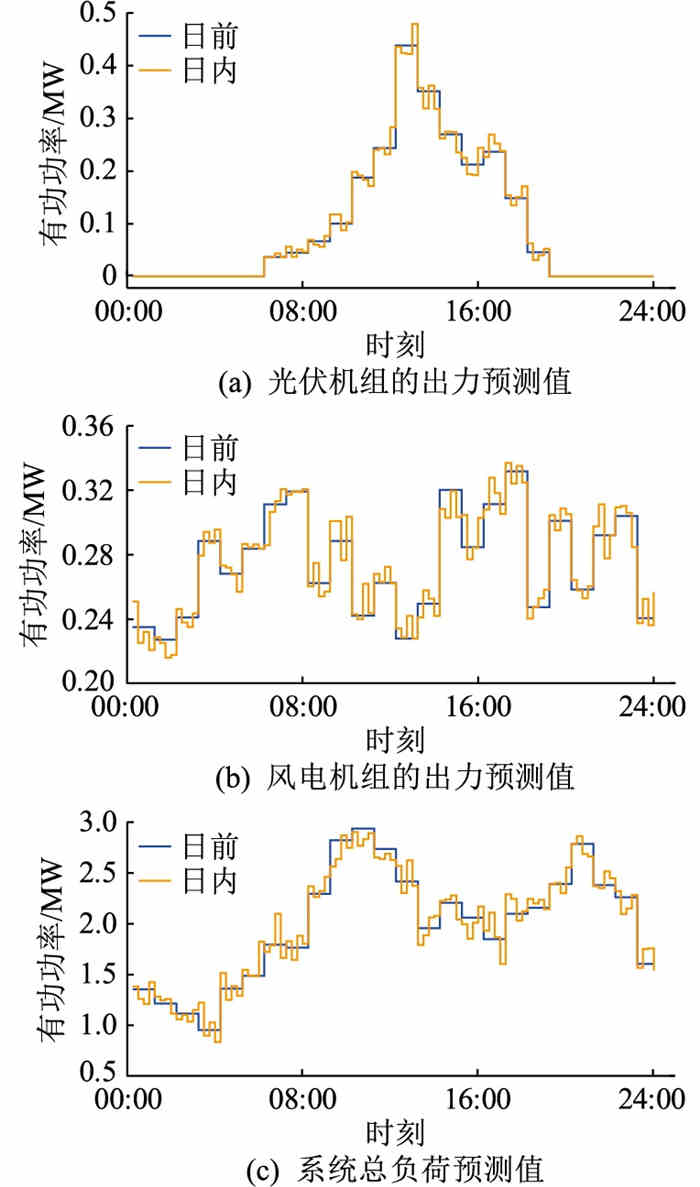
|
图 4 系统预测情况 Fig. 4 System forecast situation |
文中假设风机/光伏日前出力的参考预测误差服从均值为预测出力、方差为0.01倍预测出力的正态分布,随机生成1 000种场景进行风电/光伏出力的模拟,然后使用K-means聚类得到6种典型场景,并获取其相应的概率分布。风电机组和光伏机组聚类后的典型场景如图 5所示。
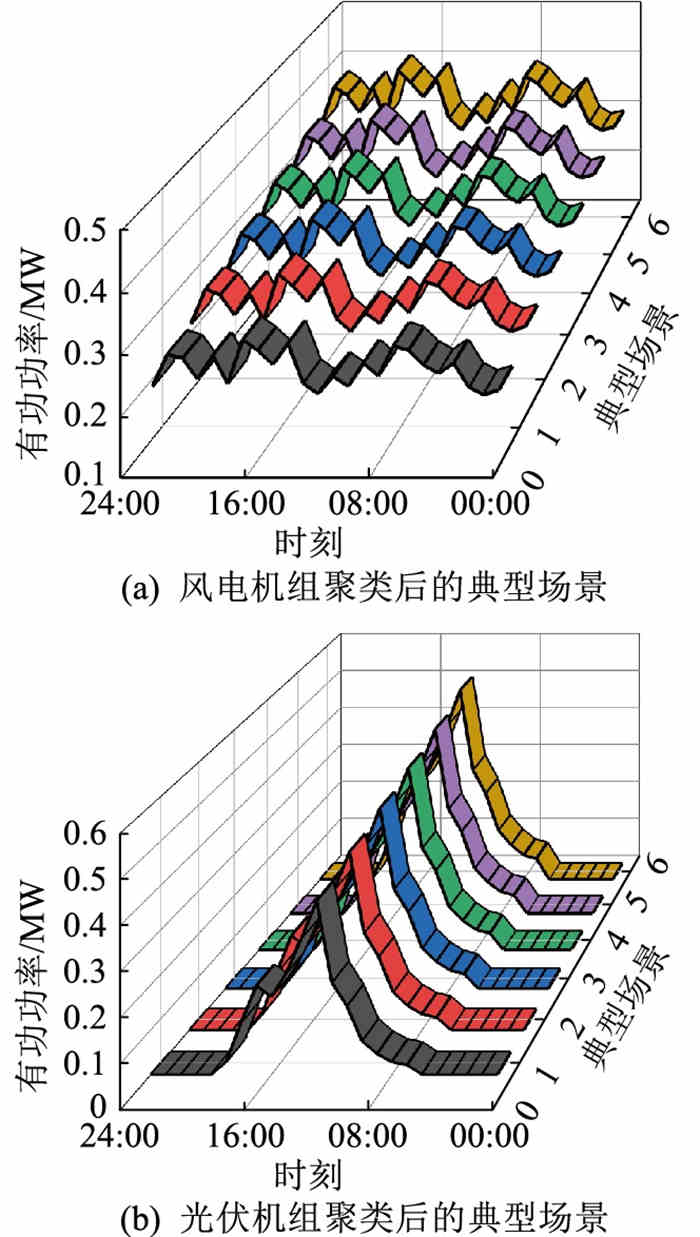
|
图 5 风电机组、光伏机组聚类后的典型场景 Fig. 5 Typical scenarios after clustering of wind turbines and photovoltaic units |
各场景对应的概率分布如表 1所示。各单元组件的运行参数如表 2所示。
3.1 不同优化方法比较分析|
|
表 1 典型场景对应概率分布 Table 1 Typical scene corresponding probability distribution |
|
|
表 2 各单元组件运行参数 Table 2 Operation parameters of each unit component |
为了比较分析不同优化方法对于微电网优化调度方案的适用性,分别采用以下3种方案对微电网调度成本进行分析比较。
方案1:基于场景的SO,选取6个聚类典型场景所示的近似正态分布作为其概率分布,并进行固定。
方案2:基于场景的RO,选取最恶劣场景下的调度结果作为优化结果。
方案3:基于数据驱动和多场景不确定集合的DRO,置信水平分别设置为α1=0.5、α∞=0.99,典型场景与方案2一致。
3种不确定性分析方法均采用相同的历史数据进行计算,结果如表 3所示。微电网的日运行成本方案1最低,方案2最高,方案3介于二者之间,这与理论分析的结果保持一致,即在一定大小不确定性的作用下,RO的优化结果保守性最高,SO的优化结果经济性最高。
|
|
表 3 各种优化方法日运行成本与新能源消纳量对比 Table 3 Daily operation cost and new energy consumption comparison of various optimization methods |
实际工程中考虑到系统运行的安全性往往难以高风险地去消纳如此多新能源,通常会留出一定安全运行裕度,而DRO综合考虑了RO的保守性和SO的经济性,相较于RO多消纳了17.08%新能源,提升了9.41%的经济效益,相较于SO则仅以牺牲4.40%经济为代价,提升了10.39%的安全性,得到适中的调度方案,避免调度结果过于极端。
3.2 参数设置影响分析针对1.1节提出的多离散场景分布鲁棒优化模型,将不确定集合中的置信度作为权衡调度方案安全裕度的指标,分析不同置信水平,即保守度指标(考虑偏差允许限值标幺化)对调度结果的影响,并通过安全运行所留出的裕度来分析调度方案的安全性。结果对比如表 4和表 5所示,对比分析考虑综合范数约束(同时考虑1-范数和∞-范数)、仅考虑∞-范数约束和仅考虑1-范数约束的优化结果可以发现,考虑综合范数约束相对于仅考虑某一单独范数约束可以获得更低的优化调度成本。此外,综合范数约束下的优化调度成本随着置信水平取值的增大而增大,这是由于置信区间会随着置信水平的增大而增大,从而使得模型中概率偏差范围变大,可以得到更差的场景概率分布,使调度安全性更高。
|
|
表 4 综合范数与∞-范数的结果对比 Table 4 Comparison of the results of integrated norm and the ∞-norm |
|
|
表 5 综合范数与1-范数的结果对比 Table 5 Comparison of the results of integrated norm and the 1-norm |
综上可知,考虑综合范数约束相比于仅考虑1-范数或者∞-范数约束有更低的保守度和更好的经济性,可避免制定过于保守的决策结果,并且可以通过灵活调整参数来调整微电网优化方案,有利于微电网系统在运行成本和运行风险间进行合理选择。
3.3 调度结果分析依据前文所提出的微电网整体架构、相关运行控制策略以及基于MPC的多时间尺度分布鲁棒优化调度模型,分析日运行的优化调度结果。
3.3.1 储能设备调度情况分析综合考虑日前和日内多时间尺度,将分析精度取为日内的15 min,范围为96个时刻,日前与日内趋势基本一致,仅有部分时间阶段存在一定偏差。在前文所建立的模型中,已经设定日内阶段的储能设备荷电状态尽量跟随日前阶段,但允许日内阶段的储能设备充放电功率在更小的时间间隔内根据实际情况进行调整,如图 6所示。
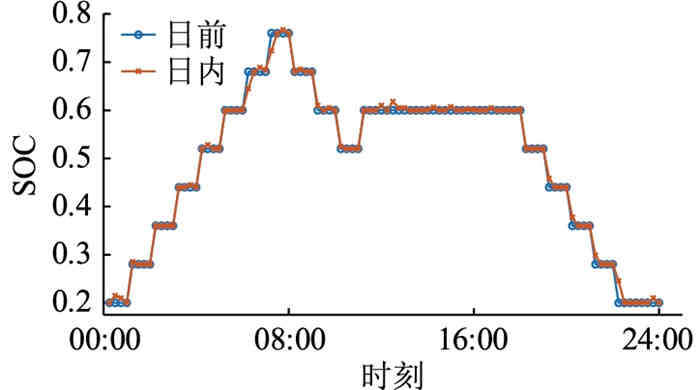
|
图 6 储能设备ESS1荷电状态变化曲线 Fig. 6 The change curves of the SOC of energy storage device ESS1 |
分析图 6中的2条曲线可以发现其与图 5相同,具有2组“峰谷”,但峰谷位置有所前移。这是因为通过一系列调度流程,利用储能设备一定程度上平抑了风光出力和负荷需求的波动,完成削峰填谷。储能设备初始状态为0.2,即标幺化后的20%,在00:00—08:00时段,此时虽然没有光伏出力,但电价较低且负荷需求不高,故而可以对储能设备进行充电,其SOC持续上升,最大值为0.76;在08:00—11:00时段,此时虽然光伏出力和负荷需求开始增加,但电价较高,储能放电成本较低,为达到更高的经济性,其SOC下降;同理,另一组波峰、波谷产生原理与上述2个时间段基本相同。
3.3.2 DG调度情况分析可控分布式电源在微电网中的主要作用是备用以及提高微电网运行的经济性,虽然其发电成本偏高但比峰值电价稍低,故在用电负荷需求较大且电价偏高时可采用可控分布式电源进行功率补充。
图 7中曲线呈现阶梯状,这是因为考虑启停成本和实际情况,对可控分布式电源运行加入了爬坡约束。该曲线波峰波谷与负荷需求曲线和电价曲线基本一致,变化趋势也相同,说明在调度过程中,可控分布式电源保障了微电网运行的可靠性与经济性。
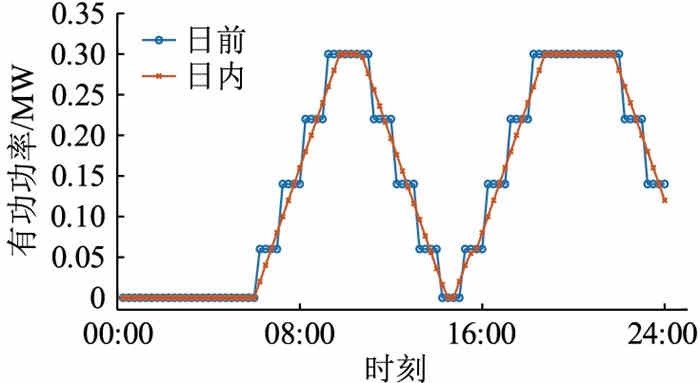
|
图 7 可控分布式电源DG2出力曲线 Fig. 7 Output curves of controllable distributed generation DG2 |
离网型微电网发生故障和停电现象的概率相对较高,而通过微/配电网的功率交互可以在保障可靠运行的基础上有效提高其经济性。
微/配电网的交互功率曲线如图 8所示,其整体也同样呈现2组波峰波谷的形状,但具体位置与前文调度结果和光伏出力等曲线相反。在00:00—03:00时段,曲线呈现一个短阶段的阶梯状上下浮动,这是由于此时进入深夜,负荷需求有所下降且新能源出力较低;在03:00—08:00时段,曲线有所回升,说明清晨用电需求上涨;在08:00—11:00时段,曲线持续下降,微电网向配电网取用的有功功率持续变少并转变为向其售电,这与实时售/购电电价相关,为兼顾安全可靠和经济成本,选择在高电价时减少向配电网购电或选择向其售电,功率缺额由新能源出力和储能设备进行补充,在可控分布式电源单位功率发电成本低于实时电价时,可采用可控分布式电源进行发电;其余阶段的曲线变化同理。值得一提的是,与储能设备SOC类似,2个调度阶段的微/配电网交互功率也需要尽量保持一致,但由于将时间尺度缩小后情况会更加复杂,所以二者均会存在一定偏差,但需要整体保持一致,这也体现了模型预测控制滚动优化的特点。
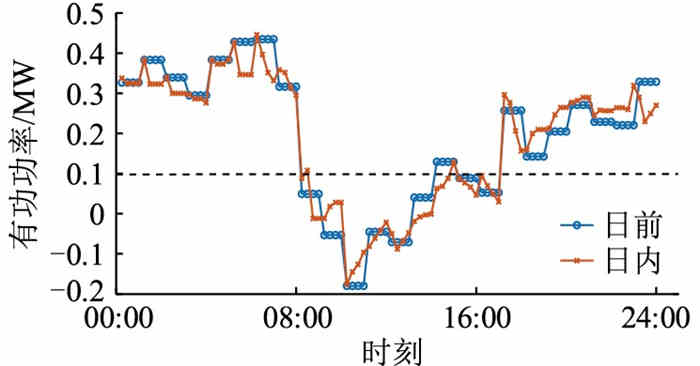
|
图 8 微/配电网售/购电功率曲线 Fig. 8 Micro/distribution grid sales/purchase power curves |
综上,通过对微电网各个组件设备的调度变化情况分析,首先能够合理运行即说明了在该场景下系统具有一定安全稳定运行能力,在保证安全可靠性的基础上,分析储能设备调度曲线、可控分布式电源调度曲线及微/配电网联络线功率变化曲线,整体可以论证其为了提升经济性,在跟随分时电价机制趋势而变化,能够调控各组件设备进行“削峰填谷”,达成微电网系统安全性和经济性的双赢。
4 结论文中基于综合范数约束不确定集合,提出一种基于数据驱动的两阶段分布鲁棒优化调度模型。并结合多时间尺度调度策略和MPC理论,构建了微电网日前-日内协同优化调度模型,通过算例分析,可以得到以下结论:
(1) 考虑新能源DG出力和负荷功率的不确定性,对比3类不确定性分析方法对调度结果的影响,发现基于数据驱动的DRO调度模型兼顾经济性与保守性,较RO经济性提升了9.41%,较SO安全性提升了10.39%。
(2) 所提出的综合范数约束不确定集合较单一范数能有效提升经济性,并且通过改变置信度参数能够调整微电网优化方案,有利于微电网系统在运行成本和运行风险间进行合理选择。
(3) 通过对比各时间尺度的调度结果,证明文中提出的日前-日内优化调度策略可以根据微电网当前调度时段的预测信息和实际情况进行实时调整,抵抗不确定性波动,保证微电网的安全、经济运行。
| [1] |
桑博, 张涛, 刘亚杰, 等. 多微电网能量管理系统研究综述[J]. 中国电机工程学报, 2020, 40(10): 3077-3093. SANG Bo, ZHANG Tao, LIU Yajie, et al. Energy management system research of multi-microgrid: a review[J]. Proceedings of the CSEE, 2020, 40(10): 3077-3093. (  0) 0) |
| [2] |
HAN Y, ZHANG K, LI H, et al. MAS-based distributed coordinated control and optimization in microgrid and microgrid clusters: a comprehensive overview[J]. IEEE Transactions on Power Electronics, 2018, 33(8): 6488-6508. DOI:10.1109/TPEL.2017.2761438 (  0) 0) |
| [3] |
曹敬, 金玉龙, 郑涛, 等. 计及分布式电源集群不确定性的配电网分散鲁棒电压控制[J]. 电力系统保护与控制, 2023, 51(22): 155-166. CAO Jing, JIN Yulong, ZHENG Tao, et al. A decentralized robust voltage control method for distribution networks considering the uncertainty of distributed generation clusters[J]. Power System Protection and Control, 2023, 51(22): 155-166. (  0) 0) |
| [4] |
石铖, 安锐, 高红均, 等. 基于柔性多状态开关和动态重构的配电网灵活运行方法[J]. 电力系统保护与控制, 2023, 51(22): 133-144. SHI Cheng, AN Rui, GAO Hongjun, et al. Flexible operation method for a distribution network based on flexible multi-state switching and dynamic reconfiguration[J]. Power System Protection and Control, 2023, 51(22): 133-144. (  0) 0) |
| [5] |
尉耀稳, 李跃龙, 陈思超, 等. 多类型源储协调互动的配电网分布鲁棒优化调度[J]. 电力工程技术, 2021, 40(5): 192-199. YU Yaowen, LI Yuelong, CHEN Sichao, et al. Distributionally robust optimal dispatch of distribution network considering multiple source-storage coordinated interaction[J]. Electric Power Engineering Technology, 2021, 40(5): 192-199. (  0) 0) |
| [6] |
CHE L, ZHANG X P, SHAHIDEHPOUR M, et al. Optimal interconnection planning of community microgrids with renewable energy sources[J]. IEEE Transactions on Smart Grid, 2017, 8(3): 1054-1063. DOI:10.1109/TSG.2015.2456834 (  0) 0) |
| [7] |
宁阳天, 罗翠云, 赵梓淇, 等. 计及核电调峰的新能源电力系统两阶段随机优化调度[J]. 电力工程技术, 2020, 39(2): 66-74, 126. NING Yangtian, LUO Cuiyun, ZHAO Ziqi, et al. A two-stage stochastic optimization for power system nuclear power plants participating in peak regulation with the consideration of renewable energy uncertainty[J]. Electric Power Engineering Technology, 2020, 39(2): 66-74, 126. (  0) 0) |
| [8] |
李英俊, 张耀, 许志军, 等. 基于数据驱动的电-热综合能源系统两阶段鲁棒备用优化[J]. 全球能源互联网, 2022, 5(2): 127-137. LI Yingjun, ZHANG Yao, XU Zhijun, et al. Data-driven based two-stage robust reserve optimization of integrated electric-heat systems[J]. Journal of Global Energy Interconnection, 2022, 5(2): 127-137. (  0) 0) |
| [9] |
SUNDAR K, NAGARAJAN H, ROALD L, et al. Chance-constrained unit commitment with N-1 security and wind uncertainty[J]. IEEE Transactions on Control of Network Systems, 2019, 6(3): 1062-1074. DOI:10.1109/TCNS.2019.2919210 (  0) 0) |
| [10] |
于馨玮, 陈继明, 仉志华. 分布鲁棒优化在综合能源系统调度与规划中的应用综述[J]. 全球能源互联网, 2023, 6(2): 207-215. YU Xinwei, CHEN Jiming, ZHANG Zhihua. A review of the application of distributionally robust optimization in integrated energy system dispatching and planning[J]. Journal of Global Energy Interconnection, 2023, 6(2): 207-215. (  0) 0) |
| [11] |
臧云帆, 夏晟, 李嘉文, 等. 含共享储能的微电网群分布鲁棒博弈优化调度方法[J]. 电力系统保护与控制, 2023, 51(24): 90-101. ZANG Yunfan, XIA Sheng, LI Jiawen, et al. A robust game optimization scheduling method for shared energy storage micro electric network group distribution[J]. Power System Protection and Control, 2023, 51(24): 90-101. (  0) 0) |
| [12] |
刘一欣, 郭力, 王成山. 微电网两阶段鲁棒优化经济调度方法[J]. 中国电机工程学报, 2018, 38(14): 4013-4022, 4307. LIU Yixin, GUO Li, WANG Chengshan. Economic dispatch of microgrid based on two stage robust optimization[J]. Proceedings of the CSEE, 2018, 38(14): 4013-4022, 4307. (  0) 0) |
| [13] |
贺帅佳, 阮贺彬, 高红均, 等. 分布鲁棒优化方法在电力系统中的理论分析与应用综述[J]. 电力系统自动化, 2020, 44(14): 179-191. HE Shuaijia, RUAN Hebin, GAO Hongjun, et al. Overview on theory analysis and application of distributionally robust optimization method in power system[J]. Automation of Electric Power Systems, 2020, 44(14): 179-191. (  0) 0) |
| [14] |
YUAN W L, WANG X Q, SU C G, et al. Stochastic optimization model for the short-term joint operation of photovoltaic power and hydropower plants based on chance-constrained programming[J]. Energy, 2021, 222: 119996. DOI:10.1016/j.energy.2021.119996 (  0) 0) |
| [15] |
李运龙, 李志刚, 郑杰辉. 考虑风电不确定性和相关性的多区域电网分布鲁棒经济调度[J]. 电力自动化设备, 2021, 41(8): 97-104. LI Yunlong, LI Zhigang, ZHENG Jiehui. Distributionally robust economic dispatch of multi-regional power grid considering uncertainty and correlation of wind power[J]. Electric Power Automation Equipment, 2021, 41(8): 97-104. (  0) 0) |
| [16] |
WANG C, GAO R, WEI W, et al. Risk-based distributionally robust optimal gas-power flow with Wasserstein distance[J]. IEEE Transactions on Power Systems, 2019, 34(3): 2190-2204. DOI:10.1109/TPWRS.2018.2889942 (  0) 0) |
| [17] |
CHEN Y W, GUO Q L, SUN H B, et al. A distributionally robust optimization model for unit commitment based on kullback-leibler divergence[J]. IEEE Transactions on Power Systems, 2018, 33(5): 5147-5160. DOI:10.1109/TPWRS.2018.2797069 (  0) 0) |
| [18] |
税月, 刘俊勇, 高红均, 等. 考虑风电不确定性的电热综合系统分布鲁棒协调优化调度模型[J]. 中国电机工程学报, 2018, 38(24): 7235-7247, 7450. SHUI Yue, LIU Junyong, GAO Hongjun, et al. A distributionally robust coordinated dispatch model for integrated electricity and heating systems considering uncertainty of wind power[J]. Proceedings of the CSEE, 2018, 38(24): 7235-7247, 7450. (  0) 0) |
| [19] |
DING T, YANG Q R, YANG Y H, et al. A data-driven stochastic reactive power optimization considering uncertainties in active distribution networks and decomposition method[J]. IEEE Transactions on Smart Grid, 2018, 9(5): 4994-5004. DOI:10.1109/TSG.2017.2677481 (  0) 0) |
| [20] |
阮贺彬, 高红均, 刘俊勇, 等. 考虑DG无功支撑和开关重构的主动配电网分布鲁棒无功优化模型[J]. 中国电机工程学报, 2019, 39(3): 685-695, 948. RUAN Hebin, GAO Hongjun, LIU Junyong, et al. A distributionally robust reactive power optimization model for active distribution network considering reactive power support of DG and switch reconfiguration[J]. Proceedings of the CSEE, 2019, 39(3): 685-695, 948. (  0) 0) |
| [21] |
李卫东, 礼晓飞, 王海鑫, 等. 基于MPC的柔性负荷与储能系统超短期调控策略[J]. 电测与仪表, 2020, 57(10): 64-70. LI Weidong, LI Xiaofei, WANG Haixin, et al. Ultra-short-term dispatch strategy of flexible load and energy storage system based on MPC[J]. Electrical Measurement & Instrumentation, 2020, 57(10): 64-70. (  0) 0) |
| [22] |
朱兰, 田泽清, 唐陇军, 等. 计及细节层次直接负荷控制的区域综合能源系统多时间尺度优化调度[J]. 电网技术, 2021, 45(7): 2763-2774. ZHU Lan, TIAN Zeqing, TANG Longjun, et al. Multi-time-scale optimal dispatch of regional integrated energy system considering level of detail direct load control[J]. Power System Technology, 2021, 45(7): 2763-2774. (  0) 0) |
| [23] |
DOU C X, YUE D, LI X B, et al. MAS-based management and control strategies for integrated hybrid energy system[J]. IEEE Transactions on Industrial Informatics, 2016, 12(4): 1332-1349. DOI:10.1109/TII.2016.2569506 (  0) 0) |
| [24] |
BAZMOHAMMADI N, TAHSIRI A, ANVARI-MOGHADDAM A, et al. Stochastic predictive control of multi-microgrid systems[C]//2018 IEEE International Conference on Environment and Electrical Engineering and 2018 IEEE Industrial and Commercial Power Systems Europe (EEEIC / I&CPS Europe). Palermo, Italy. IEEE, 2018: 1-5.
(  0) 0) |
| [25] |
魏梅芳, 吴燕, 黎跃龙, 等. 基于分布鲁棒优化的微电网日前经济运行模型与求解方法[J]. 电力系统及其自动化学报, 2022, 34(12): 81-90. WEI Meifang, WU Yan, LI Yuelong, et al. Day-ahead economic operation model of microgrid and its solving method based on distributed robust optimization[J]. Proceedings of the CSU-EPSA, 2022, 34(12): 81-90. (  0) 0) |
| [26] |
CHEN Z, LI Z S, GUO C X, et al. Fully distributed robust reserve scheduling for coupled transmission and distribution systems[J]. IEEE Transactions on Power Systems, 2021, 36(1): 169-182. DOI:10.1109/TPWRS.2020.3006153 (  0) 0) |
| [27] |
张黎明, 李浩, 吴亚雄, 等. 基于运行优化的含储能电力系统可靠性评估方法[J]. 中国电力, 2022, 55(9): 23-28. ZHANG Liming, LI Hao, WU Yaxiong, et al. A reliability evaluation method for power system with energy storage based on operation optimization[J]. Electric Power, 2022, 55(9): 23-28. (  0) 0) |
| [28] |
MIETH R, DVORKIN Y. Data-driven distributionally robust optimal power flow for distribution systems[J]. IEEE Control Systems Letters, 2018, 2(3): 363-368. DOI:10.1109/LCSYS.2018.2836870 (  0) 0) |
| [29] |
朱光远, 林济铿, 罗治强, 等. 鲁棒优化在电力系统发电计划中的应用综述[J]. 中国电机工程学报, 2017, 37(20): 5881-5892. ZHU Guangyuan, LIN Jikeng, LUO Zhiqiang, et al. Review of robust optimization for generation scheduling in power systems[J]. Proceedings of the CSEE, 2017, 37(20): 5881-5892. (  0) 0) |
| [30] |
董燕, 杨俊林, 朱永胜, 等. 基于零和博弈的电力系统鲁棒优化调度研究[J]. 电力系统保护与控制, 2022, 50(5): 55-64. DONG Yan, YANG Junlin, ZHU Yongsheng, et al. Robust optimal dispatch of a power system based on a zero-sum game[J]. Power System Protection and Control, 2022, 50(5): 55-64. (  0) 0) |
| [31] |
吴桐, 刘丽军, 林钰芳, 等. 基于动态分区的配电网日前优化调度研究[J]. 电力系统保护与控制, 2022, 50(15): 21-32. WU Tong, LIU Lijun, LIN Yufang, et al. Day-ahead optimal dispatch for a distribution network based on dynamic partitioning[J]. Power System Protection and Control, 2022, 50(15): 21-32. (  0) 0) |
| [32] |
刘自发, 张婷, 王岩. 基于模型预测控制的主动配电网多场景变时间尺度优化调度[J]. 电力自动化设备, 2022, 42(4): 121-128. LIU Zifa, ZHANG Ting, WANG Yan. Multi-scenario variable time scale optimal scheduling of active distribution network based on model predictive control[J]. Electric Power Automation Equipment, 2022, 42(4): 121-128. (  0) 0) |
| [33] |
胡剑, 林耀玮, 阎发友, 等. 考虑光热电站接入的电力系统双层双时间尺度优化调度[J]. 电力系统保护与控制, 2022, 50(13): 23-32. HU Jian, LIN Yaowei, YAN Fayou, et al. Two-layer double-time scale optimal dispatch for a power system considering concentrating solar power plant penetration[J]. Power System Protection and Control, 2022, 50(13): 23-32. (  0) 0) |
| [34] |
李咸善, 马凯琳, 程杉. 含多区域综合能源系统的主动配电网双层博弈优化调度策略[J]. 电力系统保护与控制, 2022, 50(1): 8-22. LI Xianshan, MA Kailin, CHENG Shan. Dispatching strategy of an active distribution network with multiple regional integrated energy systems based on two-level game optimization[J]. Power System Protection and Control, 2022, 50(1): 8-22. (  0) 0) |
2. School of Electrical and Control Engineering, North China University of Technology, Beijing 100144, China;
3. State Grid Hangzhou Power Supply Company of Zhejiang Electric Power Co., Ltd., Hangzhou 311400, China
 2024, Vol. 43
2024, Vol. 43


 李嘉伟(2000),男,硕士在读,研究方向为电力系统优化调度(E-mail:
李嘉伟(2000),男,硕士在读,研究方向为电力系统优化调度(E-mail: