0 引言

我国10 kV中压配电网常采用消弧线圈接地方式^[1-5]，对于这种小电流接地方式，在线路发生单相接地故障时允许运行1~2 h，非故障相对地电压升高，在不同出线的绝缘薄弱处可能发生击穿并产生第二个接地点^[6-9]，形成同母两回线异相接地复故障。此外，受雷击、刮风等自然灾害的影响，容易发生同母两回线异相接地的情况^[10]。同母两回线异相接地复故障发生时容易造成人畜触电事故，因此需要快速选出故障线路，防止危害扩大。

目前对于消弧线圈接地系统接地故障的研究主要针对单回线接地故障方面^[11-15]，单相故障检测技术与装置并不能很好地处理两点接地故障^[16]。文献[17]针对配电网的相继接地故障，提出一种零序保护定值整定方法，但是该方法要依靠现场运行以及继电保护相关整定经验，没有经过严格的理论推导。文献[18]对消弧线圈接地系统同母多回线相继故障的发生机理进行研究，揭示了接地发生相间短路故障的原因，并提出一些抑制同母多回线相继故障发生的方法。文献[19]针对不接地系统偶发两出线相继接地故障处理难题，利用故障前后工频电气量信息，提出一种适用于不接地系统同名相两点接地故障的选线方法。文献[20]对多回线接地故障下的馈线零序电流关系进行推导，并提出一种自适应馈线零序电流保护方案，但是并不适用于异相接地的情形。文献[21]推导了小电阻接地系统中同母两回线金属性接地故障各馈线的零序电流，未考虑过渡电阻变化的情况。

文中在分析消弧线圈接地系统同母两回线异相接地复故障特征的基础上，提出一种基于零序导纳幅值比的故障选线方法。利用故障线路零序导纳幅值大于非故障线路零序导纳幅值的特征，选出所有的故障线路，最后经过PSCAD仿真表明，文中方法在故障位置、消弧线圈补偿度等因素的影响下仍能准确选出故障线路，具有较强的耐受过渡电阻的能力。

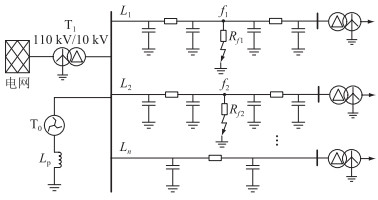
1 同母两回线异相接地复故障分析 1.1 故障点处电气量计算

图 1为10 kV消弧线圈接地系统同母两回线异相接地故障示意。从母线出来总共有n条馈线，线路采用π型等值模型，在线路L₁的f₁点发生了B相接地故障，线路L₂的f₂点发生了C相接地故障。R_f1为第一个故障点f₁处的过渡电阻；R_f2为第二个故障点f₂处的过渡电阻；T₀为接地变压器；T₁为系统侧主变压器；L_p为消弧线圈。

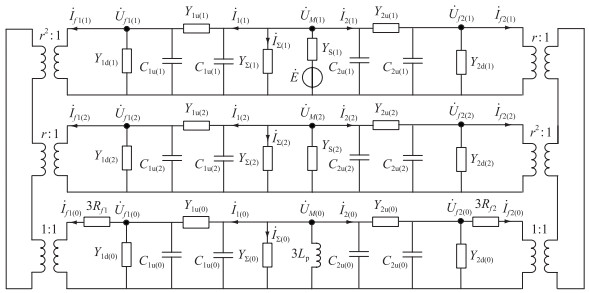
以A相为基准相，采用对称分量法，根据接地复故障边界条件，可得到同母两回线异相接地复故障的复合序网图如图 2所示，两侧为理想变压器，其变比的设计参考文献[22]，文中所有变量的下标(1)、(2)、(0)均表示正、负、零序分量。

图 2中，$\dot{U}$_f1、$\dot{I}$_f1分别为故障点f₁处的电压和电流；$\dot{U}$_f2、$\dot{I}$_f2分别为故障点f₂处的电压和电流；$\dot{U}$_M为母线电压；$\dot{I}$₁、$\dot{I}$₂为故障线路首端电流；$\dot{I}$_Σ为所有非故障线路首端的电流之和；$\dot{E}$为正序网络中的等效电势；Y_1d、Y_2d分别为故障点f₁、f₂下游的总导纳，正负序中包括线路导纳、线路对地电容以及负荷部分，而零序中不包含负荷；C_1u、C_2u分别为故障点f₁、f₂上游的线路对地电容；Y_1u、Y_2u分别为故障点f₁、f₂上游的线路导纳；Y_Σ为所有非故障线路的总导纳；Y_S为系统导纳；r为变换算子，r=e^jπ/3。

根据同母两回线异相接地复故障的复合序网图，可建立如下的节点电压方程：

$ \left\{ {\begin{array}{*{20}{l}} {{Y_{f1(1)}}{{\dot U}_{f1(1)}} - {Y_{1{\rm{u}}(1)}}{{\dot U}_{{\rm{M}}(1)}} = - r{{\dot I}_{f1(0)}}}\\ { - {Y_{{\rm{Iu}}(1)}}{{\dot U}_{f1(1)}} + {Y_{{\rm{M}}(1)}}{{\dot U}_{M(1)}} - {Y_{2{\rm{u}}(1)}}{{\dot U}_{f(1)}} = \dot E{Y_{{\rm{S}}(1)}}}\\ { - {Y_{2{\rm{u}}(1)}}{{\dot U}_{{\rm{M}}(1)}} + {Y_{f2(1)}}{{\dot U}_{f2(1)}} = - {r^2}{{\dot I}_{f2(0)}}}\\ {{Y_{f1(2)}}{{\dot U}_{f1(2)}} - {Y_{{\rm{lu}}(2)}}{{\dot U}_{{\rm{M}}(2)}} = - {r^2}{{\dot I}_{f1(0)}}}\\ { - {Y_{1{\rm{u}}(2)}}{{\dot U}_{f1(2)}} + {Y_{{\rm{M}}(2)}}{{\dot U}_{{\rm{M}}(2)}} - {Y_{2{\rm{u}}(2)}}{{\dot U}_{f2(2)}} = 0}\\ { - {Y_{2{\rm{u}}(2)}}{{\dot U}_{{\rm{M}}(2)}} + {Y_{f2(2)}}{{\dot U}_{f1(2)}} = - r{{\dot I}_{f2(0)}}}\\ {{Y_{f1(0)}}{{\dot U}_{f1(0)}} - {Y_{{\rm{lu}}(0)}}{{\dot U}_{{\rm{M}}(0)}} = - {{\dot I}_{f1(0)}}}\\ { - {Y_{1{\rm{u}}(0)}}{{\dot U}_{f1(0)}} + {Y_{{\rm{M}}(0)}}{{\dot U}_{{\rm{M}}(0)}} - {Y_{2{\rm{u}}(0)}}{{\dot U}_{f2(0)}} = 0}\\ { - {Y_{2{\rm{u}}(0)}}{{\dot U}_{{\rm{M}}(0)}} + {Y_{f2(0)}}{{\dot U}_{f1(0)}} = - {{\dot I}_{f2(0)}}} \end{array}} \right. $

(1)

式中: Y_f1、Y_f2分别为故障点f₁、f₂处的自导纳；Y_M为$\dot{U}$_M点处的自导纳。

理想变压器处的边界条件方程为：

$ \left\{\begin{array}{l} r^2 \dot{U}_{f 1(1)}+r \dot{U}_{f 1(2)}+\dot{U}_{f 1(0)}=3 \dot{I}_{f 1(0)} R_{f 1} \\ r \dot{U}_{f 2(1)}+r^2 \dot{U}_{f 2(2)}+\dot{U}_{f 2(0)}=3 \dot{I}_{f 2(0)} R_{f 2} \end{array}\right. $

(2)

根据式(1)和式(2)可求解出2个故障点f₁、f₂处的正、负、零序电压，故障点处的零序电流以及母线处的正、负、零序电压，进而可以求解出各条线路首端的正、负、零序电流。

1.2 线路零序导纳计算

采用零序分量进行分析，同母两回线的异相接地的零序网络如图 3所示，$\dot{I}$_L(0)为消弧线圈支路的电流，各线路首端的电流均以从母线流出的方向为正方向。由于系统测主变压器以及线路降压变压器的连接方式，可以看到零序网络中不包含系统阻抗以及负荷。

结合零序网络结构，2条故障线路首端零序电流为：

$ \dot{I}_{1(0)}=\left(\dot{U}_{\mathrm{M}(0)}-\dot{U}_{f 1(0)}\right) Y_{\mathrm{lu}(0)}+\frac{1}{2} \mathrm{j} \omega c_0 l_{f 1} \dot{U}_{\mathrm{M}(0)} $

(3)

$ \dot{I}_{2(0)}=\left(\dot{U}_{\mathrm{M}(0)}-\dot{U}_{f 2(0)}\right) Y_{2 \mathrm{u}(0)}+\frac{1}{2} \mathrm{j} \omega c_0 l_{f 2} \dot{U}_{\mathrm{M}(0)} $

(4)

式中: ω为系统角频率；c₀线路对地单位长度零序电容；l_f1、l_f2分别为故障点f₁、f₂到母线的距离。式(3)、式(4)中等式右边的第一部分为故障点上游线路导纳中流过的电流，第二部分为流向故障点上游对地电容的电流。

第i(i=3, 4, …, n)条非故障线路首端零序电流为：

$ \dot{I}_{i(0)}=\dot{U}_{\mathrm{M}(0)} Y_{i(0)} $

(5)

式中: Y_i(0)为第i条线路的总零序导纳。

利用线路首端的零序电流与母线零序电压比得到零序导纳，对于故障线路，其零序导纳计算见式(6)和式(7)。

$ Y_{1(0)}=\frac{\dot{I}_{1(0)}}{\dot{U}_{\mathrm{M}(0)}}=\frac{1}{2} \mathrm{j} \omega c_0 l_{f 1}+\left(1-\frac{\dot{U}_{f 1(0)}}{\dot{U}_{\mathrm{M}(0)}}\right) Y_{1 \mathrm{u}(0)} $

(6)

$ Y_{2(0)}=\frac{\dot{I}_{2(0)}}{\dot{U}_{\mathrm{M}(0)}}=\frac{1}{2} \mathrm{j} \omega c_0 l_{f 2}+\left(1-\frac{\dot{U}_{f 2(0)}}{\dot{U}_{\mathrm{M}(0)}}\right) Y_{2 \mathrm{u}(0)} $

(7)

对于第i条非故障线路，其零序导纳计算如式(8)所示。

$ Y_{i(0)}=\frac{\dot{I}_{i(0)}}{\dot{U}_{\mathrm{M}(0)}}=\frac{4 \mathrm{j} \omega c_0 l_i-\omega^2 c_0^2 z_0 l_i^3}{2\left(2+\mathrm{j} \omega c_0 z_0 l_i^2\right)} \quad i=3, 4, \cdots, n $

(8)

式中: z₀线路单位长度零序阻抗；l_i为第i条非故障线路长度。

1.3 零序导纳幅值特征分析

为了得到各线路零序导纳之间的关系，用故障线路的零序导纳比上非故障路的零序导纳，根据式(6)—式(8)可得2条故障线路与第i条非故障线路的零序导纳比为：

$ \begin{gathered} \frac{Y_{1(0)}}{Y_{i(0)}}=\left[\frac{1}{2} \mathrm{j} \omega c_0 l_{\mathrm{f} 1}+\left(1-\dot{U}_{\mathrm{f} 1 \mathrm{M}}\right) Y_{1 \mathrm{u}(0)}\right] / \\ \frac{4 \mathrm{j} \omega c_0 l_i-\omega^2 c_0^2 z_0 l_i^3}{2\left(2+\mathrm{j} \omega c_0 z_0 l_i^2\right)} \end{gathered} $

(9)

$ \begin{gathered} \frac{Y_{2(0)}}{Y_{i(0)}}=\left[\frac{1}{2} \mathrm{j} \omega c_0 l_{\mathrm{f} 2}+\left(1-\dot{U}_{\mathrm{f} 2 \mathrm{M}}\right) Y_{2 \mathrm{u}(0)}\right] / \\ \frac{4 \mathrm{j} \omega c_0 l_i-\omega^2 c_0^2 z_0 l_i^3}{2\left(2+\mathrm{j} \omega c_0 z_0 l_i^2\right)} \end{gathered} $

(10)

式中: $\dot{U}_{\mathrm{f} 1 \mathrm{M}}=\dot{U}_{f 1(0)} / \dot{U}_{\mathrm{M}(0)}, \dot{U}_{\mathrm{f} 2 \mathrm{M}}=\dot{U}_{f 2(0)} / \dot{U}_{\mathrm{M}(0)}$分别为故障点f₁、f₂处的零序电压与母线零序电压之比，可通过式(1)、式(2)求解得到。以故障线路L₁为例，根据方程的求解结果，对于$\dot{U}$_f1M，其结果可以写成如下形式：

$ \dot{U}_{\mathrm{flM}}=\frac{a_1 R_{f 1}+a_2 R_{f 2}+a_3 / R_{f 2}+a_4}{b_1 R_{f 1}+b_2 R_{f 2}+b_3 / R_{f 1}+b_4 / R_{f 2}+b_5} $

(11)

式中: a₁—a₄和b₁—b₅均是只与2条线路的故障位置有关的参数，不包含与过渡电阻有关的量。

消弧线圈接地系统中，无论是架空线还是电缆，线路零序阻抗远小于对地容抗，因此在分析故障线路与非故障线路零序导纳之间的关系时，对于式(9)有：

$ \left\{\begin{array}{l} \left|\frac{1}{2} \mathrm{j} \omega c_0 l_{f 1}\right| \ll\left|Y_{1 u(0)}\right|=\left|\frac{1}{z_0 l_{f 1}}\right| \\ \left|\omega^2 c_0^2 z_0 l_i^3\right| \ll\left|4 \mathrm{j} \omega c_0 l_i\right| \\ \left|\mathrm{j} \omega c_0 z_0 l_i^2\right| \ll 2 \end{array}\right. $

(12)

对式(9)取幅值，并忽略式(12)中幅值较小的量，可得到故障线路L₁与第i条非故障线路的零序导纳幅值比K_m1为：

$ K_{\mathrm{m} 1}=\left|\frac{Y_{1(0)}}{Y_{i(0)}}\right|=\frac{\left|1-\dot{U}_{\mathrm{flM}}\right|\left|Y_{1 \mathrm{u}(0)}\right|}{\left|\mathrm{j} \omega c_0 l_i\right|} $

(13)

式(13)由$\left|1-\dot{U}_{f \mathrm{IM}}\right|$与$\left|Y_{1 \mathrm{u}(0)} /\left(\mathrm{j} \omega c_0 l_i\right)\right|$两部分组成，$\dot{U}$_f1(0)与$\dot{U}$_M(0)之间相差一个故障点f₁上游线路阻抗的电压，即Y_1u(0)上的电压。该线路阻抗虽然与故障点位置有关，但是由于线路阻抗值较小，因此可以忽略故障位置对$\dot{U}$_f1M的影响，只考虑过渡电阻的影响。而对于$\left|Y_{\mathrm{lu}(0)} /\left(\mathrm{j} \omega c_0 l_i\right)\right|$部分，|Y_1u(0)|受第一个故障点位置的影响，并且随着l_f1的增大而减小。

故障线路L₂与故障线路L₁的分析过程一致，故参照线路L₁的分析过程同理可得故障线路L₂与第i条非故障线路的零序导纳幅值比K_m2为：

$ K_{\mathrm{m} 2}=\left|\frac{Y_{2(0)}}{Y_{i(0)}}\right|=\frac{\left|1-\dot{U}_{\mathrm{f} 2 \mathrm{M}}\right|\left|Y_{2 \mathrm{u}(0)}\right|}{\left|\mathrm{j} \omega c_0 l_i\right|} $

(14)

对于$\dot{U}$_f2M也只考虑过渡电阻的影响，$\left|Y_{2 \mathrm{u}(0)} /\left(\mathrm{j} \omega c_0 l_i\right)\right|$部分随着l_f2的增大而减小。

前面分析了故障线路与非故障线路之间的零序导纳特征，对于非故障线路，第j条故障线路的零序导纳与第i条故障线路的零序导纳比为：

$ \begin{gathered} \frac{Y_{j(0)}}{Y_{i(0)}}=\frac{4 \mathrm{j} \omega c_0 l_j-\omega^2 c_0^2 z_0 l_j^3}{2+\mathrm{j} \omega c_0 z_0 l_j^2} / \frac{4 \mathrm{j} \omega c_0 l_i-\omega^2 c_0^2 z_0 l_i^3}{2+\mathrm{j} \omega c_0 z_0 l_i^2} \\ i \neq j \end{gathered} $

(15)

根据式(12)的关系，忽略对零序导纳幅值影响较小的量，非故障线路之间的零序导纳幅值比可表示为：

$ K_{\mathrm{m} j}=\left|\frac{Y_{j(0)}}{Y_{i(0)}}\right|=\left|\frac{4 \mathrm{j} \omega c_0 l_j}{4 \mathrm{j} \omega c_0 l_i}\right|=\frac{l_j}{l_i} \quad i \neq j $

(16)

非故障线路零序导纳即为该条线路的总零序导纳，包括线路阻抗以及对地电容部分，在线路长度已知时其为一个固定量。由式(16)可以看出，非故障线路之间的零序导纳幅值比近似为线路的长度比，由于10 kV城市配电网的线路长度不超过20 km，故在一定的供电区域内，若线路长度相差不大，非故障线路之间的零序导纳幅值比很小。

2 同母两回线异相接地复故障选线原理 2.1 选线原理

根据前面的分析，非故障线路之间的零序导纳差异较小，由式(13)可以看出，|Y_1u(0)/(jωc₀l_i)|部分由于线路零序阻抗与对地容的关系，存在|jωc₀l_i|＜＜|Y_1u(0)|，在2个过渡电阻处于某个范围内时，由于|Y_1u(0)/(jωc₀l_i)|的影响，K_m1会达到很大值，远大于非故障线路之间的幅值比K_mj。对于K_m2有同样的结论，即故障线路零序导纳幅值大于非故障线路零序导纳的幅值，可利用此特征进行故障选线。以线路首端零序电流最小的线路为参考线路，该线路的零序导纳在所有线路中最小，为非故障线路，用所有线路的零序导纳幅值比上参考线路的零序导纳幅值，可构造如下的选线判据：

$ \begin{cases}K_{\mathrm{m} k}>K_{\text {set }} & \text { 故障线路 } \\ K_{\mathrm{m} k}＜K_{2 \mathrm{set}} & \text { 非故障线路 }\end{cases} $

(17)

式中: K_mk为第k条线路与参考线路的零序导纳幅值比；K_1set、K_2set为设定值。

2.2 故障启动判据

消弧线圈接地系统发生接地故障时会产生较大的零序电压，故障选线装置可以采用零序电压越限启动，当母线零序电压有效值超过设定的启动整定值U_set时，进行故障选线。因此启动判据可设为：

$ U_{\mathrm{M}(0)}>U_{\text {set }} $

(18)

考虑到未发生故障时，由于三相不平衡也会出现零序电压，因此可按照躲开三相不平衡时出现的最大零序电压设定启动值，架空馈线的不平衡度一般不超过1.5%^[23-26]，可取零序电压整定值为相电压的10%，对于10 kV配电网，U_set=577 V。

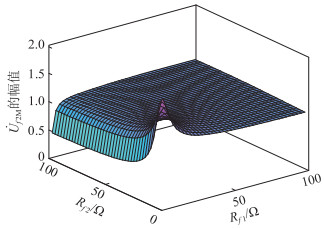
2.3 参数整定

对式(17)中的K_1set、K_2set进行整定，在式(13)、式(14)中，故障线路L₁的故障点f₁在线路末端时，|Y_1u(0)/(jωc₀l_i)|=1/(|z₀l_f1||jωc₀l_i|)取最小值，根据《工业与民用配电设计手册》：“我国10 kV电压等级线路中，架空线的供电距离为6~20 km”^[27-29]，可令l_f1=l_i=20 km，此时|Y_1u(0)/(jωc₀l_i)|达到最小，故障线路L₂的情形亦是如此。对于|1－$\dot{U}$_f1M|与|1－$\dot{U}$_f2M|部分，$\dot{U}$_f1M和$\dot{U}$_f2M的幅值与过渡电阻的关系分别如图 4和图 5所示，随着过渡电阻R_f1与R_f2的增大，$\dot{U}$_f1M和$\dot{U}$_f2M的幅值接近1，|1－$\dot{U}$_f1M|与|1－$\dot{U}$_f2M|越接近最小值。由于|Y_1u(0)/(jωc₀l_i)|与|1－$\dot{U}$_f1M|并不在同一故障位置同时取得最小值，因此实际的K_m1与K_m2的最小值并不在故障发生线路末端时取得，又因为|1－$\dot{U}$_f1M|和|1－$\dot{U}$_f2M|主要受过渡电阻的影响，并且过渡电阻越大，故障位置对K_m1与K_m2的影响越小，不妨认为故障发生在线路末端时，K_m1与K_m2均取得最小值，代入线路参数^[30-31]后，在R_f1、R_f2≤1 000 Ω范围内，对于非故障线路，由式(16)可知，对于第j条非故障线路有K_mj=l_j/l_i，则可设K_1set=k₁K_mj-max，K_mj-max为最长线路与最短线路的长度之比，为了留有一定的裕度，在此基础上乘以系数k₁，可取k₁=1.2。而对于故障线路，前面的分析可知其零序导纳幅值要大于非故障线路零序导纳幅值，根据计算可取K_2set=2K_mj-max，故障线路选线判据与非故障线路选线判据中没有重叠的部分，可以准确选出故障线路。

2.4 故障选线流程

基于零序导纳幅值比的故障选线方法流程如图 6所示。具体选线步骤如下：

(1) 判断母线电压是否满足选线启动判据，若满足则进行步骤(2), 否则继续监视线路状态。

(2) 获取各条线路首端零序电流与母线零序电压，利用线路首端零序电流与母线零序电压数据计算各条线路零序导纳。

(3) 以零序电流最小的线路作为参考线路，计算各条线路与参考线路的零序导纳幅值比。

(4) 判断各线路与参考线路的零序导纳幅值比是否大于K_1set或小于K_2set。若大于K_1set则该线路为故障线路，若小于K_2set则为非故障线路。

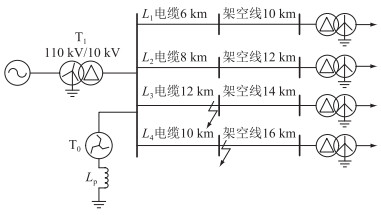
3 仿真验证

在PSCAD平台搭建10 kV消弧线圈接地系统仿真模型，如图 7所示。系统采用架空-电缆混合线路，在母线出口处设有4条出线，具体线路的长度如图 7所示，系统采用过补偿10%，系统阻抗为(7.55×10^-4+j0.360 7) Ω。架空线模型参考文献[25]中的架空线电气参数，具体参数如下。线路正序参数为：r₁=0.17 Ω/km，x₁=0.35 Ω/km，c₁=0.12 μF/km。零序参数为：r₀=0.32 Ω/km，x₀=1.12 Ω/km，c₀=6.4×10^－3 μF/km。电缆线路正序参数为：r₁=0.27 Ω/km，x₁=0.08 Ω/km，c₁=0.376 μF/km。零序参数为：r₀=2.7 Ω/km，x₀=0.35 Ω/km，c₀=0.276 μF/km。假设线路L₃发生B相接地故障，L₄发生C相接地故障。

3.1 不同故障位置的仿真结果

为验证故障发生在线路不同位置时选线方法的准确性，在低阻R_f1=R_f2=10 Ω和高阻R_f1=R_f2=1 000 Ω时，设故障分别发生在线路首端、线路中间以及线路末端。根据仿真得到的结果，上述各种情况下零序电流最小的线路均为L₁，故以此线为参考线路，用所有线路的零序导纳幅值比上该线路的零序导纳幅值，结合故障选线判据，最终得到的故障选线结果如表 1和表 2所示。

根据表 1和表 2选线结果可以看到，母线零序电压大于故障启动整定值，故障选线装置能够启动，而且无论故障发生在2条线路的哪个位置，故障线路与参考线路的零序导纳的幅值比大于非故障线路与参考线路的零序导纳幅值比，满足故障选线判据，都能够准确选出故障线路，故障选线结果不受故障位置的影响。

3.2 不同过渡电阻的仿真结果

为验证在不同过渡电阻时故障选线方法的准确性，当故障发生在线路中间时，分别设置不同的过渡电阻进行仿真。根据仿真结果，各情形下零序电流最小的线路仍为L₁，故以此线为参考线路，得到的选线结果如表 3所示。根据表 3结果，母线零序电压大于故障启动整定值，在不同过渡电阻影响下，故障线路与非故障线路的差异仍然明显，在1 000 Ω高阻时也可以判断出故障线路，具有一定的耐受过渡电阻能力。

3.3 消弧线圈补偿度不同时的仿真结果

消弧线圈的补偿度对母线电压以及各线路零序电流都有影响，为验证在不同补偿状态下是否能选出故障线路，设线路L₁发生B相接地故障，L₄发生C相接地故障，故障发生在线路中间，过渡电阻R_f1=R_f2=100 Ω时，设置消弧线圈在过补偿、完全补偿以及欠补偿3种状态进行仿真验证，仿真得到各情形下零序电流最小的线路为L₂，v为消弧线圈脱谐度，得到的选线结果如表 4所示。

根据表 4结果，在消弧线圈处于不同的补偿状态时，选线装置均能够启动，故障选线结果准确，因此文中方法在消弧线圈处于不同运行状态下仍有很好的适应性。

3.4 母线出线数量的影响

在实际电网中对于10 kV配电网存在10条以上的出线，为了验证母线出线数量对仿真结果的影响，在图 7母线中再引出一定数量的架空-电缆混合线路，多出的线路参数按照线路L₂进行设置，则K_m2的结果可反应其余线路的情况。对故障发生在线路中间，过度电阻均为20 Ω的情况进行仿真，得到的仿真结果如表 5所示。

根据表 5结果可知，母线的出线数量对于故障选线的结果并无影响，故障线路与非故障线路的零序导纳幅值之间存在明显差异，在出线数量较多的情况下仍能选出故障线路。

4 结语

文中通过对10 kV消弧线圈接地系统发生同母两回线异相接地复故障进行分析，发现故障线路零序导纳幅值比非故障线路的零序导纳幅值大得多，即使在1 000 Ω的高阻情况下也能达到非故障线路的2倍以上，进而提出基于零序导纳幅值比的故障选线方法。该方法利用线路首端的零序电流与母线零序电压之比得到零序导纳，通过各线路与参考线路的零序导纳幅值比选出故障线路，解决了同母两回线异相接地复故障难以选出所有故障线路的问题。PSCAD仿真结果表明，文中方法不受故障位置、消弧线圈补偿度的影响，能够耐受1 000 Ω过渡电阻，此外只需要单端信息，通信量小。

致谢

本文得到广州供电局有限公司科技项目(GZHKJXM20200081)资助，谨此致谢！