文章编号: 2096-3203(2024)04-0077-11 中图分类号: TM76
2. 国网江苏省电力有限公司, 江苏 南京 210024
对电力系统进行可靠性评估时[1-3],由于输电网与配电网两者电压等级间的差异,通常将其视作2个独立系统进行可靠性分析[4-7]。可采用故障枚举法对输电网与配电网进行可靠性评估[8],即通过枚举可能发生的故障场景,计算该场景对应的停电时间、频次及供电量缺额等指标,再结合故障场景发生概率,计算输电网与配电网的可靠性指标[9]。
若将输电网与配电网视作2个独立系统进行可靠性评估,在输电网可靠性分析中,与其相连的配电网被等效为节点负荷;在配电网可靠性分析中,输电网则被简化描述为配电网接入点处可靠运行的电源节点[10]。采用这2种简化假设是为了仅针对所研究系统进行可靠性分析。考虑到输配电网络在电力系统运行过程中的紧密联系,有必要将其视作一个整体进行可靠性评估[11],此时若仍沿用前述简化会降低可靠性评估结果精度。因此,需要在现有可靠性评估方法的基础上进行改进,进一步计及输电网与配电网在运行可靠性方面的交互影响,构建输配电网络整体可靠性评估模型,以获得更接近实际运行工况的可靠性评估结果。
考虑输配电网络整体,由于输电网与配电网运行状态间存在关联,输电网内部发生故障会影响配电网运行可靠性。对于输电网而言,机组与线路故障会导致节点功率与网架结构参数变化。在此过程中若出现系统潮流安全约束越限则需要进行负荷减载[12],以最小化输电网整体减载量为目标对系统潮流进行优化[13],确定输电网各负荷节点的减载量[14]。对于输配电系统而言,输电网节点的负荷减载量由下属配电网响应减载所断开的配电网节点负荷决定。配电网确定负荷切除方案时不仅要考虑整体减载量的大小,还要考虑不同电力用户中断供电的成本[15],因而输配电网络中输电网故障后的负荷减载量须细化为配电网实际可提供的响应[16]。
对于配电网而言,灵活可控的运行方式有助于为输电网负荷减载提供其所需的切负荷量。柔性互联配电网是一种新兴的配电网架构方式,应用具备功率控制能力的智能软开关(soft open point,SOP)[17]后,其具备更强的供电架构调整能力,可用于促进微网新能源发电的消纳[18]。另一方面,柔性互联配电网可将配电网传统联络开关替换为SOP,SOP具备的电压支撑能力可避免负荷大规模转供场景下的馈线末端节点电压过低情况[19-20],因而柔性互联配电网可为响应输电网负荷减载提供更为灵活的负荷切除方案。对于配电网而言,为响应输电网减载所造成的负荷损失[21],在考虑输配电网络整体时,其应当被视作影响配电网运行可靠性的外部因素纳入配电网可靠性评估模型中。
与之相对应的,将输配电网络作为一个整体进行可靠性评估时,同样需要考虑配电网故障导致的负荷损失对输电网运行可靠性的影响[22]。由配电网故障导致的负荷损失应体现在其与输电网相连接节点的供电不足指标中。对于柔性互联配电网而言,其内部SOP装置可增强配电网故障重构能力[23],通过负荷转供使部分受影响负荷节点在故障隔离后可经由重构后的配电网结构恢复供电[24]。因而在计算配电网故障引起的负荷损失时,须对此类短时供电中断的负荷单独加以考虑。此外,若配电网故障造成大量负荷损失,可能会触发输电网潮流安全约束,导致输电网内部节点负荷减载,因而在输电网可靠性评估中须计及配电网故障的影响。
文中对输电网与柔性互联配电网在应对各自内部故障时,通过输电网与配电网相连接节点作用的交互影响进行了细化考虑,构建了面向输配电网络整体的可靠性评估模型。在对输电网进行可靠性评估时,将输电网故障后的节点负荷减载细化为配电网优化后的负荷切除方案,并将应对输电网故障导致的配电网负荷损失纳入配电网可靠性评估中。对配电网进行可靠性评估时,在考虑配电网故障造成的配电网负荷损失的基础上,进一步考虑配电网故障在与之相连的输电网节点处造成的供电不足,并评估其对输电网运行可靠性的影响。在现有输电网与配电网可靠性评估的指标体系基础上[25-26],采用故障枚举法,对现有可靠性指标计算方式进行修正,构建了面向输配电网络整体的可靠性指标解析计算方法。基于可靠性测试系统进行算例分析,验证了文中方法的有效性。
1 输电网与配电网独立可靠性评估方法 1.1 输电网独立可靠性评估方法当采用故障枚举法单独评估输电网可靠性时,需要计算所枚举故障状态下的输电网潮流,判断节点电压、线路潮流、机组出力等参数是否发生越限。若发生越限则须基于潮流优化进行发电再调度,其优化目标为最小化输电网有功负荷削减量,具体数学模型如式(1)所示,约束条件包括:节点减载量大小约束、节点功率平衡约束以及线路容量约束。
| $ \left\{\begin{array}{l} \min \sum\limits_{i \in I} \Delta P_{\mathrm{L}, i} \\ \text { s.t. } 0 \leqslant \Delta P_{\mathrm{L}, i} \leqslant \Delta P_{\mathrm{L}, i}^{\max } \\ \quad 0 \leqslant \Delta Q_{\mathrm{L}, i} \leqslant \Delta Q_{\mathrm{L}, i}^{\max } \\ \Delta P_{\mathrm{L}, i}=P_{\mathrm{L}, i}-P_{\mathrm{G}, i}+ \\ \quad V_{i} \sum\limits_{j \in J} V_{j}\left(G_{i, j} \cos \theta_{i, j}+B_{i, j} \sin \theta_{i, j}\right) \\ \Delta Q_{\mathrm{L}, i}=Q_{\mathrm{L}, i}-Q_{\mathrm{G}, i}+ \\ \quad V_{i} \sum\limits_{j \in J} V_{j}\left(G_{i, j} \sin \theta_{i, j}-B_{i, j} \cos \theta_{i, j}\right) \\ S_{i, j} \leqslant S_{i, j}^{\max } \end{array}\right. $ | (1) |
式中:I、J分别为输电网负荷节点与输电网全部节点的集合;ΔPL, i、ΔQL, i分别为负荷节点i的有功与无功负荷减载量;ΔPL, imax、ΔQL, imax分别为负荷节点i的有功与无功负荷减载量的最大允许值;PL, i、QL, i分别为负荷节点i的有功与无功负荷大小;PG, i、QG, i分别为负荷节点i连接的发电机组的有功与无功出力;Vi、Vj分别为节点i、j的电压幅值;Gi, j、Bi, j分别为输电网节点导纳矩阵第i行第j列元素的实部与虚部;θi, j为节点i和节点j之间的相角差;Si, j、Si, jmax分别为连接节点i与节点j线路上的视在功率大小及其最大允许值。
结合所枚举故障状态的发生概率与发电再调度方案对应的负荷减载量,可计算得到输电网的各项可靠性指标。
1.2 柔性互联配电网独立可靠性评估方法类似地,采用故障枚举法对柔性互联配电网进行可靠性评估。首先枚举配电网故障场景,然后分析故障影响范围,最后综合全部故障场景计算得到单个用户负荷节点与配电网整体供电可靠性指标。
对于柔性互联配电网而言,其内部的SOP设备可在配电网内部元件发生故障时,使部分在故障初始时刻断开的负荷通过故障重构的方式恢复供电。受故障影响的负荷可分为短时供电中断负荷(对应为实现故障重构,柔性互联配电网相关执行机构动作所需的操作时间tr)与长时供电中断负荷(对应故障元件的修复时间tf)。
为充分利用SOP的故障负荷转供能力以最小化长时供电中断负荷,当SOP参与配电网故障重构时,其采用最大无功输出的运行方式以尽可能抬升馈线末端的电压大小,从而最大化故障负荷转供范围。SOP无功出力计算如式(2)所示,将其无功输出作为已知条件进行故障后配电网潮流计算。
| $ \begin{equation*} Q_{\mathrm{SOP}}=\sqrt{S_{\mathrm{Sop}}^{2}-\left(P_{\mathrm{L}, \mathrm{pre}}-P_{\mathrm{L}, \mathrm{pos}}\right)^{2}} \end{equation*} $ | (2) |
式中:QSOP为SOP向进行负荷转供的馈线输出的无功功率;SSOP为SOP的额定容量;PL, pre为故障重构前配电网的失负荷量,即短时与长时供电中断负荷之和;PL, pos为故障重构后的配电网失负荷量,即长时供电中断负荷;PL, pre-PL, pos对应的是转供的有功负荷大小。
2 计及输配电网络交互影响的可靠性评估文中在现有输电网与柔性互联配电网独立的可靠性评估方法基础上,计及故障场景下输电网与配电网间的交互影响,构建如图 1所示的可靠性评估模型。图中红色箭头表示的是输电网内部故障对配电网的影响,蓝色箭头表示的是配电网内部故障对输电网的影响。基于图 1所示的输配电网络整体可靠性评估模型,将模型中各个环节的具体实施方法进一步细化描述。

|
图 1 计及输电网与柔性互联配电网交互影响的可靠性评估模型 Fig. 1 Reliability evaluation model considering interaction between transmission network and flexible interconnected distribution network |
在输电网故障场景下,若输电网故障后潮流发生安全约束越限的情况,须对输电网节点负荷进行减载以保障输电网安全运行。对于输电网与柔性互联配电网组成的整体而言,输电网节点负荷减载是通过切除相连柔性互联配电网内部部分负荷实现的,因而实际减载量由配电网内部切除负荷的具体开关操作决定。须分析不同开关操作下配电网可提供的实际减载量,作为输电网发电再调度依据。
考虑到配电网内部开关元件众多,仅选取配电网各条主馈线上的开关作为可操作对象进行分析。当枚举所有可行的开关操作时,直接对所有开关进行排列组合的运算量极大,会显著增加可靠性评估方法的运算负担。通过采用基于开关连接关系的操作枚举法,可避免等效开关操作的多次枚举,提升可靠性评估方法的运算效率。
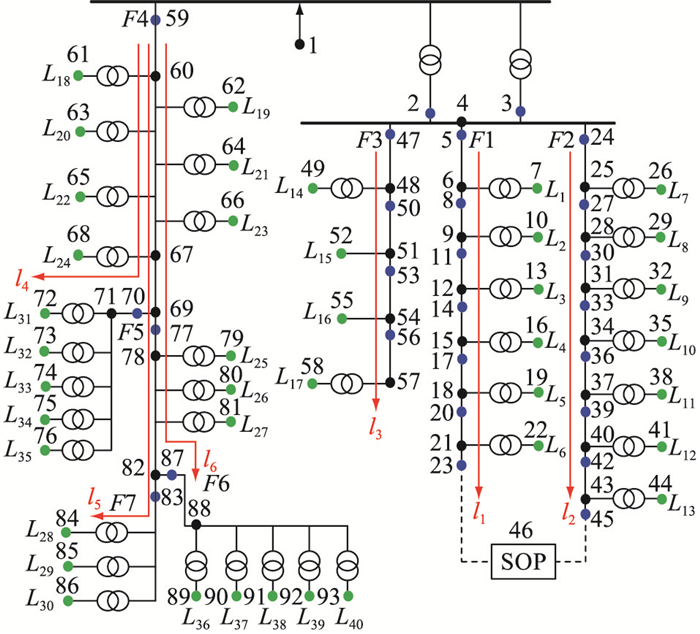
以图 2所示RBTS测试系统中节点6所连接的配电网系统为例,基于开关间的连接关系,可将配电网中所有主馈线上的开关形成开关线路(l1—l6),l1—l6箭头方向代表配电网馈线上由电源节点至负荷节点的供电方向,列出每条开关线路上的开关节点(图中蓝色点)。由于每条开关线路上断开多个开关与断开最上游的开关是等效的,所以对于配电网开关操作的枚举可先枚举开关线路组合,再枚举各开关线路上断开的单个开关,以避免大量等效开关操作的重复枚举。
|
图 2 RBTS-Bus 6连接的柔性互联配电网结构 Fig. 2 Configuration of flexible interconnected distribution network connected to Bus 6 of RBTS |
对于柔性互联配电网,还需要考虑其中SOP开关(图 2节点46处)所具备的配电网故障重构能力。若在某枚举开关操作下,2条经SOP连接的馈线中有且仅有1条馈线有开关断开,此时SOP可通过负荷转供为有开关断开的馈线末端部分负荷恢复供电,柔性互联配电网中该馈线的切负荷量即为开关下游的负荷总量减去经SOP转供的负荷量。
2.2 考虑中断成本的配电网负荷切除方案优化输电网故障后的发电再调度是以切除有功负荷最小为目标。细化至配电网内部,实际负荷减载的成本与减载量大小相关,且配电网中不同负荷类型单位缺电量的经济价值也存在差异。从配电网层面考虑,须将输电网发电再调度目标由最小化有功负荷切除量转换为最小化配电网负荷中断供电成本,确保输电网发电再调度方案的经济性。
将输电网故障后的负荷减载细化描述为配电网开关操作对应的负荷切除量,以最小化配电网负荷中断供电成本为目标,输电网发电再调度的目标函数调整为式(3),并相对应地修改式(1)中的节点有功与无功减载量约束,参见式(3)中的约束条件。
| $ \begin{cases}\min & \sum\limits_{i \in I} C\left(\Delta P_{\mathrm{L}, i}\left(M_{i}\right)\right)=\min \sum\limits_{i \in I} \sum\limits_{p=1}^{q} c_{p} \Delta P_{\mathrm{L}, i, p}\left(M_{i}\right) \\ \text { s.t. } & 0 \leqslant \Delta P_{\mathrm{L}, i}=\sum\limits_{n=1}^{k} P_{\mathrm{L}}^{M_{i, n}}-\Delta P_{\mathrm{SOP}} \leqslant \Delta P_{\mathrm{L}, i}^{\max } \\ & 0 \leqslant \Delta Q_{\mathrm{L}, i}=\sum\limits_{n=1}^{k} Q_{\mathrm{L}}^{M_{i, n}}-\Delta Q_{\mathrm{SOP}} \leqslant \Delta Q_{\mathrm{L}, i}^{\max }\end{cases} $ | (3) |
式中:C为配电网负荷中断供电的成本;Mi 为输电网节点i负荷减载时,节点i连接配电网中断开开关编号的集合,其可行范围为配电网所有开关操作组合;q为节点i连接配电网中的用户种类数;cp为第p类用户的单位停电损失;ΔPL, i, p为节点i减载负荷中第p类用户的负荷总量;k为配电网断开开关的数量;PLMi, n、QLMi, n分别为第n个断开开关所属馈线中位于断开开关下游的有功负荷与无功负荷各自的总和;ΔPSOP、ΔQSOP分别为柔性互联配电网中经SOP转供的有功负荷与无功负荷各自的总和。
计及配电网在输电网故障减载场景下的细化响应后,无法再将输电网节点减载量视作连续可调节量进行优化模型求解。为提升模型求解效率,首先采用输电网节点负荷连续可调的假设得到优化后的理想最优负荷减载量,然后基于式(4)筛选出使输电网负荷减载量在其理想最优值附近的配电网开关操作,在此范围内对配电网负荷切除方案进行进一步优化选取。
| $ \left\{\begin{array}{l} \left|\Delta P_{\mathrm{L}}(M)-\Delta P_{\mathrm{L}}\right| \leqslant m\left|\Delta P_{\mathrm{L}}\right| \\ \left|\Delta Q_{\mathrm{L}}(M)-\Delta Q_{\mathrm{L}}\right| \leqslant m\left|\Delta Q_{\mathrm{L}}\right| \end{array}\right. $ | (4) |
式中:m为与配电网开关操作筛选范围相关的系数,文中m取值为0.1。考虑到配电网开关操作的目的还是在于响应输电网的负荷减载,所以m取值不宜过大。在无法筛选得到可行的配电网开关操作场景下,可适当增大m以保证配电网负荷优化切除方案存在可行解。
在输电网故障减载场景下,考虑配电网可提供的实际响应,以最小化配电网负荷中断供电成本为目标,得到输电网节点负荷减载的优化方案,其流程具体如图 3所示。该方案可得到既考虑输电网潮流约束,又考虑输电网节点下属配电网负荷切除能力与负荷中断供电成本的输电网发电再调度方案。

|
图 3 计及配电网细化切负荷方案的输电网减载方案优化 Fig. 3 Optimization of load shedding scheme of transmission network considering detailed load cutting scheme of distribution network |
将输配电网络作为整体进行可靠性评估时,配电网可靠性分析要在计及内部故障的基础上,额外考虑为响应输电网故障减载对应切除的配电网负荷。对于特定的输电网枚举故障状态y(y为输电网枚举故障状态下的故障元件集合),首先计算该故障状态对应的可靠性指标:失负荷频率(loss of load frequency,LOLF)指标ILOLF, y与失负荷期望(loss of load expectation,LOLE)指标ILOLE, y[27]。若该故障条件下配电网内部负荷节点b被切除,则设Fb(y)=1,否则Fb(y)=0;基于式(5)修正节点b的可靠性指标(故障率λ与停运时间U),其修正量分别表示为:
| $ \left\{\begin{array}{l} \Delta \lambda_{b}=\sum\limits_{y \in Y} F_{b}(y) I_{\mathrm{LOLF}, y} \\ \Delta U_{b}=\sum\limits_{y \in Y} F_{b}(y) I_{\mathrm{LOLE}, y} \end{array}\right. $ | (5) |
式中:Y为输电网所有枚举故障状态的集合。
在此基础上可进一步修正配电网整体可靠性指标,例如系统平均停电频率指标(system average interruption frequency index,SAIFI)ISAIFI与电量不足(energy not supplied,ENS)IENS等指标[28]。
2.4 计及配电网故障的输电网可靠性指标修正配电网内部元件故障通常会导致配电网部分负荷被切除,从而在作为配电网电源节点的输电网节点处产生负荷损失,须在输电网供电可靠性评估中计及该负荷损失。此外,在配电网内部离电源节点较近的元件发生故障导致配电网负荷大量切除的场景下,须进一步评估配电网与输电网连接节点处的大幅度负荷波动对输电网潮流的影响。若其会导致输电网潮流安全约束越限,则须进一步基于发电再调度方案确定输电网的负荷节点减载,此过程中输电网与配电网间的交互影响如图 4所示。

|
图 4 配电网故障导致输电网节点负荷损失影响的评估 Fig. 4 Impact evaluation of load loss at transmission network nodes caused by distribution network failures |
将输配电网络作为整体进行可靠性评估时,输电网的可靠性分析要在计及内部故障的基础上额外考虑配电网故障导致的输电网节点负荷损失,对输电网可靠性指标进行修正。
设枚举得到的某一配电网故障场景为x(x为配电网枚举故障场景对应的故障元件集合),该故障场景的故障率、故障修复时间与配电网故障重构时间分别为λx、tf, x与tr, x,故障重构前后配电网的中断负荷量分别为PL, pre(x)与PL, pos(x)。基于式(6)—式(9)得到输电网LOLF指标ILOLF、LOLE指标ILOLE以及电量不足期望(expected energy not supplied,EENS)指标IEENS的修正量。
| $ \Delta I_{\mathrm{LOLF}}=\sum\limits_{x \in X} \lambda_{x} $ | (6) |
| $ \Delta I_{\mathrm{LOLE}}=\sum\limits_{x \in X}\left[F(x) t_{\mathrm{r}, x}+\left(1-F(x) t_{\mathrm{f}, x}\right)\right] $ | (7) |
| $ \Delta I_{\mathrm{EENS}}=\sum\limits_{x \in X}\left\{F(x) P_{\mathrm{L}, \mathrm{pre}}(x) t_{\mathrm{r}, x}+(1-F(x)) \times\right. \\ \left.\left[P_{\mathrm{L}, \mathrm{pos}}(x)\left(t_{\mathrm{f}, x}-t_{\mathrm{r}, x}\right)+P_{\mathrm{L}, \mathrm{pre}}(x) t_{\mathrm{r}, x}\right]\right\} $ | (8) |
| $ \begin{gather*} F(x)= \begin{cases}1 & P_{\mathrm{L}, \mathrm{pos}}(x)=0 \\ 0 & P_{\mathrm{L}, \mathrm{pos}}(x)>0\end{cases} \end{gather*} $ | (9) |
式中:X为配电网所有枚举故障状态的集合。
3 算例分析为验证文中可靠性评估方法的有效性,构建输配电网络整体可靠性测试系统进行算例分析,输电网结构采用IEEE RTS 24节点可靠性测试系统,其可靠性参数参见文献[29]。柔性互联配电网测试系统选取RBTS-Bus 3、Bus 5与Bus 6系统,其结构与可靠性参数参见文献[30],配电网系统中的联络开关替换为SOP。IEEE RTS 24节点测试系统中节点10、13、14、15、18、19、20连接的配电网采用RBTS-Bus 3结构;节点3、5、7、8、9连接的配电网采用RBTS-Bus 5结构;节点1、2、4、6、16连接的配电网采用RBTS-Bus 6结构;配电网负荷大小进行等比例缩放以适配输电网负荷参数,各类型负荷用户中断供电成本设定值参见文献[31],负荷用户类型参照RBTS测试系统设定。
3.1 配电网响应细化对输电网可靠性评估影响验证输电网故障场景设定为2号节点连接的发电机发生单重故障,该故障场景下基于下述3种方案得到的输电网节点负荷减载对比如表 1所示,输电网节点减载在相连配电网中断开的负荷节点编号对比如表 2所示。
|
|
表 1 3种方案下输电网发电再调度结果 Table 1 Generation re-dispatch results of transmission network with three different schemes |
|
|
表 2 方案2与方案3切除的配电网负荷节点对比 Table 2 Comparison of nodes for load cutting in distribution networks with scheme 2 and scheme 3 |
方案1:设定节点负荷减载量为连续变量,最小化负荷减载量。
方案2:基于所连接配电网具体结构确定节点负荷减载量,最小化负荷减载量。
方案3:基于所连接配电网具体结构确定节点负荷减载量,最小化负荷中断供电成本。
由表 1可以看出,当计及配电网具体结构后,得到实际可行的减载方案,其对应的输电网负荷减载量(方案2与方案3)相较采用负荷减载量连续可调假设时(方案1)有所增长。方案3从经济性角度出发确定配电网响应输电网节点减载所断开的负荷,优先保障断电成本较高的负荷节点的供电。由表 2可知,目标由最小化负荷减载量(方案2)转换至最小化负荷中断供电成本(方案3)后,配电网负荷节点的切除方案发生改变。表 1中,虽然方案3在节点负荷减载量方面相较方案2有所增长,但降低了系统的停电成本。
对于输电网,枚举其发电机单重故障G_N-1、发电机双重故障G_N-2、输电线路单重故障L_N-1、输电线路双重故障L_N-2以及输电线路与发电机混合故障L&G的故障场景进行可靠性评估。虽然现有输电网规划方案通常要满足“N-1”安全约束,但在特定运行方式下仍存在单重故障导致输电网负荷减载的场景[32],因此文中对采用的输电网可靠性测试系统进行可靠性评估时仍考虑了单重故障场景[33]。
分别采用方案1与方案3确定输电网故障后的负荷减载量,计算输电网电力不足期望(expected demand not supplied,EDNS)可靠性指标IEDNS与EENS可靠性指标IEENS,结果对比如表 3所示。将输电网故障后节点负荷减载量结合相连配电网结构进行细化描述后,计算得到的IEDNS与IEENS这2个可靠性指标均有明显增长。这表明仅基于输电网进行可靠性评估,将所连接的下级配电网视作连续可调的负荷会得到偏乐观的IEDNS与IEENS计算结果,即低估了输电网故障场景下系统供电量的缺额。
|
|
表 3 方案1与方案3计算得到的IEDNS与IEENS对比 Table 3 Comparison of IEDNS and IEENS calculated based on scheme 1 and scheme 3 |
考虑输电网发生故障后负荷减载导致的配电网切负荷,对配电网可靠性指标进行修正。以IEEE RTS 24节点系统中节点16连接的配电网为例,计及输电网故障影响前后的负荷节点可靠性指标结果对比如表 4所示。
|
|
表 4 计及输电网故障前后的配电网负荷节点可靠性指标 Table 4 Load reliability indices of distribution network before and after considering transmission network fault |
由表 4可知,当计及输电网故障影响后,计算得到的配电网内部负荷节点供电可靠性指标中负荷节点故障率λ与停运时间U都有所增长,其中部分节点(节点1与节点2)由于参与输电网故障负荷减载较多,负荷节点的供电可靠性水平显著降低。这表明仅计及配电网内部元件故障计算得到的可靠性指标计算结果对于需要参与输电网负荷减载的配电网负荷节点而言,结果偏乐观。
基于配电网内部负荷节点的可靠性指标计算结果,可进一步得到配电网整体的可靠性指标。表 5给出了部分配电网在计及输电网故障影响前后的配电网整体可靠性指标计算结果对比。
|
|
表 5 计及输电网故障前后的配电网整体可靠性指标 Table 5 Overall reliability indices of distribution network before and after considering transmission network faults |
如表 5所示,计及与配电网相连的输电网故障影响后,得到的配电网系统平均停电频率ISAIFI与电量不足IENS指标均出现了较大幅度的增长,其中IENS指标增长更为显著。考虑到IENS指标受故障持续时间与故障场景下的负荷损失量两方面因素共同影响,IENS指标较大幅度的增长可归结为以下两方面原因:一是输电网部分元件的维修时间较长,使得故障平均持续时间增长,从而导致IENS的增加;二是输电网容量较配电网大,其负荷减载量大于配电网内部故障引起的负荷损失,且配电网故障的负荷损失还可以通过故障重构的方式进一步减小。这两方面原因使得配电网可靠性评估结果在考虑其响应输电网故障减载后,IENS指标出现了显著的增长,表明在配电网可靠性评估中有必要计及上级输电网故障的影响。
3.3 计及配电网故障影响修正输电网可靠性指标在输配电网络一体化可靠性评估框架下,输电网的供电可靠性评估应当计及相连接配电网内部故障导致的负荷损失。表 6给出了节点6连接配电网内部部分开关故障导致的配电网切负荷量大小。
|
|
表 6 节点6连接配电网内部开关故障导致的切负荷量 Table 6 Load cut yielded by faults of switch within distribution network connected to node 6 |
由表 6可知,依托于柔性互联配电网内SOP等装置提供的负荷转供能力,部分受影响负荷节点在隔离故障后可恢复供电,因而柔性互联配电网内部故障导致的输电网供电不足等指标须对短时供电中断负荷与长时供电中断负荷加以区分。
评估配电网故障对输电网可靠性的影响时,首先分析配电网故障引起的配电网长时供电中断负荷,将配电网所连接输电网节点的节点负荷减去配电网负荷损失,重新进行输电网潮流计算。若输电网潮流满足其安全约束,配电网故障仅引起相连输电网节点处的负荷损失;若输电网潮流发生安全约束越限,此时须进行发电再调度,输电网其他负荷节点也会产生负荷损失。在配电网内部节点59处开关元件的故障场景下,配电网负荷的损失作用于输电网后会导致其潮流安全约束越限,需要进行减载的节点及其负荷减载量如表 7所示,此类负荷减载需要被纳入输电网可靠性指标统计中。表 8给出了计及配电网故障影响前后的输电网可靠性指标计算结果对比,其中ILOLD指标为失负荷平均持续时间(loss of load duration,LOLD),计算表达式为:
| $ \begin{equation*} I_{\text {LOLD }}=I_{\text {LOLE }} / I_{\mathrm{LOLF}} \end{equation*} $ | (10) |
|
|
表 7 配电网故障导致的输电网负荷节点减载量 Table 7 Load cut at load nodes of transmission network caused by fault occurring within distribution network |
|
|
表 8 计及配电网故障前后的输电网可靠性指标 Table 8 Reliability indices of transmission network be- fore and after considering fault of distribution network |
由表 8可以看出,当计及配电网故障对输电网供电可靠性的影响后,其失负荷期望ILOLE、失负荷频率ILOLF、以及电量不足期望IEENS等指标都有所上升,表明忽略配电网故障影响会得到偏乐观的输电网可靠性评估结果。相较输电网,柔性互联配电网的故障隔离与供电恢复能力更强,故计及配电网影响后得到的输电网失负荷平均持续时间ILOLD指标有所下降。通过将配电网故障对输电网的影响纳入其可靠性指标计算中,可得到更贴近输配电网络整体运行实际的可靠性评估结果。
3.4 配电网分布式电源(DG)故障对输配电网络可靠性影响考虑柔性互联配电网内部含分布式电源(distributed generation,DG)接入的情况,对该条件下配电网故障对输电网可靠性的影响进行评估。输电网测试系统中节点1、2、4、6、16连接的配电网采用RBTS-Bus 6结构,在图 2所示的RBTS-Bus 6配电网中将节点15与节点31处分别接入DG,其各自容量均设定为馈线l1与l2所连接负载总量的10%,DG的故障率设定为2次/a,修复时间设定为48 h。考虑到DG的接入,配电网上级的输电网节点负荷对应减去DG的容量。基于调整后的测试系统,采用文中输配电网络整体可靠性评估方法,计算柔性互联配电网内部接入DG后的输配电系统可靠性,DG接入前后的输电网可靠性指标与配电网可靠性指标对比分别如表 9、表 10所示。
|
|
表 9 配电网接入DG前后的输电网可靠性指标 Table 9 Reliability indices of transmission network be- fore and after integrating DG to distribution network |
|
|
表 10 配电网接入DG前后的配电网可靠性指标 Table 10 Reliability indices of distribution network be- fore and after integrating DG to distribution network |
由表 10中数据可以看出,柔性互联配电网接入DG后,DG自身的故障会成为配电网新的故障来源,所以表现为配电网故障频率的ISAIFI指标相较接入DG前有所增长。但另一方面,DG可通过与柔性互联配电网中的SOP互相配合,增强配电网故障后的负荷转供能力,因而表现为配电网故障后负荷损失的IENS指标则有所减小。接入DG对配电网可靠性的影响同样体现在表 9所示的计及配电网故障影响的输电网可靠性指标中。由表 9可知,由于DG的接入增加了配电网的故障频率,计及配电网故障影响的输电网ILOLE、ILOLF以及ILOLD可靠性指标均有一定程度的增长,但考虑到DG接入起到的减少配电网负荷损失的作用,输电网可靠性指标IEENS有所降低。
4 结论文中以包含输电网与柔性互联配电网的输配电网络整体可靠性评估方法为研究对象,在现有输电网与配电网仅计及自身内部元件故障的可靠性评估方法基础上,量化故障场景下输配电网络间的交互影响,基于输配电网络各自的可靠性指标体系对可靠性参数进行修正,实现面向输电网与柔性互联配电网整体的可靠性评估。基于测试系统算例分析的计算结果,得到以下结论:
(1) 将输电网故障后节点负荷的减载量不视作连续可调变量,而是基于下属配电网具体结构并考虑切负荷成本确定输电网减载量,可避免得到偏乐观的输电网可靠性评估结果。
(2) 对于输配电网络整体,配电网供电可靠性除受内部元件故障影响外,为响应输电网负荷减载而进行的配电网负荷切除会导致配电网供电可靠性发生较大幅度的下降。
(3) 配电网内部故障导致的负荷损失一方面会导致输电网供电缺额的增加;另一方面在配电网负荷大量切除的场景下,输电网会发生潮流安全约束越限,进而导致输电网内部除配电网接入点以外的其他负荷节点同样需要进行负荷减载。
致谢
本文得到国网江苏省电力有限公司科技项目“配网高效紧凑柔性互联关键技术研究”(J2022083)资助,谨此致谢!
| [1] |
蒋玮, 王铭华, 陈锦铭, 等. 基于Neo4j图数据库的配电网供电可靠性计算[J]. 电力系统自动化, 2022, 46(15): 104-111. JIANG Wei, WANG Minghua, CHEN Jinming, et al. Calculation of power supply reliability for distribution network based on Neo4j graph database[J]. Automation of Electric Power Systems, 2022, 46(15): 104-111. (  0) 0) |
| [2] |
杨庆, 朱道华. 智能变电站二次系统失效风险评估方法[J]. 电力工程技术, 2022, 41(2): 179-185. YANG Qing, ZHU Daohua. The equipment failure assessment on the secondary system in smart substation[J]. Electric Power Engineering Technology, 2022, 41(2): 179-185. (  0) 0) |
| [3] |
张宸滔, 郑永康, 卢继平, 等. 基于图神经网络的智能变电站二次回路故障定位研究[J]. 电力系统保护与控制, 2022, 50(11): 81-90. ZHANG Chentao, ZHENG Yongkang, LU Jiping, et al. Fault location of secondary circuits in a smart substation based on a graph neural network[J]. Power System Protection and Control, 2022, 50(11): 81-90. (  0) 0) |
| [4] |
LEI Y K, SUN Y G, HOU K, et al. Impact increment based hybrid reliability assessment method for transmission systems[J]. CSEE Journal of Power and Energy Systems, 2022, 8(1): 317-328. (  0) 0) |
| [5] |
王梦帆, 郑建勇, 梅飞. 基于组合赋权和改进灰色关联分析的配电网可靠性影响因素研究[J]. 电气工程学报, 2022, 17(1): 41-48. WANG Mengfan, ZHENG Jianyong, MEI Fei. Research on influencing factors of distribution network reliability based on combination empowerment and improved grey correlation analysis[J]. Journal of Electrical Engineering, 2022, 17(1): 41-48. (  0) 0) |
| [6] |
ZHANG B, JIA M, CHEN C, et al. Wind farm active power dispatching algorithm based on Grey incidence[J]. Global Energy Interconnection, 2023, 6(2): 175-183. DOI:10.1016/j.gloei.2023.04.005 (  0) 0) |
| [7] |
叶宇鑫, 李更丰, 别朝红, 等. 考虑智能软开关的有源配电网恢复力评估与提升[J]. 全球能源互联网, 2022, 5(3): 205-214. YE Yuxin, LI Gengfeng, BIE Zhaohong, et al. Resilience assessment and improvement of active distribution networks considering soft open point[J]. Journal of Global Energy Interconnection, 2022, 5(3): 205-214. (  0) 0) |
| [8] |
项波, 吴承骏, 胡伟楠, 等. 综合考虑检修策略和设备健康指数的配电网可靠性评估[J]. 重庆大学学报, 2021, 44(8): 10-20. XIANG Bo, WU Chengjun, HU Weinan, et al. Reliability evaluation of distribution networks considering maintenance strategies and equipment health indexes[J]. Journal of Chongqing University, 2021, 44(8): 10-20. (  0) 0) |
| [9] |
李生虎, 张楠, 张浩. 考虑风电出力状态转移和直流线路功率调整的AC/UHVDC系统静态可靠性及其灵敏度评估[J]. 电网技术, 2021, 45(6): 2342-2351. LI Shenghu, ZHANG Nan, ZHANG Hao. AC/UHVDC system reliability and sensitivity evaluation considering state transition of wind power and power adjustment of UHVDC[J]. Power System Technology, 2021, 45(6): 2342-2351. (  0) 0) |
| [10] |
郭雨涵, 蒋雪冬, 黄道姗, 等. 基于多目标蒙特卡洛法的全电压序列一体化电网可靠性评估[J]. 电网技术, 2016, 40(9): 2866-2870. GUO Yuhan, JIANG Xuedong, HUANG Daoshan, et al. Reliability evaluation of whole voltage level integrated power grid based on multi-objective Monte-Carlo method[J]. Power System Technology, 2016, 40(9): 2866-2870. (  0) 0) |
| [11] |
陈碧云, 陈千懿, 周恒旺. 电力系统输配电可靠性的快速协同评估方法[J]. 电力系统及其自动化学报, 2018, 30(11): 101-106. CHEN Biyun, CHEN Qianyi, ZHOU Hengwang. Rapid integrated evaluation method for transmission and distribution reliability of power system[J]. Proceedings of the CSU-EPSA, 2018, 30(11): 101-106. (  0) 0) |
| [12] |
秦砺寒, 陈丹, 李顺昕, 等. 面向配电网可靠性评估的输电网等值方法[J]. 电力系统保护与控制, 2016, 44(22): 71-76. QIN Lihan, CHEN Dan, LI Shunxin, et al. An equivalent method of transmission system for distribution network reliability assessment[J]. Power System Protection and Control, 2016, 44(22): 71-76. (  0) 0) |
| [13] |
DONG Z H, HOU K, LIU Z Y, et al. A deep-learning-based optimal energy flow method for reliability assessment of integrated energy systems[J]. IEEE Access, 2022, 10: 91092-91102. DOI:10.1109/ACCESS.2022.3202197 (  0) 0) |
| [14] |
CAO M S, SHAO C Z, HU B, et al. Reliability assessment of integrated energy systems considering emergency dispatch based on dynamic optimal energy flow[J]. IEEE Transactions on Sustainable Energy, 2022, 13(1): 290-301. DOI:10.1109/TSTE.2021.3109468 (  0) 0) |
| [15] |
汤奕, 孙大松, 周毅, 等. 含分布式电源的主配一体化电网日前-实时协调风险调度方法研究[J]. 智慧电力, 2020, 48(8): 8-14, 23. TANG Yi, SUN Dasong, ZHOU Yi, et al. Coordinated day-ahead and real-time risk dispatch method for main distribution integrated network containing distributed generation[J]. Smart Power, 2020, 48(8): 8-14, 23. (  0) 0) |
| [16] |
张漫, 王主丁, 张寓涵, 等. 高中压配电网可靠性协调评估中2参数和4N+2M参数等值电源研究[J]. 电网技术, 2018, 42(5): 1534-1540. ZHANG Man, WANG Zhuding, ZHANG Yuhan, et al. Research on 2-parameter and (4N+2M)-parameter equivalent sources for reliability coordination evaluation of HV-MV distribution network[J]. Power System Technology, 2018, 42(5): 1534-1540. (  0) 0) |
| [17] |
余云雯, 袁旭峰, 熊炜, 等. 含多端SOP柔性互联配电网供电恢复方法[J]. 电网与清洁能源, 2021, 37(10): 75-82, 90. YU Yunwen, YUAN Xufeng, XIONG Wei, et al. A power supply restoration method for the flexible interconnected distribution network with multi-terminal soft open point[J]. Power System and Clean Energy, 2021, 37(10): 75-82, 90. (  0) 0) |
| [18] |
JI H R, WANG C S, LI P, et al. Robust operation of soft open points in active distribution networks with high penetration of photovoltaic integration[J]. IEEE Transactions on Sustainable Energy, 2019, 10(1): 280-289. DOI:10.1109/TSTE.2018.2833545 (  0) 0) |
| [19] |
宋毅, 孙充勃, 李鹏, 等. 基于智能软开关的有源配电网供电恢复方法[J]. 中国电机工程学报, 2018, 38(15): 4390-4398, 4639. SONG Yi, SUN Chongbo, LI Peng, et al. SOP based supply restoration method of active distribution networks using soft open point[J]. Proceedings of the CSEE, 2018, 38(15): 4390-4398, 4639. (  0) 0) |
| [20] |
王杰, 王维庆, 王海云, 等. 主动配电网中考虑条件风险价值的智能软开关的规划方法[J]. 电力系统保护与控制, 2022, 50(2): 1-11. WANG Jie, WANG Weiqing, WANG Haiyun, et al. Planning method of soft open point for an active distribution network considering conditional value-at-risk[J]. Power System Protection and Control, 2022, 50(2): 1-11. (  0) 0) |
| [21] |
许鹏程, 陈启, 刘宗歧, 等. 考虑主网与变电站主接线影响的配电网可靠性评估[J]. 现代电力, 2016, 33(6): 46-50. XU Pengcheng, CHEN Qi, LIU Zongqi, et al. Reliability assessment of distribution network considering the influence of transmission system and substations[J]. Modern Electric Power, 2016, 33(6): 46-50. (  0) 0) |
| [22] |
HOU Z F, LIANG Y, ZHANG Y, et al. Security evaluation under N-1 for active distribution networks coordinated with transmission grid[C]//2019 IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia). Chengdu, China. IEEE, 2019: 710-715.
(  0) 0) |
| [23] |
张黎明, 李浩, 吴亚雄, 等. 基于运行优化的含储能电力系统可靠性评估方法[J]. 中国电力, 2022, 55(9): 23-28. ZHANG Liming, LI Hao, WU Yaxiong, et al. A reliability evaluation method for power system with energy storage based on operation optimization[J]. Electric Power, 2022, 55(9): 23-28. (  0) 0) |
| [24] |
解智刚, 韩蓓, 李国杰. 含SOP的配电网多阶段供电恢复优化策略[J]. 电测与仪表, 2022, 59(1): 113-119. XIE Zhigang, HAN Bei, LI Guojie. Multi-stage power supply restoration optimization strategy for distribution network with SOP[J]. Electrical Measurement & Instrumentation, 2022, 59(1): 113-119. (  0) 0) |
| [25] |
白雪岩, 樊艳芳, 刘雨佳, 等. 考虑可靠性及灵活性的风光储虚拟电厂分层容量配置[J]. 电力系统保护与控制, 2022, 50(8): 11-24. BAI Xueyan, FAN Yanfang, LIU Yujia, et al. Wind power storage virtual power plant considering reliability and flexibility tiered capacity configuration[J]. Power System Protection and Control, 2022, 50(8): 11-24. (  0) 0) |
| [26] |
张军六, 王金浩, 常潇, 等. 基于网络等值的直流配用电系统可靠性评估方法研究[J]. 电力工程技术, 2020, 39(5): 107-112. ZHANG Junliu, WANG Jinhao, CHANG Xiao, et al. Reliability evaluation of DC distribution system based on reliability network equivalent[J]. Electric Power Engineering Technology, 2020, 39(5): 107-112. (  0) 0) |
| [27] |
MIAO Y Z, LUO W, LEI W M, et al. Power supply reliability indices computation with consideration of generation systems, transmission systems and sub-transmission systems' load transfer capabilities[C]//2016 IEEE PES Asia-Pacific Power and Energy Engineering Conference, Xi'an, China: 2016: 1840-1844.
(  0) 0) |
| [28] |
张璐, 余顺江, 王辰, 等. 计及VSC运行方式与故障恢复优化的交直流混合配电网可靠性评估[J]. 电网技术, 2022, 46(1): 292-300. ZHANG Lu, YU Shunjiang, WANG Chen, et al. Reliability evaluation of AC/DC hybrid distribution network considering VSC operation mode and fault recovery optimization[J]. Power System Technology, 2022, 46(1): 292-300. (  0) 0) |
| [29] |
SUBCOMMITTEE P M. IEEE reliability test system[J]. IEEE Transactions on Power Apparatus and Systems, 1979, PAS-98(6): 2047-2054. DOI:10.1109/TPAS.1979.319398 (  0) 0) |
| [30] |
BILLINTON R, JONNAVITHULA S. A test system for teaching overall power system reliability assessment[J]. IEEE Transactions on Power Systems, 1996, 11(4): 1670-1676. DOI:10.1109/59.544626 (  0) 0) |
| [31] |
周晶晶, 袁越, 李振杰, 等. 计及供电可靠性的配电网节点电价计算方法[J]. 电力系统自动化, 2016, 40(7): 42-48. ZHOU Jingjing, YUAN Yue, LI Zhenjie, et al. Calculation method of nodal price in distribution network considering power supply reliability[J]. Automation of Electric Power Systems, 2016, 40(7): 42-48. (  0) 0) |
| [32] |
石文辉, 别朝红, 王锡凡. 大型电力系统可靠性评估中的马尔可夫链蒙特卡洛方法[J]. 中国电机工程学报, 2008, 28(4): 9-15. SHI Wenhui, BIE Zhaohong, WANG Xifan. Applications of Markov chain Monte Carlo in large-scale system reliability evaluation[J]. Proceedings of the CSEE, 2008, 28(4): 9-15. (  0) 0) |
| [33] |
李莉, 阳东升, 余梦天, 等. 基于改进混合法的电网运行可靠性评估方法研究[J]. 电测与仪表, 2021, 58(10): 74-79. LI Li, YANG Dongsheng, YU Mengtian, et al. Research on reliability assessment method of power grid operation based on improved hybrid method[J]. Electrical Measurement & Instrumentation, 2021, 58(10): 74-79. (  0) 0) |
2. State Grid Jiangsu Electric Power Co., Ltd., Nanjing 210024, China
 2024, Vol. 43
2024, Vol. 43


 史明明(1986),男,博士,研究员级高级工程师,从事电力电子技术、交直流配用电技术相关工作(E-mail:
史明明(1986),男,博士,研究员级高级工程师,从事电力电子技术、交直流配用电技术相关工作(E-mail: