文章编号: 2096-3203(2024)04-0166-11 中图分类号: TM721
2. 南京邮电大学碳中和先进技术研究院, 江苏 南京 210023
随着工业化进程的不断加快,环境和能源等方面面临着越来越大的挑战,提高能源利用率、减少碳排放已经成为解决当前环境和能源问题的最优方法。在提高能源利用率方面,综合能源系统将多种形式的能源整合,可以实现区域内的能源协调互补,为区域内的能源调度提供了灵活性,显著提升了能源利用效率[1-5]。在减少碳排放方面,可再生能源发展十分迅猛,在提供充足可靠能源的前提下大大减少了发电过程的碳排放。但是风电、光伏等清洁能源设备容易受到外界环境的影响,使得其供能产生波动,影响系统的稳定性[6-9]。因此,在享受清洁能源发电的红利时也应考虑其出力不确定性对系统的影响,这是风电、光伏等设备并网时亟需解决的问题。
楼宇级的综合能源系统相比于区域级的综合能源系统,由于其用户形式具有多样性,楼宇系统中的多元负荷更容易受到用户用能规律和天气等因素的影响,具有更强的不确定性,调度问题面临着更大的挑战[10-13]。因此如何系统地分析源荷双侧的不确定性是综合能源系统优化调度需要考虑的重要问题[14-16]。目前的研究通常采用场景分析、鲁棒优化和机会约束规划等方法来处理综合能源系统优化调度问题中的不确定因素。文献[17]构建了基于风电出力极端场景的双层鲁棒优化调度模型,其中外层为日前经济调度主问题,内层为因风电出力不确定性而引起的调控成本子问题,采用列约束生成算法对该模型进行交互迭代求解。文献[18]考虑综合能源系统中风电出力不确定性和需求侧响应,并利用随机优化方法对其进行求解。文献[19]中热电厂配置储热罐,降低低谷期的负荷,从而消纳风电,针对源侧的不确定性,通过多场景调度模型确定储热罐策略。但是上述文献仅将源侧出力不确定性作为唯一的不确定因素来考虑,忽略了用户行为导致的多元负荷不确定性的影响[20-21]。文献[22]采用蒙特卡洛模拟法和场景削减技术生成多个可再生能源出力的典型场景。文献[23]在考虑不确定因素对系统运行的影响的前提下,构建了随机优化模型,得到期望场景下的经济最优解。然而场景分析方法[24-25]获取典型性场景较为繁琐,并且场景削减过程中存在一些极端场景信息丢失的问题。文献[26]应用基于鲁棒优化的调度方法,仅考虑风电和光伏不确定集下的极端场景,但由于极端场景实际发生的概率极低,导致所得结果过于保守,经济性较差。文献[27]采用基于数据驱动的分布鲁棒优化方法处理含不确定性参数的优化问题,引入一系列矩函数描述不确定参数的概率分布信息以构建相应的模糊集,能够在一定程度上提高系统调度决策的经济性能。相比之下,机会约束规划[28-30]允许约束条件在某个置信水平下不成立,不会存在过分保守的问题,也可以满足调度精度的要求,具有较好的适用性。但一般对机会约束不等式的简化近似需要假设随机变量服从特定的分布类型(正态分布),限制了其进一步的应用。
然而上述文献大多未能充分考虑天然气网络在实际运行中的特点以及楼宇用户热负荷需求与温度的关系,对天然气网络和楼宇热负荷建模不够精细,未能详尽刻画不同能源系统和设备之间的耦合关系,从而使调度结果不能满足实际运行要求。
鉴于以上研究工作的局限,文中对天然气网络运行的实际情况进行详细分析,建立了楼宇负荷的热室模型,详细刻画了锅炉、热泵等供热设备与楼宇室内外温度以及居民的舒适度需求之间的复杂关系。相较于传统的区域级综合能源模型,该模型更能真实地反应楼宇综合能源系统内的负荷特性。并且文中充分考虑了源荷双侧不确定性,以系统运行经济性为目标,提出了一种改进的基于机会约束规划的楼宇综合能源系统日前优化调度方法,能够克服机会约束不等式对随机变量概率密度函数(probability density function, PDF)的限制条件,对服从任意分布的不确定参数具有鲁棒性。然后,通过凸松弛技术将非线性模型转化为混合整数二阶锥规划问题,在Python环境中进行建模,利用CPLEX求解器求解,并通过算例验证了所提方法的有效性。
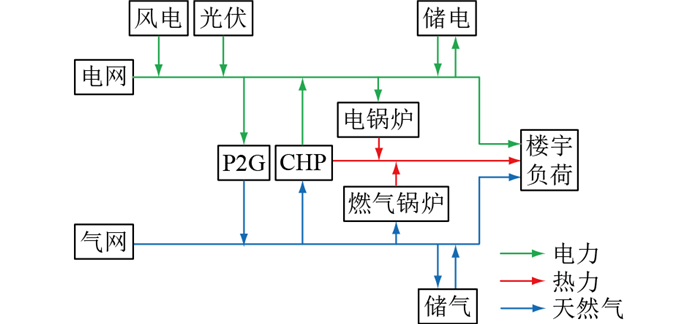
1 综合能源系统基本结构文中研究的综合能源系统负荷形式包括电负荷、热负荷和气负荷,由能量生产单元、能量转换单元和能量消耗单元组成,系统基本结构如图 1所示。
|
图 1 综合能源系统基本结构 Fig. 1 Basic structure of integrated energy system |
其中风力发电单元和光伏发电单元为可再生能源发电装置,分别通过风能和太阳能发电;系统的电能和天然气可以分别在综合能源系统与大电网、大天然气网之间双向交互;电转气(power to gas, P2G)机组通过电解的方式可以实现从电能到天然气的转换;热电联产(combined heat and power, CHP)机组通过天然气发电并收集热能的方式实现从天然气到电能和热能的转换;电锅炉与燃气锅炉可通过消耗电能和天然气产生热能以满足用户的热负荷需求。
2 综合能源系统模型 2.1 电网模型在电力系统模型中,采用最优潮流模型。电力系统的最优潮流模型包括支路电压方程、支路首端功率方程、节点功率平衡方程、节点电压幅值约束、发电机功率约束、线路电流幅值约束,如式(1)—式(6)所示。
| $V_i-V_j=z_{i j} I_{i j}$ | (1) |
| $S_{i j}=V_i I_{i j}^*$ | (2) |
| $\sum\limits_{k \rightarrow i} S_{k i}-\sum\limits_{j \rightarrow k}\left(S_{j k}-z_{j k}\left|I_{j k}\right|^2\right)=S_k$ | (3) |
| $V_{i, \min } \leqslant\left|V_i\right| \leqslant V_{i, \max }$ | (4) |
| $S_{i, \min } \leqslant\left|S_i\right| \leqslant S_{i, \max }$ | (5) |
| $\left|I_{i j}\right| \leqslant I_{i j, \max }$ | (6) |
式中:Vi、Vj分别为节点i和节点j的电压相量;zij为支路阻抗;Iij为支路i-j电流相量;Sij为支路i-j首端功率;Iij*为电流Iij的共轭;Ski为节点k流向节点i的复功率;k→i、j→k分别表示从节点k流入节点i和从节点j流入节点k;Sjk为节点j流向节点k的复功率;zjk为支路j-k阻抗;Ijk为支路j-k电流;Sk为节点k发电机的复功率;Vi, max、Vi, min分别为节点i电压Vi的最大、最小值;Si, max、Si, min分别为节点i的发电机功率Si的最大、最小值;Iij, max为支路电流相量的最大值。
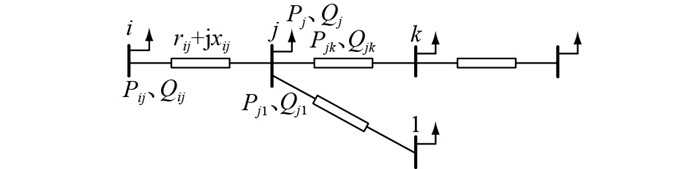
图 2为辐射状配电网示意。图中,Pij、Qij分别为支路i-j首端有功、无功功率;Pjk、Qjk分别为支路j-k首端有功、无功功率;Pj1、Qj1分别为支路1首端有功、无功功率;rij、xij分别为支路i-j电阻、电抗;Pj、Qj分别为节点j的发电机有功、无功功率。
|
图 2 辐射状配电网示意 Fig. 2 Schematic diagram of bradial distribution network |
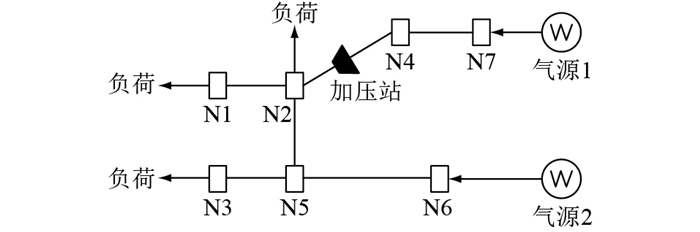
天然气网络系统主要包含气源、输气管道和气负荷等部分。天然气在网络中由气源处供应,通过输气管道配送至气负荷部分,天然气在供应时视为供需平衡的关系,即气源供给量等于用户负荷量。当前主要通过气源、管道流量、节点流量和天然气负荷模型对天然气系统建模。图 3为7节点天然气系统示意,N1—N7为天然气供电站。
|
图 3 7节点天然气系统示意 Fig. 3 Schematic diagram of seven-node natural gas system |
天然气网络中气源主要为气井,气井的天然气供应被建模为相关节点处的正注气,并受其上下边界的限制,t时刻位于节点i的气源的天然气供应量Sg, i, t的约束可表示为:
| $S_{\mathrm{g}, i, \min } \leqslant S_{\mathrm{g}, i, i} \leqslant S_{\mathrm{g}, i, \max }$ | (7) |
式中:Sg, i, min、Sg, i, max分别为节点i气源的天然气供应量的最小、最大值。
文中天然气负荷包括楼宇用户的天然气负荷、CHP机组的天然气负荷和燃气锅炉的天然气负荷,其中CHP机组和燃气锅炉的天然气负荷分别取决于发电量和供热量。由于机组的发电量和供热量存在上下限约束,故机组的天然气消耗量也存在对应的上下限约束:
| $G_{i, \text { gas }, \text { min }}^{\mathrm{L}} \leqslant G_{i, \text { gas }, t}^{\mathrm{L}} \leqslant G_{i, \text { gas }, \text { max }}^{\mathrm{L}}$ | (8) |
式中:Gi, gas, tL为t时刻节点i的消耗天然气机组的耗气量;Gi, gas, minL、Gi, gas, maxL分别为节点i的消耗天然气机组的耗气量的最小、最大值。
2.2.2 管道流量与节点流量天然气管道中的气体流向与管道两端节点的节点压力有关,即从高压节点流向低压节点。而管道流量则与管道特性相关,例如管道的长度、直径、工作温度和两端节点的压差等。管道流量与管道特性及节点压力的关系可由Weymouth方程表示:
| $\left\{\begin{array}{l}F_{i j}=\operatorname{sgn}\left(\pi_i, \pi_j\right) C_{i j} \sqrt{\left|\pi_i^2-\pi_j^2\right|} \\ \operatorname{sgn}\left(\pi_i, \pi_j\right)= \begin{cases}1 & \pi_i>\pi_j \\ 0 & \pi_i=\pi_j \\ -1 & \pi_i<\pi_j\end{cases} \\ \pi_{i, \min } \leqslant \pi_i \leqslant \pi_{i, \max }\end{array}\right.$ | (9) |
式中:Fij为天然气管道的流量;Cij为天然气管道的常数;πi、πj分别为节点i、j的压力;πi, min、πi, max分别为节点i的压力的最小、最大值。
天然气管道的流量与气源供应和负荷消耗有关,在运行中几乎没有损失。与直流潮流中的发电转移因子(generation shift factor,GSF)类似,引入TgasGSF矩阵反映节点气体注入对管道流量的影响[19]。
| $F_{i j}=\sum\limits_{m=1}^{N_{\mathrm{g}}} T_{\mathrm{gas}, m, i j}^{\mathrm{GSF}}\left(S_{\mathrm{g}, m}-G_m^{\mathrm{L}}\right)$ | (10) |
式中:Ng为天然气网络的节点数量;Tgas, m, ijGSF为节点m对管道线路i-j的天然气流量转移因子;Sg, m为节点m气源的天然气供应量;GmL为节点m消耗天然气机组的耗气量。
2.3 楼宇热需求模型居民的热负荷需求是满足居民舒适度要求的一个重要指标,该综合能源系统中楼宇的热负荷主要由消耗电能的电锅炉和消耗天然气的燃气锅炉提供,通过协调电锅炉和燃气锅炉可以使楼宇温度保持在一定的区间内。采用线性化的热室模型模拟室内温度:
| $H_{i, t}^{\mathrm{D}}=\eta_{\mathrm{EB}} P_{i, t}^{\mathrm{EB}}+\eta_{\mathrm{GF}} P_{i, t}^{\mathrm{GF}}$ | (11) |
| $\left\{\begin{array}{l}\left(T_{i, t}^{\mathrm{in}}-T_{i, t-\Delta t}^{\mathrm{in}}\right) / \Delta t=\left(H_{i, t}^{\mathrm{D}}+H_{i, t}^{\mathrm{ext}}+H_{i, t}^{\mathrm{in}, \mathrm{rad}}\right) / C_i^{\mathrm{in}}+ \\ \quad\zeta_i^{\mathrm{is}}\left(T_{i, t}^{\mathrm{sf}}-T_{i, t}^{\mathrm{in}}\right) / C_i^{\mathrm{in}}+\zeta_i^{\mathrm{ie}}\left(T_t^{\mathrm{ext}}-T_{i, t}^{\mathrm{in}}\right) / C_i^{\mathrm{in}} \\ \left(T_{i, t}^{\mathrm{sf}}-T_{i, t-\Delta t}^{\mathrm{sf}}\right) / \Delta t=H_{i, t}^{\mathrm{sf}, \mathrm{rad}} / C_i^{\mathrm{sf}}+ \\ \quad \zeta_i^{\mathrm{is}}\left(T_{i, t}^{\mathrm{in}}-T_{i, t}^{\mathrm{sf}}\right) / C_i^{\mathrm{sf}}+\zeta_i^{\mathrm{se}}\left(T_t^{\mathrm{ext}}-T_{i, t}^{\mathrm{sf}}\right) / C_i^{\mathrm{sf}}\end{array}\right.$ | (12) |
| $\sum\limits_{i \in \varOmega_{\mathrm{CHP}}} H_{i, t}^{\mathrm{ext}}=H_t^{\mathrm{CHP}}$ | (13) |
| $\left\{\begin{array}{l}T_i^{\mathrm{in}, \min } \leqslant T_{i, t}^{\mathrm{in}} \leqslant T_i^{\mathrm{in}, \max } \\ 0 \leqslant H_{i, t}^{\mathrm{D}} \leqslant H_i^{\mathrm{D}, \max } \\ 0 \leqslant H_{i, t}^{\mathrm{ext}} \leqslant H_i^{\mathrm{ext}, \max }\end{array}\right.$ | (14) |
式中:Hi, tD为t时刻第i栋楼宇综合能源系统的供热功率;ηEB、ηGF分别为电锅炉和燃气锅炉的能效比;Pi, tEB、Pi, tGF分别为t时刻第i栋楼宇电锅炉和燃气锅炉的输入功率;Ti, tin为t时刻第i栋楼宇内部的温度;Ti, t-Δtin为t-Δt时刻第i栋楼宇内部的温度;Δt为时间差;Ti, tsf为t时刻第i栋楼宇表面的温度;Ti, t-Δtsf为t-Δt时刻第i栋楼宇表面的温度;ΩCHP为CHP机组集合;Hi, text为t时刻第i栋楼宇CHP机组的供热功率;HtCHP为全部CHP机组总供热功率;Hi, tin, rad为t时刻第i栋楼宇内部的热辐射;Hi, tsf, rad为t时刻第i栋楼宇表面的热辐射;Ttext为t时刻环境温度;Ciin为第i栋楼宇内部的热容;Cisf为第i栋楼宇表面的热容;ζiis为第i栋楼宇内部与表面的传热能力;ζiie为第i栋楼宇内部与外部的传热能力;ζise为第i栋楼宇表面与外部的传热能力;Tiin, min为第i栋楼宇内部温度的最小值;Tiin, max为第i栋楼宇内部温度的最大值;HiD, max为第i栋楼宇综合能源系统供热功率的最大值;Hiext, max为第i栋楼宇CHP机组供热功率的最大值。
2.4 耦合设备模型由第1章可知,该综合能源系统的能量耦合设备包括P2G机组、CHP机组、电锅炉机组和燃气锅炉机组,对其分别建模如下。
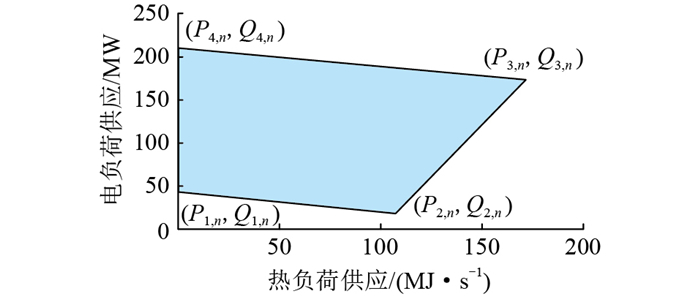
(1) CHP机组。CHP机组的可运行范围如图 4所示,CHP设备产生的电力被注入电网,热能提供给热负荷。CHP是耦合的,可用运行区域内的一个点的坐标表示,可行区域中的每个特定操作点由角点坐标的凸组合表示,即:
|
图 4 CHP设备的操作区域 Fig. 4 Operating area of CHP equipments |
| $\left\{\begin{array}{l}P_{n, t}^{\mathrm{CHP}}=\sum\limits_k^{N_{\mathrm{k}}} \alpha_{n, k, t} P_{n, k} \\ Q_{n, t}^{\mathrm{CHP}}=\sum\limits_k^{N_{\mathrm{k}}} \alpha_{n, k, t} Q_{n, k} \\ 0 \leqslant \alpha_{n, k, t} \leqslant 1 \\ \sum\limits_k^{N_{\mathrm{k}}} \alpha_{n, k, t}=1 \\ G_{n, t}^{\mathrm{CHP}}=\sum\limits_k^{N_k} \alpha_{n, k, t} G_{\mathrm{C}, k, n}\end{array}\right.$ | (15) |
式中:Pn, tCHP、Qn, tCHP分别为CHP机组的供电量和供热量;αn, k, t为CHP机组的组合系数;Nk为CHP机组的角点数;Pn, k、Qn, k分别为角点k的供电量和供热量;Gn, tCHP为CHP机组的耗气量;GC, k, n为角点k的耗气量。
(2) P2G机组。
| $\left\{\begin{array}{l}E_{i, t}^{\mathrm{P} 2 \mathrm{G}}=\eta_{\mathrm{P} 2 \mathrm{G}} D_{i, t}^{\mathrm{P} 2 \mathrm{G}} \\ 0 \leqslant D_{i, t}^{\mathrm{P} 2 \mathrm{G}} \leqslant D_{i, \max }^{\mathrm{P} 2 \mathrm{G}}\end{array}\right.$ | (16) |
式中:Ei, tP2G、Di, tP2G分别为第i个P2G机组的供气量和耗电量;ηP2G为P2G机组转化效率;Di, maxP2G为第i个P2G机组的耗电量的最大值。
(3) 电锅炉。
| $\left\{\begin{array}{l}Q_{i, t}^{\mathrm{EB}}=\eta_{\mathrm{EB}} P_{i, t}^{\mathrm{EB}} \\ P_{i, \text { min }}^{\mathrm{EB}} \leqslant P_{i, t}^{\mathrm{EB}} \leqslant P_{i, \max }^{\mathrm{EB}}\end{array}\right.$ | (17) |
式中:Qi, tEB为第i个电锅炉的产热量;Pi, tEB为第i个电锅炉的耗电量;ηEB为电锅炉的能量转化效率;Pi, minEB、Pi, maxEB分别为第i个电锅炉耗电量的最小、最大值。
(4) 燃气锅炉。
| $\left\{\begin{array}{l}Q_{i, t}^{\mathrm{GF}}=\eta_{\mathrm{GF}} P_{i, t}^{\mathrm{GF}} \\ P_{i, \text { min }}^{\mathrm{GF}} \leqslant P_{i, t}^{\mathrm{GF}} \leqslant P_{i, \max }^{\mathrm{GF}}\end{array}\right.$ | (18) |
式中:Qi, tGF为第i个燃气锅炉的产热量;Pi, tGF为第i个燃气锅炉的耗气量;ηGF为燃气锅炉的能量转化效率;Pi, minEB、Pi, maxGF分别为第i个燃气锅炉耗气量的最小、最大值。
(5) 储能模型。储能设备可以对多余电能和天然气进行存储,在供能充足时储存能量,在供能不足时便可作为能量供应单元进行供能。根据储存容量、充放能量限制和效率可以对电能储能和天然气储能进行建模。电能储能量与天然气储能量分别由式(19)、式(20)计算:
| $E_{n, t}^{\mathrm{ES}}-E_{n, t-\Delta t}^{\mathrm{ES}}=\left(\eta^{\mathrm{ES}, \text { in }} P_{n, t}^{\mathrm{ES}, \text { in }}-P_{n, t}^{\mathrm{ES}, \text { out }} / \eta^{\mathrm{ES}, \text { out }}\right) \Delta t$ | (19) |
| $\begin{gathered}E_{i, t}^{\mathrm{GS}}-E_{i, t-\Delta t}^{\mathrm{GS}}=\eta^{\mathrm{GS}, \text { in }} Q_{i, t}^{\mathrm{GS}, \text { in }} \Delta t- \\ Q_{i, t}^{\mathrm{GS}, \text { out }} \Delta t / \eta^{\mathrm{GS}, \text { out }}\end{gathered}$ | (20) |
式中:En, tES、Ei, tGS分别为电储能设备和天然气储能设备的储能量;ηES, in、ηES, out、ηGS, in、ηGS, out分别为电储能设备和天然气储能设备的充、放电效率和充、放气效率;Pn, tES, in、Pn, tES, out、Qi, tGS, in、Qi, tGS, out分别为电储能设备和天然气储能设备的充、放电功率和充、放气功率。
由于储能设备在设计时考虑了储能容量,因此储能设备的储能量应满足其对应的上、下限限制。同时,应该保证储能设备操作的一致性,即释放能量均来自供能充足时所储存的能量,储能设备不能凭空产生能量。
| $E_n^{\mathrm{ES}, \text { min }} \leqslant E_{n, t}^{\mathrm{ES}} \leqslant E_n^{\mathrm{ES}, \max }$ | (21) |
| $E_i^{\mathrm{GS}, \min } \leqslant E_{i, t}^{\mathrm{GS}} \leqslant E_i^{\mathrm{GS}, \max }$ | (22) |
| $E_{n, t, \text { end }}^{\mathrm{ES}}-E_{n, t, \text { start }}^{\mathrm{ES}} \geqslant 0$ | (23) |
| $E_{i, t, \text { end }}^{\mathrm{GS}}-E_{i, t, \text { start }}^{\mathrm{GS}} \geqslant 0$ | (24) |
式中:EnES, min、EnES, max分别为储电设备储电量的最小、最大值;EiGS, min、EiGS, max分别为储气设备储气量的最小、最大值;En, t, startES、En, t, endES分别为储电设备调度周期开始、结束时的储电量;Ei, t, startGS、Ei, t, endGS分别为储气设备调度周期开始、结束时的储气量。
为了避免储能设备同时进行充能和放能的操作,引入2个二元变量:bn, tES∈{0, 1}和bi, tGS∈{0, 1},分别约束电储能和天然气储能的充放行为。
| $0 \leqslant P_{n, t}^{\mathrm{ES}, \mathrm{in}} \leqslant b_{n, t}^{\mathrm{ES}} P_n^{\mathrm{ES}, \mathrm{in}, \max }$ | (25) |
| $0 \leqslant P_{n, t}^{\mathrm{ES}, \text { out }} \leqslant\left(1-b_{n, t}^{\mathrm{ES}}\right) P_n^{\mathrm{ES}, \text { out }, \text { max }}$ | (26) |
| $0 \leqslant Q_{i, t}^{\mathrm{GS}, \mathrm{in}} \leqslant b_{i, t}^{\mathrm{GS}} Q_i^{\mathrm{GS}, \text { in, max }}$ | (27) |
| $0 \leqslant Q_{i, t}^{\mathrm{GS} \text {, out }} \leqslant\left(1-b_{i, t}^{\mathrm{GS}}\right) Q_i^{\mathrm{GS}, \text { out }, \max }$ | (28) |
式中:PnES, in, max、PnES, out, max分别为电储能设备充、放电功率的最大值;QiGS, in, max、QiGS, out, max分别为天然气储能设备充、放气功率的最大值。式(25)和式(26)对电储能设备不能同时充放电进行约束;式(27)和式(28)对天然气储能设备不能同时充放气进行约束。
3 机会约束规划模型楼宇综合能源系统的不确定性来自多个方面,其中,受环境影响的可再生能源出力不确定性和受用户行为影响的负荷不确定性是最主要的2个方面。将可再生能源出力和负荷视为预测值和误差值之和,预测值为确定变量,误差值为随机变量,且可再生能源出力和负荷的预测误差均服从正态分布。可再生能源出力和负荷的表达式与概率密度函数具体为:
| $\left\{\begin{array}{l}P_{i, t}^{\mathrm{WT}{ }^*}=P_{i, t}^{\mathrm{WT}}+\xi_{t, \mathrm{WT}} \\ P_{i, t}^{\mathrm{PV}{ }^*}=P_{i, t}^{\mathrm{PV}}+\xi_{t, \mathrm{PV}} \\ P_{i, t}^{\mathrm{L}^*}=P_{i, t}^{\mathrm{L}}+\xi_{t, \mathrm{~L}}\end{array}\right.$ | (29) |
| $f\left(\xi_t\right)=\frac{1}{\sqrt{2 \pi} \sigma_t} \exp \left(-\frac{\xi_t^2}{2 \sigma_t^2}\right)$ | (30) |
式中:Pi, tWT*、Pi, tPV*、Pi, tL*分别为风电出力、光伏出力和负荷的实际值;Pi, tWT、Pi, tPV、Pi, tL分别为风电出力、光伏出力和负荷的预测值;ξt, WT、ξt, PV、ξt, L分别为风电出力、光伏出力和负荷的预测误差;f(·)为概率密度函数;ξt为预测误差;σt为正态分布的标准差。
通过在CHP机组中引入旋转备用约束来消除综合能源系统运行中的不确定性因素的影响,机组的正、负旋转备用具体为:
| $\left\{\begin{array}{l}\operatorname{Pr}\left\{P_{\max }^{\mathrm{CHP}}-P_{\mathrm{e}, t}^{\mathrm{CHP}} \geqslant \xi_{t, \mathrm{WT}}+\xi_{t, \mathrm{PV}}-\xi_{t, \mathrm{~L}}\right\} \geqslant \alpha_1 \\ \operatorname{Pr}\left\{P_{\mathrm{e}, t}^{\mathrm{CHP}}-P_{\min }^{\mathrm{CHP}} \geqslant \xi_{t, \mathrm{WT}}+\xi_{t, \mathrm{PV}}-\xi_{t, \mathrm{~L}}\right\} \geqslant \alpha_2\end{array}\right.$ | (31) |
式中:Pr{·}为正、负备用率大于α1、α2的概率函数;Pe, tCHP为t时刻CHP机组的旋转备用;PmaxCHP、PminCHP分别为CHP机组的最大、最小电功率。
采用逆累积分布函数f-1将上述问题转化为确定性的约束:
| $\left\{\begin{array}{l}P_{\max }^{\mathrm{CHP}}-P_{\mathrm{e}, t}^{\mathrm{CHP}} \geqslant f^{-1}\left(\alpha_1\right) \sqrt{\xi_{t, \mathrm{WT}}^2+\xi_{t, \mathrm{PV}}^2+\xi_{t, \mathrm{~L}}^2} \\ P_{\mathrm{e}, t}^{\mathrm{CHP}}-P_{\min }^{\mathrm{CHP}} \geqslant f^{-1}\left(\alpha_2\right) \sqrt{\xi_{t, \mathrm{WT}}^2+\xi_{t, \mathrm{PV}}^2+\xi_{t, \mathrm{~L}}^2}\end{array}\right.$ | (32) |
传统基于机会约束规划的不确定性建模方法通常高度依赖于随机变量PDF的先验知识。在文中的楼宇综合能源系统日前调度中,逆累积分布函数f-1(·)的计算依赖于新能源和负荷预测误差的PDF。如果能提前给定随机变量PDF的类型,则f-1(·)的计算较为简单。然而,只有当获得足够多的数据时,才能取得较为令人满意的PDF近似。事实上,分布式电源近几年才逐渐引入到楼宇综合能源系统中,其采集到的数据量非常有限。因此,所近似的新能源出力的PDF往往是不准确的,并可能给调度结果带来风险。为了解决该问题,采用基于切比雪夫不等式的分布鲁棒估计方法[31-32],只需要根据有限的输入变量数据,得到随机变量一阶和二阶矩的信息。对于任意给定的置信水平1-α,逆累积分布函数f-1(α)可以由式(33)计算得到:
| $f^{-1}(\alpha)=\sqrt{\alpha(1-\alpha)^{-1}}$ | (33) |
将式(33)代入式(32)中,得到改进后的机会约束规划模型对服从任意分布的输入随机变量具有鲁棒性。该特性对于新能源出力数据不足的楼宇综合能源系统尤为重要。关于改进的机会约束规划模型在性能上的优势将在下文的算例测试中进一步给出。
4 调度模型及其凸松弛 4.1 调度模型 4.1.1 目标函数将最优经济性作为该楼宇综合能源系统调度模型的目标函数,使得系统运行的成本最低。系统运行成本包括购电成本、购气成本、设备运行维护成本、环境治理成本和热负荷满意度惩罚成本。
楼宇的热需求被视为柔性热负荷,在关键参数满足相应的限制时可根据需要调整供热设备相应的能耗。在满足成本最小目标时,供热设备可能会运行在其供能下限以节约成本,但会影响楼宇用户的供热满意度,此处引入热负荷满意度惩罚成本χi表示用户对供热的满意度。选取楼宇内部温度上、下限的均值作为满意度惩罚的阈值,如果日均Ti, tin低于满意度阈值,则χi>0。具体为:
| $\left\{\begin{array}{l}\min F=F_1+F_2+F_3+\chi \\ F_1=\sum\limits_{t=1}^T\left(\omega_{\mathrm{g}, t}^{\mathrm{P}} P_{\mathrm{g}, t}^{\mathrm{EL}}+\omega_{\mathrm{g}, t}^{\mathrm{Q}} Q_{\mathrm{g}, t}^{\mathrm{GL}}\right) \Delta t \\ F_2=\sum\limits_{t=1}^T \sum\limits_{m=1}^M \varphi_m P_{m, t} \Delta t \\ F_3=\sum\limits_{t=1}^T \sum\limits_{n=1}^N \delta_n P_{n, t} \Delta t \\ \chi=\sum\limits_i \chi_i \\ \chi_i=\lambda_i \sum\limits_{t \in \varOmega_T}\left(\frac{T_i^{\mathrm{in}, \min }+T_i^{\mathrm{in}, \max }}{2}-T_{i, t}^{\mathrm{in}}\right)\end{array}\right.$ | (34) |
式中:F、F1、F2、F3、χ分别为综合能源系统运行总成本、购电购气成本、设备运维成本、设备的环境治理成本和热负荷满意度惩罚成本;T为运行总时段;ωg, tP、ωg, tQ分别为购售电价格和天然气价格;Pg, tEL、Qg, tGL分别为该综合能源系统消耗或产生的电功率和天然气功率;M、N分别为需要运维和环境治理的设备总数量;Pm, t为设备m的功率;φm为设备m的单位运维成本;Pn, t为设备n的功率;δn为设备n的单位环境治理成本;ΩT为日前调度时刻的集合;λi为加热设备罚款价格。
4.1.2 约束条件该调度模型的约束条件包括能量平衡约束、电网潮流约束、天然气网运行约束、CHP机组运行约束、P2G机组运行约束、电锅炉运行约束、燃气锅炉运行约束、楼宇热源约束、可再生能源出力不确定性机会约束和负荷不确定性机会约束。除能量平衡约束外,式(1)—式(28)、式(30)、式(32)详细介绍了上述约束。
能量平衡约束包括电能平衡约束、热能平衡约束和天然气平衡约束,具体为:
| $\begin{gathered}P_{\mathrm{g}, t}^{\mathrm{EL}}+P_{i, t}^{\mathrm{WT}}+P_{i, t}^{\mathrm{PV}}+P_{i, t}^{\mathrm{CHP}}+P_{n, t}^{\mathrm{ES}, \text { out }}= \\ P_{i, t}^{\mathrm{P2G} }+P_{i, t}^{\mathrm{EB}}+P_{i, t}^{\mathrm{Eload}}+P_{n, t}^{\mathrm{ES}, \mathrm{in}}\end{gathered}$ | (35) |
| $H_{i, t}^{\mathrm{CHP}}+H_{i, t}^{\mathrm{EB}}+H_{i, t}^{\mathrm{GF}}=H_{i, t}^{\mathrm{Hload}}$ | (36) |
| $Q_{\mathrm{g}, t}^{\mathrm{GL}}+Q_{i, t}^{\mathrm{P} 2 \mathrm{G}}+Q_{i, t}^{\mathrm{GS}, \text { out }}=Q_{i, t}^{\mathrm{CHP}}+Q_{i, t}^{\mathrm{GF}}+Q_{i, t}^{\mathrm{Gload}}+Q_{i, t}^{\mathrm{GS}, \text { in }}$ | (37) |
式中:Pi, tP2G为P2G机组消耗的电功率;Pi, tEload为负荷消耗的电功率;Hi, tCHP为CHP机组的制热功率;Hi, tEB为电锅炉系统的制热功率;Hi, tGF为燃气锅炉的制热功率;Hi, tHload为负荷消耗的热功率;Qi, tP2G为P2G机组产生的气功率;Qi, tCHP为CHP机组消耗的气功率;Qi, tGload为负荷消耗的气功率。
4.2 调度模型转化在电力系统潮流模型中,式(2)和式(3)中含有非线性分量,通过支路潮流的相角松弛和凸松弛将其转化为凸约束问题:
引入新变量,令
| $\left\{\begin{array}{l}p_k=\sum\limits_{k \rightarrow i} P_{k i}-\sum\limits_{j \rightarrow k}\left(P_{j k}-r_{j k} l_{j k}\right) \\ q_k=\sum\limits_{k \rightarrow i} Q_{k i}-\sum\limits_{j \rightarrow k}\left(Q_{j k}-x_{j k} l_{j k}\right)\end{array}\right.$ | (38) |
式中:pk为节点k注入有功功率;qk为节点k注入无功功率;Pki为支路k-i首端有功功率;Qki为支路k-i首端无功功率;rjk为支路j-k电阻;xjk为支路j-k电抗。
将Sij=ViIij*代入支路电压方程,并将方程两端同乘以自身的共轭,可得:
| $v_j=v_i-2\left(r_{i j} P_{i j}+x_{i j} Q_{i j}\right)+\left(r_{i j}^2+x_{i j}^2\right) l_{i j}$ | (39) |
支路首段功率方程两端同乘以自身的共轭,可以得到:
| $S_{i j}=V_i I_{i j}^* \Rightarrow l_{i j}=\frac{P_{i j}^2+Q_{i j}^2}{v_i}$ | (40) |
其中式(40)为等价变量替换, 将支路潮流方程转化为线性方程组的形式, 但等式约束的存在使得模型仍为非凸问题。考虑作如下松弛:
| $P_{i j}^2+Q_{i j}^2 \leqslant l_{i j} v_i$ | (41) |
文献[31]推导且证明了当节点负荷无上界且目标函数为支路电流的严格增函数时, 该松弛是精确的。可作如下等价转化为标准的二阶锥形式:
| $\left\|\begin{array}{c}2 P_{i j} \\ 2 Q_{i j} \\ l_{i j}-v_i\end{array}\right\|_2 \leqslant l_{i j}+v_i$ | (42) |
天然气流量采用Weymouth方程引入,其中包含非线性因素,采用增量分段线性近似方法来消除Weymouth方程中的非线性因素,引入πi2=πi*、πj2=πj*,则可改写为:
| $\operatorname{sgn}\left(\pi_i, \pi_j\right) F_{i j}^2=C_{i j}^2\left(\pi_i^*-\pi_j^*\right)$ | (43) |
引入增量分段线性化方法将式(30)改写为线性化方程:首先设定平均分段的段数K;其次将x区间等分为K段,可得到离散点x0、x1、…、xK;然后计算出离散点x0、x1、…、xK对应的f(x0)、f(x1)、…、f(xK)便可得到如下近似线性化结果。
| $\left\{\begin{array}{l}f(x)=f\left(x_0\right)+\sum\limits_{\varepsilon=0}^K\left(f\left(x_{\varepsilon+1}\right)-f\left(x_{\varepsilon}\right)\right) \delta_{\varepsilon} \\ x=x_0+\sum\limits_{\varepsilon=0}^K\left(x_{\varepsilon+1}-x_{\varepsilon}\right) \delta_{\varepsilon}\end{array}\right.$ | (44) |
则该天然气模型的Weymouth方程可表述为:
| $\left\{\begin{array}{l}C_{i j}^2\left(\pi_i^*-\pi_j^*\right)=Y_{i j, 0}+\sum\limits_{\varepsilon=0}^K\left(Y_{i j, \varepsilon+1}-Y_{i j, \varepsilon}\right) \delta_{\varepsilon} \\ F_{i j}=F_{i j, 0}+\sum\limits_{\varepsilon=0}^K\left(F_{i j, \varepsilon+1}-F_{i j, \varepsilon}\right) \delta_{i j, \varepsilon} \\ 0 \leqslant \delta_{i j, \varepsilon+1} \leqslant 1 \\ \eta_{i j, \varepsilon}=\{0, 1\}\end{array}\right.$ | (45) |
式中:Yij, 0为支路i-j首端流量平方数;Yij, ε+1为支路i-j上ε+1段的流量平方数;Yij, ε为支路i-j上ε段的流量平方数;δij, m为ε段的流量平方差斜率常数;Fij为支路i-j流量;Fij, 0为支路i-j首端流量;Fij, ε+1为支路i-j上ε+1段的流量;Fij, ε为支路i-j上ε段的流量;δij, ε+1为ε+1段的流量平方差斜率常数;ηij, ε为0、1集合。
通过上述松弛和线性化方法,可将该楼宇综合能源系统调度模型转化为混合整数二阶锥规划模型,使用集成化的数学优化软件CPLEX直接求解。
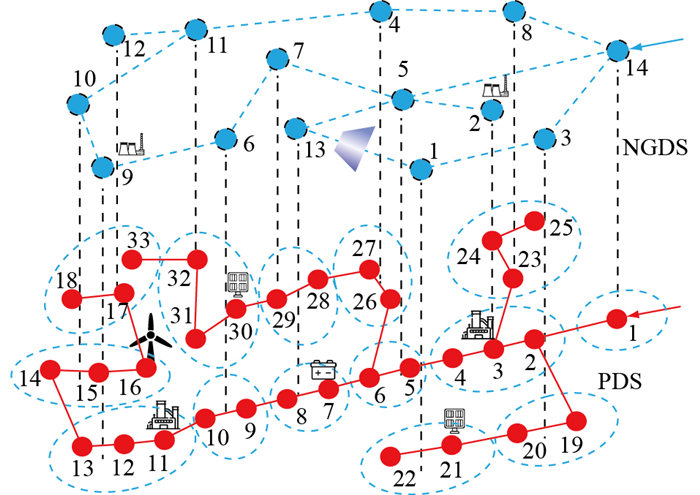
5 算例分析 5.1 测试系统介绍算例测试能源系统由图 5所示的IEEE 33节点配电网系统(power distribution system, PDS)和14节点的天然气系统(natural gas distribution system, NGDS)组成。2种系统中的分布式电源参数如表 1所示。其中,PDS的额定电压为10 kV,节点1配变容量为5 MV·A,每个节点有4户居民住宅。NGDS源节点的天然气供气量固定为80 m3/h,节点1和节点13通过压缩机连接,形成节点1到节点13的单向燃气流量。位于PDS节点3和节点11的2台热电联产机组分别从NGDS节点2和节点9消耗天然气。2座储气站分别位于NGDS节点3和节点11,储气容积均为30 m3,流量为10 m3/h。表 2还列出了一些重要的输入参数。假设新能源发电、负荷和能源价格的预测误差均服从正态分布,均值为0,标准差分别为相应预测值的5%、2%和2%。
|
图 5 测试系统拓扑 Fig. 5 Topology of test system |
|
|
表 1 楼宇综合能源系统中的分布式电源参数 Table 1 Parameters of distributed energy resources in building integrated energy systems |
|
|
表 2 仿真参数 Table 2 Simulation parameters |
测试系统采用CPLEX软件,在配置为四核3.6 GHz处理器和12 GB内存的个人计算机上进行求解。对各运行区间上的雅可比矩阵进行预处理需要2 s,重构后的模型平均求解时间为76.4 s。
为了后续进行比较,将5.1节中设置的参数定为基础场景(场景0),在场景0下优化模型的求解结果如表 3所示。
|
|
表 3 场景0的优化求解结果 Table 3 Optimized results of case 0 |
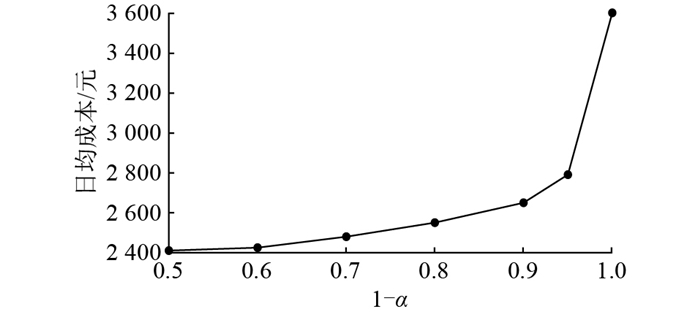
图 6比较了不同置信水平下的日均能源消费成本。当置信水平1-α增加时,可再生能源的发电量更为保守,运营商将不得不向市场购买更多的能源。因此,能源消费总成本随置信水平的增加而增加。
|
图 6 不同置信水平下日均成本 Fig. 6 Average daily cost at different confidence levels |
另一方面,λi对楼宇供暖设备的调度和室内平均温度有较大的影响。表 4比较了不同λi值下的一些关键状态量的结果,其他参数均与基础场景设置相同。由表 4可以看出,当λi=0时,室内平均温度明显低于所选择的舒适阈值(22 ℃)。虽然考虑了约束式(14),但对居民用户来说这种优化调度策略并不理想。随着λi的增加,室内平均温度升高,日内能源消耗也随之增加。当λi=3.4元/(h·℃)或变得更大时,平均室内温度和舒适阈值之间的差值可忽略不计。
|
|
表 4 不同λi值的优化调度结果 Table 4 Optimal scheduling results for different λi |
通过修改基础场景中的参数设置,可以进一步验证所提模型的有效性。表 5比较了场景0、场景1、场景2和场景3的仿真结果。
|
|
表 5 场景0、1、2和3的优化求解结果 Table 5 Optimized results of case 0, 1, 2 and 3 |
(1) 场景1:在场景0基础上增加电价波动。场景0和场景1的电价均值均为1.15元/(kW·h),场景0和场景1的标准差分别为0.34元/(kW·h)和1.50元/(kW·h)。
(2) 场景2:各个时段环境温度升高5 ℃。
(3) 场景3:各个时段环境温度降低5 ℃。
由表 5可知,电价波动更为剧烈的场景1的总能源消费成本远低于场景0。由于2个场景的日均电价相同,因此,场景1的价格数据偏差越大,说明电价峰谷差越明显。优化后的调度策略增加了“谷时”电价下的能源采购,减少了“峰时”电价下的能源消耗。这种做法能够减轻对CHP机组和储能装置的依赖,虽然总电力采购量增加了,但总能源消费成本显著降低。
场景2和场景3修改了初始环境温度数据,从而影响居民的热负荷需求。场景2和场景3的外界环境温度高于(低于)场景0,居民热负荷需求减少(增加),因此,其电力采购量及日均能源消费成本均较场景0更低(高)。此外,场景2(场景3)的CHP机组会消耗更多(更少)的天然气以产生更多(更少)的电能和热能,从而保证楼宇综合能源系统中的燃气锅炉有足够的燃料供暖。
为了比较不同不确定性处理方法所得调度结果,新增了如下的2个场景:
(1) 场景4:采用传统鲁棒优化方法求解场景0;
(2) 场景5:采用传统机会约束规划方法求解场景0,其中,式(33)中的f-1(α)由正态分布的逆累积分布函数计算得到。
表 6列出了场景0、场景4和场景5的优化求解结果。可知,相较于场景0,场景4的日均能源成本更高,新能源平均出力更低,表明采用切比雪夫不等式改进后的机会约束规划方法(场景0)能够有效减小鲁棒优化调度结果的保守性。另外,场景5的调度成本小于场景0,且新能源发电功率更高。
|
|
表 6 场景0、4和5的优化求解结果 Table 6 Optimized results of case 0, 4 and 5 |
然而,基于正态分布假设的传统机会约束方法往往会高估新能源发电能力,导致系统状态量(电压、潮流)越限。表 7进一步比较了不同新能源发电分布类型下,传统及文中改进的机会约束规划方法所得调度结果的越限率。其中,每种分布类型均采样生成10 000个数据点。
|
|
表 7 传统和改进机会约束方法所得调度结果的越限率 Table 7 Failure rate of dispatch results obtained by traditional and proposed chance constraint methods |
根据给定的置信水平及采样数据的一阶矩和二阶矩信息,可以得到新能源出力的估计区间,当采样点不在区间内,则记为“越限”。由表 7可知,当新能源随机出力服从对数正态分布或威布尔分布时,传统机会约束规划方法所得结果是可以接受的。而对于服从β分布或学生t分布的情形,传统方法很可能会低估新能源功率的波动性,导致较高的越限率。相比之下,文中改进的机会约束规划方法能始终将调度结果控制在置信范围内,对不同分布类型的随机变量具有鲁棒性。
6 结语文中针对楼宇综合能源系统的源荷双侧不确定性,以系统运行成本最低为目标函数,通过对电网、气网、楼宇热需求和各能源生产耦合设备建模,结合能量平衡约束构建了基于机会约束规划的综合能源系统日前优化调度模型。在此基础上通过凸松弛技术和增量分段线性化等方法将调度模型转化为易于求解的混合整数二阶锥规划问题。算例研究表明:所提模型中楼宇用户的满意度惩罚金额、置信水平等关键参数的选取对调度结果影响较大。从方法层面来看,利用切比雪夫不等式得到的改进机会约束规划方法具有较高的计算效率,对不同分布类型的不确定性参数都具有鲁棒性,从而避免正态分布假设带来的近似偏差。该方法能一定程度上克服鲁棒优化调度的保守性,经济性更优。
需要指出的是,文中对满意度惩罚金额、置信水平等模型参数的选取主要依赖于经验,下一步工作将研究如何优化这些参数以平衡系统运行经济性和安全性的矛盾。
致谢
本文得到国网江苏省电力有限公司科技项目(J2021194)资助,谨此致谢!
| [1] |
CHEN X Y, MCELROY M B, KANG C Q. Integrated energy systems for higher wind penetration in China: formulation, implementation, and impacts[J]. IEEE Transactions on Power Systems, 2018, 33(2): 1309-1319. (  0) 0) |
| [2] |
王伟亮, 王丹, 贾宏杰, 等. 能源互联网背景下的典型区域综合能源系统稳态分析研究综述[J]. 中国电机工程学报, 2016, 36(12): 3292-3306. WANG Weiliang, WANG Dan, JIA Hongjie, et al. Review of steady-state analysis of typical regional integrated energy system under the background of energy Internet[J]. Proceedings of the CSEE, 2016, 36(12): 3292-3306. (  0) 0) |
| [3] |
许剑, 刘松阳, 卢建生, 等. 基于递阶模型的综合能源系统多时间尺度运行优化研究[J]. 供用电, 2023, 40(1): 73-79. XU Jian, LIU Songyang, LU Jiansheng, et al. Research on multi-time scale operation optimization of integrated energy system based on hierarchical model[J]. Distribution & Utilization, 2023, 40(1): 73-79. (  0) 0) |
| [4] |
DOU Z, ZHANG C, WANG W, et al. Review on key technologies and typical applications of multi-station integrated energy systems[J]. Global Energy Interconnection, 2022, 5(3): 309-327. DOI:10.1016/j.gloei.2022.06.009 (  0) 0) |
| [5] |
黎静华, 朱梦姝, 陆悦江, 等. 综合能源系统优化调度综述[J]. 电网技术, 2021, 45(6): 2256-2272. LI Jinghua, ZHU Mengshu, LU Yuejiang, et al. Reviewon optimal scheduling of integrated energy systems[J]. Power System Technology, 2021, 45(6): 2256-2272. (  0) 0) |
| [6] |
郝然, 艾芊, 朱宇超, 等. 基于能源集线器的区域综合能源系统分层优化调度[J]. 电力自动化设备, 2017, 37(6): 171-178. HAO Ran, AI Qian, ZHU Yuchao, et al. Hierarchical optimal dispatch based on energy hub for regional integrated energy system[J]. Electric Power Automation Equipment, 2017, 37(6): 171-178. (  0) 0) |
| [7] |
郭杰, 吴杰康, 洪明志, 等. 综合能源系统碳交易优化调度模型[J]. 供用电, 2023, 40(11): 94-104. GUO Jie, WU Jiekang, HONG Mingzhi, et al. Optimal scheduling model of carbon trading in integrated energy system[J]. Distribution & Utilization, 2023, 40(11): 94-104. (  0) 0) |
| [8] |
于馨玮, 陈继明, 仉志华. 分布鲁棒优化在综合能源系统调度与规划中的应用综述[J]. 全球能源互联网, 2023, 6(2): 207-215. YU Xinwei, CHEN Jiming, ZHANG Zhihua. A review of the application of distributionally robust optimization in integrated energy system dispatching and planning[J]. Journal of Global Energy Interconnection, 2023, 6(2): 207-215. (  0) 0) |
| [9] |
张沈习, 王丹阳, 程浩忠, 等. 双碳目标下低碳综合能源系统规划关键技术及挑战[J]. 电力系统自动化, 2022, 46(8): 189-207. ZHANG Shenxi, WANG Danyang, CHENG Haozhong, et al. Key technologies and challenges of low-carbon integrated energy system planning for carbon emission peak and carbon neutrality[J]. Automation of Electric Power Systems, 2022, 46(8): 189-207. (  0) 0) |
| [10] |
SUN X R, LUH P B, CHEUNG K W, et al. An efficient approach to short-term load forecasting at the distribution level[J]. IEEE Transactions on Power Systems, 2016, 31(4): 2526-2537. DOI:10.1109/TPWRS.2015.2489679 (  0) 0) |
| [11] |
刘向向, 卢婕, 严勤, 等. 考虑热惯性的居民楼宇综合能源系统日前运行优化[J]. 可再生能源, 2020, 38(3): 409-415. LIU Xiangxiang, LU Jie, YAN Qin, et al. Day-ahead optimal operation of residential building integrated energy system considering thermal inertia[J]. Renewable Energy Resources, 2020, 38(3): 409-415. DOI:10.3969/j.issn.1671-5292.2020.03.019 (  0) 0) |
| [12] |
钟雅珊, 付聪, 钱峰, 等. 考虑广义储能和条件风险价值的综合能源系统经济调度[J]. 电力系统保护与控制, 2022, 50(9): 54-63. ZHONG Yashan, FU Cong, QIAN Feng, et al. Economic dispatch model of an integrated energy system considering generalizedenergy storage and conditional value at risk[J]. Power System Protection and Control, 2022, 50(9): 54-63. (  0) 0) |
| [13] |
张涛, 胡泽春, 张丹阳. 楼宇综合能源系统容量配置优化[J]. 电力建设, 2019, 40(8): 3-11. ZHANG Tao, HU Zechun, ZHANG Danyang. Study on optimal capacity planning of building integrated energy system[J]. Electric Power Construction, 2019, 40(8): 3-11. (  0) 0) |
| [14] |
闫梦阳, 李华强, 王俊翔, 等. 计及综合需求响应不确定性的园区综合能源系统优化运行模型[J]. 电力系统保护与控制, 2022, 50(2): 163-175. YAN Mengyang, LI Huaqiang, WANG Junxiang, et al. Optimal operation model of a park integrated energy system considering uncertainty ofintegrated demand response[J]. Power System Protection and Control, 2022, 50(2): 163-175. (  0) 0) |
| [15] |
文福拴, 鲁刚, 黄杰. 面向碳达峰、碳中和的综合能源系统[J]. 全球能源互联网, 2022, 5(2): 116-117. WEN Fushuan, LU Gang, HUANG Jie. Integrated energy system towards carbon peak and neutrality targets[J]. Journal of Global Energy Interconnection, 2022, 5(2): 116-117. (  0) 0) |
| [16] |
李红伟, 张翔, 周海林, 等. 考虑源荷不确定性的综合能源系统日前经济调度[J]. 科学技术与工程, 2021, 21(18): 7537-7543. LI Hongwei, ZHANG Xiang, ZHOU Hailin, et al. Day-ahead economic dispatch of integrated energy system considering source load uncertainty[J]. Science Technology and Engineering, 2021, 21(18): 7537-7543. (  0) 0) |
| [17] |
朱嘉远, 刘洋, 许立雄, 等. 考虑风电消纳的热电联供型微网日前鲁棒经济调度[J]. 电力系统自动化, 2019, 43(4): 40-48. ZHU Jiayuan, LIU Yang, XU Lixiong, et al. Robust day-ahead economic dispatch of microgrid with combined heat and power system considering wind power accommodation[J]. Automation of Electric Power Systems, 2019, 43(4): 40-48. (  0) 0) |
| [18] |
BAI L Q, LI F X, CUI H T, et al. Interval optimization based operating strategy for gas-electricity integrated energy systems considering demand response and wind uncertainty[J]. Applied Energy, 2016, 167: 270-279. (  0) 0) |
| [19] |
吕泉, 王海霞, 陈天佑, 等. 考虑风电不确定性的热电厂蓄热罐运行策略[J]. 电力系统自动化, 2015, 39(14): 23-29. LYU Quan, WANG Haixia, CHEN Tianyou, et al. Operation strategies of heat accumulator in combined heat and power plant with uncertain wind power[J]. Automation of Electric Power Systems, 2015, 39(14): 23-29. (  0) 0) |
| [20] |
田丰, 贾燕冰, 任海泉, 等. 计及用户行为及满意度的电-气综合能源系统优化调度[J]. 电测与仪表, 2021, 58(5): 31-38. TIAN Feng, JIA Yanbing, REN Haiquan, et al. Optimal dispatch of electricity-gas integrated energy system considering user behavior and satisfaction[J]. Electrical Measurement & Instrumentation, 2021, 58(5): 31-38. (  0) 0) |
| [21] |
张涛, 章佳莹, 王凌云, 等. 计及用户行为的电—气—热综合能源系统日前经济调度[J]. 电力系统自动化, 2019, 43(11): 86-94. ZHANG Tao, ZHANG Jiaying, WANG Lingyun, et al. Day-ahead economical dispatch of electricity-gas-heat integrated energy system considering user behaviors[J]. Automation of Electric Power Systems, 2019, 43(11): 86-94. (  0) 0) |
| [22] |
TALARI S, YAZDANINEJAD M, HAGHIFAM M R. Stochastic-based scheduling of the microgrid operation including wind turbines, photovoltaic cells, energy storages and responsive loads[J]. IET Generation, Transmission & Distribution, 2015, 9(12): 1498-1509. (  0) 0) |
| [23] |
徐辉, 焦扬, 蒲雷, 等. 计及不确定性和需求响应的风光燃储集成虚拟电厂随机调度优化模型[J]. 电网技术, 2017, 41(11): 3590-3597. XU Hui, JIAO Yang, PU Lei, et al. Stochastic scheduling optimization model for virtual power plant of integrated wind-photovoltaic-energy storage system considering uncertainty and demand response[J]. Power System Technology, 2017, 41(11): 3590-3597. (  0) 0) |
| [24] |
刘一欣, 郭力, 王成山. 微电网两阶段鲁棒优化经济调度方法[J]. 中国电机工程学报, 2018, 38(14): 4013-4022, 4307. LIU Yixin, GUO Li, WANG Chengshan. Economic dispatch of microgrid based on two stage robust optimization[J]. Proceedings of the CSEE, 2018, 38(14): 4013-4022, 4307. (  0) 0) |
| [25] |
LIU F, BIE ZH, WANG X. Day-ahead dispatch of integrated electricity and natural gas system considering reserve scheduling and renewable uncertainties[J]. IEEE Transactions on Sustainable Energy, 2019, 10(2): 646-658. (  0) 0) |
| [26] |
LI G Q, ZHANG R F, JIANG T, et al. Optimal dispatch strategy for integrated energy systems with CCHP and wind power[J]. Applied Energy, 2017, 192: 408-419. (  0) 0) |
| [27] |
LIU W J, ZHAN J P, CHUNG C Y, et al. Day-ahead optimal operation for multi-energy residential systems with renewables[J]. IEEE Transactions on Sustainable Energy, 2019, 10(4): 1927-1938. (  0) 0) |
| [28] |
张宇帆, 艾芊, 郝然, 等. 基于机会约束规划的楼宇综合能源系统经济调度[J]. 电网技术, 2019, 43(1): 108-116. ZHANG Yufan, AI Qian, HAO Ran, et al. Economic dispatch of integrated energy system at building level based on chance constrained programming[J]. Power System Technology, 2019, 43(1): 108-116. (  0) 0) |
| [29] |
周星球, 郑凌蔚, 杨兰, 等. 考虑多重不确定性的综合能源系统日前优化调度[J]. 电网技术, 2020, 44(7): 2466-2473. ZHOU Xingqiu, ZHENG Lingwei, YANG Lan, et al. Day-ahead optimal dispatch of an integrated energy system considering multiple uncertainty[J]. Power System Technology, 2020, 44(7): 2466-2473. (  0) 0) |
| [30] |
毕锐, 王孝淦, 袁华凯, 等. 考虑供需双侧响应和碳交易的氢能综合能源系统鲁棒调度[J]. 电力系统保护与控制, 2023, 51(12): 122-132. BI Rui, WANG Xiaogan, YUAN Huakai, et al. Robust dispatch of a hydrogen integrated energy system considering double sideresponse and carbon trading mechanism[J]. Power System Protection and Control, 2023, 51(12): 122-132. (  0) 0) |
| [31] |
FARIVAR M, LOW S H. Branch flow model: relaxations and convexification[C]//2012 IEEE 51st IEEE Conference on Decision and Control (CDC). Maui, HI, USA. IEEE, 2013: 3672-3679.
(  0) 0) |
| [32] |
杨明杰, 胡扬宇, 千海霞, 等. 计及碳排放的综合能源配网日前与日内多时间尺度优化调度[J]. 电力系统保护与控制, 2023, 51(5): 96-106. YANG Mingjie, HU Yangyu, QIAN Haixia, et al. Optimization of day-ahead and intra-day multi-time scale scheduling for integrated power-gas energy system considering carbon emission[J]. Power System Protection and Control, 2023, 51(5): 96-106. (  0) 0) |
2. College of Automation & College of Artificial Intelligence, Nanjing University of Posts and Telecommunications, Nanjing 210023, China
 2024, Vol. 43
2024, Vol. 43


 易文飞(1987),男,博士,高级工程师,从事直流电网运行控制、综合能源系统协调控制工作(E-mail:
易文飞(1987),男,博士,高级工程师,从事直流电网运行控制、综合能源系统协调控制工作(E-mail: