文章编号: 2096-3203(2024)03-0052-11 中图分类号: TM614;TM712
近年来,风电场发展呈规模容量越来越大、输送距离越来越远的趋势[1-2],以“直流汇集-直流传输”为特点的风电全直流系统,避免了交流电缆导致的过电压、无功充电电流等问题,无须使用沉重的工频交流变压器,是目前工业界和学术界关注的焦点之一[3-5]。
然而,风电全直流系统各级变换器将风电场与大电网解耦,使风电场无法主动响应电网频率变化,并网后给电网带来了系统惯量降低、调频能力不足等问题[6]。因此,开发风电全直流系统潜在的调频能力,实现风电全直流系统对交流电网的频率支撑已成为亟待解决的关键问题[7-8]。
在惯量响应方面, 文献[9]针对高压直流(high voltage direct current,HVDC)输电系统参与交流电网调频的问题,通过虚拟惯性控制将下垂控制电压参考值与交流侧频率进行耦合,有助于频率稳定及减小调频引起的暂态波动,但该策略仅挖掘了直流输电系统的惯量支撑能力;文献[10]针对大型海上风电场,在风电机组直流侧附加超级电容进行充放电以模拟同步机惯量,该策略附加了储能,投资成本增大;文献[11]提出直流电容和风电机组转子动能协同的惯性响应策略,可提供大范围的惯量,增加系统稳定性,但无法适应不同的频率响应阶段。
在一次调频方面,文献[12]针对受端电力系统频率稳定性问题,提出风电场利用超速减载备用容量实现系统的一次调频;文献[13]针对有HVDC受电的大负荷中心电网,利用重叠分解法和极点配置法设计HVDC辅助一次调频控制器,证实了HVDC辅助一次调频的可行性;文献[14]针对海上风电系统调频问题,提出直流电容储能分段控制策略,在直流电容提供惯量的同时,使其在风电系统频率降低时进行功率增发,两者配合能够有效改善系统最大频率偏差。
综上所述,风电经直流并网系统在不外加储能的情况下,含有直流风电机组(direct current wind turbine, DCWT)的转子动能、减载有功备用及直流系统的直流电容这3种调频资源。大多数文献只研究了部分资源参与系统调频,对于在风电全直流系统中协调三者以改善系统惯性响应及一次调频的研究较少。
基于此,文中介绍了风电全直流输电系统的结构及调频需求,提出一种改善惯性响应与一次调频的变系数风电全直流系统协调控制策略。在惯量响应方面,由网侧换流站附加的直流电容惯性同步控制实现直流电容对系统的惯量支撑以及频率信息传递,提出基于DCWT的变虚拟惯性系数的虚拟惯量控制,结合惯量需求对虚拟惯性系数进行分段整定,该控制与直流电容惯性同步控制配合,使风电全直流系统在不同频率响应阶段具备不同的等效惯量。在一次调频方面,DCWT采用超速与变桨相结合的减载运行方式为系统提供有功备用,通过变下垂控制改变其有功出力,下垂系数的整定考虑了不同风速下的备用容量,从而使风电全直流系统更充分地参与一次调频。最后基于PSCAD/EMTDC仿真软件搭建风电全直流系统仿真模型,对所提控制策略进行仿真验证。
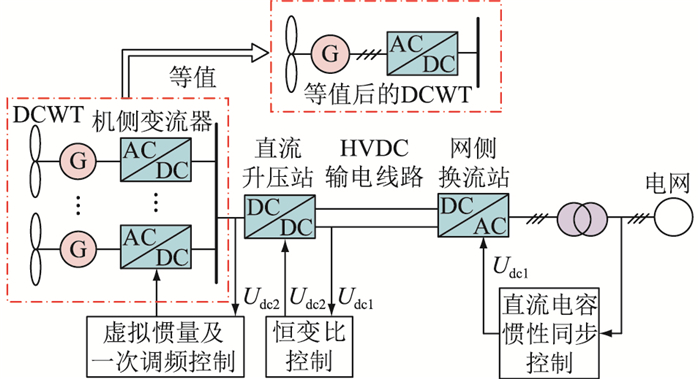
1 风电全直流系统结构及调频需求分析 1.1 风电全直流系统结构目前已有的风电全直流系统方案根据升压方式可分为升压装置升压方案和串联升压方案[4]。升压装置升压方案中的集中升压型风电全直流系统具有结构简单、升压损耗相对较少、电能传输效率高且无环流发生的优势[3],故文中采用集中升压型风电全直流系统进行研究,其结构如图 1所示,包括DCWT、直流升压站(DC/DC)、HVDC输电线路、网侧换流站。DCWT由永磁同步发电机与AC/DC换流器组成,AC/DC换流器主要控制DCWT的有功和无功功率,采用电流矢量控制策略[15];DC/DC主要控制机侧直流电压稳定并调节出口电压,文中采用恒变比控制模式;网侧换流站主要负责HVDC母线电压的稳定控制和无功功率的支撑,采用双闭环控制策略。
|
图 1 集中升压型风电全直流系统结构 Fig. 1 Structure of centralized boost wind power full DC system |
图 1中,网侧换流站附加的直流电容惯性同步控制使得直流系统中的直流电容为系统提供惯量支撑,将交流电网频率变化转变为直流高压侧直流电压Udc1的变化,直流升压站的恒变比控制将Udc1与直流低压侧直流电压Udc2建立联系,最终达到Udc2与交流电网频率实时联动的目的,两者配合实现频率信息的传递。DCWT依据Udc2感知电网频率变化,附加变系数虚拟惯量与一次调频控制参与系统调频。网侧换流站的直流电容惯性同步控制与DCWT的变系数虚拟惯量控制一同为系统提供惯量支撑,DCWT变系数一次调频控制负责一次调频阶段的有功出力。
为简化分析,采用文献[16]提出的加权法将N台并联的DCWT等值为1台风电机组。
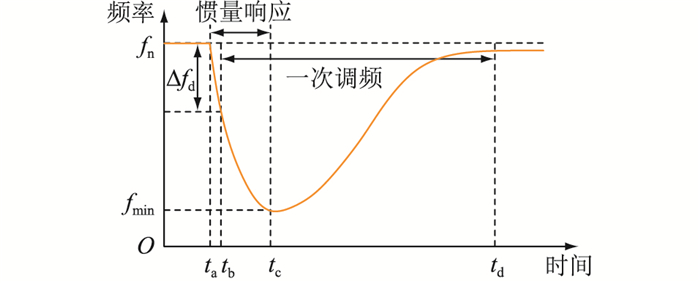
1.2 频率支撑需求分析依据图 2所示风电全直流系统接入电力系统频率响应曲线,分析其参与惯量响应和一次调频的要求。
|
图 2 风电全直流系统接入电力系统频率响应曲线 Fig. 2 Frequency response curve of wind power full DC system integration system |
(1) 惯量响应。在系统频率快速背离稳态频率fn的阶段(ta—tc),须阻止频率过快变化并优化系统频率扰动极值fmin;在系统频率达到频率扰动极值点,回归一次调频频率稳态运行点的阶段(tc—td),须加速系统频率恢复。因此要求风电全直流系统为电力系统提供惯量支撑,并在不同的频率响应阶段具备不同的惯量水平[17-18]。
(2) 一次调频。在频率偏差超过一次调频死区Δfd到一次调频结束的阶段(tb—td),须优化系统频率扰动极值并减少准稳态频率偏差。因此要求风电全直流系统具有有功功率储备,在一次调频阶段可进行持续稳定的有功输出。
2 风电全直流系统调频控制策略基于上述风电全直流系统结构和调频需求,提出适用于该系统的调频控制策略。该策略按照控制的附加对象分为两部分:在第一部分中,对网侧换流站附加直流电容惯性同步控制,利用直流电容为电力系统提供惯量,并进行频率传递的第一个环节;在第二部分中,对DCWT附加变系数虚拟惯量与一次调频控制,首先介绍频率传递的第二个环节,实现DCWT对交流电网频率的感知,接着提出DCWT的调频控制策略,利用转子动能配合直流电容一同参与惯量响应,利用有功减载备用参与一次调频,最后对调频参数进行动态整定。
2.1 基于网侧换流站的直流电容惯性同步控制(1) 惯性同步控制原理。HVDC输电线路中的直流电容可被用作功率平衡,直流高压侧直流电压的变化ΔUdc1可表示为网侧换流站输入功率Pin与输出功率Pout不平衡[11],为简化分析,忽略HVDC输电线路损耗,即线路两端电压皆为Udc1, 网侧换流站输入功率Pin可认作为DCWT的有功输出PW。
HVDC输电线路的等效电容Ceq为网侧换流站直流侧电容CGS、直流线路电容Cl与直流升压站的高压侧等效电容CDC之和。
| $ C_{\mathrm{eq}}=C_{\mathrm{DC}}+C_{1}+C_{\mathrm{GS}} $ | (1) |
设该等效电容储存的能量为Wc,直流高压侧直流电压随功率变化的方程可表示为:
| $ C_{\mathrm{eq}} U_{\mathrm{dc1}} \frac{\mathrm{d} U_{\mathrm{dc1}}}{\mathrm{d} t}=\frac{\mathrm{d} W_{\mathrm{c}}}{\mathrm{d} t}=P_{\mathrm{in}}-P_{\text {out }} $ | (2) |
网侧换流站的输出功率Pout为:
| $ \left\{\begin{array}{l} P_{\text {out }}=\frac{3 U_{\text {ref }} U_{\mathrm{g}}}{X} \sin \delta=\frac{3 m U_{\mathrm{dc1}} U_{\mathrm{g}}}{2 \sqrt{2} X} \sin \delta\\ \frac{\mathrm{d} \delta}{\mathrm{d} t}=\omega_{\text {ref }}-\omega_{\mathrm{g}} \end{array}\right. $ | (3) |
式中:Uref、ωref分别为网侧换流站输出交流电压及电角速度;m为调制比;Ug、ωg分别为电网电压幅值及电角速度;X为并网电抗、线路电抗及等效电网阻抗之和;δ为并网功角。
直流高压侧直流电压随功率变化方程和网侧换流站输出功率方程与同步发电机转子运动方程及输出方程相似。同步发电机转子运动方程为:
| $ J \omega \frac{\mathrm{d} \omega}{\mathrm{d} t}=P_{\mathrm{m}}-P_{\mathrm{e}} $ | (4) |
式中:J为同步发电机转动惯量;ω为转子转速;Pm为机械功率;Pe为并网电功率。
同步发电机输出功率为:
| $ \left\{\begin{array}{l} P_{\mathrm{g}, \text { out }}=\frac{3 E U_{\mathrm{g}}}{X} \sin \delta=\frac{3 \psi \omega_{\mathrm{m}} U_{\mathrm{g}}}{\sqrt{2} X} \sin \delta\\ \frac{\mathrm{d} \delta}{\mathrm{d} t}=\omega_{\mathrm{e}}-\omega_{\mathrm{g}} \end{array}\right. $ | (5) |
式中:E为感应电动势;ψ为气隙磁链;ωm为同步发电机转子机械频率;ωe为输出电角速度。
模拟转子转速与输出电磁频率的耦合关系, 建立直流高压侧直流电压与交流侧频率的联系[19]。
| $ \frac{U_{\mathrm{dc1}}-U_{\mathrm{dc1}, \mathrm{n}}}{U_{\mathrm{dc} 1, \mathrm{n}}}=k \frac{\omega_{\mathrm{ref}}-\omega_{\mathrm{n}}}{\omega_{\mathrm{n}}} $ | (6) |
式中:k为两者间的耦合系数[20],一般取0.2;Udc1, n为直流高压侧额定直流电压;ωn为额定输出频率。该控制框图见图 3,其中ωref, min、ωref, max分别为网侧换流站电角速度最小值和最大值;θ为调制电压相位。

|
图 3 网侧换流站惯性同步控制框图 Fig. 3 Block diagram of inertial synchronization control for grid side converter station |
将式(6)代入式(2),可得:
| $ \left\{\begin{array}{l} \frac{C_{\mathrm{eq}} U_{\mathrm{dc1}} U_{\mathrm{dc} 1, \mathrm{n}}}{k \omega_{\mathrm{n}}} \times \frac{\mathrm{d} \Delta \omega_{\mathrm{ref}}}{\mathrm{d} t}=P_{\mathrm{in}}-P_{\text {out }}\\ \frac{\mathrm{d} \delta}{\mathrm{d} t}=\omega_{\mathrm{ref}}-\omega_{\mathrm{g}} \\ P_{\text {out }}=\frac{\sqrt{3} m U_{\mathrm{dc1}} U_{\mathrm{g}}}{2 \sqrt{2} X} \sin \delta \end{array}\right. $ | (7) |
式中:Δωref为网侧换流站电角速度变化量。
在直流电容的惯性同步控制下,根据高压侧直流电压的偏差调节输出频率,可实现网侧换流站的无锁相环自同步并网以及频率信息的传递。同时直流电容电压如同同步发电机转子般响应频率变化,为系统提供惯量支撑。最后惯性同步控制环节给出调制电压的相位θ。
(2) 惯性同步控制下风电全直流系统等效惯量。同步发电机的惯量响应过程可描述为:
| $ 2 H \frac{\mathrm{d} f}{\mathrm{d} t}=P_{\mathrm{m}}-P_{\mathrm{e}} $ | (8) |
式中:H为同步发电机惯性时间常数;f为系统频率。
此时风电全直流系统仅有直流电容提供惯量支撑,类比同步发电机的惯量响应可求得此时风电全直流系统的惯性时间常数ΔH,结合式(2),Pm可看作Pin,Pe可看作Pout,可得:
| $ 2 \Delta H \frac{\mathrm{d} f}{\mathrm{d} t}=C_{\mathrm{eq}} U_{\mathrm{dc} 1} \frac{\mathrm{d} U_{\mathrm{dc} 1}}{\mathrm{d} t} $ | (9) |
对式(9)两端进行积分:
| $ \int_{f_{\mathrm{n}}}^{f} 2 \Delta H \frac{\mathrm{d} f}{\mathrm{d} t}=\int_{U_{\mathrm{dc} 1, {\rm{n}}}}^{U_{\mathrm{dc} 1}} C_{\mathrm{eq}} U_{\mathrm{dc} 1} \frac{\mathrm{d} U_{\mathrm{dc} 1}}{\mathrm{d} t} $ | (10) |
化简得:
| $ \frac{C_{\mathrm{eq}}\left(U_{\mathrm{dc} 1}^{2}-U_{\mathrm{dc1}, \mathrm{n}}^{2}\right)}{2}=2 \Delta H\left(f-f_{\mathrm{n}}\right) $ | (11) |
由于安全限制(文中取±10%的额定直流电压),直流电压只能在小范围波动,故在Udc1, n处采用一阶泰勒展开,有:
| $ C_{\mathrm{eq}} U_{\mathrm{dc1}, \mathrm{n}} \Delta U_{\mathrm{dc1}}=2 \Delta H \Delta f $ | (12) |
得到风电全直流系统的惯性时间常数为:
| $ \Delta H=\frac{C_{\mathrm{eq}} U_{\mathrm{dc1}, \mathrm{n}}}{2} \times \frac{\Delta U_{\mathrm{dc1}}}{\Delta f} $ | (13) |
直流电容提供的惯量较小,因此为了增强风电全直流系统的等效惯量,可结合DCWT的转子动能一同为电力系统提供惯量支撑。在完成DCWT对交流系统频率感知的基础上,为满足不同频率响应阶段应具备不同惯量水平的需求,提出一种基于低压侧直流电压变化率的变虚拟惯性系数的虚拟惯量控制策略。通过改变虚拟惯性系数来改变风电机组在不同阶段的有功出力,达到抑制频率恶化以及加快频率恢复的目的。
(1) DCWT对交流系统频率的感知。惯性同步控制将频率波动转换为直流高压侧电压的变化,文献[20]提出在DC/DC采用恒变比控制使直流高低压两侧直流电压耦合,实现低压侧直流电压与交流电网频率实时联动,从而实现DCWT对交流系统频率的感知。关系式为:
| $ \begin{gather*} \frac{\Delta U_{\mathrm{dc} 2}}{U_{\mathrm{dc} 2, \mathrm{n}}}=\frac{1}{1+T s} \times \frac{c \Delta U_{\mathrm{dc} 1}}{c U_{\mathrm{dc} 1, \mathrm{n}}}= \\ \frac{G(s)}{1+T s} \times \frac{\Delta \omega_{\mathrm{g}}}{\omega_{\mathrm{n}}} \approx \frac{\Delta \omega_{\mathrm{g}}}{k \omega_{\mathrm{n}}} \end{gather*} $ | (14) |
式中:ΔUdc2为直流低压侧直流电压变化量;Udc2, n为直流低压侧额定直流电压;c为恒变比控制比例系数;T为滤波时间常数;G(s)为直流电压与交流系统频率之间的传递函数[20];Δωg为电网电角速度变化量。
(2) 变虚拟惯性系数的虚拟惯量控制策略。传统虚拟惯量控制产生的有功增量ΔP1可表示为:
| $ \Delta P_{1}=-k_{1} \frac{\mathrm{d} f}{\mathrm{d} t} $ | (15) |
式中:k1为传统虚拟惯量系数。
结合式(14),可得到基于直流低压侧直流电压变化率的DCWT虚拟惯量控制。
| $ \Delta P_{1}=-k_{1} \frac{k \omega_{\mathrm{n}}}{2 {\mathsf{π}} U_{\mathrm{dc} 2, \mathrm{n}}} \times \frac{\mathrm{d} U_{\mathrm{dc} 2}}{\mathrm{d} t}=-k_{\mathrm{d}} \frac{\mathrm{d} U_{\mathrm{dc} 2}}{\mathrm{d} t} $ | (16) |
式中:kd为变虚拟惯量控制系数。
DCWT通常运行于减载模式,只有工作于次优功率跟踪区间可参与系统调频。文中主要对该区间进行讨论,当减载率为d时DCWT在该区间的输出功率[21]为:
| $ P_{\mathrm{del}}=k_{\mathrm{del}} \omega_{\mathrm{r}}^{3} \omega_{\min } \leqslant \omega_{\mathrm{r}}<\omega_{\max } $ | (17) |
其中:
| $ k_{\mathrm{del}}=\frac{(1-d) 0.5 \rho A R^{3} C_{\mathrm{p}, \max }}{\lambda_{\mathrm{opt}}^{3}} $ | (18) |
式中:Pdel为减载后DCWT的输出功率;kdel为减载功率跟踪系数;ωr为当前转速;ρ为空气密度;A为风轮机扫风面积; R为风机叶轮半径;λopt为风机捕获最大风能的最佳叶尖速比;Cp, max为风能利用系数;ωmin为DCWT转速最小限值; ωmax为DCWT转速最大限值。
加入虚拟惯量控制后DCWT的有功输出参考值Pref即为Pdel与ΔP1之和,由于在惯量支撑的作用下,转速变化量Δωd较小,满足ωr>>Δωd,可将DCWT的输出功率[22]简化为:
| $ \begin{gather*} P_{\mathrm{ref}}=P_{\mathrm{del}}+\Delta P_{1}=k_{\mathrm{del}}\left(\omega_{\mathrm{r}}+\Delta \omega_{\mathrm{d}}\right)^{3} \approx \\ k_{\mathrm{del}}\left(\omega_{\mathrm{r}}^{3}+3 \omega_{\mathrm{r}}^{2} \Delta \omega_{\mathrm{d}}\right) \end{gather*} $ | (19) |
可得到附加功率ΔP1与转速变化量的关系为:
| $ \Delta P_{1}=3 k_{\mathrm{del}} \omega_{\mathrm{r}}^{2} \Delta \omega_{\mathrm{d}} $ | (20) |
最终可得附加转速变化量Δωd为:
| $ \Delta \omega_{\mathrm{d}}=\frac{-k_{\mathrm{d}}}{3 k_{\mathrm{del}} \omega_{\mathrm{r}}^{2}} \times \frac{\mathrm{d} U_{\mathrm{dc} 2}}{\mathrm{~d} t} $ | (21) |
由式(21)可知,调节kd可改变附加转速变化量,进而改变DCWT惯量响应的有功出力。
此时,风电全直流系统的惯量响应过程为:
| $ C_{\mathrm{eq}} U_{\mathrm{dc} 1} \frac{\mathrm{d} U_{\mathrm{dc} 1}}{\mathrm{~d} t}=P_{\mathrm{in}}-k_{\mathrm{d}} \frac{\mathrm{d} U_{\mathrm{dc} 2}}{\mathrm{~d} t}-P_{\text {out }} $ | (22) |
结合式(14),对式(22)进行化简得:
| $ \left(C_{\mathrm{eq}} U_{\mathrm{dc} 1}+c k_{\mathrm{d}}\right) \frac{\mathrm{d} U_{\mathrm{dc} 1}}{\mathrm{~d} t}=P_{\mathrm{in}}-P_{\text {out }} $ | (23) |
结合式(13)进一步化简可得:
| $ \Delta H=\frac{C_{\mathrm{eq}} U_{\mathrm{dc} 1, \mathrm{n}}+c k_{\mathrm{d}}}{2} \times \frac{\Delta U_{\mathrm{dc1}}}{\Delta f} $ | (24) |
由式(24)可知,加入DCWT的虚拟惯量控制后可以显著增大风电全直流系统的等效惯性时间常数,通过调节kd即可调节风电全直流系统的惯量响应能力。
2.2.2 基于DCWT有功备用的一次调频风电全直流系统参与电网一次调频时,直流电容与转子动能只能参与短时间调频,而DCWT减载控制下留有的备用功率可满足一次调频需求。文中对DCWT采用超速和变桨相结合的减载运行方式实现全风速段的定量减载。
首先根据减载量d(文中取20%)与DCWT机组运行特性确定边界风速,即切入风速Vin、低中风速边界V1、中高风速边界V2、切出风速Vout[23]。划分风速区间后,进一步确定DCWT在不同风速下的减载方式及对应的调频控制策略。
(1) 低风速段(Vin~V1)。采用超速法实现减载,参考转速ωref为实现特定减载率下对应的转速,可由式(17)求得。
(2) 中风速段(V1~V2)。优先采用超速法进行减载且转子转速应达到最大限值ωmax,超速法无法实现的减载功率通过变桨法补充实现。参考转速[24]为:
| $ \omega_{\mathrm{ref}}=\omega_{\mathrm{mppt}}+\frac{P_{\mathrm{mppt}}-P_{\mathrm{ref}}}{P_{\mathrm{mppt}}-P_{\mathrm{del}}}\left(\omega_{\text {max }}-\omega_{\mathrm{mppt}}\right) $ | (25) |
式中:ωmppt、Pmppt分别为相应风速下最优转速、最大功率。不同风速,不同减载率下的预留桨距角可由查表法确定[23]。
(3) 高风速段(V2~Vout)。由于转速达到ωmax仅能依靠桨距角调节有功输出,则该风速段依靠变桨法实现定量减载,为系统提供有功备用。
减载控制通常与下垂控制配合使用。当电网频率变化超过一次调频死区时,可在风电机组机侧AC/DC换流器的有功控制环附加下垂控制来响应系统的有功需求。下垂控制产生的功率增量ΔP2为:
| $ \Delta P_{2}=-k_{2} \Delta f $ | (26) |
式中:k2为传统下垂控制系数。
结合式(14)可得DCWT中的下垂控制为:
| $ \Delta P_{2}=-k_{2} \frac{k \boldsymbol{\omega}_{\mathrm{n}}}{2 {\mathsf{π}} U_{\mathrm{dc} 2, n}} \Delta U_{\mathrm{dc} 2}=-k_{\mathrm{p}} \Delta U_{\mathrm{d} 2} $ | (27) |
式中:kp为变下垂控制系数。功率增量ΔP2须结合当前减载运行方式来确定由哪部分增发。
转速参与一次调频时,结合上文转速参与惯量响应时附加的转速增量,可计算出两者作用下最终的附加转速变化量Δω为:
| $ \Delta \omega=\frac{\Delta P_{1}+\Delta P_{2}}{3 k_{\mathrm{del}} \omega_{\mathrm{r}}^{2}}=\frac{1}{3 k_{\mathrm{del}} \omega_{\mathrm{r}}^{2}}\left(-k_{\mathrm{d}} \frac{\mathrm{d} U_{\mathrm{dc} 2}}{\mathrm{d} t}-k_{\mathrm{p}} \Delta U_{\mathrm{dc} 2}\right) $ | (28) |
桨距角控制参与一次调频时, 将直流电压偏差量产生功率增量对应的附加桨距角Δβ叠加至桨距角控制中的桨距角计算环节[25],进一步改变DCWT的有功出力,从而实现DCWT变速控制与附加桨距角控制参与一次调频的协调配合。其中桨距角增量Δβ为:
| $ \Delta \beta=\left(K_{\mathrm{pw}}+\frac{K_{\mathrm{iw}}}{s}\right) \Delta P_{2}=-\left(K_{\mathrm{pw}}+\frac{K_{\mathrm{iw}}}{s}\right) k_{\mathrm{p}} \Delta U_{\mathrm{dc} 2} $ | (29) |
式中:Kpw、Kiw分别为桨距角控制环中的比例、积分系数。
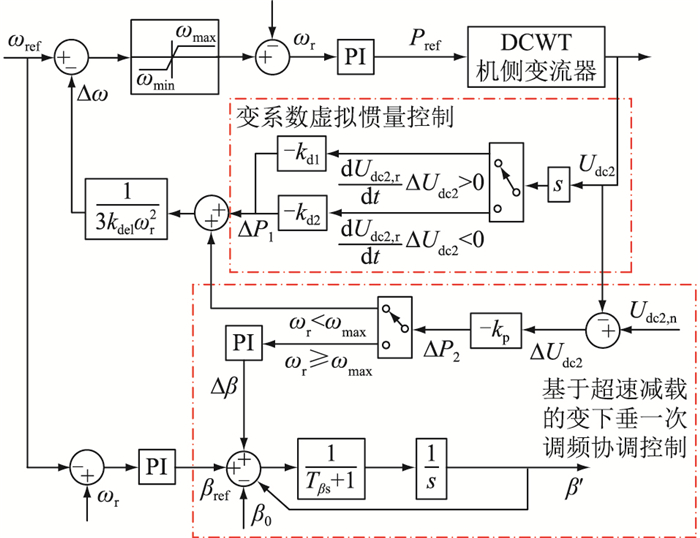
由式(28)、式(29)可知,通过调节变下垂控制系数kp即可改变风电的一次调频出力。最终DCWT的虚拟惯量及一次调频控制策略如图 4所示。图中,βref为DCWT运行于功率恒定区时的桨距角参考值;β0为查表法所得的预留桨距角;β′为桨距角输出值;Tβs为桨距角调节器时间常数。
|
图 4 DCWT虚拟惯量及一次调频控制策略 Fig. 4 DCWT virtual inertia and primary frequency modulation control strategy |
(1) 变虚拟惯量控制系数kd整定。根据上文提到的不同频率响应阶段对惯量的需求,对DCWT的虚拟惯量控制系数进行整定。
在频率背离稳态值阶段,为了阻止频率过快变化,该系数整定原则为DCWT在保证机组安全稳定运行的前提下尽可能多地释放转子动能。结合DCWT转速与直流低压侧直流电压变化率,对该阶段的虚拟惯量控制系数kd1进行整定。
DCWT转子运动方程为:
| $ \Delta P=-2 H_{\mathrm{W}} \omega \frac{\mathrm{d} \omega}{\mathrm{d} t} $ | (30) |
式中:HW为DCWT固有惯性时间常数。
假设DCWT输入输出功率差ΔP全由惯性控制环导致[26-27],结合式(16)可得:
| $ -2 {H_{\mathrm{W}} \omega} \frac{\mathrm{d} \omega}{\mathrm{d} t}=-k_{\mathrm{dl}} \frac{\mathrm{d} U_{\mathrm{dc} 2}}{\mathrm{~d} t} $ | (31) |
对式(31)两侧进行t1到t2的积分, 化简可得:
| $ k_{\mathrm{d} 1}=\frac{2 H_{\mathrm{W}}\left(\omega_{1}^{2}-\omega_{2}^{2}\right)}{U_{\mathrm{dc} 2, 1}-U_{\mathrm{de} 2, 2}} $ | (32) |
式中:ω1、Udc2, 1分别为t1时刻对应的风机转速和低压侧直流电压值;ω2、Udc2, 2分别为t2时刻对应的风机转速和低压侧直流电压值。
将式(32)中ω1、Udc2, 1替换为当前值ωr、Udc2, r,将ω2、Udc2, 2替换为边界值ωmin、Udc2, min,其中Udc2, min为DCWT被要求保持连接的频率最低值所对应的低压侧直流电压最低值。
| $ k_{\mathrm{d} 1}=\frac{2 H_{\mathrm{W}}\left(\omega_{\mathrm{r}}^{2}-\omega_{\mathrm{min}}^{2}\right)}{U_{\mathrm{dc} 2, \mathrm{r}}-U_{\mathrm{dc} 2, \text { min }}} $ | (33) |
在频率回归正常值阶段,惯性控制环会生成负的有功参考值,不利于频率恢复[28-29]。为了加快频率恢复,该阶段虚拟惯量系数kd2整定原则为令整个全直流输电系统惯量为零,此时系统中由转子动能与直流电容一同提供惯量,可令两者惯量进行抵消,结合式(24)得:
| $ k_{\mathrm{d} 2}=-\frac{C_{\mathrm{eq}} U_{\mathrm{dc} 1, \mathrm{n}}}{c} $ | (34) |
最终kd如式(35)所示,kd根据DCWT的当前转速与低压侧直流电压进行实时调整。
| $ k_{\mathrm{d}}=\left\{\begin{array}{l} \frac{2 H_{\mathrm{W}}\left(\omega_{\mathrm{r}}^2-\omega_{\min }^2\right)}{U_{\mathrm{dc} 2, \mathrm{r}}-U_{\mathrm{dc} 2, \min }} \quad \frac{\mathrm{d} U_{\mathrm{dc} 2, \mathrm{r}}}{\mathrm{d} t} \Delta U_{\mathrm{dc} 2}>0 \\ -\frac{C_{\mathrm{eq}} U_{\mathrm{dc} 1, \mathrm{n}}}{c} \quad \frac{\mathrm{d} U_{\mathrm{dc} 2, \mathrm{r}}}{\mathrm{d} t} \Delta U_{\mathrm{dc} 2}<0 \end{array}\right. $ | (35) |
(2) 变下垂控制系数kp整定。kp是影响DCWT一次调频的关键参数[30-31]。风机采用固定下垂控制会导致风机一次调频出力水平在不同风速下均相同,不能灵活高效地利用风能。所以需要合理整定kp,从而更好地平抑电网频率波动,提高电网运行稳定性。
不同风速下DCWT的减载功率不同,调频能力有所差异,文中结合DCWT的当前风速以及减载功率,对kp进行实时调整。
不同风速V下DCWT的调差系数σ为:
| $ \frac{1}{\sigma}=\frac{V^{3}}{a} $ | (36) |
式中:a为比例系数,与系统配置有关,文中取34.56。
结合当前减载功率ΔPdel, Pr为当前风机输出功率,最终kp为:
| $ k_{\mathrm{p}}=\frac{1}{\sigma} \Delta P_{\mathrm{del}}=\frac{V^{3}}{34.56} d P_{\mathrm{r}} $ | (37) |
文中策略考虑了风电全直流系统中直流电容的快速支撑性和DCWT调频的灵活性,改善了系统的惯性响应与一次调频效果。具体的调频步骤如下:
(1) 当系统负荷变化,电网频率发生波动时,网侧变流器的直流电容惯性同步控制使高压侧直流电压跟随频率变化,直流电容为系统提供少量惯量支撑。DC/DC的恒变比控制使低压侧直流电压与高压侧直流电压实时联动,DCWT根据低压侧直流电压的变化对系统频率变化作出响应。
(2) 当频率背离稳定值时,DCWT选择kd1作为虚拟惯量系数参与惯量响应,增大了系统惯量,与直流电容一同抑制频率的快速恶化。
(3) 当ΔUdc2超过一次调频死区时,DCWT启动一次调频,根据当前风速和风机的有功输出整定下垂控制系数kp;若转子转速小于额定转速,DCWT采用转速控制参与系统一次调频,若转子转速大于额定转速,则采用桨距角控制为系统提供有功支撑。
(4) 当频率恢复稳定值时,为了使系统频率快速稳定地恢复,DCWT的虚拟惯量控制系数由kd1切换为kd2,减小了系统惯量,避免了惯性控制环在频率恢复时产生的负面影响,最终系统频率恢复稳定。
4 仿真分析文中基于图 1所示风电全直流系统结构,采用PSCAD/EMTDC软件构建仿真模型,其中电网采用单同步机等效,主要仿真参数如表 1所示。
|
|
表 1 风电全直流系统主要参数 Table 1 Main parameters of wind power full DC system |
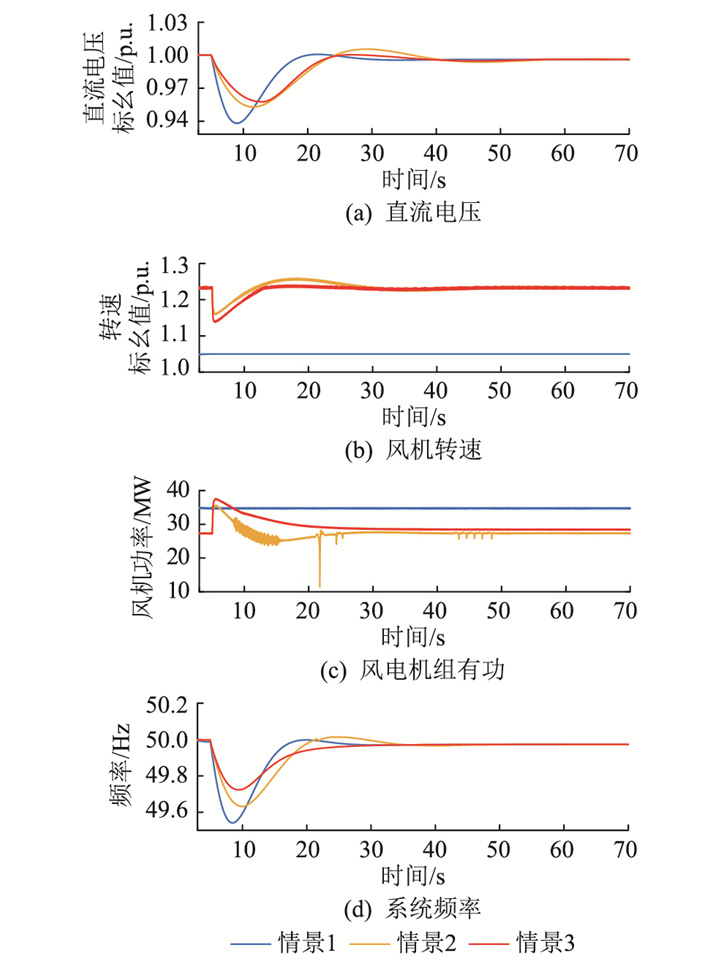
为了验证文中策略的有效性,当仿真运行到5 s时,在交流侧投入20 MW负载扰动,其中网侧换流站采用惯性同步控制。分别设置低风速(5.3 m/s)、中风速(8.3 m/s)、高风速(11.3 m/s)3种恒定风况对以下情景进行仿真对比验证,仿真结果见图 5—图 7和表 2。情景1:DCWT未附加调频控制策略;情景2:DCWT加入定系数虚拟惯量控制及定系数一次调频策略;情景3:采用文中所提变系数虚拟惯量响应与变系数一次调频控制策略。
|
图 5 低风速下仿真结果 Fig. 5 Simulation results at low wind speed |
|
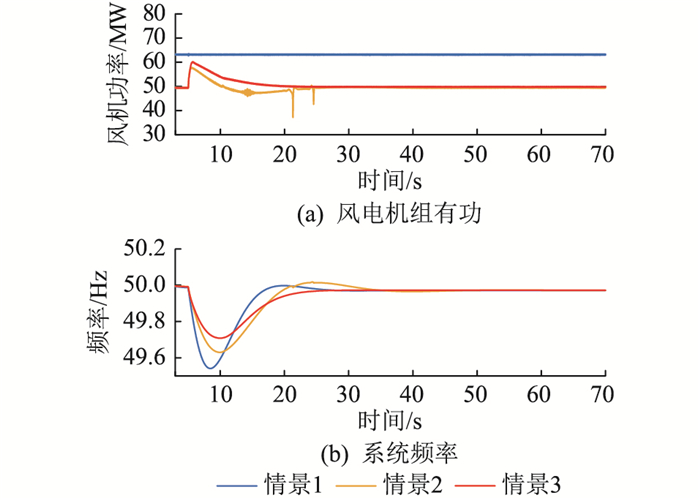
图 6 中风速下仿真结果 Fig. 6 Simulation results at medium wind speed |
|
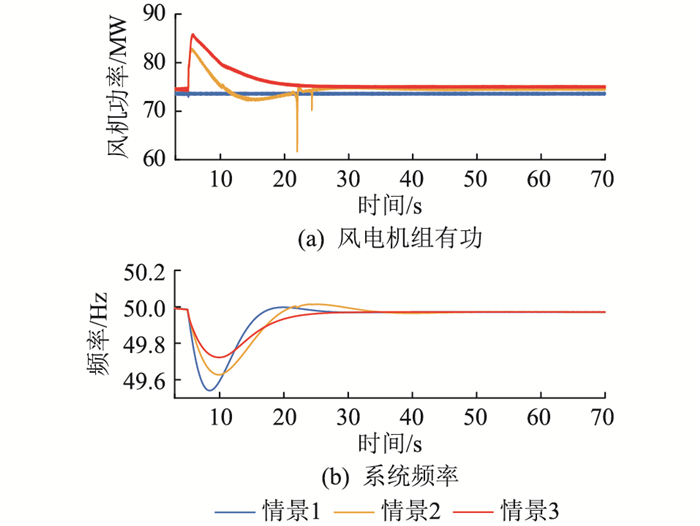
图 7 高风速下仿真结果 Fig. 7 Simulation results at high wind speed |
|
|
表 2 不同风速下的仿真结果 Table 2 Simulation results at different wind speeds |
文中选取最大频率变化率fROCOF,max、最低点频率fmin及稳态频率fss作为调频效果的评价指标。
在网侧换流站直流电容惯性同步控制下,如图 5(b)所示,直流输电线路上的直流电压跟随系统频率变化,直流电容如同发电机转子般为系统主动提供惯量支撑。
在惯量响应方面,选取图 5进行分析,当频率变化时,情景1中DCWT未附加频率控制,其有功输出保持恒定,系统频率恶化最严重。情景2加入DCWT定系数虚拟惯量控制后,DCWT的转速根据直流电压的降低而降低,其有功输出增加,转子动能与直流电容一同为系统提供惯量支撑,系统频率最低点提高,初始变化率减小,但由于虚拟惯量控制系数固定,不能适应机组运行状态变化而变化,灵活释放动能,DCWT的有功出力不稳,且在调频结束时刻会发生短暂的功率骤降,频率最低点提升有限,且在频率恢复阶段,会生成较大的负有功增量值,使频率恢复变慢,且存在超调现象。情景3加入文中所提DCWT变系数虚拟惯量控制后,在频率恶化阶段虚拟惯量控制系数根据当前可释放的转子动能进行整定,打破了固定系数的限制,DCWT的转子动能得到进一步释放,如图 5(c)和(d)所示,DCWT的转子转速下降得更多,其有功输出进一步提高,达到了改善系统频率最低点以及初始频率变化率的目的,在频率恢复阶段虚拟惯量控制系数取负值,惯性控制环生成正的转速增量值,避免了情景2中DCWT反向有功功率输出的情况,DCWT的转速及有功输出恢复加快,缩短了频率恢复时间,且无超调现象。
在一次调频方面,对比3种风速的调频效果并进行分析。情景1中DCWT不参与调频,频率最低点及稳态频率最低;情景2中DCWT附加了定系数一次调频,在直流电压降低时,其有功输出增加,但由于固定下垂控制系数的限制,DCWT的有功备用释放有限,系统频率最低点以及稳态频率得到较小幅度的提升。情景3中附加了变系数一次调频,如图 5(c)、图 6(a)、图 7(a)所示,不同风速下DCWT的有功不同,即拥有不同的减载备用功率,DCWT可根据当前风速以及有功功率对下垂控制系数进行调整,充分利用其减载备用功率,DCWT的有功增发进一步提高,进一步改善系统频率的最低点以及稳态偏差。
综上所述,在不同风速情景下,文中提出的变系数风电全直流系统惯性响应和一次调频协调控制策略在交流频率发生变化时都可充分发挥风电全直流系统的调频能力,为交流系统提供有功支撑,改善系统的惯性响应与一次调频。
4.2 随机风速下变系数风电全直流系统惯性响应与一次调频控制策略有效性仿真为验证所提变系数风电全直流系统惯性响应与一次调频控制策略在随机风速下的有效性,利用混合风速模型模拟实际自然风速,如图 8所示,设置与前文同样的负荷扰动,对情景2和情景3进行仿真对比验证,结果见图 8和表 3。
|
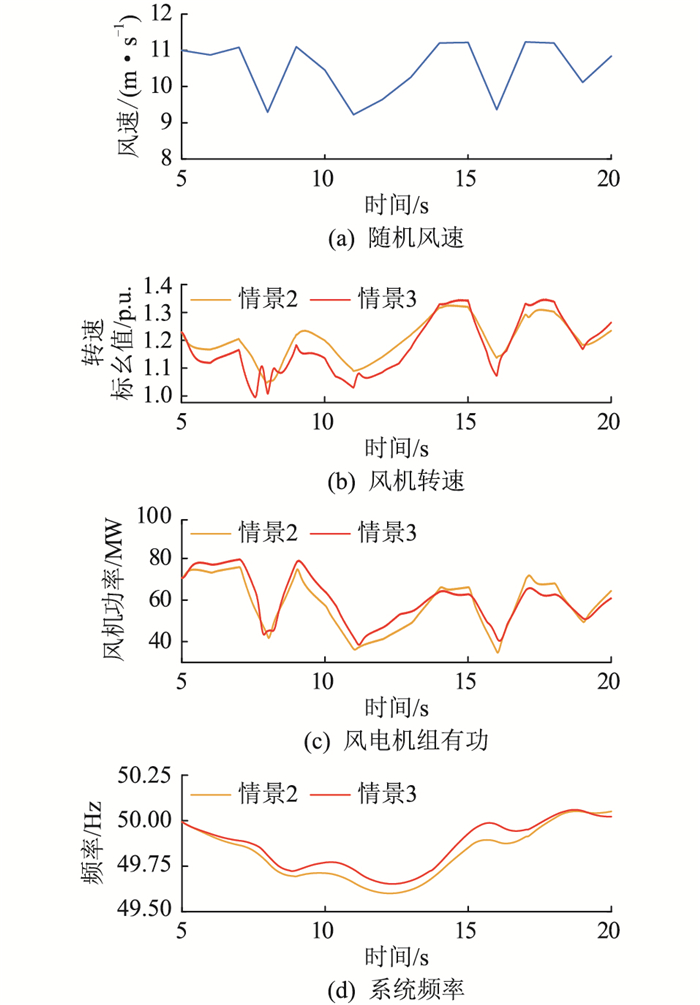
图 8 变风速下风电全直流系统调频策略仿真 Fig. 8 Simulation of frequency modulation strategy for wind power full DC system at variable wind speed |
|
|
表 3 变风速下的仿真结果 Table 3 Simulation results at variable wind speed |
在风速随机波动的情景下,5 s时发生负荷突增,在频率恶化阶段,初始风速为11 m/s,DCWT转速下降,释放转子动能,有功输出增加,情景3在变系数的惯性响应与一次调频的作用下,转速下降更多,有功增发更多,系统频率初始变化率更低;在风速发生波动时,DCWT捕获的机械功率随着风速增大而增大,其有功备用容量随之增加,意味着可释放的有功备用容量增加,根据所提策略,情景3的变虚拟惯性系数与变下垂系数根据当前风速与风机状态进行实时整定,不拘于固定系数的限制,如图 8(b)、(c)所示,情景3中DCWT的转速始终下降的幅度高于情景2,其有功输出更高,频率波动更为平缓,频率最低点更高; 在频率恢复阶段,由于情景3中虚拟惯性系数取负值,在不同风速下其DCWT的转速及有功输出皆恢复得更快。
综上所述,情景3的惯性响应与一次调频效果明显优于情景2,表明文中控制策略适用于随机风速。
4.3 电网故障下变系数风电全直流系统惯性响应与一次调频策略有效性仿真为了验证故障下文中所提变系数风电全直流系统惯性响应与一次调频控制策略的有效性,在交流电网并网母线处设置A相接地故障,故障时刻为5 s,故障持续时间为0.1 s,对3种情景进行仿真对比验证,结果如图 9和表 4所示。
|
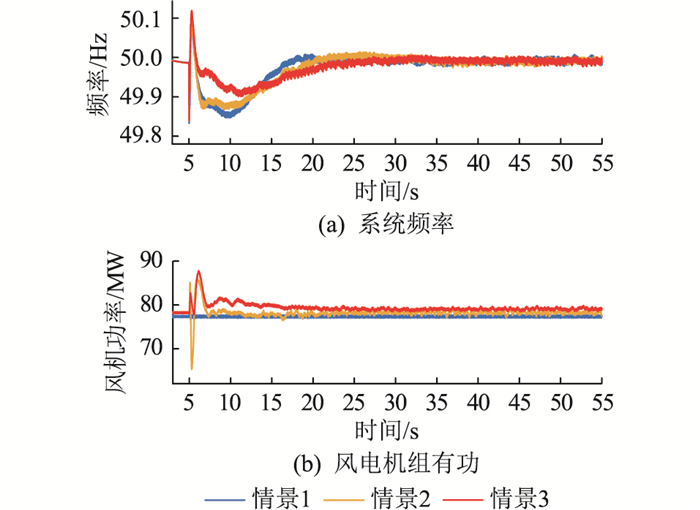
图 9 电网故障下风电全直流系统调频策略仿真 Fig. 9 Simulation of frequency modulation strategy for wind power full DC system with power grid failure |
|
|
表 4 电网故障下的仿真结果 Table 4 Simulation results with power grid failure |
仿真结果表明,情景2和情景3中的DCWT在电网故障情况下可为系统提供有功支撑,且情景3中DCWT有功出力更高,调频效果更好,可见文中所提风电全直流协调控制策略在电网故障情况时可有效改善系统的惯性响应与一次调频。综合4.1节、4.3节可得出,文中提出的控制策略适用于不同扰动程度场景。
5 结论针对风电全直流系统并网给系统带来的系统惯量降低、调频备用容量不足的问题,文中提出一种变系数的风电全直流系统惯性响应与一次调频控制策略,改善了系统的惯性响应及一次调频能力。通过仿真分析得出如下结论:
(1) 在惯量支撑方面,网侧换流站采用惯性同步控制,直流升压站采用恒变比控制,实现了直流电容对电网的惯量支撑以及直流低压侧的直流电压对交流系统频率的感知。在此基础上,对DCWT附加变虚拟惯性系数的虚拟惯量控制,使得风电全直流系统在不同频率响应阶段具备了不同的等效惯量,从而达到了抑制频率恶化以及加快频率稳定恢复的目的。
(2) 在一次调频方面,DCWT采用超速与变桨相结合的减载运行方式,通过变下垂控制来改变其有功出力,充分利用了不同风速下的备用容量,改善了风电全直流系统的一次调频。
| [1] |
徐彬, 薛帅, 高厚磊, 等. 海上风电场及其关键技术发展现状与趋势[J]. 发电技术, 2022, 43(2): 227-235. XU Bin, XUE Shuai, GAO Houlei, et al. Development status and prospects of offshore wind farms and it's key technology[J]. Power Generation Technology, 2022, 43(2): 227-235. (  0) 0) |
| [2] |
李铮, 郭小江, 申旭辉, 等. 我国海上风电发展关键技术综述[J]. 发电技术, 2022, 43(2): 186-197. LI Zheng, GUO Xiaojiang, SHEN Xuhui, et al. Summary of technologies for the development of offshore wind power industry in China[J]. Power Generation Technology, 2022, 43(2): 186-197. (  0) 0) |
| [3] |
李战龙, 王祥君, 王海云, 等. 基于直流风电机组的风电全直流输电系统综述[J]. 电测与仪表, 2022, 59(12): 14-24. LI Zhanlong, WANG Xiangjun, WANG Haiyun, et al. Review of wind power ALL-DC transmission system based on DC wind turbine[J]. Electrical Measurement & Instrumentation, 2022, 59(12): 14-24. (  0) 0) |
| [4] |
蔡旭, 施刚, 迟永宁, 等. 海上全直流型风电场的研究现状与未来发展[J]. 中国电机工程学报, 2016, 36(8): 2036-2048. CAI Xu, SHI Gang, CHI Yongning, et al. Present status and future development of offshore all-DC wind farm[J]. Proceedings of the CSEE, 2016, 36(8): 2036-2048. (  0) 0) |
| [5] |
戴礼国, 杨浩, 陈力, 等. 基于深度强化学习的风电柔直并网系统次同步振荡抑制方法[J]. 智慧电力, 2023, 51(4): 1-7, 91. DAI Liguo, YANG Hao, CHEN Li, et al. Subsynchronous oscillation suppression method for flexible direct grid-connected wind power system based on deep reinforcement learning[J]. Smart Power, 2023, 51(4): 1-7, 91. DOI:10.3969/j.issn.1673-7598.2023.04.001 (  0) 0) |
| [6] |
汪梦军, 郭剑波, 马士聪, 等. 新能源电力系统暂态频率稳定分析与调频控制方法综述[J]. 中国电机工程学报, 2023, 43(5): 1672-1694. WANG Mengjun, GUO Jianbo, MA Shicong, et al. Review of transient frequency stability analysis and frequency regulation control methods for renewable power systems[J]. Proceedings of the CSEE, 2023, 43(5): 1672-1694. (  0) 0) |
| [7] |
屈兴武, 王栋, 马天诚, 等. 支撑电网频率稳定的双馈风机一次调频控制需求分析[J]. 智慧电力, 2023, 51(10): 38-46. QU Xingwu, WANG Dong, MA Tiancheng, et al. Requirement analysis of DFIG primary frequency regulation control supporting grid frequency stability[J]. Smart Power, 2023, 51(10): 38-46. DOI:10.3969/j.issn.1673-7598.2023.10.006 (  0) 0) |
| [8] |
杨滢, 杨晓雷, 项中明, 等. 参与一次调频储能型风电场的交流外送振荡特性分析[J]. 智慧电力, 2023, 51(9): 105-112. YANG Ying, YANG Xiaolei, XIANG Zhongming, et al. Oscillation characteristic analysis of wind farm with energy storage participating primary frequency control[J]. Smart Power, 2023, 51(9): 105-112. DOI:10.3969/j.issn.1673-7598.2023.09.015 (  0) 0) |
| [9] |
刘英培, 谢乾, 梁海平. 柔性直流输电系统自适应虚拟惯性调频控制策略[J]. 电力系统自动化, 2021, 45(5): 129-136. LIU Yingpei, XIE Qian, LIANG Haiping. Frequency regulation control strategy for flexible DC transmission system based on adaptive virtual inertia[J]. Automation of Electric Power Systems, 2021, 45(5): 129-136. (  0) 0) |
| [10] |
朱介北, 史美琦, 张利, 等. 基于超级电容的海上风电柔直送出系统协调惯量支撑策略[J]. 电网技术, 2022, 46(8): 2938-2952. ZHU Jiebei, SHI Meiqi, ZHANG Li, et al. Supercapacitor-based coordinated inertia support strategy for offshore wind farms integration via VSC-HVDC[J]. Power System Technology, 2022, 46(8): 2938-2952. (  0) 0) |
| [11] |
李宇骏, 杨勇, 李颖毅, 等. 提高电力系统惯性水平的风电场和VSC-HVDC协同控制策略[J]. 中国电机工程学报, 2014, 34(34): 6021-6031. LI Yujun, YANG Yong, LI Yingyi, et al. Coordinated control of wind farms and VSC-HVDC to improve inertia level of power system[J]. Proceedings of the CSEE, 2014, 34(34): 6021-6031. (  0) 0) |
| [12] |
朱博, 徐攀腾, 刘科, 等. 柔性直流与风电协同的受端系统频率调控方法[J]. 东北电力大学学报, 2021, 41(2): 86-93. ZHU Bo, XU Panteng, LIU Ke, et al. Frequency control method for receiving end power system by DFIG and VSC-HVDC[J]. Journal of Northeast Electric Power University, 2021, 41(2): 86-93. (  0) 0) |
| [13] |
陆畅. HVDC辅助一次调频及其动态特性的研究[D]. 上海: 上海交通大学, 2007. LU Chang. Research on auxiliary primary frequency regulation by HVDC links and its dynamic characteristics[D]. Shanghai: Shanghai Jiao Tong University, 2007. (  0) 0) |
| [14] |
闫家铭, 毕天姝, 胥国毅, 等. 海上风电经VSC-HVDC并网改进频率控制策略[J]. 华北电力大学学报(自然科学版), 2021, 48(2): 11-19. YAN Jiaming, BI Tianshu, XU Guoyi, et al. An improved frequency control strategy for offshore wind farm connected by VSC-HVDC[J]. Journal of North China Electric Power University (Natural Science Edition), 2021, 48(2): 11-19. (  0) 0) |
| [15] |
王祥君, 李战龙, 王海云, 等. 基于新型直流风电机组的串联型全直流发电系统设计研究[J]. 电力系统保护与控制, 2022, 50(20): 178-187. WANG Xiangjun, LI Zhanlong, WANG Haiyun, et al. Design and research of a series all-DC power generation system based on a new DC wind turbine[J]. Power System Protection and Control, 2022, 50(20): 178-187. (  0) 0) |
| [16] |
何桂雄, 晁勤, 田易之, 等. 风电场恒速发电机动态等值参数聚合的研究[J]. 可再生能源, 2009, 27(1): 14-18, 22. HE Guixiong, CHAO Qin, TIAN Yizhi, et al. Research on the dynamic equivalent parameter aggregation of fixed-speed wind turbines in wind farm[J]. Renewable Energy Resources, 2009, 27(1): 14-18, 22. (  0) 0) |
| [17] |
李少林, 王伟胜, 张兴, 等. 基于频率响应区间划分的风电机组虚拟惯量模糊自适应控制[J]. 电网技术, 2021, 45(5): 1658-1665. LI Shaolin, WANG Weisheng, ZHANG Xing, et al. Fuzzy adaptive virtual inertia control strategy of wind turbines based on system frequency response interval division[J]. Power System Technology, 2021, 45(5): 1658-1665. (  0) 0) |
| [18] |
黎静华, 宋诚鑫, 兰飞. 基于参数模糊推理的风机虚拟惯量优化控制策略[J]. 电力系统自动化, 2023, 47(20): 125-133. LI Jinghua, SONG Chengxin, LAN Fei. Optimal control strategy of virtual inertia for wind turbine based on fuzzy inference of parameters[J]. Automation of Electric Power Systems, 2023, 47(20): 125-133. (  0) 0) |
| [19] |
杨仁炘, 施刚, 蔡旭, 等. 风电-多端柔直送出系统电压源型控制[J]. 中国电机工程学报, 2020, 40(5): 1498-1509. YANG Renxin, SHI Gang, CAI Xu, et al. Voltage source control of VSC-MTDC systems with wind farm integration[J]. Proceedings of the CSEE, 2020, 40(5): 1498-1509. (  0) 0) |
| [20] |
杨仁炘, 施刚, 蔡旭. 海上全直流型风电场的电压源型控制[J]. 电工技术学报, 2018, 33(S2): 546-557. YANG Renxin, SHI Gang, CAI Xu. Voltage source control of offshore all-DC wind farm[J]. Transactions of China Electrotechnical Society, 2018, 33(S2): 546-557. (  0) 0) |
| [21] |
LOU W H, JIN Z Y, ZHANG C H, et al. Analysis of primary frequency response based on overspeed and pitch control reserve and coordinated control strategy[C]//2023 IEEE International Conference on Power Science and Technology (ICPST). Kunming, China. IEEE, 2023: 193-198.
(  0) 0) |
| [22] |
朱家文, 陈卓, 刘人志, 等. 风电机组惯量支撑与一次调频综合控制策略[J]. 电子科技, 2023, 36(5): 9-15. ZHU Jiawen, CHEN Zhuo, LIU Renzhi, et al. Integrated control strategy of wind turbine inertia support and primary frequency regulation[J]. Electronic Science and Technology, 2023, 36(5): 9-15. (  0) 0) |
| [23] |
张留生, 谢震, 许可宝, 等. 基于超速和变桨优化协调的双馈风电机组一次调频控制[J]. 电器与能效管理技术, 2021(10): 18-27. ZHANG Liusheng, XIE Zhen, XU Kebao, et al. Primary frequency modulation control of DFIG based on optimization and coordination of overspeed and variable paddle[J]. Electrical & Energy Management Technology, 2021(10): 18-27. (  0) 0) |
| [24] |
李生虎, 朱国伟. 基于有功备用的风电机组一次调频能力及调频效果分析[J]. 电工电能新技术, 2015, 34(10): 28-33, 50. LI Shenghu, ZHU Guowei. Capability and effect of primary frequency regulation by wind turbine generators with active power reserve[J]. Advanced Technology of Electrical Engineering and Energy, 2015, 34(10): 28-33, 50. (  0) 0) |
| [25] |
彭海涛, 何山, 袁至, 等. 基于改进转子转速和桨距角协调控制的变速风电机组一次调频策略[J]. 电力自动化设备, 2023, 43(9): 87-94. PENG Haitao, HE Shan, YUAN Zhi, et al. Primary frequency regulation strategy for variable-speed wind turbines based on improved coordinated control of rotor speed and pitch angle[J]. Electric Power Automation Equipment, 2023, 43(9): 87-94. (  0) 0) |
| [26] |
WU Y K, YANG W H, HU Y L, et al. Frequency regulation at a wind farm using time-varying inertia and droop controls[C]//2018 IEEE/IAS 54th Industrial and Commercial Power Systems Technical Conference (I&CPS). Niagara Falls, ON, Canada. IEEE, 2018: 1-9.
(  0) 0) |
| [27] |
ZHANG Z S, SUN Y Z, LIN J, et al. Coordinated frequency regulation by doubly fed induction generator-based wind power plants[J]. IET Renewable Power Generation, 2012, 6(1): 38. (  0) 0) |
| [28] |
陈玮. 直驱型永磁同步风力发电系统主动频率支撑控制技术[D]. 杭州: 浙江大学, 2022. CHEN Wei. Control technology of direct-driven permanent magnet synchronous wind power generation system for active frequency support[D]. Hangzhou: Zhejiang University, 2022. (  0) 0) |
| [29] |
颜湘武, 孙雪薇, 崔森, 等. 基于转子动能与超级电容器储能的双馈风电机组惯量和一次调频改进控制策略[J]. 电工技术学报, 2021, 36(S1): 179-190. YAN Xiangwu, SUN Xuewei, CUI Sen, et al. Improved control strategy of inertia and primary frequency modulation of doubly-fed wind turbine based on rotor kinetic energy and super capacitor energy storage[J]. Transactions of China Electrotechnical Society, 2021, 36(S1): 179-190. (  0) 0) |
| [30] |
XU M T, JIN Y Q, MA J C, et al. Fuzzy frequency droop control of DFIG wind turbine generators adapted to continuous changes in wind speeds[J]. IEEE Access, 2023, 11: 115011-115024. (  0) 0) |
| [31] |
WAN T H, LI H, WANG C, et al. Variable droop control for wind farm to participate the system frequency regulation[C]//2019 IEEE 8th International Conference on Advanced Power System Automation and Protection (APAP). Xi'an, China. IEEE, 2019: 1422-1426.
(  0) 0) |
 2024, Vol. 43
2024, Vol. 43


 汝冬(1998),女,硕士在读,研究方向为新能源电力系统运行与控制(E-mail:
汝冬(1998),女,硕士在读,研究方向为新能源电力系统运行与控制(E-mail: