文章编号: 2096-3203(2024)03-0192-09 中图分类号: TM854
2. 南京航空航天大学经济与管理学院,江苏 南京 211106;
3. 杭州钱江电气集团股份有限公司,浙江 杭州 311243
油浸式电力变压器作为核心输变电装备之一,其安全可靠运行是保证电网可靠供电的重要基础[1-3]。作为反映变压器绝缘状态的关键特征,变压器油中溶解气体是判断变压器运行状态,识别潜在缺陷的有效方法[4]。通过油中溶解气体进行预测分析,可以实现变压器运行状态的预测、运行风险的预警、潜在故障的发现,为变压器状态检修策略的制定和设备健康管理提供有力的支撑[5]。
变压器油中溶解气体随着其运行时间的增长而呈现不同程度的变化,变压器状态预测本质上是一个油中溶解气体时间序列趋势预测的问题。国内外学者针对油中溶解气体的时间序列预测问题开展了大量研究,其中利用神经网络进行趋势预测广为应用。崔宇等[6]采用双重注意力机制改进长短期记忆(long short term memory, LSTM)神经网络,提取油中溶解气体参量间的关联关系,提高油中溶解气体含量的预测准确性,实现油中溶解气体含量的预测;代杰杰等[7]采用深度信念网络(deep belief network, DBN)实现油中溶解气体的趋势预测。由于神经网络参数选取标准不确定,为解决不合适的参数带来较大预测误差的问题,有学者使用智能优化算法如麻雀搜索算法[8]和粒子群算法[9]等用来对神经网络初始参数寻优,从而提高神经网络预测油中溶解气体含量的精度。上述方法虽能实现油中溶解气体的趋势预测,但由于在役变压器运行过程中复杂的工况、缺陷隐患以及监测装置的测量误差等因素的综合影响[10],实际的油中溶解气体记录值中存在明显的不确定性、非平稳性、非线性分量,这些分量的存在会导致对油中溶解气体原始序列预测的精度降低,影响变压器状态评价结果。
先分解单一的油中溶解气体时间序列,再对分解后的不同分量分别进行预测,最终将其合成为单一序列的方法(分解-预测-合成),在风电场风速预测[11-14]、太阳能发电功率预测[15]、电网负荷预测[16]、金融经济数据预测[17-18]等领域应用广泛。此类方法可以降低预测难度,有效提升预测精度[19-20]。面对变压器油中溶解气体趋势预测,采用分解-预测-合成的方法也取得了不错的成效。典型的变压器油中溶解气体趋势预测方法有变分模态分解(variational mode decomposition, VMD)结合门控循环单元(gated recurrent unit, GRU)神经网络[21]、经验小波变换(empirical wavelet transform, EWT)结合梯度提升径向基[10]、经验模态分解(empirical mode decomposition, EMD)结合LSTM[22]、集合经验模态分解(ensemble empirical mode decomposition, EEMD)结合极限学习机[23]。在上述分解算法中VMD和EWT对参数设置均较为敏感,而这些参数没有固定的选取原则,依赖人工调试。对于EMD算法而言,其结果存在模态混叠的现象。为了解决这一问题,EEMD通过叠加辅助噪声的方法来消除EMD中存在的模态混叠现象,但叠加的噪声信号难以完全去除[24-25]。作为EEMD的改进算法,自适应噪声完备集合经验模态分解(complete ensemble empirical mode decomposition with adaptive noise,CEEMDAN),借鉴了EEMD中的叠加噪声消除模态混叠的方法并通过多次叠加噪声的方式抵消噪声,克服了EEMD分解效率低以及信号重构不完整的缺陷[26]。相比于EMD和EEMD,CEEMDAN具有更好的去噪能力、稳定性、物理解释性和更高的精度。因此,采用CEEMDAN对油中溶解气体数据进行分解,并以其相应的分量进行趋势预测,能有效提高预测精度。
时间序列预测模型的选取对预测效果也有着极为显著的影响。目前,循环神经网络(recurrent neural network, RNN)由于其在时间序列上的优异表现而备受关注,但其在训练过程中存在着梯度爆炸或梯度消失的问题。LSTM和GRU在RNN的基础上改进网络结构,从而缓解梯度消失和梯度爆炸的问题,但RNN及其变种计算复杂度高,无法并行实现,会导致在数据量较大的情况下网络结构的训练时间过长。卷积神经网络(convolution neural network, CNN)有着可以实现大规模并行处理的优势,通常应用于机器视觉等领域,而时间卷积网络(time convolution network, TCN)作为CNN的一种改进形式,引入空洞卷积和因果卷积来适应序列预测问题,具有可变长的输入、计算效率高等优点,同时加入残差模块可以解决梯度爆炸和梯度消失问题,TCN在机器学习、语音识别等时序问题上有着优于RNN的精度。面对变压器油中溶解气体长序列、大数据量的任务,TCN能展现出更高的性能。
鉴于上述情况,文中提出一种基于CEEMDAN-TCN预测-重构的方法,实现在运变压器油中溶解气体含量的时序预测。首先,对油中溶解气体原始序列进行CEEMDAN,得到平稳线性和非平稳非线性的不同分量,降低不同分量之间的耦合影响;其次,对于分解得到的各个分量,分别建立TCN并根据历史数据对网络进行训练;然后,基于各个训练完成的TCN,对相应的分量序列进行预测;最后,基于CEEMDAN算法的重构特性,叠加所有分量的预测结果,重构得到油中溶解气体含量原始序列的预测结果。
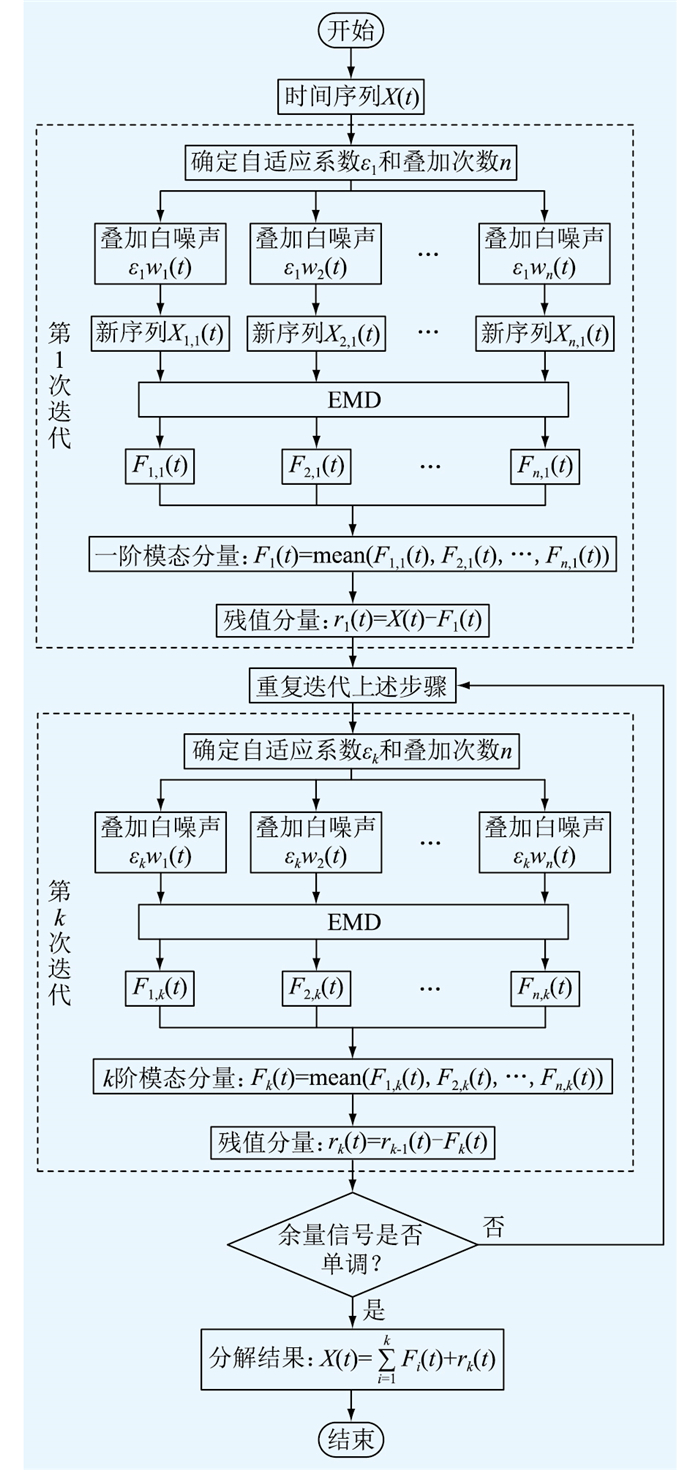
1 CEEMDAN算法在变压器的运行过程中,实际的油中溶解气体监测序列中存在着非线性和非平稳性的分量[10]。因此,将原始序列中非线性和非平稳分量分离后分别进行预测,可以有效提取序列中的隐藏信息,提高预测结果的准确性。CEEMDAN是EMD的改进算法,通过在原始信号中自适应添加高斯白噪声,消除EMD中的模态混叠问题;同时,采用多次叠加高斯白噪声取平均的方法,使得到的本征模态分量(intrinsic mode function,IMF)重构后的序列与原始序列误差接近0。CEEMDAN油中溶解气体时间序列的流程如下。
(1) 在原始油中溶解气体序列X(t)上分别叠加n个白噪声分量ε1wj(t),得到n个新序列Xj, 1(t),其中ε1为第1次迭代的自适应系数,wj(t)为随时间变化的第j个白噪声信号(j=1, 2, …, n)。对这n个序列分别进行EMD,得到第j个序列对应的一阶模态分量Fj, 1(t),对Fj, 1(t)求平均值后得到CEEMDAN的一阶IMF(简写为F1,以此类推,Fi为i阶IMF)为:
| $ F_1(t)=\frac{1}{n} \sum\limits_{j=1}^n F_{j, 1}(t) $ | (1) |
(2) 计算CEEMDAN后的第1个残差序列r1(t)为:
| $ r_1(t)=X(t)-F_1(t) $ | (2) |
(3) 在第2次迭代时,r1(t)为原始序列。在残差序列r1(t)上再次添加n个白噪声分量ε2wj(t),其中,ε2为第2次迭代的自适应系数,并进行EMD,得到n个二阶模态分量Fj, 2(t)。同样,对Fj, 2(t)求平均值后得到CEEMDAN的F2为:
| $ F_2(t)=\frac{1}{n} \sum\limits_{j=1}^n F_{j, 2}(t) $ | (3) |
(4) 重复步骤(2)和步骤(3),可以得到经过CEEMDAN后的第i个残差分量ri(t)和Fi+1(t)为:
| $ r_i(t)=r_{i-1}(t)-F_i(t) $ | (4) |
| $ F_{i+1}(t)=\frac{1}{n} \sum\limits_{j=1}^n F_{j, i+1}(t) $ | (5) |
式中:Fj, i+1为第i个残差分量添加白噪声信号后,第j个序列经过EMD后的i+1阶模态分量,i=1, 2, …, k。
(5) 当残差信号ri(t)无法再进行EMD时,CEEMDAN终止。
综上所述,CEEMDAN的油中溶解气体序列算法流程如图 1所示。
|
图 1 CEEMDAN算法流程 Fig. 1 Flow chart for CEEMDAN algorithm |
原始油中溶解气体序列X(t)经CEEMDAN后得到k个IMF(F1(t)、F2(t)、…、Fk(t))和残差rk(t),则原始序列可以表示为:
| $ X(t)=\sum\limits_{i=1}^k F_i(t)+r_k(t) $ | (6) |
TCN结合空洞卷积和残差连接,可用于序列建模的神经网络模型[27]。相比于RNN,TCN在机器翻译、语音识别等任务上能够达到更优的效果[28]。TCN的主要优势在于其可以并行处理序列数据,所需训练的参数更少,有更加灵活的应用场景[29]。
TCN中采用的空洞卷积为:
| $ G(\boldsymbol{L}, \boldsymbol{X})=\sum\limits_{m=1}^M l_m x_{t-d m} $ | (7) |
式中:X = {x1, x2, …, xt, …, xT}为输入的油中溶解气体时间序列,xt为t时刻的油中溶解气体数据,T为油中溶解气体时间序列的最终时间;L = {l1, l2, …,lm,…,lM}为M个卷积核相量;lm为第m个卷积核;d为空洞率。
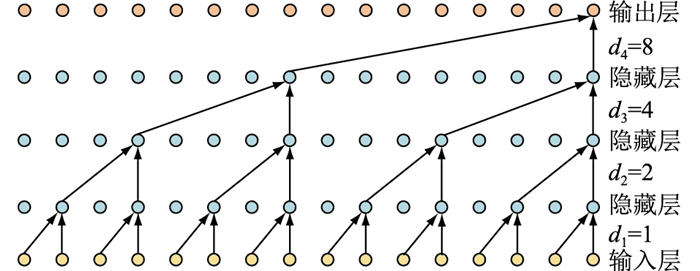
与传统卷积网络相比,空洞卷积允许卷积层的输入存在间隔采样,由空洞序列D={d1, d2, …, dp}控制,dp为p层空洞率,如图 2所示。第一层隐藏层d1=1,表示输入时对每个点进行采样;第二层隐藏层d2=2,表示对输入时间隔1个点进行采样,以此类推。因此,独特结构使得空洞卷积的感受野范围随着卷积层数的增加呈指数型增长,从而用少量的层数获得较大感受野,实现对全局信息的学习。
|
图 2 空洞卷积示意,空洞序列为D={1, 2, 4, 8} Fig. 2 Schematic diagram for dilated convolution, dilation series D={1, 2, 4, 8} |
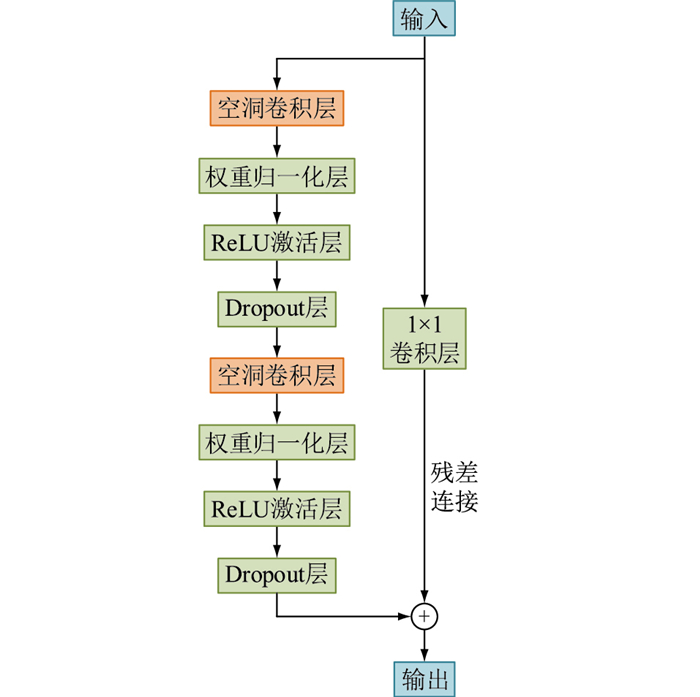
图 3为TCN的基本结构,其以空洞卷积为基础,增加权重归一化层、ReLU激活层和Dropout层。
|
图 3 TCN基本结构 Fig. 3 Basic structure of TCN |
此外,为增强网络的稳定性,防止中间层过多导致训练出现梯度消失问题,TCN中还额外引入残差连接结构,将输入序列通过1×1的卷积层后与经过空洞卷积网络计算后的数据直接相加,作为本层的最终输出。TCN中输出层相对输入层的感受野可以表示为:
| $ R_{\text {field }}=1+2(M-1) N_{\text {stack }} \sum\limits_{p=1}^{L_{\text {layer }}} d_p $ | (8) |
式中:Rfield为输出层的感受野;Nstack为堆栈个数;Llayer为隐藏层数量。
2.2 油中溶解气体预测流程文中所提出的基于CEEMDAN和TCN的变压器油中溶解气体含量预测流程如图 4所示。预测流程的基本步骤如下。

|
图 4 基于CEEMDAN和TCN的油中溶解气体含量预测流程 Fig. 4 Flow chart for dissolved gas in oil prediction based on CEEMDAN and TCN |
步骤1:对原始油中溶解气体数据进行预处理,剔除异常值和离群值;同时,对于1天内多个监测点的情况,取这些点的平均值作为当天的监测数据;对于缺失数据的情况,将该点前后最近的2个正常数据进行拼接。
步骤2:对处理后的序列进行CEEMDAN,得到k个IMF序列。
步骤3:对于每个IMF序列,分别将其划分为训练集和测试集,随后使用训练集对TCN网络进行训练,接着对每个序列进行预测,形成新的预测IMF序列。
步骤4:将TCN给出的各个IMF的预测结果进行叠加,得到最终预测结果。
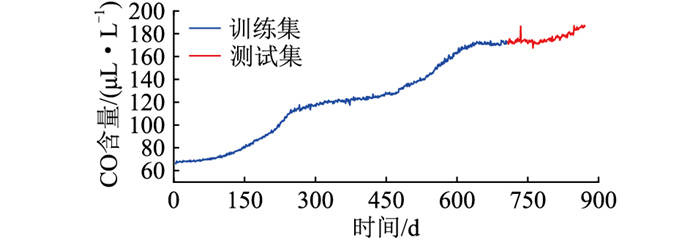
3 案例分析为验证文中提出的油中溶解气体含量预测方法,采用油浸式变压器(型号为ODFS-334000/500)油中溶解气体在线监测数据中的CO含量序列作为研究对象。该在线监测数据起止时间2020年1月1日—2022年6月8日,共有868个数据点,油中溶解气体数据如图 5所示,按照8 ∶2的比例将其划分训练集和测试集。
|
图 5 变压器CO含量在线监测数据与测试集和训练集划分 Fig. 5 Online CO concentration monitoring data of transformer and train-test data set division |
从图 5可以看出,在运行过程,CO含量呈现总体上升的趋势。同时,在该上升趋势中,由于运行工况的变化和在线监测设备检测误差,存在着局部的波动和突变情况。采用CEEMDAN对图 5所示CO含量进行分解,得到的分解结果如图 6所示。同样按照8 ∶2的比例划分训练集和测试集。
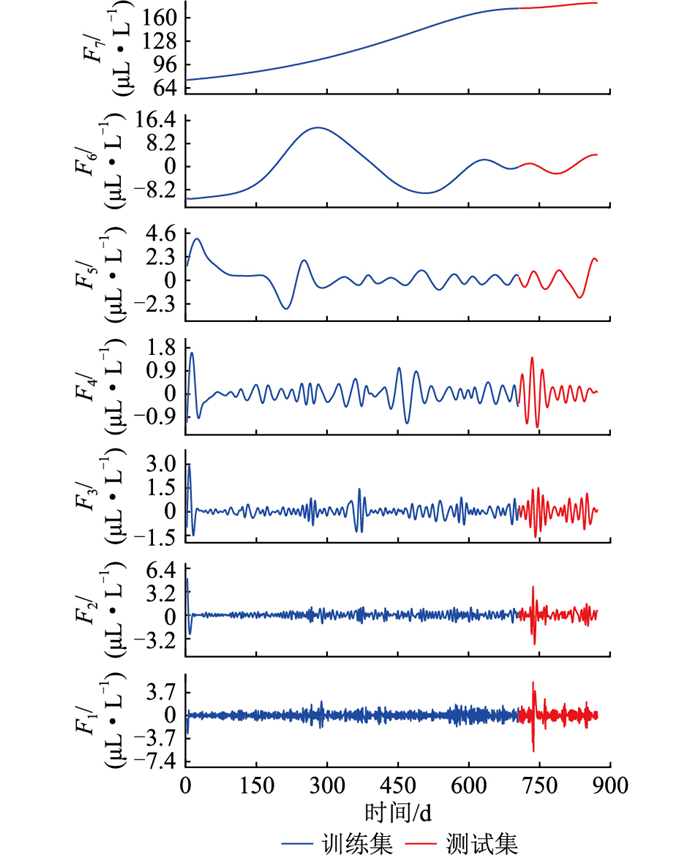
|
图 6 变压器CO含量的CEEMDAN结果与测试集和训练集划分 Fig. 6 CEEMDAN results of CO in transformer and train-test data set division |
F1—F7代表不同的频率范围和能量特征。其中F7与原始序列趋势相同,为其主要成分,而分量F1—F6呈现不稳定的波动趋势,分别代表CO含量序列中高频分量,能够反映出变压器运行过程中CO气体的突变现象和由检测设备所造成的随机误差等信息。
为验证采用CEEMDAN算法后预测精度的改进,文中首先采用相同设置的TCN对图 5和图 6所示分解前后的序列进行预测。根据神经网络结构参数的经验性原则,所用TCN参数如表 1所示。采用CEEMDAN前后的CO含量预测结果对比如图 7所示。TCN对CEEMDAN后得到的CO各IMF的预测结果如图 8所示。
|
|
表 1 TCN模型参数设置 Table 1 Parameters setting of TCN model |

|
图 7 CEEMDAN前后TCN预测CO含量结果对比 Fig. 7 Comparison of TCN prediction results for CO with and without CEEMDAN |
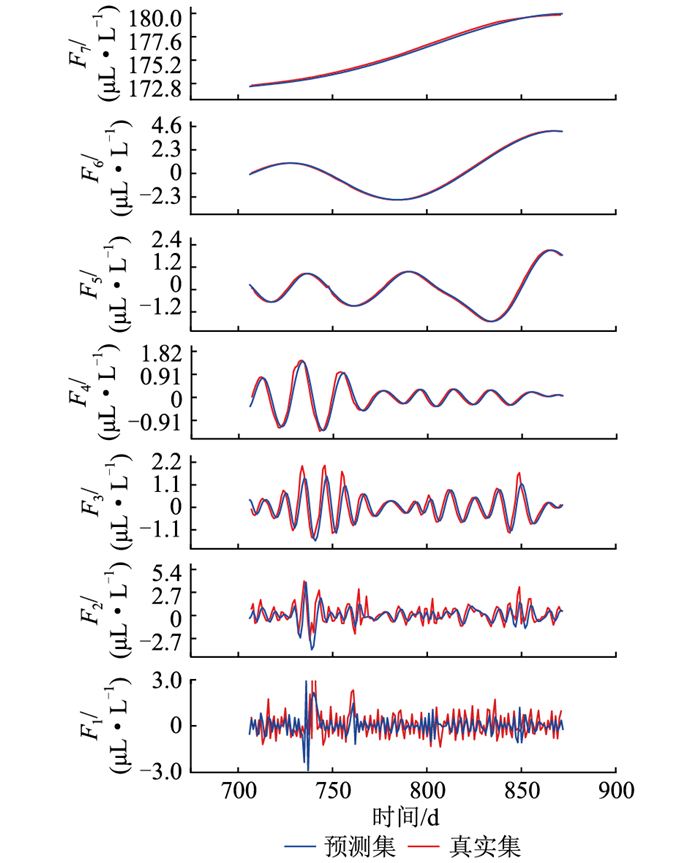
|
图 8 CEEMDAN后TCN预测CO各IMF的结果 Fig. 8 TCN prediction IMF results for CO with CEEMDAN |
使用CEEMDAN将CO分解为不同阶的IMF,然后再对每个分量进行模型训练和预测,图 8的预测结果能够更为准确地捕捉到分量的上升、下降、周期性变化,因此每个分量的预测结果都是准确有效的。在提高各分量的预测精度后,也进一步提高叠加后油中溶解气体的预测精度,可以更高效和准确地捕捉原始油中溶解气体序列的趋势和波动。
为量化分析采用CEEMDAN后给预测结果带来的精度提升,文中采用均方根误差ermse、平均绝对误差emae和最大误差emax 3个评价指标,各指标计算公式为:
| $ e_{\text {rmse }}=\sqrt{\frac{1}{n} \sum\limits_{t=1}^{t_{\text {end }}}\left(X_{\text {pred }}(t)-X(t)\right)} $ | (9) |
| $ e_{\text {mae }}=\frac{1}{m} \sum\limits_{t=1}^{t_{\text {end }}}\left(X_{\text {pred }}(t)-X(t)\right)^2 $ | (10) |
| $ e_{\text {max }}=\max \left(X_{\text {pred }}(t)-X(t)\right) $ | (11) |
式中:Xpred(t)为油中溶解气体在t时刻的预测结果;tend为油中溶解气体序列的最后时刻。
根据图 7可以计算出采用CEEMDAN前、后TCN对CO含量的预测误差,结果如表 2所示。相较于直接使用TCN预测的方法,采用CEEMDAN后再预测可以使预测精度有较大的提升,ermse、emae、emax分别提升53.47%、41.18%、13.36%,能够充分证明CEEMDAN的有效性。
|
|
表 2 采用CEEMDAN前后TCN预测CO含量精度对比 Table 2 Comparison of accuracy for TCN prediction CO with and without CEEMDAN respectively |
为进一步验证文中所提出的TCN对油中溶解气体数据预测优于其他RNN,选取时间序列预测常用的LSTM和双向长短期记忆(bi-directional long short term memory,BiLSTM)神经网络作为对比。为了排除层数对预测效果的影响,2种网络分别使用了单层和双层2种。其中,每层LSTM神经网络和BiLSTM神经网络参数设置如表 3所示。
|
|
表 3 LSTM神经网络和BiLSTM神经网络参数设置 Table 3 Parameter settings for LSTM and BiLSTM neural networks |
此外,考虑到神经网络训练过程中的随机性,对于每种预测方法均进行30轮训练,并对每轮训练得到的预测结果取均值。不同神经网络的预测精度对比结果如图 9所示。由图 9可以看出,采用CEEMDAN后,所有网络的预测精度在各个指标上均有较大的提升。对采用CEEMDAN时不同网络的预测精度进行对比,如表 4所示。由表 4可以看出,相较于其余4种神经网络结构,TCN在3个指标上均能实现最优的预测精度。
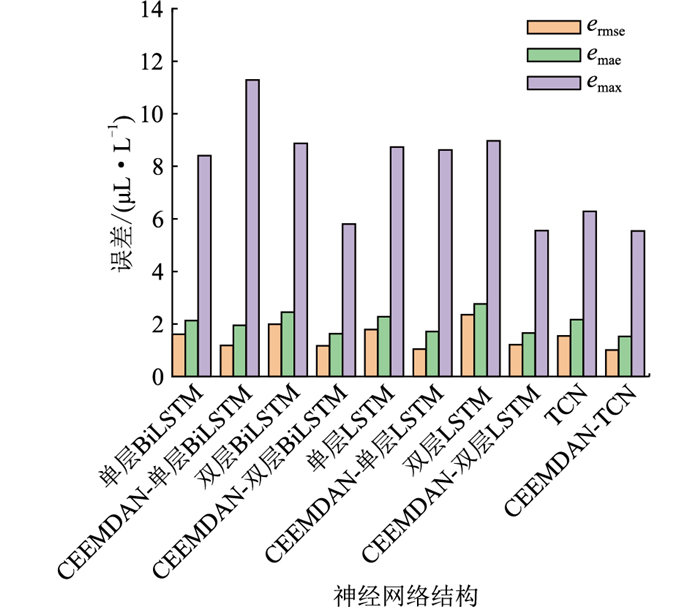
|
图 9 不同神经网络在CEEMDAN和不分解时CO含量的预测精度对比 Fig. 9 Comparison of prediction accuracy of different neural networks for CO concentration with and without CEEMDAN |
|
|
表 4 采用CEEMDAN时不同神经网络对CO含量的预测精度对比 Table 4 Comparison of prediction accuracy of different neural networks for CO concentration with CEEMDAN |
为了能够体现算法的普适性,文中又新增同地区另外2台变压器(T1、T2)的CO、CO2、H2、总烃气体作为预测对象,其中变压器T1的气体数据如图 10所示。预测结果使用ermse和emae 2种误差指标进行分析。由于神经网络训练过程中存在着一定的随机性,对于每种神经网络模型在每种气体上均进行10次训练,统计这10次训练结果中各评价指标的平均值,加粗数据表示误差最小,如表 5、表 6所示,其中,BiGRU为双向GRU。
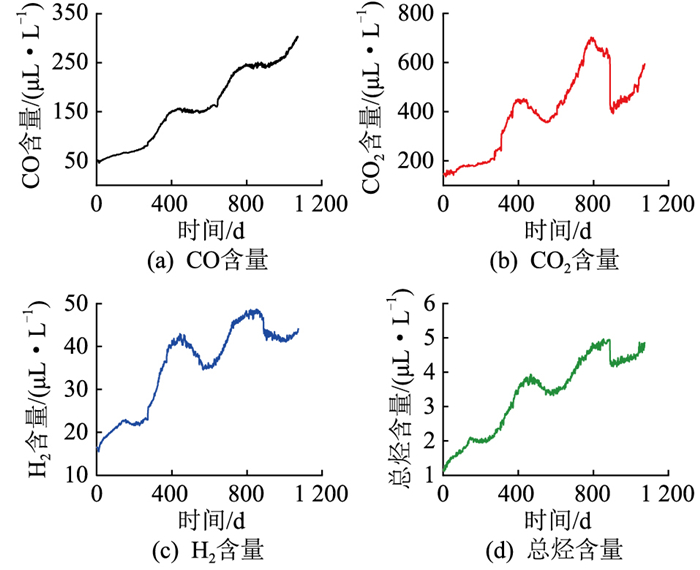
|
图 10 T1变压器中油中溶解气体变化趋势 Fig. 10 Dissolved gas in oil variation trend in transformer T1 |
|
|
表 5 2台变压器未使用CEEMDAN时各气体含量emae预测结果 Table 5 emae of dissolved gas in oil prediction results of two transformers without CEEMDAN |
|
|
表 6 2台变压器未使用CEEMDAN时各气体含量ermse预测结果 Table 6 ermse of dissolved gas in oil prediction results of two transformers without CEEMDAN |
未使用CEEMDAN时,使用TCN对2台变压器气体进行训练并预测,ermse和emae这2个误差指标均有半数达到最优。
进一步地,对上述各气体使用CEEMDAN后的IMF进行预测,结果如表 7和表 8所示。采用CEEMDAN后,2台变压器上预测结果的ermse和emae均最低,TCN预测精度相较于直接预测时有着明显的提升,预测结果也明显优于其余的神经网络。
|
|
表 7 2台变压器使用CEEMDAN时各气体含量emae预测结果 Table 7 emae of dissolved gas in oil prediction results of two transformers with CEEMDAN |
|
|
表 8 2台变压器使用CEEMDAN时各气体含量ermse预测结果 Table 8 ermse of dissolved gas in oil prediction results of two transformers with CEEMDAN |
参考文献[30-31]对在油中溶解气体预测上表现不错的2种方法进行比较。在CEEMDAN和BiLSTM神经网络的基础上,一种是增加Savitzky-Golay(SG)滤波的CEEMDAN-SG-BiLSTM气体趋势预测法;另一种是使用灰色关联分析(grey relational analysis,GRA)的GRA-CEEMDAN-BiLSTM气体趋势预测法。分别使用2种方法对文中案例中的变压器油中溶解气体(CO)进行趋势预测,同时引入CO2、H2和总烃作为辅助气体并对预测结果进行评价。
CO预测趋势如图 11所示,可以明显看出,文中方法(CEEMDAN-TCN)的预测轨迹与实际CO气体轨迹最为相近,而GRA-CEEMDAN-BiLSTM预测的轨迹偏离较远,CEEMDAN-SG-BiLSTM在气体波动较大的部分预测效果较差。
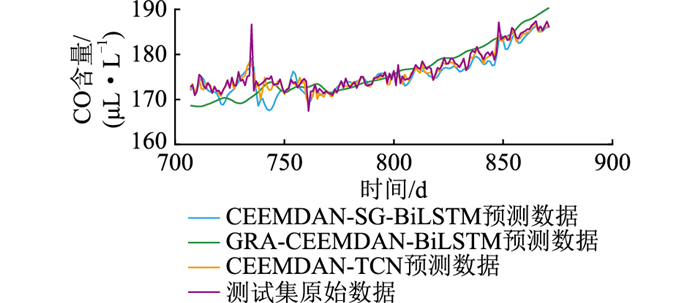
|
图 11 不同神经网络方法预测结果对比 Fig. 11 Comparison of prediction results by different neural network methods |
将3种方法与原始气体的ermse、emae、emax列于表 9。可知,相较于CEEMDAN-SG-BiLSTM和GRA-CEEMDAN-BiLSTM,文中方法的最大误差分别提升233.94%和133.75%,均方根误差分别提升1.98%和195.05%。文中方法的平均绝对误差略大于CEEMDAN-SG-BiLSTM,但相较GRA-CEEMDAN-BiLSTM提升58.83%。综合考虑3种误差结果,文中方法仍具有较为优异的性能。
|
|
表 9 文献中方法与文中方法的误差对比 Table 9 The error comparison between the method in the literature and the method in this paper |
文中提出基于CEEMDAN-TCN预测-重构的变压器油中溶解气体预测方法。相较于使用TCN直接预测和其他时间序列神经网络方法,文中方法可以有效提高预测精度,为实时在线预测变压器油中溶解气体提供一种新思路,有利于制定长期计划、调整运营策略和预防潜在问题。
(1) 相较于仅使用TCN,采用CEEMDAN-TCN预测-重构的方法对油中溶解气体进行处理,预测结果的ermse、emae、emax分别提高53.47%、41.18%、13.36%,实现了油中溶解气体预测精度的提升。
(2) TCN在油中溶解气体预测上有着良好的普适性,通过对2台变压器的4种不同油中溶解气体气体进行趋势变化预测可知,相比于不同结构的LSTM和BiLSTM,文中方法在多个气体含量预测结果上获得最小误差,适用性较强。
(3) 与2种较新且更为复杂的油中溶解气体预测方法(CEEMDAN-SG-BiLSTM和GRA-CEEMDAN-BiLSTM)进行对比,文中预测方法评价指标都有一定程度的提升,ermse、emae、emax最大提升195.05%、58.83%、233.94%,表现出优异的性能。
| [1] |
刘云鹏, 许自强, 李刚, 等. 人工智能驱动的数据分析技术在电力变压器状态检修中的应用综述[J]. 高电压技术, 2019, 45(2): 337-348. LIU Yunpeng, XU Ziqiang, LI Gang, et al. Review on applications of artificial intelligence driven data analysis technology in condition based maintenance of power transformers[J]. High Voltage Engineering, 2019, 45(2): 337-348. (  0) 0) |
| [2] |
REDIANSYAH D, PRASOJO R A, SUWARNO, et al. Artificial intelligence-based power transformer health index for handling data uncertainty[J]. IEEE Access, 2021, 9: 150637-150648. DOI:10.1109/ACCESS.2021.3125379 (  0) 0) |
| [3] |
周晶, 罗日成, 黄军. 基于改进小波阈值-CEEMDAN的变压器局部放电超声波信号白噪声抑制方法[J]. 高压电器, 2024, 60(1): 163-171. ZHOU Jing, LUO Richeng, HUANG Jun. White noise suppression method of partial discharge ultrasonic signal of transformer based on improved wavelet threshold-CEEMDAN[J]. High Voltage Apparatus, 2024, 60(1): 163-171. (  0) 0) |
| [4] |
JIANG J, CHEN R Y, CHEN M, et al. Dynamic fault prediction of power transformers based on hidden Markov model of dissolved gases analysis[J]. IEEE Transactions on Power Delivery, 2019, 34(4): 1393-1400. DOI:10.1109/TPWRD.2019.2900543 (  0) 0) |
| [5] |
QI B, WANG Y M, ZHANG P, et al. A novel deep recurrent belief network model for trend prediction of transformer DGA data[J]. IEEE Access, 2019, 7: 80069-80078. DOI:10.1109/ACCESS.2019.2923063 (  0) 0) |
| [6] |
崔宇, 侯慧娟, 胥明凯, 等. 基于双重注意力机制的变压器油中溶解气体预测模型[J]. 中国电机工程学报, 2020, 40(1): 338-347. CUI Yu, HOU Huijuan, XU Mingkai, et al. A prediction method for dissolved gas in power transformer oil based on dual-stage attention mechanism[J]. Proceedings of the CSEE, 2020, 40(1): 338-347. (  0) 0) |
| [7] |
代杰杰, 宋辉, 杨祎, 等. 基于深度信念网络的变压器油中溶解气体浓度预测方法[J]. 电网技术, 2017, 41(8): 2737-2742. DAI Jiejie, SONG Hui, YANG Yi, et al. Concentration prediction of dissolved gases in transformer oil based on deep belief networks[J]. Power System Technology, 2017, 41(8): 2737-2742. (  0) 0) |
| [8] |
刘展程, 王爽, 唐波. 基于SSA-BiGRU-Attention模型的变压器油中溶解气体含量预测[J]. 高电压技术, 2022, 48(8): 2972-2981. LIU Zhancheng, WANG Shuang, TANG Bo. Prediction of dissolved gas content in transformer oil based on SSA-BiGRU-Attention model[J]. High Voltage Engineering, 2022, 48(8): 2972-2981. (  0) 0) |
| [9] |
刘可真, 苟家萁, 骆钊, 等. 基于粒子群优化-长短期记忆网络模型的变压器油中溶解气体浓度预测方法[J]. 电网技术, 2020, 44(7): 2778-2785. LIU Kezhen, GOU Jiaqi, LUO Zhao, et al. Prediction of dissolved gas concentration in transformer oil based on PSO-LSTM model[J]. Power System Technology, 2020, 44(7): 2778-2785. (  0) 0) |
| [10] |
张鹏, 齐波, 张若愚, 等. 基于经验小波变换和梯度提升径向基的变压器油中溶解气体预测方法[J]. 电网技术, 2021, 45(9): 3745-3754. ZHANG Peng, QI Bo, ZHANG Ruoyu, et al. Dissolved gas prediction in transformer oil based on empirical wavelet transform and gradient boosting radial basis[J]. Power System Technology, 2021, 45(9): 3745-3754. (  0) 0) |
| [11] |
王渝红, 史云翔, 周旭, 等. 基于时间模式注意力机制的BiLSTM多风电机组超短期功率预测[J]. 高电压技术, 2022, 48(5): 1884-1892. WANG Yuhong, SHI Yunxiang, ZHOU Xu, et al. Ultra-short-term power prediction for BiLSTM multi wind turbines based on temporal pattern attention[J]. High Voltage Engineering, 2022, 48(5): 1884-1892. (  0) 0) |
| [12] |
关永锋, 喻敏, 胡佳. 基于自适应组合模型的超短期风速预测[J]. 电力系统保护与控制, 2022, 50(4): 120-128. GUAN Yongfeng, YU Min, HU Jia. Ultra-short-term wind speed prediction based on an adaptive integrated model[J]. Power System Protection and Control, 2022, 50(4): 120-128. (  0) 0) |
| [13] |
SUN F, JIN T D. A hybrid approach to multi-step, short-term wind speed forecasting using correlated features[J]. Renewable Energy, 2022, 186: 742-754. DOI:10.1016/j.renene.2022.01.041 (  0) 0) |
| [14] |
LI Y F, WU H P, LIU H. Multi-step wind speed forecasting using EWT decomposition, LSTM principal computing, RELM subordinate computing and IEWT reconstruction[J]. Energy Conversion and Management, 2018, 167: 203-219. DOI:10.1016/j.enconman.2018.04.082 (  0) 0) |
| [15] |
ZHENG J Q, ZHANG H R, DAI Y H, et al. Time series prediction for output of multi-region solar power plants[J]. Applied Energy, 2020, 257: 114001. DOI:10.1016/j.apenergy.2019.114001 (  0) 0) |
| [16] |
LV L L, WU Z Y, ZHANG J H, et al. A VMD and LSTM based hybrid model of load forecasting for power grid security[J]. IEEE Transactions on Industrial Informatics, 2022, 18(9): 6474-6482. DOI:10.1109/TII.2021.3130237 (  0) 0) |
| [17] |
YAN H J, OUYANG H B. Financial time series prediction based on deep learning[J]. Wireless Personal Communications, 2018, 102(2): 683-700. DOI:10.1007/s11277-017-5086-2 (  0) 0) |
| [18] |
ALHNAITY B, ABBOD M. A new hybrid financial time series prediction model[J]. Engineering Applications of Artificial Intelligence, 2020, 95: 103873. DOI:10.1016/j.engappai.2020.103873 (  0) 0) |
| [19] |
YAN Y, XU W, BU H, et al. Method for housing price forecasting based on TEI@I methodology[J]. Systems Engineering-Theory & Practice, 2007, 27(7): 1-9. (  0) 0) |
| [20] |
汤铃, 余安乐, 李建平, 等. 复杂时间序列预测技术研究: 数据特征驱动分解集成方法论[M]. 北京: 科学出版社, 2016. TANG Ling, YU Anle, LI Jianping, et al. Research on prediction technology of complex time series: data feature-driven decomposition integration methodology[M]. Beijing: Science Press, 2016. (  0) 0) |
| [21] |
谢乐, 仇炜, 李振伟, 等. 基于变分模态分解和门控循环单元神经网络的变压器油中溶解气体预测模型[J]. 高电压技术, 2022, 48(2): 653-660. XIE Le, QIU Wei, LI Zhenwei, et al. Prediction model of dissolved gas in transformer oil based on variational modal decomposition and recurrent neural network with gated recurrent unit[J]. High Voltage Engineering, 2022, 48(2): 653-660. (  0) 0) |
| [22] |
刘云鹏, 许自强, 董王英, 等. 基于经验模态分解和长短期记忆神经网络的变压器油中溶解气体浓度预测方法[J]. 中国电机工程学报, 2019, 39(13): 3998-4008. LIU Yunpeng, XU Ziqiang, DONG Wangying, et al. Concentration prediction of dissolved gases in transformer oil based on empirical mode decomposition and long short-term memory neural networks[J]. Proceedings of the CSEE, 2019, 39(13): 3998-4008. (  0) 0) |
| [23] |
周锋, 孙廷玺, 权少静, 等. 基于集合经验模态分解和极限学习机的变压器油中溶解气体体积分数预测方法[J]. 高电压技术, 2020, 46(10): 3658-3665. ZHOU Feng, SUN Tingxi, QUAN Shaojing, et al. Predication of dissolved gases concentration in transformer oil based on ensemble empirical mode decomposition and extreme learning machine[J]. High Voltage Engineering, 2020, 46(10): 3658-3665. (  0) 0) |
| [24] |
舒畅, 金潇, 李自品, 等. 基于CEEMDAN的配电变压器放电故障噪声诊断方法[J]. 高电压技术, 2018, 44(8): 2603-2611. SHU Chang, JIN Xiao, LI Zipin, et al. Noise diagnosis method of distribution transformer discharge fault based on CEEMDAN[J]. High Voltage Engineering, 2018, 44(8): 2603-2611. (  0) 0) |
| [25] |
江友华, 朱毅轩, 杨兴武, 等. 基于Hankel-SVD-CEEMDAN改进阈值的局部放电特征提取方法[J]. 电网技术, 2022, 46(11): 4557-4567. JIANG Youhua, ZHU Yixuan, YANG Xingwu, et al. Hankel-SVD-CEEMDAN improved threshold partial discharge feature extraction method[J]. Power System Technology, 2022, 46(11): 4557-4567. (  0) 0) |
| [26] |
CAO J, LI Z, LI J. Financial time series forecasting model based on CEEMDAN and LSTM[J]. Physica A: Statistical Mechanics and Its Applications, 2019, 519: 127-139. DOI:10.1016/j.physa.2018.11.061 (  0) 0) |
| [27] |
郑豪丰, 杨国华, 康文军, 等. 基于多负荷特征和TCN-GRU神经网络的负荷预测[J]. 中国电力, 2022, 55(11): 142-148. ZHENG Haofeng, YANG Guohua, KANG Wenjun, et al. Super short term power load forecasting based on multi-load feature combination and TCN-GRU neural network[J]. Electric Power, 2022, 55(11): 142-148. (  0) 0) |
| [28] |
BAI S J, KOLTER J Z, KOLTUN V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling[EB/OL]. [2023-11-04]. https://doi.org/10.48550/arXiv.1803.01271
(  0) 0) |
| [29] |
唐贤伦, 陈洪旭, 熊德意, 等. 基于极端梯度提升和时间卷积网络的短期电力负荷预测[J]. 高电压技术, 2022, 48(8): 3059-3067. TANG Xianlun, CHEN Hongxu, XIONG Deyi, et al. Short-term power load forecasting based on extreme gradient boosting and temporal convolutional network[J]. High Voltage Engineering, 2022, 48(8): 3059-3067. (  0) 0) |
| [30] |
陈铁, 陈一夫, 李咸善, 等. 基于CEEMDAN-SG-BiLSTM的变压器油中溶解气体浓度预测[J]. 高压电器, 2023, 59(12): 168-175. CHEN Tie, CHEN Yifu, LI Xianshan, et al. Prediction for dissolved gas concentration in power transformer oil based on CEEMDAN-SG-BiLSTM[J]. High Voltage Apparatus, 2023, 59(12): 168-175. (  0) 0) |
| [31] |
李佳, 邓科, 侯玉莲, 等. 基于GRA-CEEMDAN-BiLSTM的变压器油中溶解气体浓度预测[J]. 变压器, 2022, 59(6): 42-47. LI Jia, DENG Ke, HOU Yulian, et al. Prediction of dissolved gas concentration in transformer oil based on GRA-CEEMDAN-BiLSTM[J]. Transformer, 2022, 59(6): 42-47. (  0) 0) |
2. College of Economics and Management, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China;
3. Hangzhou Qiantang River Electric Group Co., Ltd., Hangzhou 311243, China
 2024, Vol. 43
2024, Vol. 43


 张文乾(1997),男,硕士在读,研究方向为变压器故障诊断及寿命评估(E-mail:
张文乾(1997),男,硕士在读,研究方向为变压器故障诊断及寿命评估(E-mail: