文章编号: 2096-3203(2024)03-0161-11 中图分类号: TM614
近年来,全球气候变暖现象逐渐加深[1-3],南北极作为地球的两大极区[4-6],其气象要素的波动对全球的气候变化有着举足轻重的影响,因此国内外学者们纷纷着眼于极地要素的课题研究[7]。目前,柴油发电机是极地的主要电力供应手段[8-9],但其会造成环境污染,故需要合适的清洁能源发电代替柴油发电机给科考站供电。南极地区常年处于大风天气,拥有可观的风力资源,而年平均风速高于5 m/s的任何地点都可以被认为是潜在的风力发电区域[10-11]。南极同样拥有丰富的光资源,极昼时光照强度大,持续时间长。因此充分利用南极的风、光资源发电,既可保护环境,又能实现能源互补供电[12-13]。
风光资源不确定性大[14-18],无法稳定供电,因此,通常利用储能装置辅助独立供能系统,实现独立、清洁、稳定供电[19]。在极地环境下,孤岛微电网中储能容量保持率会影响微电网的可靠性,因此,在考虑经济性与可靠性进行风光储优化配置时,考虑储能电池的容量衰减十分必要。
文献[20]基于交换功率和放电深度建立了储能电池衰减模型,进而分析了不同运行方式下规模化电池储能的发电计划优化问题。文献[21]考虑储能循环寿命,建立了计及储能容量衰减的储能运营优化模型,基于运营策略进行储能的容量配置优化。上述文献中对储能容量衰减的分析,多考虑循环次数、充放电深度等因素,环境较为温和,未考虑恶劣环境对系统优化配置的影响。而极地气候寒冷,冬季平均气温为-20~-16 ℃,夏季平均气温为-10~-4 ℃,常年的低温将会影响储能电池寿命。文献[22]通过测试商用软包锂离子电池在不同温度下的容量衰减,验证了温度对储能电池寿命的影响,建立了商用锂离子电池的容量衰减模型。文献[23]分析了温度、充放电倍率和充放电深度对储能容量衰减的影响机理,并建立考虑多因素聚合的储能寿命模型,但各因素的权重较为主观,并不符合实际应用的需求。
灰色关联分析法是一种客观的多因素分析法,通过数学方法建立因素与因变量的关系,进而确定各因素的权重,避免了人为主观因素对结果的影响[24-26],但其本身在求解过程中存在跟随效果差等问题。
因此,文中结合储能电池容量衰减问题对传统灰色关联分析法进行改进,提出一种自适应灰色关联分析法。基于此,考虑温度、充放电倍率和循环次数等因素,建立针对南极特殊环境的多因素耦合储能电池容量衰减数学模型;将所提电池容量衰减模型纳入微电网优化配置模型中,建立考虑经济性、可靠性与储能容量衰减的风光储优化配置模型;使用改进粒子群算法对所提模型进行求解,并对典型日的运行结果进行分析,验证所提风光储优化配置模型的有效性。
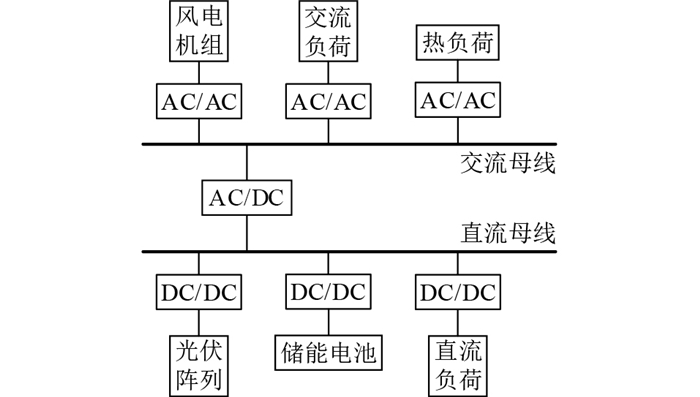
1 微电网系统结构文中采用的交直流混合微电网结构如图 1所示。不可控源包括风电机组和光伏阵列,可控源为储能电池。
|
图 1 交直流混合微电网 Fig. 1 AC/DC hybrid microgrid |
南极环境对风机、光伏影响不大,故不需要重新建立模型,仅对储能电池重新建模即可。
文中基于大量锂电池老化循环实验数据,分析了单一因素温度、充放电倍率、循环次数与锂电池容量的关系,根据经验建模方法建立简单模型。然而,电池老化是多种因素共同作用的结果,且非单一因素的影响依次累加的结果,故文中提出一种基于自适应灰色关联分析法的多因素耦合电池容量衰减模型。
(1) 电池数据选取以及说明。研究电池老化需要整个生命周期的实验数据,文中使用美国桑迪亚国家实验室(Sandia national laboratory,SNL)测试的LFP 18650型电池。数据集根据充放电倍率的不同可以分为A、B、C、D四大类,循环倍率分别为0.5 C、1 C、2 C、3 C,每一类分别在不同温度下展开2组电池特性相同的老化测试。
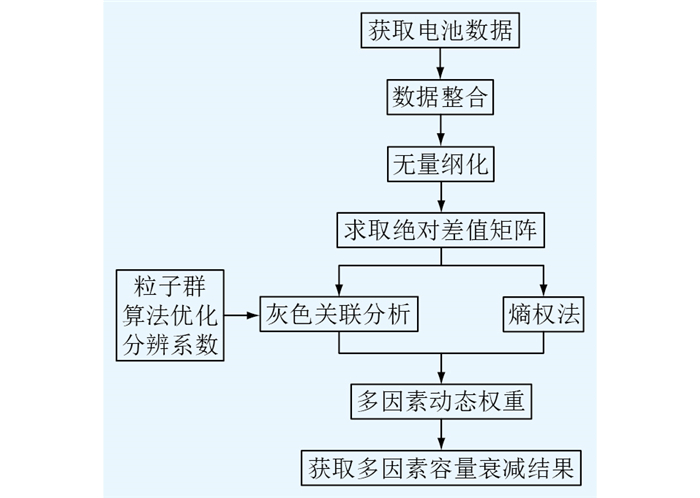
(2) 自适应灰色关联分析法。传统灰色关联分析法在计算关联度时整体采用均值方式,未体现变化趋势,导致最终差异较大,为更加准确地估算多因素下的电池容量,引入熵权法,改进灰色关联分析法。灰色关联分析法的分辨系数按照经验选取为0.5,且在整个老化阶段,求取的因素权重为固定值,无法准确跟踪曲线的变化趋势。故改进灰色关联分析法后,可采用动态权重,即在电池整个老化过程中,各个权重不再固定,而是随电池使用不断改变的值,分辨系数在可选范围(0, 1)内选择最佳值。自适应灰色关联分析法的具体流程见图 2。
|
图 2 自适应灰色关联分析法 Fig. 2 Adaptive grey relational analysis method |
(3) 多因素电池容量衰减模型。在电化学中,温度导致产品失效的Arrhenius方程[25]可以引入电气特性的等效领域。为了求取一段时间的变化量,可以在两侧同时积分,如式(1)、式(2)所示,表征电池对温度的依赖性。
| $\frac{\mathrm{d} M}{\mathrm{~d} t}=A \mathrm{e}^{-E_{\mathrm{a}} /(R T)}$ | (1) |
| $Q_{\text {loss }}(T)=A \mathrm{e}^{-E_{\mathrm{a}} /(R T)} \Delta t$ | (2) |
式中:M为状态量;dM/dt为化学反应速率;A为反应常量;Ea为活化能;R为摩尔常数;T为绝对温度;Qloss(T)为不同温度下的电池容量衰减百分数;Δt为相邻时间间隔。
非线性倍率、循环次数模型包括指数模型和二次模型,如式(3)、式(4)所示。
| $Q_{\text {loss }}(C)=a \mathrm{e}^{b C} $ | (3) |
| $ Q_{\text {loss }}(X)=p_0 X^2+p_1 X+p_2$ | (4) |
式中:C、X分别为充放电倍率和循环次数;a、b、p0、p1、p2为常系数;Qloss(C)、Qloss(X)分别为不同倍率、不同循环次数下的电池容量衰减百分数。
2.1 多因素模型基于对电池老化过程的了解,将温度、倍率、循环次数作为电池老化指标,并采用自适应灰色关联分析法将各个特征融合在一起,建立多因素模型。
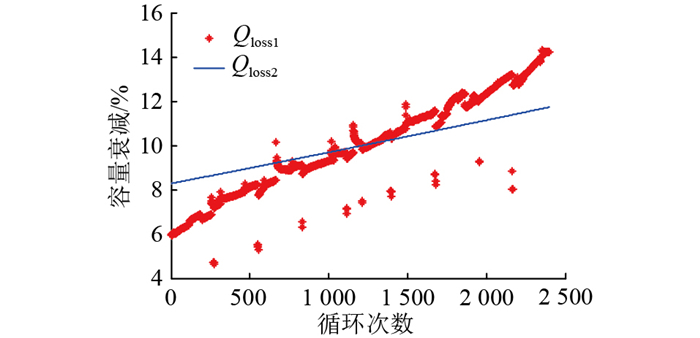
图 3为某组工况下使用传统灰色关联分析法得到的容量衰减曲线。图中,Qloss1为电池原始实验数据,Qloss2为使用传统灰色关联分析法得到的衰减曲线,二者偏差较大。
|
图 3 传统灰色关联分析法下的容量衰减曲线 Fig. 3 Capacity decay curve under conventional grey relational analysis |
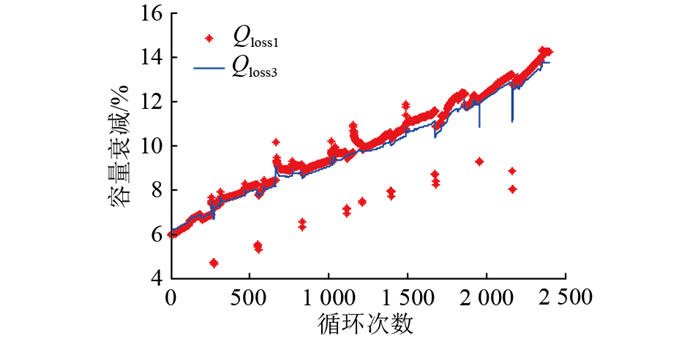
图 4为采用自适应灰色关联分析法得到的容量衰减曲线。图中,Qloss3为使用自适应灰色关联分析法得到的衰减曲线,与传统灰色关联分析法相比,其跟随效果明显增强,精度更高。
|
图 4 自适应灰色关联分析法下的容量衰减曲线 Fig. 4 Capacity decay curve under adaptive grey relational analysis |
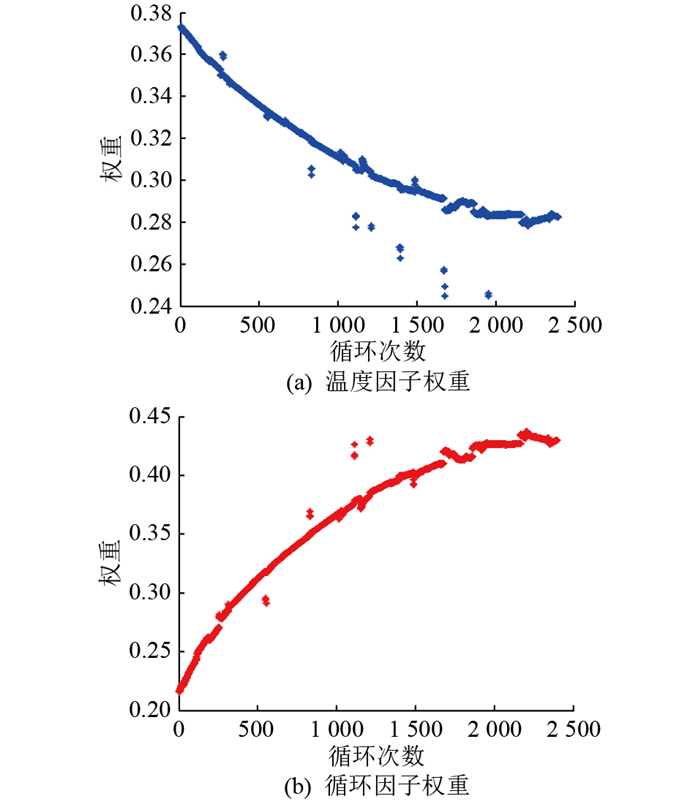
采用自适应灰色关联分析法得到的各个因素的权重如图 5所示。
|
图 5 权重因子变化趋势 Fig. 5 Variation trend of weighting factors |
图 5(a)为生命周期中温度衰减因子所占权重变化曲线,倍率衰减因子的权重变化趋势与之类似,图 5(b)为生命周期中循环衰减因子所占权重变化曲线,三者权重之和为1。通过采用复合权重法分析可知,在整个生命周期中,每个因素的权重并非一成不变,而是随着寿命周期变换。首先是温度和放电倍率对电池容量衰减的影响,温度和放电倍率权重值在最初处于最大值,之后在寿命周期内逐渐减小,即这两者对电池容量衰减的影响逐渐减小;其次是循环使用对电池容量衰减的影响,与前2个因素相反,其权重值在最初处于最小值,之后不断增大,即对电池容量衰减的影响逐渐增大。
经多组工况的实验数据验证可知,采用自适应灰色关联分析法可以精确表示电池的容量衰减规律,且只需要知道该工况最初周期的权重变化,即可预估出后期衰减变化结果。基于自适应灰色关联分析法的多因素电池容量衰减模型可以表示为:
| $Q_{\text {loss }}=\omega_{\mathrm{T}} Q_{\text {loss }}(T)+\omega_{\mathrm{C}} Q_{\text {loss }}(C)+\omega_{\mathrm{X}} Q_{\text {loss }}(X)$ | (5) |
式中:ωT、ωC、ωX分别为影响电池容量衰减的温度、倍率、循环次数动态权重因子,均可以由二次函数表示。
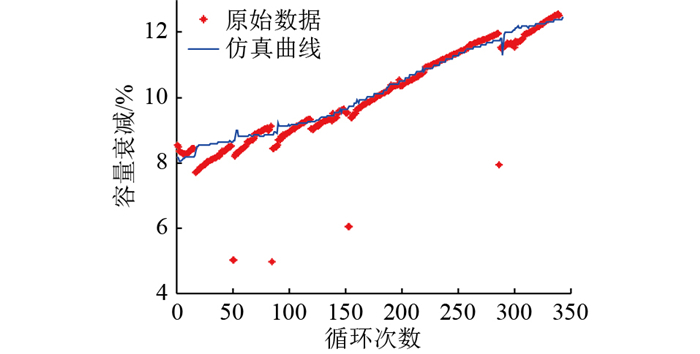
通过分析大量实验数据,验证了自适应灰色关联分析法的实用性。因文中锂电池的使用环境较为恶劣,而图 4是在较为温和的环境下得到的结果,故需要在-20 ℃、1 C下对文中方法的跟随效果进行验证,其结果如图 6所示。
|
图 6 低温容量衰减曲线 Fig. 6 Low temperature capacity decay curves |
磷酸铁锂电池作为储能元件,其容量对环境相当敏感。极地环境恶劣,故在前期容量配置时须考虑极地环境对储能电池的影响。储能电池实际容量为:
| $C_{\text {bat }}(t)=\left(1-Q_{\text {loss }}(t)\right) C_{\text {rated }}$ | (6) |
式中:Cbat(t)为蓄电池在t时刻的实际容量;Qloss(t)为采用自适应灰色关联分析法得到的t时刻多因素电池容量衰减百分数;Crated为标准状况下蓄电池额定容量。
电池充电状态模型为:
| $C_{\text {bat }}(t)=(1-\delta) C_{\text {bat }}(t-1)+P_{\text {res }}(t) \eta_{\mathrm{c}}$ | (7) |
电池放电状态模型为:
| $C_{\text {bat }}(t)=(1-\delta) C_{\text {bat }}(t-1)+P_{\text {res }}(t) / \eta_{\mathrm{d}}$ | (8) |
式中:δ为蓄电池自放电率;ηc、ηd分别为蓄电池的充、放电效率;Pres(t)为t时刻净负荷功率。
3 微电网容量优化配置模型在偏远的南极地区建立孤岛型微电网时,规划期间须重点研究储能与分布式电源容量优化,配置过程中要充分考虑合理利用当地的资源情况、当地环境对各设备的影响、微电网中的负荷分配平衡等问题,配置方案优劣直接关系到后期微电网运行的经济效益与可靠性。
3.1 目标函数微电网容量优化的主要目的在于,在满足系统各个设备协调运行条件的同时,选择最合适的设备容量使得经济效益最优,找到经济性指标与可靠性指标的最佳平衡点。
(1) 经济性指标。该微电网项目考虑寿命周期为20 a,在南极运行期间,须定期检查设备状况,并进行维护工作,且储能系统需要中期更换一次,因此除了考虑投资成本,还要计入运维成本和部分设备的置换成本。文中采用等年值综合成本Ceac作为科考站微电网的经济指标,模型如下:
| $C_{\mathrm{eac}}=C_{\mathrm{aic}}+C_{\mathrm{arc}}+C_{\mathrm{aomc}}$ | (9) |
式中:Caic、Carc、Caomc分别为该微电网系统的等年值初始投资成本、中期置换成本和运维成本。
南极科考站常年风资源充足,除极夜无光,其余时期皆可利用光资源,故微电网中包含了在时序上可以互补的分布式电源以及锂电池设备。因此初始投资成本为:
| $C_{\mathrm{aic}}=f_{\mathrm{CRF}}\left(C_{\mathrm{WT}, \mathrm{aic}}+C_{\mathrm{PV}, \mathrm{aic}}+C_{\mathrm{BAT}, \mathrm{aic}}\right)$ | (10) |
| $f_{\mathrm{CRF}}=\frac{r(1+r)^Y}{(1+r)^Y-1}$ | (11) |
式中:CWT, aic、CPV, aic、CBAT, aic分别为风电机组、光伏阵列、锂电池的初始投资成本;fCRF为计算等年值成本时的折算系数;r为折现率;Y为该项目的研究周期。
该项目设计与研究周期为20 a,除了锂电池以外,其余设备的使用周期均可超过20 a,期间不需要更换,而锂电池在理想情况下只需要更换一次。考虑到南极环境下低温、充放电倍率、电池的循环会造成电池容量不可逆的衰减,电池的使用寿命不再是固定的理想年限,因此锂电池的置换成本为:
| $C_{\mathrm{arc}}=C_{\mathrm{BAT}} \frac{r}{(1+r)^L-1} N_{\mathrm{fr}}$ | (12) |
| $N_{\mathrm{fr}}=\lceil 20 / L\rceil$ | (13) |
式中:CBAT为置换一次的成本;Nfr为项目周期内电池所需更换次数;L为电池的实际使用寿命;
运维成本主要包括:设备运行过程中设备本身以及辅助设备的费用;设备运行对设备本身造成性能损耗,定期维护以保持设备最佳状态而产生的费用。等年值运维成本则是为期1 a的微电网系统各组件运维成本之和,即:
| $C_{\mathrm{aomc}}=\left(\sum\limits_{n=1}^{N_{\mathrm{pc}}} C_{\mathrm{tom}}(n)\right) / N_{\mathrm{pc}}$ | (14) |
| $C_{\mathrm{tom}}(n)=C_{\mathrm{tom}}(1)(1+f)^n$ | (15) |
式中:Npc为项目周期;Ctom(1)为微电网第一年的运维成本;Ctom(n)为微电网第n年的运维成本;f为年通胀率。
(2) 可靠性指标。相较于传统电网的持续供电方式,在设计微电网系统时,因其新能源的随机性与机组出力波动性,供电可靠性作为基本要求就成为了一个被重视的指标。文中选择全年负荷缺电率(loss of power supply probability,LPSP)衡量系统的可靠性,定义LPSP为一年无法满足供电的负载占正常运行时总电量的比值,用δLPSP表示,LPSP越低则可靠性越高。
| $\delta_{\mathrm{LPSP}}=\frac{\sum\limits_{t=1}^{8760}\left(P_{\text {load }}(t)-P_{\mathrm{op}}(t)\right)}{\sum\limits_{t=1}^{8760} P_{\text {load }}(t)} \times 100 \%$ | (16) |
| $P_{\mathrm{op}}(t)=\left(P_{\mathrm{PV}}(t)+P_{\mathrm{WT}}(t)+P_{\mathrm{dis}}(t)\right) \Delta t$ | (17) |
式中:Pload(t) 为t时刻负荷正常运行所需电量;Pop(t) 为t时刻系统可供电的设备输出有功总和;PPV(t)、PWT(t)、Pdis(t) 分别为t时刻光伏电池、风电机组、锂电池的出力值。
3.2 约束条件为了保证系统优化的容量结果切实可行,不仅需要达到系统要实现的目标,还要对模型采用必要的约束。
3.2.1 功率平衡约束在南极,微电网没有大电网的支撑,只能孤立运行,为了满足负载用量,保证平稳运行,各个单元的出力要满足功率平衡。
| $\left\{\begin{array}{l}P_{\mathrm{PV}}(t)+P_{\mathrm{WT}}(t)+P_{\mathrm{dis}}(t)=P_{\text {load }}(t)+P_{\mathrm{ch}}(t) \\ 0<P_{\mathrm{PV}}(t)<P_{\mathrm{PV}, \text { max }} \\ 0<P_{\mathrm{WT}}(t)<P_{\mathrm{WT}, \max }\end{array}\right.$ | (18) |
式中:Pch(t)为t时刻锂电池充电功率;PPV, max、PWT, max分别为光伏阵列、风机的最大功率限制。
3.2.2 储能系统约束。(1) 锂电池的剩余容量约束。为了保证微电网孤立工作时稳定运行,须配备一定容量的储能,所使用的锂电池清洁无污染,为延长锂电池的使用周期,在运行中每时每刻的剩余容量都应满足以下约束:
| $\left\{\begin{array}{l}C_{\mathrm{b}}(t)=C_{\mathrm{b}}(t-1)-P_{\mathrm{dis}}(t) \eta_{\mathrm{d}} \Delta t+\frac{P_{\mathrm{ch}}(t) \Delta t}{\eta_{\mathrm{c}}} \\ C_{\mathrm{bat}, \text { min }}(t) \leqslant C_{\mathrm{b}}(t) \leqslant C_{\mathrm{bat}, \text { max }}(t)\end{array}\right.$ | (19) |
式中:Cb(t)为t时刻锂电池的剩余容量;Cbat, max(t)、Cbat, min(t)分别为综合考虑多方因素并计及容量衰减后修正的t时刻电池实际最大、最小容量。
(2) 锂电池的充、放电功率约束。锂电池任意时刻充放电不能同时进行,运行功率也不能过大,即:
| $\left\{\begin{array}{l}I_{\mathrm{dis}}(t) I_{\mathrm{ch}}(t)=0 \\ 0 \leqslant I_{\mathrm{ch}}(t) P_{\mathrm{ch}}(t) \leqslant P_{\mathrm{ch}, \max } \\ 0 \leqslant I_{\mathrm{dis}}(t) P_{\mathrm{dis}}(t) \leqslant P_{\mathrm{dis}, \max }\end{array}\right.$ | (20) |
式中:Ich(t)、Idis(t)为0-1变量,分别表征锂电池t时刻的充、放电状态,取0则电池既不充电也不放电,取1则电池处于充电或放电状态,由约束条件可知,两者为互斥状态;Pch, max、Pdis, max分别为最大充、放电功率。
但若储能系统在某一时刻的剩余容量与放电功率不符,则不能按照式(20)的条件约束,应当按照此时的放电能力调整其功率。
| $P_{\mathrm{dis}}(t)=\min \left\{P_{\mathrm{dis}}(t), \frac{\left(C_{\mathrm{b}}(t-1)-C_{\text {bat }, \text { min }}(t)\right) \eta_{\mathrm{d}}}{\Delta t}\right\}$ | (21) |
同理,当储能系统的剩余可充电容量无法满足充电所需时,按照式(22)对其充电能力进行调整。
| $P_{\mathrm{ch}}(t)=\min \left\{P_{\mathrm{ch}}(t), \frac{C_{\mathrm{bat}, \max }(t)-C_{\mathrm{b}}(t-1)}{\eta_{\mathrm{c}} \Delta t}\right\}$ | (22) |
南极没有传统电网,系统可靠工作更为重要,因此需要添加以下约束:
| $\delta_{\mathrm{LPSP}} \leqslant \delta_{\max }$ | (23) |
式中:δmax为文中设置的最大LPSP。
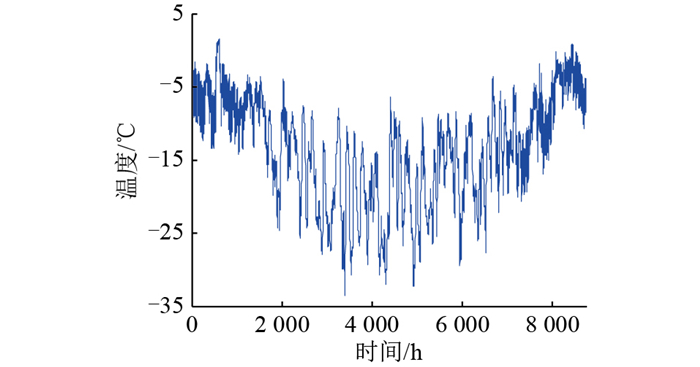
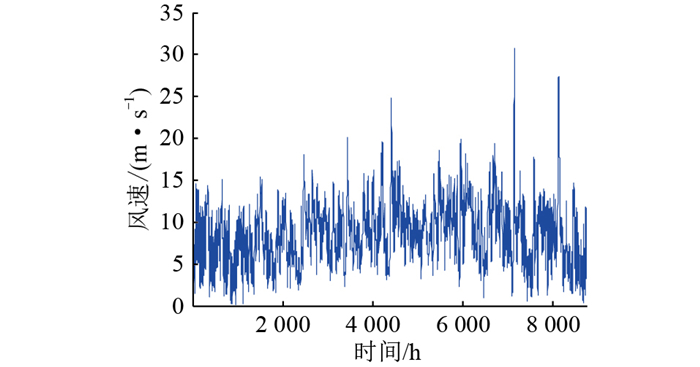
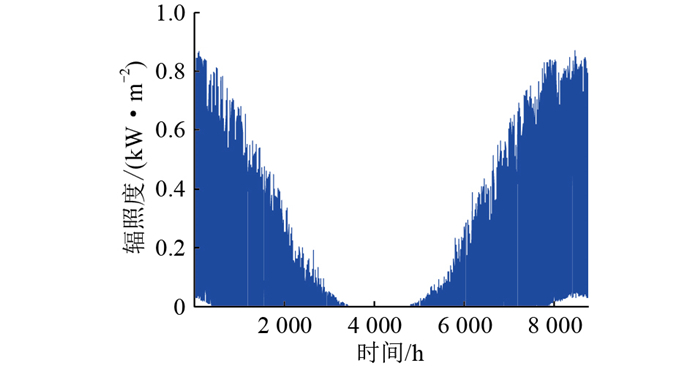
3.3 算例分析文中以南极科考站为研究背景,建立小型新能源微电网,替代部分柴油发电机。南极科考站位于南极大陆的维斯托登半岛,坐标为东经76°22′,南纬69°22′,靠近大海,水源充足,只有类比春秋的平时阶段以及类比夏冬的极昼、极夜阶段。在美国太空总署平台(NASA)上可以查询该地的气候情况,对科考站全年的温度、实时风速以及当地光照数据进行统计,将所得数据整合处理得到全年趋势图,即图 7—图 9。
|
图 7 科考站全年温度数据 Fig. 7 Annual temperature data of scientific research station |
|
图 8 科考站全年风速数据 Fig. 8 Annual wind speed data of scientific research station |
|
图 9 科考站全年光照强度数据 Fig. 9 Annual irradiance data of scientific research station |
可见,科考站风向在内陆冰盖下降风的影响下,全年东南偏东,风资源充足,年平均风速超过7 m/s。在每年五月下旬到七月中旬,科考站处于极夜状态,大约58 d内科考站环境温度极低,光照强度为0,期间光伏发电系统不能正常运行,但风资源比常日更盛。
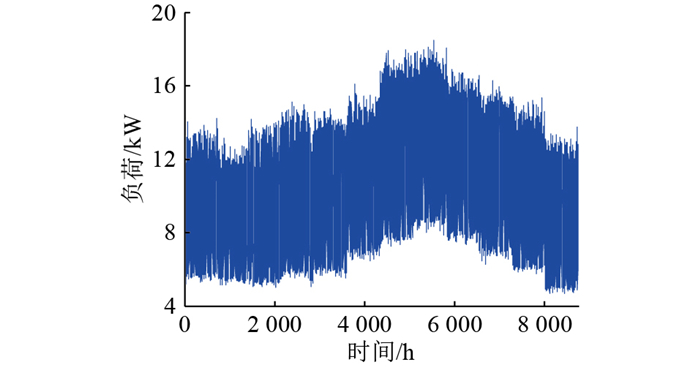
为了在南极引入微电网,逐步取代柴油发电机,同时保证科考站供电系统不至瘫痪,文中仅选取科考站部分负荷作为微电网负载,图 10为科考站部分负荷数据。表 1为微电网系统中所需的风机、光伏、锂电池的相关成本数据。
|
图 10 科考站全年负荷数据 Fig. 10 Annual load data of scientific research station |
|
|
表 1 微电网系统所需设备相关数据 Table 1 Data related to equipments required for microgrid system |
在MATLAB中采用改进粒子群算法对文中所建优化模型进行求解,能较好地求解微电网容量优化问题。本次优化设定种群规模为50,最大迭代次数为100,决策变量为风机、光伏、储能的容量,目标函数为适应度函数,约束为可靠性指标,在约束条件满足的情况下求解出最佳配置组合,使得目标函数最小。优化中设定微电网生命周期为20 a,期间,按照厂家给定参数,储能电池须更换一次。
为分析科考站恶劣的环境对微电网系统中储能容量配置的影响,更好地选择适合科考站的设备与容量,设置4种优化方案,并对优化结果进行分析。方案1:不考虑极昼极夜的微电网容量优化配置。方案2:考虑极昼极夜的微电网容量优化配置。方案3:考虑极昼极夜且简单考虑储能容量衰减的微电网容量优化配置。方案4:考虑极昼极夜与多因素耦合电池容量衰减模型的微电网容量优化配置。
针对方案1—3进行4次优化,结果见表 2。
|
|
表 2 方案1—3容量配置结果 Table 2 Solution 1, 2 and 3 capacity configuration results |
配置结果1是在未考虑极昼极夜的情况下得到的,优化结果为风电机组容量15.02 kW,光伏机组容量36.84 kW,储能容量仅55.37 kW·h。
为便于比较,针对方案2进行了2种优化,其结果分别为表 2中的配置结果2、3。配置结果2是在与方案1相同新能源机组配置容量下考虑极昼极夜优化储能容量,即在相同风光资源利用情况下,储能配置急剧增加,所需储能容量为93.73 kW·h,与方案1相比储能增加了69.28%,经济成本仅仅增加了4.65%,但在此特殊环境中系统仍能够保证平稳运行,没有缺负荷,整体可靠性增加。配置结果3是对计及极昼极夜的新能源机组与储能容量的重新优化,与配置结果2相比,因科考站全年风资源充足,光资源只有在极昼期间保持不间断,因此光伏机组容量减少19.98%,风电机组容量增加21.04%,使得所需储能容量有所削减,等年值综合成本下降到16.73万元。
配置结果4对应方案3,在整体配置时不仅考虑极昼极夜这类极端情况,还简单地将储能容量的衰减考虑进去,此时储能电池寿命不再是默认的10 a,而是减少到8.12 a。在项目周期内,电池更换将会超过2次,以此保证微电网系统内储能设备始终保持在良好的工作状态,虽导致综合成本增加到17.35万元,但及时更换废旧的储能设备保障了系统的可靠性。
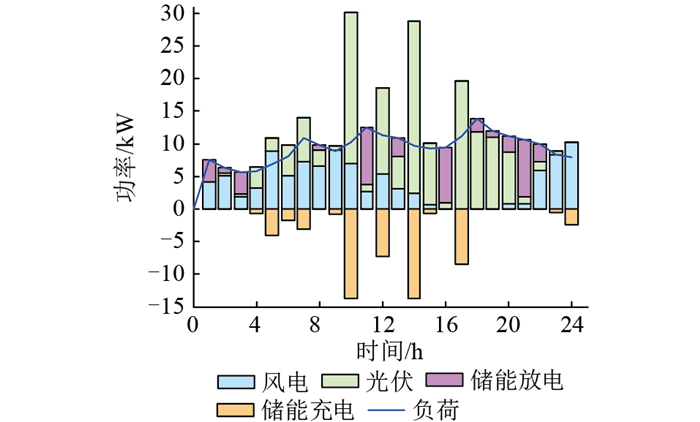
3.3.1 方案1优化配置与运行结果分析图 11为在方案1的配置结果下典型日的运行结果,因未考虑极昼极夜这类特殊气候,仅选择一个典型日验证该配置的合理性即可。图 12为对应运行过程中锂电池的荷电状态曲线。
|
图 11 方案1典型日运行结果 Fig. 11 Opeation results for solution 1 on a typical day |

|
图 12 方案1典型日荷电状态 Fig. 12 State of charge for solution 1 on a typical day |
分析图 11、图 12可知,在南极,1时—4时,太阳升起之时,负荷需求较低,太阳能发电量很少,主要靠可再生能源中的风电机组发电,且风机出力不能满足全部负荷需求,锂电池释放电能以补充缺额,此时荷电状态在允许范围内持续下降;5时—11时,随着日出科考队员依次开始进行科考任务,负荷需求不断提升,光伏输出功率也在不断增加,风光机组同时为负荷供电,并为锂电池充电,锂电池在光辐射强度低或者风资源较少时释放电能;12时—19时,风力逐渐减小,直至风速为0,光伏发电在满足负载需求的同时为储能系统充电;20时—24时,进入夜间状态,风电机组以及荷电状态较高的锂电池共同为负载供电。
3.3.2 方案2优化配置与运行结果分析为保证该微电网系统能够可持续运行,锂电池作为核心设备,要在风光资源均不足时,保证科考工作不至中断。故以1 d为周期,保证在一天开始与结束时刻储能系统剩余容量相差不大,避免下一周期储能系统出现过放、过充的现象,损害储能设备的寿命,造成负荷缺额,降低系统可靠性。
方案2考虑极昼极夜,对风、光机组与锂电池全部重新进行容量优化,优化结果即为表 2中的配置结果3,在该配置结果下,针对科考站分别选取了日常过渡阶段、极昼、极夜3个典型日,通过运行结果验证该配置的有效性。
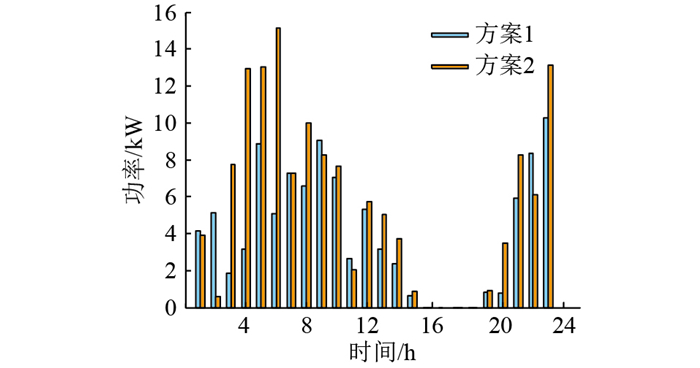
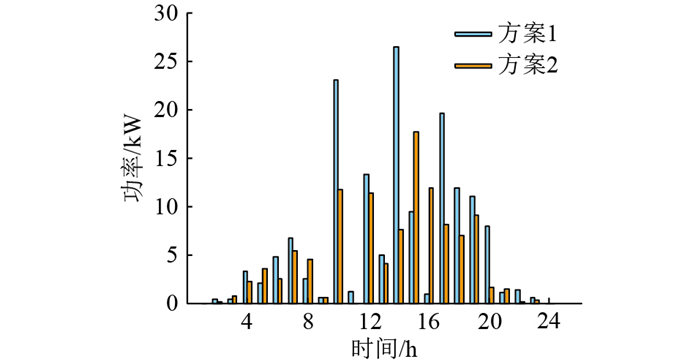
图 13—图 16依次为在方案2配置结果3下日常过渡阶段所选取的典型日与方案1配置结果下的风机出力、光伏出力、锂电池承担的负荷需求以及荷电状态对比。方案2在容量优化时兼顾了极昼极夜的极端情况,利用科考站全年风力旺盛的特点,对各个机组的配置容量重新优化,最终减少了光伏容量,更加充分利用风资源,风电机组出力整体上增加,光伏发电整体上有所削减。在运行过程中,如图 13、图 14所示,虽然储能系统承担的负荷需求整体上有所增加,但锂电池的荷电状态仍可保持在一个较高的状态,没有出现过放的现象,在增加系统可靠性的同时等年值综合成本减少了1.78万元,经济性更好。
|
图 13 风电机组出力对比 Fig. 13 Comparison of wind turbine output |
|
图 14 光伏出力对比 Fig. 14 Comparison of photovoltaic output |
|
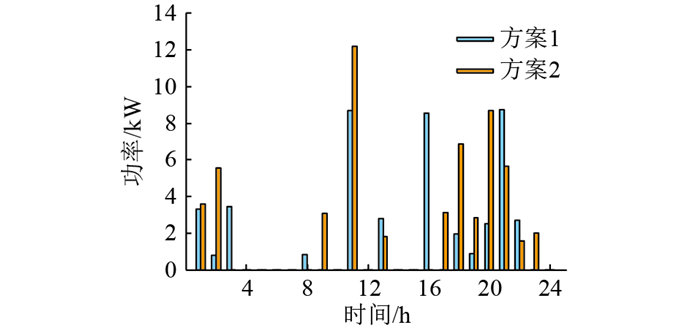
图 15 电池承担负荷对比 Fig. 15 Comparison of battery loads |
|
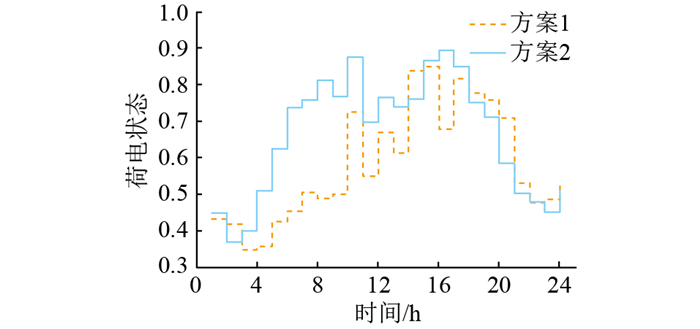
图 16 荷电状态对比 Fig. 16 Comparison of charge states |
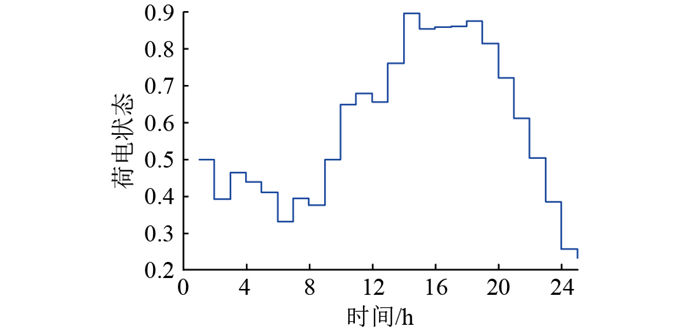
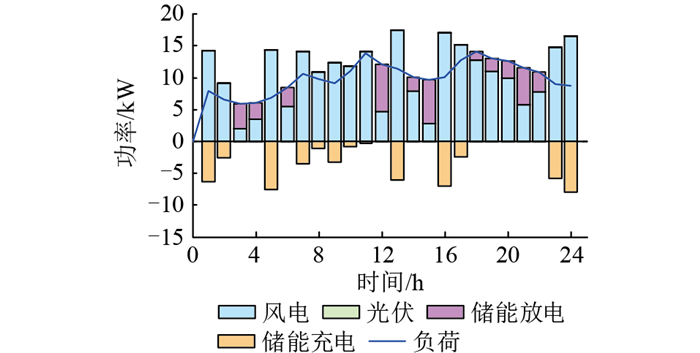
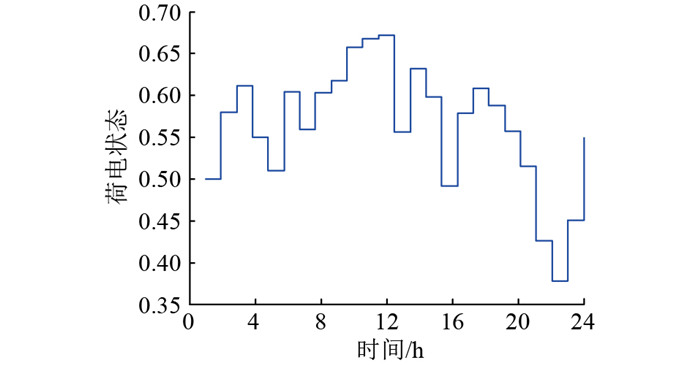
针对极昼、极夜,分别选取一个典型日与方案1进行对比分析。在方案1的配置结果下,遇到极端天气,微电网系统电力供不应求,存在较大的负荷缺额,甚至会因中断供电而损坏部分对电能要求严格的设备,增加了额外成本损耗。而在方案2配置结果3下,极昼、极夜典型日的运行出力如图 17—图 20所示,可见在极端气候下微电网系统亦能可靠地为负荷供电,验证了配置结果3的合理性与可靠性,且与配置结果2相比,并未因锂电池的增加而增加成本。在极昼期间,光资源充足,风力虽没有完全消失但多数较小,主要靠光伏阵列以及锂电池维持系统供需平衡。在极夜期间,黑暗笼罩,光伏阵列出力降为0,只有风电机组与锂电池共同承担负荷需求,并保证每个周期始末荷电状态的水平。
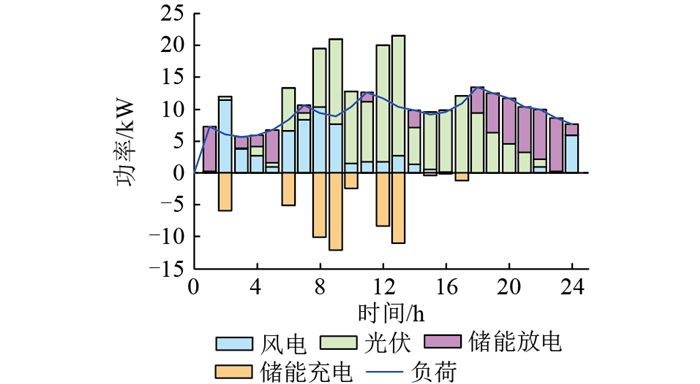
|
图 17 方案2极昼典型日运行结果 Fig. 17 Operational results for solution 2 on a typical polar-day |
|
图 18 方案2极昼典型日荷电状态 Fig. 18 State of charge for solution 2 on a typical polar-day |
|
图 19 方案2极夜典型日运行结果 Fig. 19 Operational results for solution 2 on a typical polar-night |
|
图 20 方案2极夜典型日荷电状态 Fig. 20 State of charge for solution 2 on a typical polar-night |
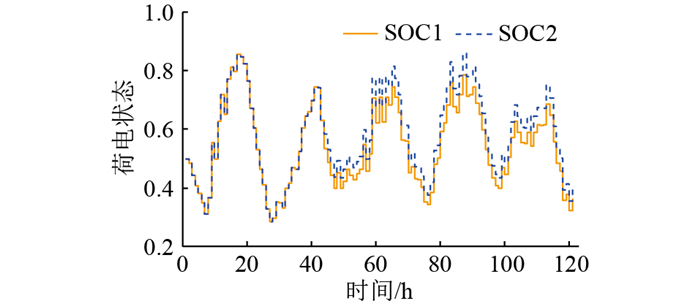
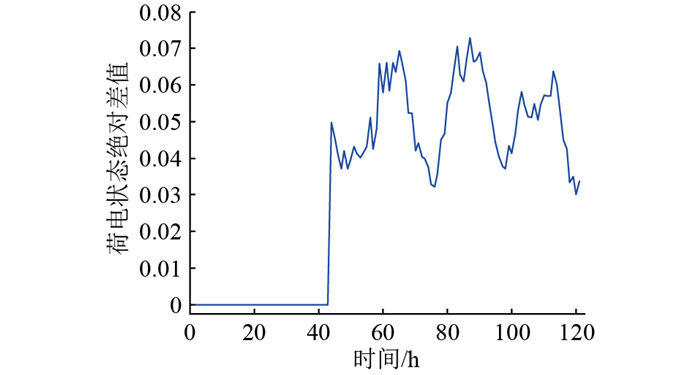
与方案2相比,在相同风光利用情况下,方案3的优化结果中储能最佳配置容量为95.31 kW·h,增加了23.49%,综合成本增加了3.71%。图 21为考虑电池容量衰减前后的荷电状态对比,其中SOC1为在方案2未考虑储能容量衰减的配置结果下为期5 d的运行荷电状态,SOC2为考虑简单的储能容量衰减的荷电状态。图 22为SOC1与SOC2的绝对差值曲线。图 21和图 22证明了在微电网优化中考虑储能容量衰减的必要性与方案3的优越性,并为考虑多因素储能容量衰减提供了理论基础。由图 21可以看出,在初始时刻,储能处于全新状态,以额定状态运行,SOC1与SOC2的曲线是重合的。随着储能的持续使用,电池容量开始出现衰减现象,同样配置下荷电状态SOC1略高于SOC2,即不考虑储能容量衰减时电池剩余可用容量会高于实际可放电容量。经年累月,绝对差值越来越大,电池渐渐会出现过放情况,造成不可逆的损坏,且使得整个微电网系统中能够提供给负荷的电能逐渐缩小,造成负荷缺电,可靠性低。缺电不仅会对部分精密的科考设备造成损害,也会影响科考人员的生活质量与身体健康。相比之下,考虑电池容量衰减虽然会增加投资成本,但综合考虑了使用年限以及维护成本,整体经济性反而有所提高。
|
图 21 简单考虑电池容量衰减前后荷电状态 Fig. 21 The charge states before and after considering the battery capacity decays |
|
图 22 荷电状态绝对差值变化趋势 Fig. 22 Trend of absolute difference of charge states |
经上述对比分析可知,在微电网优化时充分考虑锂电池容量状态,对估计电池的荷电状态十分重要,能充分提高微电网系统的供电可靠性。表 3为方案4的配置结果,因在不同的温度、充放电倍率下电池容量衰减不同,故容量优化配置方案以及锂电池的寿命、微电网寿命周期内的综合成本均有所不同。
|
|
表 3 多因素配置结果 Table 3 Results of multivariate configuration |
使用锂电池的地区环境一般较为温和,一年虽然有四季的变化,但极寒、极热期极短,与厂家测试的标况相差不大。而南极常年低温,锂电池所处环境恶劣,低温下充放电倍率对锂电池使用周期内总的等值循环次数影响较为明显,不可忽视,因此在前期优化时须考虑这些环境因素的影响。
表 3中,设置的锂电池充放电倍率越大,微电网中配置的锂电池容量越小,这也意味着锂电池的工作强度随倍率的增大而增强,同时电池损耗增大,容量衰减加快,使用周期缩短。而锂电池充放电倍率偏小时,锂电池的工作强度随倍率的减小而削弱,因此微电网中配置的锂电池容量变大,但同时因工作强度不高,持续运行下的容量衰减就较慢,寿命周期更长。锂电池测试时并非在高温低温这类特殊环境,若长期处于高温运行,虽然化学反应更加充分,充放电量相比其他情况单次较多,但造成的衰减也更快;若长期处于低温运行,则锂电池只能完成小倍率充放电工作,所需配置容量大大增加,且在低温环境下使用周期大大缩减,全寿命周期内置换次数随之增加,综合成本增加。
4 结论文中在MATLAB中采用改进粒子群算法求解极地环境下优化配置模型,为了分析极地恶劣环境对配置结果的影响设置了4种不同的优化方案进行对比分析,得出以下结论:
(1) 在考虑极地环境影响下建立基于自适应灰色关联分析法的多因素耦合电池容量衰减模型,可以更加精确地得出电池的荷电状态。
(2) 极地微电网中所需电池容量会随着工况的不同而有所改变,基于此进行的微电网容量优化经济性和可靠性更高。
(3) 考虑储能容量衰减的微电网配置方案降低了电池过充、过放概率,延长了电池的使用寿命,更适用于极地。
致谢
本文得到山西省能源互联网研究院重大科研支撑项目“极地极端环境下清洁能源供储装备与调控系统关键技术”(SXEI2023A001)资助,谨此致谢!
| [1] |
刘维康, 王丹, 余晓丹, 等. 考虑电气转换储能和可再生能源集成的微能源网多目标规划[J]. 电力系统自动化, 2018, 42(16): 11-20, 72. LIU Weikang, WANG Dan, YU Xiaodan, et al. Multi-objective planning of micro energy network considering P2G-based storage system and renewable energy integration[J]. Automation of Electric Power Systems, 2018, 42(16): 11-20, 72. DOI:10.7500/AEPS20180228003 (  0) 0) |
| [2] |
周立志, 张鹏飞, 麻常辉, 等. 南非碳中和实现路径及减排措施研究[J]. 全球能源互联网, 2022(1): 85-96. ZHOU Lizhi, ZHANG Pengfei, MA Changhui, et al. Study on carbon neutrality pathway and emission reduction measures inSouth Africa[J]. Journal of Global Energy Interconnection, 2022(1): 85-96. (  0) 0) |
| [3] |
贺旭辉, 王灿, 李欣然, 等. 计及CLHG-SOFC碳捕集的多能源系统低碳优化调度[J]. 智慧电力, 2023(5): 57-64. HE Xuhui, WANG Can, LI Xinran, et al. Low carbon optimal scheduling of multi-energy system considering CLHG-SOFC carbon capture[J]. Smart Power, 2023(5): 57-64. DOI:10.3969/j.issn.1673-7598.2023.05.010 (  0) 0) |
| [4] |
左广宇. 极区独立可再生能源供电系统关键技术研究[D]. 太原: 太原理工大学, 2020. ZUO Guangyu. Research on key technologies of polar independent renewable energy power supply system[D]. Taiyuan: Taiyuan University of Technology, 2020. (  0) 0) |
| [5] |
鄂栋臣, 沈强, 徐莹, 等. 基于ASTER立体数据和ICESat/GLAS测高数据融合高精度提取南极地区地形信息[J]. 中国科学(D辑: 地球科学), 2009, 39(3): 351-359. E Dongchen, SHEN Qiang, XU Ying, et al. High-precision terrain information extraction in Antarctic based on fusion of ASTER stereo data and ICESat/GLAS altimetry data[J]. Science in China (Series D: Earth Sciences), 2009, 39(3): 351-359. (  0) 0) |
| [6] |
张静. 中美欧在气候问题上的竞争与合作[D]. 上海: 华东师范大学, 2009. ZHANG Jing. Competition and cooperation between China, the United States and Europe on climate issues[D]. Shanghai: East China Normal University, 2009. (  0) 0) |
| [7] |
谭继强. 南极地理信息资源建设与应用服务关键技术研究[D]. 武汉: 武汉大学, 2016. TAN Jiqiang. Research on the key technologies of Antarctic geographic information resources construction and application service[D]. Wuhan: Wuhan University, 2016. (  0) 0) |
| [8] |
田立新, 封录. 实证分析二氧化碳排放量主要影响因素[J]. 北京理工大学学报(社会科学版), 2013, 15(2): 23-27, 59. TIAN Lixin, FENG Lu. An empirical analysis of the main factors influencing carbon dioxide emissions[J]. Journal of Beijing Institute of Technology (Social Sciences Edition), 2013, 15(2): 23-27, 59. (  0) 0) |
| [9] |
GUICHARD A, MAGILL P, GODON P, et al. Potential for significant wind power generation at Antarctic stations[C]//Seventh Symposium on Antarctic and Logistics Operations (SCALOP). 1996.
(  0) 0) |
| [10] |
周正斌, 张艺丹, 罗坤, 等. 基于高分辨率再分析资料的西南地区风资源特征分析[J]. 成都信息工程大学学报, 2023, 38(1): 75-82. ZHOU Zhengbin, ZHANG Yidan, LUO Kun, et al. Analysis of wind resources in southwest China based on high-resolution reanalysis data[J]. Journal of Chengdu University of Information Technology, 2023, 38(1): 75-82. (  0) 0) |
| [11] |
秦跃进, 王有春, 范黎, 等. 微网中分布式电源的容量优化配置方法[J]. 武汉大学学报(工学版), 2014, 47(3): 359-364. QIN Yuejin, WANG Youchun, FAN Li, et al. Optimal sizing method of distributed generations in a stand-alone microgrid[J]. Engineering Journal of Wuhan University, 2014, 47(3): 359-364. (  0) 0) |
| [12] |
梁硕, 王艳松. 基于改进云物元模型的工业园区综合能源系统规划方案评价[J]. 电力系统保护与控制, 2023, 51(9): 165-176. LIANG Shuo, WANG Yansong. Evaluation of an integrated energy system planning scheme for an industrial park based on an improved cloud matter-element model[J]. Power System Protection and Control, 2023, 51(9): 165-176. (  0) 0) |
| [13] |
周业荣, 李相锐, 绳博宇, 等. 水风光蓄互补发电系统中风光容量配置研究[J]. 水利水电技术(中英文), 2023, 54(11): 1-14. ZHOU Yerong, LI Xiangrui, SHENG Boyu, et al. Study of wind-photovoltaic capacity configuration in hydro-wind-photovoltaic-pumped storage complementary power generation system[J]. Water Resources and Hydropower Technology, 2023, 54(11): 1-14. (  0) 0) |
| [14] |
刘兴杰, 杜哲, 严逍. 独立交直流混合微电网电源优化配置[J]. 电力建设, 2016, 37(10): 16-23. LIU Xingjie, DU Zhe, YAN Xiao. Optimal allocation of power supply in AC/DC hybrid stand-alone microgrid[J]. Electric Power Construction, 2016, 37(10): 16-23. (  0) 0) |
| [15] |
周金辉, 田龙刚, 潘浩. 交直流混合微电网规划设计研究[J]. 合肥工业大学学报(自然科学版), 2015, 38(2): 166-170, 238. ZHOU Jinhui, TIAN Longgang, PAN Hao. Study of planning and design of hybrid AC/DC micro-grid[J]. Journal of Hefei University of Technology (Natural Science), 2015, 38(2): 166-170, 238. (  0) 0) |
| [16] |
孙伟卿, 罗静, 张婕. 高比例风电接入的电力系统储能容量配置及影响因素分析[J]. 电力系统保护与控制, 2021, 49(15): 9-18. SUN Weiqing, LUO Jing, ZHANG Jie. Energy storage capacity allocation and influence factor analysis of a power system with a high proportion of wind power[J]. Power System Protection and Control, 2021, 49(15): 9-18. (  0) 0) |
| [17] |
丁明, 潘浩, 张晶晶. 分布式电源接入交直流混合微电网群优化规划研究[J]. 太阳能学报, 2021, 42(6): 54-62. DING Ming, PAN Hao, ZHANG Jingjing. Research on optimal planning of AC/DC hybrid microgrid cluster with distributed generation access[J]. Acta Energiae Solaris Sinica, 2021, 42(6): 54-62. (  0) 0) |
| [18] |
BEHRANGRAD M. A review of demand side management business models in the electricity market[J]. Renewable and Sustainable Energy Reviews, 2015, 47: 270-283. (  0) 0) |
| [19] |
王质素, 杜欣慧, 陈惠英, 等. 考虑动力电池梯次利用的混合发电厂容量配置[J]. 太阳能学报, 2022, 43(5): 533-540. WANG Zhisu, DU Xinhui, CHEN Huiying, et al. Capacity optimization of hybrid power plants considering power battery ladder utilization[J]. Acta Energiae Solaris Sinica, 2022, 43(5): 533-540. (  0) 0) |
| [20] |
王荔妍, 陈启鑫, 何冠楠, 等. 考虑电池储能寿命模型的发电计划优化[J]. 电力系统自动化, 2019, 43(8): 93-100. WANG Liyan, CHEN Qixin, HE Guannan, et al. Optimization of generation scheduling considering battery energy storage life model[J]. Automation of Electric Power Systems, 2019, 43(8): 93-100. (  0) 0) |
| [21] |
刘凡, 李凤婷, 张高航, 等. 计及循环寿命和运营策略的风电汇集区域储能电站优化配置[J]. 电力系统保护与控制, 2023, 51(8): 127-139. LIU Fan, LI Fengting, ZHANG Gaohang, et al. Optimal configuration of storage power stations in a wind power gathering area considering cycle life and operation strategy[J]. Power System Protection and Control, 2023, 51(8): 127-139. (  0) 0) |
| [22] |
赵俊年, 金翼, 王绥军, 等. 商用Li4Ti5O12电池的温度特性及容量衰减模型[J]. 中国电机工程学报, 2017, 37(17): 5069-5075, 5226. ZHAO Junnian, JIN Yi, WANG Suijun, et al. Temperature characteristics and capacity attenuation model of commercial Li4Ti5O12 battery[J]. Proceedings of the CSEE, 2017, 37(17): 5069-5075, 5226. (  0) 0) |
| [23] |
张莲, 赵梦琪, 廖宗毅, 等. 计及多因素聚合储能寿命的微电网容量优化配置[J]. 重庆理工大学学报(自然科学), 2023(1): 196-203. ZHANG Lian, ZHAO Mengqi, LIAO Zongyi, et al. Optimal configuration of microgrid capacity for multi-factor polymerized energy storage life[J]. Journal of Chongqing University of Technology (Natural Science), 2023(1): 196-203. (  0) 0) |
| [24] |
刘思峰, 蔡华, 杨英杰, 等. 灰色关联分析模型研究进展[J]. 系统工程理论与实践, 2013, 33(8): 2041-2046. LIU Sifeng, CAI Hua, YANG Yingjie, et al. Advance in grey incidence analysis modelling[J]. Systems Engineering-Theory & Practice, 2013, 33(8): 2041-2046. (  0) 0) |
| [25] |
唐夏菲, 殷旭锋, 刘镂志, 等. 基于熵权—灰色关联变权重的有序用电决策方法[J]. 电力科学与技术学报, 2022, 37(5): 164-173. TANG Xiafei, YIN Xufeng, LIU Louzhi, et al. The decision-making method of orderly power consumption based on variable weights given by the entropy weight-grey relation[J]. Journal of Electric Power Science and Technology, 2022, 37(5): 164-173. (  0) 0) |
| [26] |
邹阳, 林锦茄, 李安娜, 等. 基于灰色关联分析和聚类云模型的变压器油纸绝缘状态评估[J]. 电力系统保护与控制, 2023, 51(21): 35-43. ZOU Yang, LIN Jinjia, LI Anna, et al. Evaluation of transformer oil-paper insulation status based on grey relational analysis and a cluster cloud model[J]. Power System Protection and Control, 2023, 51(21): 35-43. (  0) 0) |
 2024, Vol. 43
2024, Vol. 43


 李婷婷(1997), 女, 硕士在读, 研究方向为交直流混合微电网优化(E-mail:
李婷婷(1997), 女, 硕士在读, 研究方向为交直流混合微电网优化(E-mail: