文章编号: 2096-3203(2024)03-0121-09 中图分类号: TM614
2. 阳江海上风电实验室,广东 阳江 529500;
3. 华南理工大学广东省绿色能源技术重点实验室,广东 广州 510640
双碳背景下,风电作为清洁能源得到了快速发展[1-4]。随着风电并网规模的不断增加,传统同步电源的无功主动支撑能力无法保障电力系统的安全稳定运行,必须提高风电对电网的无功主动支撑能力。尤其是海上风电场正处于大规模、集中式发展阶段,提升海上风电场的无功主动支撑能力势在必行。
国内外学者对海上风电场的无功控制做了大量研究。文献[5]构建无功优化模型,以网损和电压偏差量最小为优化目标。文献[6]以配电网的有功网损最小为优化目标,将节点电压作为约束条件之一构建了无功优化模型。文献[7]提出一种基于高压侧电压控制理论的含双馈风机(doubly-fed induction generator, DFIG)风电场的电压控制策略。文献[8]提出一种风电场电压分层控制策略,以等功率因数算法计算各风机的无功功率参考值。文献[9]针对典型故障场景,提出一种分区无功储备多目标优化方法。文献[10]以风机端电压波动最小为优化目标,建立基于模型预测控制的无功优化模型。文献[11]提出一种包含多场景多组合的无功运行优化策略。文献[12]提出一种基于电压灵敏度的相干无功功率控制方法,并通过两级优化实现。文献[13]详细分析了变压器抽头失速、无功功率补偿输出和电网功率因数对系统功率损耗和母线电压的影响。文献[14]针对含DFIG的电力系统,建立基于无功优化的振荡稳定约束最优潮流模型。文献[15]提出一种无功快速跟踪优化方法,实现对时段内风机功率短期波动的跟踪优化。文献[16]提出一种基于储能和无功优化的控制方案, 依据评价指标结果对风电场中各台风电机组低电压穿越能力进行评估, 有效提高了整个风电场的无功输出能力。文献[17]以海上风电场无功补偿容量和节点电压偏差量最小为优化目标,建立无功优化模型。文献[18]分析了风电机组功率因数对配电网各节点电压、有功和无功网损影响规律。
上述研究考虑了多种无功优化的目标函数,包括网损最小、节点电压偏差量最小、所需无功补偿容量最小等,但仅考虑了固定权重系数的优化目标函数,在电网工况保持稳定或发生细微改变时对各优化目标能达到较好的优化效果。但随着新能源发电在电网中的占比逐渐增大,新型电力系统的工况随着新能源发电出力波动会频繁发生变化,上述多目标无功优化策略中各优化目标的权重系数为固定值,无法根据电网工况实时调节,可能会导致如下情况发生:当并网点电压发生较大偏离时,优化目标以网损最小为主从而影响电力系统的安全运行;反之,在电压偏离量较小时,优化目标以电压偏离量最小为主可能会导致补偿能力浪费,增加网损并降低系统的经济性。针对现有海上风电场在无功优化控制方面存在的问题,文中提出一种自适应多目标无功优化控制策略。该策略可以根据电网工况自适应调整各优化目标的优先级,以满足电网实时需求,保证新型电力系统的安全、稳定和经济性。
1 海上风电场无功控制模型针对海上风电机组输出功率特性和风电场并网点电压波动特性,建立可支撑海上风电场并网点电压恢复的无功控制模型。
1.1 海上风电场无功控制量分配模型海上风电场的无功控制总量跟随风电场并网点电压波动而波动,而这个波动的无功控制总量通过风电场自动电压控制(automatic voltage control, AVC)下发指令分配到单台风机,即:
| $ Q_*=\sum\limits_{k=1}^n Q_{\mathrm{G}, k}+\sum\limits_{l=1}^m Q_{\mathrm{S}, l} $ | (1) |
式中:Q*为整风场接收的无功功率指令;QG, k为第k台风机输出的无功功率;QS, l为第l台静止无功发生器(static var generator,SVG)输出的无功功率;n、m分别为风机和SVG的数量。
海上风电场进行无功功率分配时需要考虑风电场内部的潮流约束,将各风机及静止无功发生器SVG定义为PQ节点,用节点导纳矩阵表示为:
| $ \dot{I}_i=\sum\limits_{j=1}^{N_1} Y_{i, j} \dot{U}_i \quad i=1, 2, \cdots, N_1 $ | (2) |
式中:Yi, j为节点导纳矩阵的元素;
实际应用中普遍关注节点的功率注入,令
| $ \frac{P_i-\mathrm{j} Q_i}{\dot{U}_i}=\sum\limits_{j=1}^{N_1} Y_{i, j} \dot{U}_i \quad i=1, 2, \cdots, N_1 $ | (3) |
令
| $ \left\{\begin{array}{l} P_i=U_i \sum\limits_{j=1}^{N_1} U_j\left(G_{i, j} \cos \varphi_{i, j}+B_{i, j} \sin \varphi_{i, j}\right) \\ Q_i=U_i \sum\limits_{j=1}^{N_1} U_j\left(G_{i, j} \sin \varphi_{i, j}-B_{i, j} \cos \varphi_{i, j}\right) \end{array}\right. $ | (4) |
式中:Pi、Qi分别为节点i输入的有功功率和无功功率;Uj为节点j的电压;Gi, j、Bi, j分别为节点导纳矩阵中各元素的实部与虚部;φi, j为节点i和节点j之间的相角差。
利用牛顿-拉夫森法对式(4)所述潮流方程进行线性化,有:
| $ \left\{\begin{array}{l} \Delta P_i=\sum\limits_{j=1}^{N_1} \frac{\partial P_i}{\partial \varphi_{i, j}} \Delta \varphi_j+\sum\limits_{j=1}^{N_1} \frac{\partial P_i}{\partial U_j} \Delta U_j \\ \Delta Q_i=\sum\limits_{j=1}^{N_1} \frac{\partial Q_i}{\partial \varphi_{i, j}} \Delta \varphi_j+\sum\limits_{j=1}^{N_1} \frac{\partial Q_i}{\partial U_j} \Delta U_j \end{array}\right. $ | (5) |
式中:ΔUj为节点j的电压变化量;ΔPi、ΔQi分别为节点i的有功、无功变化量;Δφj为节点j的相位角变化量。
将式(5)化为矩阵形式,即:
| $ \left[\begin{array}{c} \Delta \boldsymbol{P} \\ \Delta \boldsymbol Q \end{array}\right]=-\left[\begin{array}{ll} \boldsymbol{H} & \boldsymbol N \\ \boldsymbol K & \boldsymbol L \end{array}\right]\left[\begin{array}{c} \Delta \boldsymbol\varphi \\ \boldsymbol U^{-1} \Delta \boldsymbol U \end{array}\right]=-\boldsymbol J\left[\begin{array}{c} \Delta \boldsymbol \varphi \\ \boldsymbol U^{-1} \Delta \boldsymbol U \end{array}\right] $ | (6) |
式中:ΔP、ΔQ分别为风电场内节点有功、无功变化量组成的向量;Δφ、ΔU分别为风电场内节点相位角变化量、电压变化量组成的向量;H、N、K、L为雅可比矩阵J的参数矩阵。
式(6)等号两边同时乘以雅可比矩阵的逆矩阵,可得:
| $ \left[\begin{array}{c} \Delta \boldsymbol{\varphi} \\ \boldsymbol{U}^{-1} \Delta \boldsymbol U \end{array}\right]=\boldsymbol{J}^{-1}\left[\begin{array}{c} \Delta \boldsymbol{P} \\ \Delta \boldsymbol Q \end{array}\right]=-\left[\begin{array}{ll} \boldsymbol{A} & \boldsymbol{B} \\ \boldsymbol{C} & \boldsymbol{D} \end{array}\right]\left[\begin{array}{c} \Delta \boldsymbol{P} \\ \Delta \boldsymbol{Q} \end{array}\right] $ | (7) |
式中:A、B、C、D为参数矩阵,由雅可比矩阵求逆得到。
由式(7)可以看出,海上风电场内各节点的电压增量与节点注入的有功、无功功的率增量有关,因此,整风场分配无功功率时须兼顾节点电压的稳定性。
1.2 海上风电机组无功控制模型单台机组分配到的无功控制量随着海上风电场无功控制总量的变化而不断变化,于是,海上风电机组需要不断跟随这个变化的无功控制目标实现精准的无功控制。
以采用双脉宽调制(pulse width modulation, PWM)全功率变换器实现变速恒频运行的直驱型海上风电机组为研究对象,构建风机的控制框图,如图 1所示。其中,风力发电机为永磁同步电机(permanent magnet synchronous generator, PMSG), 风机采用最大功率跟踪(maximum power point tracking, MPPT)模式以实现最大功率输出,
图 1中,isa、isb、isc分别为输入机侧变流器的a、b、c三相电流值;ωr为风机的电磁角速度;ωr*为风机的电磁角速度参考值;ωg为电网角速度;isd、isq分别为机侧变流器输入电流的d轴及q轴分量;isd*为机侧变流器输入电流d轴的参考值;usd*、usq*分别为PWM输入电压参考值的d轴及q轴分量;udc、udc*分别为直流电容C电压的实际值和参考值;Lgd、Lgq分别为网侧电感值的d轴及q轴分量;uga、ugb、ugc分别为电网侧的三相上的电压;ugα、ugβ分别为电网侧电压的α轴及β轴分量;igq*为机侧变流器输入电流q轴的参考值;Q*为网侧变流器输出无功功率参考值;iga、igb、igc分别为网侧a、b、c三相输入电流;igd、igq分别为网侧输出电流的d轴及q轴分量;Ug为电网电压。

|
图 1 直驱型风电机组控制框图 Fig. 1 Control diagram of direct-driven wind turbine |
对于直驱型风机,通过控制网侧变流器即可控制风机的有功、无功输出[19],网侧PWM变换器的拓扑如图 2所示,idc为流过直流电容C的电流值,RL为负载电阻。

|
图 2 网侧PWM变换器拓扑 Fig. 2 Network side PWM converter topology |
在三相静止坐标系中,网侧变换器的数学表达式为:
| $ \left\{\begin{array}{l} L_{\mathrm{ga}} \frac{\mathrm{d} i_{\mathrm{ga}}}{\mathrm{d} t}=u_{\mathrm{ga}}-i_{\mathrm{ga}} R_{\mathrm{ga}}-\frac{u_{\mathrm{ga}}+u_{\mathrm{gb}}+u_{\mathrm{gc}}}{3}-V_{\mathrm{ga}} \\ L_{\mathrm{gb}} \frac{\mathrm{d} i_{\mathrm{gb}}}{\mathrm{d} t}=u_{\mathrm{gb}}-i_{\mathrm{gb}} R_{\mathrm{gb}}-\frac{u_{\mathrm{ga}}+u_{\mathrm{gb}}+u_{\mathrm{gc}}}{3}-V_{\mathrm{gb}} \\ L_{\mathrm{gc}} \frac{\mathrm{d} i_{\mathrm{gc}}}{\mathrm{d} t}=u_{\mathrm{gc}}-i_{\mathrm{gc}} R_{\mathrm{gc}}-\frac{u_{\mathrm{ga}}+u_{\mathrm{gb}}+u_{\mathrm{gc}}}{3}-V_{\mathrm{gc}} \\ C \frac{\mathrm{d} u_{\mathrm{dc}}}{\mathrm{d} t}=S_{\mathrm{a}} i_{\mathrm{ga}}+S_{\mathrm{b}} i_{\mathrm{gb}}+S_{\mathrm{c}} i_{\mathrm{gc}}-i_{\mathrm{L}} \end{array}\right. $ | (8) |
式中:Lga、Lgb、Lgc为三相电感值;Rga、Rgb、Rgc为三相电阻值;Vga、Vgb、Vgc为变换器交流侧三相相对电压;Sa、Sb、Sc为整流桥中各相桥臂的开关常数,取值为1或0。
将式(8)变换到dq坐标系中,即:
| $ \left\{\begin{array}{l} u_{\mathrm{g} d}=L_{\mathrm{g} d} \frac{\mathrm{d} i_{\mathrm{g} d}}{\mathrm{~d} t}+R_{\mathrm{g} d} i_{\mathrm{g} d}-\omega_{\mathrm{g}} L_{\mathrm{g} d} i_{\mathrm{g} d}+V_{\mathrm{g} d} \\ u_{\mathrm{g} q}=L_{\mathrm{g} q} \frac{\mathrm{d} i_{\mathrm{g} q}}{\mathrm{~d} t}+R_{\mathrm{g} q} i_{\mathrm{g} q}-\omega_{\mathrm{g}} L_{\mathrm{g} q} i_{\mathrm{g} q}+V_{\mathrm{g} q} \\ C \frac{\mathrm{d} u_{\mathrm{dc}}}{\mathrm{d} t}=\frac{3}{2}\left(S_d i_{\mathrm{g} d}+S_q i_{\mathrm{g} q}\right)-i_{\mathrm{L}} \end{array}\right. $ | (9) |
式中:ugd、ugq分别为交流侧电压的d轴及q轴分量;Lgd、Lgq分别为网侧电感值的d轴及q轴分量;Rgd、Rgq分别为网侧电阻值的d轴及q轴分量;Vgd、Vgq分别为交流侧电压的d轴及q轴分量;Sd、Sq为开关函数,取值为1或0。
令dq坐标系的d轴方向与电网电压方向一致,有:
| $ \left\{\begin{array}{l} u_{\mathrm{g} d}=U_{\mathrm{g}} \\ u_{\mathrm{g} q}=0 \end{array}\right. $ | (10) |
结合式(9)与式(10)可得:
| $ \left\{\begin{array}{l} V_{\mathrm{g} d}=u_{\mathrm{g} d}-L_{\mathrm{g} d} \frac{\mathrm{d} i_{\mathrm{g} d}}{\mathrm{~d} t}-R_{\mathrm{g} d} i_{\mathrm{g} d}+\omega_{\mathrm{g}} L_{\mathrm{g} q} i_{\mathrm{gq}} \\ V_{\mathrm{g} q}=-L_{\mathrm{g} q} \frac{\mathrm{d} i_{\mathrm{g} q}}{\mathrm{~d} t}-R_{\mathrm{g} q} i_{\mathrm{g} q}-\omega_{\mathrm{g}} L_{\mathrm{g} d} i_{\mathrm{g} d} \end{array}\right. $ | (11) |
网侧变流器向电网输送的有功、无功功率为:
| $ \left\{\begin{array}{l} P=-\frac{3}{2}\left(u_{\mathrm{g} d} i_{\mathrm{g} d}+u_{\mathrm{g} q} i_{\mathrm{g} q}\right) \\ Q=-\frac{3}{2}\left(u_{\mathrm{g} q} i_{\mathrm{g} d}-u_{\mathrm{g} d} i_{\mathrm{g} q}\right) \end{array}\right. $ | (12) |
结合式(10)与式(12),可得:
| $ \left\{\begin{array}{l} P=-\frac{3}{2} u_{\mathrm{g} d} i_{\mathrm{g} d} \\ Q=\frac{3}{2} u_{\mathrm{g} d} i_{\mathrm{g} q} \end{array}\right. $ | (13) |
通过式(13)可以看出,控制igq即可控制网侧变流器注入电网的无功功率[20-22]。
SVG通过对送入内部调节器的无功参考值进行分配,从而调整其输出的无功功率,可表示为:
| $ Q_{\mathrm{S}}^{\prime}=Q_{\mathrm{S}, 0}+K_{\mathrm{S}, \mathrm{P}}\left(U_{\mathrm{S}}^{\prime}-U_{\mathrm{S}}\right)+K_{\mathrm{S}, \mathrm{I}}\left(U_{\mathrm{S}}^{\prime}-U_{\mathrm{S}}\right) $ | (14) |
式中:QS′、QS, 0分别为SVG输出无功功率的设定值和在工作点下的无功功率;KS, P、KS, I分别为SVG内部比例积分(proportional integral, PI)控制器的比例增益常数和积分增益常数;US′、US分别为SVG输出电压的参考值和实际值。
通过式(14)可以看出,通过调节SVG输出电压参考值的相位和幅值,可以使SVG吸收或者发出满足要求的无功功率,实现功率无功补偿的目的[23-24]。
2 海上风电场自适应多目标无功优化控制策略针对海上风电场的有功网损和并网点电压波动,设置无功优化控制的目标函数,其中各子目标的权重系数基于并网点电压偏差量自适应调整,基于风机的输出特性和风电场的运行特性,构建无功优化的约束条件集,并利用粒子群优化(particle swarm optimization,PSO)算法进行策略求解,以实现对海上风电场各无功源无功输出的精准控制。
2.1 海上风电场无功控制目标函数的自适应权重设计将目标函数设置为系统有功网损与并网点电压偏差的加权和最小,优化变量包含直驱风机及SVG的无功出力、可调变压器分接头位置,据此建立无功优化模型。具体实施方式为将电压偏差及有功网损作为子目标,并分别给定权重系数合并为总的优化目标,其目标函数如下:
| $ \min F=\min \left(\alpha_1 F_1+\alpha_2 F_2\right) $ | (15) |
式中:F1为电压偏离量最小的优化目标;F2为风电场内有功网损最小的优化目标;α1、α2分比为电压偏离量、有功网损的权重系数。
风机并网点电压波动在-0.05~0.05 p.u.范围内符合要求,当|ΔU|>0.05 p.u.时,并网点电压超过安全范围,此时风电场的无功控制策略主要使并网点电压偏差减少至规定范围内;当|ΔU|<0.03 p.u.时,并网点电压波动较小,无功控制策略主要使风电场的有功网损最小。为满足上述要求,文中电压偏离量F1的权重采用sin函数自适应调节:
| $ \alpha_1=\sin (y \pi / 2) $ | (16) |
其中:
| $ y=\left|\frac{U_0-U_{\text {ref }}}{\Delta U_{\max } / 2}\right| $ | (17) |
式中:U0为并网点电压实测值;Uref为电网电压参考值;ΔUmax为国标规定风机不脱网运行的最大偏离范围的差值, 为0.1 p.u.。
有功网损F2的权重系数标定方式为:
| $ \alpha_2=1-\alpha_1 $ | (18) |
则总的目标函数为:
| $ \min F(\boldsymbol{x})=\alpha_1\left|U_0-U_{\mathrm{ref}}\right|+\alpha_2 \sum\limits_{w=1}^{N_2} R_w \frac{P_w^2+Q_w^2}{\left|U_w\right|^2} $ | (19) |
式中:x为优化变量,
等式约束为海上风电场潮流约束,见式(4)。
不等式约束为:
| $ Q_{\mathrm{G}, k, \text { min }} <Q_{\mathrm{G}, k}<Q_{\mathrm{G}, k, \text { max }} $ | (20) |
| $ P_{\mathrm{G}, k, \text { min }} <P_{\mathrm{G}, k}<P_{\mathrm{G}, k, \text { max }} $ | (21) |
| $ Q_{\mathrm{S}, l, \text { min }} <Q_{\mathrm{S}, l}<Q_{\mathrm{S}, l, \text { max }} $ | (22) |
| $ T_{\mathrm{tr}, p, \text { min }} <T_{\mathrm{tr}, p}<T_{\mathrm{tr}, p, \text { max }} $ | (23) |
| $ U_{i, \text { min }} <U_i<U_{i, \text { max }} $ | (24) |
式中:PG, k,QG, k分别为第k台风机的有功、无功功率输出;PG, k, min、PG, k, max、QG, k, min、QG, k, max分别为第k台风机的有功、无功功率输出最小值与最大值;QS, l, min、QS, l, max分别为第l台SVG的无功输出最小值与最大值;Ttr, p, min、Ttr, p, max分别为第p台可调变压器分接头位置的最小值与最大值;Ui, min、Ui, max分别为第i个节点的电压最小值与最大值。
2.3 策略求解流程PSO算法具有搜索速度快、效率高等优势,能够快速高效地求解多变量的优化问题,快速收敛到最优解[25-27]。基于PSO算法求解海上风电场在自适应权重目标函数下的多目标优化控制策略的流程如图 3所示。

|
图 3 PSO算法流程 Fig. 3 Flow chart of PSO algorithm |
具体步骤如下。
步骤1:输入海上风电场中直驱风机的台数、装机容量、运行参数、所处位置的风速等数据。
步骤2:基于输入的数据及直驱风机的功率特性曲线求出每台风机的有功输出功率。
步骤3:假定风电场中单个风机的初始功率因数为1,根据步骤2求出的风机有功功率进行潮流计算,得出风电场并网点电压。
步骤4:根据每个风机有功输出确定相应的无功输出范围,即每个风机的无功调节能力。
步骤5:设置粒子群的种群大小为K、加速系数c1和c2、最大迭代次数M,将各风机及SVG的无功调节能力、变压器分接头位置作为优化变量进行编码。
步骤6:在保证随机性的条件下初始化粒子群,得到K个粒子,即K个可行解。将初始化后的粒子值代入到潮流计算中,求出各粒子的适应度值,并将其作为当前的粒子最优位置代入下次运算,同时选取适应度最小的粒子的当前位置作为种群的最优位置代入下次运算。
步骤7:基于粒子群迭代次数,对惯性权重ω进行更新;同时,在保证随机性的条件下,更新各粒子的速度和位置数据。若存在粒子速度超出规定速度的情况,则将该粒子的速度设置为就近的极值代入到下次运算。
步骤8:对更新后的粒子进行适应度值计算,并更新相关信息,包括适应度值、粒子历史最优位置、种群历史最优位置等。
步骤9:若达到最大迭代次数,则停止迭代,解码并输出得到的无功控制策略;否则重新进入步骤7。
基于上述流程进行无功优化策略的求解,确定实时工况下各风电机组和SVG的出力策略以及可调变压器分接头的位置,从而对不同无功源的无功输出进行控制,以实现海上风电场对复杂工况下电力系统的无功主动支撑。
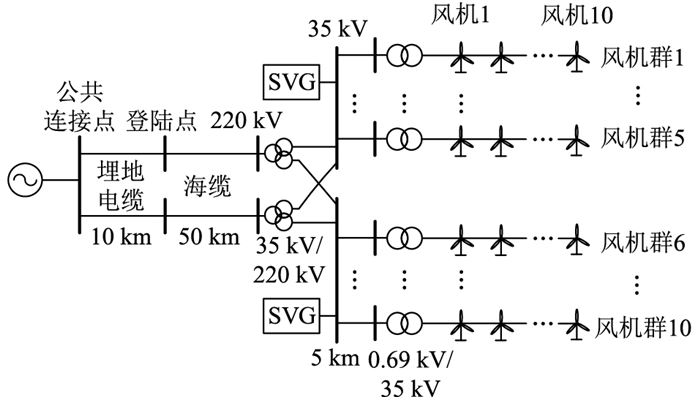
3 算例分析 3.1 仿真场景设计文中采用的海上风电场结构模型见图 4。该风电场容量为300 MW,由100台3 MW的永磁同步风电机组组成,风电机组经箱变(0.69 kV/35 kV)升压后并联,每10台风机构成一个支路,共有10路汇集线,经过35 kV海缆集电线接至海上升压站的低压侧,再由2台主变压器(35 kV/220 kV)升压至220 kV后,最后经过2路陆地电缆接入陆上并网点,海上升压站至陆上并网点的距离约100 km。海缆的单位直流电阻值为0.268 Ω/km,单位交流阻值为0.342 Ω/km。其中3 MW永磁同步风机的基本参数如表 1所示。
|
图 4 海上风电场结构 Fig. 4 Structure of offshore wind farm |
|
|
表 1 3 MW永磁同步风机参数表 Table 1 Parameters of 3 MW permanent magnet synchronous wind generator |
针对这一海上风电场,分别针对传统无功优化策略和自适应无功优化策略进行仿真设计。
固定权重系数多目标无功优化策略:为比较多目标优化中各不同权重系数的优化效果,设置3个权重组合。其中,组合1将电压偏差量的权重系数设为0.75,有功网损的权重系数设为0.25;组合2将电压偏差量的权重系数设为0.5,有功网损的权重系数设为0.5;组合3将电压偏差量的权重系数设为0.25,有功网损的权重系数设为0.75。在这3个权重组合设置下,对应的3个目标函数如下。
(1) 组合1:
| $ \min F_3(\boldsymbol{x})=0.75\left|U_0-U_{\text {ref }}\right|+0.25 \sum\limits_{w=1}^{N_2} R_w \frac{P_w^2+Q_w^2}{\left|U_w\right|^2} $ | (25) |
(2) 组合2:
| $ \min F_4(\boldsymbol{x})=0.5\left|U_0-U_{\text {ref }}\right|+0.5 \sum\limits_{w=1}^{N_2} R_w \frac{P_w^2+Q_w^2}{\left|U_w\right|^2} $ | (26) |
(3) 组合3:
| $ \min F_5(\boldsymbol{x})=0.25\left|U_0-U_{\text {ref }}\right|+0.75 \sum\limits_{w=1}^{N_2} R_w \frac{P_w^2+Q_w^2}{\left|U_w\right|^2} $ | (27) |
自适应权重系数多目标无功优化策略的目标函数见式(19)。
为比较不同工况下上述无功优化策略的优化效果,将风电场并网点电压分别设置为1.01 p.u.、1.06 p.u.、1.10 p.u.,采用上述多种无功优化策略进行仿真分析。
3.2 仿真分析不同工况下各无功优化策略的优化效果如表 2、表 3所示,可以看出,不同的电压、网损权重系数设置会对优化效果产生影响。以并网点初始电压为1.06 p.u.为例,在3种固定权重系数组合对应的优化策略中,电压、网损权重系数为0.75、0.25的组合1对应的优化策略获得了最佳的电压优化效果,此时并网点电压从1.06 p.u.降低至1.016 p.u.,但优化后的网损为10.33 MW,对网损的优化效果最差;电压、权重权重系数为0.25、0.75的组合3对应的优化策略对于并网点电压的优化效果最差,并网点电压仅降低至1.030 p.u.,但其网损降低至10.18 MW,取得了最好的网损优化效果;电压、网损权重系数为0.5、0.5的组合2对应的优化策略对于并网点电压的优化效果优于组合1,但劣于组合3,对于网损的优化效果优于组合3,但劣于组合1。
|
|
表 2 不同工况下各优化策略网损优化对比 Table 2 Comparison of optimization effect of each optimization strategy on network loss under different working conditions |
|
|
表 3 不同工况下各优化策略电压优化对比 Table 3 Comparison of voltage optimization effects of various optimization strategies under different working conditions |
由以上数据分析可知,在多目标优化中,优化目标对应权重系数越大,对该目标的优化效果越好。但对于复杂工况下的电网,风电场并网点电压会持续处于波动状态,不同时刻的并网点电压偏离量可能相差较大,固定权重系数的无功优化策略可能无法持续取得较好的优化效果。
当电网工况处于持续变化的场景下,风电场并网点电压可能会持续剧烈变化,对比表 2、表 3中自适应权重系数与固定权重系数无功优化策略的优化效果可见:(1) 当并网点电压保持在安全范围内时(对应表 2、表 3中1.01 p.u.一行),自适应无功优化策略对于并网点电压的优化效果弱于固定权重无功优化策略,但对于有功网损的优化效果远优于固定权重无功优化策略,有功网损降低至10.08 MW;(2) 当并网点电压临近或超出安全阈值时(对应表 2、表 3中1.06 p.u.、1.10 p.u.两行),自适应无功优化策略对于有功网损的优化效果弱于固定权重无功优化策略,但对于并网点电压的优化效果明显优于固定权重系数的无功优化策略,能有效保证并网点电压处于安全范围内。当并网点电压为1.10 p.u.时,经权重系数比为0.25 ∶0.75的优化策略优化后的并网点电压为1.052 p.u.,依旧超出安全阈值,此时风电场的安全运行受到严重影响。
综上,相比于传统固定权重无功优化策略,自适应无功优化策略在并网点电压出现较大波动时,对电压的优化效果更好,能使电压偏离量快速降低至安全范围;当并网点电压处于安全范围内时,能够最大降低有功网损,优化效果优于固定权重无功优化策略。
4 结语当电压偏离量较大时,优化目标以网损最小为主,影响电力系统的安全运行;反之,在电压偏离量较小时,优化目标以电压偏离量最小为主,可能会导致补偿能力浪费,增加网损并降低系统的经济性。针对海上风电场在无功主动支撑控制方面存在的电压偏离较大或补偿能力浪费问题,文中在建立海上风电场及其风电机组的无功主动支撑控制模型的基础上,提出基于并网点电压偏离量的自适应实时变权重的目标函数,并利用PSO算法求解该模型在动态约束下的无功控制策略。仿真结果表明:所提出的策略可保证复杂工况下海上风电场并网点的电压偏离处于安全范围内的条件下,且能够最小化有功网损,从而精准实现海上风电场对复杂工况下电力系统的无功主动支撑。
致谢
本文得到南方电网数字电网研究院有限公司科技项目(670000KK52220011)资助,谨此致谢!
| [1] |
刘文元, 任必兴, 李海峰, 等. 直驱风电场和串补之间的次同步振荡风险[J]. 电力工程技术, 2022, 41(4): 25-32. LIU Wenyuan, REN Bixing, LI Haifeng, et al. Sub-synchronous oscillation risk between PMSG farm and series complement[J]. Electric Power Engineering Technology, 2022, 41(4): 25-32. DOI:10.12158/j.2096-3203.2022.04.004 (  0) 0) |
| [2] |
王渝红, 宋雨妍, 廖建权, 等. 风电电压主动支撑技术现状与发展趋势[J]. 电网技术, 2023, 47(8): 3193-3205. WANG Yuhong, SONG Yuyan, LIAO Jianquan, et al. Review and development trends of DFIG-based wind power voltage active support technology[J]. Power System Technology, 2023, 47(8): 3193-3205. (  0) 0) |
| [3] |
朱瑛, 饶军, 郭旭滨. 风电场无功补偿工况下级联H桥STATCOM电压平衡控制[J]. 电力系统自动化, 2022, 46(21): 97-105. ZHU Ying, RAO Jun, GUO Xubin. Voltage balance control of cascaded H-bridge STATCOM for wind farm under reactive power compensation condition[J]. Automation of Electric Power Systems, 2022, 46(21): 97-105. (  0) 0) |
| [4] |
肖晃庆, 黄小威, 李岩, 等. 适用于二极管不控整流送出的海上风电机组无功功率同步控制策略[J]. 高电压技术, 2022, 48(10): 3820-3828. XIAO Huangqing, HUANG Xiaowei, LI Yan, et al. Reactive pow er-synchronization control for offshore wind turbines connected to diode rectifier[J]. High Voltage Engineering, 2022, 48(10): 3820-3828. (  0) 0) |
| [5] |
唐云辉, 马跃江, 王超, 等. 基于量子粒子群算法的含风电场配电网无功优化[J]. 电测与仪表, 2015, 52(19): 79-83. TANG Yunhui, MA Yuejiang, WANG Chao, et al. Reactive power optimization in distribution network with wind farm based on quantum particle swarm optimization algorithm[J]. Electrical Measurement & Instrumentation, 2015, 52(19): 79-83. (  0) 0) |
| [6] |
王玲玲, 王昕, 郑益慧, 等. 计及多个风电机组出力相关性的配电网无功优化[J]. 电网技术, 2017, 41(11): 3463-3469. WANG Lingling, WANG Xin, ZHENG Yihui, et al. Reactive power optimization of distribution network considering output correlation of multiple wind turbines[J]. Power System Technology, 2017, 41(11): 3463-3469. (  0) 0) |
| [7] |
李晓利, 高金峰. 用于配电网多目标无功优化的改进粒子群优化算法[J]. 电力自动化设备, 2019, 39(1): 106-111. LI Xiaoli, GAO Jinfeng. Improved particle swarm optimization algorithm for multi-objective reactive power optimization of distribution network[J]. Electric Power Automation Equipment, 2019, 39(1): 106-111. (  0) 0) |
| [8] |
栗然, 唐凡, 刘英培, 等. 双馈风电场新型无功补偿与电压控制方案[J]. 中国电机工程学报, 2012, 32(19): 16-23, 180. LI Ran, TANG Fan, LIU Yingpei, et al. A new scheme of reactive power compensation and voltage control for DFIG based wind farm[J]. Proceedings of the CSEE, 2012, 32(19): 16-23, 180. (  0) 0) |
| [9] |
陈光宇, 吴文龙, 戴则梅, 等. 计及故障场景集的风光储混合系统区域无功储备多目标优化[J]. 电力系统自动化, 2022, 46(17): 194-204. CHEN Guangyu, WU Wenlong, DAI Zemei, et al. Multi-objective optimization of regional reactive power reserve in hybrid system with wind, photovoltaic and energy storage considering fault scenario set[J]. Automation of Electric Power Systems, 2022, 46(17): 194-204. (  0) 0) |
| [10] |
崔挺, 李雪萍, 颜畅, 等. 基于模型预测控制的风电场故障穿越有功无功优化控制策略[J]. 电力系统保护与控制, 2022, 50(2): 12-20. CUI Ting, LI Xueping, YAN Chang, et al. Active and reactive power optimization control strategy for wind farm fault ride-through based on model predictive control[J]. Power System Protection and Control, 2022, 50(2): 12-20. (  0) 0) |
| [11] |
董海鹰, 陈彦求, 汪宁渤, 等. 含前端调速式风电机组风电场的无功运行优化[J]. 太阳能学报, 2020, 41(11): 254-260. DONG Haiying, CHEN Yanqiu, WANG Ningbo, et al. Optimizatton in reactive power operation of wind farm with front-end speed controlled wind turbine[J]. Acta Energiae Solaris Sinica, 2020, 41(11): 254-260. (  0) 0) |
| [12] |
LIU J H, CHENG J S. Online voltage security enhancement using voltage sensitivity-based coherent reactive power control in multi-area wind power generation systems[J]. IEEE Transactions on Power Systems, 2021, 36(3): 2729-2732. DOI:10.1109/TPWRS.2021.3053139 (  0) 0) |
| [13] |
WANG Y, WANG T, ZHOU K P, et al. Reactive power optimization of wind farm considering reactive power regulation capacity of wind generators[C]//2019 IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia). Chengdu, China. IEEE, 2019: 4031-4035.
(  0) 0) |
| [14] |
李生虎, 蒋以天. 基于无功优化的DFIG并网电力系统OSC-OPF算法[J]. 电力系统自动化, 2020, 44(15): 70-76. LI Shenghu, JIANG Yitian. Oscillatory stability constrained optimal power flow algorithm based on reactive power optimization for DFIG integrated power system[J]. Automation of Electric Power Systems, 2020, 44(15): 70-76. (  0) 0) |
| [15] |
刘承锡, 张兆毅, 赖秋频. 考虑风电功率短期波动的风电场无功快速跟踪优化[J]. 中国电机工程学报, 2023, 43(15): 5850-5863. LIU Chengxi, ZHANG Zhaoyi, LAI Qiupin. Fast-tracking optimization of reactive power for wind farm considering short-term fluctuations of windgenerations[J]. Proceedings of the CSEE, 2023, 43(15): 5850-5863. (  0) 0) |
| [16] |
黄肖琪, 周羽生, 周文晴, 等. 基于储能和无功优化的直驱机组海上风电场低电压穿越策略[J/OL]. 电测与仪表: 1-9[2023-04-18]. http://kns.cnki.net/kcms/detail/23.1202.TH.20230215.1719.024.html. HUANG Xiaoqi, ZHOU Yusheng, ZHOU Wenqing, et al. Low voltage ride through strategy of the D-PMSG offshore wind power farm based on energy storage and reactive power optimization[J]. Electrical Measurement & Instrumentation: 1-9[2023-04-18]. http://kns.cnki.net/kcms/detail/23.1202.TH.20230215.1719.024.html. (  0) 0) |
| [17] |
吴星, 刘天羽, 江秀臣, 等. 基于改进遗传算法的海上风电场无功优化[J]. 电测与仪表, 2020, 57(4): 108-113. WU Xing, LIU Tianyu, JIANG Xiuchen, et al. Research on reactive power optimization of offshore wind farm based on improved genetic algorithm[J]. Electrical Measurement & Instrumentation, 2020, 57(4): 108-113. (  0) 0) |
| [18] |
刘昊, 王玮, 唐芬. 基于变功率因数的分散式风电场优化运行策略[J]. 太阳能学报, 2019, 40(2): 387-395. LIU Hao, WANG Wei, TANG Fen. Optimal operation strategy for dispersed wind farms based on variable power factor[J]. Acta Energiae Solaris Sinica, 2019, 40(2): 387-395. (  0) 0) |
| [19] |
沈可心, 薛博文, 朱晓荣. 直流微网中直驱风机的类虚拟同步发电机惯性控制策略[J]. 高电压技术, 2023, 49(6): 2526-2537. SHEN Kexin, XUE Bowen, ZHU Xiaorong. Inertia control strategy of direct-driven wind generation system in DC microgrid based on analogous virtual synchronous generator[J]. High Voltage Engineering, 2023, 49(6): 2526-2537. (  0) 0) |
| [20] |
吴昊天, 顾雪平, 李航. 基于MMC-HVDC的永磁直驱风机并网控制策略[J]. 电网与清洁能源, 2018, 34(7): 51-56. WU Haotian, GU Xueping, LI Hang. Grid connection control strategy of permanent magnet direct drive fan based on MMC-HVDC[J]. Power System and Clean Energy, 2018, 34(7): 51-56. (  0) 0) |
| [21] |
王德胜, 颜湘武, 贾焦心, 等. 永磁直驱风机基于虚拟同步技术的高、低电压连续故障穿越策略[J]. 中国电机工程学报, 2022, 42(6): 2164-2175. WANG Desheng, YAN Xiangwu, JIA Jiaoxin, et al. High/low voltage continuous fault ride through strategy of PMSGs based on virtual synchronization technology[J]. Proceedings of the CSEE, 2022, 42(6): 2164-2175. (  0) 0) |
| [22] |
杨航, 周羽生, 许振华, 等. 基于储能和序分量控制的直驱永磁风电系统非对称故障穿越研究[J]. 电力系统保护与控制, 2022, 50(2): 60-68. YANG Hang, ZHOU Yusheng, XU Zhenhua, et al. Asymmetric fault ride-through of a direct-drive permanent magnet wind power system based on the control of energy storage and sequence components[J]. Power System Protection and Control, 2022, 50(2): 60-68. (  0) 0) |
| [23] |
张明慧, 张逸, 刘必杰, 等. 考虑供用电双方无功补偿潜力的省级技术降损互动管控平台[J]. 电力系统保护与控制, 2023, 51(23): 160-169. ZHANG Minghui, ZHANG Yi, LIU Bijie, et al. Provincial technology loss reduction interactive management and control platform consideringreactive power compensation potential of power supply and consumption sides[J]. Power System Protection and Control, 2023, 51(23): 160-169. (  0) 0) |
| [24] |
陈鸿琳, 熊馨瑶, 余浩, 等. SVG对海上风电交流并网系统稳定性影响分析[J]. 电力系统保护与控制, 2022, 50(19): 119-129. CHEN Honglin, XIONG Xinyao, YU Hao, et al. Analysis on the influence of an SVG on the stability of AC grid-connected offshore wind farms[J]. Power System Protection and Control, 2022, 50(19): 119-12. (  0) 0) |
| [25] |
鞠浩, 王旭东, 陆佳红. 基于混合参数化与粒子群算法的风力机翼型气动优化设计[J]. 太阳能学报, 2023, 44(5): 473-479. JU Hao, WANG Xudong, LU Jiahong. Aerddynamic optimization design of wind turbine airfoil based on hybrid parameterization and particle swarm algorithm[J]. Acta Energiae Solaris Sinica, 2023, 44(5): 473-479. (  0) 0) |
| [26] |
陈际, 袁守利, 刘志恩. 基于BAS改进PSO算法对PEMFC温度的控制[J]. 太阳能学报, 2023, 44(5): 67-73. CHEN Ji, YUAN Shouli, LIU Zhien. Temperature control of PEMFC based on BAS improved PSO algorithm[J]. Acta Energiae Solaris Sinica, 2023, 44(5): 67-73. (  0) 0) |
| [27] |
朱娟娟, 段奕琳, 闫群民, 等. 基于BAS-IMOPSO算法的风电系统储能优化配置[J]. 电力工程技术, 2023, 42(2): 180-187. ZHU Juanjuan, DUAN Yilin, YAN Qunmin, et al. Optimal allocation of energy storage in wind power system based on BAS-IMOPSO algorithm[J]. Electric Power Engineering Technology, 2023, 42(2): 180-187. DOI:10.12158/j.2096-3203.2023.02.021 (  0) 0) |
2. Yangjiang Offshore Wind Energy Laboratory, Yangjiang 529500, China;
3. Guangdong Key Laboratory of Clean Energy Technology, South China University of Technology, Guangzhou 510640, China
 2024, Vol. 43
2024, Vol. 43


 杨铎烔(1988),男,博士,研究员级高级工程师,从事新能源边缘控制、电力系统仿真与人工智能应用相关工作(E-mail:
杨铎烔(1988),男,博士,研究员级高级工程师,从事新能源边缘控制、电力系统仿真与人工智能应用相关工作(E-mail: