文章编号: 2096-3203(2024)03-0088-11 中图分类号: TM73
2. 天津市复杂系统控制理论及应用重点实验室,天津 300384;
3. 天津市新能源电力变换传输与智能控制重点实验室,天津 300384
随着对环境变化关注度的不断提高,低碳经济已经成为了全球的共识[1]。作为低碳经济的核心组成部分之一,碳交易优化是降低碳排放的有效途径。能源枢纽(energy hub, EH)在综合能源系统(integrated energy system, IES)中负责能源的协调和优化调度[2],通过协调各种能源形态之间的转换和利用,提高能源利用率[3],从而促进碳交易发展、减少碳排放。然而,基于EH的复杂性和不确定性,有效实现EH的低碳优化是一个具有挑战性的目标。
目前,已有大量研究针对EH优化问题进行探讨。文献[4]首次提出EH的概念,利用能量耦合矩阵,抽象地描述了IES内部的耦合关系,为IES运行研究奠定了重要基础。文献[5]将多类型的需求响应资源纳入EH优化模型中,提出以运行成本最小为目标的EH优化运行策略。文献[6]详细描述了考虑综合需求响应的基于分时电价的IES模型。上述研究均从经济性方面对EH进行研究,得出了关键的结论,但未考虑碳排放等环境效益的影响。
为保证可持续发展,有必要引入阶梯型碳交易机制[7],以有效减少系统碳排放量。文献[8]针对传统碳交易机制在减排力度方面的不足,提出阶梯型碳交易模型。文献[9]基于碳交易机制,提出基于EH的分散调度模型。然而,上述研究均是以精确的可再生能源为前提展开研究,未考虑源-荷预测误差对系统实际运行的影响。
模型预测控制(model predictive control, MPC)具有滚动优化和反馈校正的特点,能有效降低源-荷预测误差对系统实际运行的影响,在EH优化调度中有着广泛的应用[10-11]。文献[12]采用双层MPC算法,上层通过MPC对火电机组的高、低频指令进行再分配,下层利用MPC完成频率的动态调节。文献[13]在对园区EH中各设备建模的基础上,建立滚动优化和实时调整两阶段的多时间尺度调度模型,可以快速响应各设备和负荷的变化。然而,随着我国经济水平的快速增长以及电力系统的不断建设,电网结构和运行方式愈加复杂,传统MPC求解效率偏低、不易拓展[14],而分布式模型预测控制(distributed model predictive control, DMPC)可以预测未来的电力需求和能源供应情况,从而制定最佳的电力调度计划。DMPC在MPC的基础上,将整个能源系统分解为多个智能体,每个智能体负责局部的优化求解,因此系统能够并行处理数据,不仅提高了计算效率,而且能够适应大规模复杂系统的需求,从而有效解决传统MPC在控制方法上面的不足。文献[15]提出一种基于DMPC加权一致性算法的电池储能阵列分布式控制策略,实现各单元功率的合理分配。文献[16]基于DMPC,将整体配电网模型分解为多个子系统,协调配电网中大规模分布式电源、储能等可控资源。EH是一种大规模复杂系统,其优化问题涉及多种变量和约束[17],因此,将DMPC应用于EH优化调度具有重要研究意义。
为此,文中以现有文献研究为基础,针对源-荷不确定性和低碳政策,提出基于DMPC和奖惩阶梯型碳价机制的考虑源-荷预测误差的EH多时间尺度低碳优化调度策略。首先,基于奖惩阶梯型碳价机制,建立日前低碳优化调度、日内滚动优化调度和实时调整的多时间尺度低碳优化调度模型;其次,基于DMPC,在实时调整阶段通过对各智能体的有序控制,实现对系统的整体优化;最后,设置不同场景进行仿真对比,验证文中方法在考虑源-荷不确定性和低碳政策下,实现EH优化调度的可行性。
1 EH数学模型为了描述EH的运行特性和约束条件,文中建立EH数学模型。文中研究的EH结构如图 1所示,包含供能侧、EH侧和负荷侧。供能侧包括外部电网、外部气网、光伏机组(photovoltaic, PV)和风电机组(wind turbine, WT);EH侧包括余热锅炉(waste heat boiler, WHB)、燃气轮机(gas turbine, GT)、燃气锅炉(gas boiler, GB)、冰蓄冷空调(ice-storage air-conditioner, ISAC)、吸收式制冷机(absorption refrigerator, AR),储能装置有蓄电池(storage cell, SC)、蓄热槽(heat storage tank, HST);负荷侧包括冷、热、电3种负荷。图 1展示了不同能源形式之间的转换,以及各参与者之间的协作关系。

|
图 1 EH结构示意 Fig. 1 Schematic diagram of EH structure |
冷热电联产(combined cooling, heating and power, CCHP)系统是一种集制冷、制热和发电于一体的能源利用系统,通过燃烧天然气发电,发电过程中产生的余热可通过WHB和AR实现热能和冷能的转化。CCHP可同时满足用户的冷气、热力和电能需求,提高能源利用率,减少能源消耗和排放。
1.2 电转气设备电转气(power to gas, P2G)设备可以利用可再生能源产生的多余电能电解水获得氢气,并进一步将氢气与二氧化碳等合成甲烷等气体,实现电能和气体能量的互通。P2G技术可以促进可再生能源的利用并减少碳排放量。其中,电功率和天然气功率之间须满足如下关系:
| $ \left\{\begin{array}{l} G_{\mathrm{P} 2 \mathrm{G}}(t)=\eta_{\mathrm{P} 2 \mathrm{G}} P_{\mathrm{P} 2 \mathrm{G}}(t) \\ 0 \leqslant G_{\mathrm{P} 2 \mathrm{G}}(t) \leqslant G_{\mathrm{P} 2 \mathrm{G}}^{\max } \end{array}\right. $ | (1) |
式中:GP2G(t)、PP2G(t)分别为P2G输出的天然气功率和P2G输入的电功率;ηP2G为P2G的能源转换效率;GP2Gmax为P2G的最大输出功率。
1.3 储能设备储能设备的作用类似柔性负荷,可以平衡能源的供需,对系统能源进行合理的规划以提高能源利用效率并降低运行成本,文中考虑的储能装置为SC和HST。储能装置的约束条件如下:
| $ \left\{\begin{array}{l} S_x(t)=S_x(t-1)\left(1-\gamma_x\right)+ \\ \quad\left(P_{x, \mathrm{chr}}(t) \eta_{x, \mathrm{chr}}-P_{x, \mathrm{dis}}(t) / \eta_{x, \mathrm{dis}}\right) \Delta t \\ S_x^{\min } \leqslant S_x(t) \leqslant S_x^{\max } \\ S_{x, 24}=S_{x, 1} \\ B_{x, \mathrm{chr}}(t) P_{x, \mathrm{chr}}^{\min } \leqslant P_{x, \mathrm{chr}}(t) \leqslant B_{x, \mathrm{chr}}(t) P_{x, \mathrm{chr}}^{\max } \\ B_{x, \mathrm{dis}}(t) P_{x, \mathrm{dis}}^{\min } \leqslant P_{x, \mathrm{dis}}(t) \leqslant B_{x, \mathrm{dis}}(t) P_{x, \mathrm{dis}}^{\max } \\ B_{x, \mathrm{chr}}(t)+B_{x, \mathrm{dis}}(t) \leqslant 1 \end{array}\right. $ | (2) |
式中:Sx(t)为t时刻储能装置x的储能状态量,x∈{SC, HST};γx为储能装置x的能量自损系数;Px, chr(t)、Px, dis(t)分别为储能装置x在t时刻的充、放能功率;ηx, chr、ηx, dis分别为储能装置x的充、放能效率;Δt为时间跨度;Sxmax、Sxmin分别为储能装置x的储能状态量上、下限;Sx, 1、Sx, 24分别为储能装置x一天调度周期开始和结束时的储能状态量;Bx, chr(t)、Bx, dis(t)分别为t时刻储能装置x的充、放能状态标志位;Px, chrmax、Px, chrmin分别为储能装置x充能功率的上、下限;Px, dismax、Px, dismin分别为储能装置x放能功率的上、下限。
1.4 冰蓄冷空调(ISAC)ISAC主要包括一个冰蓄冷装置(蓄冰罐)和一个空气处理装置。在夜间低峰电时段,制冷机组利用电能制造冰块并储存在蓄冰罐中,白天高峰电时段,空气处理装置利用冰块来提供制冷效果。ISAC系统可以显著降低电力需求峰值、减少电能消耗、提高电网稳定性。蓄冰罐是ISAC的重要设备,模型主要考虑了制冷效率、损耗系数和最大储存容量。
| $ \left\{\begin{array}{l} C_{\mathrm{ice}}(t)=C_{\mathrm{ice}}(t-1)\left(1-\gamma_{\mathrm{Q}}\right)+ \\ \quad\left(\eta_{\mathrm{ice}, \mathrm{chr}} Q_{\mathrm{c}}(t)-Q_{\mathrm{d}}(t) / \eta_{\mathrm{ice}, \mathrm{dis}}\right) \Delta t \\ C_{\mathrm{ice}}^{\mathrm{down}} \leqslant C_{\mathrm{ice}}(t)-C_{\mathrm{ice}}(t-1) \leqslant C_{\mathrm{ice}}^{\mathrm{up}} \end{array}\right. $ | (3) |
式中:Cice(t)为蓄冰罐t时刻储存的冷能;γQ为自损系数;ηice, chr、ηice, dis分别为蓄冰和融冰系数;Qc(t)、Qd(t)分别为t时刻制冷机蓄冰功率和蓄冰罐融冰功率;Ciceup、Cicedown分别为蓄冰罐的爬坡率上、下限。
2 奖惩阶梯型碳价机制模型 2.1 EH碳排放配额的分配机制为促进EH系统减少碳排放,文中设计一种奖惩阶梯型碳价机制模型。根据企业CO2排放情况,对应不同的碳排放配额(称为碳配额):如果企业的碳排放量低于其碳配额,则可以获得相应的奖励补贴。奖惩阶梯型碳价机制的设定可以有效激励企业降低碳排放量。文中EH的无偿碳配额在调度前基于国家碳排放指标分配方案确定。
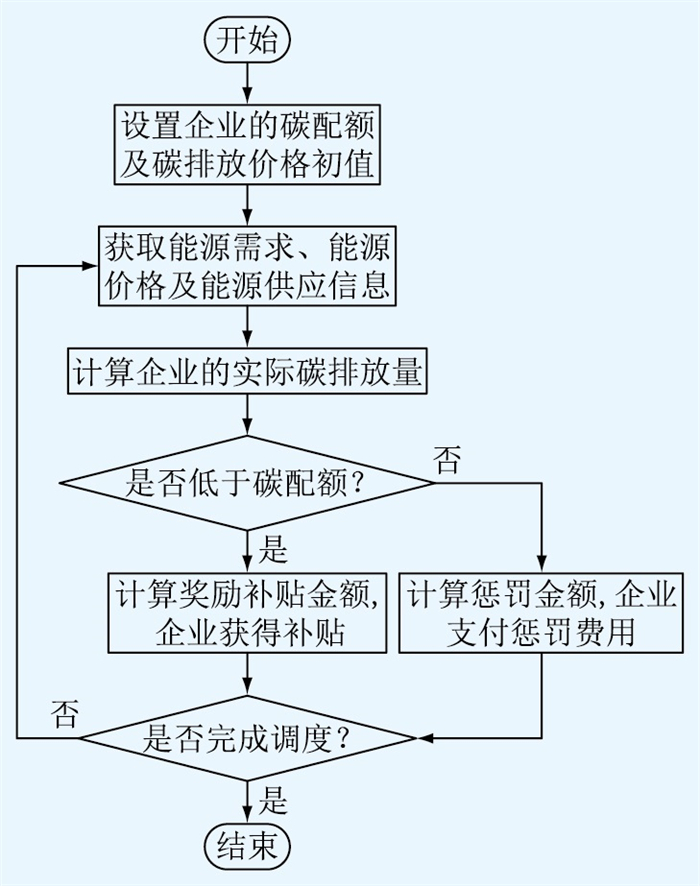
将碳排放量作为EH调度的一个目标,将多时间尺度调度问题转化为一个动态规划问题。考虑能源需求、能源价格、能源供应等多种因素,并根据奖惩阶梯型碳价机制,设定不同的碳配额及碳排放价格。通过不断调整碳配额及价格,可以逐步优化EH的调度方案、降低系统碳排放量,同时保证能源供应的可靠性。具体流程如图 2所示。
|
图 2 奖惩阶梯型碳价计算流程 Fig. 2 The calculation flowchart of incentive and penalty ladder carbon price |
文中EH的碳排放源主要分为三部分,分别为GB、CCHP和外部购电,其中认为外部购电均来自于燃煤机组。EH的碳配额分配如下:
| $ E_{\mathrm{EH}}=E_{\mathrm{GB}}+E_{\mathrm{CCHP}}+E_{\mathrm{Grid}} $ | (4) |
式中:EEH为EH总的碳配额;EGB、ECCHP、EGrid分别为GB、CCHP和外部购电所分配的碳配额。
考虑到P2G在转换过程中能够吸收部分CO2作为原料[18],故实际碳排放量可以表示为:
| $ \left\{\begin{array}{l} E_{\mathrm{EH}}^{\text {act }}=E_{\mathrm{Grid}}^{\text {act }}+E_{\mathrm{CCHP}}^{\text {act }}+E_{\mathrm{GB}}^{\text {act }}-E_{\mathrm{P} 2 \mathrm{G}}^{\text {act }} \\ E_{\mathrm{Grid}}^{\text {act }}=\sum\limits_{t=1}^T\left(a_1+b_1 P_{\text {buy }}(t)+c_1 P_{\text {buy }}^2(t)\right) \\ E_{\mathrm{CCHP}}^{\text {act }}=\sum\limits_{t=1}^T\left(a_2+b_2 P_{\text {total }}(t)+c_2 P_{\text {total }}^2(t)\right) \\ E_{\mathrm{GB}}^{\text {act }}=\sum\limits_{t=1}^T\left(a_3+b_3 H_{\mathrm{GB}}(t)+c_3 H_{\mathrm{GB}}^2(t)\right) \\ P_{\text {total }}(t)=P_{\mathrm{GT}}(t)+H_{\mathrm{WHB}}(t)+Q_{\mathrm{AR}}(t) \\ E_{\mathrm{P} 2 \mathrm{G}}^{\text {act }}=\sum\limits_{t=1}^T \delta P_{\mathrm{P} 2 \mathrm{G}}(t) \end{array}\right. $ | (5) |
式中:EEHact为EH总的实际碳排放量;EGridact、ECCHPact、EGBact分别为外部购电、CCHP、GB的实际碳排放量;EP2Gact为P2G吸收的CO2量;T为总时刻;a1、b1、c1为外部购电的碳排放量计算参数;Pbuy(t)为EH向外部电网购电功率;a2、b2、c2为CCHP的碳排放量计算参数;Ptotal(t)为总的清洁机组的等效输出功率;a3、b3、c3为GB的碳排放量计算参数;HGB(t)为GB在t时刻输出的热功率;PGT(t)、HWHB(t)、QAR(t)分别为CCHP在t时刻输出的电、热、冷功率;δ为碳捕获系数。
为进一步减少系统碳排放量,激发能源企业减排潜力,建立奖惩阶梯型碳价数学模型,可表示为:
| $ F_{\mathrm{c}}=\left\{\begin{array}{l} -c(1+2 \mu)\left(E_{\mathrm{EH}}-h-E_{\mathrm{EH}}^{\text {act }}\right) \\ \ \ \ \ \ \ \ \ \ \ \ \ E_{\mathrm{EH}}^{\text {act }}-E_{\mathrm{EH}}<-h \\ -c(1+2 \mu) h-c(1+\mu)\left(E_{\mathrm{EH}}-E_{\mathrm{EH}}^{a c t}\right) \\ \ \ \ \ \ \ \ \ \ \ \ \ -h \leqslant E_{\mathrm{EH}}^{\text {act }}-E_{\mathrm{EH}} \leqslant 0 \\ c\left(E_{\mathrm{EH}}^{\text {act }}-E_{\mathrm{EH}}\right) \quad 0<E_{\mathrm{EH}}^{\text {act }}-E_{\mathrm{EH}} \leqslant h \\ c h+c(1+\lambda)\left(E_{\mathrm{EH}}^{\text {act }}-E_{\mathrm{EH}}-h\right) \\ \ \ \ \ \ \ \ \ \ \ \ \ h<E_{\mathrm{EH}}^{a \mathrm{at}}-E_{\mathrm{EH}} \leqslant 2 h \\ c(2+\lambda) h+c(1+2 \lambda)\left(E_{\mathrm{EH}}^{\text {act }}-E_{\mathrm{EH}}-2 h\right) \\ \ \ \ \ \ \ \ \ \ \ \ \ 2 h<E_{\mathrm{EH}}^{\text {act }}-E_{\mathrm{EH}} \leqslant 3 h \\ c(3+3 \lambda) h+c(1+3 \lambda)\left(E_{\mathrm{EH}}^{\text {act }}-E_{\mathrm{EH}}-3 h\right) \\ \ \ \ \ \ \ \ \ \ \ \ \ E_{\mathrm{EH}}^{\text {act }}-E_{\mathrm{EH}}>3 h \end{array}\right. $ | (6) |
式中:Fc为EH中承担的奖惩阶梯型碳价;c为碳交易价格;μ、λ分别为奖、惩系数;h为碳排放区间长度。图 3展示了奖惩阶梯型碳价的数学模型,其中Fcu为碳排放区间内单位碳排放的价格。

|
图 3 奖惩阶梯型碳价模型示意 Fig. 3 Schematic diagram of incentive and penalty ladder carbon price model |
DMPC将大型系统分解为多个具有交互能力的小型子系统,从而将整体优化问题转化为多个子系统求解问题[19]。在DMPC下,各智能体系统在假定其他M-1个智能体系统最优解已知的情况下,其整体的控制策略可由M个智能体系统共同表示,则第i个智能体系统的控制策略的目标函数为:
| $ \begin{gathered} \min f_i=k_i \sum\limits_{x=1}^l\left[\alpha_i\left(y_i(h+x \mid h)-p_i(h+x \mid h)\right)^2+\right. \\ \left.\beta_i\left(w_i(h+x)-w_i(h+x-1)\right)^2\right]+ \\ g_i \sum\limits_{x=1}^l\left[p_i(h+x \mid h)-\alpha_i\left(y_i(h+x \mid h)-\right.\right. \\ \left.\sum\limits_{a=1, a \neq i}^M y_a(h+x \mid h)\right)^2+ \\ \left.\beta_i\left(w_i(h+x)-w_i(h+x-1)\right)^2\right] \end{gathered} $ | (7) |
式中:ki、gi为第i个智能体系统的权重系数,用于调节不同智能体系统之间的优先级和协调性;αi、βi分别为第i个智能体系统的输出变量和控制变量的权重系数;l为未来预测的时刻数;yi(h+x|h)为第i个智能体系统在h+x时刻的预测输出变量,根据第i个智能体系统的模型和当前状态计算得到;pi(h+x|h)为第i个智能体系统在h+x时刻的参考轨迹,根据第i个智能体系统的期望输出确定;wi(h+x)为第i个智能体系统在h+x时刻的控制变量。式(7)为最小化问题,目的是使第i个智能体系统的输出变量和控制变量与参考轨迹的偏差最小。
在DMPC中,各个智能体系统之间的控制策略相互联系、相互依赖,需要进行协同计算和通信,以实现整个系统的协同控制。因此,在计算第i个智能体系统的控制策略时,需要考虑其他M-1个智能体系统的状态变量,并纳入目标函数进行优化。同时,须满足上、下限约束。
| $ \left\{\begin{array}{l} w_{i, \min }(h+l) \leqslant w_i(h+l) \leqslant w_{i, \max }(h+l) \\ \Delta w_{i, \min }(h+l) \leqslant w_i(h+l+1)-w_i(h+l) \leqslant \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \Delta w_{i, \max }(h+l) \\ y_{i, \min }(h+l) \leqslant y_i(h+l) \leqslant y_{i, \max }(h+l) \end{array}\right. $ | (8) |
式中:wi, max(h+l)、wi, min(h+l)分别为h+l时刻控制变量的上、下限;Δwi, max(h+l)、Δwi, min(h+l)分别为h+l时刻控制变量增量的上、下限;yi(h+l)为h+l时刻第i个智能体的输出变量;yi, max(h+l)、yi, min(h+l)分别为h+l时刻输出变量的上、下限。
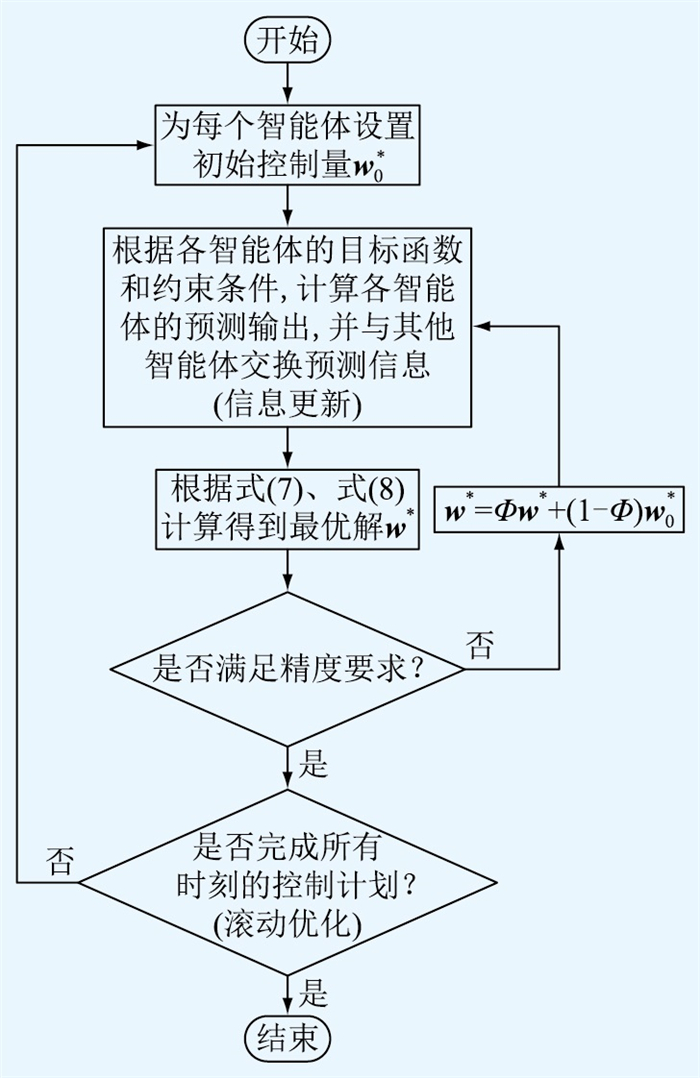
DMPC的具体求解流程如图 4所示,其中Φ为权重系数,表示对上一次迭代结果的信任程度。文中使用CPLEX商业求解器对DMPC内部优化问题进行求解,所使用算法为分支定界法。
|
图 4 DMPC算法流程 Fig. 4 The flow chart of DMPC algorithm |
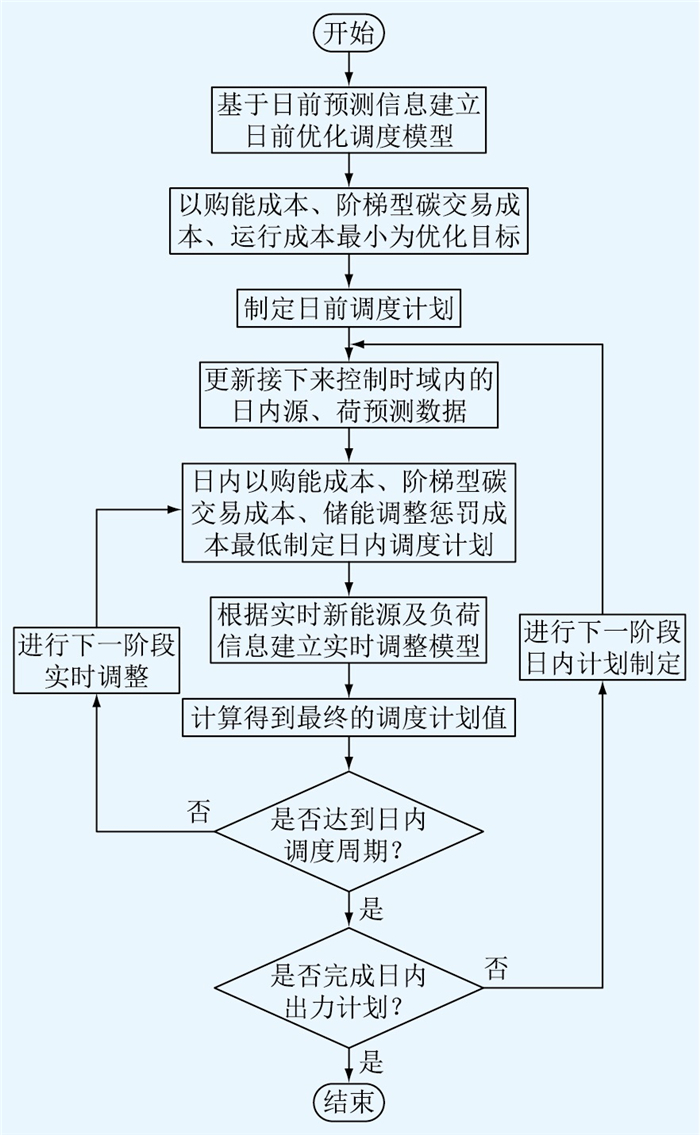
为了充分利用EH的多能互补和协同优化特性,提出一种多时间尺度调度策略。当预测的时间范围减小时,不确定性对预测的影响也降低[20]。这是因为较短时间尺度内的预测受到外部因素影响较少,天气、用电行为等相对较为稳定,而随着时间尺度增加,外部因素变化更加复杂和不确定。为降低可再生能源和负荷预测不确定性对系统优化调度的影响,基于源-荷预测精度随时间尺度的减小而增加的原理,提出日前-日内-实时多时间尺度的优化调度模型,求解流程如图 5所示。
|
图 5 多时间尺度调度流程 Fig. 5 The flow chart of multi-timescale scheduling |
以1 h为时间尺度制定1 d的调度计划:考虑到EH的环境效益,在日前调度阶段引入阶梯型碳交易机制,以EH日前调度的总成本最小为优化目标,建立日前低碳调度模型。
| $ \min F_{\mathrm{DA}}=F_{\mathrm{Grid}}^{\mathrm{DA}}+F_{\text {Gas }}^{\mathrm{DA}}+F_{\mathrm{m}}^{\mathrm{DA}}+F_{\mathrm{c}}^{\mathrm{DA}} $ | (9) |
式中:FDA为EH日前调度的总成本费用;FGridDA、FGasDA、FmDA、FcDA分别为电网交互成本、购气成本、设备运行维护成本和日前的奖惩阶梯碳价。其中FcDA计算参考式(6),其余各项计算如下:
| $ \left\{\begin{array}{l} F_{\text {Grid }}^{\mathrm{DA}}=\sum\limits_{i=1}^{24}\left(c_{\mathrm{g}}^{\mathrm{b}}(t) P_{\mathrm{buy}}(t)+c_{\mathrm{g}}^{\mathrm{s}}(t) P_{\mathrm{sell}}(t)\right) \Delta t \\ F_{\mathrm{Gas}}^{\mathrm{DA}}=\sum\limits_{t=1}^{24} \frac{c_{\mathrm{gas}}(t) G_{\mathrm{gas}}(t)}{H_{\mathrm{ng}}} \Delta t \\ F_{\mathrm{m}}^{\mathrm{DA}}=\sum\limits_{t=1}^{24} \sum\limits_{i=1}^N r_i P_i(t) \Delta t \end{array}\right. $ | (10) |
式中:cgb(t)、cgs(t)分别为EH与外部电网交互时t时刻的购、售电价格;Psell(t)为t时刻EH与外部电网交互的售电功率;cgas(t)、Ggas(t)分别为t时刻的购气价格和购气功率;Hng为天然气低热值;ri为设备i的单位运行维护费用;Pi(t)为设备i在t时刻的输出功率。
系统须满足功率平衡约束:
| $ \left\{\begin{array}{l} P_{\mathrm{WT}}(t)+P_{\mathrm{PV}}(t)+P_{\mathrm{GT}}(t)+P_{\mathrm{buy}}(t)+P_{\mathrm{SC}, \mathrm{dis}}(t)= \\ \ \ \ \ L_{\mathrm{e}}(t)+P_{\mathrm{sell}}(t)+P_{\mathrm{P} 2 \mathrm{G}}(t)+P_{\mathrm{SC}, \mathrm{chr}}(t)+P_{\mathrm{ISAC}}(t) \\ H_{\mathrm{GB}}(t)+H_{\mathrm{WHB}}(t)+H_{\mathrm{HST}, \mathrm{dis}}(t)=L_{\mathrm{h}}(t)+H_{\mathrm{HST}, \mathrm{chr}}(t) \\ Q_{\mathrm{AR}}(t)+Q_{\mathrm{c}}(t)+Q_{\mathrm{d}}(t)=L_{\mathrm{q}}(t) \end{array}\right. $ | (11) |
式中:PWT(t)、PPV(t)、PGT(t)分别为WT、PV和GT在t时刻的输出功率;PSC, chr(t)、PSC, dis(t)分别为SC在t时刻的充、放电功率;Le(t)、Lh(t)、Lq(t)分别为t时刻实际电、热、冷负荷;PISAC(t)为ISAC在t时刻消耗的电功率;HHST, chr(t)、HHST, dis(t)分别为HST在t时刻的充、放热功率。
3.2.2 日内滚动优化模型(15 min)在日内调度中,从第k时段开始,以15 min为时间尺度,更新后续控制时段内的源、荷预测信息;然后以系统总成本最低为目标,确定控制时段内各机组最优出力的调整量;最后,从第k+1时段开始,使用更新后的源、荷数据信息,重复以上步骤,实现预测信息的滚动优化。
基于日前调度计划,在滚动优化时,须先更新控制时域内可再生能源和负荷的预测信息,文中控制时域取4 h。为避免储能装置的频繁充放能,使优化结果遵循日前计划,须在日内滚动优化中增加能反映储能装置长期特征的储能惩罚项[21]。基于此,日内滚动优化目标函数可表示如下:
| $ \min F_{\mathrm{ID}}=F_{\text {Grid }}^{\mathrm{ID}}+F_{\text {Gas }}^{\mathrm{ID}}+F_{\mathrm{Pun}}^{\mathrm{ID}}+F_{\mathrm{c}}^{\mathrm{ID}} $ | (12) |
式中:FID为日内优化的总成本;FGridID为日内EH与电网的交互成本;FGasID为日内EH的购气成本;FPunID为日内各储能设备的调整惩罚成本;FcID为日内的奖惩阶梯碳价,其计算参考式(6)。
| $ \left\{\begin{aligned} F_{\text {Grid }}^{\mathrm{ID}} & =\sum\limits_{t=k+1}^{k+4}\left(c_{\mathrm{g}}^{\mathrm{b}}(t) P_{\text {buy }}(t)+c_{\mathrm{g}}^{\mathrm{s}}(t) P_{\mathrm{sell}}(t)\right) \Delta t \\ F_{\text {Gas }}^{\mathrm{ID}} & =\sum\limits_{t=k+1}^{k+4} \frac{c_{\text {Gas }}(t) G_{\text {Gas }}(t)}{H_{\mathrm{ng}}} \Delta t \\ F_{\mathrm{Pun}}^{\mathrm{ID}} & =\sum\limits_{t=k+1}^{k+4}\left[\mu_{\mathrm{e}}\left(S_{\mathrm{SC}}^{\mathrm{ID}}(t)-S_{\mathrm{SC}}^{\mathrm{DA}}(t)\right)^2+\right. \\ & \left.\mu_{\mathrm{h}}\left(S_{\mathrm{HST}}^{\mathrm{ID}}(t)-S_{\mathrm{HST}}^{\mathrm{DA}}(t)\right)^2\right] \end{aligned}\right. $ | (13) |
式中:μe、μh分别为SC和HST的惩罚系数;SSCID(t)、SHSTID(t)分别为SC和HST在日内调度中t时刻的实际储能量;SSCDA(t)、SHSTDA(t)分别为SC和HST在日前计划中t时刻的储能量。
日内调度阶段不仅需要满足日前调度阶段中的能源设备约束和功率平衡约束,还需要与日前调度的能源设备运行状态约束一致[22]。
| $ \left\{\begin{array}{l} B_{\mathrm{GT}}^{\mathrm{DA}}(t)=B_{\mathrm{GT}}^{\mathrm{ID}}(t) \\ B_{x, \mathrm{chr}}^{\mathrm{DA}}(t) / B_{x, \mathrm{dis}}^{\mathrm{DA}}(t)=B_{x, \mathrm{chr}}^{\mathrm{ID}}(t) / B_{x, \mathrm{dis}}^{\mathrm{ID}}(t) \\ B_{\mathrm{ISAC}}^{\mathrm{DA}}(t)=B_{\mathrm{ISAC}}^{\mathrm{ID}}(t) \end{array}\right. $ | (14) |
式中:BGTDA(t)、BGTID(t)分别为日前、日内GT在t时刻的运行状态标志位;Bx, chrDA(t)/Bx, disDA(t)、Bx, chrID(t)/Bx, disID(t)分别为日前、日内储能装置x在t时刻的充/放能状态标志位,x∈{SC, HST};BISACDA(t)、BISACID(t)分别为日前、日内ISAC在t时刻的运行状态标志位。
3.2.3 实时调整模型(5 min)在实时调整阶段,随着时间的推移,测量数据和预测数据不断更新,各个智能体可以使用最新的信息进行微调并更新控制策略以满足不断变化的能源需求。根据实时更新的源、荷预测信息,实时调整与日内滚动优化嵌套执行,以5 min为时间尺度,以后续1 h内的设备总调整量最低为目标,确定调整后的最终调度计划[23]。以部分设备为例,利用式(15)作为实时调整的预测模型:
| $ \begin{array}{c} {\left[\begin{array}{c} P_{\mathrm{GT}}(t+1) \\ P_{\mathrm{AR}}(t+1) \\ P_{\mathrm{ISAC}}(t+1) \\ P_{\mathrm{Grid}}(t+1) \\ G_{\mathrm{Gas}}(t+1) \end{array}\right]=\left[\begin{array}{ccccc} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{array}\right]\left[\begin{array}{c} P_{\mathrm{GT}}(t) \\ P_{\mathrm{AR}}(t) \\ P_{\mathrm{ISAC}}(t) \\ P_{\mathrm{Grid}}(t) \\ G_{\mathrm{Gas}}(t) \end{array}\right]+} \\ {\left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ -1 & 1 & 1 \\ \frac{\eta_{\mathrm{GT}}}{1-\eta_{\mathrm{GT}}-\eta_{\mathrm{S}}} & 0 & 0 \end{array}\right]\left[\begin{array}{c} \Delta P_{\mathrm{GT}}(t) \\ \Delta P_{\mathrm{AR}}(t) \\ \Delta P_{\mathrm{ISAC}}(t) \end{array}\right]+} \\ \left[\begin{array}{ccccc} 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & -1 & -1 \\ 0 & 0 & 0 & 0 & 0 \end{array}\right]\left[\begin{array}{c} \Delta L_{\mathrm{e}}(t) \\ \Delta L_{\mathrm{h}}(t) \\ \Delta L_{\mathrm{q}}(t) \\ \Delta P_{\mathrm{WT}}(t) \\ \Delta P_{\mathrm{PV}}(t) \end{array}\right] \end{array} $ | (15) |
式中:PAR(t)为t时刻AR消耗的电功率;PGrid(t)为t时刻IES与电网的交互功率;ηGT、ηS分别为GT的发电效率和散热损失系数。等式左侧表示最终的调度计划值,右侧的第一项和第二项分别表示上一阶段的优化值和实时的调整量,第三项为负荷、风电以及光伏波动所产生的扰动量。
文中将DMPC应用于EH的多时间尺度低碳优化调度。首先,根据EH的结构和功能,将其划分为若干个子系统,分别为WT、PV、WHB、GT、GB、ISAC、AR、SC、HST,并分别作为智能体系统。各智能体系统之间可以进行信息交换,从而获得其他智能体系统前一次计算得到的输入序列,然后优化局部性能指标[24],各智能体控制策略的目标函数如式(7)所示。
文中所有智能体共享一个全局目标函数,该函数包括电网交互成本、购气成本、储能调整惩罚成本和奖惩阶梯型碳价。根据目标函数可确定各能源耦合设备的出力,即系统的控制变量,然后可进一步得到系统的输出变量,继而确定最终的出力计划。因此,该阶段的优化目标可转换成各智能体系统的优化问题,其目标函数为:
| $ \min F_i^{\mathrm{TZ}}=\left(\boldsymbol{Y}_{i, \mathrm{r}}-\boldsymbol{Y}_{i, \mathrm{f}}\right)^{\mathrm{T}} \alpha_i\left(\boldsymbol{Y}_{i, \mathrm{r}}-\boldsymbol{Y}_{i, \mathrm{f}}\right)+\left(\Delta \boldsymbol{w}_i\right)^{\mathrm{T}} \boldsymbol{\beta}_i \Delta \boldsymbol{w}_i $ | (16) |
其中:
| $ \boldsymbol{Y}_{i, \mathrm{r}}=\left[\begin{array}{ccc} P_{i, \text { Grid }}^{\text {ref }}(h+\Delta t) & \cdots & P_{i, \text { Grid }}^{\text {ref }}(h+d \Delta t) \\ G_{i, \text { Gas }}^{\text {ref }}(h+\Delta t) & \cdots & G_{i, \text { Gas }}^{\text {ref }}(h+d \Delta t) \end{array}\right] $ | (17) |
| $ \boldsymbol{Y}_{i, \mathrm{f}}=\left[\begin{array}{lll} P_{i, \text { Grid }}(h+\Delta t \mid h) & \cdots & P_{i, \text { Grid }}(h+d \Delta t \mid h) \\ G_{i, \text { Gas }}(h+\Delta t \mid h) & \cdots & G_{i, \text { Gas }}(h+d \Delta t \mid h) \end{array}\right] $ | (18) |
| $ \Delta \boldsymbol{w}_i=\left[\begin{array}{lll} \Delta w_i(h+\Delta t) & \cdots & \Delta w_i(h+d \Delta t) \end{array}\right] $ | (19) |
式中:Pi, Gridref(h+Δt)、Gi, Gasref(h+Δt)分别为第i个智能体系统在h+Δt时刻的电网交互功率和购气功率的参考值;Pi, Grid(h+Δt|h)、Gi, Gas(h+Δt|h)分别为第i个智能体系统在h+Δt时刻的电网交互功率和购气功率的预测值;Δwi(h+Δt)为第i个智能体系统在h+Δt时刻的控制变量增量。
实时调整阶段的具体流程如图 6所示,其中σ为权重系数,表示对上一次迭代结果的信任程度;εn为第n个智能体的迭代精度。

|
图 6 实时调整阶段DMPC实施流程 Fig. 6 The flow chart of DMPC at real-time adjustment stage |
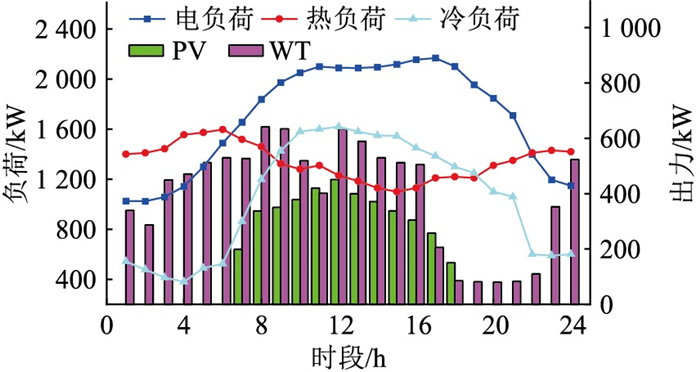
以某社区EH为案例进行算例分析。冷、热、电负荷预测曲线以及WT、PV预测出力如图 7所示。
|
图 7 风机、光伏和负荷预测曲线 Fig. 7 The forecasting curves of WT, PV, and load |
分时电价见表 1,EH内部各设备参数见表 2。购气价格为3.24元/m3,日内滚动优化的控制时域取4 h。实际碳排放模型参数见文献[18],单位发电量的碳配额δe为0.728 t/(MW·h),单位供热量的碳配额δh为0.102 t/GJ,μ、λ分别取0.2、0.15。仿真均基于64-bit Windows11系统,16 GB RAM,16 cores 3.4 GHz-i7 CPU,软件平台为MATLAB R2021a,CPLEX 12.9.0,Yalmip R2021。
|
|
表 1 分时电价 Table 1 Time-of-use electricity prices |
|
|
表 2 模型参数 Table 2 Model parameters |
为验证奖惩阶梯型碳价机制的有效性,设置以下3种运行情景进行对比分析。情景1:仅考虑购能成本、运行成本,不考虑碳交易成本;情景2:在情景1的基础上,考虑传统碳交易成本;情景3:在情景1的基础上,加入奖惩阶梯型碳价机制。表 3为3种情景的调度结果。
|
|
表 3 不同方案的调度结果对比 Table 3 Comparison of scheduling results for different scenarios |
由表 3可知,当日前调度的目标函数中考虑碳交易成本时,系统的碳排放量会大幅下降。这是由于IES向外部电网购电时会产生较多的碳排放量,因此,为减少系统碳排放量,IES会选择增加系统内CCHP和GB的出力。其中,情景2的碳排放量相比情景1下降了14.72%,而情景3的碳排放量相比情景2又进一步下降了4.31%。虽然CCHP和GB输出功率的增加会导致EH运行成本上升,但由于情景2和情景3承担的碳交易成本较低,所以,与情景1相比,情景2和情景3的总成本也有所下降。综上所述,奖惩阶梯型碳价机制能有效降低EH的碳排放量,实现EH低碳经济调度。
4.2.2 奖励系数对EH调度的影响在EH运营过程中,若EH实际的碳排放量低于碳配额,则会根据奖励系数获得相应的奖励值。奖励系数越高,意味着奖励值越大,对EH的运营成本影响越大。
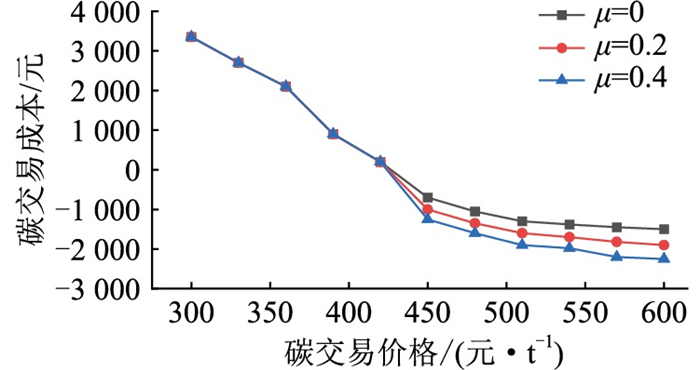
图 8为奖励系数μ对情景3中EH承担的碳交易成本的影响。EH的碳交易成本为正时,奖励系数的改变对EH承担的碳交易成本没有影响,这是因为EH只承担碳交易惩罚费用,没有获得奖励;碳交易成本为负时,即EH获得碳交易收益时,奖励系数越大,EH的收益越多,并且EH获得的碳交易收益也随着碳交易价格的增加而逐渐上升。原因是EH获得的碳交易收益增加,使EH主动增加CCHP和GB的输出功率,因此减少了EH向外部电网的外购电量,EH碳排放总量减少。因此,在EH的调度中,需要综合考虑奖励系数和碳交易成本之间的关系,寻求一个最优的平衡点,在实现碳减排的同时保证调度的经济性。
|
图 8 奖励系数对EH碳交易成本的影响 Fig. 8 The impact of reward coefficient on carbon trading cost of EH |
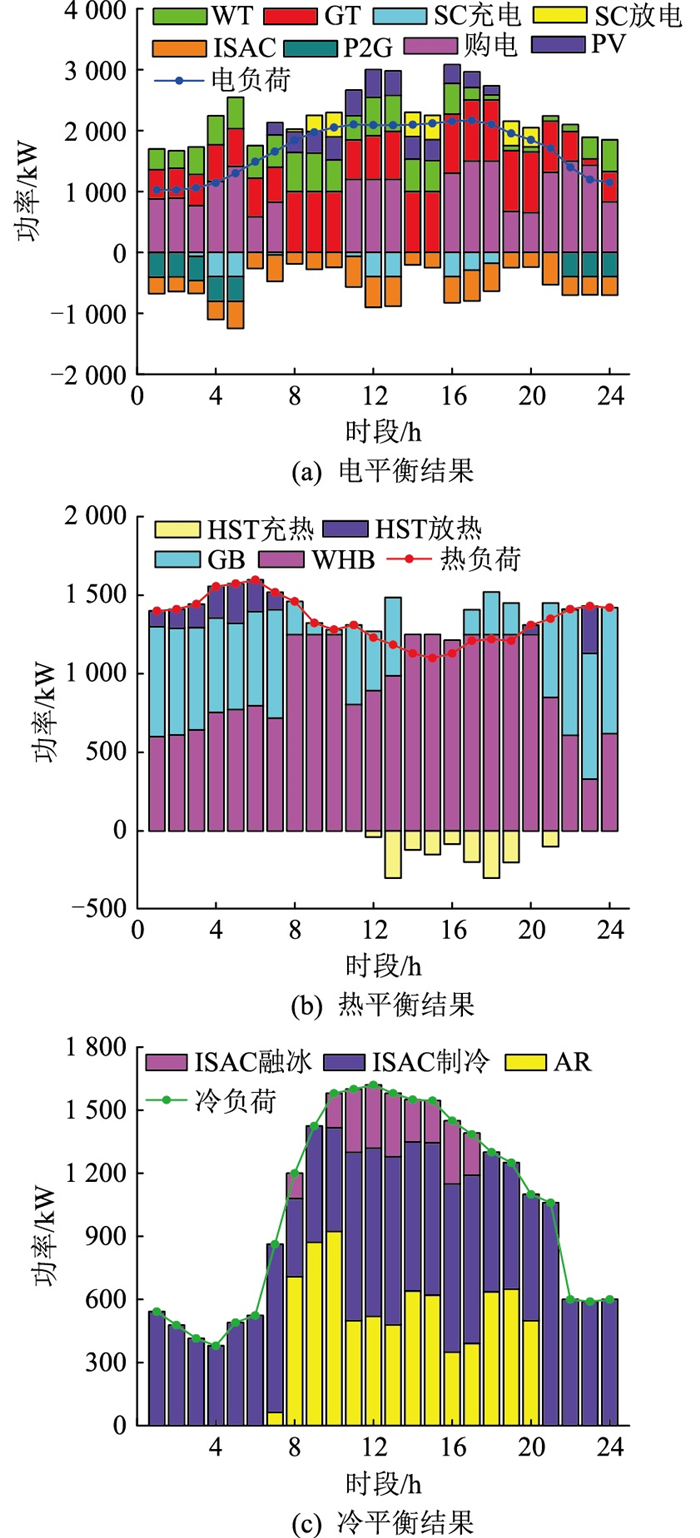
图 9为情景3优化后EH的电、热、冷调度结果。在21:00—05:00电价谷时段,由于电负荷较低,主要通过外购电力和WT满足电负荷;由于此时热负荷较高,根据GT以热定电的工作模式,GT存在部分出力,热负荷主要通过WHB和GB共同满足;而冷负荷此时较低,主要通过ISAC的制冷模式满足。在08:00—10:00、14:00—15:00和19:00—20:00电价峰时段,基本无外购电量,主要通过GT、WT、PV等满足电负荷,不足的部分由SC提供;热负荷主要通过WHB满足,不足的部分由GB和HST提供;冷负荷主要由ISAC制冷和AR共同提供。而在剩余电价平时段,其工作模式处于电价峰时段与谷时段之间,其中,11:00—13:00和16:00—17:00时段冷负荷处于峰值,ISAC制冷模式和AR不能满足冷负荷,故ISAC通过融冰模式满足冷能需求。
|
图 9 日前调度结果 Fig. 9 Day-ahead scheduling results |
综上所述,通过对调度结果进行分析,验证了奖惩阶梯型碳价机制更有利于清洁机组的上网,在奖励系数等参数适当的情况下,能够有效减少系统碳排放量;同时,由于储能、P2G等技术的加持,还可以起到削峰填谷的作用。
4.3 日内优化调度分析 4.3.1 不同策略下的对比结果为了验证文中所提基于DMPC的多时间尺度协调优化策略的有效性,将其与基于MPC的多时间尺度策略进行对比。表 4为2种策略的对比结果。
|
|
表 4 不同策略对比结果 Table 4 Comparative results of different strategies |
首先, 从求解效率上,采用DMPC时求解时间相比MPC缩短了19.43%。虽然DMPC优化属于分布式优化,其求解次数会多于MPC优化,但是每个智能体系统在求解时可以利用其他智能体系统的信息,相对于MPC优化的集中式求解,显著降低了优化模型的阶数,使模型更易于求解。
其次,从经济和环境效益,DMPC的总成本减少了206.7元,且交互功率波动率和系统碳排放量分别减少了2.90%和1.54%,原因是DMPC策略将调度任务分配至各智能体系统,各系统只须实现自身最优控制,从而减少了各类设备功率的波动率,也降低了购能成本和设备调整成本,提高了系统经济性和环保性。
综上所述,DMPC策略在反复滚动优化的同时更新了源、荷预测信息,提高了预测精度,并且利用实时调整对机组出力进行调整,可以有效降低源-荷预测误差对系统的不利影响。
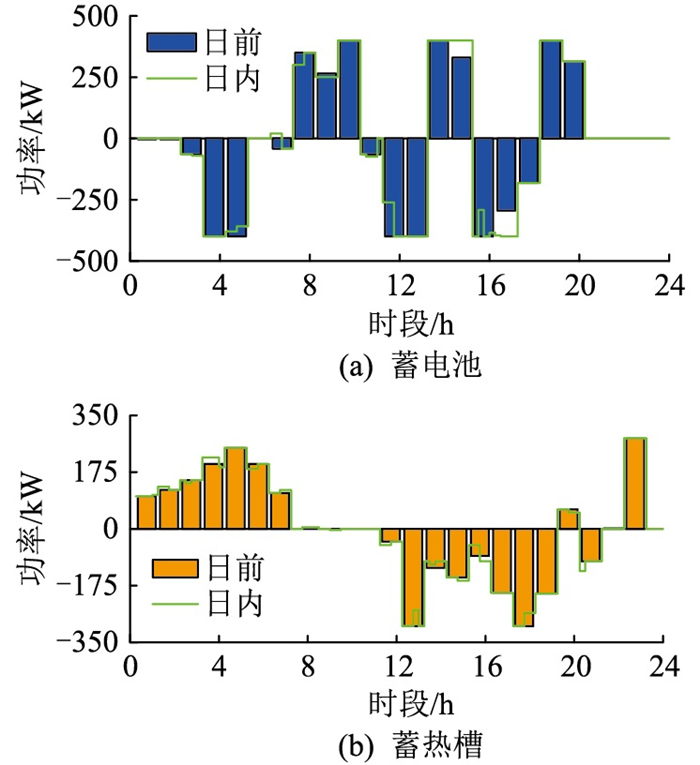
4.3.2 设备调整结果分析图 10为SC和HST在日前和日内阶段的功率调整。为了延长储能装置的使用寿命,避免储能设备频繁充、放能,储能装置只参与日内滚动优化,实时阶段的功率波动由其他能源转换设备平抑。由于日内调度阶段考虑了反映长期储能特征的储能量惩罚项,故日内阶段各储能装置的充、放能状态与日前阶段相似,但由于预测误差带来的影响,部分误差须由储能设备进行调整。
|
图 10 储能装置功率调度 Fig. 10 The power scheduling of energy storage devices |
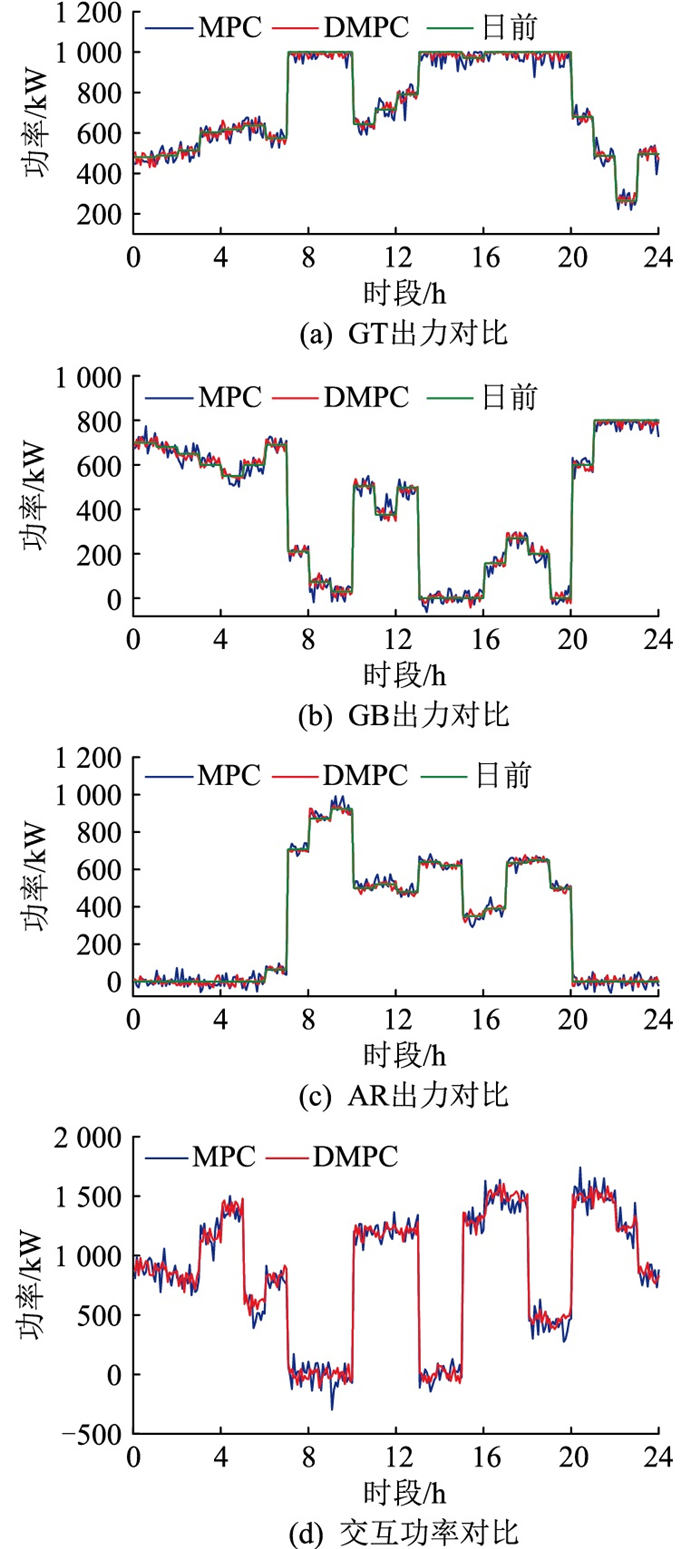
图 11(a)—(c)为各机组在DMPC和MPC下与日前调度的对比结果。实时调度以5 min为时间尺度进行优化,并且对源、荷预测信息实时更新,在2种优化方法下,对各能源设备出力调整都有一定的修正,使优化结果更符合实际情况。可以看出,相对于MPC在优化过程中出现了多个尖峰,DMPC下各能源设备功率波动相对平缓,调整幅度较小。图 11(d)对比了不同场景下的交互功率,在DMPC方式下,各能源设备能更快地响应系统功率波动,使设备之间协调能力加强,从而进一步降低交互功率波动率。结合表 3、表 4可知,基于DMPC的多时间尺度策略可较大提升EH经济性和稳定性。
|
图 11 各设备调整结果及交互功率对比结果 Fig. 11 The results of scheduling for each device and the comparison of interactive power |
文中提出一种基于奖惩阶梯型碳价机制和DMPC算法的EH日前-日内-实时的多时间尺度低碳优化调度策略,能够降低碳排放水平、减小源-荷不确定性的影响。
仿真结果表明:采用奖惩阶梯型碳价机制模型能更大程度地发挥清洁机组的低碳特性,提升系统的经济和环境效益;采用多时间尺度策略既提高了各机组出力精确性,又缓解了联络线交互功率波动,实现了EH经济、稳定、可靠运行;DMPC不仅可以减小由可再生能源预测误差带来的系统功率波动,还能提高求解效率和系统稳定性。
| [1] |
王宏, 闫园, 文福拴, 等. 国内外综合能源系统标准现状与展望[J]. 电力科学与技术学报, 2019, 34(3): 3-12. WANG Hong, YAN Yuan, WEN Fushuan, et al. Standards associated with integrated energy systems: current situation and research prospects[J]. Journal of Electric Power Science and Technology, 2019, 34(3): 3-12. DOI:10.3969/j.issn.1673-9140.2019.03.001 (  0) 0) |
| [2] |
MANSOURI S A, AHMARINEJAD A, JAVADI M S, et al. Two-stage stochastic framework for energy hubs planning considering demand response programs[J]. Energy, 2020, 206: 118124. DOI:10.1016/j.energy.2020.118124 (  0) 0) |
| [3] |
LI P, WANG Z X, YANG W H, et al. Hierarchically partitioned coordinated operation of distributed integrated energy system based on a master-slave game[J]. Energy, 2021, 214: 119006. DOI:10.1016/j.energy.2020.119006 (  0) 0) |
| [4] |
FAVRE-PERROD P. A vision of future energy networks[C]//2005 IEEE Power Engineering Society Inaugural Conference and Exposition in Africa. Durban, South Africa. IEEE, 2006: 13-17.
(  0) 0) |
| [5] |
蒋文超. 考虑电-气-热的能源枢纽运行优化问题研究[D]. 上海: 上海交通大学, 2018. JIANG Wenchao. Research on operation optimization of energy hub considering electricity-gas-heat[D]. Shanghai: Shanghai Jiao Tong University, 2018. (  0) 0) |
| [6] |
郭尊, 李庚银, 周明, 等. 计及综合需求响应的商业园区能量枢纽优化运行[J]. 电网技术, 2018, 42(8): 2439-2448. GUO Zun, LI Gengyin, ZHOU Ming, et al. Optimal operation of energy hub in business park considering integrated demand response[J]. Power System Technology, 2018, 42(8): 2439-2448. (  0) 0) |
| [7] |
文云峰, 瞿小斌, 肖友强, 等. 耦合能量枢纽多区域电—气互联能源系统分布式协同优化调度[J]. 电力系统自动化, 2019, 43(9): 22-30. WEN Yunfeng, QU Xiaobin, XIAO Youqiang, et al. Distributed coordinated optimal dispatch of multi-regional electricity-gas integrated energy systems with energy hubs[J]. Automation of Electric Power Systems, 2019, 43(9): 22-30. (  0) 0) |
| [8] |
陈志, 胡志坚, 翁菖宏, 等. 基于阶梯碳交易机制的园区综合能源系统多阶段规划[J]. 电力自动化设备, 2021, 41(9): 148-155. CHEN Zhi, HU Zhijian, WENG Changhong, et al. Multi-stage planning of park-level integrated energy system based on ladder-type carbon trading mechanism[J]. Electric Power Automation Equipment, 2021, 41(9): 148-155. (  0) 0) |
| [9] |
瞿凯平, 黄琳妮, 余涛, 等. 碳交易机制下多区域综合能源系统的分散调度[J]. 中国电机工程学报, 2018, 38(3): 697-707. QU Kaiping, HUANG Linni, YU Tao, et al. Decentralized dispatch of multi-area integrated energy systems with carbon trading[J]. Proceedings of the CSEE, 2018, 38(3): 697-707. (  0) 0) |
| [10] |
靳小龙, 穆云飞, 贾宏杰, 等. 集成智能楼宇的微网系统多时间尺度模型预测调度方法[J]. 电力系统自动化, 2019, 43(16): 25-33. JIN Xiaolong, MU Yunfei, JIA Hongjie, et al. Model predictive control based multiple-time-scheduling method for microgrid system with smart buildings integrated[J]. Automation of Electric Power Systems, 2019, 43(16): 25-33. DOI:10.7500/AEPS20180629016 (  0) 0) |
| [11] |
JIN X L, WU J Z, MU Y F, et al. Hierarchical microgrid energy management in an office building[J]. Applied Energy, 2017, 208: 480-494. DOI:10.1016/j.apenergy.2017.10.002 (  0) 0) |
| [12] |
余洋, 王紫阳, 张瑞丰, 等. 基于VMD和MPC的电动汽车-火电机组联合调频控制[J]. 电力工程技术, 2023, 42(2): 29-39. YU Yang, WANG Ziyang, ZHANG Ruifeng, et al. Combined frequency regulation control of electric vehicles and thermal power units based on VMD and MPC[J]. Electric Power Engineering Technology, 2023, 42(2): 29-39. DOI:10.12158/j.2096-3203.2023.02.004 (  0) 0) |
| [13] |
王成山, 吕超贤, 李鹏, 等. 园区型综合能源系统多时间尺度模型预测优化调度[J]. 中国电机工程学报, 2019, 39(23): 6791-6803, 7093. WANG Chengshan, LÜ Chaoxian, LI Peng, et al. Multiple time-scale optimal scheduling of community integrated energy system based on model predictive control[J]. Proceedings of the CSEE, 2019, 39(23): 6791-6803, 7093. (  0) 0) |
| [14] |
李群, 张宁宇, 王新宝, 等. 电力潮流灵活控制技术应用综述[J]. 电力工程技术, 2023, 42(1): 50-60. LI Qun, ZHANG Ningyu, WANG Xinbao, et al. Review on application of flexible power flow control technology[J]. Electric Power Engineering Technology, 2023, 42(1): 50-60. DOI:10.12158/j.2096-3203.2023.01.007 (  0) 0) |
| [15] |
郭伟, 赵洪山. 基于DMPC加权一致性算法的电池储能阵列分组控制策略[J]. 电力自动化设备, 2020, 40(1): 133-140. GUO Wei, ZHAO Hongshan. Grouping control strategy of battery energy storage array based on DMPC weighted consensus algorithm[J]. Electric Power Automation Equipment, 2020, 40(1): 133-140. (  0) 0) |
| [16] |
李桂鑫, 徐科, 刘英英, 等. 基于分布式模型预测控制的含分布式储能有源配电网动态电压控制[J]. 电力建设, 2021, 42(6): 116-126. LI Guixin, XU Ke, LIU Yingying, et al. Dynamic voltage control based on DMPC for active distribution network with distributed energy storage systems[J]. Electric Power Construction, 2021, 42(6): 116-126. (  0) 0) |
| [17] |
周连俊, 李群, 殷明慧, 等. 面向风电机组最大功率点跟踪的转矩曲线增益动态优化[J]. 电工技术学报, 2023, 38(13): 3447-3458. ZHOU Lianjun, LI Qun, YIN Minghui, et al. Torque curve gain dynamic optimization for maximum power point tracking of wind turbines[J]. Transactions of China Electrotechnical Society, 2023, 38(13): 3447-3458. (  0) 0) |
| [18] |
秦婷, 刘怀东, 王锦桥, 等. 基于碳交易的电—热—气综合能源系统低碳经济调度[J]. 电力系统自动化, 2018, 42(14): 8-13, 22. QIN Ting, LIU Huaidong, WANG Jinqiao, et al. Carbon trading based low-carbon economic dispatch for integrated electricity-heat-gas energy system[J]. Automation of Electric Power Systems, 2018, 42(14): 8-13, 22. (  0) 0) |
| [19] |
高瑜隆. 多智能体系统的分布式模型预测控制[D]. 北京: 北京理工大学, 2016. GAO Yulong. Distributed model predictive control of multi-agent systems[D]. Beijing: Beijing Institute of Technology, 2016. (  0) 0) |
| [20] |
李彬, 杜亚彬, 曹望璋, 等. 计及负载特性的数据中心微电网双层优化配置[J]. 电力工程技术, 2023, 42(2): 75-83. LI Bin, DU Yabin, CAO Wangzhang, et al. Bi-level optimal con figuration of microgrid in data center considering load characteristics[J]. Electric Power Engineering Technology, 2023, 42(2): 75-83. DOI:10.12158/j.2096-3203.2023.02.009 (  0) 0) |
| [21] |
朱娟娟, 段奕琳, 闫群民, 等. 基于BAS-IMOPSO算法的风电系统储能优化配置[J]. 电力工程技术, 2023, 42(2): 180-187. ZHU Juanjuan, DUAN Yilin, YAN Qunmin, et al. Optimal allocation of energy storage in wind power system based on BAS-IMOPSO algorithm[J]. Electric Power Engineering Technology, 2023, 42(2): 180-187. DOI:10.12158/j.2096-3203.2023.02.021 (  0) 0) |
| [22] |
郑毅, 李少远. 网络信息模式下分布式系统协调预测控制[J]. 自动化学报, 2013, 39(11): 1778-1786. ZHENG Yi, LI Shaoyuan. Networked cooperative distributed model predictive control for dynamic coupling systems[J]. Acta Automatica Sinica, 2013, 39(11): 1778-1786. (  0) 0) |
| [23] |
李天格, 胡志坚, 陈志, 等. 计及电-气-热-氢需求响应的综合能源系统多时间尺度低碳运行优化策略[J]. 电力自动化设备, 2023, 43(1): 16-24. LI Tiange, HU Zhijian, CHEN Zhi, et al. Multi-time scale low-carbon operation optimization strategy of integrated energy system considering electricity-gas-heat-hydrogen demand response[J]. Electric Power Automation Equipment, 2023, 43(1): 16-24. (  0) 0) |
| [24] |
程杉, 陈诺, 徐建宇, 等. 考虑综合需求响应的楼宇综合能源系统能量管理优化[J]. 电力工程技术, 2023, 42(2): 40-47, 57. CHENG Shan, CHEN Nuo, XU Jianyu, et al. Optimal energy management of residential integrated energy system with consideration of integrated demand response[J]. Electric Power Engineering Technology, 2023, 42(2): 40-47, 57. DOI:10.12158/j.2096-3203.2023.02.005 (  0) 0) |
2. Tianjin Key Laboratory of Control Theory and Application for Complex Systems, Tianjin 300384, China;
3. Tianjin Key Laboratory of New Energy Power Conversion, Transmission and Intelligent Control, Tianjin 300384, China
 2024, Vol. 43
2024, Vol. 43


 吴艳娟(1973),女,博士,教授,研究方向为智能电网、电力系统优化与控制、智能控制(E-mail:
吴艳娟(1973),女,博士,教授,研究方向为智能电网、电力系统优化与控制、智能控制(E-mail: