文章编号: 2096-3203(2024)03-0130-10 中图分类号: TM73
2. 东南大学软件学院,江苏 苏州 210018
在“双碳”目标的驱动下,推进新能源汽车的发展是我国成为汽车强国的必要途径,也是实现交通能源转型战略的重要举措。2020年,国务院印发的《新能源汽车产业发展规划(2021—2035年)》[1]指出,至2035年,纯电动汽车(electric vehicle, EV)将占据汽车销售市场,公共交通领域也将全面采用EV,这将有助于提高能源利用效率,减少污染排放,同时提高社会运行效率。因此,电网生产和资源配置将不可避免地受到大规模EV负荷接入的影响,而预测EV充电负荷的准确性,不仅可以为EV充电设施的建设、电力配送网络的优化和充电管理提供数据支持,还可以帮助合理配置资源,促进电网的稳定运行。
近几年,专家学者对EV充电负荷的预测进行了大量研究[2-9]。文献[4-5]将区域划分成住宅区、工作区、商业区,按照各个功能区中EV的不同充电特性计算充电负荷的时空分布,但忽略了EV行程中用户选择出行路径的主观性。文献[6]将“起点-终点”分析运用于EV移动性建模中,但未考虑EV用户出行的随机性。文献[7]考虑了EV的移动性,基于停车生成率思想建立了EV移动储能模型,但缺少对EV用户出行行为方式与实际道路交通信息的考虑。文献[8]根据出行链对EV用户的时空分布进行建模,根据启动时间从小到大对每个响应周期进行排序,但忽略了目标区域功能特性对EV用户出行行为的影响。EV的移动性和随机性决定了充电需求预测要以准确分析用户出行行为规律为基础,文献[10]考虑在交通系统中行驶的单个车辆的动态运动,提出了一种基于Agent元胞自动机模型的充电需求仿真方法,但未考虑其他因素对EV用户出行行为的影响。文献[11-12]引入图论分析方法和Dijkstra路径搜索算法,运用蒙特卡洛模拟EV行驶行为与充电行为,从而对EV负荷时空分布特性进行分析;文献[13]计及实时交通与温度,提出一种基于马尔可夫决策过程(Markov decision process, MDP)随机路径模拟的EV充电负荷时空分布预测方法,但在EV用户出行决策规划方面,文献[11-13]均未考虑全面用户的出行规律。文献[14-16]计及耦合因素对EV充电负荷的时空特性进行预测,基于算例对比分析EV及其充电负荷在不同情况下的时空分布,但其算例模型较为简单,需要根据实际地理信息提高算例模型的准确度。
针对上述问题,文中以私家车为例,基于出行链理论模拟EV用户出行特性,建立EV充电需求因素模型,并将目标区域按功能进行区域划分,利用最优路径算法规划EV的行驶路线,模拟EV用户一天内在各个目的地之间的移动与停留情况,以此模拟出各个区域充电站的负荷需求特性。文中充分考虑了目标区域功能特性对EV用户出行行为的影响、交通路网对EV用户行驶路径的影响,增强了“车-路-网”之间的耦合程度。最后以某城市为例,对比分析EV充电负荷在不同功能区、不同行政区域的分布规律,并验证了所提方法的有效性和优越性。
1 EV时空转移及充电模型 1.1 基于出行链的EV时空分布模型 1.1.1 出行链结构假设EV用户出行的首次出发点均为居民区,经过一条完整的出行链后,EV最后返回起始出发点结束一次行程[17-18]。EV一次完整出行示意如图 1所示。

|
图 1 汽车模拟行驶 Fig. 1 Car simulation driving |
将一天内EV的总出行次数设为n,mi为EV第i次出行时的行程级数。闭环出行链示意如图 2所示。

|
图 2 出行链示意 Fig. 2 Travel chain diagram |
一天内,单辆EV第i次出行时,到达第j个目的地时的行驶状态可由
| $ T_{i, j}=t_{i-1, \text { total }}+\sum\limits_{k=1}^j t_{\mathrm{d}, i, k}+\sum\limits_{k=1}^j t_{\mathrm{p}, i, k} $ | (1) |
式中:k为EV行程中的目的地索引变量;ti-1, total为一天内第i-1次出行结束的时刻;td, i, k为第i次出行时从第k-1个目的地行驶到第k个目的地的行驶时间;tp, i, k为第i次出行时在第k个目的地的停车时长。
| $ t_{i, \text { total }}=t_{i-1, \text { total }}+\sum\limits_{k=1}^{m_i} t_{\mathrm{d}, i, k}+\sum\limits_{k=1}^{m_i} t_{\mathrm{p}, i, k} $ | (2) |
式中:ti, total为一天内第i次出行结束的时刻。
| $ t_{\mathrm{d}, i, k}=\frac{d_{i, k}}{v_{i, k}} $ | (3) |
式中:di, k为EV第i次出行时从第k-1个目的地行驶到第k个目的地的行驶里程,由路径规划模拟得到;vi, k为EV第i次出行时从第k-1个目的地行驶到第k个目的地的平均行驶速度,由时间和路段性质决定。
1.1.2 转移概率文中使用马尔可夫状态转移矩阵[19-20]来描述EV在居民区、工作区、商业区以及其他区域之间的转移规律。设gi, j仅与gi, j-1有关,与第1个—第j-2个出行目的地无关。如果用精确的数学定义来描述,EV第j个出行目的地为gi, j的概率为:
| $ p\left(g_{i, j} \mid g_{i, j-1}, g_{i, j-2}, \cdots, g_{i, 1}\right)=p\left(g_{i, j} \mid g_{i, j-1}\right) $ | (4) |
针对文中的功能区类型划分,状态转移矩阵可表示为:
| $ \boldsymbol{P}=\left[\begin{array}{llll} p_{11} & p_{12} & p_{13} & p_{14} \\ p_{21} & p_{22} & p_{23} & p_{24} \\ p_{31} & p_{32} & p_{33} & p_{34} \\ p_{41} & p_{42} & p_{43} & p_{44} \end{array}\right] $ | (5) |
式中:p11、p22、p33、p44分别为居民区、工作区、商业区和其他区域的自转移概率,其余元素均为对应功能区之间的互转移概率,可根据当地居民出行调研数据统计确定。
根据EV转移特性,式(5)满足以下约束条件:
| $ \left\{\begin{array}{l} 0 \leqslant p_{h z} \leqslant 1 \\ \sum\limits_{z=1}^4 p_{h z}=1 \end{array} \quad h, z=1, 2, 3, 4\right. $ | (6) |
式中:h、z分别为式(5)中矩阵元素的行序和列序。
1.2 考虑实时转移特性的EV充电负荷模型为准确描述EV用户的出行行为以及停车规律,对EV用户首次出行时间分布概率、停车时长分布概率以及EV充电概率等特征量进行建模。
1.2.1 EV用户出行时间特性(1) 首次出行时间。据文献[21]统计,EV用户每日首次出行时间符合正态分布规律函数,如式(7)所示。
| $ f\left(T_{\text {first }}, \mu_s, \sigma_s\right)=\frac{1}{\sigma_s \sqrt{2 \pi}} \exp \left(-\frac{\left(T_{\text {first }}-\mu_s\right)^2}{2 \sigma_s^2}\right) $ | (7) |
式中:Tfirst为EV用户首次出行时间;μs、σs分别为该分布概率函数的均值和方差,μs、σs在工作日分别取7.82与1.50,在休息日分别取9.46与0.68。
(2) 停车时长。EV在目的地的停车时长由该目的地的场所性质决定。研究表明,EV在居民区停车时长的概率密度符合Weibull分布,如式(8)所示;而在工作区、商业区和其他区域停车时长的概率密度则符合广义极值分布,如式(9)所示。
| $ f_1\left(t_{\mathrm{p}, i, j}\right)=\frac{k}{\theta}\left(\frac{t_{\mathrm{p}, i, j}}{\theta}\right)^{k-1} \exp \left(-\left(\frac{t_{\mathrm{p}, i, j}}{\theta}\right)^k\right) $ | (8) |
| $ \begin{gathered} f_2\left(t_{\mathrm{p}, i, j}\right)= \\ \frac{1}{\sigma}\left(1+\xi \frac{t_{\mathrm{p}, i, j}-\mu}{\sigma}\right)^{-\frac{1}{\xi}-1} \exp \left(\left(1+\xi \frac{t_{\mathrm{p}, i, j}-\mu}{\sigma}\right)^{-\frac{1}{\xi}}\right) \end{gathered} $ | (9) |
式中:θ为分布概率函数f1(tp, i, j)的尺度参数;μ为未知参数;σ>0,为分布概率函数f2(tp, i, j)的尺度参数;ξ为形状参数,决定分布的尾部形状。
1.2.2 EV用户充电功率计算模型文中将二阶段方法[22]作为EV在居民区的充电方式,即“先恒流限压,后恒压限流”。利用等面积法则定义整数C,使得整数C满足不等式CTM≤TC≤(C+1)TM,其中TC为EV电池恒流充电时间;TM为EV电池充电总时长。EV充电机分阶段充电功率模型如式(10)所示。
| $ P_{\vartheta}=\left\{\begin{array}{l} U_{\max } I_{\max }\left[\frac{(1-\chi)(2 \vartheta-1) T_M}{2 T_C}-\chi\right] \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 0<\vartheta \leqslant C \\ U_{\max } I_{\max }\left[\frac{(1-\chi)\left(T_C^2-C^2 T_M^2\right)}{2 T_C}+\right. \\ \ \ \ \ \left.\chi\left(T_C-C T_M\right)-\frac{\mathrm{e}^{\alpha\left(T_C-C T_M-T_M\right)}-1}{\alpha}\right] \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \vartheta=C+1 \\ U_{\max } I_{\max }\left\{\mathrm{e}^{\alpha\left[T_C-(\vartheta-1) T_M\right]}-\mathrm{e}^{\alpha\left(T_C-\vartheta T_M\right)}\right\} / \alpha \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ C+1<\vartheta \leqslant M \end{array}\right. $ | (10) |
式中:
以某热门EV为例,该车采用磷酸铁锂电池,其基本参数如表 1所示。
|
|
表 1 某EV电池组基本参数 Table 1 Basic parameters of an EV battery pack |
假设EV的充电起始荷电状态(state of charge,SOC)为25%,以1 h为单位分阶段充电,考虑电池组连续充电约束条件,由式(10)计算得到电池组各阶段的平均充电功率,如表 2所示。
|
|
表 2 电池组各阶段平均充电功率 Table 2 Average charging power of battery pack in stages |
EV在居民区采用上述分阶段充电方法,而在商业区和工作区,根据用户充电习惯及实际充电桩特性采用快充的方式进行充电。
以国家电网建设的直流充电桩为例,目前市面上大部分充电桩的充电功率为37.5 kW。因此,文中采用37.5 kW作为商业区和工作区的充电桩充电功率。
1.2.3 EV充电需求判断模型EV用户到达目的地gi, j后,将根据剩余电量及下一段行驶里程判断是否进行充电。EV的剩余电量由上一阶段SOC及行驶路径长度共同决定。
| $ s_{i, j}=s_{i, j-1}-\frac{d_{i, j}}{d_{\max }} $ | (11) |
式中:si, j为EV在gi, j的SOC;di, j为EV第i次出行时从第j-1个目的地行驶到第j个目的地的行驶路径长度;dmax为EV可行驶的最大里程。
假设SOC小于25%或剩余电量不能支持下一段行驶里程均能导致EV用户强制充电行为,则EV在目的地gi, j的充电概率为:
| $ p_{\mathrm{c}}\left(g_{i, j}\right)= \begin{cases}1 & s_{i, j}<25 \% \\ 1 & s_{i, j} \geqslant 25 \%\text { 且 } t_{\mathrm{r}, i, j}<t_{\mathrm{d}, i, j+1} \\ 0 & s_{i, j} \geqslant 25 \% \text { 且 } t_{\mathrm{r}, i, j} \geqslant t_{\mathrm{d}, i, j+1}\end{cases} $ | (12) |
式中:pc(gi, j)为EV在目的地gi, j的充电概率,1表示充电,0表示不充电;tr, i, j为EV在目的地gi, j的可行驶时长。
| $ t_{\mathrm{r}, i, j}=\frac{s_{i, j} C}{\rho_{\max } \bar{v}} $ | (13) |
式中:ρmax为EV每公里耗电量的最大值;v为EV在该路段的平均行驶速度,由路段的道路等级及交通情况共同决定。
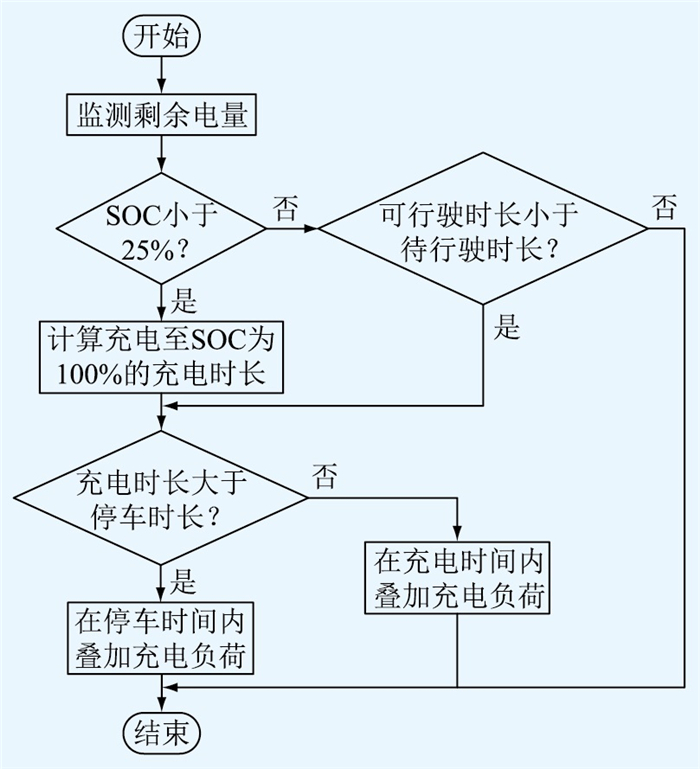
EV用户充电需求判断流程如图 3所示。
|
图 3 充电需求判断流程 Fig. 3 Flow chart of charging demand judgment |
图 3中,充电时长可表示为:
| $ t_{\mathrm{c}, i, k}= \begin{cases}t_{\mathrm{p}, i, k} & t_{\mathrm{r}, i, j}>t_{\mathrm{p}, i, k} \\ \frac{s_{i, j} C}{c} & t_{\mathrm{r}, i, j} \leqslant t_{\mathrm{p}, i, k}\end{cases} $ | (14) |
式中:tc, i, k为EV在第i次出行时第k个目的地的充电时长;c为EV的充电功率。
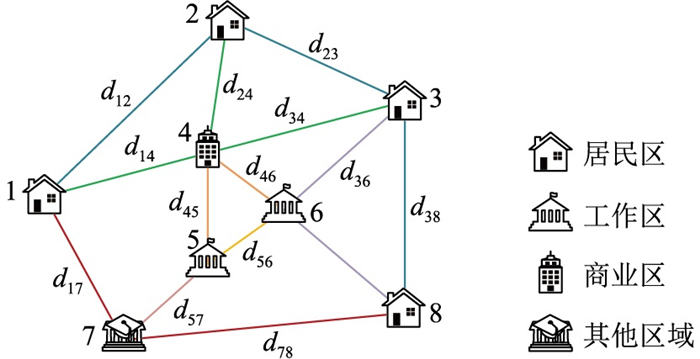
2 基于路网融合及出行链理论的EV充电需求预测方法分析 2.1 路网拓扑模型为简化计算,文中将实际路网进行抽象,利用图论[23-25]的方法来描述。简单交通路网如图 4所示。
|
图 4 交通路网图 Fig. 4 Traffic network map |
路网由
假设路网中所有路段均可双向通行,则X节点路网的邻接矩阵为:
| $ \boldsymbol{\psi}_G=\left[\begin{array}{ccccccc} 0 & d_{12} & d_{13} & \cdots & d_{1 y} & \cdots & d_{1 X} \\ d_{21} & 0 & d_{23} & \cdots & d_{2 y} & \cdots & d_{2 X} \\ d_{31} & d_{32} & 0 & \cdots & d_{3 y} & \cdots & d_{3 X} \\ \vdots & \vdots & \vdots & & \vdots & & \vdots \\ d_{x 1} & d_{x 2} & d_{x 3} & \cdots & d_{x y} & \cdots & d_{x X} \\ \vdots & \vdots & \vdots & & \vdots & & \vdots \\ d_{X 1} & d_{X 2} & d_{X 3} & \cdots & d_{X y} & \cdots & 0 \end{array}\right] $ | (15) |
式中:dxy为路网中两节点间的路径长度。若节点vx与节点vy不连通,则dxy为无穷大。
将居民区、工作区、商业区和其他区域的节点功能区属性分别赋值为1、2、3、4,如式(16)所示。
| $ q_{x y}= \begin{cases}1 & \left\langle v_x, v_y\right\rangle \text { 属于居民区 } \\ 2 & \left\langle v_x, v_y\right\rangle \text { 属于工作区 } \\ 3 & \left\langle v_x, v_y\right\rangle \text { 属于商业区 } \\ 4 & \left\langle v_x, v_y\right\rangle \text { 属于其他区域 }\end{cases} $ | (16) |
根据全局优化思想,假设EV在城市内的平均行驶速度为60 km/h,最优路径规划即转化为最短路径规划。
Floyd也被称为Floyd-Warshall算法,是一种用于求解所有节点对之间最短路径的动态规划算法[26-28]。因此,在求解多源最短路径的问题上,Floyd算法能快速获得所有节点之间的最短路径,且速度、内存占优。该算法的基本思想为:若有X个路网节点,则可递推产生一个矩阵序列
| $ a_r(x, y)=\min \left(a_{r-1}(x, y), a_{r-1}(x, r), a_{r-1}(r, y)\right) $ | (17) |
插点试探完成时,r=X,AX即为各个节点之间的最短距离值所组成的矩阵。
2.3 充电负荷计算及仿真流程基于上述理论,在模拟生成完整出行链之前,需要先获得日出行次数、行程级数,将问题转化成单辆车一天出行的模拟。
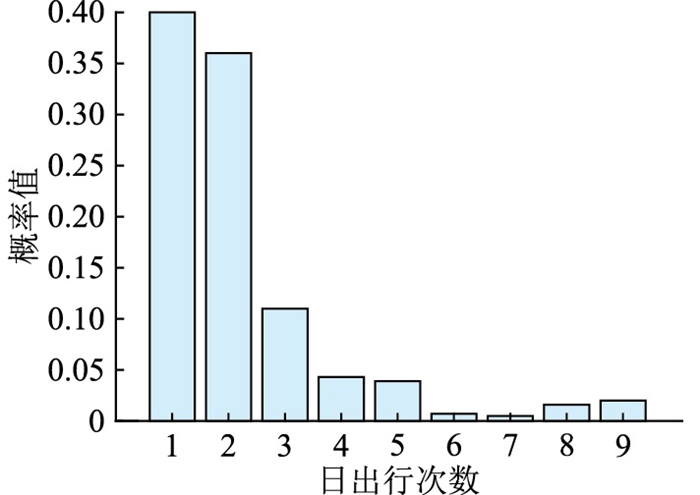
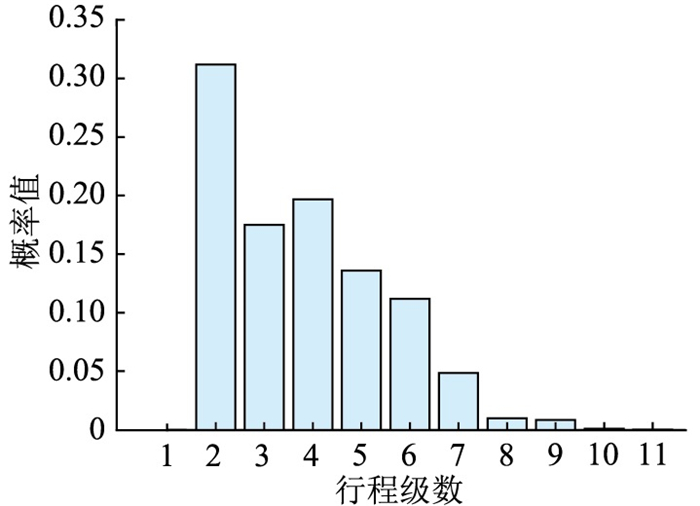
全国家庭出行调查(national household travel survey,NHTS)数据统计分析如图 5、图 6所示,可知日出行次数最多达9次,普遍集中在1~4次之间;行程级数最高达11级,普遍集中在2~7级之间。
|
图 5 出行次数概率分布 Fig. 5 Probability distribution of trips |
|
图 6 行程级数概率分布 Fig. 6 Probability distribution of stroke series |
基于上述研究获得的相关变量分布,结合仿真模拟EV充电的时空场景。仿真流程如图 7所示,具体步骤如下。
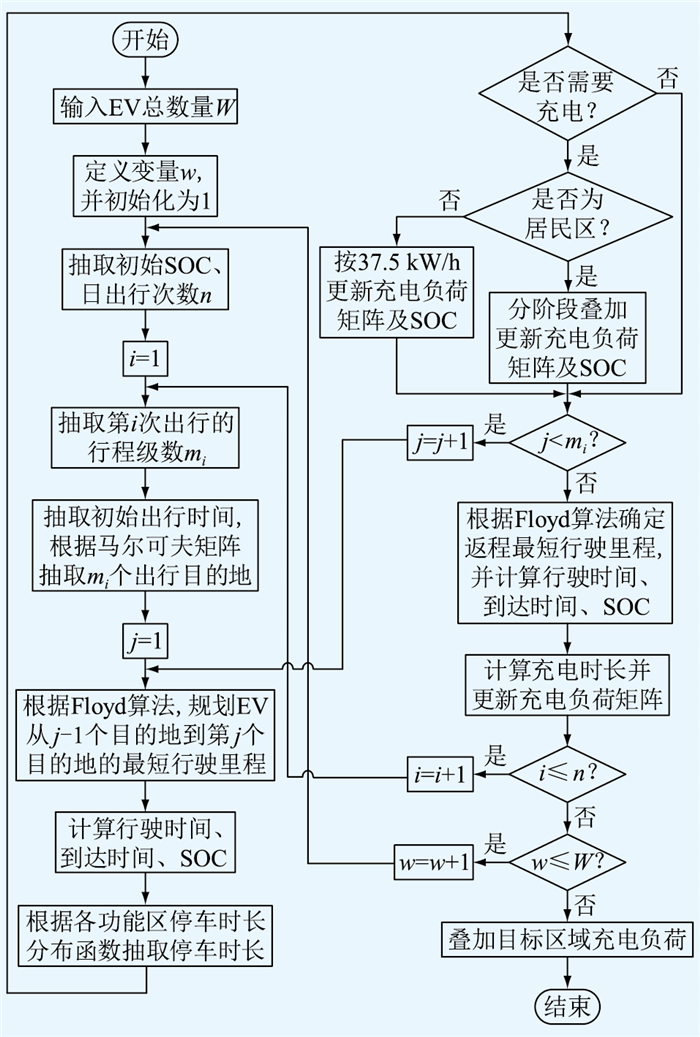
|
图 7 EV充电需求预测流程 Fig. 7 Flow chart of EV charging demand forecasting |
(1) 输入EV总数量W。
(2) 定义变量w为EV在程序中的循环编号,并初始化为1。
(3) 抽取第w辆EV的初始SOC、日出行次数n。
(4) 抽取第w辆EV第i次出行时的行程级数mi。
(5) 根据拟合分布概率函数,抽取第w辆EV第i次出行的初始出行时间。根据马尔可夫转移矩阵,抽取此次出行的mi个出行目的地。
(6) 根据Floyd最短路径规划算法,确定EV从第j-1个目的地到第j个目的地的最短行驶里程,并根据该里程计算行驶时间、到达时间、SOC。
(7) 根据各功能区的停车时长分布函数,抽取第w辆EV在第j个目的地的停车时长。
(8) 进行充电判断,若需要充电,则计算充电时长并更新充电负荷矩阵及SOC;若不需要,则充电负荷矩阵及SOC不变。
(9) 重复步骤(6)—步骤(8),直至j=mi时结束该循环。
(10) 按Floyd算法,确定EV从第mi-1个目的地返回出发点的最短行驶里程,并计算行驶时间、到达时间、SOC。
(11) 计算EV在该目的地的充电时长并更新充电时段内的负荷矩阵。
(12) 重复步骤(4)—步骤(11),直至i>n时结束该循环。
(13) 重复步骤(3)—步骤(12),直至w>W时结束该循环。
(14) 根据目标曲线,累加得到目标区域负荷。
3 算例仿真与结果分析 3.1 算例背景对模拟的EV及EV用户做出如下假设:①将模拟的EV用户设定为私家车用户群体;②用户仅在其停车时间内充电,用户出发去下一个目的地或电池充电完成都会导致充电停止;③所有道路均可双向通行;④所有EV在任意停车地点均可以进行充电且不受充电桩的限制;⑤ EV用户行驶里程由路径规划模拟。
文中算例基于我国某市的实际地理信息,将该市的8个行政区域分别设为a区、b区、c区、d区、e区、f区、g区、h区,并对其进行功能区(居民区、工作区、商业区以及其他区域)划分。该“路-网”试验区总面积为6 587.02 km2。根据实际地理信息,将该市划分为191个功能区,其中,a区功能区划分示意如图 8所示。
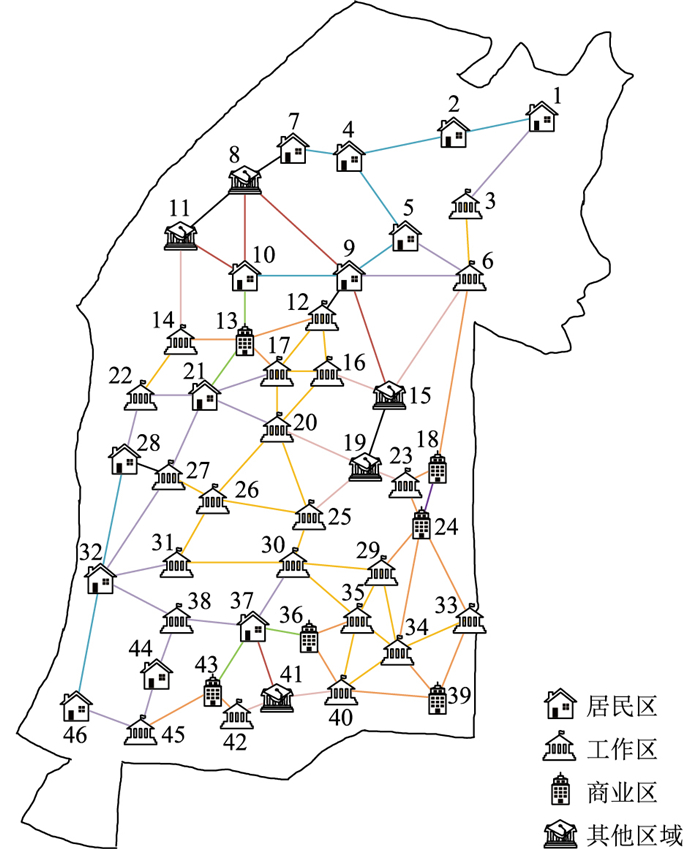
|
图 8 a区功能区划分示意 Fig. 8 Schematic diagram of functional area division in area a |
按照算例背景设定的某市实际汽车保有量,设EV总量为10万辆,按面积比分布在居民区内。该市居民区、工作区和商业区的占地面积百分比及充电桩数量如表 3所示。
|
|
表 3 某市功能区划分结果 Table 3 Results of functional zoning in a city |
以a区和b区的功能区划分结果为例进行分析,如表 4所示。
|
|
表 4 a区及b区功能区划分结果 Table 4 Results of functional zoning in area a and area b |
由统计结果可知,在a区的功能区中,工作区数量最多;而b区的居民区占比达到57.45%,数量远超工作区和商业区。
3.2 仿真结果该市总负荷变化及居民区、工作区充电负荷分布规律如图 9所示。
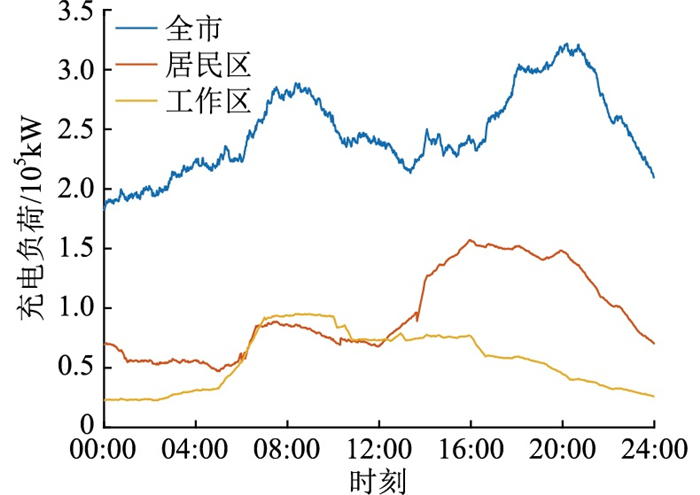
|
图 9 全市充电负荷预测分布规律 Fig. 9 Distribution law of the city′s charging load forecast |
从负荷变化来看,全市总负荷呈现“双高峰”趋势,并且一天的负荷高峰集中在08:00和22:00左右。从00:00开始,负荷逐步攀升,在07:00左右充电功率上升至第一个高峰,持续2 h左右后迅速下降18.41%;而在13:00—15:00时间段内,充电负荷需求处于一天中的低谷阶段,经过约6 h平稳期后又迅速上升至一天中需求最高峰,为日负荷均值的1.28倍,之后又逐渐下降。
对于居民区,一天内的负荷呈现“先波动上升,达到峰值后下降”的变化趋势。特别地,在工作日19:00—24:00这个下班时段,居民区的充电需求较大,充电负荷峰值约为谷值的1.65倍。
对于工作区,一天内的负荷呈现“先上升,达到峰值后下降”的变化趋势。由于大部分工作时间主要分布在白天,01:00—07:00负荷处于最低水平,为负荷均值的0.40倍。在06:00后,工作区的EV充电需求随着人们的活动增加而上升,最早在07:00达到负荷峰值,这与居民区第一次负荷峰值时间相比,提前了约10 h。该峰值维持一段时间后于10:00左右开始下降。
相对来看,除了06:00—12:00之间居民区和工作区的充电负荷曲线接近,其余时间居民区的充电负荷功率总体高于工作区,特别是在21:00—24:00之间,居民区充电负荷远远高于工作区负荷,百分比差值高达134.17%。这与大部分用户晚上下班回家充电的行为相一致。
在工作日和休息日,居民区及工作区的充电负荷如图 10所示。
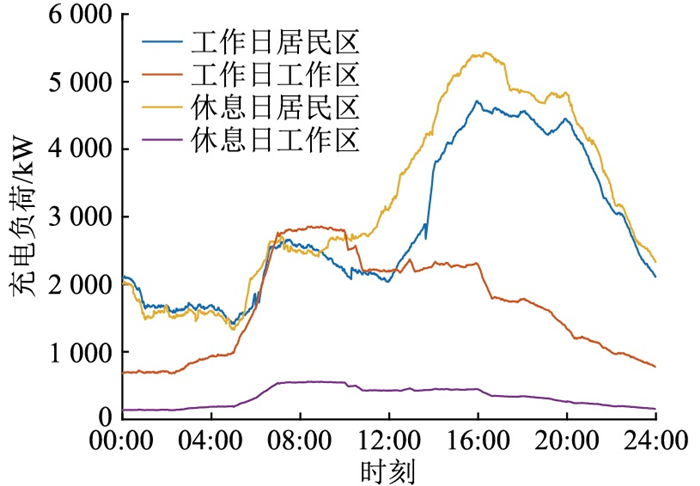
|
图 10 日充电功率需求 Fig. 10 Daily charging power demand |
由图 10可知,在居民区,相较于普通工作日,休息日的EV充电负荷总体显著增加,同比增长12.34%,但工作日EV充电负荷需求峰值基本不变。在工作区,由于工作日与休息日EV用户前往工作区的概率相差很大,因此日期属性对EV充电负荷需求影响很大,具体表现在工作日负荷均值为休息日负荷均值的5.12倍,因此休息日充电需求远低于工作日。
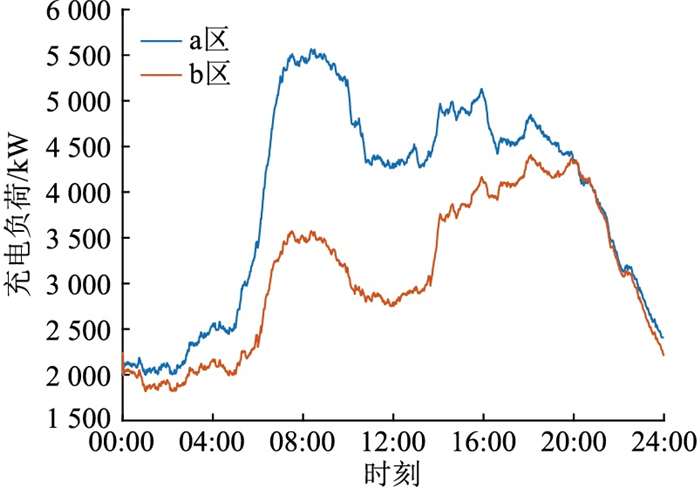
a区及b区的充电负荷变化曲线如图 11所示。
|
图 11 a区及b区的充电负荷变化曲线 Fig. 11 Charging load variation curves of area a and area b |
将图 11的充电负荷变化曲线与图 9中的全市充电负荷变化曲线对比可知,a区的充电负荷总曲线变化情况与工作区相似,在06:00—10:00时段出现尖峰,之后平缓下降;b区的充电负荷总曲线变化情况与居民区相似,在波动后于16:00—23:00达到尖峰。这与a区、b区的功能区划分结果相一致。
3.3 仿真验证抽取单辆EV的日出行行程如表 5所示,可知该辆EV日出行次数为2次,第一次出行的行程级数为4,第二次出行的出行级数为3。运用文中算法对该EV进行路径规划,规划结果如表 6所示。经检验,符合最短路径要求。
|
|
表 5 EV路径规划算例背景(n=2) Table 5 Background of EV route planning algorithm example (n=2) |
|
|
表 6 EV路径规划算例验证(n=2) Table 6 Verification of EV route planning algorithm example (n=2) |
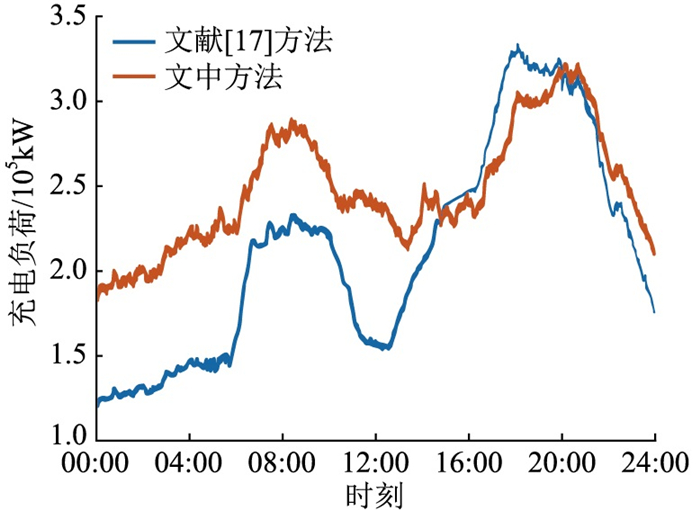
在同一工作日下和统一仿真参数的情况下,采用文中所提方法和文献[17]提出的方法对EV充电负荷进行预测并对比,仿真结果如图 12所示。
|
图 12 工作日充电功率 Fig. 12 Charging power on weekdays |
由图 12可知,采用文中方法和文献[17]方法预测的充电负荷变化趋势大致相同,同样呈现“先出现小高峰,再出现大高峰,之后下降”的变化趋势。两者的不同之处在于16:00之前,采用文中方法预测的变化曲线要高于文献[17]的方法,其原因为工作日EV白天在工作区和商业区的充电比例要高于在居民区的充电比例,相比于文献[17],文中考虑了居民区充电桩多为慢充,商业区和工作区充电桩多为快充的情况。同时,文中方法预测的变化曲线的峰谷差较小,其主要原因在于文献[17]中的EV用户一天只有一次出行行为,而文中考虑了多出行次数、多行程级数的情况。
4 结论文中计及EV、路网、电网等多方因素,提出了一种基于路网融合及出行链理论的EV负荷时空特性分析方法,并结合我国某市实际地理信息,按照区域功能特性进行仿真分析。结果表明:
(1) 基于实际地理信息考虑时空分布的EV充电负荷预测方法结合了功能区划分、图论以及路径规划Floyd算法,模拟EV用户的出行轨迹,可以有效预测一天内EV充电负荷的时空变化规律。
(2) 大规模EV充电负荷接入后,充电负荷主要集中在居民区,因此在充电站建设中,应优先考虑居民区充电桩建设。
(3) EV的出行行为受到不同功能区的影响,在不同功能区中的充电负荷变化规律不同,有着明显的区域特性。如居民区夜间充电负荷峰值最高,持续时间最长,而工作区峰值出现在上午等。功能区占比数量不同时,不同的行政区域所展现的充电负荷变化规律不同,一般变化特性更接近于占比最高的功能区充电负荷变化特性。如a区、b区的充电负荷总变化曲线与占比最高的功能区充电负荷变化曲线相似。
(4) 将a区及b区算例进行比较可知,不同功能区占比将直接影响该区域的充电负荷变化规律。居民选择错峰充电时,可通过分析区域类型来合理选择充电时间。
| [1] |
国务院办公厅. 国务院办公厅关于印发新能源汽车产业发展规划(2021—2035年)的通知[J]. 中华人民共和国国务院公报, 2020(31): 16-23. General Office of the State Council. Circular of the general office of the state council on printing and issuing the development plan of new energy automobile industry (2021-2035)[J]. Gazette of the State Council of the People's Republic of China, 2020(31): 16-23. (  0) 0) |
| [2] |
陈丽丹, 张尧, Antonio Figueiredo. 电动汽车充放电负荷预测研究综述[J]. 电力系统自动化, 2019, 43(10): 177-191. CHEN Lidan, ZHANG Yao, FIGUEIREDO A. Overview of charging and discharging load forcasting for electric vehicles[J]. Automation of Electric Power Systems, 2019, 43(10): 177-191. DOI:10.7500/AEPS20180814001 (  0) 0) |
| [3] |
蔡黎, 葛棚丹, 代妮娜, 等. 电动汽车入网负荷预测及其与电网互动研究进展综述[J]. 智慧电力, 2022, 50(7): 96-103. CAI Li, GE Pengdan, DAI Nina, et al. Review of research progress on load prediction and grid interaction of electric vehicles[J]. Smart Power, 2022, 50(7): 96-103. DOI:10.3969/j.issn.1673-7598.2022.07.015 (  0) 0) |
| [4] |
李瑶虹, 陈良亮, 刘卫东, 等. 基于用户出行链和调控意愿的城市级私家电动汽车调控能力评估[J]. 电力建设, 2021, 42(5): 100-112. LI Yaohong, CHEN Liangliang, LIU Weidong, et al. Regulation ability estimation of private EVs at city level considering users' trip chain and regulation willingness[J]. Electric Power Construction, 2021, 42(5): 100-112. (  0) 0) |
| [5] |
TAO S, LIAO K Y, XIAO X N, et al. Charging demand for electric vehicle based on stochastic analysis of trip chain[J]. IET Generation, Transmission & Distribution, 2016, 10(11): 2689-2698. (  0) 0) |
| [6] |
MU Y F, WU J Z, JENKINS N, et al. A spatial-temporal model for grid impact analysis of plug-in electric vehicles[J]. Applied Energy, 2014, 114: 456-465. DOI:10.1016/j.apenergy.2013.10.006 (  0) 0) |
| [7] |
陈中, 刘艺, 陈轩, 等. 考虑移动储能特性的电动汽车充放电调度策略[J]. 电力系统自动化, 2020, 44(2): 77-85. CHEN Zhong, LIU Yi, CHEN Xuan, et al. Charging and discharging dispatching strategy for electric vehicles considering characteristics of mobile energy storage[J]. Automation of Electric Power Systems, 2020, 44(2): 77-85. (  0) 0) |
| [8] |
BIAN H H, GUO Z Y, ZHOU C G, et al. Research on orderly charge and discharge strategy of EV based on QPSO algorithm[J]. IEEE Access, 2992, 10: 66430-66448. (  0) 0) |
| [9] |
张美霞, 叶睿琦, 杨秀, 等. 基于多维状态空间MCMC充电负荷预测的充电站规划[J]. 电力科学与技术学报, 2022, 37(4): 78-87. ZHANG Meixia, YE Ruiqi, YANG Xiu, et al. Charging station planning for electric vehicle based on charging load forecast by MCMC method in multi-dimensional state space[J]. Journal of Electric Power Science and Technology, 2022, 37(4): 78-87. (  0) 0) |
| [10] |
SU S, HUI Y, NING D, et al. Spatial-temporal distribution model of electric vehicle charging demand based on a dynamic evolution process[C]//2018 2nd IEEE Conference on Energy Internet and Energy System Integration (EI2). Beijing, China. IEEE, 2018: 1-8.
(  0) 0) |
| [11] |
XIANG Y, LIU Z P, LIU J C, et al. Integrated traffic-power simulation framework for electric vehicle charging stations based on cellular automaton[J]. Journal of Modern Power Systems and Clean Energy, 2018, 6(4): 816-820. DOI:10.1007/s40565-018-0379-3 (  0) 0) |
| [12] |
李晓辉, 李磊, 刘伟东, 等. 基于动态交通信息的电动汽车充电负荷时空分布预测[J]. 电力系统保护与控制, 2020, 48(1): 117-125. LI Xiaohui, LI Lei, LIU Weidong, et al. Spatial-temporal distribution prediction of charging load for electric vehicles based on dynamic traffic information[J]. Power System Protection and Control, 2020, 48(1): 117-125. (  0) 0) |
| [13] |
张谦, 王众, 谭维玉, 等. 基于MDP随机路径模拟的电动汽车充电负荷时空分布预测[J]. 电力系统自动化, 2018, 42(20): 59-66. ZHANG Qian, WANG Zhong, TAN Weiyu, et al. Spatial-temporal distribution prediction of charging load for electric vehicle based on MDP random path simulation[J]. Automation of Electric Power Systems, 2018, 42(20): 59-66. DOI:10.7500/AEPS20171117007 (  0) 0) |
| [14] |
程杉, 赵子凯, 陈诺, 等. 计及耦合因素的电动汽车充电负荷时空分布预测[J]. 电力工程技术, 2022, 41(3): 194-201, 208. CHENG Shan, ZHAO Zikai, CHEN Nuo, et al. Prediction of temporal and spatial distribution of electric vehicle charging load considering coupling factors[J]. Electric Power Engineering Technology, 2022, 41(3): 194-201, 208. DOI:10.12158/j.2096-3203.2022.03.023 (  0) 0) |
| [15] |
张琦, 杨健维, 向悦萍, 等. 计及气象因素的区域电动汽车充电负荷建模方法[J]. 电力系统保护与控制, 2022, 50(6): 14-22. ZHANG Qi, YANG Jianwei, XIANG Yueping, et al. Regional electric vehicle charging load modeling method considering meteorological factors[J]. Power System Protection and Control, 2022, 50(6): 14-22. (  0) 0) |
| [16] |
牛牧童, 廖凯, 杨健维, 等. 考虑季节特性的多时间尺度电动汽车负荷预测模型[J]. 电力系统保护与控制, 2022, 50(5): 74-85. NIU Mutong, LIAO Kai, YANG Jianwei, et al. Multi-time-scale electric vehicle load forecasting model considering seasonal characteristics[J]. Power System Protection and Control, 2022, 50(5): 74-85. (  0) 0) |
| [17] |
陈丽丹, 张尧, Antonio Figueiredo. 融合多源信息的电动汽车充电负荷预测及其对配电网的影响[J]. 电力自动化设备, 2018, 38(12): 1-10. CHEN Lidan, ZHANG Yao, FIGUEIREDO A. Charging load forecasting of electric vehicles based on multi-source information fusion and its influence on distribution network[J]. Electric Power Automation Equipment, 2018, 38(12): 1-10. (  0) 0) |
| [18] |
刘志强, 张谦, 朱熠, 等. 计及车-路-站-网融合的电动汽车充电负荷时空分布预测[J]. 电力系统自动化, 2022, 46(12): 36-45. LIU Zhiqiang, ZHANG Qian, ZHU Yi, et al. Spatial-temporal distribution prediction of charging loads for electric vehicles considering vehicle-road-station-grid integration[J]. Automation of Electric Power Systems, 2022, 46(12): 36-4. (  0) 0) |
| [19] |
董锴, 蔡新雷, 崔艳林, 等. 基于马尔科夫链的电动汽车聚合建模及多模式调频控制策略[J]. 电网技术, 2022, 46(2): 622-634. DONG Kai, CAI Xinlei, CUI Yanlin, et al. Aggregation modeling based on Markov chain and multi-mode control strategies of aggregated electric vehicles for frequency regulation[J]. Power System Technology, 2022, 46(2): 622-634. (  0) 0) |
| [20] |
YU Y, NDUKA O S, NAZIR F U, et al. A three-stage stochastic framework for smart electric vehicle charging[J]. IEEE Access, 2023(11): 655-666. (  0) 0) |
| [21] |
王浩林, 张勇军, 毛海鹏. 基于时空特征变量数据分析的共享汽车充电负荷预测方法[J]. 电力自动化设备, 2019, 39(12): 169-175. WANG Haolin, ZHANG Yongjun, MAO Haipeng. Charging load prediction method of shared vehicles based on data analysis of spatiotemporal characteristic variables[J]. Electric Power Automation Equipment, 2019, 39(12): 169-175. (  0) 0) |
| [22] |
强浩. 计及无线充电的电动汽车对电网的影响研究[D]. 南京: 东南大学, 2015. QIANG Hao. Research on the impacts of EVs involving wireless charging mode on the power grid[D]. Nanjing: Southeast University, 2015. (  0) 0) |
| [23] |
卢少平, 应黎明, 王霞, 等. 基于用户出行模拟的电动汽车快充站负荷预测及其优化调度[J]. 电力建设, 2020, 41(11): 38-48. LU Shaoping, YING Liming, WANG Xia, et al. Charging load prediction and optimized scheduling of electric vehicle quick charging station according to user travel simulation[J]. Electric Power Construction, 2020, 41(11): 38-48. (  0) 0) |
| [24] |
李含玉, 杜兆斌, 陈丽丹, 等. 基于出行模拟的电动汽车充电负荷预测模型及V2G评估[J]. 电力系统自动化, 2019, 43(21): 88-96. LI Hanyu, DU Zhaobin, CHEN Lidan, et al. Trip simulation based charging load forecasting model and vehicle-to-grid evaluation of electric vehicles[J]. Automation of Electric Power Systems, 2019, 43(21): 88-96. (  0) 0) |
| [25] |
李娇, 杨伟. 考虑出行路径决策的电动汽车充电负荷时空预测方法[J]. 电力电容器与无功补偿, 2023, 44(4): 62-71. LI Jiao, YANG Wei. Spatial-temporal forecast method of electric vehicles charging load considering decision-making of trip path[J]. Power Capacitor & Reactive Power Compensation, 2023, 44(4): 62-71. (  0) 0) |
| [26] |
黄登一, 刘灏, 毕天姝, 等. 基于扰动传播时空相关性的电网扰动事件快速定位方法[J]. 中国电机工程学报, 2022, 42(6): 2045-2060. HUANG Dengyi, LIU Hao, BI Tianshu, et al. A novel method for fast event location based on the temporal and spatial relevance of disturbance propagation[J]. Proceedings of the CSEE, 2022, 42(6): 2045-2060. (  0) 0) |
| [27] |
杨军亭, 马振祺, 梁鹏霄, 等. 考虑多源互补特性的孤岛供电故障恢复方法[J]. 电力需求侧管理, 2022, 24(3): 22-27. YANG Junting, MA Zhenqi, LIANG Pengxiao, et al. Isolated island power supply fault recovery method considering multi-source complementarity[J]. Power Demand Side Management, 2022, 24(3): 22-27. (  0) 0) |
| [28] |
MA K, HU X Y, YUE Z Y, et al. Voltage regulation with electric taxi based on dynamic game strategy[J]. IEEE Transactions on Vehicular Technology, 2022, 71(3): 2413-2426. (  0) 0) |
2. School of Software, Southeast University, Suzhou 210018, China
 2024, Vol. 43
2024, Vol. 43


 沈筱琦(1998),女,硕士在读,研究方向为电动汽车负荷预测(E-mail:
沈筱琦(1998),女,硕士在读,研究方向为电动汽车负荷预测(E-mail: