文章编号: 2096-3203(2024)03-0042-10 中图分类号: TM341;TM464
为实现能源的可持续性发展,以逆变器为主要接口的分布式电源越来越多地接入到电网中[1],然而大量分布式电源接入电网势必会影响电网安全稳定运行[2-6]。
针对以上问题,国内外学者提出了虚拟同步发电机(virtual synchronous generator,VSG)技术[7-8],通过引入转子运动方程以及调频、调压机制来模拟同步发电机的工作特性,为整个系统增加阻尼和惯性,同时为电网提供电压和频率支撑,维持了电网的稳定运行[9-11]。
目前,传统的VSG控制技术多是应用在电网电压正常的工况下[12-15]。但在实际运行中,配电网易受短路故障影响而出现电网电压跌落的情况,此时须要求并网逆变器有足够的低电压穿越能力来保证电网在故障下的稳定运行。而传统VSG控制技术在电压跌落期间无法抑制过流,也难以提供足够的无功支撑,从而造成电网运行失稳[16-19]。
针对传统VSG控制技术难以实现低电压穿越的问题,国内外相关学者提出了一些切实可行的低电压穿越方法。文献[20-21]提出了一种额外增加电流环的控制方法,但无法在低电压穿越期间提供无功功率支撑。文献[22-23]提出了一种通过平滑切换模式的VSG低电压穿越控制方法,但没有考虑到功率振荡过大的问题。文献[24]在低电压穿越期间加入定量的虚拟阻抗,通过增大系统的阻抗值来减小故障时的电流大小,但忽略了电网电压跌落与恢复时均会引起相位变化的问题,不能有效解决因相位变化而引起的VSG输出电压和电网电压之间电压差过大的问题。文献[25]通过有功与无功指令相结合的方式来保持功角的稳定,并通过无功指令与虚拟电抗相结合的方式来限制短路过电流,但该方案在弱电网中的适应性还有待验证。文献[26]通过相位补偿来抑制短路过电流和维持有功功率的稳定输出,但需要监测大量的实时数据来计算所需补偿的物理量,增加了实际操作的困难性,降低了控制的精确性,并且没有考虑频率稳定性的问题。文献[27]通过模拟同步发电机励磁状态的调整方式,改进了基于VSG的低电压穿越方法,但无法在低电压穿越期间灵活地调整有功和无功功率。文献[28]提出了在电网发生故障时,控制模式由电压型控制切换成电流型控制,从而有效抑制短路电流,但故障过程中无法为电网提供有效的电压支撑。
以上各种常规的低电压穿越控制策略在电网电压跌落的场景下均有一定的效果,但是大都仅仅考虑了电网电压幅值下降造成的过流影响,忽略了电网电压相位的变化,或者在考虑相位跳变时所提的控制策略较为复杂,难以应用于工程实践。而电网电压相位与幅值的跳变均会造成VSG输出电压与电网之间的电压差过大,从而产生过流、输出功率不稳定等问题。
为此,文中首先介绍了VSG的基本数学模型。其次,分析了在VSG控制方法下电网电压跌落时存在的问题。然后,提出了一种基于相位与幅值补偿的VSG低电压穿越控制策略。该策略整体上分为两部分,一是在电网电压跌落期间,兼顾抑制过流、稳定输出功率、频率以及无功支撑4个目标,设计了相位补偿与加入虚拟阻抗进行幅值补偿的环节;二是在电网电压恢复之后,以抑制过流为目标,设计了相位与幅值快速补偿环节。最后,通过仿真结果验证了所提控制策略的有效性。
1 VSG建模及故障特性分析 1.1 VSG数学建模图 1为传统VSG控制下的逆变器系统框图[29-31]。其中ugabc为三相电网电压;uabc、igabc分别为VSG输出三相电压、三相电流;Zg为等效线路阻抗;Ze为并网点和逆变器端口之间的等效阻抗,滤波结构为电感Le和电容C组成的LC滤波;egabc为VSG内电势;Udc为直流电压源;ωN为系统额定角频率;ω为系统实际角频率;Δω为ω与ωN之差;Kp、Kq分别为有功-频率、无功-电压下垂系数;Pref为设定的有功参考值;Pm为虚拟机械功率;Pe为VSG实际输出的有功功率;J为VSG的虚拟转动惯量;D为VSG的阻尼系数;s为拉普拉斯算子;θref为VSG内电势的参考相位;Qref为无功功率参考值;Qe为VSG实际输出的无功功率;E为VSG内电势幅值;Eref为内电势参考幅值。
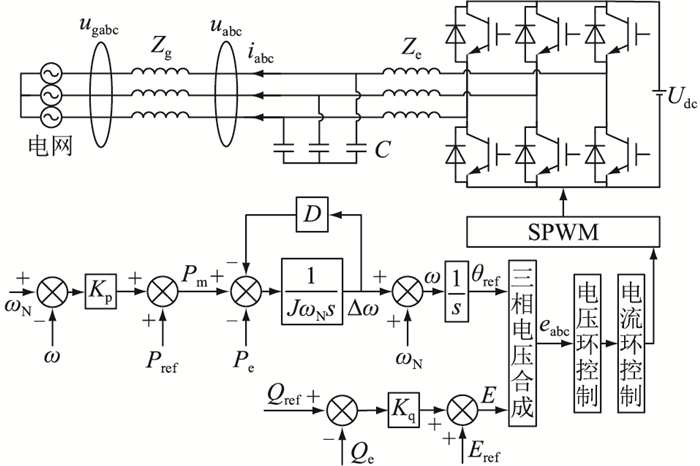
|
图 1 VSG主电路及控制结构 Fig. 1 VSG main circuit and control structure |
VSG控制主要由有功-频率环和无功-电压环组成。利用有功下垂控制模拟同步发电机的原动机调速器,利用转子运动方程来模拟同步发电机的惯性和阻尼特性,两者共同组成了有功-频率环;利用无功下垂控制模拟同步发电机的励磁调压部分来调节输出的无功功率;并利用电压电流双闭环解耦控制以及正弦脉宽调制(sinusoidal pulse width modulation,SPWM)技术控制逆变器,从而维持系统电压的稳定。其基本控制方程为:
| $ \left\{\begin{array}{l} P_{\mathrm{m}}=P_{\text {ref }}-K_{\mathrm{p}}\left(\omega-\omega_{\mathrm{N}}\right) \\ J \omega_{\mathrm{N}} \frac{\mathrm{d} \omega}{\mathrm{d} t}=P_{\mathrm{m}}-P_{\mathrm{e}}-D\left(\omega-\omega_{\mathrm{N}}\right) \\ E=E_{\text {ref }}-K_{\mathrm{q}}\left(Q_{\mathrm{e}}-Q_{\text {ref }}\right) \end{array}\right. $ | (1) |
当电网系统正常工作时,传统VSG控制下电压相量如图 2所示,VSG输出电压相量和电网电压相量之间的相位差为δ0(因为线路阻抗Zg很小,所以在系统正常工作时δ0非常小,
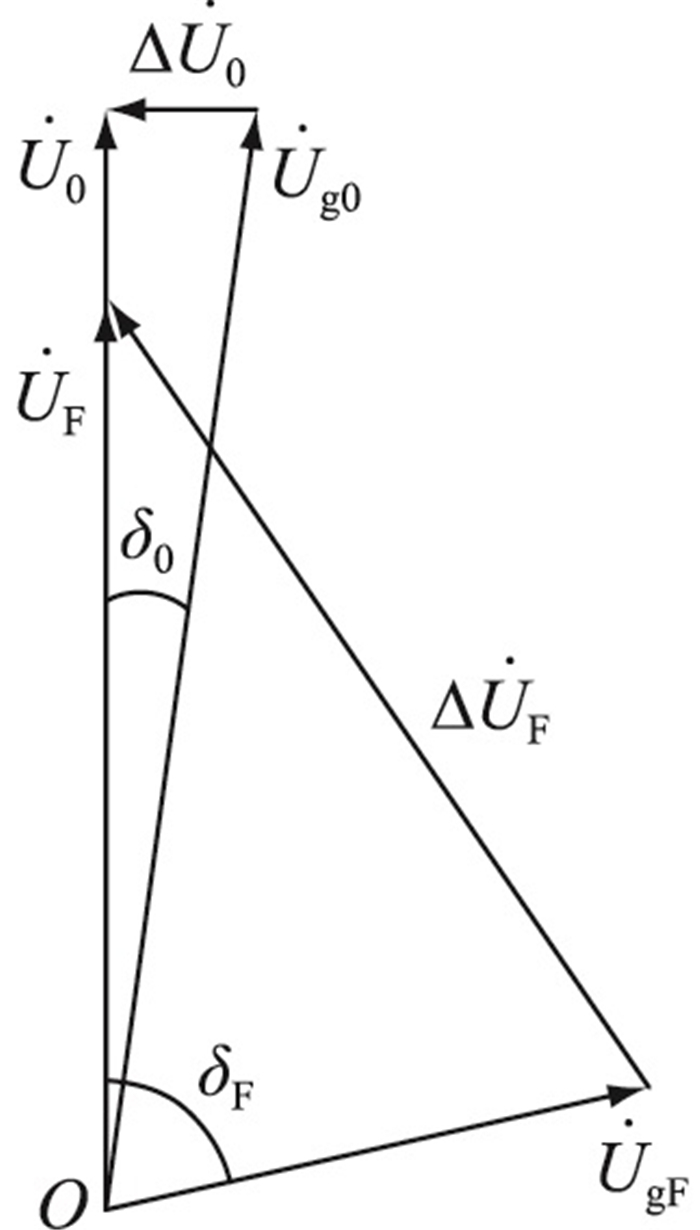
|
图 2 传统VSG控制下电压相量 Fig. 2 Voltage phasor under traditional VSG control |
结合图 2可知,在电网电压跌落后,VSG输出电压和电网电压之间存在较大的电压相量差
由上文分析可知,在电网电压跌落后,电网电压的幅值与相位都发生了相应的变化,使电网存在过流的风险,因此文中在考虑解决这2个问题的基础上,提出了图 3所示的基于幅值与相位补偿的VSG低电压穿越控制策略。其中,红色部分为加入的补偿环节;Zv为虚拟阻抗;ΔθF、ΔθR为相位补偿量;ΔUR为幅值补偿量。
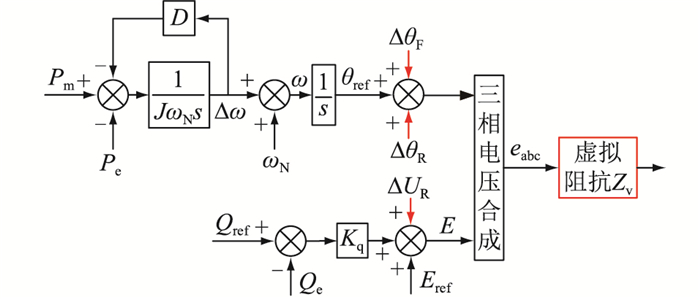
|
图 3 VSG低电压穿越改进控制框图 Fig. 3 VSG low voltage ride-through improvement control block diagram |
当忽略传输线路中的阻性成份时,VSG向电网输送的有功功率和无功功率分别为:
| $ P_{\mathrm{e}}=\frac{3}{2} \times \frac{U U_{\mathrm{g}}}{X_{\mathrm{e}}} \sin \delta $ | (2) |
| $ Q_{\rm{e}}=\frac{3}{2} \times \frac{U_{\mathrm{g}}\left(U \cos \delta-U_{\mathrm{g}}\right)}{X_{\mathrm{e}}} $ | (3) |
式中:U为VSG输出相电压的幅值;Ug为电网相电压的幅值;Xe为VSG输出电压和电网电压之间的总阻抗;δ为VSG输出电压和电网电压之间的功角。
由1.2节的分析可知,为减小VSG输出电压和电网电压之间的电压差,需要减小两者之间的相位差。易知,当两者之间的相位差δF减小为0时,两者之间的电压相量差
文中将频率波动范围-0.2~0.2 Hz作为电网频率的标准要求。当电网电压跌落时,VSG输出侧功率必然小于输入侧功率,所以电网频率必然大于工频50 Hz,那么此时频率在标准要求内的波动范围为0~0.2 Hz。由式(2)、式(3)可知,随着功角δ的变化,有功功率Pe和无功功率Qe呈现相反的变化趋势,而为了提供更多的无功支撑,须要求VSG尽可能多地输出无功功率,尽可能少地输出有功功率,此时就需要控制频率波动为0.2 Hz这一最低要求,即要控制VSG输出电压和电网电压之间有最小相位差δmin,以保证电网频率稳定。并且因电压电流双闭环的响应时间远小于虚拟同步控制环的响应时间,可认为egabc与ugabc相等,所以可以通过调节VSG内电势与电网电压相量之间的相位差来调节有功功率的输出。
以电网电压的实时相位为d轴定向,对VSG内电势egabc进行dq变换,VSG内电势Ė在dq轴上的分量Ėd、Ėq如图 4所示。在电网电压跌落期间冻结VSG的无功-电压环,令Qref=Qe, 从而控制VSG始终以内电势参考幅值Eref运行。根据图 4可知,控制VSG内电势与电网电压之间的功角δ为最小值δmin,等效为将幅值Eq控制为符合频率波动最低要求的最小值Eq-min,二者之间满足:
| $ E_{q-\min }=2 {\mathsf{π}}\left(K_{\mathrm{p}-{\mathsf{δ}}}+\frac{K_{\mathrm{i}-{\mathsf{δ}}}}{s}\right)(f-50.2) $ | (4) |
| $ \delta_{\text {min }}=\arcsin \left(\frac{E_{q-\text {min }}}{E_{\text {ref }}}\right) $ | (5) |
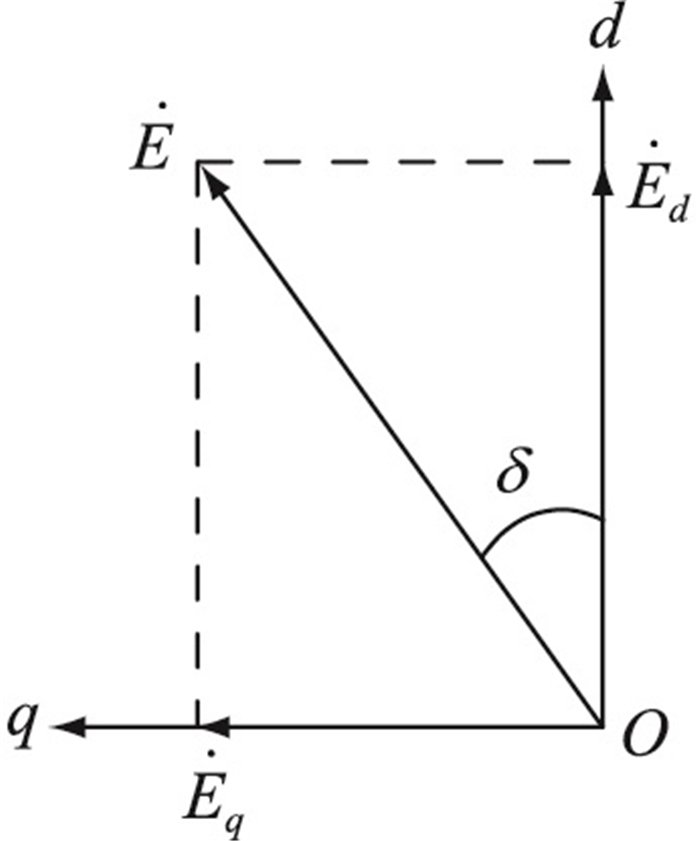
|
图 4 VSG内电势dq轴分量 Fig. 4 dq axis component of potential in VSG |
式中:Kp-δ、Ki-δ分别为将电网频率快速调整至50.2 Hz的自适应比例、积分系数,系统稳定运行时为常数;f为电网的实际频率。
利用比例积分(proportional-integral,PI)控制,根据式(6)计算得到电网电压跌落期间的相位补偿量ΔθF。
| $ \Delta \theta_{\mathrm{F}}=\left(K_{\mathrm{p}-{\mathsf{ω}}}+\frac{K_{\mathrm{i}-{\mathsf{ω}}}}{s}\right)\left(E_{q-\min }-E_{q}\right) $ | (6) |
式中:Kp-ω、Ki-ω分别为将VSG输出电压和电网电压的相位差快速补偿到所需最小量的自适应比例、积分系数,系统稳定运行时为常数。
图 5为相位补偿后的电压相量图。其中,Ė0为故障发生后未进行相位补偿之前的VSG内电势;ĖF为进行相位补偿之后的VSG内电势。由图 5可知,经过相位补偿之后,VSG输出电压和电网电压之间的相量差变为了

|
图 5 相位补偿后的电压相量 Fig. 5 Voltage phasor after phase compensation |
文中采用模糊控制对相位补偿过程中的PI参数进行调节,对输入误差进行模糊控制,如图 6所示,其中r为模糊自适应PI控制过程的初始输入值;y为输出值;ΔKp、ΔKi为根据模糊推理产生的PI参数修正量。根据各参数的模糊控制模型和各模糊子集的隶属度赋值表,利用模糊规则推理设计PI参数的模糊矩阵表,实时对PI参数进行修正,修正公式如式(7)所示。
| $ \left\{\begin{array}{l} K_{{\rm{p}}-{\mathsf{δ}}}=K_{{\rm{p}}-{\mathsf{δ}}0}+\Delta K_{{\rm{p}}-{\mathsf{δ}}}\\ K_{\mathrm{i}-{\mathsf{δ}}}=K_{\mathrm{i}-{\mathsf{δ}}0}+\Delta K_{\mathrm{i}-{\mathsf{δ}}} \\ K_{{\rm{p}}-{\mathsf{ω}}}=K_{\mathrm{p}-{\mathsf{ω}}0}+\Delta K_{\mathrm{p}-{\mathsf{ω}}} \\ K_{\mathrm{i}-{\mathsf{ω}}}=K_{\mathrm{i}-{\mathsf{ω}}0}+\Delta K_{\mathrm{i}-{\mathsf{ω}}} \end{array}\right. $ | (7) |

|
图 6 模糊自适应PI控制框图 Fig. 6 Fuzzy adaptive PI control block diagram |
式中:ΔKp-δ、ΔKi-δ、ΔKp-ω、ΔKi-ω为PI参数修正量;Kp-δ0、Ki-δ0、Kp-ω0、Ki-ω0为由传统PI整定方法得到的初始值。文中设置Kp-δ0=Kp-ω0=10,Ki-δ0=Ki-ω0=20。
2.2 幅值补偿由于冻结无功-电压环之后,VSG以内电势参考幅值Eref运行,所以当电网电压跌落程度较深时,VSG输出电压幅值与电网电压幅值差较大。由图 5可知,当VSG输出电压和电网电压幅值相差过大时,进行相位补偿后,两者之间的相量差
因此,文中考虑在无功-电压环中加入虚拟阻抗来减小VSG输出电压的幅值。假设虚拟阻抗Zv=Rv+jLv,则虚拟阻抗上产生的虚拟电压降为:
| $ \Delta U_{{\rm{v}}}=\mid I \mid \sqrt{R_{{\rm{v}}}^{2}+L_{{\rm{v}}}^{2}} $ | (8) |
式中:Rv、Lv分别为虚拟电阻和虚拟电感;I为VSG输出电流。
此时VSG输出电压幅值为:
| $ U_{\mathrm{F}_{2}}=\left|\dot{E}_{\mathrm{F}}-\Delta \dot{U}_{\mathrm{v}}\right| $ | (9) |
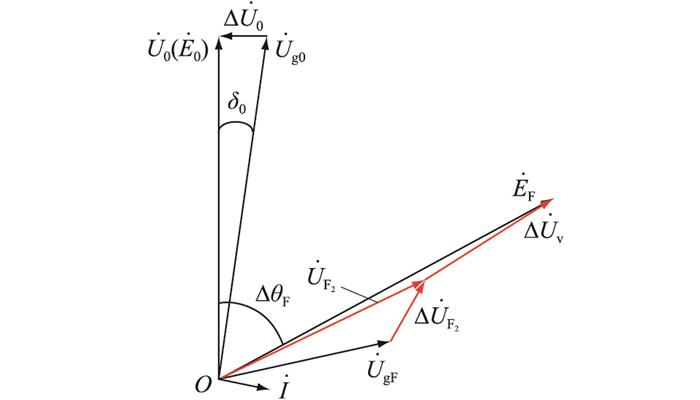
如图 7所示,在加入虚拟阻抗之后,VSG输出电压和电网电压之间的相量差变为
|
图 7 幅值补偿后的电压相量 Fig. 7 Voltage phasor after amplitude compensation |
其中,可根据式(10)设计虚拟阻抗的值。
| $ \left|Z_{\mathrm{v}}+Z_{\mathrm{g}}\right|=\frac{\left|\dot{E}_{\mathrm{F}}-\dot{U}_{\mathrm{g} F}\right|}{I_{\text {lim }}} $ | (10) |
式中:Ilim为电流限幅值,短路情况下对任意相电流起到限值作用。同时设置Ilim≤1.3Iset,Iset为VSG输出电流额定值。
当需要实现VSG对电网最大的电压支撑时,设置Ilim=1.3Iset。同时为更便捷地调整虚拟阻抗值的大小,文中设置虚拟阻抗、阻感比为1 ∶1,即虚拟电阻Rv和虚拟电感Lv存在以下关系:
| $ R_{{\rm{v}}} / L_{{\rm{v}}}=1 $ | (11) |
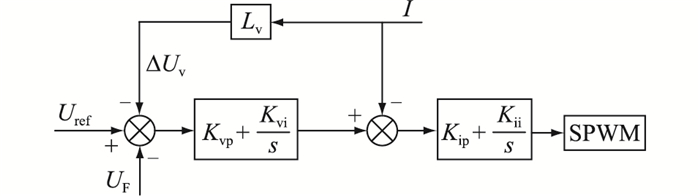
图 8为加入虚拟阻抗后的电压电流双闭环控制框图,图中Uref、UF分别为故障发生后VSG输出电压参考值及VSG输出电压实际值;Kvp、Kvi、Kip、Kii分别为传统电压电流双闭环解耦控制结构中的比例、积分系数。
|
图 8 加入虚拟阻抗后的电压电流双闭环控制框图 Fig. 8 Block diagram of voltage and current double closed-loop control after adding virtual impedance |
故障恢复后,解除无功-电压环的冻结,去除虚拟阻抗,使VSG恢复到正常的工作状态。去除虚拟阻抗之后,VSG内电势与VSG输出电压相等,且由于无功-电压环调节时间的滞后,在电网电压恢复后,VSG输出无功功率值在额定值附近振荡,因此VSG输出电压值也在额定值附近振荡。受虚拟机械惯性的影响,在电网电压恢复之后,VSG内电势的相位也不能发生快速变化。
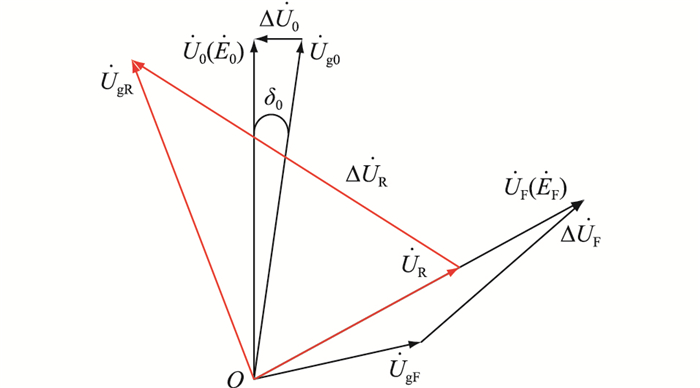
电网电压恢复后,同样存在幅值与相位的跳变,如图 9所示,在故障恢复瞬间,电网电压从
|
图 9 故障恢复后的电压相量 Fig. 9 Voltage phasor diagram after fault recovery |
在进行相位补偿时,电网电压已恢复至额定值,有功负载吸收的功率也基本达到了额定值,因此不需要VSG向电网提供额外的有功功率来维持电网频率的稳定。所以为了尽可能地维持电网的稳定运行,可将两者之间的相位差控制为0。
由于VSG无功-电压环调节时间的滞后,VSG输出电压不能快速达到额定值,因此也需要加入相应的幅值补偿策略来使其快速达到额定值,以消除其与电网电压之间的幅值差。为此,文中提出了低电压穿越控制策略,以保证故障恢复之后,系统能够稳定运行。
与电网电压跌落期间的补偿原理类似,仍以电网电压实时相位为d轴定向,对VSG输出电压ugabc进行dq变换,根据上述分析可知,此时需要控制ugabc在d轴上的分量值等于Eref,在q轴上的分量值为0,即可满足幅值与相位的补偿要求。利用PI调节器根据式(12)、式(13)计算得到故障恢复期间的相位与幅值补偿量。
| $ \Delta \theta_{\mathrm{R}}=\left(K_{{\rm{p}}-{\mathsf{ω}}^{\prime}}+\frac{K_{\mathrm{i} \cdot {\mathsf{ω}}^{\prime}}}{s}\right)\left(0-U_{q}\right) $ | (12) |
| $ \Delta U_{\mathrm{R}}=\left(K_{\mathrm{p}-\mathrm{U}^{\prime}}+\frac{K_{\mathrm{i}-\mathrm{U}^{\prime}}}{s}\right)\left(E_{\mathrm{ref}}-U_{d}\right) $ | (13) |
式中:Ud、Uq分别为ugabc在d、q轴上的分量值;Kp-ω′、Kp-U′、Ki-ω′、Ki-U′分别为自适应的比例系数和积分系数,系统稳定运行时为常数,其作用为快速跟踪电网电压,将VSG输出电压快速补偿至与电网电压相同,此处自适应的比例和积分系数的设计方法和2.1节中的PI参数调节方法一致。
电网电压恢复后,在进行相位与幅值补偿的同时,检测VSG输出电流的峰值。当VSG输出电流值能够稳定在电流额定值的1.3倍以内时,撤去相位与幅值补偿环节,系统恢复到正常的工作状态。
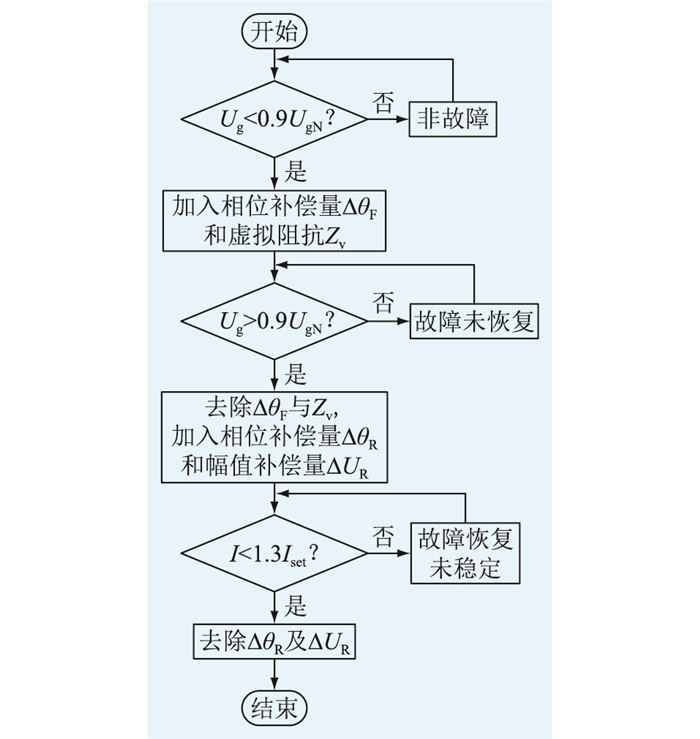
综上所述,文中所提的低电压穿越控制策略的流程如图 10所示。通过比较电网电压幅值与阈值,判断其是否发生跌落。文中电网相电压额定值UgN为311 V,据国标要求,当电网电压幅值低于0.9UgN时,可认为发生电压跌落故障,当电网电压幅值高于0.9UgN时,可认为恢复正常。
|
图 10 低电压穿越控制流程 Fig. 10 Flow chart of low voltage ride-through control |
为验证文中所提低电压穿越控制策略的有效性,在MATLAB/Simulink中搭建了图 1所示的VSG并网仿真模型。VSG额定有功功率PN为15 kW、额定无功功率QN为0,内电势参考幅值Eref和额定频率fN分别为311 V和50 Hz,主要的仿真参数如表 1所示。
|
|
表 1 VSG并网仿真参数 Table 1 VSG grid connection simulation parameters |
为验证文中所提的加入补偿量的低电压穿越控制策略的有效性,分别设定不加补偿量和加入补偿量2种控制情形下的仿真实验,对比2种情况下的波形并分析。整体仿真时间为2 s,前0.7 s,VSG运行于额定状态;0.7 s时电网电压跌落至0.5 p.u.;1.3 s时恢复正常,恢复后运行于额定状态。
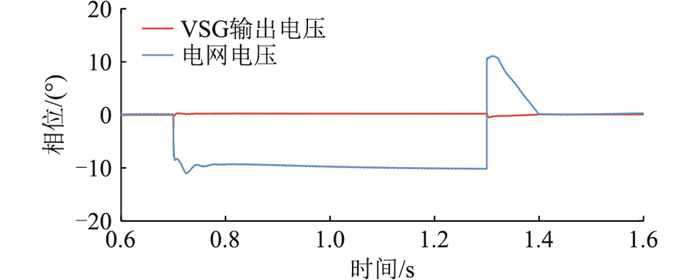
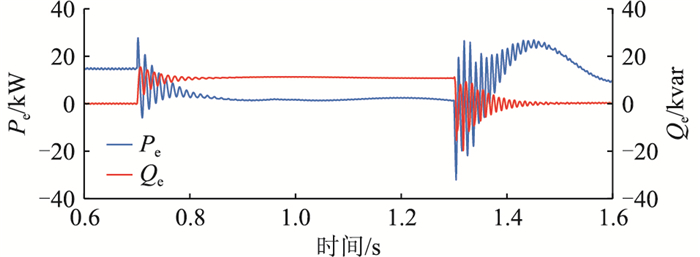
4.1 不加补偿量的常规控制策略图 11为电网电压跌落至0.5 p.u.时的VSG输出电压和电网电压的相位波形。正常运行时,两者的相位十分相近;当发生故障时,电网电压相位向后发生了跳变,两者之间的相位差增大,从0°增加到了10°左右;故障恢复后,电网电压同样发生了跳变,且该跳变使得电网电压超前于VSG输出电压,电网电压相位与VSG输出电压相位差最大达到了12°。VSG输出有功和无功功率波形如图 12所示。在故障发生与恢复时,有功和无功都存在很明显的振荡现象,并且在故障恢复时,VSG出现了吸收有功功率的情形,严重威胁了电网的稳定运行。
|
图 11 不加补偿量时的相位波形 Fig. 11 Phase waveforms without compensation |
|
图 12 不加补偿量时的VSG输出功率波形 Fig. 12 VSG output power waveforms without compensation |
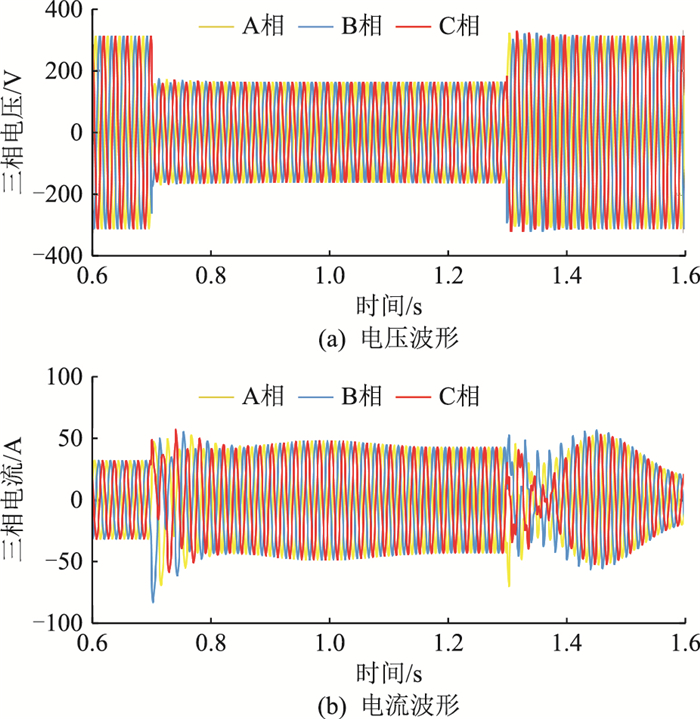
图 13为不加补偿量时电网电压跌落至0.5 p.u.时的电压波形和电流波形。由图 13(b)可知,额定电流为32.1 A,故障发生后最大冲击电流达到了83.5 A,稳态过流为48.2 A,故障恢复后最大冲击电流达到了70.6 A。
|
图 13 不加补偿量时的电压、电流波形 Fig. 13 Voltage and current waveforms without compensation |
由4.1节仿真分析可知,若不加入补偿环节,在整个故障阶段以及故障恢复阶段都会出现明显的过流现象。因此文中设计相位补偿与幅值补偿环节,并进行仿真验证。
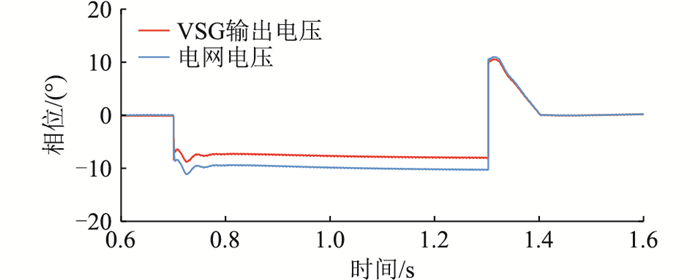
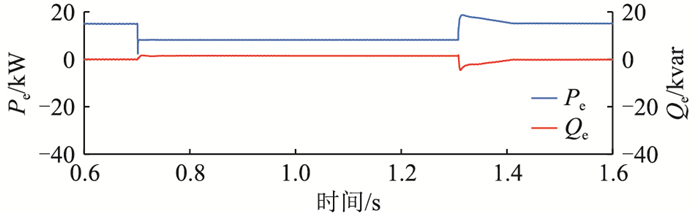
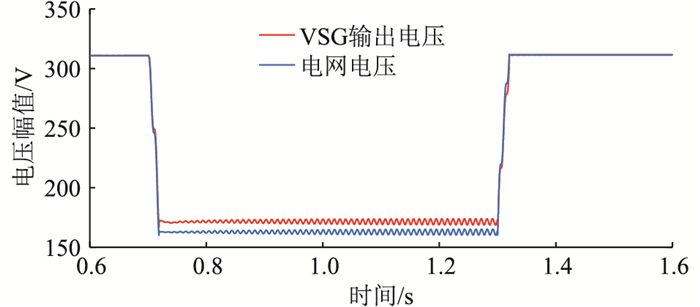
图 14为加入补偿量之后的VSG输出电压和电网电压的相位波形,可以看出,由于相位补偿量的加入,故障发生后VSG输出电压相位可以快速接近电网电压相位,两者之间的相位差维持在2.5°左右,从而避免了冲击电流的出现,同时两者之间仍然留有一定的余量差来保证VSG输出足够的有功功率,达到稳定频率的目的。图 15为VSG输出有功和无功功率波形,可以看出,故障发生时,功率振荡现象基本消除,故障恢复后,输出功率可在短时间内达到额定值。图 16为加入补偿量后的VSG输出电压及电网电压幅值波形,在低电压穿越期间,VSG输出电压幅值为171 V, 电网电压幅值为163 V。
|
图 14 加入补偿量后的相位波形 Fig. 14 Phase waveforms after adding compensation |
|
图 15 加入补偿量后的VSG输出功率波形 Fig. 15 VSG output power waveforms after adding compensation |
|
图 16 加入补偿量后的VSG输出电压及电网电压幅值波形 Fig. 16 VSG output voltage and grid voltage amplitude waveforms after adding compensation |
图 17(a)为VSG输出电压和电网电压相位差为0时的频率波形,可知VSG有功输出的不足导致了电网频率的波动范围过大,峰值处达到了50.4 Hz。图 17(b)为VSG输出电压和电网电压相位差为δmin(文中理论分析所设置的仿真条件下为2.5°)时的频率波形,可知相位差δmin的存在可以保证VSG输出足够的有功功率,从而稳定了电网频率。

|
图 17 加入补偿量后的频率波形 Fig. 17 Frequency waveforms after adding compensation |
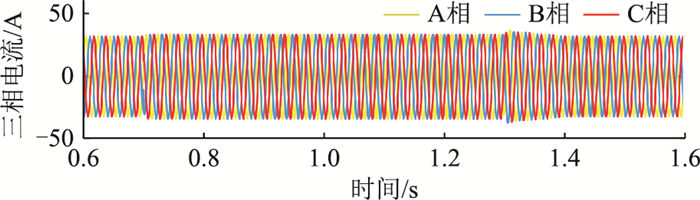
图 18为加入补偿量后电网电压跌落至0.5 p.u.时的电流波形,可知故障阶段的最大冲击电流峰值为34 A,稳态过电流为33.7 A,故障恢复阶段的最大冲击电流峰值为37.2 A,均在电流安全运行的1.3Iset范围内,整个故障过程均不存在过流现象。并且在1.3 s电网电压恢复之后,经过0.1 s的调节时间,整个系统恢复到了正常的工作状态。
|
图 18 加入补偿量后的电流波形 Fig. 18 Current waveforms after adding compensation |
由上述实验可知,加入补偿环节之后,故障阶段VSG输出电压和电网电压之间的相量差明显减小,输出功率振荡现象被消除,电网频率得以稳定,限流效果也明显提升,验证了文中所提控制策略的有效性。同时由于文中所用的补偿方法利用了PI调节器,可以达到快速跟踪并减小误差的效果,因此可以很大程度上减小检测延时对补偿策略的影响。
5 结论针对电网发生对称短路故障以及故障恢复时产生的逆变器过流及输出功率不稳定等问题,文中提出了一种基于相位与幅值补偿的VSG低电压穿越控制策略,实现了VSG与电网并网工作时的低电压穿越过程。文中结论及下一步工作展望如下:
(1) 电网发生电压跌落与恢复时,电网电压相位与幅值均会发生跳变,逆变器并网时,在传统VSG控制下,会出现过流及逆变器输出功率不稳定等问题。
(2) 文中提出的低电压穿越控制策略通过在故障发生过程中加入相位与幅值补偿的方法,来减小VSG输出电压与电网电压之间的相量差,从而避免了过流等问题的发生,并消除了VSG输出功率振荡现象,同时达到了稳定电网频率的效果。
(3) 故障恢复期间,文中提出的控制策略依然具有适应性,能够快速消除VSG输出电压和电网电压之间的相量差,在解决过流问题的同时使系统快速恢复到额定状态。
(4) 文中仅针对单个逆变器并网发生对称故障时的情况提出了相应的低电压穿越控制策略。但当多个逆变器同时接入电网时,系统工况更加复杂,发生短路故障产生的影响也会更加复杂,后续将进一步展开相关的研究工作。
| [1] |
张若微, 秦博宇, 李恒毅, 等. 基于干扰抑制的双馈风机低电压穿越控制策略[J]. 电力系统自动化, 2020, 44(20): 112-120. ZHANG Ruowei, QIN Boyu, LI Hengyi, et al. Low voltage ride-through control strategy for DFIG-based wind turbine based on disturbance attenuation[J]. Automation of Electric Power Systems, 2020, 44(20): 112-120. (  0) 0) |
| [2] |
罗嘉, 赵浩然, 高术宁, 等. 基于显式模型预测控制和改进虚拟阻抗的双馈风机低电压穿越策略[J]. 电网技术, 2021, 45(5): 1716-1723. LUO Jia, ZHAO Haoran, GAO Shuning, et al. LVRT strategy for DFIG based on explicit model predictive control and improved virtual impedance[J]. Power System Technology, 2021, 45(5): 1716-1723. (  0) 0) |
| [3] |
韦徵, 姬秋华, 王伟, 等. 适用于电网不对称下的自同步电压源逆变器控制策略[J]. 电力系统自动化, 2021, 45(10): 124-131. WEI Zheng, JI Qiuhua, WANG Wei, et al. Control strategy of self-synchronous voltage source inverter for asymmetric power grid[J]. Automation of Electric Power Systems, 2021, 45(10): 124-131. DOI:10.7500/AEPS20200805003 (  0) 0) |
| [4] |
丁一凡, 季亮, 常潇, 等. 不对称电压跌落下虚拟同步机改进低电压穿越控制策略[J]. 电力系统保护与控制, 2022, 50(16): 76-85. DING Yifan, JI Liang, CHANG Xiao, et al. Improved low voltage ride-through control strategy of a virtual synchronous generator during unbalanced voltage sags[J]. Power System Protection and Control, 2022, 50(16): 76-85. (  0) 0) |
| [5] |
王德胜, 颜湘武, 贾焦心, 等. 永磁直驱风机基于虚拟同步技术的高、低电压连续故障穿越策略[J]. 中国电机工程学报, 2022, 42(6): 2164-2175. WANG Desheng, YAN Xiangwu, JIA Jiaoxin, et al. High/low voltage continuous fault ride through strategy of PMSGs based on virtual synchronization technology[J]. Proceedings of the CSEE, 2022, 42(6): 2164-2175. (  0) 0) |
| [6] |
ZHAO T, CHEN D L. Analysis and suppression of active power backflow of three-phase common DC-bus cascaded H-bridge PV grid-connected inverter during LVRT[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 10(1): 745-759. DOI:10.1109/JESTPE.2021.3071091 (  0) 0) |
| [7] |
颜湘武, 崔森, 宋子君, 等. 基于超级电容储能控制的双馈风电机组惯量与一次调频策略[J]. 电力系统自动化, 2020, 44(14): 111-120. YAN Xiangwu, CUI Sen, SONG Zijun, et al. Inertia and primary frequency regulation strategy of doubly-fed wind turbine based on super-capacitor energy storage control[J]. Automation of Electric Power Systems, 2020, 44(14): 111-120. (  0) 0) |
| [8] |
彭星, 姜飞, 涂春鸣, 等. 不对称故障下光伏逆变器的最优电压支撑策略[J]. 电网技术, 2021, 45(11): 4259-4268. PENG Xing, JIANG Fei, TU Chunming, et al. Optimal voltage support strategy for photovoltaic inverters under asymmetric faults[J]. Power System Technology, 2021, 45(11): 4259-4268. (  0) 0) |
| [9] |
王继磊, 张兴, 朱乔华, 等. 虚拟同步发电机暂态稳定性分析与控制策略[J]. 电机与控制学报, 2022, 26(12): 28-37. WANG Jilei, ZHANG Xing, ZHU Qiaohua, et al. Transient stability analysis and control strategy of virtual synchronous generator[J]. Electric Machines and Control, 2022, 26(12): 28-37. (  0) 0) |
| [10] |
房志学, 苏建徽, 王华锋, 等. 微网逆变器低电压穿越控制策略[J]. 电力系统自动化, 2019, 43(2): 143-149, 161. FANG Zhixue, SU Jianhui, WANG Huafeng, et al. Low voltage ride-through control strategy of microgrid inverter[J]. Automation of Electric Power Systems, 2019, 43(2): 143-149, 161. (  0) 0) |
| [11] |
李帅虎, 胡耀尹, 罗滇生, 等. 基于模型预测控制的光储发电系统VSG频率控制方法[J]. 全球能源互联网, 2022, 5(4): 348-355. LI Shuaihu, HU Yaoyin, LUO Diansheng, et al. VSG frequency control method of photovoltaic system with storage based on model predictive control[J]. Journal of Global Energy Interconnection, 2022, 5(4): 348-355. (  0) 0) |
| [12] |
秦世耀, 齐琛, 李少林, 等. 电压源型构网风电机组研究现状及展望[J]. 中国电机工程学报, 2023, 43(4): 1314-1334. QIN Shiyao, QI Chen, LI Shaolin, et al. Review of the voltage-source grid forming wind turbine[J]. Proceedings of the CSEE, 2023, 43(4): 1314-1334. (  0) 0) |
| [13] |
王若谷, 张若微, 王明杰, 等. 提升双馈风力发电系统低电压穿越能力的跟踪控制方法[J]. 电力工程技术, 2021, 40(2): 185-191. WANG Ruogu, ZHANG Ruowei, WANG Mingjie, et al. A tracking control method for doubly-fed induction generator to enhance the low voltage ride through capability[J]. Electric Power Engineering Technology, 2021, 40(2): 185-191. DOI:10.12158/j.2096-3203.2021.02.026 (  0) 0) |
| [14] |
张冠锋, 杨俊友, 王海鑫, 等. 基于虚拟同步机技术的风储系统协调调频控制策略[J]. 电工技术学报, 2022, 37(S1): 83-92. ZHANG Guanfeng, YANG Junyou, WANG Haixin, et al. Coordinated frequency modulation control strategy of wind storage system based on virtual synchronous machine technology[J]. Transactions of China Electrotechnical Society, 2022, 37(S1): 83-92. (  0) 0) |
| [15] |
杨效, 曾成碧, 赖辉, 等. 弱电网下基于谐波状态空间模型的光储-虚拟同步发电机稳定性分析与优化控制研究[J]. 电力系统保护与控制, 2023, 51(16): 34-47. YANG Xiao, ZENG Chengbi, LAI Hui, et al. A stability analysis method and optimal control of a photovoltaic energy storage-virtual synchronous generator based on a harmonic state space model in a weak grid[J]. Power System Protection and Control, 2023, 51(16): 34-47. (  0) 0) |
| [16] |
董纪清, 潘佳清, 毛行奎. 自适应正负序复合控制的VSG低电压穿越策略[J]. 电网技术, 2023, 47(2): 815-822. DONG Jiqing, PAN Jiaqing, MAO Xingkui. Low voltage ride-through strategy of VSG based on adaptive positive and negative sequence composite control[J]. Power System Technology, 2023, 47(2): 815-822. (  0) 0) |
| [17] |
高长伟, 黄翀阳, 郑伟强, 等. 虚拟阻抗制动可再生能源机组低电压穿越控制[J]. 电力系统保护与控制, 2023, 51(10): 142-152. GAO Changwei, HUANG Chongyang, ZHENG Weiqiang, et al. Low voltage ride-through control of a renewable energy unit with virtual impedance braking[J]. Power System Protection and Control, 2023, 51(10): 142-152. (  0) 0) |
| [18] |
江世明, 唐杰. 基于暂态阻尼增强的改进VSG控制策略[J]. 电力系统保护与控制, 2023, 51(19): 144-154. JIANG Shiming, TANG Jie. Improved VSG control strategy based on transient damping enhancement[J]. Power System Protection and Control, 2023, 51(19): 144-154. (  0) 0) |
| [19] |
邢鹏翔, 贾璇悦, 许长清, 等. VSG低电压穿越的特性分析及控制方法研究[J]. 电网与清洁能源, 2022, 38(8): 130-137, 143. XING Pengxiang, JIA Xuanyue, XU Changqing, et al. A study on characteristic analysis and control methods of low voltage ride through for the VSG[J]. Power System and Clean Energy, 2022, 38(8): 130-137, 143. (  0) 0) |
| [20] |
马磊, 刘国荣, 毛云坤, 等. 基于VSG的永磁直驱风电机组惯量支撑控制策略[J]. 电网与清洁能源, 2020, 36(12): 115-120. MA Lei, LIU Guorong, MAO Yunkun, et al. Inertia support con trol strategy for permanent magnet direct-drive wind turbines based on VSG[J]. Power System and Clean Energy, 2020, 36(12): 115-120. (  0) 0) |
| [21] |
马铱林, 杨欢, 屈子森, 等. 改善虚拟同步发电机阻尼特性的设计方法[J]. 电网技术, 2021, 45(1): 269-275. MA Yilin, YANG Huan, QU Zisen, et al. Design method for improving damping characteristics of virtual synchronous generator[J]. Power System Technology, 2021, 45(1): 269-275. (  0) 0) |
| [22] |
CHEN T Y, CHEN L J, ZHENG T W, et al. General control strategy to limit peak currents of virtual synchronous generator under voltage sags[C]//2016 IEEE Power and Energy Society General Meeting (PESGM). Boston, MA, USA. IEEE, 2016: 1-5.
(  0) 0) |
| [23] |
SHI K, SONG W T, XU P F, et al. Low-voltage ride-through control strategy for a virtual synchronous generator based on smooth switching[J]. IEEE Access, 1809, 6: 2703-2711. (  0) 0) |
| [24] |
刘航, 王跃, 刘永慧, 等. 基于定量设计虚拟阻抗的VSG低电压穿越策略[J]. 高电压技术, 2022, 48(1): 245-256. LIU Hang, WANG Yue, LIU Yonghui, et al. The LVRT strategy for VSG based on the quantitatively designed virtual impedance[J]. High Voltage Engineering, 2022, 48(1): 245-256. (  0) 0) |
| [25] |
李清辉, 葛平娟, 肖凡, 等. 基于功角与电流灵活调控的VSG故障穿越方法研究[J]. 中国电机工程学报, 2020, 40(7): 2071-2080, 2387. LI Qinghui, GE Pingjuan, XIAO Fan, et al. Study on fault ride-through method of VSG based on power angle and current flexible regulation[J]. Proceedings of the CSEE, 2020, 40(7): 2071-2080, 2387. (  0) 0) |
| [26] |
郑涛, 王子鸣, 邹芃蓥. 基于相位跳变补偿的虚拟同步发电机低电压穿越控制策略研究[J]. 电网技术, 2023, 47(1): 100-109. ZHENG Tao, WANG Ziming, ZOU Pengying. Research on low voltage ride-through control strategy of virtual synchronous generator based on phase jump compensation[J]. Power System Technology, 2023, 47(1): 100-109. (  0) 0) |
| [27] |
张国荣, 沈聪, 彭勃, 等. 馈线故障下柔性多状态开关的平滑切换策略[J]. 高电压技术, 2019, 45(10): 3050-3058. ZHANG Guorong, SHEN Cong, PENG Bo, et al. Smooth switching strategy of flexible multi-state switchin the case of feeder fault[J]. High Voltage Engineering, 2019, 45(10): 3050-3058. (  0) 0) |
| [28] |
OUREILIDIS K O, DEMOULIAS C S. A fault clearing method in converter-dominated microgrids with conventional protection means[J]. IEEE Transactions on Power Electronics, 2016, 31(6): 4628-4640. (  0) 0) |
| [29] |
杨银国, 戴耀辉, 陆秋瑜, 等. 虚拟同步发电机暂态全局稳定分析与阻尼调制方法[J]. 高电压技术, 2023, 49(6): 2505-2515. YANG Yinguo, DAI Yaohui, LU Qiuyu, et al. Transient global stability analysis and damping tuning method of virtual synchronous generator[J]. High Voltage Engineering, 2023, 49(6): 2505-2515. (  0) 0) |
| [30] |
沈可心, 薛博文, 朱晓荣. 直流微网中直驱风机的类虚拟同步发电机惯性控制策略[J]. 高电压技术, 2023, 49(6): 2526-2535. SHEN Kexin, XUE Bowen, ZHU Xiaorong. Inertia control strategy of direct-driven wind generation system in DC microgrid based on analogous virtual synchronous generator[J]. High Voltage Engineering, 2023, 49(6): 2526-2535. (  0) 0) |
| [31] |
LIU M Y, PAN W X, RAO Y F, et al. An electromagnetic transient analysis model for DFIG considering LVRT hardware protection[J]. IEEE Access, 1809, 9: 32591-32598. (  0) 0) |
 2024, Vol. 43
2024, Vol. 43


 陈智勇(1998),男,硕士在读,研究方向为新能源并网的运行与控制(E-mai:
陈智勇(1998),男,硕士在读,研究方向为新能源并网的运行与控制(E-mai: