文章编号: 2096-3203(2024)03-0063-08 中图分类号: TM71
2. 智能电网保护和运行控制国家重点实验室,江苏 南京 211106;
3. 国网北京市电力公司,北京 100031
为满足能源需求持续快速增长和能源体系绿色低碳转型,经过近十年的快速发展,我国在新能源发电技术方面取得了突破并实现规模化应用[1]。然而,新能源电源与常规电源的出力特性不同,各时间尺度均存在不确定性,其大规模并网给电网调度运行和计划安排带来了巨大的挑战[2-5]。
受制于气候、天气等不确定性因素,现有新能源功率预测技术通常无法精确预测新能源场站输出功率,其预测结果必然存在一定误差,即新能源功率预测给出的是一定置信概率下的预测误差带[6-9]。各级电力调度控制中心现有调度计划安全稳定校核功能通常未考虑新能源功率预测的不确定性,仍采用发生概率最高的新能源预测功率曲线进行确定性安全稳定校核[10-12],导致调度计划安全稳定校核结论与电网实际情况相差较大,无法有效指导实际电网调度运行。因此,如何在调度计划安全稳定校核中计及新能源功率预测的不确定性,提高校核结果的准确性,是调度计划安全稳定校核亟待解决的问题。
对于考虑新能源功率预测不确定性的调度计划安全稳定校核方法,现有研究主要包括概率潮流法[13-15]、场景分析法[16-19]和区间潮流法[20-21]。概率潮流法采用随机变量来描述不确定性变量,运用蒙特卡洛仿真、半不变量法等概率分析方法得到潮流结果的概率性分布情况,计算量较大且仅能够获取状态变量的概率分布,难以适应静态、暂态、动态安全稳定校核等应用场景。场景分析法采用抽样组合方法生成一系列可能出现的确定性运行场景来表征不确定性变量,存在场景组合数过多导致计算效率下降的问题。虽然可以通过场景聚类和缩减技术降低计算量,但是聚类中心选择不合理时可能存在风险泄露情况。区间潮流法根据一定置信水平确定不确定性变量的取值范围,在此基础上生成相应的最大/最小运行方式进行安全校核,可极大缩减需要安全校核的运行方式数量,但最大/最小运行方式并不一定是安全稳定裕度最小的高风险运行状态,无法据此准确判断调度计划能否执行,存在计算结论可能过于保守的问题。因此,亟须提出准确可靠的考虑新能源不确定性的调度计划安全稳定校核方法,以满足在线应用对计算速度和准确性的要求。
针对现有技术的不足,文中提出一种考虑新能源不确定性的调度计划安全稳定校核方法,采用置信区间描述新能源有功出力的波动范围,通过求解计及新能源功率预测不确定性约束的安全稳定裕度最小化模型,快速识别出可能导致调度计划安排无法正常执行的高风险计划方式集,基于高风险计划方式集对考核故障集进行安全稳定量化评估,得到考虑新能源不确定性的调度计划安全稳定校核结果。
1 基本原理调度计划安全稳定校核的主要目的是确定调度计划安排是否存在不满足电网安全稳定要求的高风险时段及高风险时段的分布情况。基于新能源场站功率预测置信区间及其对电网安全稳定性影响因子,可以生成大量用于描述新能源功率预测不确定性的待校核计划方式。其中,大部分待校核计划方式并不是导致调度计划安排难以执行的高风险计划方式,反而容易出现大量计算资源浪费和关键信息湮没的问题。因此,考虑新能源不确定性的调度计划安全稳定校核的关键在于如何高效、准确地识别出可能导致调度计划安排无法正常执行的高风险计划方式,有效降低高风险计划方式识别过程中风险泄露的概率,并实现高风险计划方式集的快速校核。
1.1 高风险计划方式识别由于电网安全稳定特性与电网运行状态紧密相关,电网设备投退状态和节点功率注入决定了电网的运行状态[22]。基于确定性计划数据和发生概率最高的新能源功率预测数据,可以生成确定性的参考计划方式。考虑新能源不确定性的待校核计划方式与确定性的参考计划方式的区别在于新能源场站预测功率不同。当待校核计划方式和参考计划方式的差异程度不大时,已知参考计划方式安全稳定校核结果的情况下,可根据2个计划方式的变化程度及相关安全稳定影响因子,估算出待校核计划方式的安全稳定裕度指标,计算公式如下:
| $ \eta_{t . s}=\min\limits_{c \in C, k \in K} f\left(H_{t . c . k .0}, \hat{\boldsymbol{S}}_{t . c. k .0}, \hat{\boldsymbol{P}}_t, \hat{\boldsymbol{P}}_{t .0}\right) $ | (1) |
式中:ηt.s为计划时段t待校核计划方式的安全稳定裕度指标;C为考核故障集;K为监视元件或稳定模式集;f(·)为安全稳定裕度指标估算公式(不同安全稳定问题采用不同估算公式);Ht.c.k.0为计划时段t对应参考计划方式下考核故障c的监视元件或稳定模式k的安全稳定裕度指标;Ŝt.c.k.0为计划时段t对应参考计划方式下考核故障c的新能源场站有功功率对监视元件或稳定模式k的安全稳定裕度影响因子向量;$\hat{\boldsymbol{P}}_t$为计划时段t待校核计划方式下新能源场站有功功率向量;$\hat{\boldsymbol{P}}_{t.0}$为计划时段t对应参考计划方式下新能源场站有功功率向量。
待校核计划方式的安全稳定裕度指标越小,表明待校核计划方式安全稳定违约程度越严重。因此,各个计划时段的高风险计划方式识别问题变成求解对应计划时段下一系列安全稳定裕度最小化问题,这些问题可以表达为:
| $ \left\{\begin{array}{l} \min f \\ \text { s.t. } P_{t.\text {min }} \leqslant P_t \leqslant P_{t . \max } \end{array}\right. $ | (2) |
式中:Pt为计划时段t新能源场站的预测功率;Pt.max、Pt.min分别为计划时段t新能源场站的功率预测置信区间上限和下限。
考虑到调度计划安全稳定校核的主要目的是确定调度计划能否正常执行,通常不直接涉及调度计划编排,因此文中所提裕度最小化模型仅考虑新能源不确定性约束。求解式(2)得到与安全稳定裕度最小值对应的待校核计划方式,即为可能导致计划时段t的调度计划无法正常执行的高风险计划方式。不同计划时段的高风险计划方式总和构成了考虑新能源不确定性的调度计划安全稳定校核的高风险计划方式集。
1.2 风险泄露降低策略当待校核计划方式和参考计划方式的差异程度较大时,待校核计划方式与参考计划方式的安全稳定模式可能会发生变化,根据式(1)和式(2)筛选高风险计划方式集可能出现风险泄露的情况。为了有效降低调度计划安全稳定校核过程中出现的风险泄露概率,文中提出如下改进策略:(1) 在安全稳定裕度最小化模型中引入反映新能源场站有功功率变化对安全稳定裕度指标的影响参数,并根据相似原理从历史数据中选取参与详细计算的考核故障的安全稳定裕度指标对影响参数进行优化,提高安全稳定裕度最小化模型的准确性;(2) 将安全稳定裕度较小的考核故障或监视元件纳入需要参与安全稳定裕度最小化模型求解的计算队列,通过适当扩大考核故障集或监视元件集的方式降低风险泄露的概率。
1.3 高风险计划方式校核由于调度计划安全稳定校核需要校核未来一段时间内多个时段的计划方式,即使每个时段仅考虑一个高风险计划方式,其计算量仍然非常庞大。因此,如何提高考虑新能源不确定性的调度计划安全稳定校核的计算效率显得尤为重要。另外,由于电力系统安全稳定问题的复杂性和非线性,高风险计划方式识别过程中基于安全稳定裕度最小模型得到的安全稳定裕度估算值与实际值可能存在一定偏差,临界情况下甚至存在颠覆性的定性结论。因此,对于安全稳定裕度估算值远离临界值的高风险时段,可直接采用高风险计划方式识别过程中得到的估算结果作为其安全稳定校核结果,以提高调度计划安全稳定校核的计算效率。对于临界安全的高风险时段,在得到对应新能源有功计划的基础上,结合其他确定性计划数据,采用文献[23]的方法整合生成高风险计划方式数据,利用并行计算平台的集群计算能力形成调度队列,采用文献[24]的方法进行多方式分组并行安全校核,得到临界安全的高风险时段的安全稳定校核结果,以提高安全稳定校核结论的可靠性和准确性。
2 裕度最小化模型针对不同安全稳定问题可以构建不同安全稳定裕度最小化模型,文中以过载安全稳定为例进一步阐述安全稳定裕度最小化模型构建及求解过程。基于安全稳定量化分析可以获得参考计划方式下各个考核故障的过载裕度、过载安全薄弱支路及新能源场站有功功率对过载安全薄弱支路有功功率的灵敏度等安全稳定量化指标。考虑到实际系统中新能源功率预测误差区间一般不大,待校核计划方式与参考计划方式的过载安全薄弱支路及有功灵敏度基本一致。因此,可基于参考计划方式安全稳定量化指标,构建待校核计划方式计及新能源功率预测置信区间约束的安全稳定裕度最小化模型。
2.1 目标函数文中设定的安全稳定裕度最小化模型的目标函数如下:
| $ \min \left(\eta_{t . c . l .0}-\frac{\alpha}{P_{\mathrm{lmt} . l}} \sum\limits_{i=1}^N s_{t . c . l . i .0}\left(P_{t . i}-P_{t . i .0}\right)\right) $ | (3) |
式中:ηt.c.l.0为计划时段t对应参考计划方式下考核故障c的过载安全薄弱支路l的过载安全裕度;α为反映新能源场站有功功率变化对过载安全裕度的影响参数;Plmt.l为过载安全薄弱支路l的有功功率限值;N为新能源场站数;st.c.l.i.0为计划时段t对应参考计划方式下考核故障c的新能源场站i有功功率对过载安全薄弱支路l有功功率的灵敏度;Pt.i为计划时段t对应待校核计划方式下新能源场站i的有功功率;Pt.i.0为计划时段t对应参考计划方式下的新能源场站i的有功功率。
2.2 约束条件文中设定的安全稳定裕度最小化模型的约束条件为各个新能源场站有功出力不超过其置信区间上下限,如式(4)所示。
| $ P_{t, i \min } \leqslant P_{t, i} \leqslant P_{t, i \max } $ | (4) |
式中:Pt.i.max、Pt.i.min分别为计划时段t新能源场站i有功功率预测置信区间的上限和下限。
2.3 求解方法考虑到有功灵敏度较小的新能源场站对考核故障的设备过载安全性影响不大,因此可以忽略部分有功灵敏度较小的新能源场站的不确定性,并将有功灵敏度相近的新能源场站合并,有效减少不确定性变量维数,提高安全稳定裕度最小化模型的求解效率。按照式(5)对新能源场站的有功灵敏度进行标幺,可得到各个新能源场站的有功灵敏度标幺值。
| $ s_{t . c . l . i .0}^{\prime}=\frac{s_{t . c . l . i .0}}{\max \left(\left|s_{t . c . l . i .0}\right|, l \in L\right)} $ | (5) |
式中:st.c.l.i.0′为计划时段t对应参考计划方式下考核故障c的新能源场站i有功功率对过载安全薄弱支路l的有功功率灵敏度的标幺值;L为过载安全薄弱支路数。
基于标幺后的新能源场站有功灵敏度,将有功灵敏度绝对值小于指定门槛值的新能源场站剔除,可得到各个考核故障的关联新能源场站集G。按照有功灵敏度对关联新能源场站集从大到小进行排序,将满足式(6)的新能源场站合并,可得到聚合后的关联等值新能源场站集G′。
| $ \left|s_{t.c. l. i .0}^{\prime}-s_{t . c. l. j .0}^{\prime}\right|<\varepsilon \quad i, j \in G^{\prime} $ | (6) |
式中:st.c.l.j.0′为计划时段t对应参考计划方式下考核故障c的新能源场站j的有功功率对过载安全薄弱支路l的有功功率灵敏度标幺值;ε为有功灵敏度分档间距,ε>0。
对于安全稳定裕度最小化模型中的影响参数α,可采用后评估方式进行优化,公式如下:
| $ \left\{\begin{array}{l} \min \sum\limits_{c=1}^{C^{\prime}} \sum\limits_{l=1}^{L}\left(1-\eta_{t . c . l}\right)\left(\eta_{t . c . l}^{\prime}-\eta_{t . c . l}\right)^{2}\\ \text { s.t. } \alpha>0 \end{array}\right. $ | (7) |
式中:C′为高风险计划方式下参与详细计算的考核故障个数;ηt.c.l为计划时段t对应高风险计划方式下考核故障c的过载安全薄弱支路l的安全稳定裕度指标计算值;ηt.c.l′为根据式(3)得到的计划时段t对应高风险计划方式下考核故障c的过载安全薄弱支路l的安全稳定裕度指标估算值。
对于等值新能源场站的有功灵敏度,可取其关联新能源场站有功灵敏度的平均值。对于等值新能源场站预测功率置信区间,可基于电网海量历史采样数据,通过统计分析新能源场站功率预测误差的概率分布关系得到。求解安全稳定裕度最小化模型得到每个考核故障的所有过载安全薄弱支路的过载安全裕度及其对应等值新能源场站有功出力,再按照新能源场站可调空间将等值新能源场站有功出力分解到对应新能源场站。
对考核故障集的所有过载安全薄弱支路均求解安全稳定裕度最小化模型,其计算量非常大。为进一步提高计算效率,将考核故障集的所有过载安全薄弱支路的安全稳定裕度最小化模型的计算任务提交到计算集群,采用分组并行方法进行计算,得到考核故障集中所有过载安全薄弱支路的过载安全裕度及其对应新能源场站有功出力,再从中选取过载安全裕度最小值对应的新能源场站有功出力作为对应高风险计划方式的新能源有功计划。
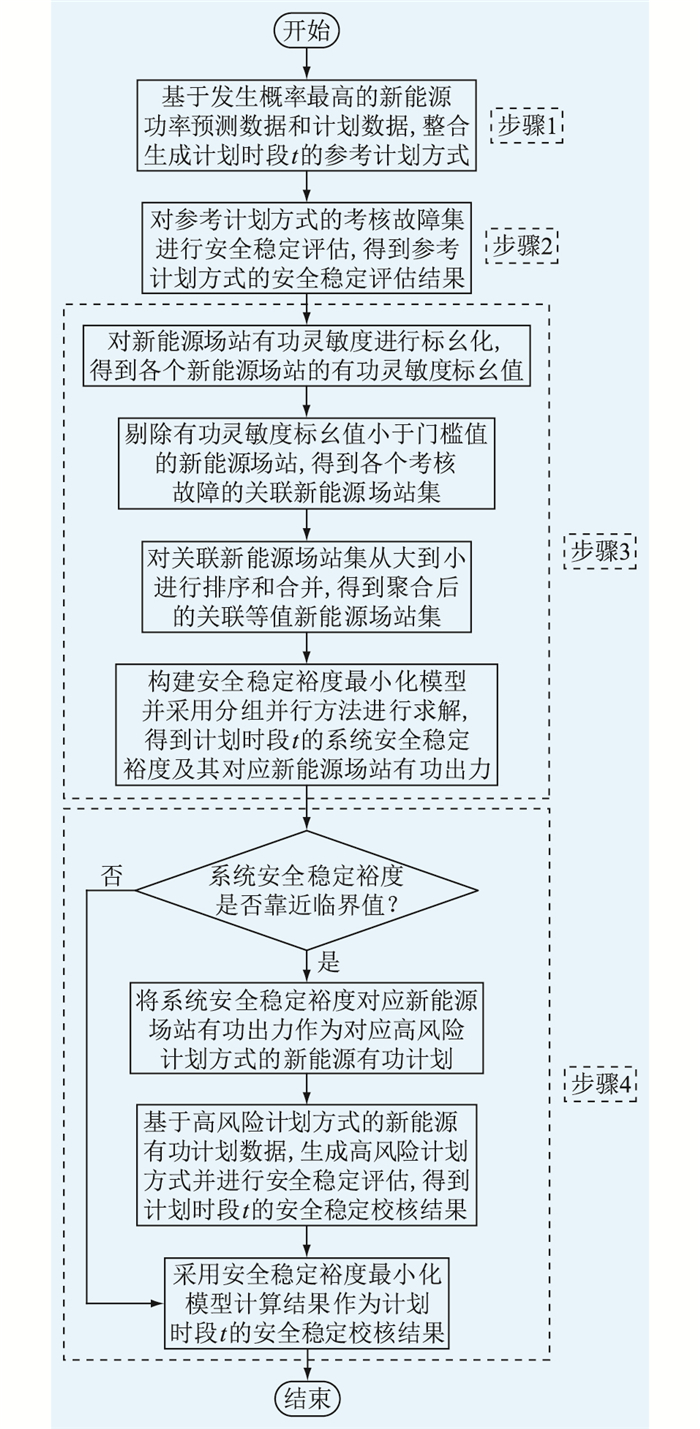
3 安全校核流程设计多个计划时段的调度计划安全稳定校核可采用多方式分组并行模式进行计算,单个计划时段的调度计划安全稳定校核流程如图 1所示,具体步骤如下。
|
图 1 安全校核流程示意 Fig. 1 Schematic diagram of safety verification process |
步骤1:基于发生概率最高的新能源功率预测数据,结合常规机组发电计划、负荷预测、联络线计划和停复役计划,生成确定性的参考计划方式。
步骤2:基于参考计划方式对考核故障集进行安全稳定量化评估,得到参考计划方式的安全稳定量化评估结果。
步骤3:基于参考计划方式的安全稳定量化指标,构建计及新能源功率预测不确定性约束的安全稳定裕度最小化模型,求解得到该计划时段的系统安全稳定裕度及其对应新能源有功出力。
步骤4:对于临界安全的计划时段,基于裕度最小化模型计算结果对应新能源有功出力生成待校核高风险计划方式并进行安全稳定评估,得到该时段的调度计划安全稳定校核结果;对于安全的计划时段,直接采用裕度最小化模型计算结果作为该时段的调度计划安全稳定校核结果。
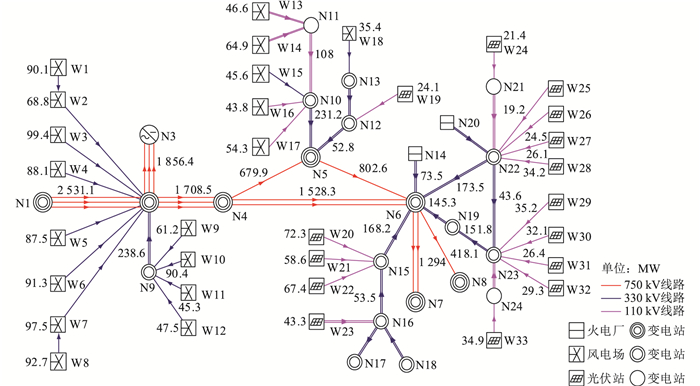
4 应用实例文中提出的调度计划安全稳定校核方法已在某高比例新能源区域电网日前计划安全稳定校核系统中得到应用。以2022年某日数据为例,该区域电网的局部网络示意如图 2所示,W1—W18为风电场,W19—W33为光伏站;N1—N24中N3为换流站,N14和N20为火电厂,其余为变电站。图中有功潮流分布为该日10:30根据常规机组发电计划、负荷预测、联络线计划和停复役计划整合生成的参考计划方式运行状态,新能源发电占比约为24%。
|
图 2 某区域电网局部网络示意 Fig. 2 Schematic diagram of local network of a regional power grid |
基于新能源有功预测、常规机组发电计划、负荷预测、联络线计划和停复役计划整合生成确定性的96点日前参考计划方式。日前计划安全校核的考核故障集共有331个预想故障,设备过载安全监视元件集共有735条支路。基于96点日前参考计划方式对考核故障进行设备过载安全评估,设备过载安全裕度最小的故障为N4—N6双线N-2故障,该预想故障下部分计划时段的设备过载安全薄弱支路如表 1所示。
|
|
表 1 设备过载安全薄弱支路 Table 1 Equipment overload and weak safety equipment |
设新能源场站有功灵敏度标幺值分档间距为0.01,基于参考计划方式有功灵敏度和历史数据对新能源场站进行场站聚合和概率统计,可得等值新能源场站聚合结果,如表 2所示。
|
|
表 2 有功灵敏度计算结果 Table 2 Calculation results of active power sensitivity |
根据式(3)、式(4)构建设备过载安全薄弱支路的裕度最小化模型并求解,可得N4—N6双线N-2故障下设备过载安全薄弱支路裕度最小估算值及其对应新能源有功计划,分别如表 3和表 4所示。
|
|
表 3 过载安全裕度估算结果 Table 3 Estimation results of overload safety margin |
|
|
表 4 10:30裕度最小值对应新能源有功计划 Table 4 Minimum margin of 10:30 corresponds to new energy active power plan |
对于裕度最小值远离临界值的断面时刻(如表 3中的13:30和22:30),直接采用估算结果作为其安全稳定校核结果。对于裕度最小估算值靠近临界值的计划时段(如表 3中的10:30),基于表 4所示新能源有功计划,结合常规机组发电计划、负荷预测、联络线计划和停复役计划,整合生成高风险计划方式,采用并行计算集群对临界状态计划方式进行安全校核,计算结果如表 5所示。
|
|
表 5 高风险计划方式校核结果 Table 5 Verification results of high-risk planning methods |
以断面时刻10:30为例,相同计算参数条件下,通过调整新能源装机容量和新能源有功预测模拟新能源发电占比变化,计算得到不同新能源发电占比情况下高风险计划方式校核结果,如表 6所示。
|
|
表 6 不同新能源发电占比下高风险计划方式校核结果 Table 6 Verification results of high-risk planning methods under different new energy generation ratios |
由表 6可知,新能源发电占比越大,系统不确定性越大,系统安全稳定裕度变化越大。
4.3 风险泄露分析采用基于蒙特卡洛仿真的概率潮流法进行安全稳定校核,如果样本数量足够大,其计算结果足够精确,可以认为其不存在风险泄露情况。因此,以断面时刻10:30为例,对场景分析法和文中方法进行比对分析。假设新能源场站等值聚合和置信区间与文中方法保持一致,采用场景分析法对等值新能源场站进行抽样组合,可得到13 284个场景,不同聚类数目下的设备过载安全评估结果如表 7所示。
|
|
表 7 场景分析法校核结果 Table 7 Scene method verification results |
由表 7可知,聚类数目变化较大时,场景分析法得到的设备过载安全裕度偏差值较大。当聚类数目较少时,极端情况下可能存在风险泄露的情况,而文中所提方法不存在该问题。
4.4 计算性能分析并行计算集群共配置40台服务器,每台服务器有4个CPU、16个核,主频2.27 GHz、L2缓存1 M,测试程序采用Fortran和C/C++语言编写。
考虑方式并行计算能力为4个,任务并行计算能力为640,单方式单故障过载安全裕度最小化模型求解耗时约为0.2 s,单方式单故障设备过载安全评估详细计算耗时约为0.8 s,临界安全的高风险计划方式占比约为10%,则针对日前计划96点计划时段、331个预想故障,通过24轮迭代可完成设备过载安全裕度最小模型计算,通过3轮迭代可完成详细设备过载安全评估,进一步考虑数据交互等耗时,文中所提方法耗时约为10 min。
相同计算资源条件下,采用基于蒙特卡洛仿真的概率潮流法对相同计划数据进行安全稳定校核,由于蒙特卡洛模拟法的计算量(即抽样次数)与抽样精度的平方呈反比,一般情况下取5 000~10 000才能保证模拟的有效性,假设抽样次数为5 000,单方式单故障设备过载安全评估详细计算耗时约为0.8 s,则针对日前计划96点计划时段、331个预想故障,通过120 000轮迭代才能完成设备过载安全评估,进一步考虑数据交互等耗时,概率潮流法耗时约为56 h。采用场景分析法对相同计划数据进行安全稳定校核,假设场景聚类数目小于等于20,单方式单故障设备过载安全评估详细计算耗时约为0.8 s,则针对日前计划96点计划时段、331个预想故障,通过480轮迭代可完成设备过载安全评估,进一步考虑场景聚类、数据交互等耗时,场景分析法耗时约为30 min。由此可知,文中所提方法在计算性能上有较大优势,可满足在线应用要求。
5 结论文中针对传统确定性计划校核难以应对新能源预测不确定性的问题,提出一种考虑新能源不确定性的调度计划安全稳定校核方法,将不确定性计划校核问题转化为计及新能源预测置信区间约束的安全稳定裕度最小化模型求解问题,以某高比例新能源电网为例,验证了所提方法的准确性和时效性。主要结论如下:
(1) 通过求解计及新能源功率预测不确定性约束的安全稳定裕度最小化模型,快速识别出可能导致调度计划安排无法正常执行的高风险计划方式集,极大缩减了需要安全校核的计划方式,并有效降低风险泄露的概率;
(2) 通过新能源场站聚合有效减少不确定性变量维数,并采用集群并行计算技术进行安全稳定裕度最小化模型求解和高风险计划方式安全稳定校核,进一步提高安全稳定校核的计算速度,可以满足在线应用要求。
后续需要进一步考虑调度计划安全稳定校核与调度计划编排的互动,提高调度计划安全稳定校核功能的实用性。
| [1] |
陈国平, 董昱, 梁志峰. 能源转型中的中国特色新能源高质量发展分析与思考[J]. 中国电机工程学报, 2020, 40(17): 5493-5506. CHEN Guoping, DONG Yu, LIANG Zhifeng. Analysis and reflection on high-quality development of new energy with Chinese characteristics in energy transition[J]. Proceedings of the CSEE, 2020, 40(17): 5493-5506. (  0) 0) |
| [2] |
徐潇源, 王晗, 严正, 等. 能源转型背景下电力系统不确定性及应对方法综述[J]. 电力系统自动化, 2021, 45(16): 2-13. XU Xiaoyuan, WANG Han, YAN Zheng, et al. Overview of power system uncertainty and its solutions under energy transition[J]. Automation of Electric Power Systems, 2021, 45(16): 2-13. (  0) 0) |
| [3] |
王丹, 杨俊涛, 曾燕, 等. 考虑源荷不确定性的配电网风光储综合规划[J]. 电力需求侧管理, 2023, 25(5): 65-72. WANG Dan, YANG Juntao, ZENG Yan, et al. Comprehensive planning of wind-PV-storage in distribution network considering uncertainty of source and load[J]. Power Demand Side Management, 2023, 25(5): 65-72. DOI:10.3969/j.issn.1009-1831.2023.05.011 (  0) 0) |
| [4] |
HONG P Z, QIN Z J. Distributed active power optimal dispatching of wind farm cluster considering wind power uncertainty[J]. Energies, 2022, 15(7): 1-16. (  0) 0) |
| [5] |
侯慧, 王晴, 薛梦雅, 等. 计及源荷不确定性及需求响应的离网型微电网两阶段日前经济调度[J]. 电力系统保护与控制, 2022, 50(13): 74-85. HOU Hui, WANG Qing, XUE Mengya, et al. Two-stage economic day-ahead dispatch of an islanded microgrid considering uncertainty and demand response[J]. Power System Protection and Control, 2022, 50(13): 74-85. (  0) 0) |
| [6] |
王伟胜, 王铮, 董存, 等. 中国短期风电功率预测技术现状与误差分析[J]. 电力系统自动化, 2021, 45(1): 17-27. WANG Weisheng, WANG Zheng, DONG Cun, et al. Status and error analysis of short-term forecasting technology of wind power in China[J]. Automation of Electric Power Systems, 2021, 45(1): 17-27. (  0) 0) |
| [7] |
赵永宁, 李卓, 叶林, 等. 基于时空相关性的风电功率超短期自适应预测方法[J]. 电力系统保护与控制, 2023, 51(6): 94-105. ZHAO Yongning, LI Zhuo, YE Lin, et al. A very short-term adaptive wind power forecasting method based on spatio-temporal correlation[J]. Power System Protection and Control, 2023, 51(6): 94-105. (  0) 0) |
| [8] |
XING Z X, QU B Y, LIU Y, et al. Comparative study of reformed neural network based short-term wind power forecasting models[J]. IET Renewable Power Generation, 2022, 16(5): 885-899. DOI:10.1049/rpg2.12384 (  0) 0) |
| [9] |
TAWN R, BROWELL J. A review of very short-term wind and solar power forecasting[J]. Renewable and Sustainable Energy Reviews, 2022, 153: 111758. DOI:10.1016/j.rser.2021.111758 (  0) 0) |
| [10] |
吴迪, 王正风, 刘航. 全时间维度调度计划安全校核的设计与应用[J]. 中国电力, 2020, 53(5): 48-55. WU Di, WANG Zhengfeng, LIU Hang. Design and application of full-time dimension dispatching schedule safety check[J]. Electric Power, 2020, 53(5): 48-55. DOI:10.3969/j.issn.1007-3361.2020.05.031 (  0) 0) |
| [11] |
路轶, 蔡帜, 张国芳, 等. 适应电力现货市场运营的省级电网安全校核实现方案[J]. 电力系统自动化, 2021, 45(16): 216-223. LU Yi, CAI Zhi, ZHANG Guofang, et al. Implementation scheme of security check in provincial power grid suitable for operation of electricity spot market[J]. Automation of Electric Power Systems, 2021, 45(16): 216-223. (  0) 0) |
| [12] |
常俊晓, 卢姬, 叶仁杰, 等. 基于概率潮流的主动配电网静态安全校核方法[J]. 浙江电力, 2020, 39(7): 36-41. CHANG Junxiao, LU Ji, YE Renjie, et al. Static security verification method of active distribution network based on probabilistic load flow[J]. Zhejiang Electric Power, 2020, 39(7): 36-41. (  0) 0) |
| [13] |
曹瑞琳, 邢洁, 李征. 基于改进级数展开的含风电电力系统概率潮流计算方法[J]. 电网技术, 2022, 46(9): 3447-3454. CAO Ruilin, XING Jie, LI Zheng. Improved series expansion based probabilistic load flow calculation for power system with wind power[J]. Power System Technology, 2022, 46(9): 3447-3454. (  0) 0) |
| [14] |
WANG D W, ZHENG K D, CHEN Q X, et al. A data-driven probabilistic power flow method based on convolutional neural networks[J]. International Transactions on Electrical Energy Systems, 2020, 30(7): 1-20. (  0) 0) |
| [15] |
程杉, 傅桐, 李沣洋, 等. 含高渗透可再生能源的配电网灵活性供需协同规划[J]. 电力系统保护与控制, 2023, 51(22): 1-12. CHENG Shan, FU Tong, LI Fengyang, et al. Flexible supply demand collaborative planning for distribution networks with high penetration of renewable energy[J]. Power System Protection and Control, 2023, 51(22): 1-12. (  0) 0) |
| [16] |
杨晶显, 刘俊勇, 韩晓言, 等. 基于深度嵌入聚类的水光荷不确定性源场景生成方法[J]. 中国电机工程学报, 2020, 40(22): 7296-7306. YANG Jingxian, LIU Junyong, HAN Xiaoyan, et al. An uncertain hydro/PV/load typical scenarios generation method based on deep embedding for clustering[J]. Proceedings of the CSEE, 2020, 40(22): 7296-7306. (  0) 0) |
| [17] |
LIU Y N, GUAN X, LI J, et al. Evaluating smart grid renewable energy accommodation capability with uncertain generation using deep reinforcement learning[J]. Future Generation Computer Systems, 2020, 110: 647-657. DOI:10.1016/j.future.2019.09.036 (  0) 0) |
| [18] |
唐锦, 张书怡, 吴秋伟, 等. 基于Copula函数与等概率逆变换的风电出力场景生成方法[J]. 电力工程技术, 2021, 40(6): 86-94. TANG Jin, ZHANG Shuyi, WU Qiuwei, et al. Wind power output scenario generation method based on Copula function and equal probability inverse transformation[J]. Electric Power Engineering Technology, 2021, 40(6): 86-94. DOI:10.12158/j.2096-3203.2021.06.011 (  0) 0) |
| [19] |
代江, 田年杰, 单克, 等. 基于极端场景分析的中长期交易校核方法[J]. 电力工程技术, 2021, 40(1): 65-71. DAI Jiang, TIAN Nianjie, SHAN Ke, et al. Long and medium-term power market security check based on extreme scenario analysis[J]. Electric Power Engineering Technology, 2021, 40(1): 65-71. DOI:10.12158/j.2096-3203.2021.01.009 (  0) 0) |
| [20] |
王晨旭, 唐飞, 刘涤尘, 等. 基于双层代理模型的概率-区间潮流计算及灵敏度分析[J]. 电工技术学报, 2022, 37(5): 1181-1193. WANG Chenxu, TANG Fei, LIU Dichen, et al. Probabilistic-interval power flow and sensitivity analysis using double layer surrogate method[J]. Transactions of China Electrotechnical Society, 2022, 37(5): 1181-1193. (  0) 0) |
| [21] |
鲍海波, 郭小璇. 求解含风电相关性区间潮流的仿射变换最优场景法[J]. 电力系统保护与控制, 2020, 48(18): 114-122. BAO Haibo, GUO Xiaoxuan. Optimal scenario algorithm based on affine transformation applied to interval power flow considering correlated wind power[J]. Power System Protection and Control, 2020, 48(18): 114-122. (  0) 0) |
| [22] |
吴亚宁, 罗毅, 周生存, 等. 计及源-荷功率波动性的静态电压稳定故障快速筛选和排序方法[J]. 中国电力, 2022, 55(11): 29-40. WU Yaning, LUO Yi, ZHOU Shengcun, et al. A fast static voltage stability contingency screening and ranking method considering source-load power fluctuation[J]. Electric Power, 2022, 55(11): 29-40. (  0) 0) |
| [23] |
周海锋, 徐伟, 鲍颜红, 等. 基于相似日选择的调度计划安全校核潮流数据生成[J]. 电力系统保护与控制, 2015, 43(18): 87-93. ZHOU Haifeng, XU Wei, BAO Yanhong, et al. Power flow data generation of security check for scheduling plans based on similar day selection[J]. Power System Protection and Control, 2015, 43(18): 87-93. (  0) 0) |
| [24] |
徐伟, 徐泰山, 胡昊明, 等. 适用于调度计划滚动更新的安全校核计算策略研究[J]. 陕西电力, 2017, 45(2): 10-14. XU Wei, XU Taishan, HU Haoming, et al. Security check calculation strategy for rolling update scheduling plan[J]. Shaanxi Electric Power, 2017, 45(2): 10-14. (  0) 0) |
2. State Key Laboratory of Smart Grid Protection and Control, Nanjing 211106, China;
3. State Grid Beijing Electric Power Company, Beijing 100031, China
 2024, Vol. 43
2024, Vol. 43


 周海锋(1983),男,硕士,高级工程师,从事电力系统运行分析与控制相关工作(E-mail:
周海锋(1983),男,硕士,高级工程师,从事电力系统运行分析与控制相关工作(E-mail: