文章编号: 2096-3203(2024)02-0055-10 中图分类号: TM732
随着全球能源危机和环境问题的日益凸显,能源系统面临着提质增效与节能减排的发展任务。园区作为区域经济发展的空间载体,往往配置有风光发电机组和多能耦合设备,具有电、热、气等多种用能需求,是能源生产、转换与消费的重要场所[1]。氢气在燃烧过程中绿色无污染,是助力能源系统清洁低碳发展的重要载体,电制氢(power to hydrogen, P2H)技术被视为促进多能耦合和新能源消纳的重要手段,在推动园区综合能源系统低碳经济运行以及内部可再生能源高效利用等方面具有重大潜力[2-5]。
近年来,我国发布了一系列涉及氢能的文件政策[6-8],旨在推动氢能在制、储、输、用等环节的全方位发展。将氢气混入天然气进行使用,可以减少天然气燃烧的碳排放量、降低输氢管道及燃料电池等设备的建设投资,加快氢能的推广应用。21世纪初欧洲就开始了天然气混氢的示范工程建设,掺氢比例多数分布在2%~50%之间[9]。2018年国家电投集团在辽宁朝阳启动了中国首项天然气混氢示范工程,将可再生能源制得的“绿氢”,按照10%体积百分比掺入天然气,供燃气锅炉及民用终端设备使用[10]。
另一方面,园区综合能源系统的电热气能源需求、风光清洁能源发电能力以及天然气价格存在季节性差异,氢储能相较于传统的电、热储能,自损耗较小,适合长时间存储,可以更好地应对日间乃至季节性的能源供需差异[11-13]。
目前, 国内外学者在含氢综合能源系统优化方面已开展了大量的理论研究,文献[14]提出电制取氢气后混入天然气的光伏消纳途径,并通过模型的搭建模拟了电-气网络的耦合交互机理。文献[15]考虑风光清洁能源的不确定性,以经济成本、风光消纳和能源供应等多因素最优为目标,建立含氢综合能源系统混合规划模型。文献[16]考虑风电和负荷的双重不确定性,以年化成本最小为目标,建立低碳能源系统优化配置模型,验证了风电制氢系统可降低系统总体运行成本,提高能源利用率。文献[17]考虑电制取氢气直接混入燃气管道供用气负荷使用,建立混氢综合能源系统的优化运行模型。文献[18]考虑天然气混氢使用,以经济成本最优为目标,提出园区综合能源系统氢储能优化配置模型。但上述文献大多从日内时间尺度考虑储氢的作用,未计及氢气的跨季节存储。
综合上述分析,文中将在天然气混氢使用的基础上,考虑氢气的跨季节存储,同时引入碳交易机制,以系统低碳经济运行为目标,提出P2H系统的容量规划模型。构建含氢综合能源系统的运行框架,建立天然气混氢、氢能跨季节存储以及能源耦合设备的数学模型。以设备的年化投资成本、园区的年度运行成本和碳交易成本最优为目标,结合典型日源荷数据,得出P2H及储氢装置的配置容量,为园区综合能源系统的规划运行提供参考。
1 含氢园区综合能源系统架构文中考虑的含氢园区综合能源系统架构如图 1所示。该园区将外购市电、天然气以及风光等自然资源作为能源输入,内部具有风机、光伏、热电联产(combined heat and power, CHP)机组、燃气锅炉和P2H装置实现能源的转换,同时蓄电池、蓄热罐和储氢罐可以对能源进行存储,实现供需的跨时段转移,最终满足负荷终端的用电及用热需求。
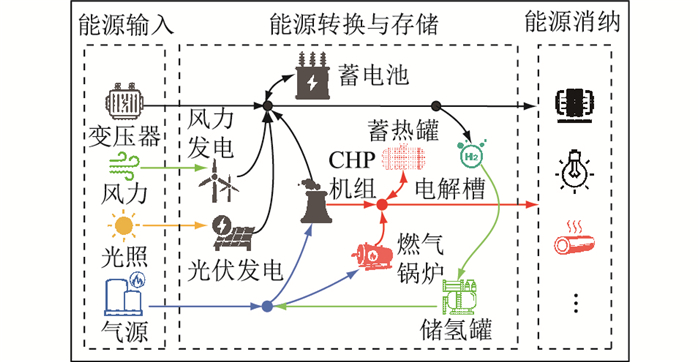
|
图 1 含氢园区综合能源系统架构 Fig. 1 Park integrated energy system architecture with hydrogen |
面向园区综合能源系统,文中以经济性和低碳性为目标,考虑天然气掺氢利用和氢气的跨季节存储,在原有风光发电、CHP机组等能源转换装置和蓄电池、蓄热罐等能源存储装置基础上,对P2H及储氢罐进行优化配置。其中,由于电力及热力存储存在自损耗问题,文中蓄电池和蓄热罐主要用于日内时间尺度能源供需平移,其运行约束满足日内能量充放平衡;储氢罐可用于跨季节时间尺度的能量转移,其运行约束满足年度能量充放平衡。
1.1 风光出力建模园区具有风力和光伏2种新能源发电机组,其出力约束满足:
| $ \left\{\begin{array}{l} 0 \leqslant P_{\mathrm{w}, i} \leqslant P_{\mathrm{wf}, i}\\ 0 \leqslant P_{\mathrm{p}, i} \leqslant P_{\mathrm{pf}, i} \end{array}\right. $ | (1) |
式中:Pw, i、Pp, i分别为i时刻风力发电和光伏发电的运行功率,MW;Pwf, i、Ppf, i分别为i时刻风电和光伏的典型日曲线出力值,MW。
1.2 耦合设备建模 1.2.1 CHP机组CHP机组通过消耗天然气输出电能和热能,是实现电-热-气耦合的重要能源转换设备,其数学模型可表示如下:
| $ G_{\text {chp }, i}=\frac{3\;600 P_{\text {chp }, i}}{\eta_{\text {chp }} H_{\mathrm{NG}}} $ | (2) |
| $ H_{\text {chp }, i}=c_{\mathrm{m}} P_{\text {chp }, i} $ | (3) |
| $ u_{\text {chp }, i} P_{\text {chp }, \text { min }} \leqslant P_{\text {chp }, i} \leqslant u_{\text {chp }, i} P_{\text {chp }, \text { max }} $ | (4) |
| $ -R_{\text {d, chp }} \leqslant P_{\text {chp }, i}-P_{\text {chp }, i-1} \leqslant R_{\mathrm{u}, \text { chp }} $ | (5) |
式中:Gchp, i为i时刻CHP机组的耗气速率,m3/h;Pchp, i、Hchp, i分别为i时刻CHP机组的电功率和热功率输出,MW;ηchp、cm分别为CHP机组的发电效率和热电比;HNG为天然气的热值,MJ/m3;Pchp, max、Pchp, min分别为CHP机组的发电功率上、下限,MW;Ru, chp、Rd, chp分别为CHP机组的向上、下爬坡速率,MW/h;uchp, i为表示CHP机组运行状态的0-1变量,取1时表示i时刻CHP机组处于运行状态,取0时表示i时刻CHP机组处于关停状态。
1.2.2 燃气锅炉燃气锅炉通过消耗天然气输出热能,其数学模型可表示如下:
| $ H_{\mathrm{gb}, i}=\frac{\eta_{\mathrm{gb}} G_{\mathrm{gb}, i} H_{\mathrm{NG}}}{3\;600} $ | (6) |
| $ u_{\mathrm{gb}, i} H_{\mathrm{gb}, \min } \leqslant H_{\mathrm{gb}, i} \leqslant u_{\mathrm{gb}, i} H_{\mathrm{gb}, \max } $ | (7) |
| $ -R_{\mathrm{d}, \mathrm{gb}} \leqslant H_{\mathrm{gb}, i}-H_{\mathrm{gb}, i-1} \leqslant R_{\mathrm{u}, \mathrm{gb}} $ | (8) |
式中:Hgb, i为燃气锅炉在i时刻的产热功率,MW;ηgb为燃气锅炉的产热效率;Ggb, i为i时刻燃气锅炉的耗气速率,m3/h;Hgb, max、Hgb, min分别为燃气锅炉的产热功率上、下限,MW;Ru, gb、Rd, gb分别为燃气锅炉的向上、向下爬坡速率,MW/h;ugb, i为表示燃气锅炉运行状态的一组0-1变量,取1时表示i时刻燃气锅炉处于运行状态,取0时表示i时刻燃气锅炉处于关停状态。
1.2.3 P2HP2H,即电解槽通电后水电解产生氢气和氧气。根据电解质的不同,可将电解槽分为碱性电解槽、质子交换膜电解槽和固体氧化物电解槽,其中碱性电解槽的技术成熟度最高,已广泛商业化,能量转换率可达60%,单位投资成本约2 000~10 000元/kW, 其数学模型可表示为:
| $ P_{\mathrm{H}_{2}, i}=\eta_{\mathrm{p} 2 \mathrm{h}} P_{\mathrm{p} 2 \mathrm{h}, i} $ | (9) |
| $ F_{\mathrm{H}_{2}, i}=\frac{P_{\mathrm{H}_{2}, i}}{3\;600 H_{\mathrm{H}_{2}}} $ | (10) |
| $ 0 \leqslant P_{\mathrm{p} 2 \mathrm{h}, i} \leqslant P_{\mathrm{p} 2 \mathrm{h}, \max } $ | (11) |
式中:PH2, i、Pp2h, i分别为i时刻电解槽的氢能输入和电能输出功率,MW;ηp2h为电解槽的制氢效率;FH2, i为i时刻电解槽的产气速率,m3/h;HH2为氢气的热值,MJ/m3;Pp2h, max为电解槽的输入功率上限,MW。
1.3 储能设备建模 1.3.1 蓄电池蓄电池通过电能的充放平抑新能源出力波动。目前蓄电池的投资成本较高,且通过蓄电池进行电能的长期存储会发生自放电损耗,文中考虑其用于日内电力供需调节,其数学模型可表示为:
| $ E_{\mathrm{bt}, i}= E_{\mathrm{bt}, i-1}+\eta_{\mathrm{bt}, \mathrm{c}} P_{\mathrm{bt}, \mathrm{c}, i}-P_{\mathrm{bt}, \mathrm{d}, i} / \eta_{\mathrm{bt}, \mathrm{d}} $ | (12) |
| $ E_{\mathrm{bt}, 0}=E_{\mathrm{bt}, 24} $ | (13) |
| $ E_{\mathrm{bt}, \min } \leqslant E_{\mathrm{bt}, i} \leqslant E_{\mathrm{bt}, \max } $ | (14) |
| $ \left\{\begin{array}{l} 0 \leqslant P_{\mathrm{bt}, \mathrm{c}, i} \leqslant I_{\mathrm{bt}, \mathrm{c}, i} P_{\mathrm{bt}, \max } \\ 0 \leqslant P_{\mathrm{bt}, \mathrm{d}, i} \leqslant I_{\mathrm{bt}, \mathrm{d}, i} P_{\mathrm{bt}, \max } \end{array}\right. $ | (15) |
| $ 0 \leqslant I_{\mathrm{bt}, \mathrm{c}, i}+I_{\mathrm{bt}, \mathrm{d}, i} \leqslant 1 $ | (16) |
式中:Ebt, i为蓄电池在i时刻的储电量,MW ·h;Pbt, c, i、Pbt, d, i分别为蓄电池在i时刻的充、放电功率,MW;ηbt, c、ηbt, d分别为蓄电池的充、放电效率;Ebt, 0、Ebt, 24分别为每个典型日初始及结束时刻蓄电池的储电量,MW ·h;Ebt, max、Ebt, min分别为蓄电池的蓄电量上、下限,MW ·h;Pbt, max为蓄电池的充、放电功率上限,MW;Ibt, c, i、Ibt, d, i为一组0-1变量,分别表示i时刻蓄电池的充、放状态。
1.3.2 蓄热罐类似地,蓄热罐可实现短时间尺度的热力供需调节,其数学模型为:
| $ E_{\mathrm{hst}, i}=E_{\mathrm{hst}, i-1}+\eta_{\mathrm{hst}, \mathrm{c}} H_{\mathrm{hst}, {\rm{c}}, i}-H_{\mathrm{hst}, \mathrm{d}, i} / \eta_{\mathrm{hst}, \mathrm{d}} $ | (17) |
| $ E_{\mathrm{hst}, 0}=E_{\mathrm{hst}, 24} $ | (18) |
| $ E_{\mathrm{hst}, \text { min }} \leqslant E_{\mathrm{hst}, i} \leqslant E_{\mathrm{hst}, \text { max }} $ | (19) |
| $ \left\{\begin{array}{l} 0 \leqslant H_{\mathrm{hst}, \mathrm{c}, i} \leqslant I_{\mathrm{hst}, {\rm{c}}, i} H_{\mathrm{hst}, \text { max }} \\ 0 \leqslant H_{\mathrm{hst}, \mathrm{d}, i} \leqslant I_{\mathrm{hst}, \mathrm{d}, i} H_{\mathrm{hst}, \text { max }} \end{array}\right. $ | (20) |
| $ 0 \leqslant I_{\mathrm{hst}, \mathrm{c}, i}+I_{\mathrm{hst}, \mathrm{d}, i} \leqslant 1 $ | (21) |
式中:Ehst, i为蓄热罐在i时刻的储热量,MW ·h;Hhst, c, i、Hhst, d, i分别为蓄热罐在i时刻的充、放热功率,MW;ηhst, c、ηhst, d分别为蓄热罐的充、放热效率;Ehst, 0、Ehst, 24分别为每个典型日初始及结束时刻蓄热罐的储热量,MW ·h;Ehst, max、Ehst, min分别为蓄热罐的蓄热量上、下限,MW ·h;Hhst, max为蓄热罐的充、放热功率上限,MW;Ihst, c, i、Ihst, d, i为一组0-1变量,分别表示i时刻蓄热罐的充、放状态。
1.3.3 蓄氢罐电解生成的氢气经压缩机及管道进入储氢罐,同时,氢气也可由储气罐注入燃气管道,与天然气按照一定的体积百分比混合后,传输至用气负荷处供用户使用。天然气混氢后,其热值会发生变化,变化的大小与混氢比例有关。为保证用气负荷的用能需求,应保证混氢前后气体提供的总能量不变,用气速率随着热值的变化而增减。为保证系统安全可靠运行,储氢罐的充放气速率以及天然气混氢体积系数均应满足一定的限制。考虑氢气可实现跨季节存储,其运行约束满足年度能量充放平衡,即:
| $ E_{\mathrm{H}_{2}, i}=E_{\mathrm{H}_{2}, i-1}+F_{\mathrm{H}_{2} \text { in }, i}-F_{\mathrm{H}_{2} \text { out }, i} \quad i=1, 2, \cdots, 8\;760 $ | (22) |
| $ 0 \leqslant E_{\mathrm{H}_{2}, i} \leqslant S_{\mathrm{H}_{2}, \text { max }} $ | (23) |
| $ E_{\mathrm{H}_{2}, 0}=E_{\mathrm{H}_{2}, 8\;760} $ | (24) |
| $ \left\{\begin{array}{l} 0 \leqslant F_{\mathrm{H}_{2} \text {in }, i} \leqslant F_{\mathrm{H}_{2}, \text {max }} \\ 0 \leqslant F_{\mathrm{H}_{2} \text {out }, i} \leqslant F_{\mathrm{H}_{2}, \text {max }} \end{array}\right. $ | (25) |
| $ F_{\mathrm{H}_{2} \text {out }, i} H_{\mathrm{H}_{2}}+F_{\mathrm{NG}_{\text {mix }}, i} H_{\mathrm{NG}}=F_{\mathrm{NG}_{0}, i} H_{\mathrm{NG}} $ | (26) |
| $ \omega=\frac{F_{\mathrm{H}_2 \text {out }, i}}{F_{\mathrm{H}_2 \text {out }, i}+F_{\mathrm{NG}_{\text {mix }}, i}} $ | (27) |
| $ 0 \leqslant \omega \leqslant \omega_0 $ | (28) |
式中:EH2, i为i时刻储氢罐的储氢量,m3;FH2in, i、FH2out, i分别为i时刻储氢罐的进、出气速率,m3/h;SH2, max为储氢罐的额定容量,m3;EH2, 0、EH2, 8 760分别为调度周期的初始及结束时刻储氢罐的储气量,m3;FH2, max为储氢罐的进出气速率上限,m3/h;FNG0, i、FNGmix, i分别为混氢前、后i时刻用户的天然气耗量,m3/h;ω、ω0分别为混氢体积系数和允许的混氢体积系数上限。
2 考虑低碳经济运行的P2H配置模型文中提出的计及天然气混氢使用和跨季节存储的P2H优化配置研究以经济性和低碳性为目标,其中经济性由设备的年化投资成本和园区综合能源系统的年度运行成本表征,低碳性由园区的碳交易成本表征,即:
| $ \min C_{\text {total }}= \tau_{1}\left(C_{\text {cap }}+C_{\text {ope }}\right)+\tau_{2} C_{\mathrm{co}_{2}} $ | (29) |
| $ \tau_{1}+\tau_{2}=1 $ | (30) |
式中:Ctotal为园区的年度加权成本,元;Ccap、Cope、Cco2分别为P2H系统的年化投资成本、园区综合能源系统的年度运行成本和碳交易成本,元;τ1、τ2为经济及低碳性成本的权重系数。
2.1 年化投资成本设备的投资成本由电解槽和储氢罐两部分组成,考虑系统设备的全寿命周期等年值成本,即:
| $ C_{\text {cap }}=P_{\mathrm{p} 2 \text {h cap }} c_{\mathrm{p} 2 \mathrm{h}, \text {unit }} R_{\mathrm{p} 2 \mathrm{h}}+S_{\mathrm{H}_{2}, \text {cap }} c_{\mathrm{H}_{2}, \text {unit }} R_{\mathrm{H}_{2}} $ | (31) |
| $ R_{*}=\frac{d(1+d)^{n}}{(1+d)^{n}-1} $ | (32) |
式中:SH2, cap为储氢罐储气容量,m3;Pp2h, cap为电解槽的额定功率,MW;cp2h, unit为电解槽的单位投资成本,元/MW;cH2, unit为储氢罐的单位投资成本,元/m3;R*为资金回收系数,与设备的寿命年限n和折现率d有关。
2.2 年度运行成本园区综合能源系统的年度运行经济成本Cope由购能成本Cen、运维成本Cma、弃风弃光成本Ccur以及上级P2H电价补贴收益Csub四部分组成,其数学表达式如下:
| $ C_{\mathrm{ope}}=C_{\mathrm{en}}+C_{\mathrm{ma}}+C_{\mathrm{cur}}-C_{\mathrm{sub}} $ | (33) |
购能成本表示园区综合能源系统向上级电网和气网购买电力及天然气的费用,其中电力价格考虑分时电价,天然气价格考虑季节性波动,即:
| $ C_{\text {en }}=N_{\text {day }} \sum\limits_{i=1}^{24}\left(P_{\text {main }, i} K_{\text {main }, i}+G_{\text {source }, i} K_{\text {source }, i}\right) $ | (34) |
式中:Nday为调度周期的天数;Pmain, i为i时刻向上级电网的平均购电功率,MW;Kmain, i为i时刻向上级电网的购电价格,元/(MW ·h);Gsource, i为i时刻向上级气网的购气速率,m3/h;Ksource, i为i时刻向上级气网的购气价格,元/m3。
2.2.2 运维成本运维成本表示园区内部能量转换与存储设备的运行与维护成本,即:
| $ \begin{gather*} C_{\mathrm{ma}}=N_{\mathrm{day}} \sum\limits_{i=1}^{24}\left[K_{\mathrm{w}, \mathrm{ma}} P_{\mathrm{w}, i}+K_{\mathrm{p}, \mathrm{ma}} P_{\mathrm{p}, i}+K_{\mathrm{chp}, \mathrm{ma}} P_{\mathrm{chp}, i}+\right. \\ K_{\mathrm{gb}, \mathrm{ma}} H_{\mathrm{gb}, i}+K_{\mathrm{p2h}, \mathrm{ma}} P_{\mathrm{p} 2 \mathrm{h}, i}+K_{\mathrm{H}_{2}}\left(F_{\mathrm{H}_{2 \mathrm{in}}, i}+F_{\mathrm{H}_{2 \mathrm{out}}, i}\right)+ \\ \left.K_{\mathrm{bt}}\left(P_{\mathrm{bt}, {\rm{c}}, i}+P_{\mathrm{bt}, \mathrm{d}, i}\right)+K_{\mathrm{hst}}\left(H_{\mathrm{hst}, {\rm{c}}, i}+H_{\mathrm{hst}, \mathrm{d}, i}\right)\right] \end{gather*} $ | (35) |
式中;Kw, ma、Kp, ma、Kchp, ma、Kgb, ma、Kp2h, ma、Kbt、Khst分别为风力发电、光伏发电、CHP机组、燃气锅炉、电解槽、蓄电池、蓄热罐的运维成本,元/(MW ·h);KH2为储氢罐充放气过程的费用成本,元/m3。
2.2.3 弃风弃光成本弃风弃光成本以园区内部风光可再生能源发电能力与就地消纳能力的差值乘以相应的单位经济惩罚系数表示,即:
| $ \begin{gather*} C_{\mathrm{cur}}=N_{\mathrm{day}} \sum\limits_{i=1}^{24}\left[K_{\mathrm{w}, \mathrm{cur}}\left(P_{\mathrm{wf}, i}-P_{\mathrm{w}, i}\right)+\right. \\ \left.K_{\mathrm{p}, \mathrm{cur}}\left(P_{\mathrm{pf}, i}-P_{\mathrm{p}, i}\right)\right] \end{gather*} $ | (36) |
式中:Kw, cur、Kp, cur分别为风电和光伏的弃电成本,元/(MW ·h)。
2.2.4 P2H补贴收益电解槽是P2H系统的核心设备,其投资及运行成本较高,为促进氢能产业的健康发展,成都、潍坊等多地先后发布P2H补贴政策[19-20]。因此,文中将进一步考虑上级政府对园区综合能源系统的P2H电价补贴[21],补贴收益Csub可表示为:
| $ C_{\text {sub }}=N_{\text {day }} \sum\limits_{i=1}^{24} K_{\mathrm{H}_{2}, \text {sub }} P_{\mathrm{p} 2 \mathrm{h}, i} $ | (37) |
式中:KH2, sub为上级政府的电价补贴,元/(MW ·h)。
2.3 碳交易成本将碳排放权视为一种可交易的商品,碳市场的引入有利于控制社会的整体碳排放量。目前,我国电力行业现行的主流碳配额分配方式为无偿分配[22-23],当碳市场交易主体实际碳排放量大于获得的初始分配额时,需要从其他用户处购买超出部分的碳排放额度;当碳市场交易主体实际碳排放量小于获得的初始分配额时,可以通过碳交易市场出售富余碳排放额度获益。为了促进园区综合能源系统的低碳运行,文中引入无偿分配的碳配额机制。文中所研究的园区综合能源系统的终端用能需求包括电力和热力两部分,其初始分配额度EC,0可表示为:
| $ E_{\mathrm{C}, 0}=\lambda_{\mathrm{e}} W_{\mathrm{e}}+\lambda_{\mathrm{h}} W_{\mathrm{h}} $ | (38) |
式中:λe、λh分别为单位用电、用热量的碳配额系数,分别取0.728 t/(MW ·h)、0.102 t/GJ[24];We、Wh分别为单位时间内园区的历史用电、热量,MW ·h。
园区综合能源系统以外购电力、燃气以及风光等自然资源为能量输入,文中认为光伏及风电在运行阶段近似零碳排,则园区综合能源系统的实际碳排放量可表示为:
| $ E_{\mathrm{C}}=\lambda_{\text {main }} W_{\text {main }, \text {sum }}+\lambda_{\text {gas }} G_{\text {gas }, \text {sum }} $ | (39) |
式中:λmain为变电站的碳排放系数,t/(MW ·h);λgas为天然气的碳排放系数,t/m3; Wmain, sum为园区年度购电量,MW ·h;Ggas, sum为园区年度购气量,m3。
故碳交易成本Cco2可表示为:
| $ C_{\mathrm{co}_{2}}=K_{\mathrm{co}_{2}}\left(E_{\mathrm{C}}-E_{\mathrm{C}, 0}\right) $ | (40) |
式中:Kco2为单位碳交易价格,元/t。
2.4 模型约束条件 2.4.1 设备规划约束电解槽功率及储氢罐容量的规划结果应不低于0,可表示为:
| $ \left\{\begin{array}{l} S_{\mathrm{H}_{2}, \text {cap }} \geqslant 0\\ S_{\text {p2h, cap }} \geqslant 0 \end{array}\right. $ | (41) |
式中:SH2, cap为储氢罐的规划容量,m3; Sp2h, cap为电解槽的规划功率,MW。
2.4.2 电热气能量平衡约束| $ \left\{\begin{array}{l} P_{\mathrm{main}, i}+P_{\mathrm{w}, i}+P_{\mathrm{v}, i}+P_{\mathrm{chp}, i}+P_{\mathrm{bt}, \mathrm{d}, i}= \\ \;\;\;\;\;\;\;\;\;\;\;\; P_{\mathrm{el}, i}+P_{\mathrm{bt}, \mathrm{c}, i}+P_{\mathrm{p} 2 \mathrm{h}, i} \\ H_{\mathrm{gb}, i}+H_{\mathrm{chp}, i}+H_{\mathrm{hst}, \mathrm{d}, i}=H_{\mathrm{hl}, i}+H_{\mathrm{hst}, \mathrm{c}, i} \\ G_{\mathrm{source}, i}=F_{\mathrm{NG}_{\text {mix }, i}} \\ \text {s.t. } \quad \text {式 }(1) \text {- 式 }(28) \end{array}\right. $ | (42) |
式中:Pel, i、Hhl, i分别为电力负荷和热力负荷的平均功率,MW。
2.4.3 与园区外部的能量交互约束考虑园区内部可再生能源就地消纳且变压器正向传输功率存在一定的限制,不允许园区综合能源系统向上级气网倒送天然气,同时各时刻购买天然气平均速率存在上限,即:
| $ \left\{\begin{array}{l} 0 \leqslant P_{\text {main }, i} \leqslant P_{\text {main }, \max } \\ 0 \leqslant G_{\text {source }, i} \leqslant G_{\text {source }, \max } \end{array}\right. $ | (43) |
式中:Pmain, max为变压器的传输功率上限,MW;Gsource, max为购买天然气的速率上限,m3/h。
3 算例分析 3.1 基础数据文中以含高比例可再生能源的园区综合能源系统为参考,其基本参数如下:(1) 园区4个典型日的风光出力及电热负荷标幺曲线如图 2所示[18],其中风、光发电的基准值均取6 MW,电、热负荷的基准值均取10 MW;(2) 变压器碳排放系数取0.4 t/(MW ·h),天然气碳排放系数[25]取5.61×10-5t/MJ,天然气及氢气热值[17]分别取39 MJ/m3、12.75 MJ/m3,单位碳交易价格参考国家碳交易第一个履约周期成交均价[26],取42.85元/t;(3) 混氢体积分数上限取20%,上级政府的P2H电价补贴取0.15元/(kW ·h),折现率取8%,τ1、τ2均取0.5[23];(4) 园区向上级电网的购电价格参考江苏省现行工业用电峰谷分时电价,如表 1所示,天然气价格考虑季节性波动,春、夏、秋、冬四季单位价格分别取2.113、1.934、1.936和3.272元/m3[12];(5) 设备的运行参数及运维成本见表 2[18]。
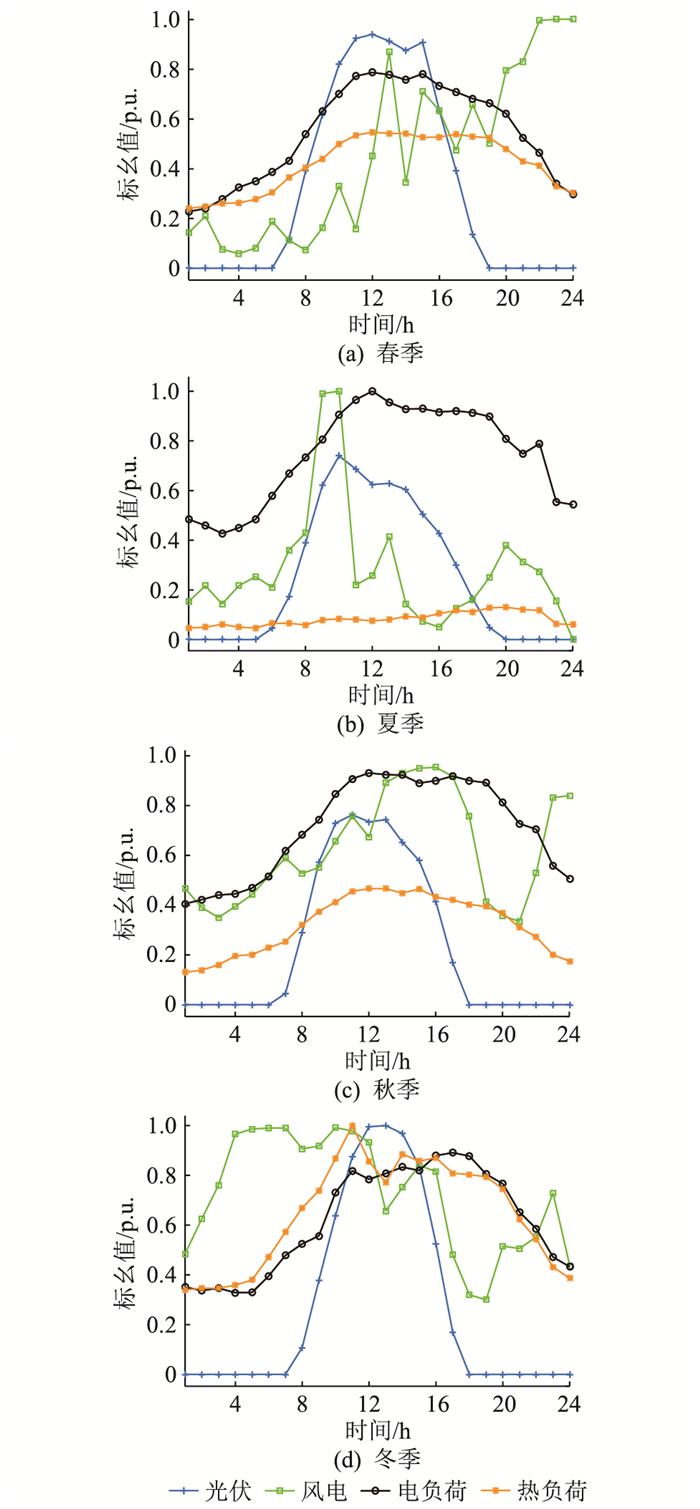
|
图 2 源荷标幺值曲线 Fig. 2 Unit value curve of source and load |
|
|
表 1 江苏省现行工业用电峰谷分时电价 Table 1 The current industrial time of use electricity price in Jiangsu province |
|
|
表 2 设备参数 Table 2 Equipment parameters |
文中建立的模型为多约束下的线性优化问题,基于MATLAB 2016a的YALMIP平台进行搭建,并调用优化求解器Mosek进行求解。
3.2 仿真结果结合3.1节基础数据,根据第2章提出的目标函数和约束条件,电解槽功率及储氢罐容量的配置结果分别为2.26 MW、3 789.25 m3。
3.2.1 电力源荷对比结果为分析配置P2H系统后对园区综合能源系统的影响,将对规划前后的系统运行结果进行展示对比。规划前后电力子系统各典型日的能量供需结果分别如图 3和图 4所示,规划前后的电力基本负荷不变,故不再对其开展分析。
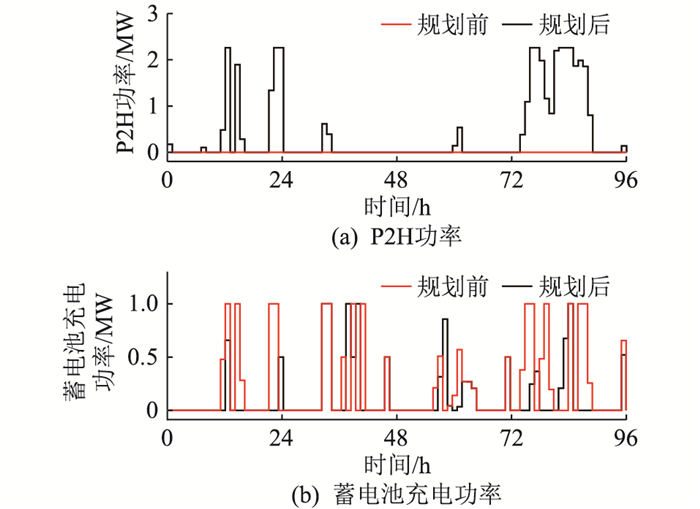
|
图 3 电力子系统需求情况对比 Fig. 3 Comparison of power subsystem demand |

|
图 4 电力子系统供给情况对比 Fig. 4 Comparison of power subsystem supply |
观察图 3及图 4可知,考虑P2H系统配置及天然气混氢使用后:(1) 电解槽的输出功率主要集中在春冬季节。受风光资源分布、电力基础负荷以及CHP机组“以热定电”工作模式的影响,春冬季节的风光发电富余量较大,P2H系统规划后,风光年度发电量增加2 957 MW ·h,较规划前提升了7.67%;(2) P2H装置的引入,降低了电力净负荷波动,P2H系统规划后,蓄电池的年度充放总电量减少1 313 MW ·h,较规划前降低42.86%;(3) P2H系统规划后,对外购电量及CHP机组出力影响较小,其中外购电量略有降低,CHP机组出力略有提升。
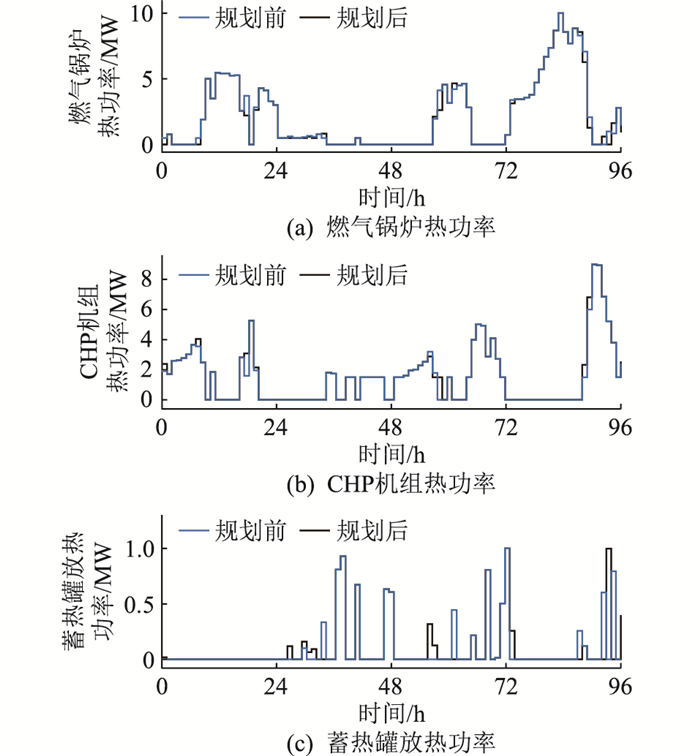
3.2.2 热力源荷对比结果规划前后热力子系统各典型日的能量供需结果分别如图 5和图 6所示,同理,此处不再对热力基本负荷展开分析。
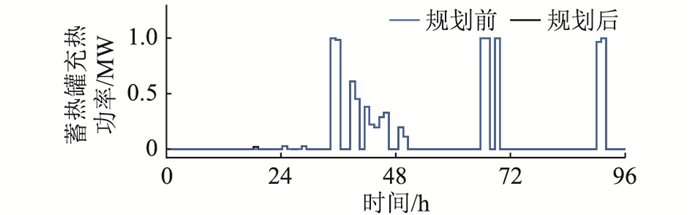
|
图 5 蓄热罐充热情况对比 Fig. 5 Comparison of thermal storage power of heat storage tank |
|
图 6 热力子系统供给情况对比 Fig. 6 Comparison of heat subsystem supply |
观察图 5及图 6可知,考虑P2H系统配置及天然气混氢使用后,对热力子系统的整体影响较小:(1) P2H装置的引入,减弱了CHP机组的出力限制,CHP机组的热力输出略有上升,燃气轮机的热力输出略有降低,两者的年度产热增减量为488 MW ·h;(2) 蓄热罐的年度充放总热量变化不大,其中充热功率几乎不变,放热功率的大小及时段均受到了一定的影响。
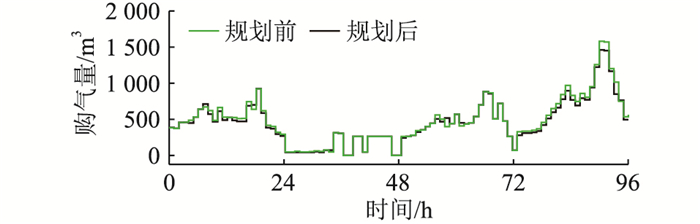
3.2.3 天然气供需对比结果规划前后各典型日的天然气购买量及储氢罐的进出气量情况分别如图 7和图 8所示。
|
图 7 购气量情况对比 Fig. 7 Comparison of gas purchase volume |

|
图 8 储氢罐的进出气量 Fig. 8 Inlet and outlet gas volume of hydrogen storage tank |
由图可知:(1) 考虑混氢使用后,电-气间的能量转换更加畅通,P2H系统产生的氢气对天然气起到了替代作用,P2H系统规划后,园区综合能源系统的年度购气量减少1.56×105 m3,较规划前降低3.74%;(2) 受天然气价格、风光发电能力及热力负荷分布的影响,氢气的充放主要集中于冬季和春季,春冬两季总的充、放气量各占储氢罐全年充、放气量的95.62%和95.49%,氢气的跨季节存储主要体现在夏季和秋季,其中夏季的氢气储存增量为3 022.4 m3,秋季的氢气储存增量为-3 696.7 m3。
3.3 模型灵敏度分析 3.3.1 电解槽价格及混氢体积分数上限影响分析随着氢能在制、储、输、用等方面技术及市场的进一步发展,未来电解槽这一核心设备的寿命年限将有所提高,投资成本进一步降低,上级政府的P2H电价补贴也会相应减少。可以预见,天然气混氢技术也将得到进一步发展。为对比上述因素对P2H规划配置的影响,比较分析以下6个场景。
(1) 场景一:不考虑电解槽及储氢罐的规划;
(2) 场景二:考虑电解槽和储氢罐的规划,同时考虑天然气混氢使用,混氢体积分数上限取20%,即文中3.1节基础算例;
(3) 场景三:电解槽年化投资成本降低25%,上级政府P2H电价补贴降至0.05元/(kW ·h),其余设置与场景二相同;
(4) 场景四:电解槽年化投资成本降低50%,上级政府取消P2H电价补贴,其余设置与场景二形同;
(5) 场景五:混氢体积分数上限取10%,其余设置与场景二相同;
(6) 场景六:混氢体积分数上限取30%,其余设置与场景二相同。
上述算例场景的P2H系统的规划、园区的运行和碳交易成本等结果如表 4所示。
|
|
表 4 6种场景下的结果对比 Table 4 Comparison of results in six cases |
由表 4可知:(1) 相较于场景一,配置P2H系统且考虑天然气混氢使用后,场景二下园区综合能源系统的年度加权总成本、购能成本、弃电成本及碳排放量分别降低5.4%、2.9%、96.8%和2.3%,运维成本及碳交易收益有所提升;(2) 对比场景二、场景三及场景四的优化结果可知,随着氢能相关技术及市场的进步,上级政府逐步取消P2H电价补贴,P2H技术也能实现健康有序发展;(3) 对比场景二、场景五及场景六可知,随着天然气混氢体积分数上限的提高,电-气之间的能源转换将更加畅通,氢能的替代能力将进一步增强。其中,混氢体积分数上限取30%时,为追求园区综合能源系统的年度加权总成本最优,电解槽将在谷电价时段增加功率输出,以获取更多的电价补贴,故场景六下的外购能源成本、运维成本、P2H补贴以及碳排放量相较于场景二均有所提升。
3.3.2 经济性及低碳性权重系数取值影响分析同理,为进一步分析经济性及低碳性系数取值大小对P2H规划配置及园区综合能源系统运行结果的影响,对以下3种场景做比较分析。
(1) 场景七:τ1、τ2分别取0.3、0.7,其余设置与场景二相同;
(2) 场景八:τ1、τ2均取0.5,即所有设置与场景二相同;
(3) 场景九:τ1、τ2分别取0.7、0.3,其余设置与场景二相同。
上述3种场景的电解槽及储氢罐的规划容量相同,分别为2.26 MW和3 789.3 m3,这主要是受限于混氢体积分数上限和可再生能源富余量的影响,且规划设备的年化投资成本相较于园区年度运行成本占比较小,故经济性及低碳性权重系数主要影响P2H规划后园区的运行阶段,相关结果见表 5。
|
|
表 5 3种场景下的结果对比 Table 5 Comparison of results in three cases |
由表 5可知:(1) 对比场景七和场景八可知,随着低碳性权重系数的提升,购能成本、运维成本及碳交易收益略有上升,相较于场景八,场景七的年度碳排放量降低1.2%,此外,外购电量降低3.6%,外购天然气增加1%;(2) 对比场景八及场景九可知,随着经济性权重系数的提升,购能成本及运维成本反而略有升高,相较于场景八,场景九的碳排放量增加1.3%,这主要是由于为了追求更高的电制氢电价补贴,园区增加了年度整体购能量。
4 结论引入具有工程基础和发展前景的P2H及天然气混氢技术,文中提出计及天然气混氢使用及跨季节储氢的园区综合能源系统P2H优化配置方法。首先梳理了含氢园区综合能源系统架构和能量流动关系,其次以低碳性和经济性为目标,建立P2H优化配置模型。最后通过算例分析,可以得出以下结论:
(1) 文中所提模型可为园区综合能源系统电解槽和储氢罐的规划配置、能源的购买、存储与生产等提供参考;
(2) P2H和天然气混氢技术的引入可有效提升电-气能源系统间的耦合互补能力,促进风光可再生能源的就地消纳,降低园区综合能源系统的年度加权成本和碳排放量;
(3) 随着氢能制、储、输、用等方面技术的全方位发展,P2H技术在促进可再生能源消纳、降低碳排放等方面的优势将进一步凸显。
致谢
本文得到国网江苏省电力有限公司科技项目(J2022122)资助,谨此致谢!
| [1] |
胡博, 孙铠彬, 邵常政, 等. 面向全过程碳足迹的园区综合能源系统碳感知与优化方法[J]. 高电压技术, 2022, 48(7): 2495-2504. HU Bo, SUN Kaibin, SHAO Changzheng, et al. Carbon perception and optimization method of the integrated community energy system oriented to the whole process carbon footprint[J]. High Voltage Engineering, 2022, 48(7): 2495-2504. (  0) 0) |
| [2] |
胡兵, 徐立军, 何山, 等. 碳达峰与碳中和目标下PEM电解水制氢研究进展[J]. 化工进展, 2022, 41(9): 4595-4604. HU Bing, XU Lijun, HE Shan, et al. Researching progress of hydrogen production by PEM water electrolysis under the goal of carbon peak and carbon neutrality[J]. Chemical Industry and Engineering Progress, 2022, 41(9): 4595-4604. (  0) 0) |
| [3] |
潘光胜, 顾钟凡, 罗恩博, 等. 新型电力系统背景下的电制氢技术分析与展望[J]. 电力系统自动化, 2023, 47(10): 1-13. PAN Guangsheng, GU Zhongfan, LUO Enbo, et al. Analysis and prospect of electrolytic hydrogen technology under background of new power systems[J]. Automation of Electric Power System, 2023, 47(10): 1-13. (  0) 0) |
| [4] |
潘光胜, 顾伟, 张会岩, 等. 面向高比例可再生能源消纳的电氢能源系统[J]. 电力系统自动化, 2020, 44(23): 1-10. PAN Guangsheng, GU Wei, ZHANG Huiyan, et al. Electricity and hydrogen energy system towards accomodation of high proportion of renewable energy[J]. Automation of Electric Power Systems, 2020, 44(23): 1-10. (  0) 0) |
| [5] |
ZHAO P F, LU X, CAO Z D, et al. Volt-VAR-pressure optimization of integrated energy systems with hydrogen injection[J]. IEEE Transactions on Power Systems, 2021, 36(3): 2403-2415. DOI:10.1109/TPWRS.2020.3028530 (  0) 0) |
| [6] |
中华人民共和国中央人民政府. 新时代的中国能源发展白皮书[EB/OL]. (2020-12-21)[2023-04-06]. http://www.scio.gov.cn/zfbps/32832/Document/1695117/1695117.htm. The Central People′s Government of the China. White paper on China′s energy development in a new era [EB/OL]. (2020-12-21)[2023-04-06]. http://www.scio.gov.cn/zfbps/32832/Document/1695117/1695117.htm. (  0) 0) |
| [7] |
中华人民共和国中央人民政府. 2030年前碳达峰行动方案[EB/OL]. (2021-10-26)[2023-04-06]. http://www.gov.cn/zhengce/content/2021-10/26/content_5644984.htm. The Central People′s Government of the China. Action plan for carbon dioxide peaking before 2030[EB/OL]. (2021-10-26)[2023-04-06]. http://www.gov.cn/zhengce/content/2021-10/26/content_5644984.htm. (  0) 0) |
| [8] |
中华人民共和国中央人民政府. 中华人民共和国国民经济和社会发展第十四个五年规划和2035年远景目标纲要[EB/OL]. (2021-01-13)[2023-04-06]. http://www.gov.cn/xinwen/2021-03/13/content_5592681.htm. The Central People′s Government of the China. Outline of the 14th Five-Year plan for national economic and so-cial development and vision 2035 of the People′s Republic of China [EB/OL]. (2021-01-13)[2023-04-06]. http://www.gov.cn/xinwen/2021-03/13/content_5592681.htm. (  0) 0) |
| [9] |
邱玥, 周苏洋, 顾伟, 等. "碳达峰、碳中和" 目标下混氢天然气技术应用前景分析[J]. 中国电机工程学报, 2022, 42(4): 1301-1321. QIU Yue, ZHOU Suyang, GU Wei, et al. Application prospect analysis of hydrogen enriched compressed natural gas technologies under the target of carbon emission peak and carbon neutrality[J]. Proceedings of the CSEE, 2022, 42(4): 1301-1321. (  0) 0) |
| [10] |
严思韵, 周登极. 综合能源天然气网混氢输运的仿真与调度综述[J]. 中国电机工程学报, 2022, 42(24): 8816-8832. YAN Siyun, ZHOU Dengji. Review of simulation and scheduling of hydrogen-blended transportation in natural gas net-work of integrated energy system[J]. Proceedings of the CSEE, 2022, 42(24): 8816-8832. (  0) 0) |
| [11] |
姜海洋, 杜尔顺, 朱桂萍, 等. 面向高比例可再生能源电力系统的季节性储能综述与展望[J]. 电力系统自动化, 2020, 44(19): 194-207. JIANG Haiyang, DU Ershun, ZHU Guiping, et al. Review and prospect of seasonal energy storage for power system with high proportion of renewable energy[J]. Automation of Electric Power Systems, 2020, 44(19): 194-207. (  0) 0) |
| [12] |
YU K, CEN Z G, CHEN X Y, et al. Optimization of urban multi-energy flow systems considering seasonal peak shaving of natural gas[J]. CSEE Journal of Power and Energy Systems, 2022, 8(4): 1183-1193. (  0) 0) |
| [13] |
葛怀宇, 贾燕冰, 韩肖清. 考虑季节互补特性的电-气综合能源系统容量规划[J]. 中国电机工程学报, 2023, 43(1): 147-158. GE Huaiyu, JIA Yanbing, HAN Xiaoqing. Capacity planning of integrated electricity-gas energy systems considering seasonal complementarity[J]. Proceedings of the CSEE, 2023, 43(1): 147-158. (  0) 0) |
| [14] |
CAVANA M, MAZZA A, CHICCO G, et al. Electrical and gas networks coupling through hydrogen blending under increasing distributed photovoltaic generation[J]. Applied Energy, 2021, 290: 116764. DOI:10.1016/j.apenergy.2021.116764 (  0) 0) |
| [15] |
侯慧, 刘鹏, 黄亮, 等. 考虑不确定性的电-热-氢综合能源系统规划[J]. 电工技术学报, 2021, 36(S1): 133-144. HOU Hui, LIU Peng, HUANG Liang, et al. Planning of electricity-heat-hydrogen integrated energy system considering uncertainties[J]. Transactions of China Electrotechnical Society, 2021, 36(S1): 133-144. (  0) 0) |
| [16] |
袁铁江, 曹继雷. 计及风电-负荷不确定性的风氢低碳能源系统容量优化配置[J]. 高电压技术, 2022, 48(6): 2037-2044. YUAN Tiejiang, CAO Jilei. Capacity optimization allocation of wind hydrogen low-carbon energy system considering wind power-load uncertainty[J]. High Voltage Engineering, 2022, 48(6): 2037-2044. (  0) 0) |
| [17] |
FU C, LIN J, SONG Y H, et al. Optimal operation of an integrated energy system incorporated with HCNG distribution networks[J]. IEEE Transactions on Sustainable Energy, 2020, 11(4): 2141-2151. DOI:10.1109/TSTE.2019.2951701 (  0) 0) |
| [18] |
熊宇峰, 陈来军, 郑天文, 等. 考虑电热气耦合特性的低碳园区综合能源系统氢储能优化配置[J]. 电力自动化设备, 2021, 41(9): 31-38. XIONG Yufeng, CHEN Laijun, ZHENG Tianwen, et al. Optimal configuration of hydrogen energy storage in low-carbon park integrated energy system considering electricity-heat-gas coupling characteristics[J]. Electric Power Automation Equipment, 2021, 41(9): 31-38. (  0) 0) |
| [19] |
成都市人民政府. 关于促进氢能产业高质量发展的若干意见[EB/OL]. (2020-07-10)[2023-04-06]. http://www.chengdu.gov.cn/chengdu/c131029/zcwjney.shtml?id=119605&tn=6&index=AO0B0200322202000030&wz=%E6%88%90%E5%8A%9E%E5%8F%91. Chengdu Municipal People′s Government. Promoting high-quality development of hydrogen energy industry[EB/OL]. (2020-07-10)[2023-04-06]. http://www.chengdu.gov.cn/chengdu/c131029/zcwjney.shtml?id=119605&tn=6&index=AO0B0200322202000030&wz=%E6%88%90%E5%8A%9E%E5%8F%91. (  0) 0) |
| [20] |
潍坊市人民政府. 关于支持氢能产业发展的若干政策的通知[EB/OL]. (2021-12-23)[2023-04-06]. http://www.weifang.gov.cn/162/55329/1478640467267686400.html. Weifang Municipal People′s Government. Notice on several policies to support the development of hydrogen energy industry[EB/OL]. (2021-12-23)[2023-04-06]. http://www.weifang.gov.cn/162/55329/1478640467267686400.html. (  0) 0) |
| [21] |
滕越, 赵骞, 张红, 等. 新能源-质子交换膜电解槽电制氢容量双层规划模型研究[J]. 热力发电, 2021, 50(11): 37-46. TENG Yue, ZHAO Qian, ZHANG Hong, et al. Study on double-layer planning model for hydrogen production capacity of new energy proton exchange membrane electrolyzer[J]. Thermal Power Generation, 2021, 50(11): 37-46. (  0) 0) |
| [22] |
颜宁, 马广超, 李相俊, 等. 基于季节性碳交易机制的园区综合能源系统低碳经济调度[J]. 中国电机工程学报, 2024, 44(3): 918-932. YAN Ning, MA Guangchao, LI Xiangjun, et al. Low-carbon economic dispatch of park integrated energy system based on seasonal carbon trading mechanism[J]. Proceedings of the CSEE, 2024, 44(3): 918-932. (  0) 0) |
| [23] |
邱纯, 应展烽, 冯奕, 等. 计及碳配额的混合储能综合微能源网优化运行研究[J]. 电力工程技术, 2022, 41(2): 119-127. QIU Chun, YING Zhanfeng, FENG Yi, et al. Optimal operation of hybrid energy storage integrated micro-energy network considering carbon quote[J]. Electric Power Engineering Technology, 2022, 41(2): 119-127. (  0) 0) |
| [24] |
刘英培, 黄寅峰. 考虑碳排权供求关系的多区域综合能源系统联合优化运行[J]. 电工技术学报, 2023, 38(13): 3459-3472. LIU Yingpei, HUANG Yinfeng. Joint optimal operation of multi-regional integrated energy system considering the supply and demand of carbon emission rights[J]. Transactions of China Electrotechnical Society, 2023, 38(13): 3459-3472. (  0) 0) |
| [25] |
CRUZ M R M, FITIWI D Z, SANTOS S F, et al. Multi-flexibility option integration to cope with large-scale integration of renewables[J]. IEEE Transactions on Sustainable Energy, 2020, 11(1): 48-60. DOI:10.1109/TSTE.2018.2883515 (  0) 0) |
| [26] |
中华人民共和国生态环境部. 全国碳排放权交易市场第一个履约周期报告[EB/OL]. (2022-12-30)[2023-04-06]. https://www.mee.gov.cn/ywgz/ydqhbh/wsqtkz/202212/P020221230799532329594.pdf. Ministry of Ecology and Environment of the Ministry of Ecology and Environment. Report on the first performance cycle of the national carbon emissions trading market[EB/OL]. (2022-12-30)[2023-04-06]. https://www.mee.gov.cn/ywgz/ydqhbh/wsqtkz/202212/P020221230799532329594.pdf. (  0) 0) |
 2024, Vol. 43
2024, Vol. 43


 岑增光(1997), 男, 硕士, 从事配电运检相关工作(E-mail:
岑增光(1997), 男, 硕士, 从事配电运检相关工作(E-mail: