文章编号: 2096-3203(2024)02-0105-09 中图分类号: TM761;TP273
2. 江南大学物联网工程学院, 江苏 无锡 214122;
3. 武汉理工大学自动化学院, 湖北 武汉 430070
在“碳达峰、碳中和”以及构建新型电力系统的目标下,新能源发电比例快速增长。由于其间接性和不确定性导致发电量难以预测,易造成电压波动问题[1-2],电压波动在严重的情况下极易对用电设备造成破坏。为此,控制电压波动已成为新能源发电中亟待解决的问题之一。电力弹簧[3] (electric spring,ES)的提出为稳定新能源发电系统的电压波动提供新思路,其控制目标之一是将关键负载(critical load,CL)上的电压波动控制在一定的范围内,从而使CL达到稳定的参考电压;其次ES与其串联的非关键负载(non-critical load,NCL)构成智能负载(smart load,SL),可以承担不稳定的交流电源产生的电压波动,其特点为快速实现电力供应和需求的平衡。
基于在新能源发电方面的应用优势和潜力,ES近年来引起学者的广泛关注[4-16]。在ES拓扑研究方面,文献[4-7]研究了ES的3种拓扑。文献[8-9]对ES的原理、拓扑和应用进行分析,并且对ES的控制方法进行综述。在ES控制研究方面,目前对ES的控制方法仍以比例积分(proportional-integral,PI)控制为主,文献[10]提出ES在传统PI控制上改进的最优PI算法,提高系统的适应性与鲁棒性,但仍然无法很好地克服参数的不确定性所带来的影响。文献[11]提出直、交流电压双环控制,实现ES可以向电网提供电压支持以响应电网的动态需求,但是该控制策略输出的电压谐波含量较高。文献[12]通过无源控制理论实现ES对功率的跟踪和CL电压的稳定,但是当电网电压变化的瞬间,CL电压波动较为明显。文献[13]提出相位控制法,实现ES有功无功混合补偿,但是该控制方法需要采集的系统参数信息较多,并且对参数敏感。文献[14]提出一种径向弦向分解(radial-chordal decomposition,RCD)方法,RCD法可以保证CL电压稳定的同时,实现SL功率幅值以及相角的独立控制,对线路参数的依赖较小。文献[15]采用指令滤波器逼近非线性函数,解决永磁同步电机反步控制策略中的计算膨胀问题。
ES属于典型的多变量、强非线性系统,传统的PI控制方法存在控制精度差、鲁棒性弱等问题,特别是电压发生大幅度波动时,很难达到ES理想的控制效果。为此,文中将反步控制策略首次应用于ES系统中。反步控制[16-18]在设计非线性系统的鲁棒或自适应控制器方面具有明显的优越性,在控制无人机[19]、机器人[20]等领域得到广泛的应用。文中设计一种适用于非线性系统的ES反步控制策略来实现对CL电压的稳定。根据ES的数学模型,构造Lyapunov函数并利用反步法设计虚拟控制器,同时引入指令滤波器[21]来解决此过程中的计算膨胀问题,利用Lyapunov函数稳定性验证系统的全局稳定。最后通过仿真将ES的PI控制与文中控制策略作比较,进行验证分析。
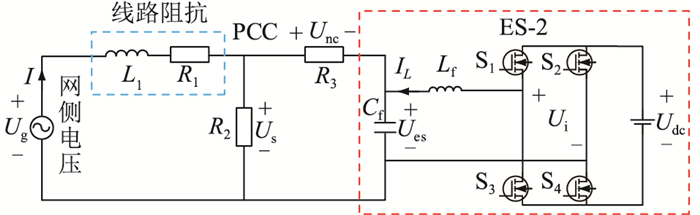
1 ES的工作原理第2代电力弹簧ES-2的拓扑[5-6, 22]如图 1所示,由1个直流电压源、4个晶闸管(metal oxide semiconductor field effect transistor,MOSFET)S1—S4组成的单相电压源逆变器和1个LC低通滤波器构成,其中,Unc为NCL上的电压;Udc为逆变器直流侧电压。ES-2与非关键负载R3串联组成SL,SL与关键负载R2并联。当电网侧电压和能量发生波动时,ES将电网侧的波动转移到NCL上,通过改变NCL的电压来实现CL电压实时自主跟踪电压参考值。文献[22]对典型的ES-2的拓扑和状态方程进行详细的描述与推导,此处不再赘述。
|
图 1 ES-2应用系统拓扑 Fig. 1 Topology of ES-2 application system |
ES-2的状态方程为:
| $ \frac{\mathrm{d} I_{L}}{\mathrm{d} t}=-\frac{U_{\text {es }}}{L_{\mathrm{f}}}+\frac{U_{\mathrm{i}}}{L_{\mathrm{f}}} $ | (1) |
| $ \frac{\mathrm{d} U_{\mathrm{es}}}{\mathrm{d} t}=\frac{I_{L}}{C_{\mathrm{f}}}+\frac{U_{\mathrm{es}}}{C_{\mathrm{f}}\left(R_{2}+R_{3}\right)}+\frac{R_{2} I}{C_{\mathrm{f}}\left(R_{2}+R_{3}\right)} $ | (2) |
| $ \frac{\mathrm{d} I}{\mathrm{d} t}=-\frac{R_{2} U_{\mathrm{es}}}{L_{1}\left(R_{2}+R_{3}\right)}-\frac{\left(R_{1} R_{2}+R_{2} R_{3}+R_{1} R_{3}\right) I}{L_{1}\left(R_{2}+R_{3}\right)}+\frac{U_{\mathrm{g}}}{L_{1}} $ | (3) |
| $ U_{\mathrm{s}}=\frac{R_{2}}{R_{2}+R_{3}} U_{\mathrm{es}}+\frac{R_{2} R_{3}}{R_{2}+R_{3}} I $ | (4) |
式中:Ug为网侧电压;R1、L1分别为线路电阻、电感;R2、R3分别为CL和NCL电阻;I为电网注入公共节点(point of common coupling,PCC)的电流;Lf为滤波电感;Cf为滤波电容;IL为滤波电感电流;Us为CL的电压;Ui为单相电压源逆变器输出电压;Ues为滤波电容Cf输出的电压即ES-2输出的电压。
2 控制器设计文中主要利用反步控制法,针对上述ES数学模型设计虚拟控制器,并将指令滤波加入到虚拟控制器中,避开对虚拟控制器的反复求导,使得CL电压能够良好地跟踪参考电压有效值Usref。
2.1 虚拟控制器设计由逆变电路的原理可知,单相电压源逆变器的输出电压Ui与脉冲宽度调制(pulse width modulation,PWM)信号m的关系为Ui=Udcm,因此式(1)可改写为:
| $ \frac{\mathrm{d} I_{L}}{\mathrm{d} t}=-\frac{U_{\mathrm{es}}}{L_{\mathrm{f}}}+\frac{U_{\mathrm{dc}} m}{L_{\mathrm{f}}} $ | (5) |
定义CL的电压与参考电压的误差量:
| $ e_{1}=U_{\mathrm{s}}-U_{\text {sref }} $ | (6) |
对式(6)求导可得:
| $ \frac{\mathrm{d} e_{1}}{\mathrm{d} t}=\frac{\mathrm{d} U_{\mathrm{s}}}{\mathrm{d} t}-\frac{\mathrm{d} U_{\text {sref }}}{\mathrm{d} t} $ | (7) |
定义Lyapunov函数:
| $ V_{1}=\frac{1}{2} e_{1}^{2} $ | (8) |
定义虚拟控制器参数为k1,对式(8)进行求导并将式(7)代入可得:
| $ \begin{align*} & \frac{\mathrm{d} V_{1}}{\mathrm{d} t}=e_{1} \frac{\mathrm{d} e_{1}}{\mathrm{d} t}=e_{1}\left(\frac{\mathrm{d} U_{\mathrm{s}}}{\mathrm{d} t}-\frac{\mathrm{d} U_{\text {sref }}}{\mathrm{d} t}\right)= \\ & -k_{1} e_{1}^{2}+e_{1}\left(k_{1} e_{1}+\frac{\mathrm{d} U_{\mathrm{s}}}{\mathrm{d} t}-\frac{\mathrm{d} U_{\text {sref }}}{\mathrm{d} t}\right) \end{align*} $ | (9) |
对式(4)进行求导:
| $ \frac{\mathrm{d} U_{\mathrm{s}}}{\mathrm{d} t}=\frac{R_{2}}{R_{2}+R_{3}} \times \frac{\mathrm{d} U_{\mathrm{es}}}{\mathrm{d} t}+\frac{R_{2} R_{3}}{R_{2}+R_{3}} \times \frac{\mathrm{d} I}{\mathrm{d} t} $ | (10) |
根据Lyapunov稳定性定理,若使系统保持稳定,则必须满足
| $ \begin{gather*} I_{L}^{\mathrm{d}}=-\frac{\left(R_{2}+R_{3}\right) C_{\mathrm{f}}}{R_{2}}\left(k_{1} e_{1}-\frac{\mathrm{d} U_{\text {sref }}}{\mathrm{d} t}\right)-\frac{R_{3} C_{\mathrm{f}}}{L_{1}} U_{\mathrm{g}}+ \\ {\left[\frac{1}{R_{2}+R_{3}}+\frac{R_{2} R_{3} C_{\mathrm{f}}}{L_{1}\left(R_{2}+R_{3}\right)}\right] U_{\text {es }}+} \\ {\left[\frac{\left(R_{1} R_{2}+R_{2} R_{3}+R_{1} R_{3}\right) R_{3} C_{\mathrm{f}}}{L_{1}\left(R_{2}+R_{3}\right)}-\frac{R_{2}}{R_{2}+R_{3}}\right] I} \end{gather*} $ | (11) |
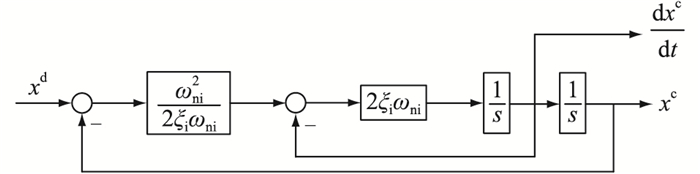
高阶的非线性系统中,在设计反步控制器时,会对虚拟控制器进行反复求导,易造成计算出现“微分膨胀问题”,从而会影响虚拟控制器对系统的控制效果[23]。为解决此问题,文中在虚拟控制器中引入指令滤波器,即将文中设计的虚拟控制器电流ILd通过指令滤波器得到输出电流ILc和输出电流微分dILc/dt。指令滤波器结构如图 2所示,xd为指令滤波器的输入信号;xc、dxc/dt分别为指令滤波器的输出信号和输出信号微分;ωni、ξi分别为指令滤波器的带宽和阻尼。
|
图 2 指令滤波器结构 Fig. 2 Command filtering structure |
指令滤波器的状态方程为:
| $ \left[\begin{array}{c} \frac{\mathrm{d} y_{1}}{\mathrm{d} t}\\ \frac{\mathrm{d} y_{2}}{\mathrm{d} t} \end{array}\right]=\left[\begin{array}{cc} 0 & 1 \\ -\omega_{\mathrm{ni}}^{2} & -\zeta_{\mathrm{i}} \omega_{\mathrm{ni}} \end{array}\right]\left[\begin{array}{l} y_{1} \\ y_{2} \end{array}\right]+\left[\begin{array}{c} 0 \\ \omega_{\mathrm{ni}}^{2} \end{array}\right] x^{\mathrm{d}} $ | (12) |
式中:y1、y2分别为指令滤波器的输出信号xc和输出信号微分dxc/dt。为实现控制目标,指令滤波器需要将输入的信号xd和输出的信号xc的误差尽可能减少,此时只要将指令滤波器内部的带宽ωni尽可能地取大,则可以使xd和xc的误差接近于0。
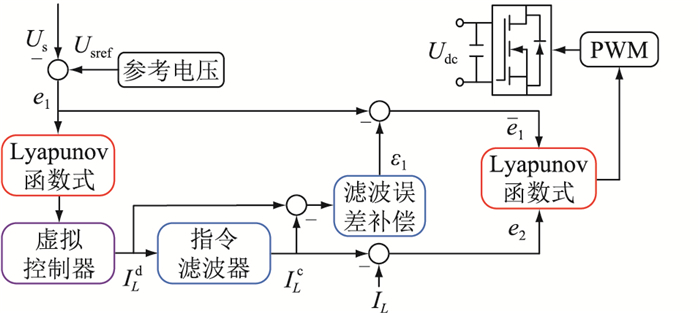
2.3 指令滤波反步控制器设计带有指令滤波的ES反步控制流程见图 3。
|
图 3 带有指令滤波的ES反步控制流程 Fig. 3 ES backstepping control flow with command filtering |
为补偿指令滤波器的滤波误差,重新定义误差量为:
| $ \bar{e}_{1}=e_{1}-\varepsilon_{1} $ | (13) |
式中:ε1为指令滤波器的误差补偿信号,并将其导数设计为式(14)所示。
| $ \frac{\mathrm{d} \varepsilon_{1}}{\mathrm{d} t}=-k_{1} \varepsilon_{1}+\frac{R_{2}}{\left(R_{2}+R_{3}\right) C_{\mathrm{f}}}\left(I_{L}^{\mathrm{c}}-I_{L}^{\mathrm{d}}\right) $ | (14) |
定义输出逆变器电流误差量为:
| $ e_{2}=I_{L}-I_{L}^{\mathrm{c}} $ | (15) |
对式(15)求导可得:
| $ \frac{\mathrm{d} e_{2}}{\mathrm{d} t}=\frac{\mathrm{d} I_{L}}{\mathrm{d} t}-\frac{\mathrm{d} I_{L}^{\mathrm{c}}}{\mathrm{d} t} $ | (16) |
为稳定整个系统,再次定义Lyapunov函数为:
| $ V_{2}=\frac{1}{2} \bar{e}_{1}^{2}+\frac{1}{2} e_{2}^{2} $ | (17) |
对式(16)进行求导可得:
| $ \frac{\mathrm{d} V_{2}}{\mathrm{d} t}=\bar{e}_{1} \frac{\mathrm{d} \bar{e}_{1}}{\mathrm{d} t}+e_{2} \frac{\mathrm{d} e_{2}}{\mathrm{d} t} $ | (18) |
为求得
| $ \begin{gather*} \frac{\mathrm{d} \bar{e}_{1}}{\mathrm{d} t}=\frac{\mathrm{d} e_{1}}{\mathrm{d} t}-\frac{\mathrm{d} \varepsilon_{1}}{\mathrm{d} t}=\frac{\mathrm{d} U_{\mathrm{s}}}{\mathrm{d} t}-\frac{\mathrm{d} U_{\text {sref }}}{\mathrm{d} t}+k_{1} \varepsilon_{1}- \\ \frac{R_{2}}{\left(R_{2}+R_{3}\right) C_{\mathrm{f}}}\left(I_{L}^{\mathrm{c}}-I_{L}^{\mathrm{d}}\right)=-k_{2} \bar{e}_{1}+\frac{R_{2}}{\left(R_{2}+R_{3}\right) C_{\mathrm{f}}} e_{2} \end{gather*} $ | (19) |
定义指令滤波反步控制器参数为k2,将式(19)代入(18)可得:
| $ \begin{gather*} \frac{\mathrm{d} V_{2}}{\mathrm{d} t}=\bar{e}_{1} \frac{\mathrm{d} \bar{e}_{1}}{\mathrm{d} t}+e_{2} \frac{\mathrm{d} e_{2}}{\mathrm{d} t}=-k_{1} \bar{e}_{1}^{2}-k_{2} e_{2}^{2}+ \\ \quad e_{2}\left[\frac{R_{2}}{\left(R_{2}+R_{3}\right) C_{\mathrm{f}}} \bar{e}_{1}+\frac{\mathrm{d} e_{2}}{\mathrm{d} t}+k_{2} e_{2}\right] \end{gather*} $ | (20) |
为满足Lyapunov稳定性使系统稳定,必须满足
| $ m^{\mathrm{d}}=\frac{L_{\mathrm{f}}}{U_{\mathrm{dc}}}\left[-k_{2} e_{2}-\frac{R_{2}}{\left(R_{2}+R_{3}\right) C_{\mathrm{f}}} \bar{e}_{1}+\frac{1}{L_{\mathrm{f}}} U_{\mathrm{es}}+\frac{\mathrm{d} I_{L}^{\mathrm{c}}}{\mathrm{d} t}\right] $ | (21) |
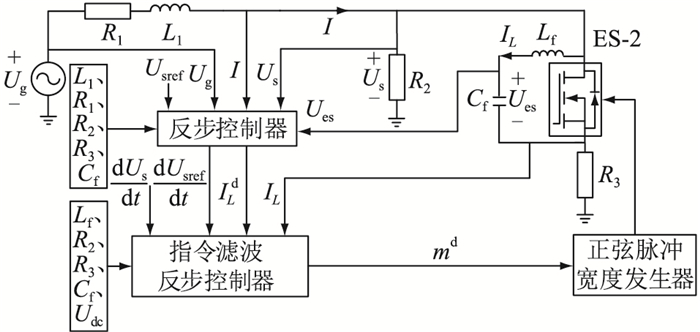
系统控制策略结构如图 4所示。
|
图 4 ES控制策略结构 Fig. 4 ES control strategy structure |
在设计虚拟控制器电流和控制率过程中,使用Lyapunov函数来保持系统的稳定性,系数k1、k2均为大于0的常数,由式(8)、式(17)可知,所构造的2个Lyapunov函数式均为正定函数。
对上述2个Lyapunov函数式进行求导,并将设计的虚拟控制器和控制律的式(11)、式(21)分别代入式(9)、式(20)中可得:
| $ \frac{\mathrm{d} V_{1}}{\mathrm{d} t}=e_{1} \frac{\mathrm{d} e_{1}}{\mathrm{d} t}=-k_{1} e_{1}^{2} \leqslant 0 $ | (22) |
| $ \frac{\mathrm{d} V_{2}}{\mathrm{d} t}=\bar{e}_{1} \frac{\mathrm{d} \bar{e}_{1}}{\mathrm{d} t}+e_{2} \frac{\mathrm{d} e_{2}}{\mathrm{d} t}=-k_{1} \bar{e}_{1}^{2}-k_{2} e_{2}^{2} \leqslant 0 $ | (23) |
根据Lyapunov稳定性理论可知,所设计的虚拟控制器电流ILd和控制率md在原点处渐进稳定,从而确保整个系统的稳定性。
2.5 ES稳态运行界限分析为确保ES能在允许的运行范围内达到理想的控制效果,须对其稳态运行界限进行分析。根据图 1所示经典ES-2拓扑,利用基尔霍夫定理可得:
| $ U_{\mathrm{g}}=I\left(R_{1}+L_{1}\right)+U_{\mathrm{s}} $ | (24) |
| $ U_{\mathrm{s}}=U_{\mathrm{es}}+U_{\mathrm{nc}} $ | (25) |
| $ I=I_{\mathrm{nc}}+I_{\mathrm{c}}=\frac{U_{\mathrm{s}}}{R_{2}}+\frac{U_{\mathrm{nc}}}{R_{3}} $ | (26) |
式中:Inc为NCL上的电流;Ic为流过CL的电流。
联立式(24)—式(26)可得:
| $ U_{\text {es }}=U_{\mathrm{s}}\left(1+\frac{R_{3}}{R_{1}+L_{1}}+\frac{R_{3}}{R_{2}}\right)-\frac{R_{3}}{R_{1}+L_{1}} U_{\mathrm{g}} $ | (27) |
根据式(27)分析可知,ES输出电压Ues与线路电阻R1和电感L1、CL电阻R2、NCL电阻R3、CL电压Us和电网电压Ug有关。则ES输出电压Ues须满足的运行约束界限为:
| $ \left\{\begin{array}{l} U_{\mathrm{es}, \text { min , rated }} \leqslant U_{\mathrm{es}} \leqslant U_{\mathrm{es}, \text { max, rated }}\\ U_{\mathrm{sref}}-U_{\mathrm{nc}, \text { max, rated }} \leqslant U_{\mathrm{es}} \leqslant U_{\mathrm{sref}}-U_{\mathrm{nc}, \text { min }, \text { rated }} \\ U_{\mathrm{sref}}-R_{3} I_{\mathrm{nc}, \text { max }, \text { rated }} \leqslant U_{\mathrm{es}} \leqslant U_{\mathrm{sref}}-R_{3} I_{\mathrm{nc}, \text { min, rated }} \end{array}\right. $ | (28) |
式中:Ues, min, rated、Ues, max, rated分别为ES输出电压额定值下、上边界;Unc, min, rated、Unc, max, rated分别为NCL上的输出电压额定值下、上边界;Inc, min, rated、Inc, max, rated分别为流过SL上的电流额定值下、上边界。
根据式(27)、式(28)可得,ES在其稳态运行边界内输出的电压Ues为:
| $ U_{\mathrm{es}}=\left\{\begin{array}{l} U_{\mathrm{es}, \max } \quad U_{\mathrm{g}}<U_{\mathrm{g}, \min }\\ U_{\mathrm{s}} \frac{R_{2} R_{3}+R_{3}\left(R_{1}+L_{1}\right)}{\left(R_{1}+L_{1}\right) R_{2}}-\frac{R_{3}}{R_{1}+L_{1}} U_{\mathrm{g}} \\ \quad\quad U_{\mathrm{g}, \min } \leqslant U_{\mathrm{g}} \leqslant U_{\mathrm{g}, \max } \\ U_{\mathrm{es}, \min } \quad U_{\mathrm{g}}>U_{\mathrm{g}, \max } \end{array}\right. $ | (29) |
式中:Ues, max、Ues, min分别为ES输出电压的最大值和最小值;Ug, max、Ug, min分别为网侧电源电压的最大值和最小值。
通过式(5)可知逆变器的输出方程:
| $ U_{\mathrm{dc}} m=U_{\mathrm{es}}+L_{\mathrm{f}} \frac{\mathrm{d} I_{L}}{\mathrm{d} t} $ | (30) |
结合式(29)、式(30),可得ES直流侧电压Udc稳态运行边界为:
| $ \begin{gather*} U_{\mathrm{dc}}= \\ \left\{\begin{array}{l} U_{\mathrm{dc}, \max } U_{\mathrm{g}}<U_{\mathrm{g}, \text { min }} \\ U_{\mathrm{s}}\left[1+\frac{R_{2} R_{3}+R_{3}\left(R_{1}+L_{1}\right)}{\left(R_{1}+L_{1}\right) R_{2}}\right]-\frac{R_{3}}{R_{1}+L_{1}} U_{\mathrm{g}}+L_{\mathrm{f}} \frac{\mathrm{d} I_{\mathrm{L}}}{\mathrm{d} t} \\ \quad\quad\quad\quad\quad U_{\mathrm{g}, \min } \leqslant U_{\mathrm{g}} \leqslant U_{\mathrm{g}, \max } \\ U_{\mathrm{dc}, \min } U_{\mathrm{g}}>U_{\mathrm{g}, \max } \end{array}\right. \end{gather*} $ | (31) |
式中:Udc, min、Udc, max分别为ES直流侧电压的最小值和最大值。
分析式(31)可知,ES的输出电压运行界限与线路阻抗、CL阻值、NCL阻值以及直流侧电压的大小相关。若电网网侧电压发生超过稳态运行范围的波动,使ES失去稳态运行的能力,可调节上述电阻值以及增大直流侧电压,来扩大ES输出电压稳态运行界限范围。
3 仿真及结果分析为验证文中提出的带有指令滤波的反步控制策略的可行性和优越性,在MATLAB/Simulink对其进行仿真实验,并将带有指令滤波的反步控制策略和PI控制[24-25]策略进行对比分析。ES仿真模型中的各元件的参数如表 1所示。
|
|
表 1 系统模型参数 Table 1 System model parameters |
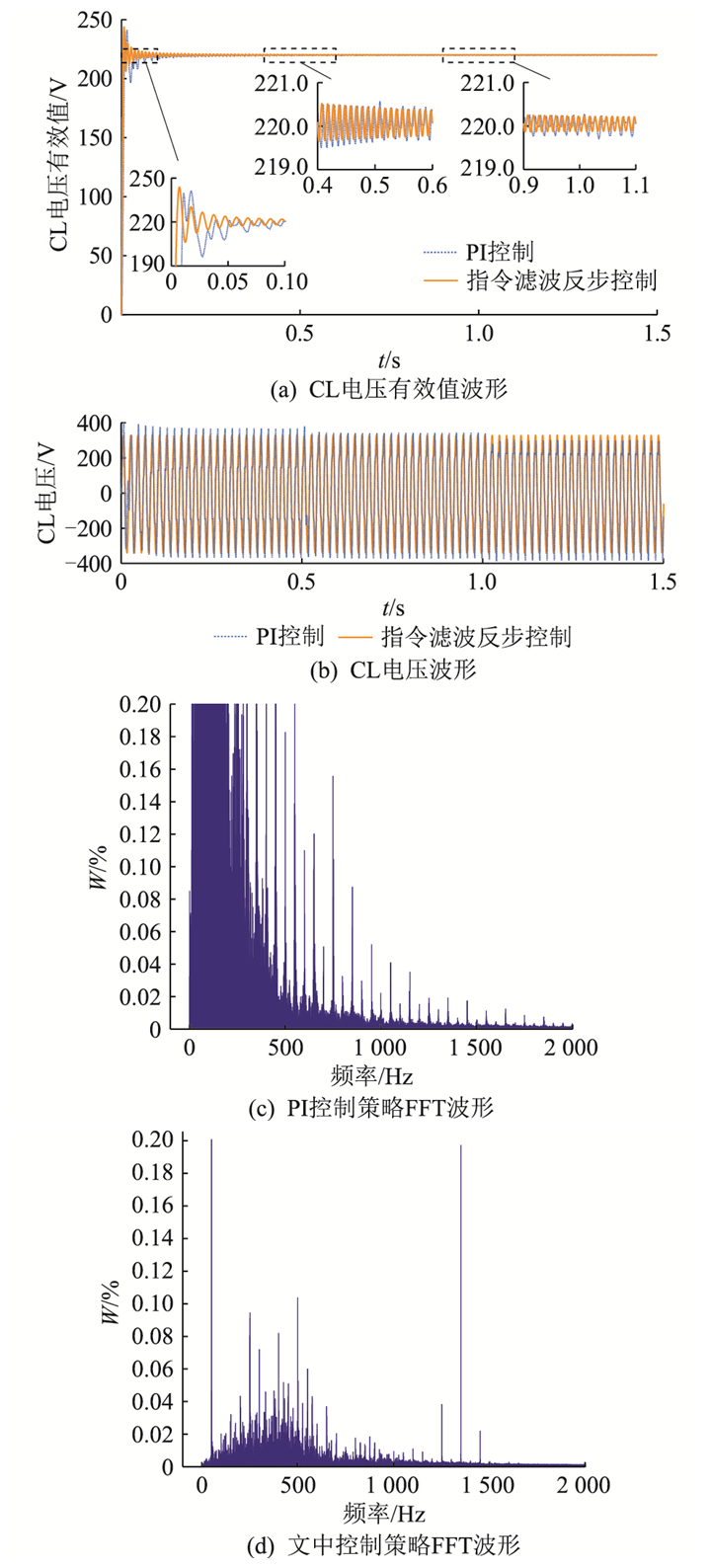
为验证新能源发电系统网侧电压瞬间突变时ES的控制效果,整个仿真过程时长设计为1.5 s,在0.5 s时网侧输出电压幅值从320 V下降至300 V;在1 s时,从300 V下降至280 V。仿真结果如图 5所示,其中图 5(a)为CL电压的有效值波形;图 5(b)为CL电压波形。从图 5(a)中可以看出,文中所提控制策略的CL电压在0.03 s附近达到相对稳定,PI控制策略的CL电压在0.1 s附近达到相对稳定,文中控制策略比PI控制电压达到稳定快0.07 s。在0.5 s和1.0 s网侧电压瞬变时刻,PI控制下,CL电压出现明显的波动和抖振,并且不能良好地跟踪参考电压,文中所提出的控制策略未出现明显的电压波动,同时也能将CL的电压牢牢地锁定在220 V附近。图 5(c)、(d)分别为2种控制方式下快速傅里叶变换(fast Fourier transformation,FFT)波形,其中,W为关键负载电压失真波形幅值的最大值减最小值与标准基波最大值减最小值的比值,整个仿真过程中可以看出PI控制策略下,CL电压波形总谐波失真度(total harmonic distortion,THD)为31.57%,幅值为296.7 V;文中提出的控制策略CL电压波形THD为0.57%,幅值为310.9 V,波形畸变率降低31%。相比于PI控制,文中提出的控制策略使CL的电压波形谐波含量大大减少、波形畸变率更低、CL电压更加稳定。
|
图 5 电网侧电压变化时CL电压 Fig. 5 CL voltage when grid-side voltage changes |
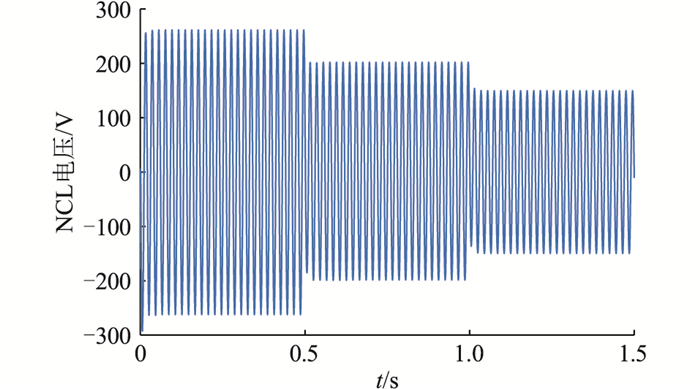
图 6为文中控制策略下的NCL电压波形,当网侧电压高于参考电压时,ES处于降压运行模式,NCL电压升高;当网侧电压低于参考电压时,ES处于升压运行模式,NCL电压降低,同时系统的电压波动转移给NCL。
|
图 6 电网侧电压变化时NCL电压 Fig. 6 NCL voltage when the grid-side voltage changes |
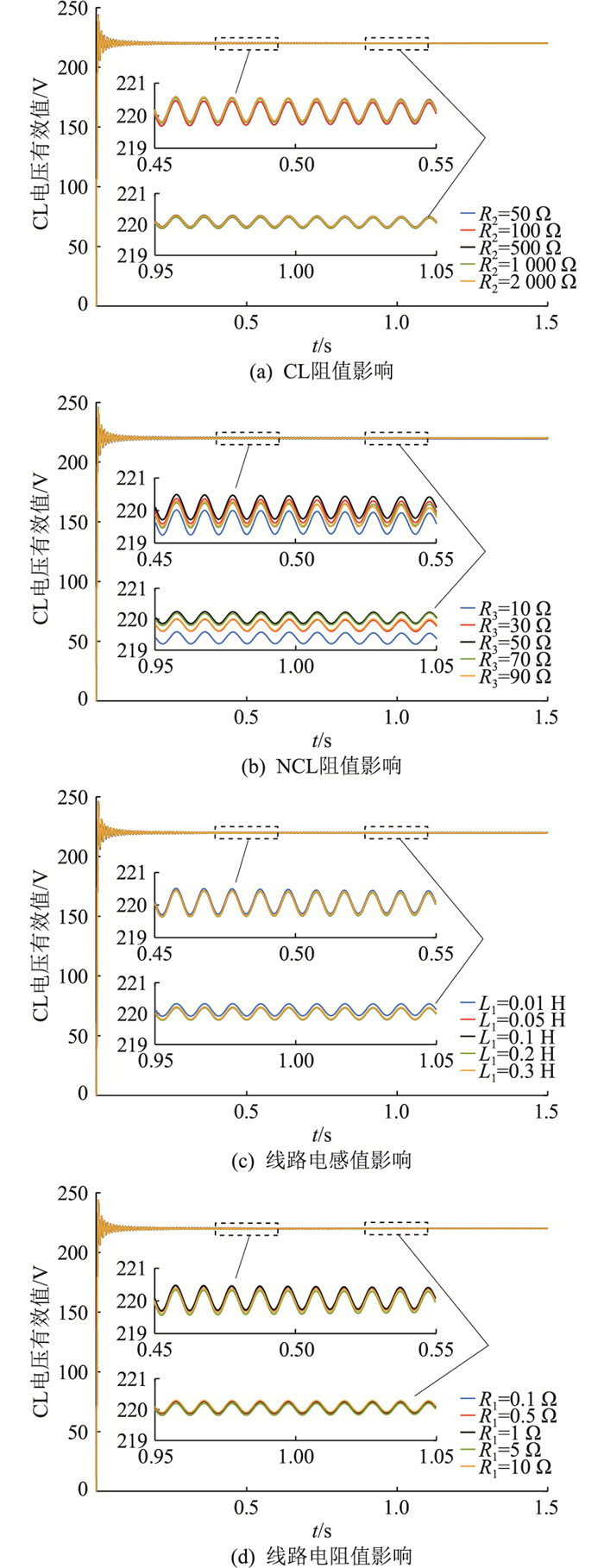
为验证系统参数对文中控制策略的影响程度,进行系统参数敏感性分析。保留3.1节中实验的电压突变情况和表 1的系统参数,仅改变研究对象参数的值。图 7(a)—(d)分别为CL阻值、NCL阻值、线路电感值和电阻值对CL电压有效值影响的分析,在系统参数改变时研究文中控制策略对CL电压的控制效果。结果显示当系统参数发生变化时,CL电压的有效值都能稳定趋于220 V,图 7(b)中,NCL阻值的变化对控制效果影响最大,但是最大电压偏差也能控制在0.7 V左右, 偏差率约为0.318%,说明文中的控制策略对系统参数的敏感性较低。
|
图 7 系统参数敏感性分析结果 Fig. 7 Analysis results of system parameter sensitivity |
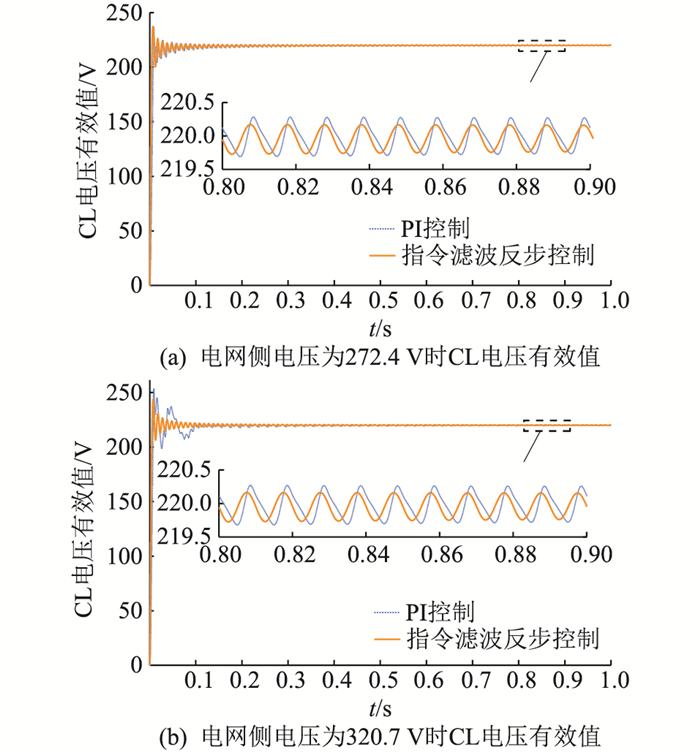
为比较2种控制方式下ES所能承受尽可能大的网侧电压波动范围,文中通过改变网侧电压的幅值不断逼近ES所能承受电压波动范围的临界值。仿真结果如图 8所示,其中图 8(a)、(b)分别为网侧电压幅值为272.4 V和320.7 V时,即传统PI控制策略下ES在极限运行电压时,2种控制策略下CL电压有效值波形。
|
图 8 电网侧电压为272.4 V和320.7 V时CL电压有效值 Fig. 8 The CL effective voltage values when the grid-side voltage is 272.4 V and 320.7 V |
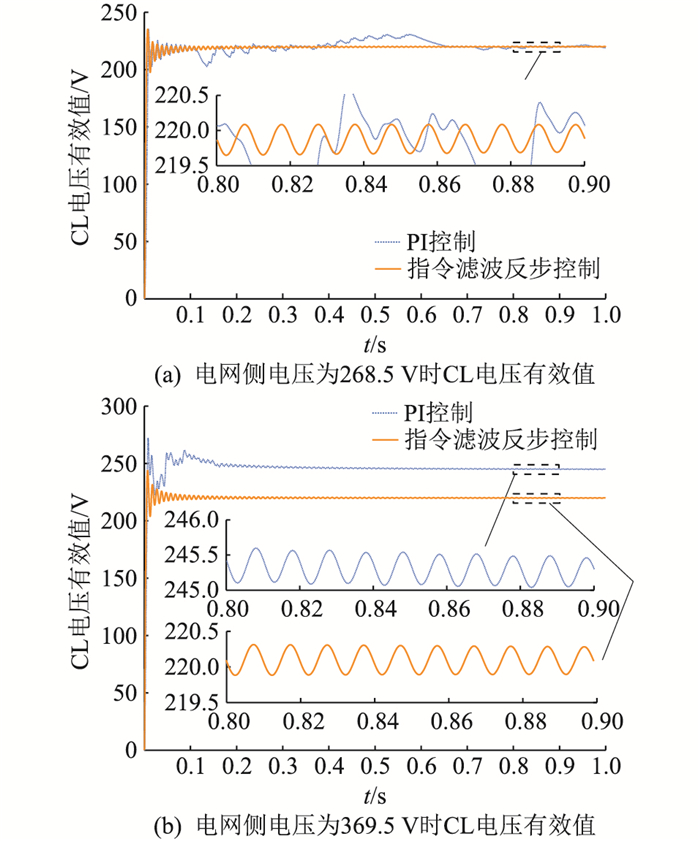
图 9(a)、(b)分别为网侧电压幅值为268.5 V和369.5 V时,即文中控制策略下,ES在极限运行电压时,2种控制策略下CL电压有效值波形。
|
图 9 电网侧电压为268.5 V和369.5 V时CL电压有效值 Fig. 9 The CL effective voltage values when the grid-side voltage is 268.5 V and 369.5 V |
经分析可知PI控制策略下,实现ES对CL电压稳定的控制目标,能够承受系统网侧的电压波动范围为272.4~320.7 V(有效值为192.62~226.77 V);带指令滤波反步控制策略下,实现CL电压稳定的控制目标,能够承受的网侧电压波动范围为268.5~369.7 V(有效值为189.85~261.27 V)。验证了文中所提出的策略能够使ES具有更大承受电压波动范围的能力,抗干扰能力强。
4 结论文中提出一种带有指令滤波的反步控制策略,应用于ES系统中,并且结合新能源发电系统模拟分布式电源发电过程中出现的间接性和不确定性所带来的电压波动问题。通过理论分析和推导以及仿真实验证明带有指令滤波的反步控制策略的优越性,同时得出下列结论:
(1) 在新能源发电系统网侧电压发生波动时,文中提出的控制策略相比PI控制达到稳定速度快0.07 s,动态响应速度快;波形畸变率降低31%,且基波幅值(310.9 V)能良好地跟踪参考电压幅值(311 V),相比PI控制电压波形谐波含量减少、畸变率降低,且对CL电压稳定效果更好。同时在电压突变时刻,PI控制下CL电压发生较明显的波动,而文中控制策略下CL电压波动较小且平滑过度。
(2) 文中所提出的控制策略对系统参数的敏感性较低,NCL阻值对控制效果有一定的影响,在敏感性分析实验中CL电压有效值偏差最大为0.7 V,偏差率为0.318%。
(3) PI控制策略下ES能承受电压幅值波动范围为48.3 V, 文中控制策略下ES能承受电压幅值波动范围为101.2 V,提高了52.9 V。文中的控制策略抗干扰能力更强。
(4) 文中仿真实验仅对网侧电压波动进行了仿真分析,未对其他波动(如频率波动、谐波污染、功率波动等)进行仿真分析。今后将进一步对文中控制策略进行研究和改进。
| [1] |
刘畅, 卓建坤, 赵东明, 等. 利用储能系统实现可再生能源微电网灵活安全运行的研究综述[J]. 中国电机工程学报, 2020, 40(1): 1-18, 369. LIU Chang, ZHUO Jiankun, ZHAO Dongming, et al. A review on the utilization of energy storage system for the flexible and safe operation of renewable energy microgrids[J]. Proceedings of the CSEE, 2020, 40(1): 1-18, 369. (  0) 0) |
| [2] |
袁志昌, 郭佩乾, 刘国伟, 等. 新能源经柔性直流接入电网的控制与保护综述[J]. 高电压技术, 2020, 46(5): 1460-1475. YUAN Zhichang, GUO Peiqian, LIU Guowei, et al. Review on control and protection for renewable energy integration through VSC-HVDC[J]. High Voltage Engineering, 2020, 46(5): 1460-1475. (  0) 0) |
| [3] |
HUI S Y, LEE C K, WU F F. Electric springs-a new smart grid technology[J]. IEEE Transactions on Smart Grid, 2012, 3(3): 1552-1561. DOI:10.1109/TSG.2012.2200701 (  0) 0) |
| [4] |
LEE C K, CHAUDHURI B, HUI S Y. Hardware and control implementation of electric springs for stabilizing future smart grid with intermittent renewable energy sources[J]. IEEE Journal of Emergingand Selected Topics in Power Electronics, 2013, 1(1): 18-27. DOI:10.1109/JESTPE.2013.2264091 (  0) 0) |
| [5] |
TAN S C, LEE C K, HUI S Y. General steady-state analysis and control principle of electric springs with active and reactive power compensations[J]. IEEE Transactions on Power Electronics, 2013, 28(8): 3958-3969. DOI:10.1109/TPEL.2012.2227823 (  0) 0) |
| [6] |
董丙伟, 薛花, 胡英俊, 等. 基于电力弹簧的可再生能源供电系统电压平稳控制方法[J]. 电测与仪表, 2020, 57(10): 100-107. DONG Bingwei, XUE Hua, HU Yingjun, et al. Voltage stabilization control method of renewable energy power supply system based on electric spring[J]. Electrical Measurement & Instrumentation, 2020, 57(10): 100-107. (  0) 0) |
| [7] |
AKHTAR Z, CHAUDHURI B, HUI S Y R. Smart loads for voltage control in distribution networks[J]. IEEE Transactions on Smart Grid, 2015, 1-10. (  0) 0) |
| [8] |
程明, 王青松, 张建忠. 电力弹簧理论分析与控制器设计[J]. 中国电机工程学报, 2015, 35(10): 2436-2444. CHENG Ming, WANG Qingsong, ZHANG Jianzhong. Theoretical analysis and controller design of electric springs[J]. Proceedings of the CSEE, 2015, 35(10): 2436-2444. (  0) 0) |
| [9] |
尹发根, 王淳. 电力弹簧研究进展: 原理、拓扑结构、控制和应用[J]. 电网技术, 2019, 43(1): 174-184. YIN Fagen, WANG Chun. Review of electric spring: principle, topologies, control and applications[J]. Power System Technology, 2019, 43(1): 174-184. (  0) 0) |
| [10] |
吴捷, 王宝华. 基于最优比例积分的电力弹簧控制器设计[J]. 电气自动化, 2017, 39(4): 39-43. WU Jie, WANG Baohua. Design of an electric spring controller based on optimal PI[J]. Electrical Automation, 2017, 39(4): 39-43. (  0) 0) |
| [11] |
SHUO Y, TAN S C, LEE C K, et al. Electric spring for power quality improvement[C]//2014 IEEE Applied Power Electronics Conference and Exposition-APEC 2014. Fort Worth, TX, USA. IEEE, 2014: 2140-2147.
(  0) 0) |
| [12] |
鲍克勤, 吴浩强, 程启明, 等. 基于E-L模型的电力弹簧无源控制策略[J]. 高电压技术, 2022, 48(12): 4986-4995. BAO Keqin, WU Haoqiang, CHENG Qiming, et al. Passive-based control strategy of electric springs based on E-L model[J]. High Voltage Engineering, 2022, 48(12): 4986-4995. (  0) 0) |
| [13] |
WANG Q S, CHENG M, CHEN Z, et al. Steady-state analysis of electric springs with a novel δ control[J]. IEEE Transactions on Power Electronics, 2015, 30(12): 7159-7169. DOI:10.1109/TPEL.2015.2391278 (  0) 0) |
| [14] |
MOK K T, TAN S C, RON HUI S Y. Decoupled power angle and voltage control of electric springs[J]. IEEE Transactions on Power Electronics, 2016, 31(2): 1216-1229. DOI:10.1109/TPEL.2015.2424153 (  0) 0) |
| [15] |
赵科淇, 于金飞, 刘加朋, 等. 永磁同步电动机指令滤波离散容错控制[J/OL]. 控制工程: 1-7[2023-12-03]. https://doi.org/10.14107/j.cnki.kzgc.20220761. ZHAO Keqi, YU Jinfei, LIU Jiapeng, et al. Discrete fault tolerant control of permanent magnet synchronous motor via command filtering[J/OL]. Contorl Engineering of China: 1-7[2023-12-03]. https://doi.org/10.14107/j.cnki.kzgc.20220761. (  0) 0) |
| [16] |
EL MAJDOUB K, GIRI F, CHAOUI F Z. Adaptive backstepping control design for semi-active suspension of half-vehicle with magnetorheological damper[J]. CAA Journal of Automatica Sinica, 2021, 8(3): 582-596. DOI:10.1109/JAS.2020.1003521 (  0) 0) |
| [17] |
STOLZLE M, DELLA SANTINA C. Piston-driven pneumatically-actuated soft robots: modeling and backstepping control[J]. IEEE Control Systems Letters, 2022, 6: 1837-1842. (  0) 0) |
| [18] |
ELIKER K, ZHANG W D. Finite-time adaptive integral backstepping fast terminal sliding mode control application on quadrotor UAV[J]. International Journal of Control, Automation and Systems, 2020, 18(2): 415-430. (  0) 0) |
| [19] |
TONG S C, LI Y M, SHI P. Observer-based adaptive fuzzy backstepping output feedback control of uncertain MIMO pure-feedback nonlinear systems[J]. IEEE Transactions on Fuzzy Systems, 2012, 20(4): 771-785. (  0) 0) |
| [20] |
BINH N T, TUNG N A, NAM D P, et al. An adaptive backstepping trajectory tracking control of a tractor trailer wheeled mobile robot[J]. International Journal of Control, Automation and Systems, 2019, 17(2): 465-473. (  0) 0) |
| [21] |
张加伟, 于金鹏, 刘加朋, 等. 基于观测器的异步电动机指令滤波离散控制[J]. 控制工程, 2023, 30(10): 1891-1899. ZHANG Jiawei, YU Jinpeng, LIU Jiapeng, et al. Observer- based command filtered discrete-time control for induction motor[J]. Control Engineering of China, 2023, 30(10): 1891-1899. (  0) 0) |
| [22] |
王青松. 电力弹簧若干关键技术研究[D]. 南京: 东南大学, 2016. WANG Qingsong. Research on key issues of electric springs[D]. Nanjing: Southeast University, 2016. (  0) 0) |
| [23] |
路遥. 基于跟踪微分器的高超声速飞行器Backstepping控制[J]. 航空学报, 2021, 42(11): 524737. LU Yao. Backstepping control for hypersonic flight vehicles based on tracking differentiator[J]. Acta Aeronautica et Astronautica Sinica, 2021, 42(11): 524737. (  0) 0) |
| [24] |
CHAUDHURI N R, LEE C K, CHAUDHURI B, et al. Dynamic modeling of electric springs[J]. IEEE Transactions on Smart Grid, 2014, 5(5): 2450-2458. (  0) 0) |
| [25] |
詹俊. 电气弹簧若干关键技术的研究[D]. 上海: 上海电机学院, 2018. ZHAN Jun. Research on key technology of electric spring[D]. Shanghai: Shanghai Dianji University, 2018. (  0) 0) |
2. School of Internet of Things Engineering, Jiangnan University, Wuxi 214122, China;
3. School of Automation, Wuhan University of Technology, Wuhan 430070, China
 2024, Vol. 43
2024, Vol. 43


 杨成顺(1984), 男, 博士, 副教授, 研究方向为新能源系统优化运行与先进控制方法(E-mail:
杨成顺(1984), 男, 博士, 副教授, 研究方向为新能源系统优化运行与先进控制方法(E-mail: