文章编号: 2096-3203(2024)02-0083-11 中图分类号: TM721
2. 南方电网科学研究院有限责任公司, 广东 广州 510700;
3. 云南电网有限责任公司电力科学研究院, 云南 昆明 650217
在“双碳”目标与能源转型的驱动下,可再生能源发电装置规模化接入电力系统。以风电、光伏为代表的可再生能源发电装置已成为我国电力系统的重要电力来源[1-3]。总体上,我国大规模风电、光伏资源集中于“三北”地区,电力负荷集中于东部地区,因而广泛应用高压直流输电(high voltage direct current, HVDC)技术以减小远距离输电过程中的损耗。现阶段,电网换相换流器型高压直流输电(line commutated converter based high voltage direct current, LCC-HVDC)技术凭借其建设成本的优势已经在多个直流输电示范工程中实践应用[4-6]。
然而,由于移相调制原理的限制,LCC-HVDC线路换流站运行时所吸收的无功功率大约为线路传输有功功率的40%~60%,因此新能源送端换流站需要装设大量的无功补偿装置(如电力电容器)[7]。一旦直流闭锁、换相失败等故障导致某条直流输电线路退出运行,电力电容器由于机械开关的时延难以立即退出,LCC-HVDC送端换流站将会出现大量过剩无功并引发暂态过电压。2011年2月24日的西北电网直流闭锁造成的暂态过电压引起风机脱网达598台,损失有功出力83.7万千瓦,严重威胁电网安全稳定运行[8-10]。为避免暂态过电压引起的新能源发电装置大规模脱网,现有工程常采取将直流线路传输容量限制在额定容量以下的方式[11-13]。
现阶段,抑制LCC-HVDC送端暂态过电压的方法主要有2类。一类是利用风力发电机组换流器吸收过剩的无功,优势是不需要投入额外的设备。文献[14]基于对送端暂态过电压发展过程的定量分析,提出了一种双馈异步发电机(doubly fed induction generator, DFIG)转子侧换流器(rotor side converter, RSC)与网侧换流器(grid side converter, GSC)协同控制的风机高压故障穿越策略,在故障期间向LCC-HVDC系统注入合理的无功抑制暂态过电压。在文献[15]中,电网电压测量环路所引入的时延被证明是暂态过电压的主导因素,因此将一个附加的信号引入风力发电装置的功率控制环路补偿电压测量环路时延,从而抑制暂态过电压。尽管这类方法在理论上具有吸收过剩无功并抑制送端过电压的应用潜力,但是改造成熟的风机控制系统在工程实践上具有一定的困难。另一类是在系统中配置快速无功补偿装置。静止无功补偿器(static var compensator, SVC)和静止同步补偿器(static synchronous compensator, STATCOM)[16-18]可根据本地电压偏差快速改变无功注入,从而实现抑制新能源送端暂态过电压。一般来说,SVC和STATCOM的电压-无功动态响应特性会随着电压测量环路的带宽和交流电压控制环路的增益增大而提升,但带宽和电压控制环路增益由于稳定运行约束而被限制在一定范围内[19]。另外,SVC和STATCOM的电力电子多时间尺度级联控制环路不可避免地会引入一定的时延,导致具有电流源外特性的补偿设备无功响应不是即时的。因此,具有电压动态自然支撑能力的电压源外特性补偿装备——同步调相机(synchronous condenser, SC)被尝试应用于抑制送端暂态过电压[20-21],但由于成本高昂、提升短路电流等问题,应用范围十分有限。
近年来,通过部分或全部模拟同步发电机动态特性的变流器虚拟同步发电机(virtual synchronous generation, VSG)控制技术已被广泛研究与应用[22-26]。基于VSG控制的换流器能够独立构建系统的频率和电压,因而是一种构网型控制技术,其通过虚拟惯量特性能够有效抑制频率快速变化,改善频率动态特性。然而,构网型控制技术用于改善电压动态特性的能力尚未被广泛注意。
为此,文中提出一种应用构网型无功补偿装置(grid-forming based reactive power compensation device, GFM-RPC)抑制新能源送端暂态过电压的方法,GFM-RPC由储能装置、变流器、构网型控制器组成。与SVC和STATCOM不同,具有电压源外特性的GFM-RPC能够提供即时、自然的无功响应,避免了电压外环-电流内环级联控制环路引入的时延,从而有效抑制新能源送端暂态过电压。首先建立GFM-RPC的控制系统模型,并简要分析主要参数对电压动态的影响规律。然后构建基于微分-代数方程的简单系统电压动态分析模型,阐明GFM-RPC对于电压动态的改善机理,并分析基于GFM-RPC的电压动态改善方法相比现有基于SVC或STATCOM的电压动态改善方法的优势。最后通过仿真验证了GFM-RPC抑制新能源送端暂态过电压的作用。
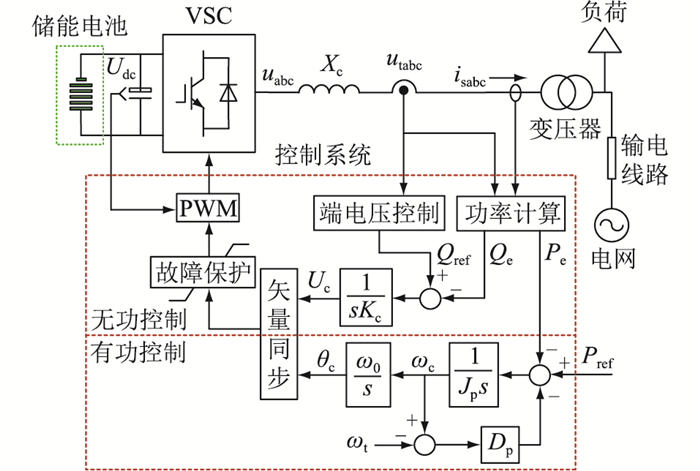
1 GFM-RPC 1.1 GFM-RPC的拓扑及控制系统文中所提GFM-RPC的拓扑及控制系统如图 1所示。GFM-RPC采用包含有功控制支路和无功控制支路在内的电压矢量控制策略,其中有功控制支路的有功参考指令设置为0。有功控制支路和无功控制支路分别直接控制电压源型换流器(voltage source converter, VSC)内电势的相角和幅值,进而在不需要电流控制环的前提下控制GFM-RPC与电网交换的有功及无功功率。其中,Udc为VSC直流侧电容电压值;uabc、utabc分别为VSC输出电压三相瞬时值和VSC并网点电压三相瞬时值;isabc为VSC输出电流三相瞬时值;Xc为VSC滤波电抗值。脉冲宽度调制(pulse width modulation, PWM)模块用于调制VSC输出电压三相瞬时值。
|
图 1 GFM-RPC的拓扑及控制系统 Fig. 1 The topology and control system of GFM-RPC |
有功控制支路的数学表达式为:
| $ \left\{\begin{array}{l} \theta_{\rm{c}}=\frac{\omega_0}{s} \omega_{\mathrm{c}} \\ \omega_{\mathrm{c}}=\frac{1}{J_{\mathrm{p}} s}\left[P_{\mathrm{ref}}-P_{\mathrm{e}}-D_{\mathrm{p}}\left(\omega_{\mathrm{c}}-\omega_{\mathrm{t}}\right)\right] \end{array}\right. $ | (1) |
式中:θc为GFM-RPC的内电势输出相角;ω0为系统额定频率,取值为50 Hz;ωc、ωt分别为GFM-RPC的内电势和端电压的角频率;Pref、Pe分别为GFM-RPC的有功参考值和有功输出实际值;Jp、Dp分别为GFM-RPC的虚拟惯量系数和阻尼系数。
无功控制支路的数学表达式为:
| $ U_{\mathrm{c}}=\frac{1}{s K_{\mathrm{c}}}\left(Q_{\mathrm{ref}}-Q_{\mathrm{e}}\right) $ | (2) |
式中:Uc为GFM-RPC的内电势幅值;Qref、Qe分别为GFM-RPC的无功参考值和无功输出实际值;Kc为GFM-RPC的电压刚度系数。
与具有电流源外特性的STATCOM不同,GFM-RPC具有电压源外特性,使得其内电势在扰动下具有保持相对稳定的能力。当电网电压快速变化时,STATCOM不具备保持内电势相对稳定的能力,如图 2(a)所示。另外,级联控制环路时延带来的“反调”特性使得STATCOM不仅不能向系统提供快速无功支撑,反而会短时吸收无功恶化端电压动态,如图 2(b)、(c)所示。而具有电压主动支撑能力的GFM-RPC能够在电网扰动发生后保持其内电势相对稳定,并且自然、即时地向系统提供无功支撑以抑制电压快速波动。

|
图 2 电网电压扰动下STATCOM和GFM-RPC的内电势、端电压及无功动态响应 Fig. 2 The inner potential, terminal voltage and reactive power dynamic response of STATCOM and GFM-RPC under grid voltage disturbance |
在MATLAB/Simulink中建立图 1所示的单机无穷大系统以研究主要参数对端电压动态特性的影响规律。
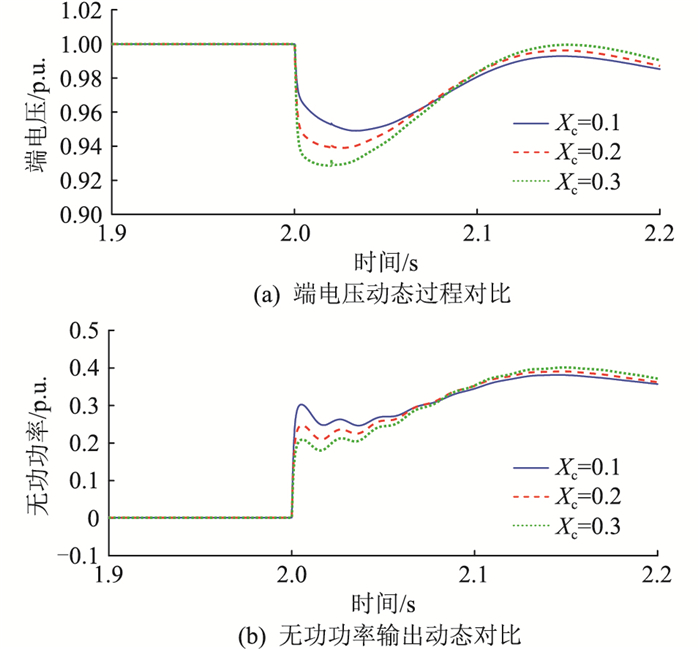
保持GFM-RPC的电压刚度系数Kc不变,在2 s时设置无功负荷从0跳变至0.4 p.u.,如图 3所示,随着滤波电抗Xc的减小,GFM-RPC提供的无功功率增大,而端电压的波动随之减小。
|
图 3 不同滤波电抗Xc下的端电压动态与GFM-RPC无功响应 Fig. 3 The terminal voltage dynamics and the reactive power response of GFM-RPC with different filter impedances |
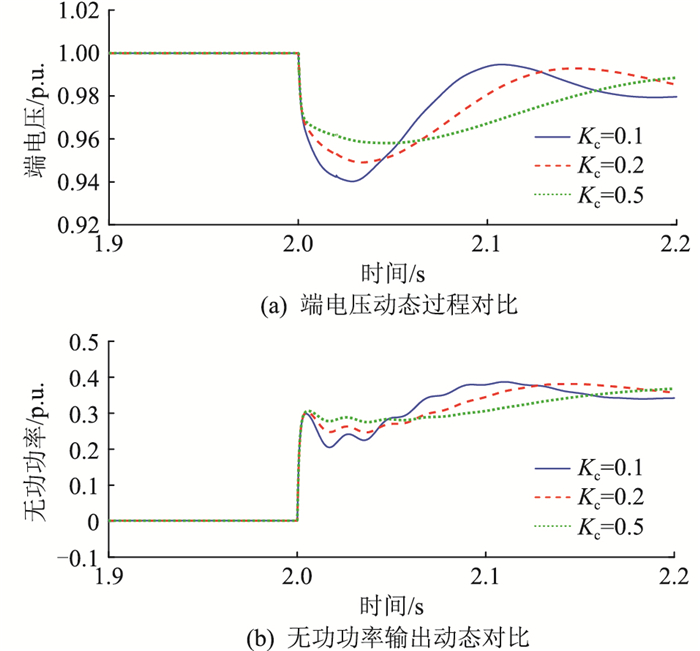
保持滤波电抗Xc不变,在2 s时设置无功负荷从0跳变至0.4 p.u.,如图 4所示,随着电压刚度系数Kc增大,GFM-RPC在扰动发生瞬间提供的无功功率幅值不变,端电压和无功功率的波动减小。
|
图 4 不同电压刚度系数Kc下的端电压动态与GFM-RPC无功响应 Fig. 4 The terminal voltage dynamics and the reactive power response of GFM-RPC with different voltage resilience coefficients |
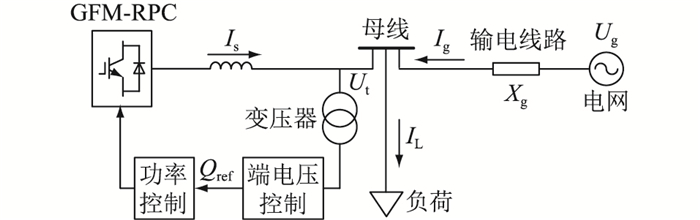
文中采用图 5所示的简化电力系统研究GFM-RPC对于暂态过电压动态的影响。GFM-RPC和恒定负荷连接在并网点母线上,并网点母线通过输电线路连接至无穷大电网。端电压Ut通过GFM-RPC的交流电压及功率控制环路实现调节。图 5中,IL、Ig、Is分别为流入负荷的电流、电网输出电流以及GFM-RPC输出电流;Ug、Xg分别为电网电压幅值和输电线路电抗。
|
图 5 用于暂态过电压动态分析的简化电力系统 Fig. 5 Simplified power system for dynamic analysis of transient overvoltage |
交流电压控制环路的数学表达式为:
| $ G_{\mathrm{ac}}=\frac{K_{\mathrm{A}}}{1+s T_{\mathrm{A}}} $ | (3) |
式中:Gac为交流电压控制环路的传递函数;KA、TA分别为交流电压控制的增益系数和时间常数。
系统中的电流可以表示为:
| $ \left\{\begin{array}{l} I_{\mathrm{L}}=I_{\mathrm{g}}+I_{\mathrm{s}}\\ I_{\mathrm{g}}=\left(U_{\mathrm{g}}-U_{\mathrm{t}}\right) / X_{\mathrm{g}} \end{array}\right. $ | (4) |
系统中的有功、无功功率可以表示为:
| $ \left\{\begin{array}{l} P_{\mathrm{L}}=P_{\mathrm{e}}+P_{\mathrm{g}}\\ Q_{\mathrm{L}}=Q_{\mathrm{e}}+Q_{\mathrm{g}} \end{array}\right. $ | (5) |
式中:PL、QL分别为流入负荷的有功、无功功率;Pg、Qg分别为电网输出有功、无功功率。
Pg和Qg可以表示为:
| $ \left\{\begin{array}{l} P_{\mathrm{g}}=U_{\mathrm{t}} U_{\mathrm{g}} \sin \left(\theta_{\mathrm{g}}-\theta_{\mathrm{t}}\right) / X_{\mathrm{g}}\\ Q_{\mathrm{g}}=\left(U_{\mathrm{t}} U_{\mathrm{g}} \cos \left(\theta_{\mathrm{g}}-\theta_{\mathrm{t}}\right)-U_{\mathrm{t}}^{2}\right) / X_{\mathrm{g}} \end{array}\right. $ | (6) |
式中:θg、θt分别为电网电压和端电压的相角。
Pe和Qe可以表示为:
| $ \left\{\begin{array}{l} P_{\mathrm{e}}=U_{\mathrm{t}} U_{\mathrm{c}} \sin \left(\theta_{\mathrm{c}}-\theta_{\mathrm{t}}\right) / X_{\mathrm{c}}\\ Q_{\mathrm{e}}=\left(U_{\mathrm{t}} U_{\mathrm{c}} \cos \left(\theta_{\mathrm{c}}-\theta_{\mathrm{t}}\right)-U_{\mathrm{t}}^{2}\right) / X_{\mathrm{c}} \end{array}\right. $ | (7) |
稳态时,GFM-RPC的输出有功功率为0,即:
| $ \left\{\begin{array}{l} \theta_{\mathrm{c} 0}=\theta_{\mathrm{t} 0}\\ \sin \left(\theta_{\mathrm{c} 0}-\theta_{\mathrm{t} 0}\right)=0 \\ \cos \left(\theta_{\mathrm{c} 0}-\theta_{\mathrm{t} 0}\right)=1 \end{array}\right. $ | (8) |
式中:θc0、θt0分别为GFM-RPC的内电势输出相角初值和端电压相角初值。
扰动下,无功功率的变化量可以表示为:
| $ \Delta Q_{\mathrm{L}}=\Delta Q_{\mathrm{e}}+\Delta Q_{\mathrm{g}} $ | (9) |
其中:
| $ \left\{\begin{align*} \Delta Q_{\mathrm{e}}= & \frac{U_{\mathrm{c} 0}-2 U_{\mathrm{t} 0}}{X_{\mathrm{c}}} \Delta U_{\mathrm{t}}+\frac{U_{\mathrm{t0}}}{X_{\mathrm{c}}} \Delta U_{\mathrm{c}}\\ \Delta Q_{\mathrm{g}}= & \frac{U_{\mathrm{g} 0}\cos \left(\theta_{\mathrm{g} 0}-\theta_{\mathrm{t0}}\right)-2 U_{\mathrm{t} 0}}{X_{\mathrm{g}}} \Delta U_{\mathrm{t}}+ \\ & \frac{U_{\mathrm{t} 0} U_{\mathrm{g} 0} \sin \left(\theta_{\mathrm{g} 0}-\theta_{\mathrm{t} 0}\right)}{X_{\mathrm{g}}} \Delta \theta_{\mathrm{t}} \end{align*}\right. $ | (10) |
式中:Uc0、Ut0分别为GFM-RPC内电势幅值初值和端电压幅值初值;Ug0、θg0分别为电网电压幅值初值和相角初值;ΔUc、ΔUt分别为内电势幅值变化量和端电压幅值变化量;Δθt为端电压相角变化量。
GFM-RPC和电网的输出有功变化量可以表示为:
| $ \left\{\begin{array}{l} \Delta P_{\mathrm{e}}=\frac{U_{\mathrm{c} 0} U_{\mathrm{t} 0}}{X_{\mathrm{c}}}\left(\Delta \theta_{\mathrm{c}}-\Delta \theta_{\mathrm{t}}\right)\\ \Delta P_{\mathrm{g}}=\frac{U_{\mathrm{g} 0} \sin \left(\theta_{\mathrm{g} 0}-\theta_{\mathrm{t} 0}\right)}{X_{\mathrm{g}}} \Delta U_{\mathrm{t}}- \\ \frac{U_{\mathrm{t0}} U_{\mathrm{g} 0} \cos \left(\theta_{\mathrm{g} 0}-\theta_{\mathrm{t} 0}\right)}{X_{\mathrm{g}}} \Delta \theta_{\mathrm{t}} \end{array}\right. $ | (11) |
GFM-RPC的内电势幅值及相角变化量为:
| $ \left\{\begin{array}{l} \Delta U_{\mathrm{c}}=\frac{1}{s K_{\mathrm{c}}}\left(\Delta Q_{\text {ref }}-\Delta Q_{\mathrm{e}}\right)\\ \Delta \theta_{\mathrm{c}}=\frac{\omega_{0}}{J_{\mathrm{p}} s}\left(\Delta P_{\text {ref }}-\Delta P_{\mathrm{e}}-D_{\mathrm{p}} \frac{s}{\omega_{0}} \Delta \theta_{\mathrm{c}}+D_{\mathrm{p}} \frac{s}{\omega_{0}} \Delta \theta_{\mathrm{t}}\right) \end{array}\right. $ | (12) |
式中:ΔPref、ΔQref分别为有功、无功输出参考值变化量。
将式(12)代入(11)可得:
| $ \Delta P_{\mathrm{e}}=\frac{-J_{\mathrm{p}} U_{\mathrm{t} 0} U_{\mathrm{c} 0} s^{2}}{J_{\mathrm{p}} X_{\mathrm{c}} s^{2}+X_{\mathrm{c}} D_{\mathrm{p}} s+U_{\mathrm{t0}} U_{\mathrm{c} 0} \omega_{0}} \Delta \theta_{\mathrm{t}} $ | (13) |
假设负荷类型为恒阻抗负荷,随着端电压的变化,负荷有功功率变化可以表示为:
| $ \Delta P_{\mathrm{L}}=\Delta P_{\mathrm{e}}+\Delta P_{\mathrm{g}}=\frac{2 U_{\mathrm{t0}}}{R} \Delta U_{\mathrm{t}} $ | (14) |
式中:R为输电线路电阻值。
将式(11)代入(14)可得:
| $\begin{array}{*{20}{c}} \Delta \theta_{\mathrm{t}}=\left[\left(\frac{2 U_{\mathrm{t} 0}}{R}-\frac{U_{\mathrm{g} 0} \sin \left(\theta_{\mathrm{g} 0}-\theta_{\mathrm{t} 0}\right)}{X_{\mathrm{g}}}\right) \Delta U_{\mathrm{t}}-\Delta P_{\mathrm{e}}\right] \times \\ \frac{-X_{\mathrm{g}}}{U_{\mathrm{t} 0} U_{\mathrm{g} 0} \cos \left(\theta_{\mathrm{g} 0}-\theta_{\mathrm{t} 0}\right)} \end{array} $ | (15) |
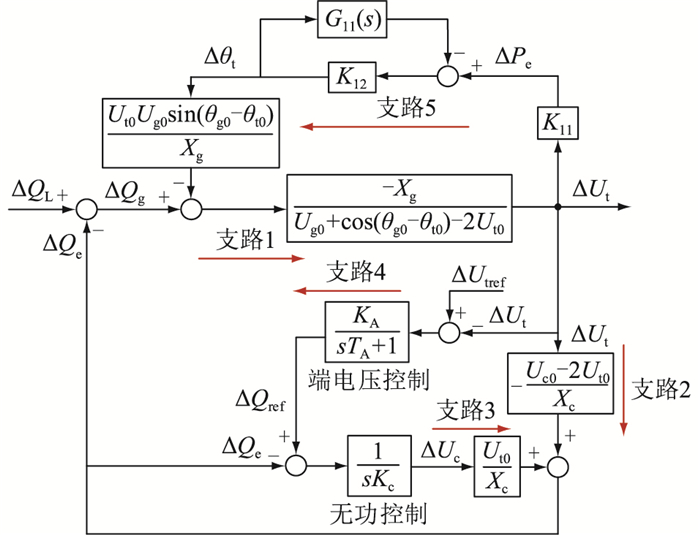
将式(8)—式(15)线性化,可得含GFM-RPC的系统电压动态线性化分析模型,其传递函数框图如图 6所示。其中,参数K11、K12以及传递函数G11(s)可以表示为:
| $ \begin{align*} & \left\{\begin{array}{l} K_{11}=\frac{2 U_{\mathrm{t} 0}}{R}-\frac{U_{\mathrm{g} 0} \sin \left(\theta_{\mathrm{g} 0}-\theta_{{\rm{t0}}}\right)}{X_{\mathrm{g}}} \\ K_{12}=\frac{-X_{\mathrm{g}}}{U_{{\rm{t0}}} U_{\mathrm{g} 0} \cos \left(\theta_{\mathrm{g} 0}-\theta_{{\rm{t0}}}\right)} \end{array}\right.\\ \end{align*} $ | (16) |
| $ G_{11}(s)=\frac{-J_{\mathrm{p}} U_{{\rm{t0}}} U_{\mathrm{c} 0} s^{2}}{J_{\mathrm{p}} X_{\mathrm{c}} s^{2}+X_{\mathrm{c}} D_{\mathrm{p}} s+U_{{\rm{t0}}} U_{\mathrm{c} 0} \omega_{0}} $ | (17) |
|
图 6 含GFM-RPC的系统电压动态线性化分析模型 Fig. 6 Linearized voltage dynamic model of system with GFM-RPC |
图 6中,ΔUtref为交流电压控制参考值变化量,在文中所关注的电压动态过程中ΔUtref忽略不计;支路1为负荷无功变化引起母线电压变化的路径,与系统有功运行点和传输线路阻抗有关;支路2为母线电压变化引起GFM-RPC无延时自然无功响应的路径;支路3为GFM-RPC无功功率控制的作用路径;支路4为交流电压控制的作用路径;支路5为母线电压幅值通过影响母线电压相位间接影响电网输出无功功率的作用路径,与系统有功运行点、线路阻抗、GFM-RPC有功控制参数等因素有关。
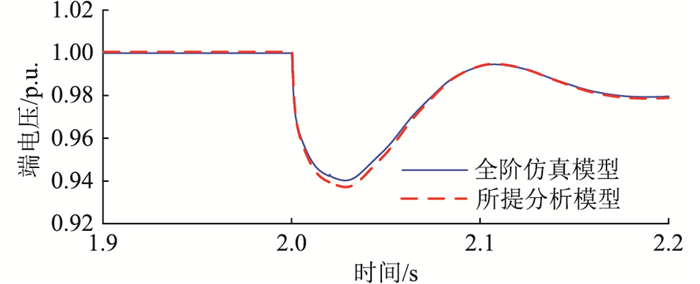
在MATLAB/Simulink仿真软件中对上述电压动态线性化分析模型和图 5所示电压分析系统的全阶仿真模型进行无功扰动仿真实验,仿真结果如图 7所示。所提分析模型的仿真结果与全阶仿真模型的运行结果具有较高的拟合性,因此该分析模型对于系统在外界无功扰动时的电压动态特性分析具有较高的可参考度。
|
图 7 所提电压动态分析模型的验证 Fig. 7 Validation of the proposed voltage dynamic analysis model |
对图 6所示模型中支路5的传递函数做伯德图分析,结果如图 8所示,支路5增益不超过-15 dB。这说明母线电压幅值通过影响母线电压相位间接影响电网输出无功功率的作用效果很小,可以忽略。

|
图 8 支路5的传递函数伯德图 Fig. 8 The bode diagram of branch 5 |
根据图 6所示模型,结合图 5的电压分析系统仿真模型,将受到扰动时,GFM-RPC作用下系统电压变化过程分为如下3个阶段。
阶段1:自然响应阶段,从受到外界无功扰动到无功控制生效。
阶段2:回归阶段,无功控制生效到交流电压控制生效。
阶段3:补偿阶段,交流电压控制下电压恢复。
在仿真中设置GFM-RPC无功控制前不加交流电压控制,在2 s时负荷无功从消耗0.2 p.u.增至0.4 p.u.,对照组使用一恒定无功功率源代替GFM-RPC,输出功率与GFM-RPC初始值一致。
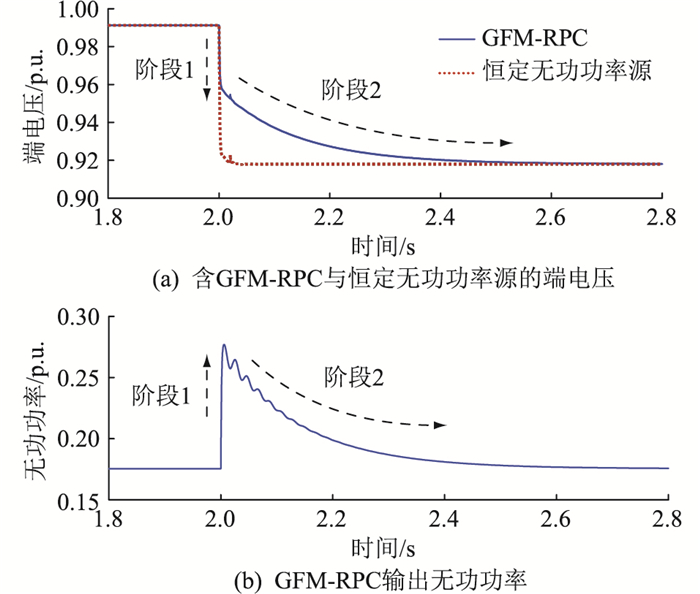
阶段1的变化主要受图 6所示模型中支路1和支路2的影响,支路1只与传输线路阻抗和系统有功运行点有关。对于GFM-RPC,支路2的增益为(Uc0-2Ut0)/Xc,符号为负,Xc较小,一般约为0.1 p.u.甚至更小,因此支路2的增益较大,约为10。当端电压在外界无功干扰下下降时,即ΔUt < 0,通过支路2中GFM-RPC产生的自然无功响应为正,ΔQe>0,如图 9(b)所示,抑制电压下降。类似地,当端电压上升时,GFM-RPC将产生负的自然无功响应,抑制电压升高。因此,当无功扰动引发系统电压变化时,GFM-RPC的电压刚度特性会使其被动产生正调性质的无功响应,达到抑制电压变化、为系统提供电压支撑的目的。图 9(a)中,GFM-RPC端电压下降的幅度远小于对照组,这表明在外界无功扰动下,GFM-RPC产生的正调性质的自然无功响应可以在第一时间很大程度地抑制电压变化。
|
图 9 阶段1、2中端电压动态以及GFM-RPC输出无功功率的仿真结果 Fig. 9 The simulation results of the terminal voltage dynamics and the reactive power output by GFM-RPC in stage 1 and 2 |
阶段2时受到支路3补偿器无功控制的影响,自然响应过后,在无功控制的作用下,GFM-RPC输出的无功功率从自然响应向无功参考值(无功初始值)回归,如图 9(b)所示,端电压也随之回归,如图 9(a)所示。
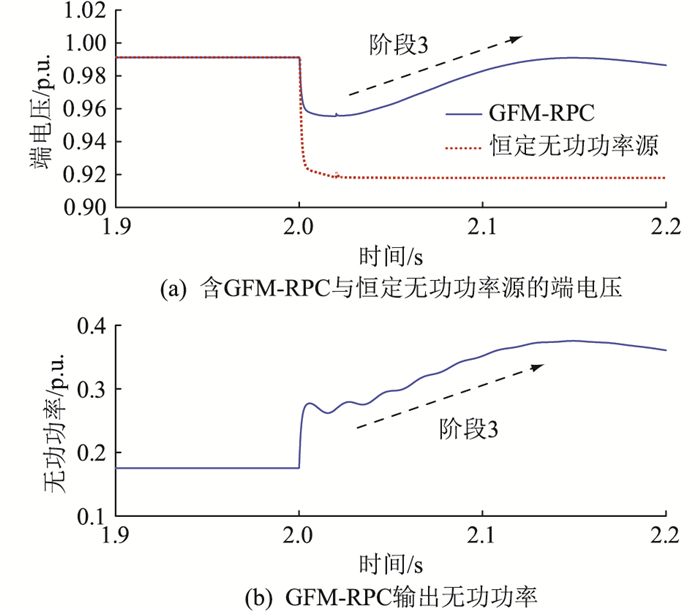
阶段3,在交流电压控制的作用下,阶段2的回归过程被截断,GFM-RPC无功参考值在交流电压控制下变化,端电压下降的情况下,无功参考值被调高,GFM-RPC输出无功功率上升,端电压随之上升,如图 10所示。
|
图 10 阶段3中端电压动态以及GFM-RPC输出无功功率的仿真结果 Fig. 10 The simulation results of the terminal voltage dynamics and the reactive power output by GFM-RPC in stage 3 |
总结GFM-RPC作用下系统电压在外界无功干扰下发展的整个过程。在系统电压变化时,GFM-RPC由于其自身的电压刚度特性会被动地产生正调性质的自然无功响应,在第一时间抑制系统电压的变化,随后在交流电压控制和无功控制作用下,GFM-RPC进一步产生更多的无功输出从而恢复电压水平。GFM-RPC自身的电压刚度特性在系统电压受到扰动,尤其是快速扰动时,可以为系统提供电压支撑,平抑电压变化。
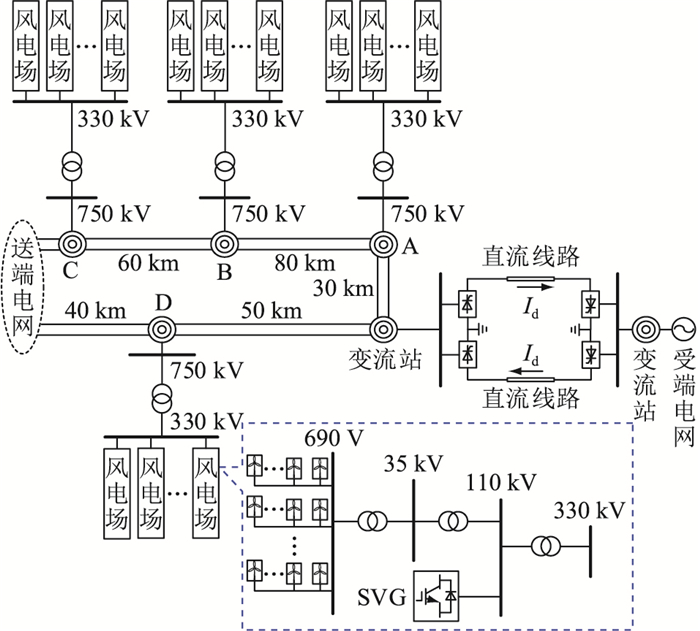
3 仿真案例 3.1 仿真系统描述为验证第2章中构建的电压动态线性化分析模型的正确性,在MATLAB/Simulink仿真软件中搭建特高压直流输电送端系统网架拓扑,如图 11所示。汇集站A、B、C、D均接有大规模全功率风电机组,各站线路距离如图 11所示,其中A站装机4 000 MW、B站装机6 000 MW、C站和D站装机各2 000 MW,交流系统主网电压等级为750 kV。全功率风电机组依次经690 V、35 kV、110 kV、330 kV、750 kV层级升压接入主网,直流换流站两回输电,每回直流输电额定直流电压为±800 kV, 每回直流额定容量为4 000 MW,直流总输电容量为8 000 MW。文中通过GFM-RPC对直流闭锁暂态过电压进行抑制实验。风电场110 kV母线处装设了静止无功发生器(static var generatior, SVG)。
|
图 11 GFM-RPC对LCC-HVDC送端暂态过电压影响的简化分析系统 Fig. 11 Simplified analysis system for effect of GFM-RPC on the transient overvoltage at sending area of LCC-HVDC |
选取3个暂态过电压情况较严重的汇集站A、B、D,在各站110 kV电压等级线路处装设占各站风机容量1/3的GFM-RPC或STATCOM,进行3组直流单极闭锁实验。实验组一:各站装设GFM-RPC;实验组二:各站装设STATCOM;实验组三:各站不装设任何类型的补偿器。
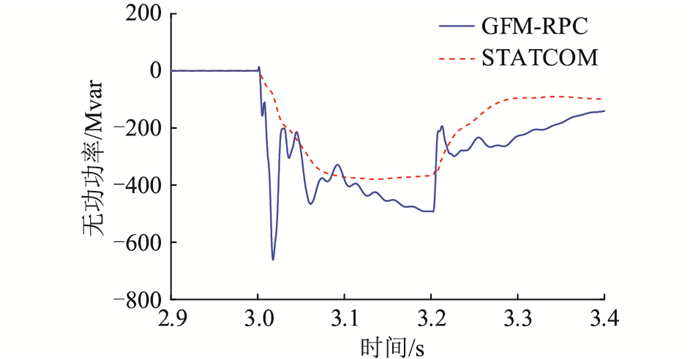
以汇集站A为例,不同补偿类型下A站机端暂态过电压以及各类型补偿器无功输出情况如图 12和图 13所示。可见GFM-RPC的补偿效果整体优于STATCOM,无功响应更加匹配电压动态过程。STATCOM由于其无功响应不及时,反而在暂态过电压结束时出现了低电压的现象,加剧了整体电压波动范围。B、D两站情况类似。

|
图 12 配置GFM-RPC和STATCOM的系统暂态过电压对比 Fig. 12 Comparison of the transient overvoltage in the system with GFM-RPC and STATCOM |
|
图 13 GFM-RPC和STATCOM的无功响应 Fig. 13 Reactive power response of GFM-RPC and STATCOM |
不同补偿类型作用下,各站机端暂态过电压情况如表 1所示。
|
|
表 1 不同补偿类型的过电压抑制效果 Table 1 Overvoltage suppression effect of different compensation types |
依旧选取3个暂态过电压情况较严重的汇集站A、B、D,在各站110 kV电压等级线路处装设占各站风机容量不同比例的GFM-RPC,进行3组直流单极闭锁实验。实验组一:各站装设相当于各站风电装机容量1/3的GFM-RPC;实验组二:各站装设相当于各站风电装机容量1/5的GFM-RPC;实验组三:各站装设相当于各站风电装机容量1/8的GFM-RPC。
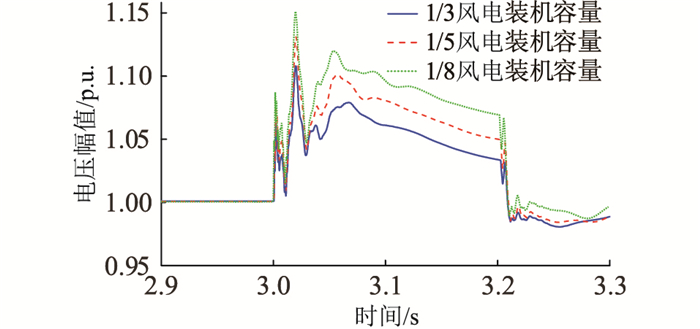
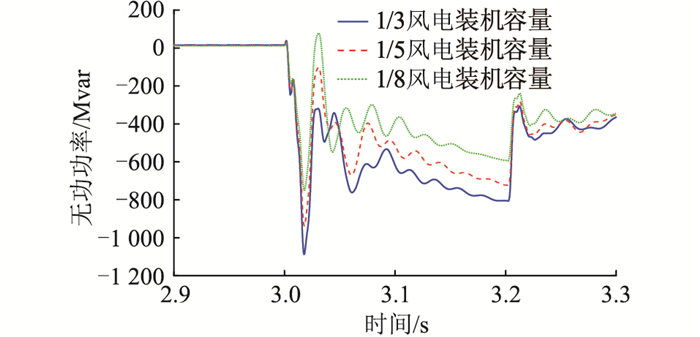
以汇集站A为例,不同GFM-RPC装机容量下A站机端暂态过电压以及GFM-RPC输出无功情况如图 14和图 15所示,可见GFM-RPC容量的增加可以显著增强暂态过电压抑制效果。B、D两站情况类似。
|
图 14 不同GFM-RPC装机容量下暂态过电压对比 Fig. 14 Comparison of transient overvoltage with different installed capacities of GFM-RPC |
|
图 15 不同GFM-RPC装机容量下的无功响应 Fig. 15 Reactive power response with different installed capacities of GFM-RPC |
不同GFM-RPC装机容量作用下,各站风电机端暂态过电压情况如表 2所示。
|
|
表 2 不同GFM-RPC装机容量下各站机端过电压 Table 2 Overvoltage on each station with different installed capacities of GFM-RPC |
同样选取过电压情况较为严重的A、B、D汇集站,在每个汇集站装设相当于各站风电装机容量1/3的GFM-RPC,进行3组单极闭锁实验。实验组一:各站GFM-RPC装设于110 kV电压等级线路处;实验组二:各站GFM-RPC装设于330 kV电压等级线路处;实验组三:各站GFM-RPC装设于750 kV电压等级线路处。
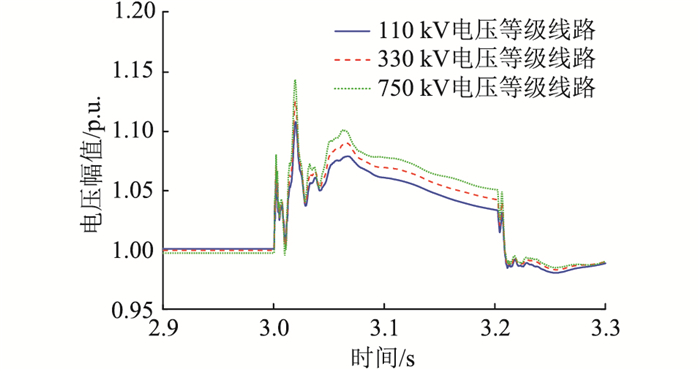
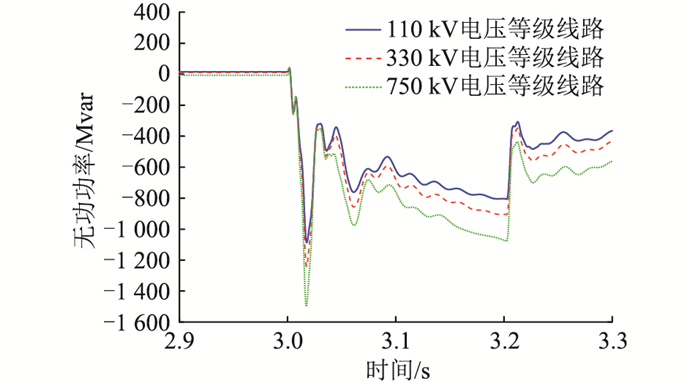
以汇集站A为例,不同电压等级GFM-RPC装设位置下A站机端暂态过电压以及GFM-RPC输出无功情况如图 16和图 17所示。可见GFM-RPC装设于110 kV电压等级线路处用最小输出无功量取得了对暂态过电压最好的抑制效果,装设于330 kV电压等级线路处的效果次之。可以得出结论,在低电压等级线路处装设GFM-RPC对风电机端暂态过电压的抑制效果优于在高电压等级处装设GFM-RPC。B、D两站情况类似。
|
图 16 GFM-RPC配置在不同位置的暂态过电压对比 Fig. 16 Comparison of transient overvoltage of the GFM-RPC at different locations |
|
图 17 GFM-RPC配置在不同位置的无功响应 Fig. 17 Reactive power response of the GFM-RPC at different locations |
不同GFM-RPC装设位置下,各站风电机端暂态过电压情况如表 3所示。
|
|
表 3 不同GFM-RPC装设位置下各站机端过电压 Table 3 Overvoltage on each station with different locations of GFM-RPC |
首先研究有功控制参数的影响。选取暂态过电压情况较严重的汇集站A、B、D,在各站110 kV电压等级线路处装设占各站风电装机容量1/3的GFM-RPC,进行3组直流单极闭锁实验。实验组一:GFM-RPC有功控制参数(Jp, Dp)设为(0.1, 5);实验组二:GFM-RPC有功控制参数(Jp, Dp)设为(0.5, 25);实验组三:GFM-RPC有功控制参数(Jp, Dp)设为(1, 50)。3个实验组中GFM-RPC无功控制参数Kc均设为0.5。
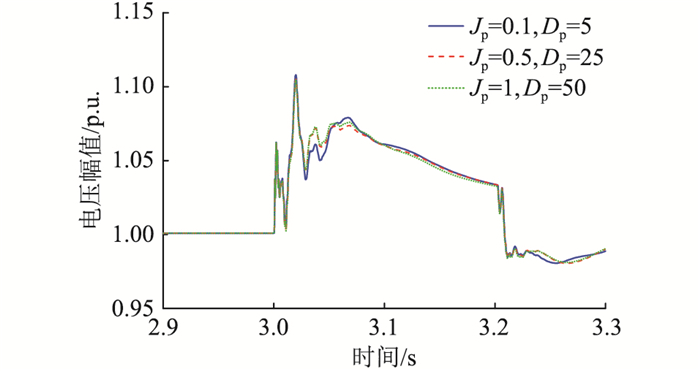
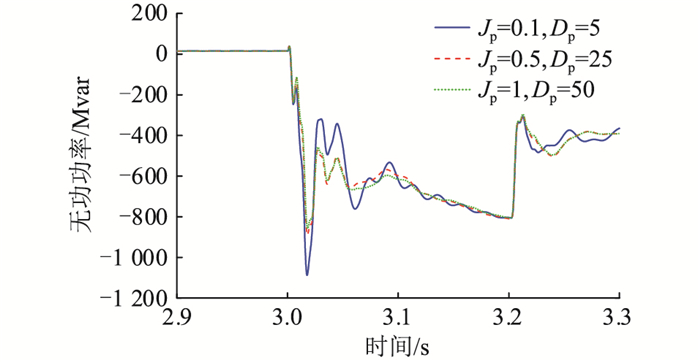
以汇集站A为例,不同GFM-RPC有功控制参数下A站机端暂态过电压以及GFM-RPC输出无功情况如图 18和图 19所示。可见有功控制参数的改变对A站机端暂态过电压的影响较小。B、D两站情况类似。
|
图 18 不同GFM-RPC有功控制参数下的暂态过电压对比 Fig. 18 Comparison of transient overvoltage with different active power control parameters of GFM-RPC |
|
图 19 不同GFM-RPC有功控制参数下的无功响应 Fig. 19 Reactive power response with different active power control parameters of GFM-RPC |
不同GFM-RPC有功控制参数下各站风电机端暂态过电压如表 4所示。
|
|
表 4 不同GFM-RPC有功控制参数下各站机端过电压 Table 4 Overvoltage on each station with different active power contorl parameters of GFM-RPC |
然后研究无功控制参数的影响。依旧选取汇集站A、B、D,在各站110 kV电压等级线路处装设占各站风电装机容量1/3的GFM-RPC,进行3组直流单极闭锁实验。实验组一:GFM-RPC无功控制参数Kc设为0.5;实验组二:GFM-RPC无功控制参数Kc设为1.0;实验组三:GFM-RPC无功控制参数Kc设为2.0。3个实验组中GFM-RPC有功控制参数(Jp, Dp)均设为(0.1, 5)。
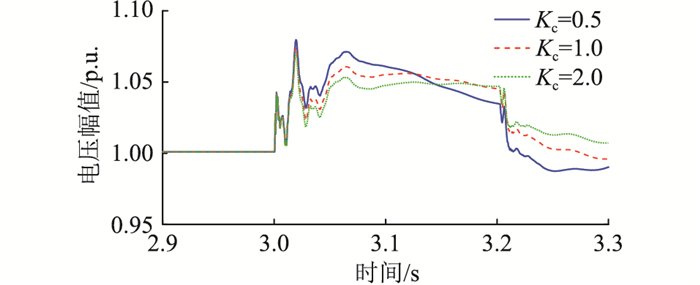
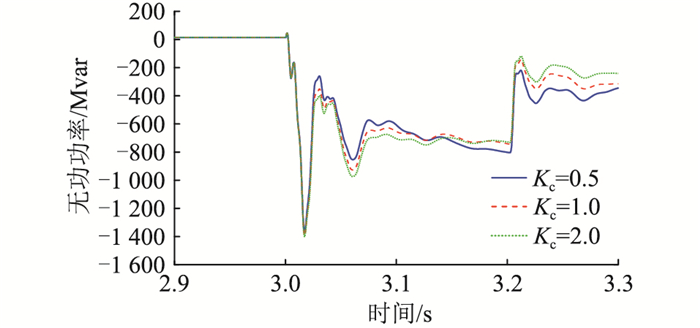
以汇集站A为例,不同GFM-RPC无功控制参数下A站机端暂态过电压以及GFM-RPC输出无功情况如图 20和图 21所示。可见在一定范围内,越小的刚度系数Kc使GFM-RPC无功控制增益越大,在过电压发展后期无功响应速度更快,过电压受到更大程度的抑制。但在另一方面,刚度系数Kc减小了GFM-RPC的电压刚度特性,由图 20可知,刚度系数Kc越小,暂态过电压的波动范围越大。B、D两站情况类似。
|
图 20 不同GFM-RPC无功控制参数下的暂态过电压对比 Fig. 20 Comparison of transient overvoltage with different reactive power control parameters of GFM-RPC |
|
图 21 不同GFM-RPC无功控制参数下的无功响应 Fig. 21 Reactive power response with different parameters of GFM-RPC |
不同GFM-RPC无功控制参数下各站风电机端暂态过电压变化范围如表 5所示。
|
|
表 5 不同GFM-RPC无功控制参数下各站机端电压变化范围 Table 5 Voltage range of each station with different reactive power control parameters of GFM-RPC |
文中提出一种应用GFM-RPC抑制新能源送端暂态过电压的方法。基于微分-代数方程构建了含GFM-RPC的系统电压多阶段分析模型,厘清了新能源送出系统动态过程中的无功-电压多阶段演化关系,揭示了构网型无功补偿控制对于电压幅值的瞬时支撑原理及电压动态改善机理。并利用大规模风电经LCC-HVDC送出的暂态过电压抑制仿真,对比了GFM-RPC和传统跟网型无功补偿装置STATCOM在电压动态改善方面的作用。结果表明,GFM-RPC借助其功率瞬时响应与内电势支撑特性可有效抑制直流闭锁瞬间的暂态过电压幅值,而STATCOM难以实现快时间尺度的电压动态控制。另外,仿真研究分析了GFM-RPC容量、装设位置、功率控制参数等因素对电压动态改善的影响,可指导后续GFM-RPC的实际工程应用与参数设计。
最后,在现有实际工程中,SC被广泛应用于解决新能源送端暂态过电压的问题,然而大型旋转设备的维护及挂网损耗增大了系统运行成本,文中所提构网型无功补偿方案与现有SC方案在技术经济性、工程适用性方面的对比是后续研究所考虑的重点。
| [1] |
李文竹, 寇汉鹏. 考虑暂态过电压抑制的新能源送出型电网无功优化方法[J]. 电瓷避雷器, 2023(6): 117-125. LI Wenzhu, KOU Hanpeng. Reactive power optimization method of new energy outgoing grid considering transient overvoltage suppression[J]. Insulators and Surge Arresters, 2023(6): 117-125. (  0) 0) |
| [2] |
张智刚, 康重庆. 碳中和目标下构建新型电力系统的挑战与展望[J]. 中国电机工程学报, 2022, 42(8): 2806-2819. ZHANG Zhigang, KANG Chongqing. Challenges and prospects for constructing the new-type power system towards a carbon neutrality future[J]. Proceedings of the CSEE, 2022, 42(8): 2806-2819. (  0) 0) |
| [3] |
尚磊, 董旭柱, 刘超. 惯量-刚度补偿器增强接入弱电网风电场直流电压时间尺度小干扰稳定的作用机理分析[J]. 中国电机工程学报, 2021, 41(7): 2321-2331. SHANG Lei, DONG Xuzhu, LIU Chao. Mechanism analysis of stability improvement of wind farm connected into weak grid by inertia-stiffness compensator in DC-link voltage time scale[J]. Proceedings of the CSEE, 2021, 41(7): 2321-2331. (  0) 0) |
| [4] |
MIRSAEIDI S, DONG X Z, SAID D M. A fault current limiting approach for commutation failure prevention in LCC-HVDC transmission systems[J]. IEEE Transactions on Power Delivery, 2019, 34(5): 2018-2027. DOI:10.1109/TPWRD.2019.2907558 (  0) 0) |
| [5] |
王梓懿, 肖华锋, 高博, 等. 考虑故障状态的LCC-HVDC建模方法研究[J]. 电力工程技术, 2021, 40(5): 78-86. WANG Ziyi, XIAO Huafeng, GAO Bo, et al. Modeling method of LCC-HVDC considering fault state[J]. Electric Power Engineering Technology, 2021, 40(5): 78-86. (  0) 0) |
| [6] |
王秋楠, 晋宏杨, 刘东, 等. LCC-HVDC换流站无功电压控制问题综述[J]. 电力电容器与无功补偿, 2023, 44(2): 10-17. WANG Qiunan, JIN Hongyang, LIU Dong, et al. Review on reactive voltage control of LCC-HVDC converter station[J]. Power Capacitor & Reactive Power Compensation, 2023, 44(2): 10-17. (  0) 0) |
| [7] |
赵成勇, 郭春义, 刘文静. 混合直流输电[M]. 北京: 科学出版社, 2014. ZHAO Chengyong, GUO Chunyi, LIU Wenjing. Hybrid high voltage direct current transmission system[M]. Beijing: Science Press, 2014. (  0) 0) |
| [8] |
孙华东, 张振宇, 林伟芳, 等. 2011年西北电网风机脱网事故分析及启示[J]. 电网技术, 2012, 36(10): 76-80. SUN Huadong, ZHANG Zhenyu, LIN Weifang, et al. Analysis on serious wind turbine generators tripping accident in Northwest China power grid in 2011 and its lessons[J]. Power System Technology, 2012, 36(10): 76-80. (  0) 0) |
| [9] |
杜维柱, 罗亚洲, 李蕴红, 等. 风电汇集系统无功盈余导致暂态过电压问题的研究综述[J]. 中国电机工程学报, 2022, 42(9): 3224-3239. DU Weizhu, LUO Yazhou, LI Yunhong, et al. Reviews of transient overvoltage problem cause by extra reactive power in large scale wind power systems[J]. Proceedings of the CSEE, 2022, 42(9): 3224-3239. (  0) 0) |
| [10] |
吕哲, 葛怀畅, 郭庆来, 等. 面向受端电网暂态电压稳定的高压直流系统主动控制研究[J]. 中国电机工程学报, 2022, 42(22): 8041-8053. LYU Zhe, GE Huaichang, GUO Qinglai, et al. Research on active control of HVDC system for transient voltage stability of receiving-end grid[J]. Proceedings of the CSEE, 2022, 42(22): 8041-8053. (  0) 0) |
| [11] |
YIN C Y, LI F T. Reactive power control strategy for inhibiting transient overvoltage caused by commutation failure[J]. IEEE Transactions on Power Systems, 2021, 36(5): 4764-4777. DOI:10.1109/TPWRS.2021.3063276 (  0) 0) |
| [12] |
周莹坤, 谢恒, 孙华东, 等. 新能源机组低电压穿越控制参数对机端工频过电压的影响[J]. 电网技术, 2022, 46(5): 1907-1916. ZHOU Yingkun, XIE Heng, SUN Huadong, et al. Influence of renewable energy low voltage ride-through control parameters on overvoltage[J]. Power System Technology, 2022, 46(5): 1907-1916. (  0) 0) |
| [13] |
孙大卫, 吴林林, 刘辉, 等. 弱电网直驱风机低电压穿越特性及其对机端暂态电压的影响[J]. 中国电机工程学报, 2021, 41(14): 4777-4786. SUN Dawei, WU Linlin, LIU Hui, et al. Effect of the low voltage ride through characteristics on PMSG terminal transient voltage in weakly-synchronized gird[J]. Proceedings of the CSEE, 2021, 41(14): 4777-4786. (  0) 0) |
| [14] |
JIN X, NIAN H, ZHAO C, et al. Optimal power coordinated control strategy for DFIG-based wind farm to increase transmission capacity of the LCC-HVDC system considering commutation failure[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 10(3): 3129-3139. DOI:10.1109/JESTPE.2021.3124794 (  0) 0) |
| [15] |
JIN X, NIAN H. Overvoltage suppression strategy for sending AC grid with high penetration of wind power in the LCC-HVdc system under commutation failure[J]. IEEE Transactions on Power Electronics, 2021, 36(9): 10265-10277. DOI:10.1109/TPEL.2021.3066641 (  0) 0) |
| [16] |
张文亮, 汤广福, 查鲲鹏, 等. 先进电力电子技术在智能电网中的应用[J]. 中国电机工程学报, 2010, 30(4): 1-7. ZHANG Wenliang, TANG Guangfu, ZHA Kunpeng, et al. Application of advanced power electronics in smart grid[J]. Proceedings of the CSEE, 2010, 30(4): 1-7. (  0) 0) |
| [17] |
王永辉, 宋广磊, 刘冰. 动态无功补偿装置的能力比较[J]. 电力电容器与无功补偿, 2022, 43(5): 18-26. WANG Yonghui, SONG Guanglei, LIU Bing. Capability comparison of dynamic reactive power compensation device[J]. Power Capacitor & Reactive Power Compensation, 2022, 43(5): 18-26. (  0) 0) |
| [18] |
任丕德, 刘发友, 周胜军. 动态无功补偿技术的应用现状[J]. 电网技术, 2004, 28(23): 81-83. REN Pide, LIU Fayou, ZHOU Shengjun. Application status of dynamic reactive power compensation technology[J]. Power System Technology, 2004, 28(23): 81-83. (  0) 0) |
| [19] |
LIU J, JIANG R R, LIU Q, et al. Study on transient overvoltage of wind farm caused by fault of HVDC system and its suppression measures[C]//20182nd IEEE Conference on Energy Internet and Energy System Integration (EI2). Beijing, China. IEEE, 2018: 1-6.
(  0) 0) |
| [20] |
HUANG S H, SCHMALL J, CONTO J, et al. Voltage control challenges on weak grids with high penetration of wind generation: ERCOT experience[C]//2012 IEEE Power and Energy Society General Meeting. San Diego, CA, USA. IEEE, 2012: 1-7.
(  0) 0) |
| [21] |
TELEKE S, ABDULAHOVIC T, THIRINGER T, et al. Dynamic performance comparison of synchronous condenser and SVC[J]. IEEE Transactions on Power Delivery, 2008, 23(3): 1606-1612. DOI:10.1109/TPWRD.2007.916109 (  0) 0) |
| [22] |
MENDIS N, MUTTAQI K M, PERERA S. Management of battery-supercapacitor hybrid energy storage and synchronous condenser for isolated operation of PMSG based variable-speed wind turbine generating systems[J]. IEEE Transactions on Smart Grid, 2014, 5(2): 944-953. DOI:10.1109/TSG.2013.2287874 (  0) 0) |
| [23] |
ZHONG Q C, NGUYEN P L, MA Z Y, et al. Self-synchronized synchronverters: inverters without a dedicated synchronization unit[J]. IEEE Transactions on Power Electronics, 2014, 29(2): 617-630. DOI:10.1109/TPEL.2013.2258684 (  0) 0) |
| [24] |
尚磊, 胡家兵, 袁小明, 等. 电网对称故障下虚拟同步发电机建模与改进控制[J]. 中国电机工程学报, 2017, 37(2): 403-412. SHANG Lei, HU Jiabing, YUAN Xiaoming, et al. Modeling and improved control of virtual synchronous generators under symmetrical faults of grid[J]. Proceedings of the CSEE, 2017, 37(2): 403-412. (  0) 0) |
| [25] |
石荣亮, 兰才华, 王国斌, 等. 基于有功前馈补偿的储能VSG并网有功振荡抑制策略[J]. 电力系统保护与控制, 2023, 51(14): 118-126. SHI Rongliang, LAN Caihua, WANG Guobin, et al. Grid-connected active power oscillation suppression strategy of an energy storage VSG based on active power feed-forward compensation[J]. Power System Protection and Control, 2023, 51(14): 118-126. (  0) 0) |
| [26] |
丁一凡, 季亮, 常潇, 等. 不对称电压跌落下虚拟同步机改进低电压穿越控制策略[J]. 电力系统保护与控制, 2022, 50(16): 76-85. DING Yifan, JI Liang, CHANG Xiao, et al. Improved low voltage ride-through control strategy of a virtual synchronous generator during unbalanced voltage sags[J]. Power System Protection and Control, 2022, 50(16): 76-85. (  0) 0) |
2. Research Institute of China Southern Power Grid Co., Ltd., Guangzhou 510700, China;
3. CSG Yunnan Electric Power Research Institute, Kunming 650217, China
 2024, Vol. 43
2024, Vol. 43


 尚磊(1986), 男, 博士, 副教授, 研究方向为电力电子化电力系统频率/电压分析与优化控制技术、能源互联网技术等(E-mail:
尚磊(1986), 男, 博士, 副教授, 研究方向为电力电子化电力系统频率/电压分析与优化控制技术、能源互联网技术等(E-mail: