文章编号: 2096-3203(2024)02-0229-10 中图分类号: TM73
2. 南方电网调峰调频发电有限公司(广东)储能材料有限公司, 广东 广州 510630;
3. 梯级水电站运行与控制湖北省重点实验室, 湖北 宜昌 443000
2022年6月,国家能源局强调新型储能作为构建新型电力系统的重要组成部分,要求持续完善价格机制,最终实现新型储能独立地参与市场[1]。目前,节点边际电价(locational marginal price,LMP)的结算方式已经在部分电力市场运行[2-4]。理论和实践表明,LMP机制难以削弱传统电厂的市场操控力。市场出清的本质是一个机组组合问题,当储能参与市场报价时,发电厂采取降低申报价格等策略,挤占市场份额形成垄断地位,阻碍储能电站参与市场获得公正利益,这显然不符合我国鼓励储能作为市场主体独立参与电力市场的改革目标。当线路发生堵塞或者供需关系紧张时,具有垄断操控能力的发电商会趁机提高申报价格以获得较大利润,间接增加了电网系统运行成本,不利于电力市场机制的稳定运行。
现阶段对于储能经济收益的研究可分为联合互补参与市场出清模式的探讨以及对市场本身规则的设计与改革。联合互补模式参与市场出清的相关研究可分为以下几类:在发电侧与风光等联合互补参与电力市场[5];在配电侧参与辅助市场,增加电网的稳定性[6];在用户侧与分布式电源、柔性负荷等组成虚拟电厂,实现负荷的时间转移[7]。这些研究仅关注优化储能充放电控制策略,实现整体利润最大化,并不能实现储能本身合理的收益。除了对于储能联合出清模式参与电力市场的研究外,电力市场运行机制规则设计的相关研究正逐步成为热点[8-9]。文献[10]将保险机制引入电力市场,提出一种现货市场下的售电公司优化运营方法,解决售电用户侧的不确定性引起的市场波动,从而提升需求响应收益,但该运营方法不符合实际情况,容易引起市场纠纷,市场运营较为复杂。文献[11]提出一种大规模新能源参与下的电力市场价值分配机制,但未考虑网络损耗对于线路堵塞约束有效性的影响。基于Vickrey-Clarke-Groves(VCG)机制,文献[12]中风电商参与日前市场结算机制,促进新能源参与日前市场。文献[13]提出在日前市场结算中考虑发电机组和柔性负荷的电价模型。根据哈维茨不可能定理,在设计满足激励相容机制时,必定会造成系统整体的收支不平衡,文献[12-13]均未提出如何解决收支不平衡问题。文献[14]提出一种按贡献价值分配的出清机制,将发电机组的贡献定义为对其他发电商的代替作用,但只考虑发电侧承担不平衡资金,违背了市场买卖双方的公平性。文献[15]通过比较LMP与VCG 2种电价机制,得出VCG机制下的调度成本低于LMP机制下的发电成本,能够有效降低系统运行成本。电动汽车作为一种典型的分布式储能与其他发电商联合互补参与电力市场,文献[16]中风力发电和电动汽车组成虚拟电厂的模式参与市场出清,按照出清电量占比的市场结算规则分配利润,在该出清模式下,风电商打压挤占市场利润份额,储能处于劣势地位。在充分实现市场公平分配收益的背景下,现阶段针对市场结算机制改革设计、扶持储能作为市场主体独立参与市场的研究较少。因此,设计合理的价格形成机制,将利益公平分配,同时削弱传统发电商的市场操控力,将成为未来电力市场改革的重点方向。
对于鼓励新型储能独立参与电力市场的倡议,上述研究均未考虑适合储能参与日前市场竞争的结算机制以及如何解决由于市场力削弱而导致系统收支不平衡的问题。基于上述分析,文中建立了含储能的日前市场出清模型;基于VCG机制,该发电商所获收益等于其参与市场出清前后系统总运行成本的变化量;同时,文中进行合理的扣除机制设计,进一步完善机制中收支不平衡的问题;最后,采用IEEE 30节点系统为例,证明VCG结算机制的合理性,并且储能参与市场结算可以极大削弱传统发电厂的市场操控力,有效降低系统出清总成本、减小市场电价的剧烈波动,保障了电力市场平稳、可靠运行。
1 日前市场出清模型 1.1 储能参与市场模型在电力市场化改革中,各级政府为储能电站独立参与市场出清提供了环境和政策支持。根据日前市场出清规则,市场出清结算间隔为1 h[17-20],发电商需要提前一天向独立运营商(independent system operator,ISO)申报发电信息与状态,由ISO根据各发电参与商的信息制定日前市场出清计划。基于上述分析,文中研究储能电站参与日前市场的运行策略,以实现储能的收益最大化,从而推动储能规模的发展[21-22]。储能获得的收益为:
| $ \varphi_j=\varphi_{j, \text { shed }}\left(P_{\text {shed }, k}^{\text {wind }}\right)+\varphi_{j, \text { re }}\left(m_j\right) $ | (1) |
式中:φj为储能电站j参与电力市场出清获得的总收益;Pshed, kwind为由于新能源风电商k不确定性而导致的切负载功率;φj, shed(Pshed, kwind)为储能电站j在实时市场提供给风电商k切负载功率Pshed, kwind所获得的收益;φj, re(mj)为储能电站j在日前市场提供功率mj所获得的收益。
在日前市场中,由于风电等新能源出力不稳定,当真实出力不满足出清量时,系统运营商将会在实时市场切负载来满足功率平衡,此时储能将获得提供切负载功率的收益为:
| $ \varphi_{j, \text { shed }}\left(P_{\text {shed }, k}^{\text {wind }}\right)=\lambda_{\text {shed }} P_{\text {shed }, k}^{\text {wind }} $ | (2) |
式中:λshed为实时市场切负载电价。
储能电站的成本包括单位充电功率成本、单位功率投资建设成本以及电池老化成本,因此储能电站获得的利润为:
| $ F_j\left(m_j\right)=\varphi_j-\gamma_j m_j $ | (3) |
| $ \gamma_j=\tau_j+\kappa_j+v_j $ | (4) |
式中:Fj(mj)为储能电站j提供出清功率mj所获得的最终利润;γj为储能电站j需要向ISO申报的真实放电功率成本系数;τj为储能电站j的单位功率充电成本系数;κj为储能电站j的单位放电功率材料老化成本系数;υj为储能电站j的单位功率投资建设成本系数。
考虑储能电站在日前市场中不同时段投标量以及辅助调频市场的预留量,日前储放功率须在其能力范围内进行申报出清[18]。
| $ m_{j, \mathrm{ch}}^{\min } \leqslant m_{j, \mathrm{ch}} \leqslant m_{j, \mathrm{ch}}^{\max } $ | (5) |
| $ m_{j, \text { dis }}^{\min } \leqslant m_{j, \mathrm{dis}} \leqslant \theta_{j, \mathrm{dis}} m_{j, \mathrm{dis}}^{\max } $ | (6) |
| $ \theta_{j, \text { dis }} \leqslant 1 $ | (7) |
| $ m_j \leqslant m_{j, \mathrm{dis}}=\eta_j m_{j, \mathrm{ch}} $ | (8) |
| $ E_{t+1}=E_t+m_{j, \mathrm{ch}} \eta_j \Delta t-\frac{m_{j, \mathrm{dis}}}{\eta_j} \Delta t $ | (9) |
| $ S_t=\frac{E_t}{E_{\max }} $ | (10) |
式中:mj, chmax、mj, chmin、mj, dismax、mj, dismin分别为储能电站j充电与放电的功率上限和下限;mj, ch、mj, dis分别为储能电站j的充电功率与放电功率;θj, dis为对应的储能电站j辅助市场预留容量系数;ηj为储能电站j的充放电功率转化效率因数;Δt为市场出清结算间隔;Et为储能电站j在t时刻的剩余电量;Emax为储能电站j的总电量;St为储能电站j在t时刻荷电状态。
为保证储能电站可以连续地参与日前市场,还应对当日初始状态电量等于次日相同时刻的初始状态电量进行约束,即:
| $ E_0=E_{24} $ | (11) |
式中:E0为当日初始0时刻的初始状态电量;E24为次日0时刻的初始状态电量。
1.2 其他发电商参与市场模型随着双碳战略的推进,新能源开始逐步参与电力市场,文中以风电为例,建立风电参与市场出清模型[23]。当风电商参与日前市场竞标时,由于出力具有较大不确定性,风力发电商k的投标出力Pkwind和实际出力Pk, relwind之间通常会存在偏差,即Pkwind≠Pk, relwind,发电商面临惩罚。那么,在实时市场的出清中:即Pk, relwind>Pkwind时,风电商选择弃风措施,弃风量为Pab, kwind;当Pkwind>Pk, relwind时,系统运营商则在实时市场切负载,切负载功率为Pshed, kwind。
故目标函数为:
| $ \min \left\{P_{\text {wind }, k}\left(P_{k, \text { rel }}^{\text {wind }}, \beta_k\right)\right\}=\lambda_{\text {shed }} P_{\text {shed }, k}^{\text {wind }} $ | (12) |
约束条件为:
| $ 0 \leqslant P_{k, \text { rel }}^{\text {wind }} \leqslant P_k^{\max } \quad k=1, 2, \cdots, K $ | (13) |
| $ P_{\mathrm{ab}, k}^{\mathrm{wind}} \geqslant 0 \quad k=1, 2, \cdots, K $ | (14) |
| $ P_{\text {shed }, k}^{\text {wind }} \geqslant 0 \quad k=1, 2, \cdots, K $ | (15) |
式中:βk为风电商k向ISO申报其模拟的功率概率分布函数;Pwind, k(Pk, relwind, βk)为在日前市场出清中,风电商k由于出力的不确定性所面临的切负载功率;Pkmax为风电商k机组模拟的功率概率分布函数βk出力的上限;K为全部的风电商数量。
1.3 目标函数文中以n个节点构成的输电网络作为分析案例,以市场运行总成本F(整体系统运行成本)最低为目标函数。假设所有发电商向ISO上报各自的真实发电成本,含储能的日前市场出清模型如下。
目标函数为:
| $ \begin{gathered} \min F=\sum\limits_{i=1}^G f_i\left(P_i\right)+\sum\limits_{j=1}^J M_j\left(m_j\right)+ \\ E\left(P_{\text {wind }, k}\left(P_{k, \text { rel }}^{\text {wind }}, \beta_k\right)\right) \end{gathered} $ | (16) |
式中:fi(Pi)为传统发电商i提供功率Pi所需要的成本;Mj(mj)为储能电站j提供功率mj所需要的成本;E(·)为期望;G为传统常规发电商的总个数;J为储能电站的总个数。
1.4 约束条件考虑忽略网络损耗,网络堵塞的计算结果可能会有误差,影响网络堵塞约束的有效性,因此必须修正网损功率。在电网实际调度中,通常采用功率传输分布系数计算网损。在标幺值计算下,假设所有节点的电压均等于其额定电压。
边际传输系数的定义如下:
| $ D_m=1-L_m=1-\frac{\partial P_{\text {loss }}}{\partial P_m} $ | (17) |
| $ \frac{\partial P_{\text {loss }}}{\partial P_m}=\frac{\partial}{\partial P_m}\left(\sum\limits_{l=1}^L I_l^2 R_l\right)=\left(\sum\limits_{l=1}^L 2 I_l D_{m, l}\right) \sum\limits_{m=1}^n D_{m, l} P_m $ | (18) |
式中:Dm为节点m处边际传输系数;Lm为节点m处边际网络损耗系数;Pm为节点m处注入功率;Ploss为网络损耗;Il为线路l的电流幅值;Rl为线路l的电阻;Dm, l为节点m和线路l之间的功率传输分布系数;n为网络总节点个数;L为网络中总线路条数。
约束条件分为以下3种。
(1) 功率平衡约束。
| $ \sum\limits_{m=1}^n D_m\left(P_i+m_j+t_k-P_{m, \mathrm{D}}\right)-P_{\mathrm{loss}}=0 $ | (19) |
式中: tk为风力发电商k参与市场出清的发电功率;Pm, D为节点m处系统所需要的负荷功率。
(2) 网络堵塞约束。通过网络的功率应当在输送容量限制内,即:
| $ \begin{gathered} -P_{\lim , l} \leqslant \sum\limits_{m=1}^n D_{m, l}\left(P_i+m_j+t_k-P_{m, \mathrm{D}}\right) \leqslant P_{\lim , l} \\ l=1, 2, \cdots, L \end{gathered} $ | (20) |
式中:Plim, l为线路l的最大传输功率容量。
(3) 传统发电商机组约束。机组发电功率应在其限制范围内,即:
| $ P_{\min , i} \leqslant P_i \leqslant P_{\text {max }, i} \quad i=1, 2, \cdots, G $ | (21) |
式中:Pmax, i、Pmin, i分别为传统发电商i有功功率的上、下限。
上述考虑实时市场的日前市场出清模型是一个二阶段随机规划问题,采用样本均值近似(sample average approximation,SAA)求解该随机规划模型[24],得到各发电商的最优发电功率与风电商的出力计划。
2 基于改进VCG结算机制的运行策略为激励各发电参与商申报自身真实发电成本,从而削弱市场操控力,进而实现系统运行总成本最小,文中基于VCG机制设计理论,提出一种储能电站参与的日前市场结算机制。VCG机制只改变原有的结算方式,对于此前所建设的电力市场规则没有较大改变,因此该结算机制具有较强的实用性。
2.1 基于VCG的结算机制已知传统发电商i申报自身发电成本报价Ci,储能电站j申报自身发电成本系数γj,风力机组k申报模拟的功率概率分布函数βk,则在市场出清中,传统发电商i获得的收益为:
| $ \varphi_i\left(P_{\mathrm{G}, i}\right)=Q_{-i}\left(P_{\mathrm{G}, i}\right)-\left(Q(P)-f_i\left(P_{\mathrm{G}, i}, c_i\right)\right) $ | (22) |
式中:φi(PG, i)为传统发电商i所获得的日前市场收益;Q-i(PG, i)为传统发电商i不参与市场出清下ISO所需要的总成本;Q(P)为全部发电商参与市场出清下ISO所需要的总成本;fi(PG, i, ci)为传统发电商i提供功率为PG, i所申报的成本。
储能电站j获得的日前市场收益为:
| $ \varphi_j\left(P_j\right)=Q_{-j}\left(P_j\right)-\left(Q(P)-M\left(P_j, \gamma_j\right)\right) $ | (23) |
式中:φj(Pj)为储能电站j提供功率为Pj所获得的日前市场出清的收益;Q-j(Pj)为储能电站j不参与市场出清下ISO所需要的成本;M(Pj, γj)为储能电站j提供功率为Pj时所申报的成本。
2.2 改进后电价机制性质证明现有的LMP结算机制不满足激励相容,难以削弱市场力,不能提高社会福利[12]。文中将从理论出发,证明基于VCG结算机制满足激励相容,可促使发电商真实报价,削弱发电商的市场操控力。
2.2.1 传统发电商假设每一个发电商都上报自身真实发电费用。
(1) 当传统发电商i上报真实费用ci, 1,则得到的收益为:
| $ \varphi_i\left(P_{\mathrm{G}, i, 1}, c_{i, 1}\right)=Q_{-i}\left(P_{\mathrm{G}, i}\right)-\left(Q(P)-f_i\left(P_{\mathrm{G}, i, 1}, c_{i, 1}\right)\right) $ | (24) |
式中:φi(PG, i, 1, ci, 1)为传统发电商i上报真实费用ci, 1时所获得的收益;PG, i, 1为在传统发电商i上报真实费用ci, 1时系统调度传统发电商i的最优出力;fi(PG, i, 1, ci, 1)为系统调度传统发电商i的真实成本。
当传统发电商i上报真实费用ci, 1时,利润为:
| $ \begin{gathered} \varphi_i\left(P_{\mathrm{G}, i, 1}, c_{i, 1}\right)-f_i\left(P_{\mathrm{G}, i, 1}, c_{i, 1}\right)=Q_{-i}\left(P_{\mathrm{G}, i}\right)- \\ \left(Q(P)-f_i\left(P_{\mathrm{G}, i, 1}, c_{i, 1}\right)\right)-f_i\left(P_{\mathrm{G}, i, 1}, c_{i, 1}\right)= \\ Q_{-i}\left(P_{\mathrm{G}, i}\right)-\left(\sum\limits_{k \neq i} f\left(\hat{P}_k\right)+f_i\left(P_{\mathrm{G}, i, 1}, c_{i, 1}\right)\right) \end{gathered} $ | (25) |
式中:
(2) 当传统发电商i虚报发电费用ci, 2,则获得的收益为:
| $ \varphi_i\left(P_{\mathrm{G}, i, 2}, c_{i, 2}\right)=Q_{-i}\left(P_{\mathrm{G}, i}\right)-\left(Q(P)-f_i\left(P_{\mathrm{G}, i, 2}, c_{i, 2}\right)\right) $ | (26) |
式中:φi(PG, i, 2, ci, 2)为传统发电商i上报虚假费用ci, 2时所获得的收益;PG, i, 2为在传统发电商i上报虚报费用ci, 2时系统调度传统发电商i的最优出力;fi(PG, i, 2, ci, 2)为传统发电商i最优出力PG, i, 2时,申报给ISO的成本费用。
因此,当传统发电商i虚报费用ci, 2时,利润为:
| $ \begin{gathered} \varphi_i\left(P_{\mathrm{G}, i, 2}, c_{i, 2}\right)-f_i\left(P_{\mathrm{G}, i, 2}, c_{i, 1}\right)=Q_{-i}\left(P_{\mathrm{G}, i}\right)- \\ \left(Q(P)-f_i\left(P_{\mathrm{G}, i, 2}, c_{i, 2}\right)\right)-f_i\left(P_{\mathrm{G}, i, 2}, c_{i, 1}\right)= \\ Q_{-i}\left(P_{\mathrm{G}, i}\right)-\left(\sum\limits_{k \neq i} f\left(\hat{P}_k^{\prime}\right)+f_i\left(P_{\mathrm{G}, i, 2}, c_{i, 1}\right)\right) \end{gathered} $ | (27) |
式中:fi(PG, i, 2, ci, 2)为在传统发电商i虚报费用为ci, 2以及最优出力为PG, i, 2时,该发电商i申报给ISO发电成本费用;fi(PG, i, 2, ci, 1)为该传统发电商i真实发电费用为ci, 1以及最优出力为PG, i, 2时,自身真实的发电成本;
对于式(25)和式(27),Q-i(PG, i)与该机组i申报给系统运营商的发电成本系数无关,PG, i, 1为在该机组i上报真实的发电成本费用ci, 1时,系统调度该机组i的最优出力;
| $ \sum\limits_{k \neq i} f\left(\hat{P}_k\right)+f_i\left(P_{\mathrm{G}, i, 1}, c_{i, 1}\right) \leqslant \sum\limits_{k \neq i} f\left(\hat{P}_k^{\prime}\right)+f_i\left(P_{\mathrm{G}, i, 2}, c_{i, 1}\right) $ | (28) |
即:
| $ \begin{gathered} \varphi_i\left(P_{\mathrm{G}, i, 1}, c_{i, 1}\right)-f_i\left(P_{\mathrm{G}, i, 1}, c_{i, 1}\right) \geqslant \\ \varphi_i\left(P_{\mathrm{G}, i, 2}, c_{i, 2}\right)-f_i\left(P_{\mathrm{G}, i, 2}, c_{i, 1}\right) \end{gathered} $ | (29) |
根据上述证明,在VCG机制下,常规发电机组i只有如实上报发电成本系数,才能获得更高的利润。
2.2.2 储能电站假设其他储能电站也按照ISO要求上报自身发电成本系数γ-j,那么储能电站j可以选择真实申报发电成本系数γj, 1,也可以选择虚报发电成本系数γj, 2。
(1) 当储能电站j真实申报发电成本系数γj, 1时,在VCG机制下,其获得的收益为:
| $ \varphi_j\left(P_{j, 1}, \gamma_{j, 1}\right)=Q_{-j}\left(P_j\right)-\left(Q(P)-M\left(P_{j, 1}, \gamma_{j, 1}\right)\right) $ | (30) |
式中:φj(Pj, 1, γj, 1)为储能电站j所获得的ISO支付的费用;M(Pj, 1, γj, 1)为储能电站j真实申报发电成本系数γj, 1时,系统出清分配储能出力Pj, 1下,储能电站j的真实发电成本。
储能电站参与市场出清的目的是为了获得更高的利益,当储能电站j真实申报发电成本系数γj, 1,所获得利润为:
| $ \begin{aligned} & \varphi_j\left(P_{j, 1}, \gamma_{j, 1}\right)-M\left(P_{j, 1}, \gamma_{j, 1}\right)=Q_{-j}\left(P_j\right)- \\ & \left(Q(P)-M\left(P_{j, 1}, \gamma_{j, 1}\right)\right)-M\left(P_{j, 1}, \gamma_{j, 1}\right)= \\ & Q_{-j}\left(P_j\right)-\left(\sum\limits_{k \neq j} f_k\left(P_{k, 1}\right)+M\left(P_{j, 1}, \gamma_{j, 1}\right)\right) \end{aligned} $ | (31) |
式中:
(2) 当储能电站j选择虚报发电成本系数γj, 2时,在VCG机制下,其获得的收益为:
| $ \varphi_j\left(P_{j, 2}, \gamma_{j, 2}\right)=Q_{-j}\left(P_j\right)-\left(Q(P)-M\left(P_{j, 2}, \gamma_{j, 2}\right)\right) $ | (32) |
式中:φj(Pj, 2, γj, 2)为储能电站j在虚报成本系数γj, 2时所获得的收益;M(Pj, 2, γj, 2)为储能电站j虚报发电成本系数γj, 2时,系统出清分配储能出力Pj, 2下,储能电站j申报的虚假发电成本。
当储能电站j选择虚报发电成本系数,所获得利润为:
| $ \begin{gathered} \varphi_j\left(P_{j, 2}, \gamma_{j, 2}\right)-M\left(P_{j, 2}, \gamma_{j, 1}\right)=Q_{-j}\left(P_j\right)- \\ \left(Q(P)-M\left(P_{j, 2}, \gamma_{j, 2}\right)\right)-M\left(P_{j, 2}, \gamma_{j, 1}\right)= \\ Q_{-j}\left(P_j\right)-\left(\sum\limits_{k \neq j} f_k\left(P_{k, 2}\right)+M\left(P_{j, 2}, \gamma_{j, 1}\right)\right) \end{gathered} $ | (33) |
式中:M(Pj, 2, γj, 1)为储能电站j在真实发电系数γj, 1以及出力Pj, 2时的自身真实成本;
对比式(31)和式(33)可知,Q-j(Pj)与储能电站j的报价无关;Pj, 2为储能电站j在虚报发电成本系数γj, 2时,储能电站j的最优出力;Pk, 2为其他参与商的最优出力。发电商为了获得更高的利润,会选择虚报发电成本系数,进而导致系统总运行成本增大,所以有:
| $ \begin{gathered} \sum\limits_{k \neq j} f_k\left(P_{k, 1}\right)+M\left(P_{j, 1}, \gamma_{j, 1}\right) \leqslant \\ \sum\limits_{k \neq j} f_k\left(P_{k, 2}\right)+M\left(P_{j, 2}, \gamma_{j, 1}\right) \end{gathered} $ | (34) |
进一步推出:
| $ \begin{gathered} \varphi_j\left(P_{j, 1}, \gamma_{j, 1}\right)-M\left(P_{j, 1}, \gamma_{j, 1}\right) \geqslant \\ \varphi_j\left(P_{j, 2}, \gamma_{j, 2}\right)-M\left(P_{j, 2}, \gamma_{j, 1}\right) \end{gathered} $ | (35) |
由上述证明可知,在VCG机制下,任何发电商只有如实上报发电成本系数,才能获得更高的利润。该出清结算机制有利于削弱市场操控力,促进储能等新型发电商积极地参与电力市场。
2.3 针对收支不平衡性质的机制改进哈维茨不可能定理证明,结算机制不会同时满足激励相容和收支平衡。在VCG结算机制提高社会福利、削弱市场操控力和满足激励相容的同时,不能满足收支平衡。将系统所产生的不平衡资金记为ΔE,表示为ISO支付给所有发电商的总费用和ISO从用户侧收取的总用电费用的差额。即:
| $ \Delta E=\sum\limits_{m=1}^n F_m^{\mathrm{VCG}}-\sum\limits_{m=1}^n \lambda_m^{\mathrm{LMP}} P_{m, \mathrm{D}} \geqslant 0 $ | (36) |
式中:等式右边第一项为ISO按照VCG结算机制支付给节点m处并网发电商的发电费用;第二项为节点m处的负荷按照电价λmLMP以及用电功率为Pm, D支付给ISO的费用。
在VCG结算机制下,发电侧和负荷侧都参与了整个交易过程,并且双方所获得的权益都有所增加。但是,如果只是一方承担不平衡资金,必然会违反市场公平交易的原则。因此,文中综合考虑双方应共同承担不平衡资金,即:
| $ \Delta E=\Delta E_1+\Delta E_2 $ | (37) |
式中:ΔE1为在发电商的收益中扣除的资金;ΔE2为在负荷侧收取的额外电费。
(1) 从发电商所获得的利润中扣除一部分资金,但使其利润仍大于0。
| $ \varepsilon_m=\frac{w_m}{W} \Delta E_1 $ | (38) |
式中:εm为节点m处并网发电商扣除的资金;wm为该发电商扣除费用之前的利润;W为所有机组的总利润。
(2) 通过提高负荷侧电价来满足收支平衡,可以理解为用户获得真实信息而产生的成本,方法有:
① 修正实时电价,各节点按修正后的电价收费,使得系统整体收支平衡。
② 附加电费方法,不用修正实时电价,在总电费中增加一定量的额外费用,即用户电费。
文中着重考虑附加电费方法,即按节点总电费分配额外电费。
在节点m处所收取的费用为:
| $ E_m=\lambda_m^{\mathrm{LMP}} P_{m, \mathrm{D}} $ | (39) |
则节点m处所承担的附加费用βm为:
| $ \beta_m=\frac{E_m}{\sum\limits_{m=1}^n \lambda_m^{\mathrm{LMP}} P_{m, \mathrm{D}}} \Delta E_2=\frac{\lambda_m^{\mathrm{LMP}} P_{m, \mathrm{D}}}{\sum\limits_{m=1}^n \lambda_m^{\mathrm{LMP}} P_{m, \mathrm{D}}} \Delta E_2 $ | (40) |
| $ \Delta E_2=\beta_1+\beta_2+\cdots+\beta_m+\cdots+\beta_n $ | (41) |
从发电商的利润中扣除费用ΔE1,使发电商仍有所盈余;按用户电费的多少额外征收费用ΔE2,使ISO在负荷侧所收取的费用足以支付给发电商所需的费用,实现收支平衡。
2.4 电价机制运行模式激励相容是指市场参与者在制定自身效益最大化的策略后,参与竞价的行为与整个系统出清总费用最小的目标一致[25-26]。发电商虚报发电信息会降低自身利润,这将促使发电商选择申报自身真实成本,降低市场操控力,并促进包括储能在内的新型发电商参与市场出清。
以传统发电商i为例,从图 1的实施流程可以看出,无论是LMP结算机制还是VCG结算机制,发电商都需要向ISO报价,系统调度出清并生成节点电价。在LMP结算机制中,系统运营商根据发电商的中标量和节点电价进行支付,满足收支平衡;在VCG结算机制中,系统运营商根据发电商之间的替代效应计算发电商的价值,并根据替代效应进行结算,可以精准辨识发电商所产生的价值,在此过程中可能会产生不平衡费用,文中通过结算扣除机制解决不平衡费用。与LMP结算机制相比,VCG结算机制并未改变传统基于报价的交易模式,只是改变结算方式,可以有效减弱发电商的市场力,避免不合理电价现象的发生,使市场更具有效率,无论其他发电商是否策略性报价,该发电商申报真实的发电成本都将会获得最大的利润。
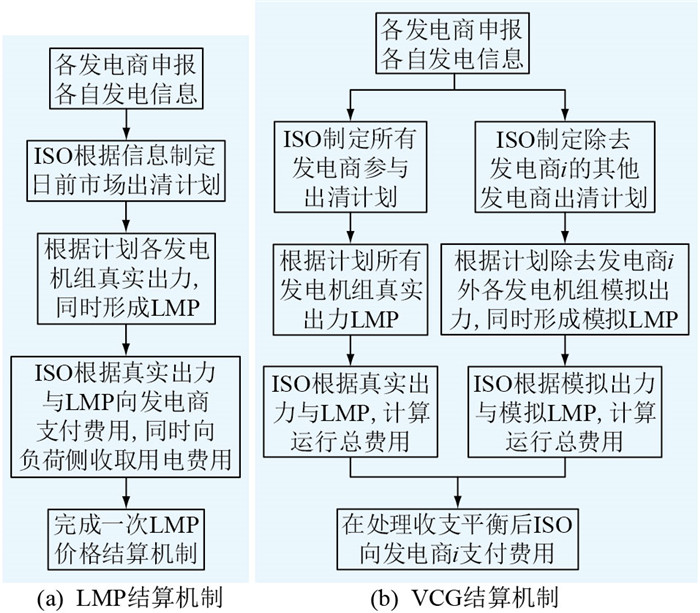
|
图 1 LMP与VCG结算机制过程对比 Fig. 1 Comparison of LMP and VCG settlement mechanism process |
文中采用含储能电站的IEEE 30节点系统,算例包括G1、G2、G3共3台常规机组,分别位于1号、2号和13号节点;1个风电商,位于22号节点;2个储能电站,分别位于23号和27号节点。系统中发电参与商的参数如表 1所示,发电机数据被市场竞标数据替代。常规机组向ISO申报其真实的发电成本一次项系数、二次项系数和发电容量;风力机组申报其模拟的功率概率分布函数和发电容量,风电商功率概率分布函数符合正态分布[12],正态分布分别记作N1(41.5, 1 452)与N2(32.8, 1 264);储能电站申报其真实放电功率成本系数[16-17]和发电容量[27],节点23和节点27处储能的真实放电成本系数分别取4.96美元/MW和5.82美元/MW。系统的负荷信息如图 2所示。
|
|
表 1 发电参与商的真实发电信息 Table 1 Real generation information for generation participants |
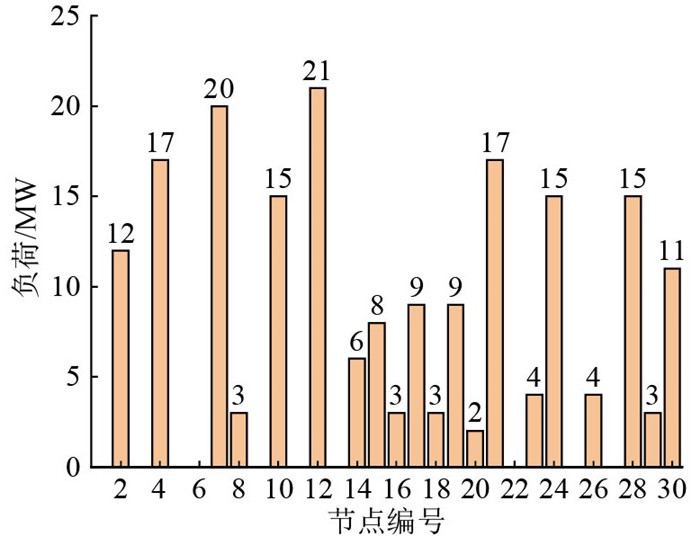
|
图 2 IEEE 30节点系统负荷分布情况 Fig. 2 IEEE 30-node system load distribution |
图 3和图 4分别为VCG机制下,各常规机组分别等比例虚报二次项系数和一次项系数时,其利润和申报真实值时利润的比值变化情况。
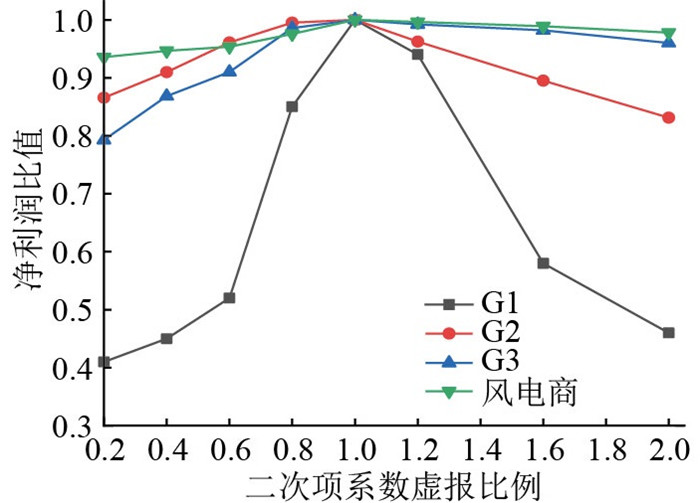
|
图 3 各发电商虚报不同比率二次项系数的收益与真实报价收益比值 Fig. 3 Ratio of each generator′s return on misrepresent- ing quadratic term coefficients at different rates to the return on the true offer |
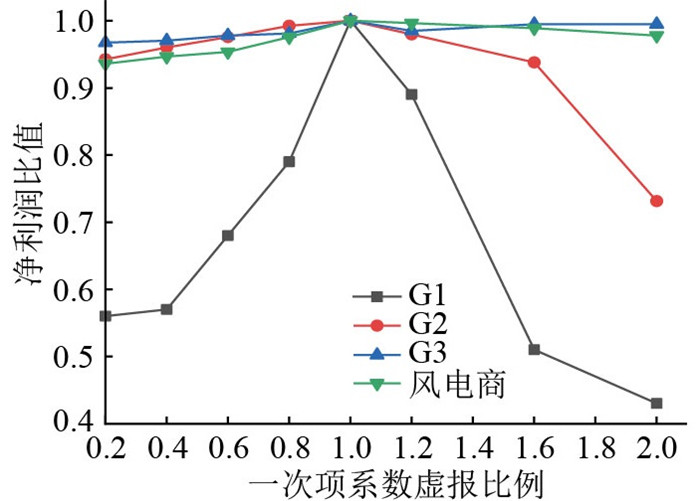
|
图 4 各发电商虚报不同比率一次项系数的收益与真实报价收益比值 Fig. 4 Ratio of each generator′s return on misrepresent- ing the primary term coefficients at different rates to the return on the true offer |
由图 3可得,无论是当储能电站参与市场出清,传统发电商选择降低申报价格,还是由于风电机组不确定性导致供求关系紧张,传统发电商选择提高价格,都将导致其利润急剧下降。只有当机组申报真实二次项系数才能获得最大利润。由图 4可得,只有当机组申报真实一次项系数时,该机组利润最大化。图 3与图 4证明了VCG结算机制满足激励相容以及社会福利最大化的性质,从而削弱了传统发电商的市场操控力,使市场价值可以得到公平公正的分配。
3.3 储能对于市场均衡的影响当常规3号机组等比例虚报二次项系数时,相连接处节点的电价变化情况如图 5所示。仿真结果表明:当虚报比例低于1时,在储能1和储能2都参与市场出清的情况下,相比于储能不参与或者只有单个储能参与出清时,系统电价最低;随着虚报比例增长,系统电价急剧上升且上升速度较快;当虚报比例大于1时,风电机组出力不稳定导致系统供求关系紧张,如果发电机组趁机抬高价格来操控市场,储能电站的参与将弥补风力发电带来的市场缺额,使系统电价增长较为平缓,降低系统价格剧烈波动的风险。
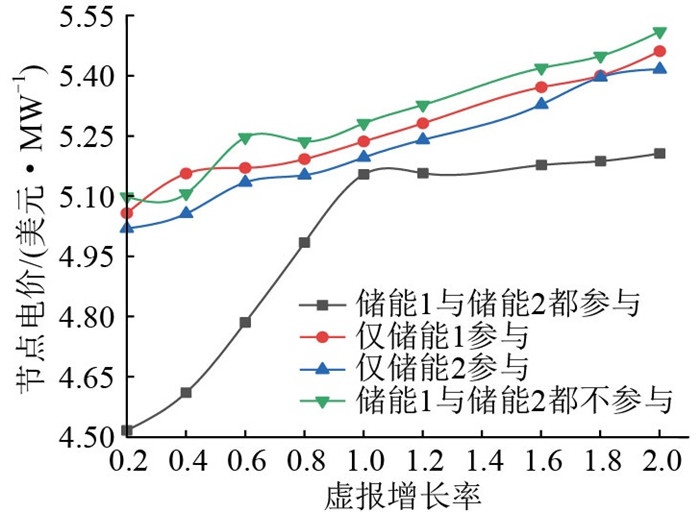
|
图 5 储能电站参与和不参与出清模式系统节点电价 Fig. 5 Node tariffs for storage plants participation and non-participation in the clearing model system |
图 6为常规3号机组等比例虚报二次项系数时的利润变化情况。基于VCG价格结算机制,通过对比4种系统不同运行模式,得出结论:常规发电商如果采取降价措施来挤占市场份额,当储能电站都参与市场出清时,常规机组的利润急剧下降,甚至会出现亏损现象。储能电站的参与将会抵制常规机组操控市场的行为,削弱常规机组的市场操控力,迫使其真实报价,促进市场公平公正。
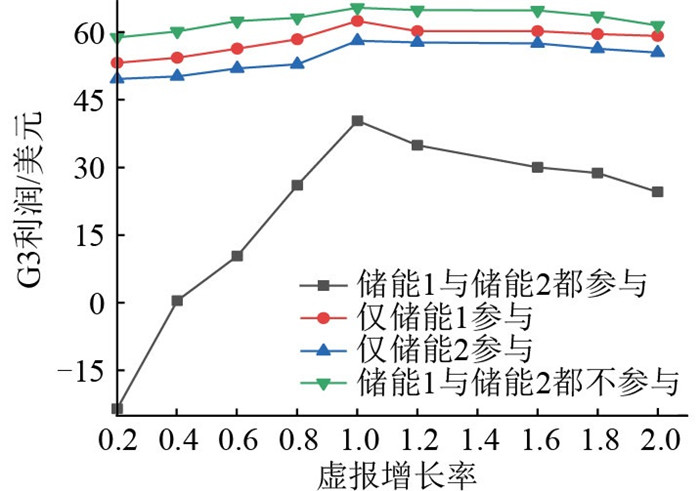
|
图 6 储能电站参与和不参与出清模式下G3利润 Fig. 6 G3 profits for storane plants participation and non-participation in the clearing model |
图 7为常规3号机组等比例虚报二次项系数时,系统ISO支付总成本的变化情况。随着虚报比例不断增大,储能电站完全参与市场出清模式相比于不完全参与市场出清模式,系统总支付成本最低并且增长率较慢。这表明储能电站积极参与市场出清可以进一步降低系统总运行成本。
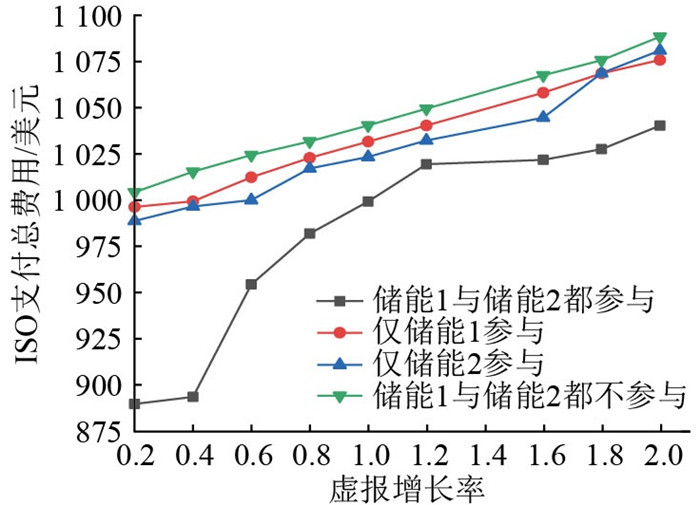
|
图 7 储能电站参与和不参与出清模式下系统总支付费用 Fig. 7 Total system payments for storage plants participation and non-participation in the clearing model |
基于VCG理论,各机组和储能电站在申报真实成本后,为满足激励相容和削弱市场操控力等性质,由式(36)以及文中2.3节分析可知,必然会造成系统收支不平衡的问题。基于2.3节针对收支不平衡性质的机制改进模式,图 8为根据式(38)从发电商的利润中按价格机制扣除部分费用后的情况,图 9为根据式(40)从负荷侧根据节点额外附加费用机制分摊的不平衡电费的情况。基于实际情况,文中考虑发电商和用户侧各承担一半的不平衡费用,并且扣除机制与各发电商报价信息无关,因此并不会削弱整体机制的激励相容性,完善系统总收支平衡。
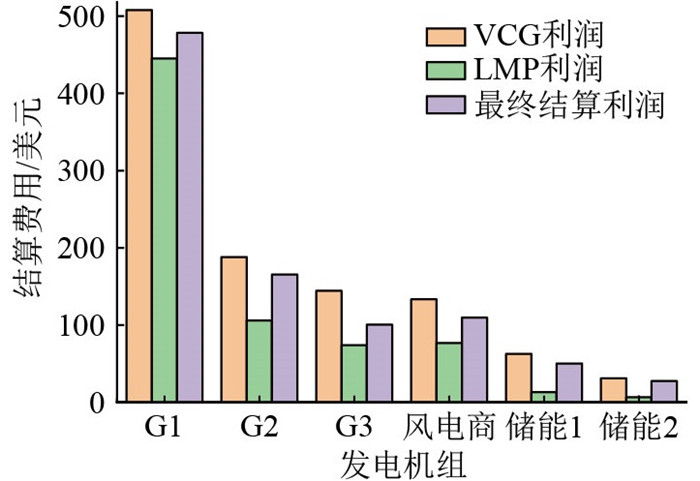
|
图 8 各发电机组的利润及扣除情况 Fig. 8 Profit and deduction of each generator set |
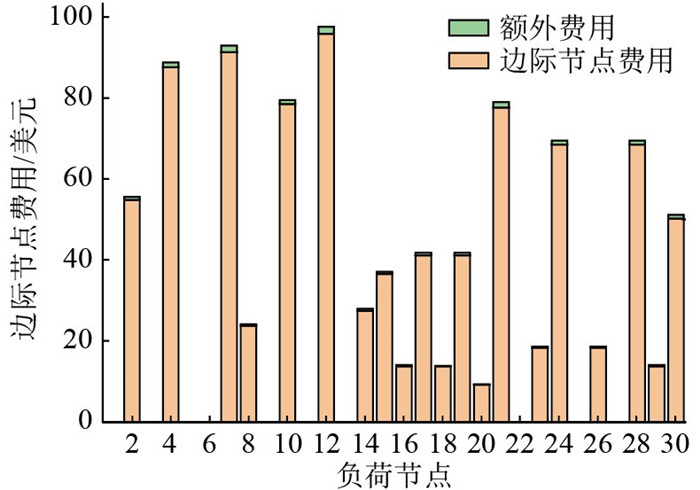
|
图 9 IEEE 30节点系统中负荷所在位置及费用 Fig. 9 Location and cost of load in IEEE 30-node system |
在边际价格机制下,当储能等新型发电商参与市场出清时,发电商为提高利润,打压并挤占了储能电站的市场份额,致使储能难以获得公正的市场利润,进而增大了系统总运行成本。
因此,文中在考虑网络损耗对于线路约束有效性影响的基础上提出一种基于VCG理论的储能电力市场出清结算机制,在满足激励相容的同时,为解决削弱市场力而产生的不平衡资金问题,考虑发电商和用户侧各承担一定量的不平衡费用,避免了因电网结构堵塞带来各节点电价差异较大的问题。通过算例分析,文中提出的市场结算机制满足激励相容以及削弱传统机组的市场操控力的要求,最终市场价值得到公正分配。同时,储能参与市场出清有利于市场机制稳定运行、减小市场运行总成本以及降低电价的剧烈波动,能够提高储能电站参与电力市场的积极性。文中研究为日后电力市场化改革提供理论参考依据,并为制定鼓励储能电站参与市场出清的政策提供参考。
| [1] |
两部委: 新型储能可独立参与电力市场交易[J]. 绿叶, 2022(6): 6. Two ministries: new energy storage can independently participate in power market transactions[J]. Green Leaf, 2022(6): 6. (  0) 0) |
| [2] |
姚星安, 曾智健, 杨威, 等. 广东电力市场结算机制设计与实践[J]. 电力系统保护与控制, 2020, 48(2): 76-85. YAO Xing'an, ZENG Zhijian, YANG Wei, et al. Electricity market settlement mechanism design and practice in Guangdong[J]. Power System Protection and Control, 2020, 48(2): 76-85. (  0) 0) |
| [3] |
叶晨, 牟玉亭, 王蓓蓓, 等. 考虑动态碳交易曲线的电-碳市场出清模型及节点边际电价构成机理分析[J]. 电网技术, 2023, 47(2): 613-624. YE Chen, MOU Yuting, WANG Beibei, et al. Mechanism of locational marginal prices and clearing model of electricity and carbon market considering dynamic carbon trading curve[J]. Power System Technology, 2023, 47(2): 613-624. (  0) 0) |
| [4] |
冯昌森, 谢方锐, 胡嘉骅, 等. 配电系统中点对点电力交易市场设计与出清方法[J]. 电力系统自动化, 2022, 46(9): 11-20. FENG Changsen, XIE Fangrui, HU Jiahua, et al. Market design and clearing method for peer-to-peer power trading in distribution system[J]. Automation of Electric Power Systems, 2022, 46(9): 11-20. (  0) 0) |
| [5] |
陈启鑫, 房曦晨, 郭鸿业, 等. 储能参与电力市场机制: 现状与展望[J]. 电力系统自动化, 2021, 45(16): 14-28. CHEN Qixin, FANG Xichen, GUO Hongye, et al. Participation mechanism of energy storage in electricity market: status quo and prospect[J]. Automation of Electric Power Systems, 2021, 45(16): 14-28. (  0) 0) |
| [6] |
梁彦杰, 陈星, 娄素华, 等. 南方(以广东起步)调频辅助服务市场卡特尔形成机理分析[J]. 电力系统自动化, 2021, 45(15): 93-100. LIANG Yanjie, CHEN Xing, LOU Suhua, et al. Formation mechanism analysis of cartel in frequency regulation ancillary service market in southern china(starting from Guangdong Province)[J]. Automation of Electric Power Systems, 2021, 45(15): 93-100. (  0) 0) |
| [7] |
李强, 朱丹丹, 黄地, 等. 虚拟电厂运营商与电动汽车用户的主从博弈定价策略[J]. 电力工程技术, 2022, 41(4): 183-191. LI Qiang, ZHU Dandan, HUANG Di, et al. Stackelberg game pricing strategy between virtual power plant operators and electric vehicle users[J]. Electric Power Engineering Technology, 2022, 41(4): 183-191. (  0) 0) |
| [8] |
荆朝霞. 新型电力系统下电力市场的建设及运行机制研究[J]. 电力工程技术, 2022, 41(1): 1. JING Chaoxia. Research on the construction and operation mechanism of power market under the new power system[J]. Electric Power Engineering Technology, 2022, 41(1): 1. (  0) 0) |
| [9] |
张超, 乔宁, 陈杰, 等. 电力市场出清机制理论与现实探索——基于市场主体对风险厌恶特性及激励相容机制的设计[J]. 价格理论与实践, 2019(10): 128-132. ZHANG Chao, QIAO Ning, CHEN Jie, et al. Exploration on the theory and practice of power market clearing mechanism——based on the characteristics of risk aversion of market subjects and the design of incentive compatibility mechanism[J]. Price: Theory & Practice, 2019(10): 128-132. (  0) 0) |
| [10] |
温钱惠, 魏震波, 张勇林, 等. 考虑保险机制与用户需求响应的售电公司优化运营[J]. 电力建设, 2023, 44(1): 47-54. WEN Qianhui, WEI Zhenbo, ZHANG Yonglin, et al. Optimized operation of electricity sales companies considering the insurance mechanism and user demand response[J]. Electric Power Construction, 2023, 44(1): 47-54. (  0) 0) |
| [11] |
安麒, 王剑晓, 武昭原, 等. 高比例可再生能源渗透下的电力市场价值分配机制设计[J]. 电力系统自动化, 2022, 46(7): 13-22. AN Qi, WANG Jianxiao, WU Zhaoyuan, et al. Benefit allocation mechanism design of electricity markets with penetration of high proportion of renewable energy[J]. Automation of Electric Power Systems, 2022, 46(7): 13-22. (  0) 0) |
| [12] |
聂涌泉, 顾慧杰, 彭超逸, 等. 激励性含风电竞标日前市场出清电价机制的建模[J]. 电力系统保护与控制, 2020, 48(19): 25-34. NIE Yongquan, GU Huijie, PENG Chaoyi, et al. Research on modeling the incentive electricity pricing mechanism in day-ahead electricity market clearing containing wind power bidding[J]. Power System Protection and Control, 2020, 48(19): 25-34. (  0) 0) |
| [13] |
顾慧杰, 彭超逸, 许丹莉, 等. 激励性含柔性负荷日前市场出清电价机制的建模[J]. 电力系统保护与控制, 2020, 48(12): 23-32. GU Huijie, PENG Chaoyi, XU Danli, et al. Research on modeling the incentive electricity pricing mechanism in day-ahead electricity market clearing containing flexible loads[J]. Power System Protection and Control, 2020, 48(12): 23-32. (  0) 0) |
| [14] |
王剑晓, 钟海旺, 夏清, 等. 基于价值公平分配的电力市场竞争机制设计[J]. 电力系统自动化, 2019, 43(2): 7-17. WANG Jianxiao, ZHONG Haiwang, XIA Qing, et al. Competitive mechanism design in electricity market based on fair benefit allocation[J]. Automation of Electric Power Systems, 2019, 43(2): 7-17. (  0) 0) |
| [15] |
XU Y J, LOW S H. An efficient and incentive compatible mechanism for wholesale electricity markets[J]. IEEE Transactions on Smart Grid, 2017, 8(1): 128-138. DOI:10.1109/TSG.2015.2483523 (  0) 0) |
| [16] |
王红野, 何俐, 王雪峰, 等. 风电与电动汽车组成虚拟电厂参与市场的多主体博弈[J]. 可再生能源, 2020, 38(12): 1686-1692. WANG Hongye, HE Li, WANG Xuefeng, et al. Game strategies among multi-agents in electrical power market with virtual power plant composed of wind power and electric vehicles[J]. Renewable Energy Resources, 2020, 38(12): 1686-1692. (  0) 0) |
| [17] |
李宏仲, 魏静怡, 吕勇荡. 考虑储能与新能源双边交易的日前市场报价策略[J]. 电网技术, 2022, 46(12): 4843-4853. LI Hongzhong, WEI Jingyi, LÜ Yongdang. Day-ahead market quotation strategy considering bilateral transaction between energy storage and new energy[J]. Power System Technology, 2022, 46(12): 4843-4853. (  0) 0) |
| [18] |
禤宗衡, 荆朝霞, 叶文圣, 等. 考虑储能灵活能量状态的新型电能量市场机制[J]. 电网技术, 2022, 46(10): 3810-3823. XUAN Zongheng, JING Zhaoxia, YE Wensheng, et al. New energy market mechanism considering flexible state of energy in energy storage[J]. Power System Technology, 2022, 46(10): 3810-3823. (  0) 0) |
| [19] |
陈洪禹, 张冶, 关艳, 等. 考虑源网荷储效益提升的电力现货市场出清优化模型研究[J]. 电测与仪表, 2022, 59(5): 50-57. CHEN Hongyu, ZHANG Ye, GUAN Yan, et al. Research on clearing optimization model of power spot market incorporating generation, network, load and storage benefit improvement[J]. Electrical Measurement & Instrumentation, 2022, 59(5): 50-57. (  0) 0) |
| [20] |
裴善鹏, 林华, 王炎, 等. 电力现货市场背景下的山东新能源储能应用模式研究[J]. 热力发电, 2021, 50(8): 30-38. PEI Shanpeng, LIN Hua, WANG Yan, et al. Study on application mode of new energy storage in Shandong under the background of power spot market[J]. Thermal Power Generation, 2021, 50(8): 30-38. (  0) 0) |
| [21] |
时智勇, 王彩霞, 胡静. 独立新型储能电站价格形成机制及成本疏导优化方法[J]. 储能科学与技术, 2022, 11(12): 4067-4076. SHI Zhiyong, WANG Caixia, HU Jing. A price formation mechanism and cost diversion optimization method for designing an independently new energy-storing power station[J]. Energy Storage Science and Technology, 2022, 11(12): 4067-4076. (  0) 0) |
| [22] |
刘凡, 李凤婷, 张高航, 等. 计及循环寿命和运营策略的风电汇集区域储能电站优化配置[J]. 电力系统保护与控制, 2023, 51(8): 127-139. LIU Fan, LI Fengting, ZHANG Gaohang, et al. Optimal configuration of storage power stations in a wind power gathering area considering cycle life and operation strategy[J]. Power System Protection and Control, 2023, 51(8): 127-139. (  0) 0) |
| [23] |
陈启鑫, 刘学, 房曦晨, 等. 考虑可再生能源保障性消纳的电力市场出清机制[J]. 电力系统自动化, 2021, 45(6): 26-33. CHEN Qixin, LIU Xue, FANG Xichen, et al. Electricity market clearing mechanism considering guaranteed accommodation of renewable energy[J]. Automation of Electric Power Systems, 2021, 45(6): 26-33. (  0) 0) |
| [24] |
WANG C, GONG Z H, LIANG Y L, et al. Data-driven wind generation admissibility assessment of integrated electric-heat systems: a dynamic convex hull-based approach[J]. IEEE Transactions on Smart Grid, 2020, 11(5): 4531-4543. DOI:10.1109/TSG.2020.2993023 (  0) 0) |
| [25] |
员江洋, 杨明, 刘宁宁, 等. 不完全信息下基于多代理深度确定策略梯度算法的发电商竞价策略[J]. 电网技术, 2022, 46(12): 4832-4844. YUN Jiangyang, YANG Ming, LIU Ningning, et al. Bidding strategy of generation companies based on multi-agent deep deterministic policy gradient algorithm under incomplete information[J]. Power System Technology, 2022, 46(12): 4832-4844. (  0) 0) |
| [26] |
李吉侗, 王洲, 达紫祺, 等. 计及恶劣天气时空相关性的弹性配电网储能电站多层规划方法[J]. 电力系统保护与控制, 2023, 51(9): 128-137. LI Jitong, WANG Zhou, DA Ziqi, et al. Multi-level planning method of energy storage stations for resilient distribution networks considering spatio-temporal correlation of severe weather[J]. Power System Protection and Control, 2023, 51(9): 128-137. (  0) 0) |
| [27] |
关立, 周蕾, 刘航航, 等. 独立储能电站参与电力现货市场机制及试运行分析[J]. 中国电力, 2022, 55(10): 185-190. GUAN Li, ZHOU Lei, LIU Hanghang, et al. Analysis of inde-pendent energy storage power station participating inpower spot market mechanism and trial operation[J]. Electric Power, 2022, 55(10): 185-190. (  0) 0) |
2. China Southern Power Grid FM Generation Co., Ltd. (Guangdong) Energy Storage Materials Co., Ltd., Guangzhou 510630, China;
3. Hubei Provincial Key Laboratory for Operation and Control of Cascaded Hydropower Station, Yichang 443000, China
 2024, Vol. 43
2024, Vol. 43


 舒征宇(1983), 男, 博士, 副教授, 研究方向为电力市场与碳市场耦合(E-mail:
舒征宇(1983), 男, 博士, 副教授, 研究方向为电力市场与碳市场耦合(E-mail: