文章编号: 2096-3203(2024)01-0157-08 中图分类号: TM715
近年来,电力系统在物联网和大数据等技术的推动下进入了电力大数据时代[1]。其中,电力负荷数据是对一定范围内的负荷对象进行用能大小、变化趋势及其分布特点的刻画与描述[2],丰富的电力负荷数据为电力系统制定决策夯实了数据基础。电力负荷受季节、天气、日类型、检修计划、生产生活及突发故障等多维因素影响,具有周期性、趋势性及随机性等典型特点[3-4]。由于电力负荷数据结构存在多元异构、数据体量大的问题,在数据采集与传输过程中极易受系统故障、设备异常、传输误码及量测误差等因素影响,导致负荷数据中掺杂了一些不易察觉的异常数据。这些异常数据将给系统规划、负荷预测及用能分析等带来负面影响[5]。因此,针对电力负荷数据异常进行检测与识别,一是可及时发现和快速诊断故障与用户窃电等异常情况,二是可及时阻止负荷异常数据继续扩散[6],防止电力系统规划因异常数据做出错误决策。
传统的数据异常检测方法可以分为6种类型,主要包括基于分类[7-9]、基于密度[10-11]、基于聚类[12-14]、基于统计[15-16]、基于信息理论[17]以及基于频谱等异常检测方法。其中,基于统计的方法往往假设数据为简单分布,无法反映出真实数据的分布情况;基于密度和基于聚类的方法无法有效提取时序数据中的细部特征;基于分类的模型则要求数据必须具备标签,对数据质量要求高,且某些特殊故障类型导致的数据异常不能满足标注需求。
由于电力负荷数据是一种典型的时序序列,当前一些研究主要聚焦于利用深度学习的范式解决时序序列异常检测问题[18-24]。文献[19]提出了基于自回归神经网络的无参数化动态阈值长短期记忆网络(long short-term memory for natural language understanding with noisy data training, LSTM-NDT)进行数据异常检测,采用无监督训练方式,对检测结果根据无参数化设定阈值进行异常判定,但模型过度依赖局部特征,忽略了长序列的全局特征。文献[20]基于长短期记忆循环神经网络架构,提出了具有生成对抗网络的多元异常检测(multiple anomaly detection using generative adversarial networks, MAD-GAN)方法,采用GAN的对抗生成机制对时间序列进行重构,通过分离异常评分实现数据异常诊断。引入GAN训练机制后,一定程度地提高了对时序序列分布特征的捕获能力。文献[21]提出了基于随机递归神经网络的OmniAnomaly多变量时间序列异常检测模型,结合门控循环单元和变分自编码器刻画时序序列的局部特征依赖和随机性特征,但模型复杂程度过高,将出现训练时间长和不易收敛的问题。针对用户窃电异常行为检测问题,文献[22]提出了深度自编码器高斯混合模型(deep auto-encoder Gaussian mixture model, DAGMM),利用压缩网络提取数据潜在特征,但由于压缩网络可能会引起特征丢失,并不能较好地保留原始特征空间的拓扑,从而降低了数据异常检测的查全率。文献[23]提出了多尺度卷积循环编码器-解码器结构,构造特征矩阵编码与解码重构,对长可变的时序序列具有较好的泛化能力。已有研究表明,虽然Transformer的掩码多头注意力层能对时间趋势性进行一定程度的推理,但是难以提取负荷异常时刻或时段前后数据的相关性特征[24]。总而言之,当前基于深度学习的数据异常检测方法研究主要致力于优化模型结构、设计异常诊断机制以及改进模型训练机制,以期在模型复杂度、训练难度、推理速度、异常检测精确率以及泛化能力上取得较好平衡。
考虑到不同负荷数据的异常时间尺度与变化趋势往往不同,即提取特征时既要关注异常持续时间又要关注突变程度。文中首先厘清电力负荷数据异常分类、原因及其特征,明确电力负荷数据异常检测技术需求。然后,为更好地捕捉负荷数据的趋势特征并提高异常检测的准确性,拟通过改进传统Transformer编码器结构,依托GAN生成器与判别器的博弈机制,提出一种改进的GAN-Transformer模型。最后,通过算例对所提电力负荷数据异常检测模型的有效性与优越性开展分析验证。
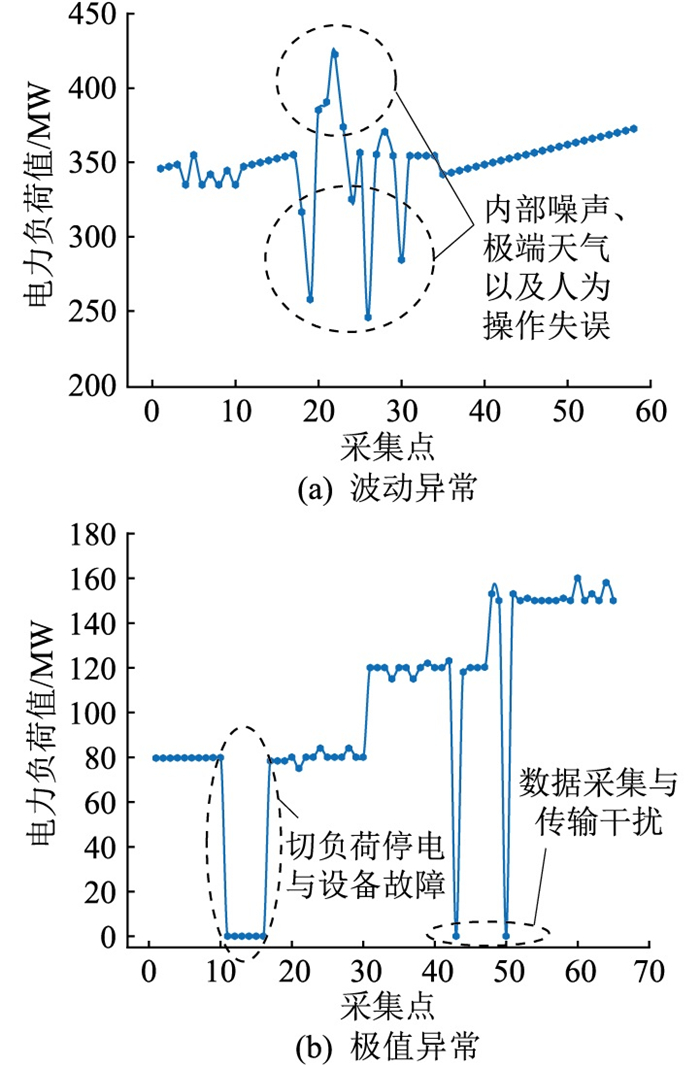
1 电力负荷数据异常分类电力负荷包括发电负荷、供电负荷以及用电负荷,通常具有周期性、自相关性与趋势性等典型特征。受极端天气、生产生活以及设备故障等不确定性因素影响,电力负荷又呈现出随机性、波动性及突变性等特征[25],电力负荷数据往往会出现异常跳变,表现为波动异常与极值异常,如图 1所示。其中,横坐标为每隔10 min采集一次的数据点。
|
图 1 电力负荷数据异常示意 Fig. 1 Anomaly schematic of power load data |
波动异常负荷曲线表现为短时间内出现大量毛刺且波动频繁,与正常的负荷波动规律相比有显著跳变。极值异常负荷曲线表现为负荷数据极值异常,在一定时间内(持续时间通常为分钟级)出现负荷尖峰、谷值或较大的峰谷差,破坏了曲线相似性与周期性。其中,波动异常的负荷数据通常由内部噪声或外界干扰引起,易在极端天气以及人为操作失误的场景下产生;极值异常的负荷数据通常由采集数据在某时刻缺损引起,易在切负荷停电、设备(变压器、电缆、保护装置等)故障、数据采集与传输干扰以及用户窃电的场景下产生。
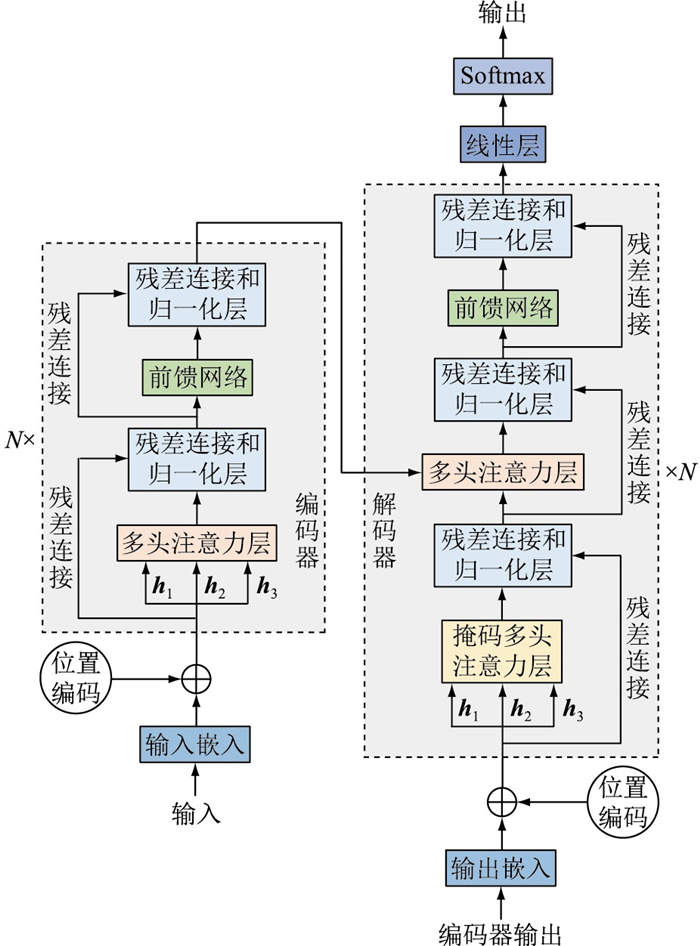
2 GAN-Transformer模型原理 2.1 Transformer模型首先,依靠Transformer架构的自注意力机制提取负荷数据中各元素的时间相关性。Transformer由N个编码器和解码器组合而成,单个编码器与解码器的结构如图 2所示。其中,h1、h2、h3为多头注意力层和掩码多头注意力层的多个特征输入。
|
图 2 Transformer模型结构 Fig. 2 Structure of Transformer model |
解码器采用掩码多头注意力层,确保解码器只关注t-1时刻数据对t时刻数据的特征映射,而不会引入t+1时刻的数据信息。与解码器相比,编码器主要由多头注意力层和前馈网络构成,多头注意力层可以使模型同时关注多个局部特征。为避免网络加深引起的序列过拟合问题,模型中引入了残差连接。
Transformer模型的多头注意力层可针对位置编码矩阵使用多组WQ, i、WK, i、WV, i得到多组 Q矩阵、K矩阵、V矩阵,从而对输入信息进行高低权重分配。WQ, i、WK, i、WV, i为多头映射过程中的权重矩阵,其中
每组 Q矩阵、K矩阵、V矩阵通过不同的线性变换分别得到一个 Z矩阵,将得到的多个 Z矩阵进行拼接。多头注意力层的计算过程可表示为:
| $ \left\{\begin{array}{l} \boldsymbol{h}_i=f_{\text {Attention }}\left(\boldsymbol{Q} \boldsymbol{W}_{\mathrm{Q}, i}, \boldsymbol{K} \boldsymbol{W}_{\mathrm{K}, i}, \boldsymbol{V} \boldsymbol{W}_{\mathrm{V}, i}\right) \\ f_{\text {MultiHead }}(\boldsymbol{Q}, \boldsymbol{K}, \boldsymbol{V})=f_{\text {Concat }}\left(\boldsymbol{h}_1, \boldsymbol{h}_2, \boldsymbol{h}_3\right) \boldsymbol{W}_\mathrm{O} \end{array}\right. $ | (1) |
式中:fAttention(·)为多头映射过程函数;fMultiHead(·)、fConcat(·)为多头注意力层运算过程函数;
考虑区域电力系统中存在多个节点,采集的数据为多变量时间序列。定义 x为电力系统中节点采集的负荷数据,W = x1, x2, …, xt,
|
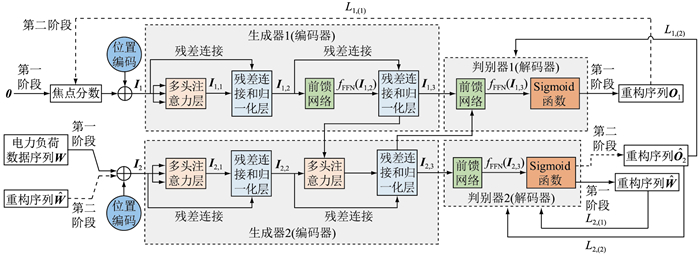
图 3 GAN-Transformer模型结构 Fig. 3 Structure of GAN-Transformer model |
生成器1用于生成包含负荷数据异常焦点分数与位置编码信息特征的重构序列。依托Transformer生成器架构,将焦点分数与位置编码信息作为输入,输出为输入序列的重构数据I1, 3。在生成器1的正向传播过程中,焦点分数初始值以零向量形式与位置编码信息I1共同作为多头注意力层的输入,输出记为I1, 1;再将I1与I1, 1共同经过残差连接和归一化层,输出记为I1, 2;输入I1, 2依次至前馈网络、第二个残差连接和归一化层,经过ReLU激活函数线性变换以及残差连接操作输出I1, 3。将生成器1表示为:
| $ \left\{\begin{array}{l} \boldsymbol{I}_{1, 1}=f_{\mathrm{MH}}\left(\boldsymbol{I}_1, \boldsymbol{I}_1, \boldsymbol{I}_1\right) \\ \boldsymbol{I}_{1, 2}=f_{\text {LayerNorm }}\left(\boldsymbol{I}_1+\boldsymbol{I}_{1, 1}\right) \\ \boldsymbol{I}_{1, 3}=f_{\text {LayerNorm }}\left(\boldsymbol{I}_{1, 2}+f_{\mathrm{FFN}}\left(\boldsymbol{I}_{1, 2}\right)\right) \end{array}\right. $ | (2) |
式中:fMH(I1, I1, I1)为对拼接后的输入矩阵I1进行多头注意力操作;fFFN(I1, 2)为对输入矩阵I1, 2进行前馈网络操作;fLayerNorm(·)为对每一层的输入值进行归一化处理。
生成器2用于重构输入电力负荷序列。在生成器2的正向传播过程中,将电力负荷序列与位置编码信息I2作为输入,通过首个多头注意力层,输出记为I2, 1;将I2与I2, 1输入第一个残差连接和归一化层,输出记为I2, 2;I2, 2经过第二层的多头注意力层以及残差连接和归一化层的操作后,输出记为I2, 3。将生成器2表示为:
| $ \left\{\begin{array}{l} \boldsymbol{I}_{2, 1}=f_{\mathrm{MH}}\left(\boldsymbol{I}_2, \boldsymbol{I}_2, \boldsymbol{I}_2\right) \\ \boldsymbol{I}_{2, 2}=f_{\text {LayerNorm }}\left(\boldsymbol{I}_2+\boldsymbol{I}_{2, 1}\right) \\ \boldsymbol{I}_{2, 3}=f_{\text {LayerNorm }}\left(\boldsymbol{I}_{2, 2}+f_{\mathrm{MH}}\left(\boldsymbol{I}_{2, 2}, \boldsymbol{I}_{2, 2}, \boldsymbol{I}_{2, 2}\right)\right) \end{array}\right. $ | (3) |
判别器1与判别器2由位置前馈网络和Sigmoid激活函数构成。第一阶段的判别器1和判别器2分别表示为:
| $ \left\{\begin{array}{l} \boldsymbol{O}_1=f_{\text {Sigmoid }}\left(f_{\mathrm{FFN}}\left(\boldsymbol{I}_{1, 3}\right)\right) \\ \hat{\boldsymbol{W}}=f_{\text {Sigmoid }}\left(f_{\mathrm{FFN}}\left(\boldsymbol{I}_{2, 3}\right)\right) \end{array}\right. $ | (4) |
第二阶段判别器2表示为:
| $ \hat{\boldsymbol{O}}_2=f_{\text {Sigmoid }}\left(f_{\mathrm{FFN}}\left(\boldsymbol{I}_{2, 3}\right)\right) $ | (5) |
式中:O1为第一阶段判别器1输出结果;
运用分阶段多次映射的思想对模型进行训练。以两阶段映射为例,将第一阶段映射的输出作为第二阶段的输入。为得到初始重构负荷序列,第一阶段定义为模型映射阶段,将焦点分数初始值0经过位置编码后输入至生成器1中,生成器1与生成器2的输出共同作为判别器1的输入,判别器1输出重构序列O1。同时将电力负荷历史数据序列W经过位置编码后输入至生成器2中,生成器1的输出将作为生成器2多头注意力层的部分输入,生成器2的输出作为判别器2的输入,此时判别器2的输出结果对应为第一阶段重构序列
为得到更优的重构负荷序列,第二阶段定义为模型训练与重映射阶段。基于第一阶段映射,模型完成对抗训练后再进行重映射。将第一阶段中判别器1的重构损失L1, (1)作为第二阶段的焦点分数,经过位置编码后再次输入至生成器1。同时将第一阶段重构序列
模型在第一阶段的目标是生成和输入负荷数据分布一致的重构序列。将重构损失结果作为焦点分数,促使生成器关注趋势异常的子序列。
定义第一阶段判别器1和判别器2的重构损失函数为L1, (1)和L2, (1)分别为:
| $ \left\{\begin{array}{l} L_{1, (1)}=\left\|\boldsymbol{O}_1-\boldsymbol{W}\right\|_2 \\ L_{2, (1)}=\|\hat{\boldsymbol{W}}-\boldsymbol{W}\|_2 \end{array}\right. $ | (6) |
模型在第二阶段进行模型训练与重映射,定义第二阶段判别器1和判别器2的重构损失函数为L1, (2)和L2, (2)分别为:
| $ \left\{\begin{array}{l} L_{1, (2)}=+\left\|\hat{\boldsymbol{O}}_2-\boldsymbol{W}\right\|_2 \\ L_{2, (2)}=-\left\|\hat{\boldsymbol{O}}_2-\boldsymbol{W}\right\|_2 \end{array}\right. $ | (7) |
将第一阶段和第二阶段的判别器1和判别器2的损失函数相结合,得出模型的整体损失函数L1和L2分别为:
| $ \left\{\begin{array}{l} L_1=\varepsilon^{-n}\left\|\boldsymbol{O}_1-\boldsymbol{W}\right\|_2+\left(1-\varepsilon^{-n}\right)\left\|\hat{\boldsymbol{O}}_2-\boldsymbol{W}\right\|_2 \\ L_2=\varepsilon^{-n}\|\hat{\boldsymbol{W}}-\boldsymbol{W}\|_2-\left(1-\varepsilon^{-n}\right)\left\|\hat{\boldsymbol{O}}_2-\boldsymbol{W}\right\|_2 \end{array}\right. $ | (8) |
式中:n为模型训练次数;ε为超参数,一般取值接近1。
2.2.3 异常数据检测机制为了准确识别输入负荷数据中的异常点,将输入负荷数据与模型第一阶段重构序列
| $ \left\{\begin{array}{l} s_t=\frac{1}{2}\left\|\boldsymbol{O}_1-\hat{\boldsymbol{W}}\right\|_2+\frac{1}{2}\left\|\hat{\boldsymbol{O}}_2-\hat{\boldsymbol{W}}\right\|_2 \\ y_t=1 \quad s_t \geqslant f_{\mathrm{POT}}\left(s_t\right) \end{array}\right. $ | (9) |
式中:st为异常得分;fPOT为使用POT方法设置的阈值;yt为异常诊断标签,yt=1为t时刻数据的异常标签,yt=0为t时刻数据的正常标签。
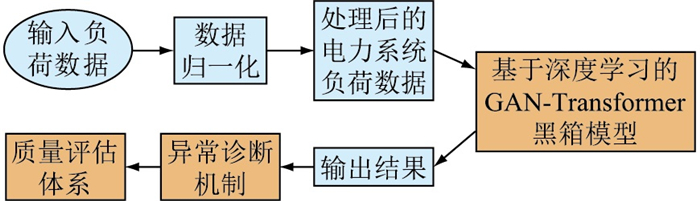
3 电力系统负荷数据异常检测实现 3.1 实现流程基于GAN-Transformer模型的电力系统负荷异常检测的实现流程如图 4所示,主要步骤为:
|
图 4 基于GAN-Transformer电力负荷异常检测流程 Fig. 4 Power load anomaly detection process based on GAN-Transformer |
(1) 获取包含丰富异常特征的典型电力系统负荷历史数据,且将采集的电力负荷历史数据分为训练样本集和测试样本集,对训练样本进行归一化处理;
(2) 将训练样本集作为模型的输入,设置超参数与训练次数,完成模型训练;
(3) 将测试样本集作为模型的输入,将模型输出结果根据异常检测机制进行异常诊断,判断是否为异常数据;
(4) 通过质量评估对测试结果与模型检测性能进行综合评价分析。
3.2 检测性能评估指标使用精确率P、召回率R和F1值来综合评估GAN-Transformer模型的数据异常检测性能:
| $ P=\frac{T_{\mathrm{P}}}{T_{\mathrm{P}}+F_{\mathrm{P}}} $ | (10) |
| $ R=\frac{T_{\mathrm{P}}}{T_{\mathrm{P}}+F_{\mathrm{N}}} $ | (11) |
| $ F_1=\frac{2 P R}{P+R} $ | (12) |
式中:TP为实际检测出的异常样本数量(检测值为1,真实值为1);FP为检测为异常但实际非异常的样本数量(检测值为1,真实值为0);FN为未被检测出的异常样本数量(检测值为0,真实值为1)。
4 电力系统负荷数据异常检测实验分析 4.1 数据预处理对负荷数据集进行归一化处理。采用最大最小归一化法,将输入的训练样本数据与输出的电力负荷重构数据均按等比例缩放,转换至[0, 1]的无量纲归一化值。
| $ \boldsymbol{x}_t^*=\frac{\boldsymbol{x}_t-\min (\boldsymbol{x})}{\max (\boldsymbol{x})-\min (\boldsymbol{x})+\boldsymbol{\varepsilon}^{\prime}} $ | (13) |
式中:xt*为t时刻的训练样本数据xt进行归一化后的向量;min(·)、max(·)分别为时间序列中的最小值和最大值函数;ε′为一个常数向量。
4.2 检测结果及分析评估为验证GAN-Transformer模型在电力负荷数据异常检测方面的有效性,基于Python 3.8解释器、Pycharm 2022.2编译环境、i5-12400F计算机处理器、32 G内存以及Windows 10操作系统搭建实验环境。数据集来源于某供电台区历史供电负荷数据与用电负荷数据,数据采集时间间隔为30 s,时间跨度为90 d,覆盖波动异常与极值异常2种典型特征。按照7 ∶3的比例随机分为训练集和测试集。模型训练结束后,从测试集中随机抽取3 d的数据进行异常检测结果分析,如图 5、图 6所示。
|
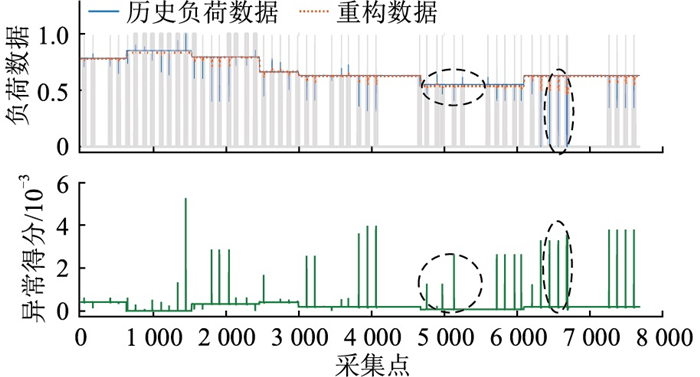
图 5 供电负荷数据异常检测结果 Fig. 5 Power load data anomaly detection results |
|
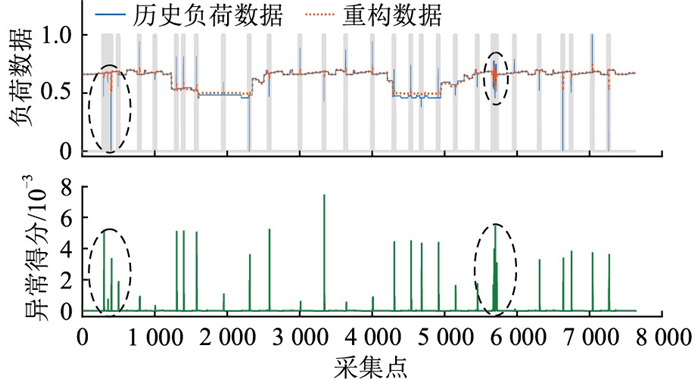
图 6 用电负荷数据异常检测结果 Fig. 6 Electricity load data anomaly detection results |
图 5与图 6中横坐标均为按等间隔时间30 s采集的电力负荷数据量,纵坐标分别为GAN-Transformer模型电力负荷数据归一化后区间为[0, 1]的重构输出与异常数据诊断得分。为便于理解,图 5中采用灰色阴影表示负荷异常出现的区域。异常得分曲线下端由不同阶段的POT组成,得分高于阈值的柱状曲线表示该点可能存在负荷异常,同时柱状曲线的幅值越大表示异常得分越高。
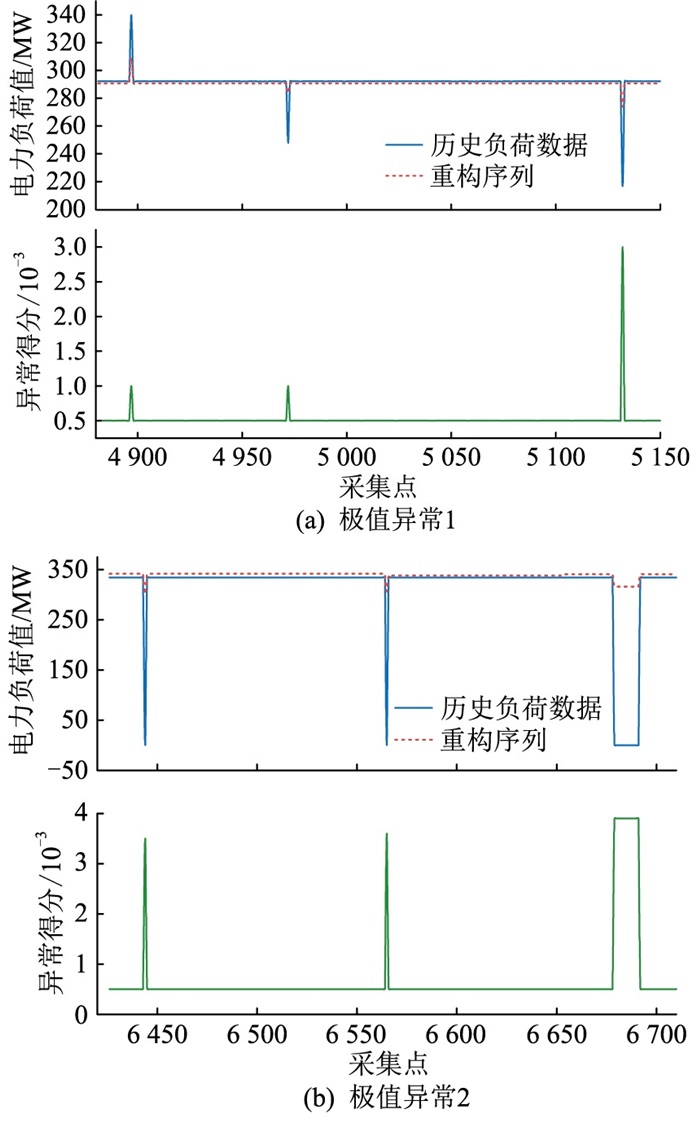
为深入分析图 5所示的供电负荷数据异常检测结果,以负荷数据极值异常为例,放大图 5的局部信息,得出重构电力数据与历史负荷数据的明显对比结果,如图 7所示,可知GAN-Transformer能够准确检测识别出供电负荷数据中的极值异常。
|
图 7 供电负荷数据异常检测结果细节 Fig. 7 Details of power load data anomaly detection results |
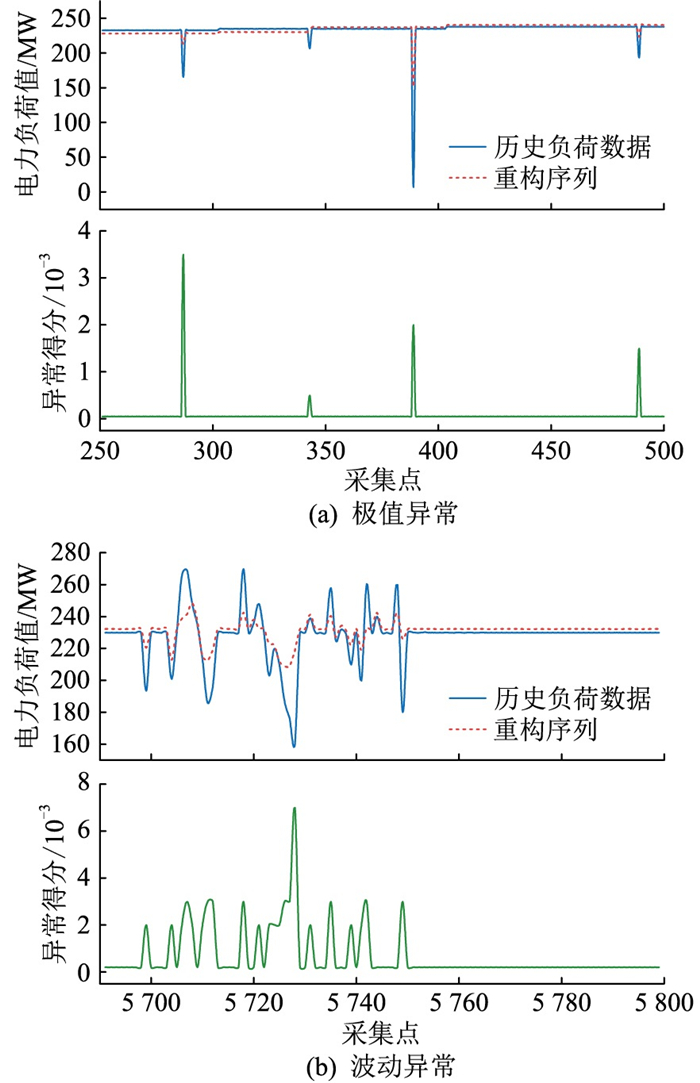
为深入分析图 6所示的用电负荷数据异常检测结果,以负荷数据极值异常为例,放大图 6中的局部历史负荷数据与重构负荷数据信息,得到图 8(a)所示的极值异常检测结果明细图;以负荷数据波动异常为例,放大图 6中的局部历史负荷数据与重构负荷数据信息,得到图 8(b)所示的波动异常检测结果明细图。图 8中,由判别器2生成的重构数据能够较好地捕捉给定电力负荷曲线变化特征。无论是历史用电负荷数据与模型重构序列,还是异常得分结果,GAN-Transformer均能够准确检测识别出用电负荷数据中的极值异常与波动异常。
|
图 8 用电负荷数据异常检测结果细节 Fig. 8 Details of electricity load data anomaly detection results |
为了验证GAN-Transformer模型对负荷数据异常检测的优越性,将其与OmniAnomaly、LSTM-NDT、MAD-GAN、DAGMM、无监督异常检测(unsupervised anomaly detection, USAD)以及Transformer等对照模型进行异常检测对比实验分析,且各模型训练次数均设置为500次。表 1和表 2分别为供电负荷数据和用电负荷数据在不同模型下的检测结果。
|
|
表 1 不同模型训练供电负荷数据的对比实验结果 Table 1 Comparative experimental results of power load data from different model training |
|
|
表 2 不同模型训练用电负荷数据的对比实验结果 Table 2 Comparative experimental results of electricity load data from different model training |
分析供电负荷数据异常检测结果,表 1中GAN-Transformer模型的检测精确率为0.949 2,相比其他模型精确率提高了10%~20%。GAN-Transformer模型的召回率为0.938 4,略低于其他模型,表明其对异常数据的查全率较低,进而表明模型的异常误检率也较低。针对用电负荷数据检测与识别,表 2中GAN-Transformer模型的检测精确率为0.976 2,相比于其他模型仍然具有优势。此时,GAN-Transformer模型的召回率为0.926 4,与其他模型相比拥有相似的查全率。综合分析精确率和召回率结果,表 1中GAN-Transformer模型的F1值为0.943 7,表 2中GAN-Transformer模型的F1值为0.950 6,均明显高于对照模型且最接近1。分析不同模型的训练时间可以得出,GAN-Transformer模型在训练次数相同、训练时间减少了70%的情况下,异常检测精确率明显提升,模型综合表现更优。
5 结语针对电力负荷数据异常检测的相关问题,首先将电力负荷数据异常按照波动异常与极值异常进行合理分类,并分析不同异常现象的负荷数据;其次,在Transformer与GAN的框架下提出了一种基于GAN-Transformer的改进模型,给出了模型的详细框架和生成器、判别器以及损失函数的数学表达;然后,将特征映射与训练过程分为2个阶段,将第一阶段的输出作为第二阶段的输入,促使模型所得到的重构负荷序列能更好地刻画电力负荷数据趋势变化特征,并通过设计焦点分数打分机制实现负荷数据异常诊断。算例分析结果表明,与对照模型相比,GAN-Transformer模型在负荷数据异常检测精确率、召回率、F1值以及训练时间方面均具有更优的性能,从而表明了所提模型的有效性和优越性。
虽然文中所提模型对电力负荷时序序列的检测准确性有一定的改进和提高,但针对电力负荷多变量时序序列检测、模型推理速度以及泛化能力尚待进一步深入研究。文中的研究工作为进一步基于深度学习实现电力负荷数据异常分类与异常数据修复提供了一定的理论与实践支撑。
| [1] |
于金镒. 向建设"具有卓越竞争力的世界一流能源互联网企业"目标奋进[J]. 国家电网, 2018(8): 54-55. YU Jinyi. Strive for the goal of building a world-class energy Internet enterprise with excellent competitiveness[J]. State Grid, 2018(8): 54-55. (  0) 0) |
| [2] |
林昱奂, 胡嘉铭, 戴伟力, 等. 基于改进K-均值联合SVDD的电力数据异常检测方法[J]. 电力电容器与无功补偿, 2023, 44(5): 99-107. LIN Yuhuan, HU Jiaming, DAI Weili, et al. Power data abnormaly detection method based on improved K-means and SVDD[J]. Power Capacitor & Reactive Power Compensation, 2023, 44(5): 99-107. (  0) 0) |
| [3] |
董骁翀, 张姝, 李烨, 等. 电力系统中时序场景生成和约简方法研究综述[J]. 电网技术, 2023, 47(2): 709-721. DONG Xiaochong, ZHANG Shu, LI Ye, et al. Review of power system temporal scenario generation and reduction methods[J]. Power System Technology, 2023, 47(2): 709-721. (  0) 0) |
| [4] |
马一杰, 陈君, 刘松. 基于长短时记忆网络的电力负荷异常检测[J]. 云南大学学报(自然科学版), 2020, 42(S2): 55-59. MA Yijie, CHEN Jun, LIU Song. Power load abnormal detection based on long short-term memory[J]. Journal of Yunnan University (Natural Sciences Edition), 2020, 42(S2): 55-59. (  0) 0) |
| [5] |
QIU X H, REN Y, SUGANTHAN P N, et al. Empirical mode decomposition based ensemble deep learning for load demand time series forecasting[J]. Applied Soft Computing, 2017, 54: 246-255. DOI:10.1016/j.asoc.2017.01.015 (  0) 0) |
| [6] |
白开峰, 赵宏斌, 张芸, 等. 电网异常业务数据检测方法综述[J]. 计算机与现代化, 2023(3): 79-83, 89. BAI Kaifeng, ZHAO Hongbin, ZHANG Yun, et al. Review of abnormal service data detection methods in power grid[J]. Computer and Modernization, 2023(3): 79-83, 89. (  0) 0) |
| [7] |
周捷, 严建峰, 杨璐, 等. LSTM模型集成方法在客户流失预测中的应用[J]. 计算机应用与软件, 2019, 36(11): 39-46. ZHOU Jie, YAN Jianfeng, YANG Lu, et al. Application of LSTM ensemble method in customer churn prediction[J]. Computer Applications and Software, 2019, 36(11): 39-46. (  0) 0) |
| [8] |
SAEED, MUSTAFA, SHEIKH, et al. Ensemble bagged tree based classification for reducing non-technical losses in Multan electric power company of Pakistan[J]. Electronics, 2019, 8(8): 860. (  0) 0) |
| [9] |
HU L J, LIU K Y, LIN Z, et al. An abnormal state detection method for power distribution network based on big data technology[C]//2018 International Conference on Cyber-Enabled Distributed Computing and Knowledge Discovery (CyberC). Zhengzhou, China. IEEE, 2019: 169-1694.
(  0) 0) |
| [10] |
SALEHI M, LECKIE C, BEZDEK J C, et al. Fast memory efficient local outlier detection in data streams[J]. IEEE Transactions on Knowledge and Data Engineering, 2016, 28(12): 3246-3260. (  0) 0) |
| [11] |
BROWN J P, ROBERTS R G, WELSH C M, et al. Nearest neigh bor anomaly detector for passively augmented LADAR[C]//2018 IEEE Research and Applications of Photonics In Defense Conference (RAPID). Miramar Beach, FL, USA. IEEE, 2018: 1-4.
(  0) 0) |
| [12] |
金晟, 苏盛, 薛阳, 等. 数据驱动窃电检测方法综述与低误报率研究展望[J]. 电力系统自动化, 2022, 46(1): 3-14. JIN Sheng, SU Sheng, XUE Yang, et al. Review on data-driven based electricity theft detection method and research prospect for low false positive rate[J]. Automation of Electric Power Systems, 2022, 46(1): 3-14. (  0) 0) |
| [13] |
肖勇, 郑楷洪, 余忠忠, 等. 基于三次指数平滑模型与DBSCAN聚类的电量数据异常检测[J]. 电网技术, 2020, 44(3): 1099-1104. XIAO Yong, ZHENG Kaihong, YU Zhongzhong, et al. Power data anomaly detection based on holt-winters model and DBSCAN clustering[J]. Power System Technology, 2020, 44(3): 1099-1104. (  0) 0) |
| [14] |
陈启鑫, 郑可迪, 康重庆, 等. 异常用电的检测方法: 评述与展望[J]. 电力系统自动化, 2018, 42(17): 189-199. CHEN Qixin, ZHENG Kedi, KANG Chongqing, et al. Detection methods of abnormal electricity consumption behaviors: review and prospect[J]. Automation of Electric Power Systems, 2018, 42(17): 189-199. (  0) 0) |
| [15] |
卓琳, 赵厚宇, 詹思延. 异常检测方法及其应用综述[J]. 计算机应用研究, 2020, 37(S1): 9-15. ZHUO Lin, ZHAO Houyu, ZHAN Siyan. Overview of anomaly detection methods and applications[J]. Application Research of Computers, 2020, 37(S1): 9-15. (  0) 0) |
| [16] |
KOLA SUJATHA P, YUVARANI S. Anomaly detection in video using Gaussian model and recurrent neural network[C]//2018 Tenth International Conference on Advanced Computing (ICoAC). Chennai, India. IEEE, 2019: 202-207.
(  0) 0) |
| [17] |
HUNDMAN K, CONSTANTINOU V, LAPORTE C, et al. Detecting spacecraft anomalies using LSTMs and nonparametric dynamic thresholding[C]//Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. London, United Kingdom. New York: ACM, 2018: 387-395.
(  0) 0) |
| [18] |
庞传军, 张波, 余建明. 基于LSTM循环神经网络的短期电力负荷预测[J]. 电力工程技术, 2021, 40(1): 175-180, 194. PANG Chuanjun, ZHANG Bo, YU Jianming. Short-term power load forecasting based on LSTM recurrent neural network[J]. Electric Power Engineering Technology, 2021, 40(1): 175-180, 194. DOI:10.12158/j.2096-3203.2021.01.025 (  0) 0) |
| [19] |
陈磊, 秦凯, 郝矿荣. 基于集成LSTM-AE的时间序列异常检测方法[J]. 华中科技大学学报(自然科学版), 2021, 49(11): 35-40. CHEN Lei, QIN Kai, HAO Kuangrong. Time series anomaly detection method based on integrated LSTM-AE[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2021, 49(11): 35-40. (  0) 0) |
| [20] |
LI D, CHEN D C, JIN B H, et al. MAD-GAN: multivariate anomaly detection for time series data with generative adversarial networks[C]//TETKO I, K URKOVÁ V, KARPOV P, et al. International Conference on Artificial Neural Networks. Cham: Springer, 2019: 703-716.
(  0) 0) |
| [21] |
SU Y, ZHAO Y J, NIU C H, et al. Robust anomaly detection for multivariate time series through stochastic recurrent neural network[C]//Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. Anchorage, AK, USA. New York: ACM, 2019: 2828-2837.
(  0) 0) |
| [22] |
刘钊瑞, 高云鹏, 郭建波, 等. 基于深度自编码器高斯混合模型的窃电行为检测[J]. 电力系统保护与控制, 2022, 50(18): 92-102. LIU Zhaorui, GAO Yunpeng, GUO Jianbo, et al. Abnormal detection of electricity theft using a deep auto-encoder Gaussian mixture model[J]. Power System Protection and Control, 2022, 50(18): 92-102. (  0) 0) |
| [23] |
ZHANG C X, SONG D J, CHEN Y C, et al. A deep neural network for unsupervised anomaly detection and diagnosis in multivariate time series data[J]. Proceedings of the AAAI Conference on Artificial Intelligence, 2019, 33(1): 1409-1416. (  0) 0) |
| [24] |
XU J H, WU H X, WANG J M, et al. Anomaly transformer: time series anomaly detection with association discrepancy[EB/OL]. [2023-04-20]. https://arxiv.org/abs/2110.02642.pdf.
(  0) 0) |
| [25] |
杨雯, 尹康涌, 鲍奕宇, 等. 基于深度置信网络的电网故障类型辨识[J]. 电力工程技术, 2021, 40(2): 169-177. YANG Wen, YIN Kangyong, BAO Yiyu, et al. Fault types identification of power grid based on deep belief network[J]. Electric Power Engineering Technology, 2021, 40(2): 169-177. DOI:10.12158/j.2096-3203.2021.02.024 (  0) 0) |
 2024, Vol. 43
2024, Vol. 43


 陆旦宏(1978),男,博士,教授,研究方向为新能源与智能电网(E-mail:
陆旦宏(1978),男,博士,教授,研究方向为新能源与智能电网(E-mail: