文章编号: 2096-3203(2024)01-0041-09 中图分类号: TM761
双碳目标的提出,标志着我国新能源建设步入快车道[1]。然而,高比例清洁能源的并网会对原有系统的频率稳定控制造成负面影响[2-3]。储能系统具有响应速度快、输入输出可控性高、配置灵活等特点,将其应用于电网调频可以有效提高电网频率稳定性[4]。
当储能系统参与电网调频时,对其采用虚拟下垂和虚拟惯性控制是目前主要的方法[5-6]。在二者基础上,为了获取更好的调频效果,有研究将虚拟惯性和下垂控制相结合,以综合控制的方式参与电网调频,优化频率响应表现[7-8]。考虑到储能系统的荷电状态(state of charge,SOC)、充放电特性与其循环使用寿命间的关联关系,设计综合调频策略使充放电系数与SOC动态匹配,能够获取更好的调频经济性表现[9]。但是,目前储能辅助电网调频的研究多聚焦于对频率偏差的控制,而当电力系统中清洁能源占比较高时,系统转动惯量将相对减小,扰动发生导致的过大频率变化率(rate of change of frequency,RoCoF)可能使同步机出现滑极现象而损坏其内部结构,故为保障电网安全运行,须将RoCoF纳入电网频率控制指标中[10]。
当综合考虑频率偏差与RoCoF来设计储能辅助调频方法时,目前的研究主要聚焦于储能的容量配置[11-12]与输出调整[13]等方面。进行容量配置调整的目的是能够更好地获得足够的系统惯性支撑,以优化RoCoF的表现。而在容量配置完成的情况下,合适的储能充放电控制方法对优化RoCoF的表现具有更直接的作用。一般而言,现有研究大多通过附加额外控制器以提高储能的输出灵活性,扩大储能输出范围,从而在RoCoF过大时有针对性地提供惯性支撑[14]。目前,储能系统输出调整的控制信号大多以频率偏差为准,频率偏差的控制虽贯穿整个调频过程,但在扰动来临瞬间往往伴随着较大的RoCoF,故用频率偏差作为控制信号在时间尺度上具有滞后性[15]。另外,稳态频率偏差与RoCoF信号之间除滞后性外,还存在不一致性,即因扰动波动引起的较大RoCoF并不一定会导致较大的稳态频率偏差,故需要合适的方法针对系统当前运行状态进行准确判断,从而实现电网频率控制模式的精细化表现。
频率控制方法针对频率偏差和RoCoF状态进行的动态调整须根据系统状态进行设计,目前实现该需求的方式有数据驱动和规则驱动2种[16]。利用数据驱动作判断时,不需要建立具体模型,根据大量数据的学习训练即可实现[17];而使用规则驱动时,需要有已知数学模型,然后根据设计的逻辑规则完成自适应驱动[18]。考虑到负荷频率控制的特征,即根据频率特性易于设计逻辑规则,故采用规则驱动对储能调频有功输出进行调整。但是,根据驱动信号调整储能输出,存在储能输出额外增强的需求,会导致储能充放电深度高,从而不利于储能循环使用。因此,针对系统处于不同状态时的储能参与度需求,综合考虑调频效果与储能循环寿命的平衡,是有待进一步考虑的问题。
文中提出一种基于频率响应特性的储能辅助电网一次调频控制策略,拟通过对系统RoCoF和频率偏差的综合判断进行储能有功输出方式的调整,并通过多目标优化问题的设计与求解,实现储能辅助电网调频的综合效能最优。
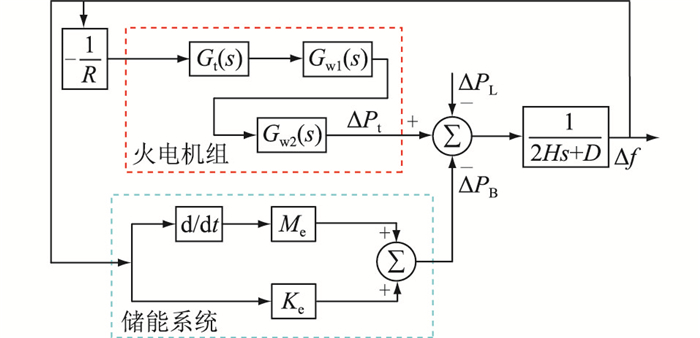
1 储能参与电网一次调频模型构建以储能辅助传统火电机组参与一次调频为研究背景,构建储能参与负荷频率控制系统结构,如图 1所示,其中R为机组调差系数;ΔPt为火电机组响应功率;ΔPB为储能响应功率;ΔPL为负荷扰动偏差;Δf为频率偏差;H为发电机转动惯量;D为负荷阻尼系数;Me为储能虚拟惯性系数;Ke为储能虚拟下垂系数。系统主要包括:火电机组、储能系统及交流电网等效模型。
|
图 1 储能参与负荷频率控制系统 Fig. 1 Energy storage participates in load frequency control system |
火电机组主要由调速器和再热式汽轮机构成[19]。调速器的传递函数为:
| $ G_{\mathrm{t}}(s)=\frac{1}{1+T_{\mathrm{g}} s} $ | (1) |
再热式汽轮机被分为两部分,传递函数如下:
| $ G_{\mathrm{w}}=G_{\mathrm{w} 1}(s) G_{\mathrm{w} 2}(s)=\frac{1}{1+T_{\mathrm{t}} s} \times \frac{K_{\mathrm{r}} T_{\mathrm{r}} s+1}{T_{\mathrm{r}} s+1} $ | (2) |
式中:Tg为调速器时间常数;Tr为再热时间常数;Tt为气容时间常数;Kr为再热系数。
储能采用虚拟惯性和虚拟下垂相结合的综合控制方式参与调频,其输出表达式[20-22]如下:
| $ \Delta P_{\mathrm{B}}=M_{\mathrm{e}} \frac{\mathrm{d} \Delta f}{\mathrm{~d} t}+K_{\mathrm{e}} \Delta f $ | (3) |
目前,我国电力系统主要以最大稳态频率偏差作为调频目标,而对RoCoF未作明确要求。随着可再生能源渗透率提高,在电力系统惯性下降的情况下,RoCoF的表现应在频率控制中予以考虑。
2.1 RoCoF与调频需求的关联性分析电网出现频率波动的根本原因是发电量与负荷需求的不平衡。在电网负荷频率控制过程中,当储能采用综合控制方式参与调频时,根据图 1,可得系统动态频率响应方程如式(4)所示。
| $ \Delta f=\left(\Delta P_{\mathrm{t}}-\Delta P_{\mathrm{L}}-M_{\mathrm{e}} \frac{\mathrm{d} \Delta f}{\mathrm{~d} t}-K_{\mathrm{e}} \Delta f\right) \frac{1}{2 H s+D} $ | (4) |
整理得:
| $ \left(2 H+M_{\mathrm{e}}\right) \frac{\mathrm{d} \Delta f}{\mathrm{~d} t}+\left(D+K_{\mathrm{e}}\right) \Delta f=\Delta P_{\mathrm{t}}-\Delta P_{\mathrm{L}} $ | (5) |
将式(5)线性化,引入功率不平衡量ΔPu表示等式右侧,扰动来临瞬间,由于惯性影响,Δf与火电机组调频输出均为0,由此可得:
| $ \begin{gathered} C\left(t_{1}\right)=\left.\frac{\mathrm{d} \Delta f}{\mathrm{~d} t}\right|_{t=t_{1}}=-\frac{\left.\Delta P_{\mathrm{u}}\right|_{t=t_{1}}}{2 H+M_{\mathrm{e}}} \\ \left.\Delta P_{\mathrm{u}}\right|_{t=t_{1}}=\left.\Delta P_{\mathrm{L}}\right|_{t=t_{1}} \end{gathered} $ | (6) |
式中:t1为扰动来临时刻,该时刻RoCoF最大,记为C(t1)。后文图中以C表示RoCoF。
扰动来临后火电机组开始动作,可得火电机组输出为:
| $ \Delta P_{\mathrm{t}}=\left(2 H+M_{\mathrm{e}}\right) \frac{\mathrm{d} \Delta f}{\mathrm{~d} t}+\left(D+K_{\mathrm{e}}\right) \Delta f+\Delta P_{\mathrm{L}} $ | (7) |
火电机组响应调频初期,其有功调整主要受RoCoF影响,故可用C(t1)近似衡量响应初期的ΔPt,即:
| $ \Delta P_{\mathrm{t}}=\left(2 H+M_{\mathrm{e}}\right) C\left(t_{1}\right)+\Delta P_{\mathrm{L}} $ | (8) |
若C(t1)过大,会使其有功输出调整幅值过高,出现机组爬坡率过高的问题,对机组安全运行造成威胁,故须采取一定措施对其进行约束。
2.2 频率响应区间划分电力系统运行过程中,对频率波动幅度有一定的要求。GB/T 15945—2008提出:电力系统正常运行条件下,频率偏差绝对值应在0.2 Hz以内,系统容量较小时可放宽至0.5 Hz。
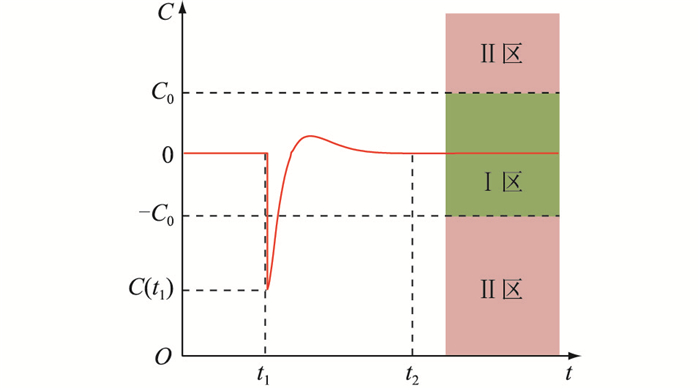
考虑到在上述要求范围内,电网的运行安全性不会受到威胁,而超出该范围后,要求频率快速回归。因此,在调频过程中,取上述标准的较小值0.2 Hz作为稳态频率偏差的阈值δ,可将稳态频率偏差Δfs的表现划分为2个区域:区间Ⅰ为0≤|Δfs|<δ,区间Ⅱ为δ≤|Δfs|,如图 2所示。当储能参与电网调频时,在区间Ⅰ采用常规调频手段,在区间Ⅱ则须强化其有功输出,加速频率调整进程。

|
图 2 频率偏差区域划分 Fig. 2 Frequency deviation area division |
图 2中t1时刻扰动来临,t2时刻系统频率偏差到达稳态值Δfs。当调频过程中同时考虑RoCoF的表现时,也需要获取RoCoF的量化表述。扰动来临瞬间,频率偏差为0,对应的功率不平衡量为:
| $ \left.\Delta P_{\mathrm{u}}\right|_{t=t_{1}}=-\left(2 H+M_{\mathrm{e}}\right) C\left(t_{1}\right) $ | (9) |
频率偏差到达稳态时,RoCoF为0,则在式(5)基础上可得式(10)。
| $ \left\{\begin{array}{l} \left.\Delta P_{\mathrm{u}}\right|_{t=t_{2}}=\left.\Delta P_{\mathrm{t}}\right|_{t=t_{2}}-\left.\Delta P_{\mathrm{L}}\right|_{t=t_{2}}=\left(D+K_{\mathrm{e}}\right) \Delta f_{\mathrm{s}} \\ \left.\Delta P_{\mathrm{t}}\right|_{t=t_{2}}=-\frac{\Delta f_{\mathrm{s}}}{R} \end{array}\right. $ | (10) |
代入稳态频率偏差阈值δ作为式(10)中的Δfs,可得造成频率波动值为0.2 Hz的临界扰动变化量。
| $ \Delta P_{\mathrm{LL}}=\left.\Delta P_{\mathrm{L}}\right|_{t=t_{2}}=-\delta\left(\frac{1}{R}+D+K_{\mathrm{e}}\right) $ | (11) |
式中:ΔPLL为临界扰动量,物理意义为发生ΔPLL大小的阶跃扰动将导致系统稳态频率偏差为δ,故ΔPLL的数值可视为该系统扰动阈值。
因系统负荷阻尼系数、储能虚拟下垂系数与机组调差系数的倒数不在一个数量级,故式(11)可简化为:
| $ \Delta P_{\mathrm{LL}}=-\delta/R $ | (12) |
ΔPLL为阶跃扰动,故t1与t2时刻ΔPL相同,大小均为ΔPLL。综合式(6)与式(9)—式(12)可得:
| $ \left.\Delta P_{\mathrm{u}}\right|_{t=t_{1}}=\Delta P_{\mathrm{LL}}=-\left(2 H+M_{\mathrm{e}}\right) C\left(t_{1}\right) $ | (13) |
将式(12)代入式(13),可求得当稳态偏差为δ时,对应扰动来临时的RoCoF,即为对应稳态频率偏差阈值δ的RoCoF阈值,令其为C1,其表达式如下:
| $ C_{1}=\frac{\delta}{\left(2 H+M_{\mathrm{e}}\right) R} $ | (14) |
例如,若发电机转动惯量H为5.92,储能虚拟惯性系数Me为3.8[23],可求得C1为0.256 Hz/s。
上述C1为RoCoF的阈值求解值,然而实际电网运行中应还有分布式电源的RoCoF保护,以英国大停电事故中扰动来临时RoCoF为0.135 Hz/s,导致约350 MW分布式电源脱网为例[24]。若综合电网实际运行与需求,可取上述两值中的较小值作为RoCoF阈值,令其为C0,即:C0=0.135 Hz/s。
由此得RoCoF区间划分:Ⅰ区为0≤|C(t1)| <|C0|,Ⅱ区为|C0|≤|C(t1)|。
RoCoF分区示意如图 3所示。与频率偏差区域划分目标类似,当C(t1)位于区间Ⅱ时,表示电网的运行安全性可能受到威胁,稳态频率偏差有超过0.2 Hz的风险,该情况下储能参与电网调频时,须强化其有功输出,以减轻发电机组的动作压力。
|
图 3 RoCoF区间划分 Fig. 3 RoCoF interval division |
根据上述分析,当频率偏差或RoCoF越过所设定的阈值到达区间Ⅱ时,需要储能在参与电网调频时能够有针对性地增大其有功输出调整幅度,以减轻火电机组调频压力,保障电网运行安全。针对此设计需求,在储能信号输入端附加比例积分(proportional integral, PI)控制器,以产生可变控制信号,对储能的输出进行调整,其表达式如式(15)所示。
| $ \Delta P_{\mathrm{B}}=\left(1+K_{\mathrm{p}}\right)\left(M_{\mathrm{e}} \frac{\mathrm{d} \Delta f}{\mathrm{~d} t}+K_{\mathrm{e}} \Delta f\right) $ | (15) |
式中:Kp为PI控制器比例系数。
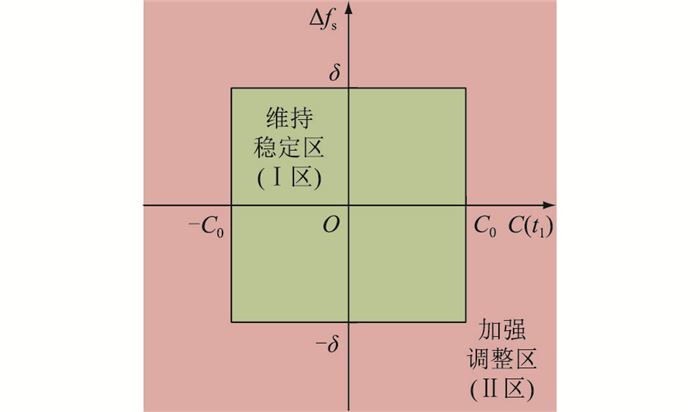
储能参与调频的有功输出将受控制器比例系数Kp、虚拟惯性系数Me与虚拟下垂系数Ke影响,对这3个参数进行调整即可改变储能参与调频的出力程度。根据对频率偏差与RoCoF特性的分析,得到驱动规则示意如图 4所示,即当判断预估稳态频率偏差或RoCoF进入加强调整区后,通过改变Kp、Me、Ke可使储能输出增强。
|
图 4 驱动规则示意 Fig. 4 Schematic diagram of driving rules |
设计驱动规则如下:
| $ X=C\left(t_{1}\right) \cup \Delta f_{\mathrm{ss}} $ | (16) |
式中:Δfss为当前扰动下一次调频完成后的稳态频率偏差预估值。
稳态频率偏差预估值Δfss的求解如式(17)所示。
| $ \left\{\begin{array}{l} \Delta f_{\mathrm{ss} 1}=-50 \times \frac{\Delta P_{\mathrm{L}} R}{1+D R+\left(1+K_{\mathrm{p}}\right) K_{\mathrm{e}} R} \\ \Delta f_{\mathrm{ss}}=\Delta f_{\mathrm{ss} 1}+\Delta f_{\mathrm{ss} 0} \end{array}\right. $ | (17) |
当负荷扰动发生,根据扰动大小,可以计算出当前扰动可能导致的频率波动为Δfss1,将其与上一时刻稳态频率偏差Δfss0叠加,即可获取Δfss,C(t1)可通过系统运行直接获取。上述二者均处于Ⅰ区时,判断系统处于维持稳定区,储能输出如式(18)所示;二者中任意一个或者均处于Ⅱ区时,判断系统处于加强调整区,储能输出如式(19)所示。
| $\Delta P_{\mathrm{B}}=\left(1+K_{\mathrm{p} 1}\right)\left(M_{\mathrm{e} 1} \frac{\mathrm{d} \Delta f}{\mathrm{~d} t}+K_{\mathrm{e} 1} \Delta f\right) $ | (18) |
| $ \Delta P_{\mathrm{B}}=\left(1+K_{\mathrm{p} 2}\right)\left(M_{\mathrm{e} 2} \frac{\mathrm{d} \Delta f}{\mathrm{~d} t}+K_{\mathrm{e} 2} \Delta f\right) $ | (19) |
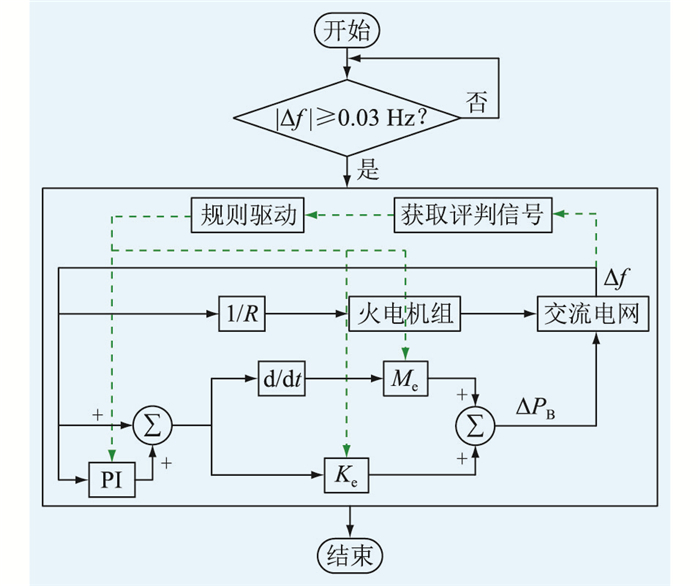
式中:Kp1、Kp2为PI控制器比例系数;Me1、Me2为虚拟惯性系数;Ke1、Ke2为虚拟下垂系数。设置死区为0.03 Hz,控制策略流程如图 5所示。
|
图 5 控制策略流程 Fig. 5 Flow chart of control strategy |
当需要储能输出增强而对储能控制参数进行调整时,储能输出增强可获得更好的调频效果,并对发电机组提供支撑,但储能充放电深度会影响其循环使用寿命,当需要储能增强其有功输出时,如何最优化储能使用,尽量降低储能寿命损耗,是需要综合考虑的问题。应综合多方面因素,进行多目标优化问题的设计与求解,以谋求调频效果与储能循环寿命之间的平衡。
3 储能输出控制多目标优化问题设计与求解 3.1 目标函数设计储能辅助电网调频时,对调频需求所展现出的矛盾性,使得在此过程中须根据储能运行特征及调频需求进行多目标优化问题的设计。
(1) 频率响应特性。维持频率稳定是电力系统频率控制的基本需求。当电网受到负荷扰动时,稳态频率偏差是判定电网频率控制效果的基础指标,故将稳态频率偏差设定为频率响应特性判断的目标函数一,即:
| $ J_{1}=\left|\Delta f_{\mathrm{s}}\right| $ | (20) |
(2) 储能循环使用寿命。电网调频过程中,储能循环使用寿命受环境、充放电深度等影响,使用环境客观可控,故讨论其与充放电深度的关系,其具体表达式[25-26]如下:
| $ \begin{gathered} N_{\mathrm{E}}=-3278 H_{\mathrm{D}}^{4}-5 H_{\mathrm{D}}^{3}+12823 H_{\mathrm{D}}^{2}- \\ 14122 H_{\mathrm{D}}+5112 \end{gathered} $ | (21) |
若忽略储能初始运行状态的影响,其充放电深度HD可视为其SOC的变化值,即:
| $ H_{\mathrm{D}}=S_{\mathrm{SOC}, t+\Delta t}-S_{\mathrm{SOC}, t}=\frac{\int_{t}^{t+\Delta t} \Delta P_{\mathrm{B}} \mathrm{d} t}{P_{\mathrm{N}}} $ | (22) |
式中:SSOC, t为储能放电前的SOC;SSOC, t+Δt为储能在SSOC, t基础上放电Δt后的SOC;PN为储能额定容量。
由式(21)、式(22)可知,储能充放电深度与循环使用寿命呈负相关,而储能输出功率与充放电深度呈正相关,由此可得储能输出与循环使用寿命也呈负相关。故以电池调频输出来衡量其循环使用寿命,设计目标函数二为:
| $ J_{2}=\left|\Delta P_{\mathrm{B}}\right| $ | (23) |
根据上述目标函数进行多目标优化求解之后,可以获取一组优化解集,即Pareto前端,如何在该解集中选择合适的具体解,需要进行综合的评估,故设计如下评价指标:
| $ J=k_{1} J_{1}+k_{2} J_{2} $ | (24) |
式中:k1、k2为权重系数,可针对不同控制需求进行任意配置,以实现满足不同需求的最优解选择。
3.2 约束条件(1) 频率偏差约束。按照国家标准,要求一次调频的稳态误差绝对值不超过0.2 Hz。故频率偏差约束为:
| $ 0 \leqslant\left|\Delta f_{\mathrm{s}}\right| \leqslant 0.2 \mathrm{~Hz} $ | (25) |
(2) RoCoF约束。国内相关研究人员推荐最大RoCoF极限值取为0.5 Hz/s[27-29],即:
| $ 0 \leqslant C\left(t_{1}\right) \leqslant 0.5 \mathrm{~Hz}/\mathrm{s} $ | (26) |
(3) 储能电池约束。储能电池约束主要是储能电池功率约束和SOC约束。对于功率约束,有:
| $ 0 \leqslant\left|\Delta P_{\mathrm{B}}\right| \leqslant \Delta P_{\mathrm{B}, \max } $ | (27) |
式中:ΔPB, max为储能电池最大输出功率。
当储能采用2.3节所述控制方式,其输出主要受PI控制器比例信号Kp、虚拟惯性系数M以及虚拟下垂系数K影响,因而电池功率约束转化为如下的参数约束:
| $ \left\{\begin{array}{l} 0 <K_{\mathrm{p}} \leqslant 1 \\ 0 \leqslant M_{\mathrm{e}} \leqslant M_{\mathrm{e}, \max } \\ 0 \leqslant K_{\mathrm{e}} \leqslant K_{\mathrm{e}, \max } \end{array}\right. $ | (28) |
式中:Me, max、Ke, max分别为最大虚拟惯性系数和最大虚拟下垂系数,分别取3.8和3.45[23]。
对于SOC约束,则是为防止过充或过放,即:
| $ S_{\mathrm{SOC}, \min } \leqslant S_{\mathrm{SOC}} \leqslant S_{\mathrm{SOC}, \max } $ | (29) |
式中:SSOC为电池SOC;SSOC, min为SOC最小值,一般取0.2;SSOC, max为SOC最大值,一般取0.8。
3.3 多目标优化问题求解多目标优化须同时对多个目标函数进行求解,取值之后再对优化结果进行筛选。考虑到如果将多目标问题转化为单目标问题之后进行求解,所保留的优化结果往往顾此失彼,容易陷入局部最优甚至极端情况,因此,拟采用基于精英策略的快速非支配排序遗传算法(non-dominated sorting genetic algorithm Ⅱ,NSGA-Ⅱ)进行求解,以更好地平衡各个目标的需求。
算法优化过程中,个体的好坏程度取决于各自的适应度,只保留适应度高的个体。将2个目标函数设计为适应度,目标函数值越小则适应度越高,待求解储能系统参数设计为个体,具体求解步骤参考文献[30]。
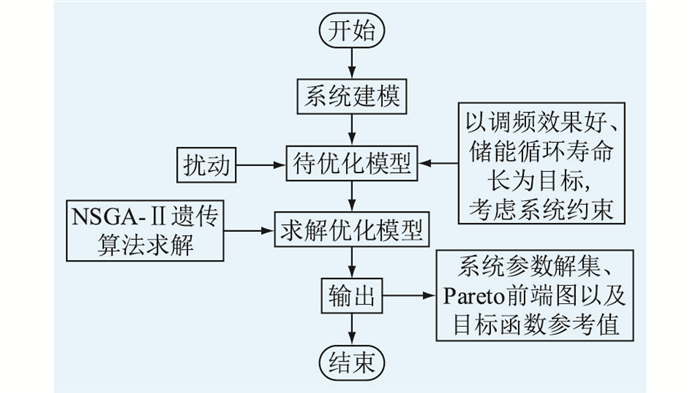
综合上述所有分析,得到所提方法的求解流程如图 6所示。
|
图 6 求解流程 Fig. 6 Solution flow chart |
为验证上述所提方法的可行性和有效性,在MATLAB/Simulink环境中进行仿真验证。建立储能辅助电网频率响应模型,其中包含一个容量为500 MW的火电厂,一个容量为12 MW/3 MW ·h的储能系统。将系统的采样周期设定为T=0.03 s,其中电池组的初始SOC设置为0.8,其余各系统仿真参数的具体取值如表 1所示。
|
|
表 1 电力系统仿真参数取值 Table 1 Power system simulation parameter value |
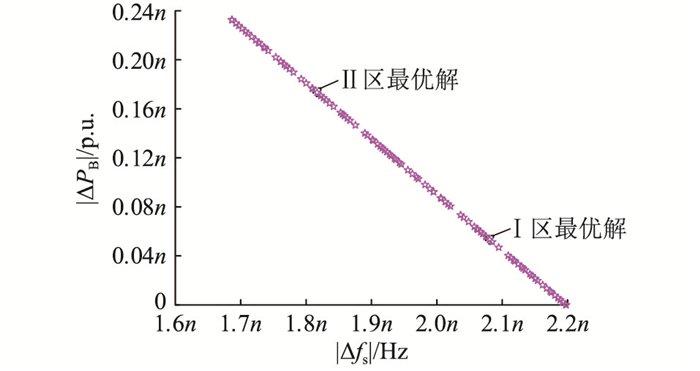
算法求解的输入为负荷扰动ΔPL,ΔPL大小设定为n,仅针对算法求解,n可为任意值,设置算法生成种群组数为300,最大迭代次数为100。运行算法得到如图 7所示的Pareto前端图。
|
图 7 Pareto前端 Fig. 7 Pareto frontend |
依照式(24)所述最优解综合评及指标,考虑到实际求解获取的Pareto前端中2个目标函数参考值不在同一数量级,自带一定偏向性,为使选解平衡化,故先将储能功率偏移在数值上扩大2.5倍,使横纵坐标轴分度值一致,从而使二者达到同一数量级。随后进行权重系数配置,针对Ⅰ区最优解选取,主要考虑储能循环使用寿命,故k1取1,k2取2;针对Ⅱ区最优解选取,主要考虑调频效果,故k1取2,k2取1。主要考虑指标的权重系数取2的目的是为了使其权重影响大于另一指标。选择出的最优解已在图 7中标识,对应的系统参数以及目标函数稳态参考值如表 2所示。
|
|
表 2 最优解参数值及目标函数稳态参考值 Table 2 Optimal solution parameter value and objective function steady-state reference value |
为便于比较分析,设置对照组无储能、储能不调整及传统储能综合控制。传统储能综合控制见式(3),Me、Ke直接取最大值;储能不调整为采用NSGA-Ⅱ对传统综合控制方式进行参数求解,求解获取最优平衡解Me与Ke分别为1.527 0和1.684 6。
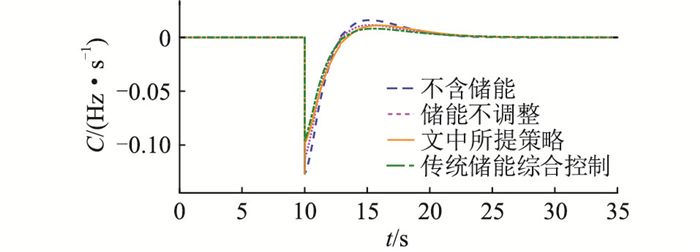
4.3 阶跃扰动分析(1) 小扰动分析。设置系统在10 s时产生0.03 p.u.的扰动,将上述参数运用于构建的电力系统模型,扰动接入后结果如图 8—图 11所示。
|
图 8 小扰动下的RoCoF波形 Fig. 8 RoCoF waveforms under small disturbance |
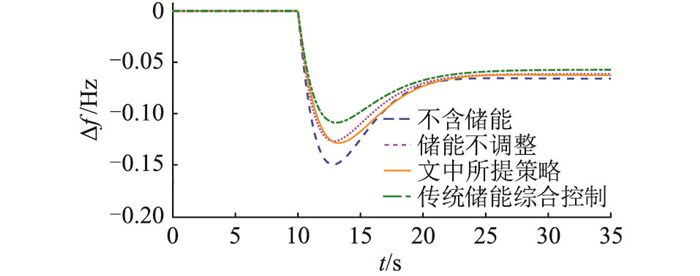
|
图 9 小扰动下的频率偏差波形 Fig. 9 Frequency deviation waveforms under small disturbance |
|
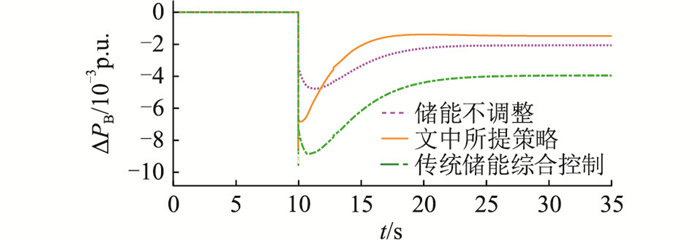
图 10 小扰动下的储能输出波形 Fig. 10 Energy storage output waveforms under small disturbance |
|
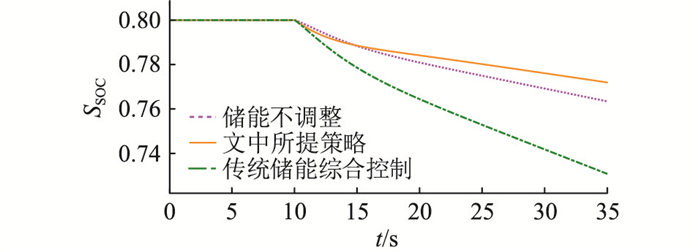
图 11 小扰动下的SOC变化波形 Fig. 11 SOC change waveforms under small disturbance |
通过仿真结果看出,小扰动时系统调频需求处于Ⅰ区,文中所提策略在调频效果上虽不占优,但充放电深度最小,即对储能循环使用寿命的延长支撑最大。
(2) 大扰动分析。设置系统在10 s时产生0.1 p.u.的扰动,扰动接入后结果如图 12—图 15所示。
|
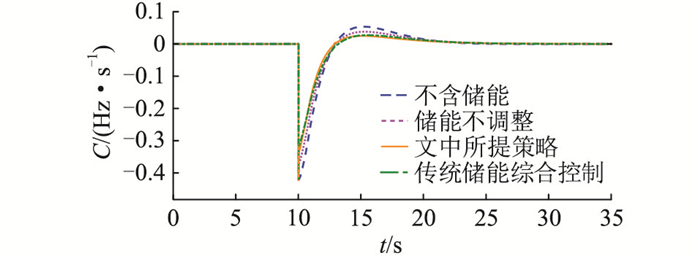
图 12 大扰动下的RoCoF波形 Fig. 12 RoCoF waveforms under large disturbance |
|
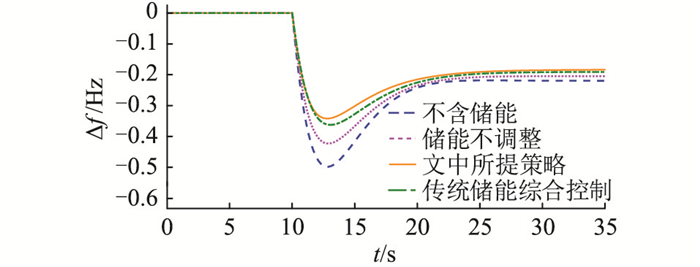
图 13 大扰动下的频率偏差波形 Fig. 13 Frequency deviation waveforms under large disturbance |

|
图 14 大扰动下的储能输出波形 Fig. 14 Energy storage output waveforms under large disturbance |
|
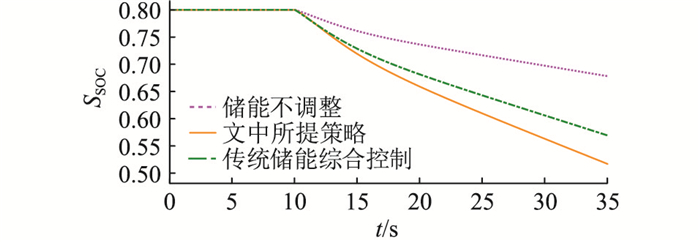
图 15 大扰动下的SOC变化波形 Fig. 15 SOC change waveforms under large disturbance |
大扰动下系统处于Ⅱ区,由仿真结果可见,扰动较大的情况下,强化储能输出可有效优化调频效果,但会加深储能充放电深度,考虑到此时的关键是使频率快速稳定,储能充放电深度的增大是必要的,而二者的平衡调整问题可以通过算法优化。
小扰动与大扰动时的具体仿真结果如表 3所示。另外,分别将对应扰动数值代入表 2,可以发现算法所求目标函数参考值与实际仿真结果高度一致,由此表明采用该算法求解的结果可靠性高。
|
|
表 3 仿真所得结果数值 Table 3 Numerical results obtained by simulation |
为进一步验证所提方法有效性,现设置如图 16所示的随机扰动。

|
图 16 随机扰动 Fig. 16 Random disturbance |
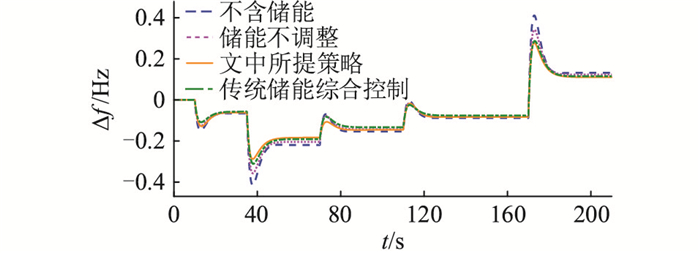
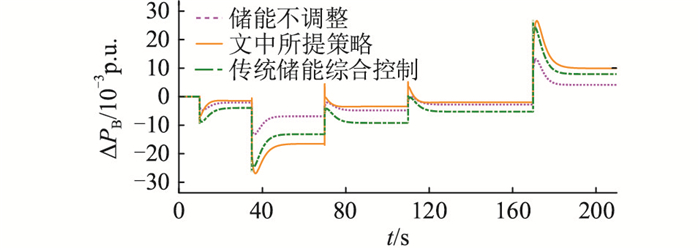
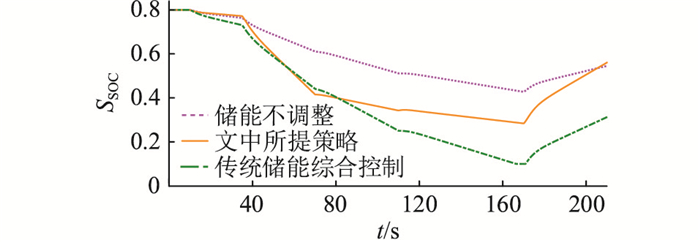
将上述扰动接入,得仿真结果如图 17—图 20所示。通过上述仿真结果可知:10 s、70 s、110 s时由于扰动波动较小,系统处于Ⅰ区,3种方法的稳态频率偏差相差极小,文中所提策略的储能输出与SOC变化幅度表现最优,说明所提策略可以有效减小电池SOC的变化幅度,从而有利于电池循环使用寿命的延长;而30 s、170 s时的大扰动波动下,系统处于Ⅱ区,所提策略的频率偏差表现最优,虽其SOC波动幅度较储能参数不调整略大,但在调频效果与储能运行经济性间能获得更好的平衡。

|
图 17 随机扰动下的RoCoF波形 Fig. 17 RoCoF waveforms under random disturbance |
|
图 18 随机扰动下的频率偏差波形 Fig. 18 Frequency deviation waveforms under random disturbance |
|
图 19 随机扰动下的储能输出波形 Fig. 19 Energy storage output waveforms under random disturbance |
|
图 20 随机扰动下的SOC变化波形 Fig. 20 SOC change waveforms under random disturbance |
为使储能辅助电网调频能兼顾更好的调频效果以及储能充放电深度的平衡,文中提出一种基于频率响应特性分析的储能辅助电网调频有功输出控制策略,通过理论分析和仿真验证得到如下结论:
(1) RoCoF、频率偏差与电网调频需求间存在一定关联性,负荷频率控制过程中,综合RoCoF及频率偏差对调频需求进行分区,并针对不同分区规划不同控制措施,可以使频率控制更具针对性。
(2) 根据调频需求的分区对储能输出做出动态调整,能够在维持稳定区获得更好的储能充放电深度表现;在加强调整区,能够通过强化储能输出获得更好的调频表现。
(3) 通过多目标优化问题的设计与求解,针对不同调频需求对储能输出动态调整,能够在调频效果与储能充放电深度的表现上获得更好的平衡。
| [1] |
郑亚先, 杨争林, 冯树海, 等. 碳达峰目标场景下全国统一电力市场关键问题分析[J]. 电网技术, 2022, 46(1): 1-20. ZHENG Yaxian, YANG Zhenglin, FENG Shuhai, et al. Key issue analysis in national unified power market under target scenario of carbon emission peak[J]. Power System Technology, 2022, 46(1): 1-20. (  0) 0) |
| [2] |
谢云云, 李虹仪, 崔红芬. 考虑电网侧储能调频能力的电力系统负荷恢复策略[J]. 电力工程技术, 2021, 40(6): 43-51. XIE Yunyun, LI Hongyi, CUI Hongfen. Load restoration strategy for power system considering the transient frequency control ability of energy storage system[J]. Electric Power Engineering Technology, 2021, 40(6): 43-51. (  0) 0) |
| [3] |
赵熙临, 龚楚峰, 付波, 等. 一种动态分层的互联电网AGC控制策略[J]. 电网技术, 2022, 46(1): 204-212. ZHAO Xilin, GONG Chufeng, FU Bo, et al. AGC control strategy of interconnected power grid based on dynamic stratification[J]. Power System Technology, 2022, 46(1): 204-212. (  0) 0) |
| [4] |
MU C X, ZHANG Y, JIA H J, et al. Energy-storage-based intelligent frequency control of microgrid with stochastic model uncertainties[J]. IEEE Transactions on Smart Grid, 2020, 11(2): 1748-1758. DOI:10.1109/TSG.2019.2942770 (  0) 0) |
| [5] |
孟建辉, 彭嘉琳, 王毅, 等. 考虑储能荷电状态及频率恢复特性的改进型灵活虚拟惯性控制[J]. 电力自动化设备, 2020, 40(6): 100-107, 114, 108. MENG Jianhui, PENG Jialin, WANG Yi, et al. Improved flexible virtual inertial control considering SOC of energy storage and characteristics of frequency recovery[J]. Electric Power Automation Equipment, 2020, 40(6): 100-107, 114, 108. (  0) 0) |
| [6] |
AZIZIVAHED A, AREFI A, GHAVIDEL S, et al. Energy management strategy in dynamic distribution network reconfiguration considering renewable energy resources and storage[J]. IEEE Transactions on Sustainable Energy, 2020, 11(2): 662-673. DOI:10.1109/TSTE.2019.2901429 (  0) 0) |
| [7] |
吴启帆, 宋新立, 张静冉, 等. 电池储能参与电网一次调频的自适应综合控制策略研究[J]. 电网技术, 2020, 44(10): 3829-3836. WU Qifan, SONG Xinli, ZHANG Jingran, et al. Study on self-adaptation comprehensive strategy of battery energy storage in primary frequency regulation of power grid[J]. Power System Technology, 2020, 44(10): 3829-3836. (  0) 0) |
| [8] |
李欣然, 崔曦文, 黄际元, 等. 电池储能电源参与电网一次调频的自适应控制策略[J]. 电工技术学报, 2019, 34(18): 3897-3908. LI Xinran, CUI Xiwen, HUANG Jiyuan, et al. The self-adaption control strategy of energy storage batteries participating in the primary frequency regulation[J]. Transactions of China Electrotechnical Society, 2019, 34(18): 3897-3908. (  0) 0) |
| [9] |
李军徽, 侯涛, 穆钢, 等. 基于权重因子和荷电状态恢复的储能系统参与一次调频策略[J]. 电力系统自动化, 2020, 44(19): 63-72. LI Junhui, HOU Tao, MU Gang, et al. Primary frequency regulation strategy with energy storage system based on weight factors and state of charge recovery[J]. Automation of Electric Power Systems, 2020, 44(19): 63-72. (  0) 0) |
| [10] |
叶畅, 柳丹, 杨欣宜, 等. 基于最小惯量评估的高比例新能源电力系统优化运行策略[J]. 电网技术, 2023, 47(2): 502-516. YE Chang, LIU Dan, YANG Xinyi, et al. Optimal operation strategy of high proportion new energy power system based on minimum inertia evaluation[J]. Power System Technology, 2023, 47(2): 502-516. (  0) 0) |
| [11] |
何锦华, 吴斌, 曹敏健, 等. 面向辅助服务的新能源场站共享储能容量优化配置[J]. 电力工程技术, 2022, 41(6): 50-57. HE Jinhua, WU Bin, CAO Minjian, et al. Capacity optimization configuration of shared energy storage in renewable energy stations for ancillary service[J]. Electric Power Engineering Technology, 2022, 41(6): 50-57. (  0) 0) |
| [12] |
CAO J, DU W J, WANG H F, et al. Optimal sizing and control strategies for hybrid storage system as limited by grid frequency deviations[J]. IEEE Transactions on Power Systems, 2018, 33(5): 5486-5495. (  0) 0) |
| [13] |
MENG L X, ZAFAR J, KHADEM S K, et al. Fast frequency response from energy storage systems—a review of grid standards, projects and technical issues[J]. IEEE Transactions on Smart Grid, 2020, 11(2): 1566-1581. (  0) 0) |
| [14] |
彭勃, 张峰, 梁军. 考虑风速分区的风: 储系统短期频率响应协同控制策略[J]. 电力系统自动化, 2018, 42(8): 57-65. PENG Bo, ZHANG Feng, LIANG Jun. Coordinated control strategy for short-term frequency response of wind-energy storage system considering wind speed partition[J]. Automation of Electric Power Systems, 2018, 42(8): 57-65. (  0) 0) |
| [15] |
单煜, 汪震, 周昌平, 等. 基于分段频率变化率的风电机组一次调频控制策略[J]. 电力系统自动化, 2022, 46(11): 19-26. SHAN Yu, WANG Zhen, ZHOU Changping, et al. Control strategy of primary frequency regulation for wind turbine based on segmented rate of change of frequency[J]. Automation of Electric Power Systems, 2022, 46(11): 19-26. (  0) 0) |
| [16] |
代浩, 金铭, 陈星, 等. 数据驱动的应用自适应技术综述[J]. 计算机研究与发展, 2022, 59(11): 2549-2568. DAI Hao, JIN Ming, CHEN Xing, et al. Survey of data-driven application self-adaptive technology[J]. Journal of Computer Research and Development, 2022, 59(11): 2549-2568. (  0) 0) |
| [17] |
MURAD ALI S M, AUGUSTO J C, WINDRIDGE D. A survey of user-centred approaches for smart home transfer learning and new user home automation adaptation[J]. Applied Artificial Intelligence, 2019, 33(8): 747-774. (  0) 0) |
| [18] |
CÁMARA J, PENG W X, GARLAN D, et al. Reasoning about sensing uncertainty and its reduction in decision-making for self-adaptation[J]. Science of Computer Programming, 2018, 167: 51-69. (  0) 0) |
| [19] |
董天翔, 翟保豫, 李星, 等. 风储联合系统参与频率响应的优化控制策略[J]. 电网技术, 2022, 46(10): 3980-3989. DONG Tianxiang, ZHAI Baoyu, LI Xing, et al. Optimal control strategy for combined wind-storage system to participate in frequency response[J]. Power System Technology, 2022, 46(10): 3980-3989. (  0) 0) |
| [20] |
李军徽, 侯涛, 严干贵, 等. 计及调频成本和荷电状态恢复的多储能系统调频功率双层优化[J]. 中国电机工程学报, 2021, 41(23): 8020-8033. LI Junhui, HOU Tao, YAN Gangui, et al. Two-layer optimization of frequency modulation power in multi-battery energy storage system considering frequency modulation cost and recovery ofstate of charge[J]. Proceedings of the CSEE, 2021, 41(23): 8020-8033. (  0) 0) |
| [21] |
高嵩, 李军, 宋辉, 等. 提升火电机组一次调频性能的火电-储能一体化系统研究[J]. 电力系统保护与控制, 2023, 51(21): 116-125. GAO Song, LI Jun, SONG Hui, et al. An integrated thermal power-energy storage system for improving primary frequency regulation performance of thermal power units[J]. Power System Protection and Control, 2023, 51(21): 116-125. (  0) 0) |
| [22] |
周霞, 刘懿诗, 戴剑丰, 等. 考虑风-储-直参与调频的电力系统频率特征定量分析[J]. 电力系统保护与控制, 2023, 51(6): 30-44. ZHOU Xia, LIU Yishi, DAI Jianfeng, et al. Quantitative analysis of power system frequency characteristics considering wind power-energy storage-flexible HVDC transmission participation in frequency modulation[J]. Power System Protection and Control, 2023, 51(6): 30-44. (  0) 0) |
| [23] |
黄际元, 李欣然, 曹一家, 等. 考虑储能参与快速调频动作时机与深度的容量配置方法[J]. 电工技术学报, 2015, 30(12): 454-464. HUANG Jiyuan, LI Xinran, CAO Yijia, et al. Capacity allocation of energy storage system considering its action moment and output depth in rapid frequency regulation[J]. Transactions of China Electrotechnical Society, 2015, 30(12): 454-464. (  0) 0) |
| [24] |
孙华东, 许涛, 郭强, 等. 英国"8 ·9"大停电事故分析及对中国电网的启示[J]. 中国电机工程学报, 2019, 39(21): 6183-6192. SUN Huadong, XU Tao, GUO Qiang, et al. Analysis on blackout in great Britain power grid on August 9th, 2019 and its enlightenment to power grid in China[J]. Proceedings of the CSEE, 2019, 39(21): 6183-6192. (  0) 0) |
| [25] |
陈艳波, 武超, 焦洋, 等. 考虑需求响应与储能寿命模型的火储协调优化运行策略[J]. 电力自动化设备, 2022, 42(2): 16-24. CHEN Yanbo, WU Chao, JIAO Yang, et al. Coordinated optimal operation strategy of thermal power-energy storage considering demand response and life model of energy storage[J]. Electric Power Automation Equipment, 2022, 42(2): 16-24. (  0) 0) |
| [26] |
张子阳, 龚一平, 邢兵, 等. 计及多重应用的电网侧分布式储能系统优化运行策略研究[J]. 供用电, 2022, 39(12): 82-88. ZHANG Ziyang, GONG Yiping, XING Bing, et al. Research on optimal operation strategy of grid-side distributed energy storage systems with multiple applications[J]. Distribution & Utilization, 2022, 39(12): 82-88. (  0) 0) |
| [27] |
贺海磊, 张彦涛, 孙骁强, 等. 考虑频率安全约束的西北电网新能源开发及直流外送规模评估方法[J]. 中国电机工程学报, 2021, 41(14): 4753-4762. HE Hailei, ZHANG Yantao, SUN Xiaoqiang, et al. Evaluation method of renewable energy development scale and DC transmission scale of China northwest power grid by considering frequency security constraints[J]. Proceedings of the CSEE, 2021, 41(14): 4753-4762. (  0) 0) |
| [28] |
陈维江, 赵国亮. 以新能源为主体的新型电力系统关键技术和装备[J]. 全球能源互联网, 2022, 5(1): 1. CHEN Weijiang, ZHAO Guoliang. Key technology and equipment of new power system based on renewable energy[J]. Journal of Global Energy Interconnection, 2022, 5(1): 1. (  0) 0) |
| [29] |
钟成元, 桂前进, 江千军, 等. 数据驱动的高比例新能源发电集群分布式电压控制[J]. 全球能源互联网, 2022, 5(3): 254-263. ZHONG Chengyuan, GUI Qianjin, JIANG Qianjun, et al. Data-driven distributed voltage control for high-penetration renewable power clusters without complete model[J]. Journal of Global Energy Interconnection, 2022, 5(3): 254-263. (  0) 0) |
| [30] |
方彤, 蒋东方, 杨洋, 等. 基于NSGA-Ⅱ和熵权法的氢综合能源系统商业运营模式[J]. 中国电力, 2022, 55(1): 110-118. FANG Tong, JIANG Dongfang, YANG Yang, et al. Research on business operation mode of hydrogen integrated energy system based on NSGA-Ⅱ and entropy weight method[J]. Electric Power, 2022, 55(1): 110-118. (  0) 0) |
 2024, Vol. 43
2024, Vol. 43


 赵熙临(1969),男,博士,教授,研究方向为电力系统保护与控制(E-mail:
赵熙临(1969),男,博士,教授,研究方向为电力系统保护与控制(E-mail: