文章编号: 2096-3203(2024)01-0117-10 中图分类号: TM715
2. 河北工业大学电气工程学院, 天津 300130;
3. 河北工业大学人工智能与数据科学学院, 天津 300401;
4. 河北工业大学实验实训中心, 天津 300401
电力负荷预测是维持电力系统电量供需平衡、保障电力系统稳定运行的基础。然而,受天气等多种因素的影响,电力负荷具有较强的不确定性特征[1],且伴随电动汽车、电采暖等新型负荷及以光伏为代表的分布式电源在配电网的持续接入和容量累积,配电网负荷的不确定性[2]进一步增加,负荷特性发生较大变化[3],负荷曲线变化规律愈加复杂[4],给超短期负荷预测带来新的挑战。建立准确的负荷预测模型对提高电力设备利用效率、降低发电成本、保障电力生产的平稳有序具有重要意义。
为降低超短期预测中负荷不确定性的影响,国内外学者开展了大量研究,主要可以分为统计学方法[5-6]、深度学习法[7-8]和组合模型法[9-10]。长短时记忆(long short-term memory, LSTM)神经网络作为循环神经网络(recurrent neural network, RNN)的一种变体结构,不仅具有较强的时序数据处理能力,还可以避免RNN学习长时间依赖问题时出现梯度消失或爆炸[11]。文献[12]在应用LSTM建立短期负荷预测模型的同时引入Attention机制,通过为隐含层神经元分配不同的权重,突出对负荷预测起关键作用的因素。实验结果表明,Attention-LSTM模型在预测精度和计算速度上较LSTM网络具有优势。然而LSTM网络只能利用历史时刻的信息,无法学习负荷数据在整个时间域的变化规律。双向长短时记忆(bidirectional long short-term memory, BiLSTM)神经网络可以依靠内部的双向LSTM结构深入挖掘负荷数据过去和未来的时序特征,在负荷预测领域得到广泛应用[13]。文献[14]建立了基于BiLSTM的日负荷峰值预测模型,与传统的机器学习算法和LSTM网络相比,其预测精度更高。文献[15]考虑到历史负荷和气象因素为影响负荷预测的重要因素,使用最大信息系数(maximum information coefficient, MIC)量化负荷与各影响因素的非线性相关性,剔除无相关因素,并基于BiLSTM网络构建负荷预测模型,但难以突出对当前负荷影响更大的因素。
由于气象、时间等诸多因素的影响,电力负荷具有较强的随机性和波动性,单一预测算法难以准确捕捉其持续变化特征,存在预测精度低、适用范围有限等问题,组合模型法成为超短期负荷预测领域的热点方向。其中,结合信号分解算法或误差修正技术的组合模型成为重要分支[16-17]。自适应噪声的完全集成经验模态分解(complete ensemble empirical mode decomposition with adaptive noise, CEEMDAN)作为一种改进经验模态分解(empirical mode decomposition, EMD),不仅可以克服分解的模态混叠现象,还具有更小的重构误差。文献[18]提出一种基于CEEMDAN和Attention-LSTM组合的短期电力负荷预测方法。首先采用CEEMDAN算法将负荷序列分解为多个负荷分量,然后基于Attention-LSTM网络建立各分量预测模型,最后叠加各预测分量获得最终预测结果。针对预测结果中包含的误差信息,文献[19]建立叠式双向门控循环单元模型,分别预测电力负荷和误差,并叠加2类预测结果修正负荷预测值。
在负荷的解耦预测方面,文献[20]针对小地区负荷特点,指出日负荷内部包含2个特征量:负荷基准值和负荷标幺曲线,提出了解耦预测机制。文献[21]采用日平均负荷和负荷标幺曲线分开预测的解耦机制,通过倍比平滑法建立日平均负荷预测模型,并采用核函数平滑法对相似日进行加权预测负荷标幺曲线。文献[22]考虑到气温累积效应对负荷预测的影响,提出一种动态相似与静态相似相结合的负荷解耦预测方法。文献[23]提出以气象条件相似、负荷曲线形状相似为前提的曲线形状修正方法,但忽略了用电习惯、突发事件等不可量化因素的影响,任意两日的曲线形状变化规律无法完全相同,曲线形状修正结果有待进一步提升。
上述解耦预测中大多采用统计方法预测负荷基准值,难以挖掘负荷序列的时序信息,且曲线形状会受多种不可量化因素影响,基于相似日加权组合的标幺曲线预测易产生偏差。为此文中提出了一种采用记忆神经网络和曲线形状修正的负荷预测方法,在分析负荷峰值和标幺曲线复杂变化特征基础上,采用MIC筛选影响负荷峰值的主要因素,并基于Attention-BiLSTM建立负荷峰值预测模型;利用加权形状相似日模型和基于CEEMDAN-BiLSTM的误差预测模型提高负荷标幺曲线预测准确度;将负荷峰值与负荷标幺曲线相乘实现负荷预测。
1 配电网负荷预测的解耦机制文献[20]指出小地区负荷结构相对单一且不同地区负荷结构和特性差异明显。针对该特点,提出了基于解耦机制的小地区负荷预测方法:以负荷水平为基准,将负荷曲线标幺化,从而将负荷预测分解为基准值和标幺曲线两部分进行预测。
| $ L_{n, t}^{\prime}=\frac{L_{n, t}}{L_{\mathrm{b}, n}} \quad t=1, 2, \cdots, T ; n=1, 2, \cdots, N $ | (1) |
式中:Ln, t′为第n日t时刻的实际负荷标幺值;Ln, t为第n日第t时刻的实际负荷;Lb, n为第n日的负荷基准值;T为每日数据点个数,T=96;N为数据集总天数,N=365。
在解耦机制的负荷预测方法中,负荷基准值可为日峰值、日最小值或日平均值。负荷标幺曲线用于表征负荷结构和曲线形状,在一段时间内保持相对稳定,这是决定解耦预测可行性的关键。
配电网负荷虽构成类型较多,但各类负荷的容量与用电量相对较大,负荷曲线形态较稳定,不易产生突变。对此图 1给出了居民、商业和工业3种典型的负荷曲线。居民负荷呈现突出的双峰特征,与人们的工作时间和用电习惯密切相关;商业负荷呈现单峰特点且波峰范围较宽;工业负荷需要稳定的电力供给,基本保持在一个固定值上下波动。这说明虽然配电网不同类型的负荷曲线特征存在差异,但各类负荷曲线具有典型的形态且相对稳定。因此,适用于小地区负荷预测的解耦机制仍然可以适用。
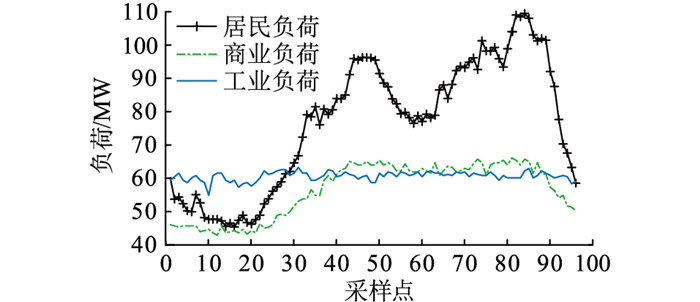
|
图 1 不同类型负荷的典型负荷曲线 Fig. 1 Typical load curves of different types of loads |
然而,随着配电网负荷预测影响因素的多元化,负荷不确定性特征明显,使得配电网负荷解耦预测问题更为复杂。对于解耦机制中的负荷峰值预测,随着配电网用电需求增加,同期负荷水平不断刷新高;伴随分布式电源的持续接入,负荷峰值受天气因素的影响更加明显,增加了配电网负荷峰值预测的难度。解耦机制中的负荷标幺曲线预测同样受到分布式电源接入和天气因素的影响,加之新型电力负荷接入容量的增加,改变了日负荷的峰谷差,负荷曲线形态更为多样,增加了标幺曲线预测难度。一种采用记忆神经网络和曲线形状修正的负荷预测方法的整体流程如图 2所示。
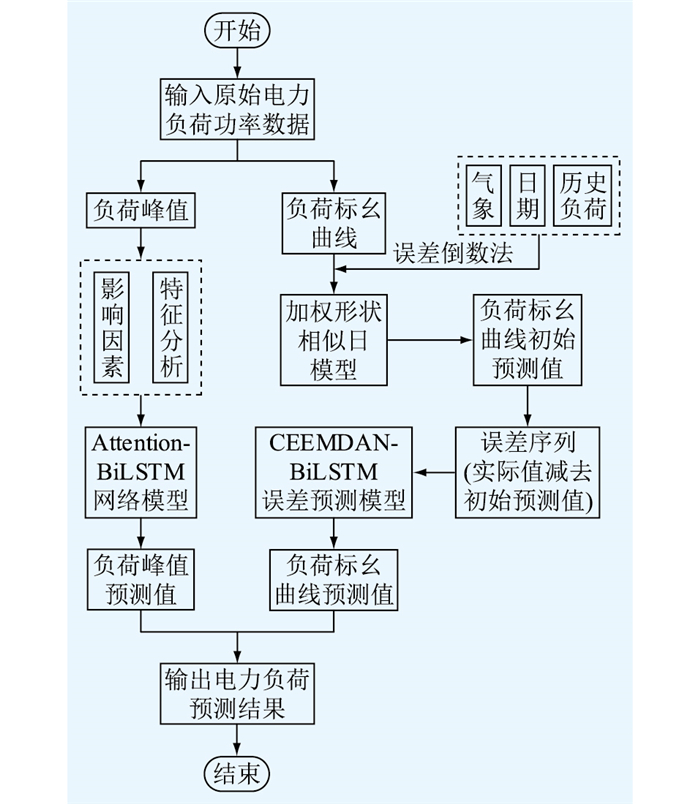
|
图 2 一种采用记忆神经网络和曲线形状修正的负荷预测方法 Fig. 2 A load prediction method using memory neural network and curve shape correction |
负荷峰值受天气、气温、日期类型以及历史负荷等多种因素的影响,且各因素对负荷峰值的影响程度不同。选择与负荷峰值存在相关性的因素作为预测模型的输入变量,不仅能够提高预测精度,还可以降低模型计算复杂度。在此重点分析天气类型、气温、季节、日期类型以及历史负荷与负荷峰值的相关性,同时对无法用具体数值描述的因素进行人为赋值、量化。对于天气类型因素,分别以1、2、3量化良好天气、突变天气和雨雪天气;对于季节因素,分别以1、2、3、4量化春季、夏季、秋季和冬季;对于日期类型因素,将工作日与非工作日分别以0、1进行量化。文中采用MIC[24]计算各影响因素与负荷峰值的相关性大小r,计算结果如表 1所示。当0≤r < 0.2时表明两序列间的相关性较弱,0.2≤r < 0.5时表明两序列间存在中度相关性,0.5≤r≤1时表明两序列间存在较强相关性。
|
|
表 1 相关性计算结果 Table 1 Correlation calculation results |
表 1中,Lmax, 1—Lmax, 7分别为待测日前一天至前七天的历史负荷峰值。由表 1可以看出,与其他影响因素相比,气温与负荷峰值的相关性r值接近0.3,相关性较高;季节和月份的相关性r值在0.2以上,与负荷峰值之间存在一定的相关性;而天气类型和日期类型与负荷峰值的相关性较弱;历史负荷峰值与待测日负荷峰值的相关性r值均大于0.5,相关性很强,是建立负荷峰值预测模型的基础。基于上述分析,将气温、季节、月份以及历史负荷峰值作为负荷峰值预测模型的输入。
2.2 负荷峰值特征分析为建立与负荷峰值相适应的预测模型,须对负荷峰值的变化特征进行分析。首先分析负荷峰值时序,如图 3所示。从图 3中可以看出,负荷峰值呈现突出的夏季高峰特点,夏季负荷峰值明显高于其他季节,冬季负荷峰值略高于春秋季节,负荷峰值序列具有明显的波动特征且夏冬两季的波动性高于春秋季节。这是因为夏季天气炎热,温度较高,制冷负荷的大量使用造成负荷峰值不断升高,冬季则与之相反。据此进一步研究负荷峰值的内在关系,得到不同间隔天数下负荷峰值的自相关系数,如图 4所示。

|
图 3 负荷峰值序列 Fig. 3 Load peak sequence |

|
图 4 负荷峰值的自相关系数 Fig. 4 Autocorrelation coefficient of load peak |
随着间隔天数的增加,自相关系数逐渐降低,但是在间隔20 d时,负荷峰值的自相关系数仍然大于0.4,相邻日的历史负荷峰值与间隔较远的历史负荷峰值都与当前负荷峰值存在不同程度的相关性,这说明负荷峰值内部存在长短期自相关性。由2.1节可知,各影响因素与负荷峰值的相关性大小不同,通过突出与负荷峰值具有强相关性的因素能够进一步提高预测精度。综合对负荷峰值影响因素及特征进行分析,文中基于Attention-BiLSTM建立负荷峰值预测模型。
2.3 基于Attention-BiLSTM的负荷峰值预测模型 2.3.1 BiLSTM网络BiLSTM网络由正向LSTM和反向LSTM构成,分别用于获取输入序列过去时刻和未来时刻的时序信息并进行正向和反向训练,同时将正反向的隐含层输出作为输出层的输入。在t时刻,BiLSTM网络隐含层的输出值由正向LSTM隐含层输出和反向LSTM隐含层输出组成。
| $ \left\{\begin{array}{l} \overrightarrow{\boldsymbol{h}}_t=\operatorname{LSTM}\left(\boldsymbol{x}_t, \overrightarrow{\boldsymbol{h}}_{t-1}\right) \\ \overleftarrow{\boldsymbol{h}}_t=\operatorname{LSTM}\left(\boldsymbol{x}_t, \overleftarrow{\boldsymbol{h}}_{t-1}\right) \\ \boldsymbol{H}_t=\left[\overrightarrow{\boldsymbol{h}}_t, \overleftarrow{\boldsymbol{h}}_t\right] \end{array}\right. $ | (2) |
式中: LSTM指传统LSTM网络的运算过程;
引入Attention机制的BiLSTM网络通过赋予隐含层状态不同的权重,放大影响负荷峰值序列的强相关因素,以提高模型的预测性能,计算过程如式(3)—式(5)所示。
| $ \boldsymbol{e}_t=\boldsymbol{v} \tanh \left(\boldsymbol{w} \boldsymbol{H}_t+\boldsymbol{b}\right) $ | (3) |
| $ \boldsymbol{\alpha}_t=\frac{\exp \left(\boldsymbol{e}_t\right)}{\sum \boldsymbol{e}_t} $ | (4) |
| $ \boldsymbol{C}_t=\sum \boldsymbol{\alpha}_t \boldsymbol{H}_t $ | (5) |
式中:v、w为采用多层感知机方式计算t时刻注意力权重时的权重矩阵;b为采用多层感知机方式计算t时刻注意力权重时的偏置;et、αt分别为t时刻不同特征对应的权重分数和权重分量;Ct为t时刻Attention层的输出。
3 负荷标幺曲线预测 3.1 基于加权形状相似日的负荷标幺曲线预测模型负荷曲线变化由气象因素产生的波动、日期因素产生的波动以及历史负荷的趋势三部分构成。为使预测的标幺曲线更贴近实际曲线形状,分别从气象因素、日期因素和历史负荷因素来选择待测日的形状相似日。
(1) 基于灰色关联分析法选取相似日,计算步骤如下。
步骤1:考虑到天气、气温是影响负荷曲线的主要气象因素以及不同日期类型间负荷曲线的差异性,选取日最高温度、日最低温度、日平均温度、天气类型和日期类型构造特征向量 V,以 V0表示待测日特征向量,Vs表示第s个历史日的特征向量。
| $ \boldsymbol{V}_s=\left[\begin{array}{lllll} v_{s, 1} & \cdots & v_{s, m} & \cdots & v_{s, 5} \end{array}\right] \quad s=1, 2, \cdots, 30 $ | (6) |
式中:vs, m为第s个历史日第m个影响因素值。
步骤2:计算各历史日特征向量与待测日特征向量的关联系数。
| $ \begin{array}{c} g_{s, m}= \\ \frac{\min\limits_s \min\limits_m\left|v_{s, m}-v_{0, m}\right|+\rho \max\limits_s \max\limits_m\left|v_{s, m}-v_{0, m}\right|}{\left|v_{s, m}-v_{0, m}\right|+\rho \max\limits_s \max\limits_m\left|v_{s, m}-v_{0, m}\right|} \end{array} $ | (7) |
式中:gs, m为第s个历史日第m个因素的关联系数;v0, m为待测日第m个影响因素值;ρ为分辨系数,设置ρ=0.5。
步骤3:以各历史日关联系数的平均值计算其灰色关联度。
| $ G_s=\frac{1}{5} \sum\limits_{m=1}^5 g_{s, m} $ | (8) |
式中:Gs为第s个历史日的灰色关联度。将历史日按照灰色关联度依次排序,选择灰色关联度最大值对应的历史日为待测日的相似日。
(2) 基于历史负荷因素确定相邻日。负荷曲线的时序性和连续性使得相邻两日负荷标幺曲线存在一定的相关性。在此分别采用Pearson相关系数、MIC和余弦相似度3种相关性分析方法计算相邻两日负荷标幺曲线的相关性,结果如图 5所示。分别从线性相关性、非线性相关性和变化趋势一致性来看,相邻两日负荷标幺曲线均具有较高的相关性。因此,将相似日和相邻日作为待测日的形状相似日建立负荷标幺曲线预测模型。
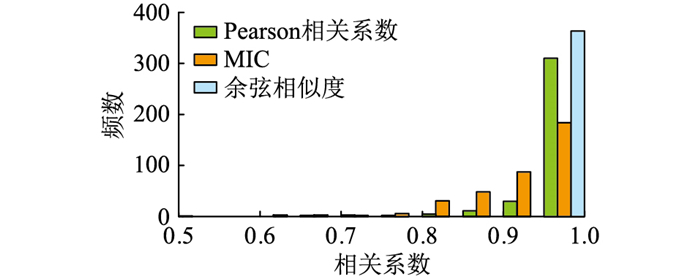
|
图 5 相关系数直方图 Fig. 5 Histogram of correlation coefficients |
(3) 权重赋予方式。采用误差倒数法对相似日和相邻日负荷标幺曲线进行加权组合计算负荷标幺曲线初始预测结果。
| $ \boldsymbol{L}_{\mathrm{p}}^{\prime}=w_1 \boldsymbol{L}_1^{\prime}+w_2 \boldsymbol{L}_2^{\prime} $ | (9) |
| $ w_1=\frac{e_{\mathrm{r} 2}}{e_{\mathrm{r} 1}+e_{\mathrm{r} 2}} $ | (10) |
| $ w_2=\frac{e_{\mathrm{r} 1}}{e_{\mathrm{r} 1}+e_{\mathrm{r} 2}} $ | (11) |
式中:Lp′为负荷标幺曲线的初始预测值;L1′、L2′分别为相似日和相邻日的负荷标幺曲线值;er1、er2分别为相似日和相邻日的预测误差;w1、w2分别为相似日和相邻日的权重。
3.2 基于CEEMDAN-BiLSTM的误差预测模型采用加权形状相似日模型分别计算训练集负荷标幺曲线初始预测值 Lp, train′和测试集负荷标幺曲线初始预测值Lp, test′。训练集前一周的负荷标幺曲线实际值 Lreal′与 Lp, train′的对比如图 6所示。从一日96个时间点的整体比较来看,负荷标幺曲线初始预测值与实际值的整体变化趋势相似,但在负荷曲线的极值点以及频繁波动时段存在一定偏差。因此有必要进一步对预测误差进行统计分析与预测,以误差预测结果修正初始预测值,进而提高负荷标幺曲线预测精度。
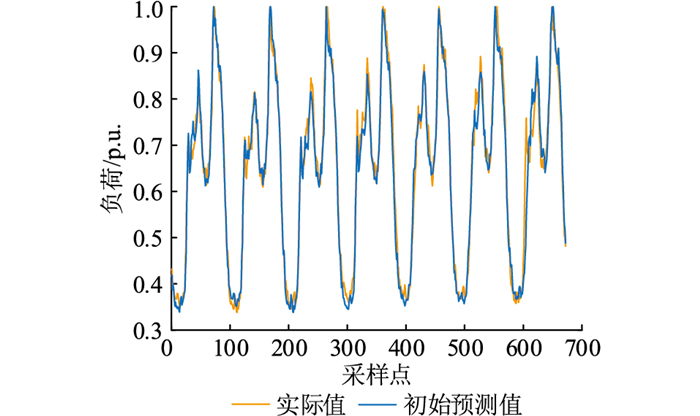
|
图 6 负荷标幺曲线初始预测值与实际值对比 Fig. 6 Comparison between initial predicted value and actual value of load per-unit curve |
在此基础上计算训练集上负荷标幺曲线实际值Lreal′与初始预测值Lp, train′的差值得到误差序列Lerror′,通过3σ异常数据检测法[25]检测误差序列异常值并采用均值法进行修复。选取异常值处理后的误差序列前一周样本点进行绘图分析,见图 7。误差序列的幅值较小,波动频率高且具有较强的非线性与不平稳特征,直接预测难以获得准确预测结果,通过对误差序列的平稳化处理可以提高误差序列的可预测性。对此建立基于CEEMDAN-BiLSTM网络的误差预测模型。
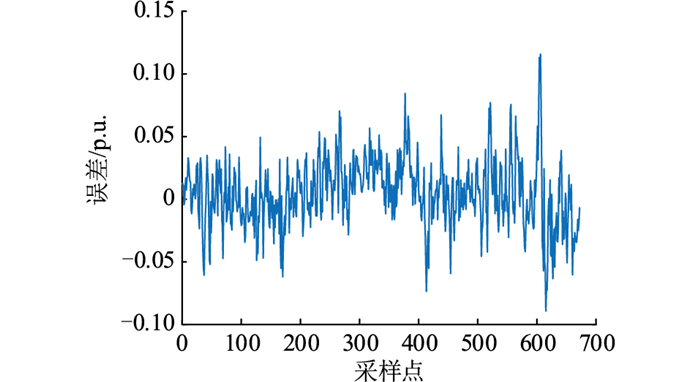
|
图 7 误差序列 Fig. 7 Error sequence |
CEEMDAN分解通过在EMD分解中引入自适应的白噪声,不仅可以解决EMD分解中的模态混叠现象,还能使重构误差接近于0,其主要计算步骤如下。
步骤1:在原始信号P(t)中添加M次高斯白噪声信号以构造M次实验的待分解信号。
| $ P_\lambda(t)=P(t)+\varepsilon_0 \delta_\lambda(t) $ | (12) |
式中:Pλ(t)为第λ次实验的待分解信号;ε0为高斯白噪声幅值;δλ(t)为第λ次实验中添加的高斯白噪声。
对Pλ(t)进行EMD分解,并将每次分解得到的第1个模态分量均值作为CEEMDAN分解的第1个模态分量,计算剩余分量。
| $ \bar{I}_1(t)=\frac{1}{M} \sum\limits_{\lambda=1}^M I_{\lambda, 1}(t) $ | (13) |
式中:
| $ R_1(t)=P(t)-\bar{I}_1(t) $ | (14) |
式中:R1(t)为第1次分解后的剩余分量。
步骤2:在R1(t)中添加高斯白噪声信号后继续进行EMD分解,得到第2个模态分量和剩余分量。
| $ \bar{I}_2(t)=\frac{1}{M} \sum\limits_{\lambda=1}^M E\left(R_1(t)+\varepsilon_1 E_1\left(\delta_\lambda(t)\right)\right) $ | (15) |
式中:
| $ R_2(t)=R_1(t)-\bar{I}_2(t) $ | (16) |
式中:R2(t)为第2次分解后的剩余分量。
步骤3:重复以上步骤,当得到的剩余分量呈单调趋势不能再分解时,停止运算。原始信号经CEEMDAN分解为:
| $ P(t)=\sum\limits_{k=1}^K \bar{I}_k(t)+R(t) $ | (17) |
式中:
近似熵是衡量时间序列复杂程度的无量纲指标,熵值越大,时间序列越复杂。对于一个样本容量为S的时间序列 U =[u(1) u(2) ⋯ u(S)],其近似熵计算过程如下。
步骤1:选取合适的嵌入维数l,将时间序列 U重构为一组维数为l的向量,即 Ui=[u(i) ⋯ u(i+l-1)],1≤i≤S-l+1。
步骤2:计算重构后向量 Ui和向量 Uj的距离dij。
| $ d_{i j}=\max \left\|\boldsymbol{U}_i-\boldsymbol{U}_j\right\| $ | (18) |
步骤3:给定阈值γ,寻找满足dij≤γ的数目A(i),并计算此数目与重构后全部向量数的比值Cl(i)。
| $ C_l(i)=\frac{A(i)}{S-l+1} $ | (19) |
计算Cl(i)的对数,并取其平均值φl,即:
| $ \varphi_l=\frac{1}{S-l+1} \sum\limits_{i=1}^{S-l+1} \ln C_l(i) $ | (20) |
步骤4:将维数l增加至l+1,重复步骤1—步骤3,计算Cl+1(i)和φl+1,据此计算近似熵AE。
| $ A_{\mathrm{E}}=\varphi_l-\varphi_{l+1} $ | (21) |
为验证所提预测模型的准确性,使用中国北方某城市的区域电网实际负荷和气象数据进行仿真实验。所用数据集的时间跨度为2018年1月—2018年12月,负荷数据的采样时间间隔为15 min,一天共96个采样点。此外,将数据集按9 ∶1的比例划分为训练集和测试集。
4.2 评价指标文中选取统计分析中常用的3个评价指标来评价预测模型的性能:平均绝对误差(mean absolute error, MAE)、均方根误差(root mean square error, RMSE)和平均绝对百分比误差(mean absolute percentage error, MAPE)。各指标计算公式见式(22)—式(24)。
| $ E_{\mathrm{MAE}}=\frac{1}{Q} \sum\limits_{q=1}^Q\left|y_q-y_q^{\prime}\right| $ | (22) |
| $ E_{\mathrm{RMSE}}=\sqrt{\frac{1}{Q} \sum\limits_{q=1}^Q\left(y_q-y_q^{\prime}\right)^2} $ | (23) |
| $ E_{\mathrm{MAPE}}=\frac{1}{Q} \sum\limits_{q=1}^Q \frac{\left|y_q-y_q^{\prime}\right|}{y_q} $ | (24) |
式中:yq为第q个样本点真实值;yq′为第q个样本点预测值;Q为数据点个数。
4.3 负荷峰值预测模型的性能分析按照2.3节建立基于Attention-BiLSTM网络的负荷峰值预测模型,将2.1节确定的5个影响因素和历史负荷峰值作为模型输入特征,输出为待预测的负荷峰值。利用训练集对模型进行学习和训练,待模型收敛后对测试集进行预测。其中,BiLSTM网络为单层结构,隐含层神经元个数为64,采用Adam算法作为优化器。
为验证文中所提负荷峰值预测模型的有效性,选取决策树、支持向量机(support vector machine, SVM)、LSTM网络和BiLSTM网络作为对比方法。表 2为测试集上各方法的平均预测误差。由表 2可知,文中方法预测误差最小。与决策树和SVM的预测结果相比,深度神经网络模型LSTM和BiLSTM的预测误差明显降低。相较于LSTM网络,BiLSTM网络预测结果的MAE、RMSE和MAPE分别降低了35.34%、31.56%和0.62%。这是因为负荷峰值序列内部存在长短期自相关性和双向信息,BiLSTM网络利用内部的正反向LSTM结构充分挖掘负荷峰值序列在整个时间域的时序信息,预测精度有所提升。与BiLSTM网络相比,文中方法的MAE、RMSE和MAPE分别降低了72.13%、68.53%和0.81%,这是因为各影响因素与负荷峰值存在不同程度的相关性,引入Attention机制的BiLSTM网络能够在预测过程中自适应地赋予输入特征不同的权重系数,突出与负荷峰值存在强相关性的因素,进一步提高负荷峰值预测精度。
|
|
表 2 不同负荷峰值模型的预测误差对比 Table 2 Prediction error comparison of different load peak models |
在采用加权形状相似日计算负荷标幺曲线初始预测值并获得训练集预测误差序列 Lerror′的基础上,使用CEEMDAN算法对异常值处理后的误差序列进行分解,结果如图 8所示。
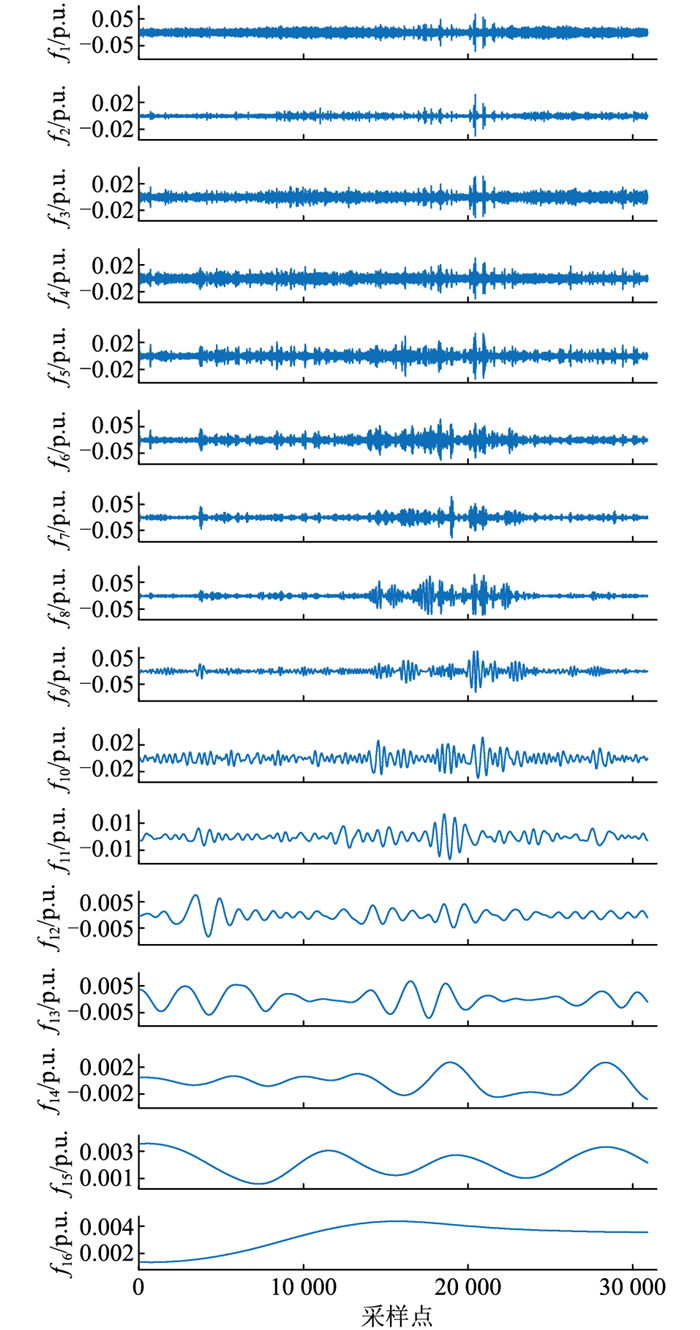
|
图 8 CEEMDAN分解结果 Fig. 8 Decomposition results of CEEMDAN |
由图 8可知,CEEMDAN将异常值处理后的误差序列分解为频率由高到低的15个模态分量和1个剩余分量,记为f1—f16,分别代表原始误差在不同时间尺度的变化特征。为提高模型整体训练预测速度,减小累加误差,利用样本熵量化各分量的复杂度,将复杂度相近的分量进行重构,结果如表 3所示。f1、f2和f3的近似熵较大,复杂度比较接近,将其重构为新的分量1;f4—f6的熵值介于[0.6, 0.8]之间,复杂度相近,将其重构为新的分量2;f7、f8的近似熵接近,将其重构为新的分量3;f9—f16的熵值均小于0.1,代表了原始误差序列的低频趋势,将其重构为新的分量4。最后利用BiLSTM网络分别建立分量1—分量4的预测模型,叠加各分量预测结果实现误差预测。
|
|
表 3 近似熵计算结果 Table 3 Calculation results of approximate entropy |
为验证文中所提负荷标幺曲线预测模型性能,将所提模型与其子模型的预测结果进行比较。子模型包括:(1) 子模型1为3.1节所建立的负荷标幺曲线预测模型,即不包含曲线形状修正;(2)子模型2在子模型1的基础上添加曲线形状修正,但是在误差预测阶段直接利用BiLSTM网络进行误差预测,不包含分解过程。由于负荷标幺曲线的预测误差无法直接利用评价指标进行计算,故在此对负荷标幺曲线预测值与负荷峰值实际值的相乘结果进行分析,结果如表 4所示。
|
|
表 4 不同负荷标幺曲线模型的预测误差对比 Table 4 Prediction error comparison of different load per-unit curve models |
从表 4可以看出,子模型1预测误差最大,这是因为子模型1建立的负荷标幺曲线预测模型仅考虑了相似的气象和相近的日期,忽略了负荷曲线形状还受到突发事件等不可量化因素的影响。与子模型1相比,子模型2的MAE、RMSE和MAPE分别降低了32.41%、35.01%和1.35%,这说明利用误差预测值修正标幺曲线初始预测结果,能够提高曲线形状预测精度。然而预测误差仍然高于所提模型,这是因为误差序列非平稳性,使得直接利用BiLSTM网络进行预测时无法准确学习其变化规律,难以完成高精度预测。与子模型2相比,文中模型的MAE、RMSE和MAPE值分别降低了33.71%、41.26%和0.79%,误差最小,说明文中模型能够通过误差修正更好地预测曲线形状。
4.5 整体预测模型的结果与分析为验证文中所提方法的整体预测性能和稳定性,将所提方法与超短期负荷预测领域的主流方法进行对比分析,包括SVM、决策树、BP网络、BiLSTM网络以及CEEMDAN-LSTM组合方法。表 5给出了测试集上各方法的平均预测误差,不同神经网络模型的计算时间如表 6所示。
|
|
表 5 不同模型的预测误差对比 Table 5 Prediction error comparison of different models |
|
|
表 6 计算时间对比 Table 6 Comparison of computing time |
结合表 5、表 6信息可知,在传统的机器学习算法中,SVM的预测误差最大且明显高于决策树。这是因为SVM的预测精度与模型参数和核函数的选择密切相关,随着样本数量的增加,负荷随机性、波动性增强,SVM难以准确捕捉负荷序列的变化规律,预测结果不理想。相较于决策树,BP网络可以更好地拟合输入输出之间的非线性映射关系,日平均预测精度提高了0.19%。BiLSTM网络利用双向LSTM结构深入挖掘输入序列的时序信息,将日平均预测精度提高到97.66%。相较于单一的预测模型,CEEMDAN-LSTM组合模型能够达到更高的预测精度。这是由于CEEMDAN能够降低负荷序列的非平稳特征,使LSTM可以更加准确地学习负荷分量的变化规律,具有更强的预测能力。相较于CEEMDAN-LSTM模型,在计算时间相近的基础上,所提方法可将日平均预测精度提高0.33%,达到98.15%。综上所述,文中所提方法的预测误差最小,精度最高。
为更加直观地展示不同日期类型的预测结果,从测试集中随机选取某一工作日和非工作日的实际值与预测值进行对比,结果分别如图 9和图 10所示。
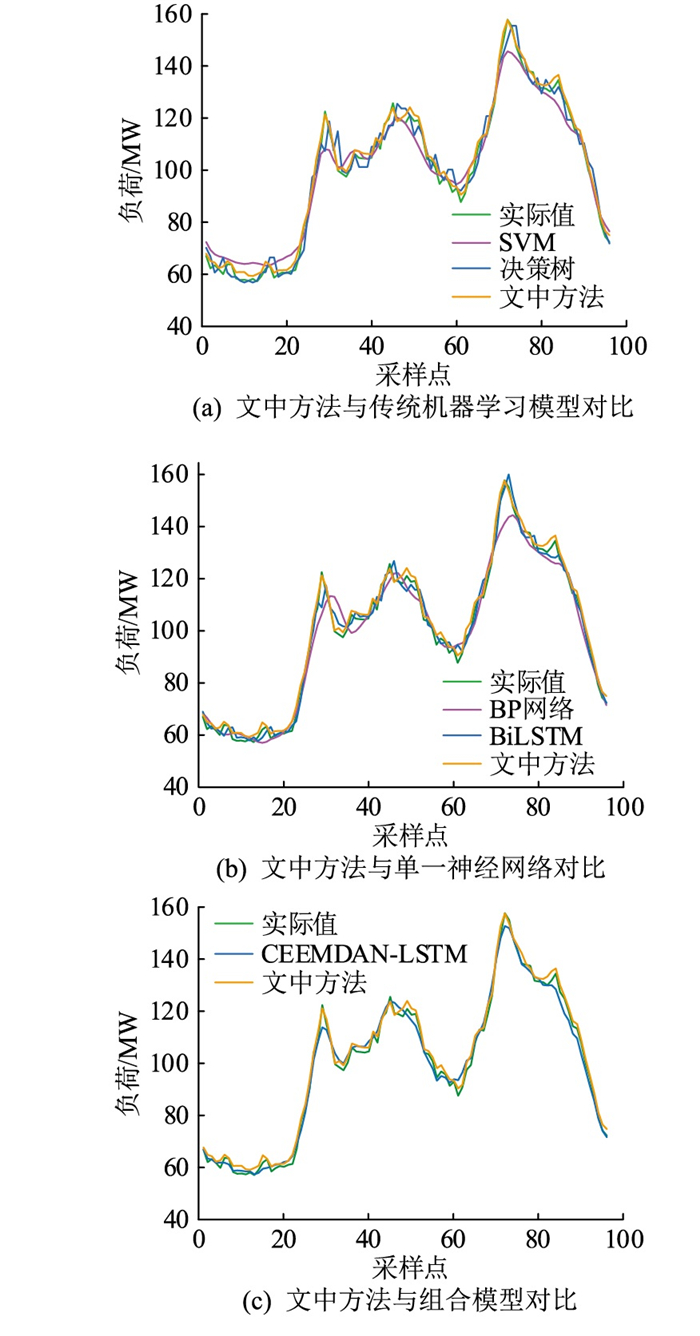
|
图 9 工作日的预测值与实际值对比 Fig. 9 Comparison between predicted value and actual value of working day |
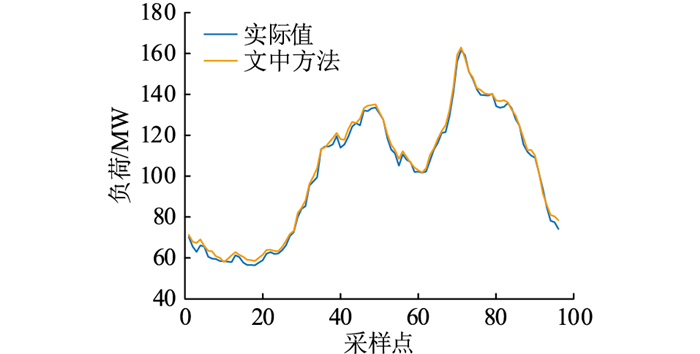
|
图 10 非工作日的预测值与实际值对比 Fig. 10 Comparison between predicted value of nonworking day and actual value |
由图 9可见,不论是负荷曲线的峰谷时段还是频繁波动时段,文中方法均具有稳定的预测能力,能准确预测配电负荷的未来变化趋势,与实际值的拟合度更高。与预测效果较好的CEEMDAN-LSTM组合模型相比,在负荷曲线的局部极值处,文中方法表现出更好的预测性能。由图 10可以看出,文中方法在非工作日仍然具有准确的预测结果。
5 结论文中提出一种采用记忆神经网络和曲线形状修正的负荷预测方法,提高了超短期负荷预测精度。基于实际数据验证所提方法的稳定性和准确度,主要结论如下:
(1) 采用MIC筛选影响负荷峰值的主要因素并分析负荷峰值的变化特征,结合Attention机制和BiLSTM网络建立与负荷峰值特征相适应的预测模型,提升负荷峰值预测精度。
(2) 建立基于加权形状相似日的负荷标幺曲线预测模型,利用误差倒数法赋予相似日和相邻日不同的权重系数,通过加权组合实现负荷标幺曲线的初始预测。
(3) 针对曲线形状预测存在的较大偏差以及误差序列的非平稳特征,建立基于CEEMDAN和BiLSTM网络的误差预测模型,以误差预测结果修正负荷标幺曲线初始预测值,提高曲线形状的预测准确度。同时引入的误差预测模型避免了传统修正方法中因片面考虑负荷曲线形状影响因素而导致的精度不高问题,进一步提升负荷解耦预测的普适性和可信度。
| [1] |
郑睿程, 顾洁, 金之俭, 等. 数据驱动与预测误差驱动融合的短期负荷预测输入变量选择方法研究[J]. 中国电机工程学报, 2020, 40(2): 487-500. ZHENG Ruicheng, GU Jie, JIN Zhijian, et al. Research on short-term load forecasting variable selection based on fusion of data driven method and forecast error driven method[J]. Proceedings of the CSEE, 2020, 40(2): 487-500. (  0) 0) |
| [2] |
张淑清, 李君, 姜安琦, 等. 基于FPA-VMD和BiLSTM神经网络的新型两阶段短期电力负荷预测[J]. 电网技术, 2022, 46(8): 3269-3279. ZHANG Shuqing, LI Jun, JIANG Anqi, et al. A novel two-stage model based on FPA-VMD and BiLSTM neural network for short-term power load forecasting[J]. Power System Technology, 2022, 46(8): 3269-3279. (  0) 0) |
| [3] |
陈国平, 梁志峰, 董昱. 基于能源转型的中国特色电力市场建设的分析与思考[J]. 中国电机工程学报, 2020, 40(2): 369-379. CHEN Guoping, LIANG Zhifeng, DONG Yu. Analysis and reflection on the marketization construction of electric power with Chinese characteristics based on energy transformation[J]. Proceedings of the CSEE, 2020, 40(2): 369-379. (  0) 0) |
| [4] |
陆臣斌, 包哲静, 于淼, 等. 基于改进自适应构造区间法的电力负荷区间预测[J]. 电测与仪表, 2022, 59(11): 34-41. LU Chenbin, BAO Zhejing, YU Miao, et al. Power load interval prediction based on improved adaptively constructed interval optimization method[J]. Electrical Measurement & Instrumentation, 2022, 59(11): 34-41. (  0) 0) |
| [5] |
LI B, LU M Z, ZHANG Y Y, et al. A weekend load forecasting model based on semi-parametric regression analysis considering weather and load interaction[J]. Energies, 2019, 12(20): 3820. DOI:10.3390/en12203820 (  0) 0) |
| [6] |
王宝财. 基于温度近因效应的多元线性回归电力负荷预测[J]. 水电能源科学, 2018, 36(10): 201-205. WANG Baocai. Load forecasting of multiple linear regression based on temperature recency effect[J]. Water Resources and Power, 2018, 36(10): 201-205. (  0) 0) |
| [7] |
IMANI M. Electrical load-temperature CNN for residential load forecasting[J]. Energy, 2021, 227: 120480. (  0) 0) |
| [8] |
AMALOU I, MOUHNI N, ABDALI A. Multivariate time series prediction by RNN architectures for energy consumption forecasting[J]. Energy Reports, 2022, 8: 1084-1091. (  0) 0) |
| [9] |
KONG X Y, LI C, WANG C S, et al. Short-term electrical load forecasting based on error correction using dynamic mode decomposition[J]. Applied Energy, 2020, 261: 114368. (  0) 0) |
| [10] |
唐贤伦, 陈洪旭, 熊德意, 等. 基于极端梯度提升和时间卷积网络的短期电力负荷预测[J]. 高电压技术, 2022, 48(8): 3059-3067. TANG Xianlun, CHEN Hongxu, XIONG Deyi, et al. Short-term power load forecasting based on extreme gradient boosting and temporal convolutional network[J]. High Voltage Engineering, 2022, 48(8): 3059-3067. (  0) 0) |
| [11] |
王继东, 杜冲. 基于Attention-BiLSTM神经网络和气象数据修正的短期负荷预测模型[J]. 电力自动化设备, 2022, 42(4): 172-177, 224. WANG Jidong, DU Chong. Short-term load prediction model based on Attention-BiLSTM neural network and meteorological data correction[J]. Electric Power Automation Equipment, 2022, 42(4): 172-177, 224. (  0) 0) |
| [12] |
彭文, 王金睿, 尹山青. 电力市场中基于Attention-LSTM的短期负荷预测模型[J]. 电网技术, 2019, 43(5): 1745-1751. PENG Wen, WANG Jinrui, YIN Shanqing. Short-term load forecasting model based on Attention-LSTM in electricity market[J]. Power System Technology, 2019, 43(5): 1745-1751. (  0) 0) |
| [13] |
欧阳福莲, 王俊, 周杭霞. 基于改进迁移学习和多尺度CNN-BiLSTM-Attention的短期电力负荷预测方法[J]. 电力系统保护与控制, 2023, 51(2): 132-140. OUYANG Fulian, WANG Jun, ZHOU Hangxia. Short-term power load forecasting method based on improved hierarchical transfer learning andmulti-scale CNN-BiLSTM-Attention[J]. Power System Protection and Control, 2023, 51(2): 132-140. (  0) 0) |
| [14] |
李玉志, 刘晓亮, 邢方方, 等. 基于Bi-LSTM和特征关联性分析的日尖峰负荷预测[J]. 电网技术, 2021, 45(7): 2719-2730. LI Yuzhi, LIU Xiaoliang, XING Fangfang, et al. Daily peak load prediction based on correlation analysis and Bi-directional long short-term memory network[J]. Power System Technology, 2021, 45(7): 2719-2730. (  0) 0) |
| [15] |
GUO Y X, LI Y, QIAO X B, et al. BiLSTM multitask learning-based combined load forecasting considering the loads coupling relationship for multienergy system[J]. IEEE Transactions on Smart Grid, 2022, 13(5): 3481-3492. (  0) 0) |
| [16] |
LAOUAFI A, LAOUAFI F, BOUKELIA T E. An adaptive hybrid ensemble with pattern similarity analysis and error correction for short-term load forecasting[J]. Applied Energy, 2022, 322: 119525. (  0) 0) |
| [17] |
WANG D Y, YUE C Q, ELAMRAOUI A. Multi-step-ahead electricity load forecasting using a novel hybrid architecture with decomposition-based error correction strategy[J]. Chaos, Solitons & Fractals, 2021, 152: 111453. (  0) 0) |
| [18] |
刘文杰, 刘禾, 王英男, 等. 基于完整自适应噪声集成经验模态分解的LSTM-Attention网络短期电力负荷预测方法[J]. 电力建设, 2022, 43(2): 98-108. LIU Wenjie, LIU He, WANG Yingnan, et al. Short-term power load forecasting method based on CEEMDAN and LSTM-attention network[J]. Electric Power Construction, 2022, 43(2): 98-108. (  0) 0) |
| [19] |
孙景钌, 胡长洪, 项烨鋆, 等. 基于多核模糊C均值聚类的配电网短期负荷预测[J]. 浙江电力, 2022, 41(3): 65-71. SUN Jingliao, HU Changhong, XIANG Yeyun, et al. Short-term load forecasting of distribution networks based on multiple kernel fuzzy C-means clustering[J]. Zhejiang Electric Power, 2022, 41(3): 65-71. (  0) 0) |
| [20] |
黎灿兵, 刘梅, 单业才, 等. 基于解耦机制的小地区短期负荷预测方法[J]. 电网技术, 2008, 32(5): 87-92. LI Canbing, LIU Mei, SHAN Yecai, et al. Short-term load forecasting method of small region based on decoupling mechanism[J]. Power System Technology, 2008, 32(5): 87-92. (  0) 0) |
| [21] |
沈沉, 秦建, 盛万兴, 等. 基于小波聚类的配变短期负荷预测方法研究[J]. 电网技术, 2016, 40(2): 521-526. SHEN Chen, QIN Jian, SHENG Wanxing, et al. Study on short-term forecasting of distribution transformer load using wavelet and clustering method[J]. Power System Technology, 2016, 40(2): 521-526. (  0) 0) |
| [22] |
方八零, 李龙, 赵家铸, 等. 动态相似与静态相似相结合的短期负荷预测方法[J]. 电力系统保护与控制, 2018, 46(15): 29-35. FANG Baling, LI Long, ZHAO Jiazhu, et al. Short-term load forecasting based on the combination of dynamic similarity and static similarity[J]. Power System Protection and Control, 2018, 46(15): 29-35. (  0) 0) |
| [23] |
覃芳璐. 考虑多因素气象的电网短期负荷预测建模研究[D]. 南宁: 广西大学, 2017. QIN Fanglu. Study on modeling of power system short term load forecasting considering multi factor meteorology[D]. Nanning: Guangxi University, 2017. (  0) 0) |
| [24] |
薛阳, 张宁, 吴海东, 等. 基于UTCI-MIC与振幅压缩灰色模型的用户侧微电网短期负荷预测方法[J]. 电网技术, 2020, 44(2): 556-563. XUE Yang, ZHANG Ning, WU Haidong, et al. Short-term load forecasting method for user side microgrid based on UTCI-MIC and amplitude compression grey model[J]. Power System Technology, 2020, 44(2): 556-563. (  0) 0) |
| [25] |
李清. 基于改进PSO-PFCM聚类算法的电力大数据异常检测方法[J]. 电力系统保护与控制, 2021, 49(18): 161-166. LI Qing. Power big data anomaly detection method based on an improved PSO-PFCM clustering algorithm[J]. Power System Protection and Control, 2021, 49(18): 161-166. (  0) 0) |
2. School of Electrical Engineering, Hebei University of Technology, Tianjin 300130, China;
3. College of Artificial Intelligence and Data Science, Hebei University of Technology, Tianjin 300401, China;
4. Experimental Training Center, Hebei University of Technology, Tianjin 300401
 2024, Vol. 43
2024, Vol. 43


 张家安(1975),男,博士,讲师,研究方向为新能源发电系统及智能化、新能源接入电网系统建模与仿真(E-mail:
张家安(1975),男,博士,讲师,研究方向为新能源发电系统及智能化、新能源接入电网系统建模与仿真(E-mail: