文章编号: 2096-3203(2023)06-0206-08 中图分类号: TM757
2. 华北电力大学(电力物联网技术河北省重点实验室),河北 保定 071003
随着近年来电力线缆的输送电压等级越来越高,输电容量越来越大,高压大截面电缆在电力系统中得到了广泛的应用[1-5]。在隧道中,高压大截面电缆一般采用蛇形敷设,以降低电缆热胀冷缩量,有效缓解电缆的机械效应带来的危害。电缆三相之间采用水平或品型排列方式,水平敷设电缆之间有一定相间距,有利于热量的散发;品型敷设电缆的三相紧靠在一起,有利于降低金属护套上的感应电压。随着隧道内敷设的电缆回路数不断增加,各相产生的电磁场彼此相互影响,使得电缆的电动力分析变得更为复杂。电缆系统中常见的短路故障有三相短路、两相短路、两相接地短路、单相接地短路[6]。三相短路故障造成的后果比其他类型更为严重[7],短路电流可达正常工作电流的十倍以上。通电导体处在交变电磁场中,受到巨大的电动力[8-10],电缆将在交变电动力作用下产生振动。若电缆及附件的机械强度不足,可能会导致缆体、接头以及夹具产生较大的机械应力,严重时将摧毁整条输电线路[11],因此准确分析计算高压大截面电缆的电动力可以为电缆敷设和金具设计提供理论依据,以避免故障的发生。
通过实际试验的方法测试电缆短路电动力不仅需要耗费巨大的人力和物力,而且会对输电系统造成不可逆转的破坏,因此目前电动力求解主要使用的是公式法和有限元法。文献[12]介绍公式法在计算电动力中的应用,该方法可以快速计算出电缆电动力,但同时存在理论性强,求解变量多,求解多回路电缆的短路电动力需要复杂的公式推导[13]等缺点。由于公式法作了大量的近似处理,因此计算得到的电动力与实际电缆电动力存在一定偏差。同时,公式法难以充分反映电动力在空间的分布情况以及其随时间的变化规律。
为了得到更精确、更充分的结果,研究人员尝试采用有限元法计算短路电动力。文献[14]建立了短路电流、电缆电动力以及夹具应力的多物理场有限元模型,模拟了短路电流下电缆和金具上的动态负载。文献[15]研究不同故障电阻、故障类型以及故障持续时间对电缆短路电动力的影响。文献[16]通过对正常运行和超负荷运行的海缆进行模拟,获得电缆在电动力下的振动情况。文献[17]对三相电缆电动力情况进行了有限元仿真,分析了不同冲击电流和不同长度电缆下电动力导致的夹具机械应力。但以上文献[14-17]仅仅针对电缆电动力或夹具应力进行计算,未从电缆的敷设角度考虑减小电动力带来的影响,未给出电缆的具体敷设建议。文献[18]建立电缆夹具的有限元模型,研究在不同相间距和跨度下,水平敷设电缆短路电动力对夹具的影响。文献[19]分析单芯电缆之间的间距对磁场强度的影响,研究平行排布的单芯电缆电动力对缆体的振动情况。虽然文献[18-19]简单分析电缆敷设方式对电动力的影响,但文献[18]未考虑短路电动力的瞬态特性,文献[19]未考虑短路电流的冲击性。上述研究为应用有限元法计算电缆短路电动力或夹具应力奠定了坚实的基础,但到目前为止,系统分析水平和品型敷设高压大截面电缆的磁场分布和电动力变化特征的文献仍较少。此外,尚无文献考虑电缆的回路间距对短路电动力的影响。随着双回路电缆的应用越来越广泛,亟须考虑如何从电缆的回路间距着手去减小短路电动力,以提高电缆传输的安全性。
文中将建立水平和品型敷设高压大截面电缆的电磁有限元模型,分析其在三相短路电流下的电磁场和短路电动力变化特点;重点分析回路间距对双回路电缆短路电动力的影响,得出短路电动力最大值随回路间距变化的规律,并通过函数拟合得到关系式。文中研究将为电力电缆短路电动力理论研究和工程设计施工提供理论依据。
1 电缆模型的建立高压大截面电缆通常采用水平和品型两种敷设方式,一条电缆隧道中可以包含双回路、三回路等多种回路[20]。文中以图 1所示ZC-YJLW02型交流330 kV交联聚乙烯绝缘电缆为研究对象,该电缆导体的标称截面为2 500 mm2。
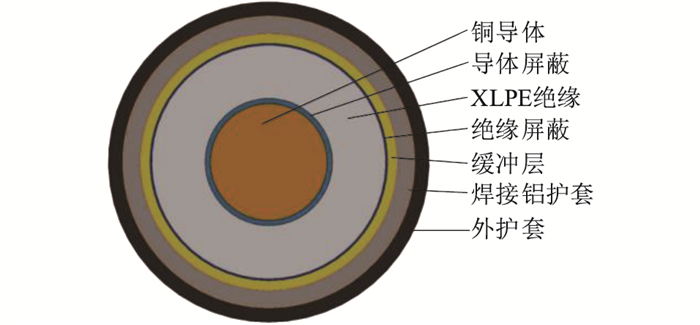
|
图 1 电缆结构 Fig. 1 Cable structure |
电缆运行过程中受到的短路电动力是短路电流下导体在磁场中产生的[21],电缆的其他层结构对电动力数值结果影响很小,因此将厚度较小的导体屏蔽、绝缘屏蔽合并到性能相近的交联聚乙烯(crosslinked polyethylene cable,XLPE)绝缘层,最终建立具有五层结构的电缆电磁有限元模型,其分别为铜导体层、XLPE绝缘层、缓冲阻水层、铝护套层以及外护套层[22]。结合西安某段高压大截面电缆在隧道中实际敷设情况,设置电缆的跨距为6 m,电缆轴向为垂直蛇形结构,波峰到波谷的距离为0.26 m,建立的三相水平和品型电缆模型如图 2所示。电缆电磁计算所用材料参数[23]见表 1。
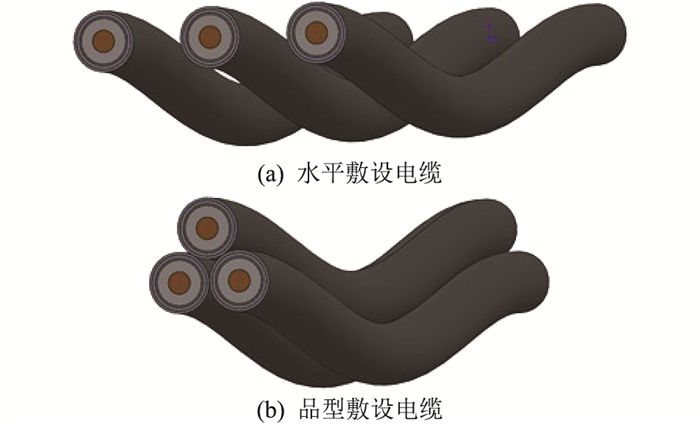
|
图 2 水平和品型敷设电缆模型 Fig. 2 Cable models in flat formation and trefoil formation |
|
|
表 1 电缆电磁材料参数 Table 1 Cable electromagnetic material parameters |
短路电流流经导体时,会在空间中产生电磁场,考虑到矢量磁位在空间中的衰减,在电缆周围设置足够的计算域,以保证短路电动力计算的准确性。计算域的材料为空气,设置计算域外边界处矢量磁位为0(第一类边界条件),电缆端面与计算域交界处边界设为磁绝缘。短路电动力求解为瞬态电磁特性分析,设置求解终止时间为60 ms,即包含3个周波,步长为0.4 ms。在交变电流下,须考虑导体集肤效应对电动力计算的影响。为了保证计算的速度和准确性,采用软件自适应剖分和手工设定剖分尺寸相结合的方式,对电缆剖分较密的网格,对计算域剖分相对稀疏的网格,如图 3所示。

|
图 3 电缆水平和品型敷设时网格的划分 Fig. 3 Grid division in flat formation and trefoil formation |
当发生短路故障时,尤其是三相接地短路,短路电流峰值可到达上百千安,电缆将产生巨大电动力。假设系统为无穷大供电系统,电缆三相母线短路时,认为电压不变,短路电流周期分量不衰减,非周期分量衰减,A、B、C三相的初始相位差为2π/3。在短路前期,电流幅值大,随着时间的推移,短路电流会逐渐衰减。瞬态三相短路电流[24]如式(1)所示,式中第一项为稳态分量,即电流周期分量,第二项为暂态分量,即电流非周期分量。
| {iA=Im(sin(ωt+φA)−e−1/Ta×sinφA)iB=Im(sin(ωt+φA−23π)−e−1/Ta×sin(φA−23π))iC=Im(sin(ωt+φA+23π)−e−1/Ta×sin(φA+23π)) | (1) |
式中:Im为短路电流周期分量的最大值;ω为角频率;t为时间;φA为A相短路电流的初相角;Ta为短路电流非周期分量衰减时间常数,一般取45 ms。
一般采用短路冲击电流ip衡量电力设备在短路电动力下的稳定性,即短路电流最大瞬时值。ip出现在短路发生后最初半周期[25],此时t=0.01 s,其表达如式(2)所示。
| ip=Im(1+e−0.01/Ta)=ImKsh | (2) |
式中:Ksh为短路电流冲击系数,表示冲击电流与短路电流周期分量间的倍数关系,取值范围为1~2。
以文中所分析的330 kV超高压大截面电缆为例,根据该回路各参数计算得到冲击电流峰值为63 kA,其三相短路电流曲线如图 4所示。

|
图 4 三相短路电流 Fig. 4 Three-phase short-circuit current |
短路发生前期,电流幅值大,电缆周围产生较强的磁场,文中利用建立的水平和品型敷设电缆有限元模型,计算其在三相短路电流下的磁场强度。图 5分别展示了0.01 s时刻水平和品型敷设电缆端面上磁场强度分布情况。由于磁场强度与电流大小成正比,电流越大,磁场强度越大,而由图 4可知在0.01 s时刻,A相和B相的短路电流值都较大,C相电流值较小,且三相电缆的几何参数与材料参数完全一致。因此由图 5可知,磁场强度较大的红色区域主要位于A相和B相电缆,并且A相和B相磁场强度最大值出现在铜导体的表面,其主要原因是电缆导体通入三相短路电流后产生了集肤效应[26],使得大部分磁场分布在导体的表面,导体内部磁场分布很小。同时由于邻近效应的作用,导体表面的磁场分布在趋向两导体靠近的一侧。整体上看,整个求解区域的磁场强度的云图分布较均匀,并沿着径向逐渐衰减,符合实际情况。

|
图 5 磁场强度分布云图 Fig. 5 Vector cloud diagram of cable magnetic field intensity |
为了更好地分析电缆轴向和径向的磁场强度变化规律,沿着水平敷设电缆B相导体的两个端面中心画一条长6 m的路径,再沿着品型敷设电缆A相端面从左到右绘制一条长169 mm的路径,如图 5红色箭头所示,分别绘制2条路径的磁场强度随时间变化分布图,如图 6所示。由图 6(a)可知,在同一时刻,随着轴向距离变化,电缆的磁场强度基本保持一致。由于绘图路径位于B相电缆导体的中心,此处的磁场强度较弱,因此图 6(a)中的最大磁场强度仅为4.168×105 A/m。由图 6(b)可知,在同一时刻,电缆径向上的磁场强度分布差异巨大,在靠近电缆铜导体表面处,即径向距离53.65 mm和115.25 mm处,出现磁场强度极大的尖峰,沿着直径方向向外,磁场强度逐渐减小。无论是电缆轴向路径还是径向路径上,随着时间的推移,由于短路电流逐渐衰减,磁场强度也都出现周期性的衰减。

|
图 6 电缆路径上随时间变化的磁场强度 Fig. 6 Magnetic field intensity over time along the cable path |
基于有限元计算原理,其瞬时电动力[27]表达如式(3)所示。
| F=dW(S,i)dS|iconst =∂∂S∫V(∫H0B dH)dV | (3) |
式中:W(s, i)为磁场储能;i为磁场电流;H为磁场强度;B为磁感应强度;S为面积;V为体积。
基于式(3),采用虚功法计算短路电动力,在三相短路电流条件下,水平和品型敷设电缆受到的短路电动力幅值如图 7所示。由图 7 (a)可知,在0.01 s时,水平敷设电缆A相和B相的瞬时电动力达到最大值,分别为11.5 kN和12.4 kN。在0.014 s时,C相的电动力最大值为5.1 kN。由于B相的短路电流较大,且处在中间相,同时受A相和C相磁场的影响,故短路电动力最大。

|
图 7 短路电动力幅值随时间变化曲线 Fig. 7 Short-circuit electromagnetic force amplitude variation curve with time |
由图 7(b)可知,相比于水平敷设电缆,品型敷设电缆的相间距较近,因此短路电动力更大。在第一个周期,在0.008 4 s时刻,A相的瞬时电动力数值达到最大,为25.3 kN;在0.010 8 s时刻,B相的瞬时电动力数值达到最大,为24.1 kN;在0.006 s时刻,C相的瞬时电动力达到最大,为11.8 kN。由于A相的短路电流峰值最大,且A、B、C三相距离较近,所处磁场强度大,因此A相所受电动力最大。对比两图可知,无论是水平敷设还是品型敷设,电缆所受的短路电动力都呈周期性的变化,周期与工频周期近似成倍数关系,每周期的短路电动力峰值随着周期的增加逐步衰减。
为了验证电磁有限元方法计算不同敷设形式电缆短路电动力的准确性,文中采用公式法对结果进行验证,参考标准IEC 61914-2015给出的发生三相短路时导体之间最大短路电动力公式,如式(4)所示。
| {Ffo=1.6×10−7×hsi2pFfm=1.7×10−7×hsi2pFt=1.7×10−7×hsi2p | (4) |
式中:Ffo为水平敷设电缆外边相短路电动力最大值;Ffm为水平敷设电缆中间相短路电动力最大值;Ft为品型敷设电缆短路电动力最大值;h为电缆跨距;s为两相邻电缆的中心距离。
三相短路下水平和品型敷设电缆短路电动力最大值的有限元计算法(finite element method, FEM)和公式法计算结果对比见表 2。由表 2可知,公式计算的结果与有限元仿真计算的结果近似相等,验证了文中有限元法计算短路电动力的正确性。虽然利用式(4)计算电动力简单快速,但是该方法只能计算电动力最大值,并且不适用于一些具有复杂铺设形式和结构的多回路电缆。因此针对相间距对双回路电缆电动力影响,须使用有限元软件进行更准确的模拟计算。
|
|
表 2 公式法和FEM结果对比 Table 2 Comparison of formula method and FEM results |
在实际中为了增加供电容量,提高电缆隧道利用率,同一隧道内通常会敷设两回路甚至更多回电缆[28]。以双回路电缆为例,电缆周围磁场强度相比单回路电缆发生了变化[29],其短路电动力也必然变化。当双回路电缆的回路间距改变时,又会引起短路电动力的复杂变化,因此有必要对双回路下的短路电动力进行深入分析。
为了分析回路间距对双回路敷设电缆短路电动力的影响,以图 8所示的电缆为例,改变其回路间距,建立水平敷设回路间距l1为350~1 300 mm,间隔d1为50 mm,以及品型敷设回路间距l2为300~850 mm,间隔d2为50 mm的电缆有限元模型,分析短路电动力最大值随回路间距变化趋势。
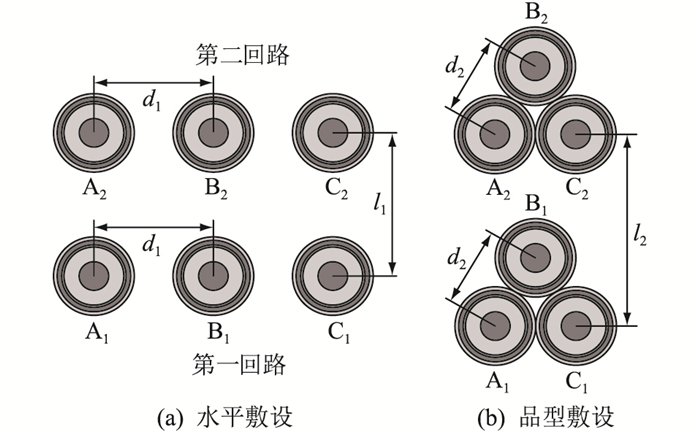
|
图 8 双回路敷设电缆 Fig. 8 Double-loop laying cables |
观察模型计算结果发现,上下布置的双回路水平敷设电缆周围磁场分布完全相同,短路电动力曲线也相同,这是由于两回路结构相同。绘制其中一个回路的短路电动力最大值随回路间距变化的曲线图,如图 9所示。

|
图 9 双回路水平敷设电缆短路电动力最大值 Fig. 9 The maximum value of short-circuit electromagnetic force of double-loop cables in flat formation |
由图 9可知,当回路间距为300 mm时,此时三相电缆距离很近,具有较大短路电流的A相和B相的电动力都在20 kN左右。
随着回路间距的增加,A、B、C三相的短路电动力先是急剧下降,随后趋于平缓,当回路的间距达到1 300 mm时趋于水平,此时A相的短路电动力最大值为11.94 kN,B相为12.86 kN,C相为5.26 kN,与图 7(a)中单回路水平敷设电缆计算得到的短路电动力最大值接近。
利用双线性回归法对电动力数据进行拟合,拟合后的效果如图 9曲线所示,由图可知,拟合曲线与数据点完全重合,拟合精度较高。拟合得到的A、B、C三相短路电动力最大值随回路间距变化的方程如式(5)所示。
| {SA=13.52×e−1.04l+30.46×e−0.0049lSB=22.69×e−0.0043l+13.87×e−6.5lSC=5.61×e−0.0000532l+11.04×e−0.0049l | (5) |
式中:SA、SB、SC分别为A相、B相和C相的最大短路电动力;l为回路间距。
由式(5)可知,短路电动力最大值与回路间距成指数关系,增大回路间距可有效降低短路电动力,但存在一个拐点,即800 mm处,其右侧电动力减少明显变缓,此值可作为工程施工的参考临界值。
上下布置的双回路品型敷设电缆不是完全对称模型,两个回路周围的磁场分布不相同,短路电动力最大值曲线不完全相同。为了对比短路电动力最大值随回路间距变化的规律,将两个回路的短路电动力最大值绘制在图 10中。
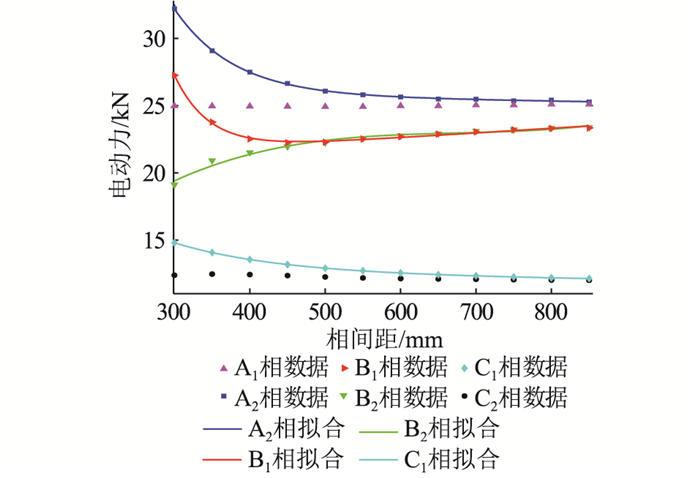
|
图 10 双回路品型敷设电缆短路电动力最大值 Fig. 10 The maximum value of short-circuit electromagnetic force of double-loop cables in trefoil formation |
由图 10可知,随着回路间距的增加,第一回路A1相的短路电动力最大值基本保持不变,为24.5 kN左右,B1相和C1相短路电动力最大值逐渐减小;第二回路的A2相短路电动力最大值逐渐减小,而B2相短路电动力最大值逐渐增大,C2相短路电动力最大值基本保持在13 kN左右。
对比图 10中两个回路短路电动力数据可知,当回路间距增大时,两个回路的A相短路电动力最大值逐渐接近,当达到850 mm时两者重合;两个回路的B相短路电动力最大值在回路间距大于500 mm时完全重合;两个回路的C相短路电动力最大值在回路间距大于750 mm时完全重合。当回路间距为850 mm时,两个回路A相的短路电动力最大值都为26.5 kN,B相都为25.3 kN,C相都为12.4 kN,与图 7(b)中单回路品型短路电动力最大值接近。
图 10中的第一回路的B1、C1相以及第二回路的A2、B2相电动力曲线变化比较明显,对其进行函数拟合,拟合的效果如图 10曲线所示。由图 10可知拟合曲线与数据点基本重合,拟合精度高。拟合得到的方程如式(6)所示。
| {SB1=3910×e−0.022l+0.000015×e−0.0049lSC1=19.61×e−0.0072l+12.78×e0.0000657lSA2=293.12×e−0.013l+26.03×e−0.0000347lSB2=(5.65×10−8)l3−(1.15×10−4)l2+0.0793l+4.4339 | (6) |
式中:SB1、SC1、SA2、SB2分别第一回路的B1相、C1相以及第二回路的A2相、B2相最大短路电动力。
由式(6)可知,第一回路的B1相、C1相和第二回路的A2相都符合指数函数,而第二回路的B2相符合三次多项式函数。短路电动力随回路间距的变化存在一个临界值,当双回路品型敷设电缆的回路间距大于850 mm时,可忽略回路之间的影响。但考虑到电缆隧道的尺寸有限,建议回路间距为600 mm左右,此时的短路电动力已基本接近最小值。
4 结论文中采用电磁耦合有限元法建立了水平和品型敷设高压大截面电缆的电动力模型,分析了三相短路下两种敷设方式的电磁分布和短路电动力特点,重点分析了回路间距对双回路电缆短路电动力的影响,得出如下结论:
(1) 三相短路发生后,在电缆径向空间维度上,导体表面处磁场强度最大,向外逐渐衰减,在时间维度上,磁场成振荡衰减,在时空图上体现为重复出现的马鞍形曲面;在电缆轴向上,磁场强度不变。电缆所受的短路电动力随时间呈周期性变化,周期与工频周期近似成倍数关系,短路电动力峰值随着周期的增加逐步衰减。水平和品型敷设电缆短路电动力最大值分别出现在B相和A相。
(2) 在双回路水平敷设电缆中,电动力与回路间距成指数关系,随着回路间距的增加,电动力先是急剧下降,随后趋于平缓,可以找到一个拐点,该点可作为回路间距折中值的参考;对于双回路品型敷设电缆的电动力与回路间距的变化,用同样方法也可找到拐点。针对ZC-YJLW02型交流330 kV交联聚乙烯绝缘电缆,综合考虑短路电动力和隧道利用率,建议水平敷设双回路间距不小于800 mm,品型敷设双回路间距不小于600 mm。
| [1] |
李盛翀, 马宏忠, 付明星, 等. 基于热力耦合的高压大截面电缆应力和形变研究[J]. 绝缘材料, 2019, 52(3): 80-85. LI Shengchong, MA Hongzhong, FU Mingxing, et al. Research on stress and deformation of high voltage cable with large section based on thermal-mechanical coupling[J]. Insulating Materials, 2019, 52(3): 80-85. (  1) 1) |
| [2] |
LI M Z, ZHOU C K, ZHOU W J. A revised model for calculating HV cable sheath current under short-circuit fault condition and its application for fault location—part 1:the revised model[J]. IEEE Transactions on Power Delivery, 2019, 34(4): 1674-1683. DOI:10.1109/TPWRD.2019.2918159 (  0) 0) |
| [3] |
梁振锋, 李天婷, 张怿宁. 高压架空-电缆混合线路电容电流补偿方法研究[J]. 电力电容器与无功补偿, 2022, 43(6): 16-21. LIANG Zhenfeng, LI Tianting, ZHANG Yining. Research on capacitance current compensation method of high voltage overhead-cable hybrid line[J]. Power Capacitor & Reactive Power Compensation, 2022, 43(6): 16-21. (  0) 0) |
| [4] |
张宇飞, 罗日成, 田迪凯, 等. 110 kV海底电缆-架空线雷击过电压分析[J]. 电瓷避雷器, 2022(2): 14-19. ZHANG Yufei, LUO Richeng, TIAN Dikai, et al. Lightning overvoltage on 110 kV submarine cable-overhead line[J]. Insulators and Surge Arresters, 2022(2): 14-19. (  0) 0) |
| [5] |
陈宗正, 张旭航, 申亚, 等. 基于500 kV长距离电缆线路的合闸过电压研究[J]. 电瓷避雷器, 2021(6): 108-112. CHEN Zongzheng, ZHANG Xuhang, SHEN Ya, et al. Closing overvoltage based on EHV long-distance cable line[J]. Insulators and Surge Arresters, 2021(6): 108-112. (  1) 1) |
| [6] |
LUO X X, XIAO Q B, WANG Q, et al. Research on short-circuit force of transformer winding with single-phase short-circuit and three-phase short-circuit[C]//2021 11th International Conference on Power and Energy Systems (ICPES). Shanghai, China. IEEE, 2022: 219-223.
(  1) 1) |
| [7] |
ZHANG C C, GE W Q, XIE Y, et al. Comprehensive analysis of winding electromagnetic force and deformation during No-load closing and short-circuiting of power transformers[J]. IEEE Access, 2021, 9: 73335-73345. DOI:10.1109/ACCESS.2021.3068054 (  1) 1) |
| [8] |
HODGSON I, SAUSE R, TAHMASEBI E, et al. Testing and analysis of dynamic response of a high-voltage substation structure to short-circuit current forces[J]. IEEE Transactions on Power Delivery, 2018, 33(5): 2097-2105. DOI:10.1109/TPWRD.2017.2769841 (  1) 1) |
| [9] |
SZULBORSKI M, ŁAPCZYNSKI S, KOLIMAS Ł, et al. Calculations of electrodynamic forces in three-phase asymmetric busbar system with the use of FEM[J]. Energies, 2020, 13(20): 5477. DOI:10.3390/en13205477 (  0) 0) |
| [10] |
SHAN Y, AI M M, LIU W H. Research on simulation calculation on short-circuit electrodynamics force of power transformer winding[J]. International Journal of Applied Electromagnetics and Mechanics, 2021, 65(3): 451-465. DOI:10.3233/JAE-200021 (  1) 1) |
| [11] |
舒乃秋, 关向雨, 康兵, 等. 基于场路耦合有限元的三相共箱气体绝缘母线暂态电动力分析[J]. 电网技术, 2015, 39(5): 1456-1462. SHU Naiqiu, GUAN Xiangyu, KANG Bing, et al. Dynamic electromagnetic force analysis of three phase enclosure type GIB based on field-circuit coupling theory[J]. Power System Technology, 2015, 39(5): 1456-1462. (  1) 1) |
| [12] |
张振鹏, 蒙绍新, 赵健康, 等. 典型敷设条件下电力电缆线路运行振动特征值的测量试验[J]. 高电压技术, 2015, 41(4): 1188-1193. ZHANG Zhenpeng, MENG Shaoxin, ZHAO Jiankang, et al. Measurement of vibration characteristics of power cable line under typical laying conditions[J]. High Voltage Engineering, 2015, 41(4): 1188-1193. (  1) 1) |
| [13] |
CAI Y, GUO W Y, SANG W J, et al. An improved multiphysics analysis model for the short-circuit fault ride-through capability evaluation of the MMC submodule busbar[J]. IEEE Access, 2021, 9: 119090-119099. DOI:10.1109/ACCESS.2021.3108048 (  1) 1) |
| [14] |
YEOMAN M S, FRIZZELL L, VARLEY R J, et al. Using a multiphysics model to ensure power cables are restrained safely[C]//2015 Petroleum and Chemical Industry Conference Europe (PCIC Europe). London, UK. IEEE, 2016: 1-9.
(  2) 2) |
| [15] |
SADEGHI A, SEYYEDBARZEGAR S M, YAZDANI-ASRAMI M. Transient analysis of a 22.9 kV/2 kA HTS cable under short circuit using equivalent circuit model considering different fault parameters[J]. Physica C: Superconductivity and Its Applications, 2021, 589: 1353935. DOI:10.1016/j.physc.2021.1353935 (  1) 1) |
| [16] |
胡宇航. 基于BOTDR的三芯海缆振动的建模及测量方法研究[D]. 北京: 华北电力大学, 2021. HU Yuhang. Research on modeling and measurement method of three-core submarine cable vibration based on BOTDR[D]. Beijing: North China Electric Power University, 2021. (  1) 1) |
| [17] |
刘博文. 基于有限元分析的三相短路实验电缆电动力三维模型的设计与建立[D]. 抚顺: 辽宁石油化工大学, 2019. LIU Bowen. Design and establishment of three-dimensional electrodynamic model of three-phase short-circuit experimental cable based on finite element analysis[D]. Fushun: Liaoning Shihua University, 2019. (  2) 2) |
| [18] |
刘航宇, 刘念, 蒲丽娟, 等. 基于ANSYS的高压大截面电缆金具短路电动力和机械应力分析[J]. 电工技术学报, 2016, 31(5): 170-176. LIU Hangyu, LIU Nian, PU Lijuan, et al. ANSYS based analysis on short-circuit force and mechanical stress of cleats for high voltage large cross-sectional cables[J]. Transactions of China Electrotechnical Society, 2016, 31(5): 170-176. (  3) 3) |
| [19] |
孙国亮, 周鋆玲, 韩璐. 面向脉冲电流的单芯电缆排布方式[J]. 船舶工程, 2022, 44(12): 97-102. SUN Guoliang, ZHOU Junling, HAN Lu. Single-core cable arrangement for pulse current[J]. Ship Engineering, 2022, 44(12): 97-102. (  3) 3) |
| [20] |
张重远, 芮皓然, 刘贺晨, 等. 高压单芯电缆单相接地故障护套过电压特性仿真分析[J]. 电测与仪表, 2018, 55(11): 115-119. ZHANG Zhongyuan, RUI Haoran, LIU Hechen, et al. Simulation analysis of sheath overvoltage characteristic for single-phase ground fault in high voltage single-core cable[J]. Electrical Measurement & Instrumentation, 2018, 55(11): 115-119. (  1) 1) |
| [21] |
JAMALI-ABNAVIA, HASHEMI-DEZAKI H. Evaluating the electromagnetic forces on the electric arc furnaces' power cables under various operation conditions[J]. Electric Power Systems Research, 2021, 201: 107553. (  1) 1) |
| [22] |
吕安强, 李静, 张振鹏, 等. 夹具对高压绝缘电缆热学特性影响的有限元分析[J]. 电工技术学报, 2022, 37(1): 283-290. LV Anqiang, LI Jing, ZHANG Zhenpeng, et al. Finite element analysis for the influence of clamp on the thermal characteristics of high voltage insulated power cable[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 283-290. (  1) 1) |
| [23] |
张宇娇, 郭梽炜, 汪振亮, 等. 基于电磁场—流场—温度场耦合分析的电缆支架温升计算及实验验证[J]. 高压电器, 2019, 55(8): 143-148, 156. ZHANG Yujiao, GUO Zhiwei, WANG Zhenliang, et al. Calculation and experimental verification of cable support's temperature rise based on electromagnetic-fluid-thermal fields[J]. High Voltage Apparatus, 2019, 55(8): 143-148, 156. (  1) 1) |
| [24] |
LI Y, XU Q Y, LU Y F. Electromagnetic force analysis of a power transformer under the short-circuit condition[J]. IEEE Transactions on Applied Superconductivity, 2021, 31: 1-3. (  1) 1) |
| [25] |
马静, 刘青, 吴佳芳, 等. 高比例变流型电源并网的输电系统三相短路电流计算[J]. 电力系统自动化, 2019, 43(5): 83-91, 113. MA Jing, LIU Qing, WU Jiafang, et al. Three-phase short-circuit current calculation for power transmission system with high penetration of converter-type sources[J]. Automation of Electric Power Systems, 2019, 43(5): 83-91, 113. (  1) 1) |
| [26] |
高俊国, 于平澜, 李紫云, 等. 基于有限元法的电缆金属护套感应电压仿真分析[J]. 高电压技术, 2014, 40(3): 714-720. GAO Junguo, YU Pinglan, LI Ziyun, et al. Simulation analysis of induced voltage on metal sheath of power cable based on finite element method[J]. High Voltage Engineering, 2014, 40(3): 714-720. (  1) 1) |
| [27] |
孙娜, 刘胜春, 许爱斌, 等. 大截面高压电缆金具电磁-结构瞬态耦合分析[J]. 中国电力, 2021, 54(4): 72-79. SUN Na, LIU Shengchun, XU Aibin, et al. Electromagnetic-structure transient coupling analysis of large cross-sectional high voltage cables[J]. Electric Power, 2021, 54(4): 72-79. (  1) 1) |
| [28] |
牛海清, 李小潇, 陈泽铭, 等. 基于改进遗传算法的隧道多回路电缆群相序优化[J]. 电力工程技术, 2023, 42(2): 147-153. NIU Haiqing, LI Xiaoxiao, CHEN Zeming, et al. Phase sequence optimization of tunnel multi-loop cable group based on improved genetic algorithm[J]. Electric Power Engineering Technology, 2023, 42(2): 147-153. (  1) 1) |
| [29] |
ZHANG P N, ZHANG H Y, LI W, et al. Study on optimization of laying mode of two parallel high voltage cables in the same phase of two circuits[J]. Energy Reports, 2022, 8: 1839-1846. (  1) 1) |
2. North China Electric Power University (Hebei Key Laboratory of Power Internet of Things Technology), Baoding 071003, China
 2023, Vol. 42
2023, Vol. 42



 吕安强(1979),男,博士,副教授,研究方向为分布式光纤传感及新型电力系统智能状态感知(E-mail:
吕安强(1979),男,博士,副教授,研究方向为分布式光纤传感及新型电力系统智能状态感知(E-mail: