文章编号: 2096-3203(2023)06-0014-08 中图分类号: TM744
2. 河北工业大学人工智能与数据科学学院,天津 300130;
3. 河北工业大学实验实训中心,天津 300401
在能源紧缺和环境问题压力下,分布式光伏发电快速发展。但随着光伏在配电网中渗透率的不断提高,功率反送、系统网损增加和节点电压幅值越限等问题也逐渐显现[1-4]。此外,为保证系统安全运行,常进行弃光处理,投资方和运营方的利益冲突问题日益突出[5]。对配电网光伏接纳能力(hosting capacity, HC)进行评估有助于缓解上述问题。
HC概念由Math Bollen和Fainan Hassan于2011年首次明确定义为:在不违反任何运行约束下,能最大程度接入电力网络的分布式电源容量[6]。基于运筹优化的方法是研究HC问题的重要方法之一[7-8]。文献[9]提出一种静态无功补偿器(static var compensator,SVC)优化模型,证明了适当提供无功补偿可提高系统对光伏的HC,但在补偿达到一定程度以后,HC不再增加。文献[10]提出一种电池储能系统参与用户侧削峰填谷的鲁棒优化调度策略,可实现对负荷和可再生能源波动的抑制,提高可再生能源渗透率。然而,当前储能系统成本较高,难以大规模推广应用[11]。文献[12]提出一种三角函数泰勒近似的潮流约束方程,以光伏接入容量最大为目标函数,以潮流方程为主要约束,考虑最坏场景法下的光伏接入容量,但使用最坏场景法所得结果过于保守。文献[13]建立以安装容量最大为目标的模型,计算临近电压越限条件下的单一接入点光伏接入容量,没有对多点接入问题进行研究。
在考虑多个目标函数时,文献多采用元启发式算法进行求解。文献[14-15]依据投资方和运营方的层级关系,建立以投资成本和网损最小为目标的双层目标函数,分别使用粒子群算法和灰狼算法对模型进行求解。文献[16]提出一种以接入容量最大和网损最小为目标的多目标函数模型,使用粒子群算法得到模型的帕累托解集合。文献[17]建立台区电压、线路损耗和电压稳定的多目标决策模型,使用粒子群算法计算光伏接入问题。文献[18]以运行成本最低和网损最小为目标,对分布式光伏接入规划进行研究,使用多种群遗传算法对模型进行求解。尽管上述文献考虑了多个目标函数,但由于元启发式算法的计算效率问题,多对单一时间断面内的数据进行计算。
基于上述研究,提出计及弃光约束的配电网光伏HC评估方法,确定配电网光伏总接入容量和各备选节点接入容量。将弃光约束引入基于DistFlow方程的评估模型,将问题转化为不同弃光阈值下的二阶锥规划问题。在模型框架下,利用利润与光伏总接入容量及弃光率的差分关系,构建风险因子,插值估算投资方利润最大时的光伏总接入容量。采用回代策略,将总接入容量和弃光率作为新的约束代入评估模型,计算确定各备选接入点的接入容量。所提方法考虑时间序列,将弃光率这一指标作为约束整合到评估模型中。通过求解评估模型,直接得到相应弃光阈值下各备选节点的光伏接入容量。在考虑网损的前提下,通过设置有限次的弃光阈值,构造了风险因子这一指标,估算得到利润最大时的光伏接入容量。
1 计及弃光约束的HC评估模型运营方可以通过限制光伏出力保证配电网整体处于安全运营状态,光伏投资方也可以在承受一定的弃光损失下获得更多收益。文中推导了典型时间序列下的弃光约束, 将弃光约束引入以网损最小为目标的评估模型。为方便对比,同时给出典型的以总接入容量最大为目标的评估模型。
1.1 弃光约束假设在某配电网中共有M个备选节点可以接入光伏,节点i的光伏接入容量为SPV, i,i=1, 2, …, M,总接入容量为Shost。则有:
| $ S_{\mathrm{host}}=\sum\limits_{i=1}^{M} S_{\mathrm{PV}, i} $ | (1) |
节点i处光伏在不弃光条件下的t时刻出力PPV, id, i, t为:
| $ P_{\mathrm{PV}, \mathrm{id}, i, t}=\alpha_{i, t} S_{\mathrm{PV}, i} $ | (2) |
式中:αi, t为t时刻节点i的理想单位光伏出力。
节点i处光伏t时刻弃光功率为:
| $ P_{\mathrm{PV}, \mathrm{ab}, i, t}=P_{\mathrm{PV}, \mathrm{id}, i, t}-P_{\mathrm{PV}, i, t} $ | (3) |
式中:PPV, i, t为节点i处接入光伏在t时刻的实际出力。
光伏在任意时刻的出力都不可能大于不限制其出力下的最大出力,即弃光功率应不小于0:
| $ P_{\mathrm{PV}, \text { ab }, i, t} \geqslant 0 $ | (4) |
假设弃光率阈值为η0,在长度为N的典型时间序列内,弃光率约束如下:
| $ \left(1-\eta_{0}\right) \sum\limits_{i=1}^{M} \sum\limits_{t=1}^{N} \alpha_{i, t} S_{\mathrm{PV}, i} \leqslant \sum\limits_{t=1}^{N} \sum\limits_{i=1}^{M} P_{\mathrm{PV}, i, t} $ | (5) |
当各节点的光伏分属不同投资方时,为兼顾各自利益,须对各自的弃光率进行约束,推导过程类似。此处假设在同一配电网下的光伏投资方为同一个,且投资方只关心整体的弃光率,而不关心单个光伏的弃光率。文中不再对每个光伏接入点处的弃光率进行约束,只设置总的弃光阈值。
1.2 其他约束及目标函数在运行过程中,任意时刻均须满足潮流约束、电压幅值约束、联络线电流约束、功率因数约束、过载约束等。为表述方便,在下文约束方程中省略了时间标注t。配电网潮流满足DistFlow方程约束[19],如式(6)所示。
| $ \left\{\begin{array}{l} P_{\mathrm{PV}, i}-P_{\mathrm{D}, i}=\sum\limits_{k} P_{i k}-\sum\limits_{j}\left(P_{j i}-r_{i j} L_{i j}\right) \\ Q_{\mathrm{PV}, i}-Q_{\mathrm{D}, i}=\sum\limits_{k} Q_{i k}-\sum\limits_{j}\left(Q_{j i}-x_{i j} L_{i j}\right) \\ v_{i}-v_{j}=2\left(r_{i j} P_{i j}+x_{i j} Q_{i j}\right)-\left(r_{i j}^{2}+x_{i j}^{2}\right) L_{i j} \\ L_{i j}=\frac{P_{i j}^{2}+Q_{i j}^{2}}{v_{i}} \end{array}\right. $ | (6) |
式中:PPV, i、QPV, i分别为节点i处光伏的有功和无功出力;PD, i、QD, i分别为节点i处有功和无功负荷;Pik、Qik分别为由节点i流向节点k的有功和无功;Pji、Qji分别为由节点j流向节点i的有功和无功;rij为节点i和节点j之间的电阻;xij为节点i和节点j之间的联络线电抗;Lij为节点i和节点j之间支路电流幅值的平方;vi、vj分别为节点i和节点j处电压幅值的平方;Pij、Qij分别为由节点i流向节点j的有功和无功。
文献[20]证明了在目标函数是联络线电流的增函数和配电网辐射状运行等必要条件下,可将式(6)中第4项二阶锥松弛为:
| $ P_{i j}^{2}+Q_{i j}^{2} \leqslant v_{i} L_{i j} $ | (7) |
节点电压幅值约束,根据《电能质量供电电压偏差》(GB/T 12325—2008[21])规定, 不同电压等级允许的电压偏差不同,如式(8)所示。
| $ V_{i, \min }^{2} \leqslant v_{i} \leqslant V_{i, \max }^{2} $ | (8) |
式中:Vi, min、Vi, max分别为节点i处电压幅值的最小、最大限值。
联络线电流约束如下:
| $ L_{i j} \leqslant I_{i j, \max }^{2} $ | (9) |
式中:Iij, max为节点i和节点j之间的联络线允许通过的最大电流值。
关口功率约束。目前我国大部分配电网无法满足功率反送的要求[22],关口处有功功率P0须不小于0,即:
| $ P_{0} \geqslant 0 $ | (10) |
光伏发电的功率因数约束如下:
| $ \cos \varphi_{1} \leqslant \cos \varphi \leqslant 1 $ | (11) |
式中:cos φ为功率因数;cos φ1为功率因数下限。在功率因数约束条件下,无功出力为:
| $ -P_{\mathrm{PV}, i}\left|\tan \varphi_{1}\right| \leqslant Q_{\mathrm{PV}, i} \leqslant P_{\mathrm{PV}, i}\left|\tan \varphi_{1}\right| $ | (12) |
视在功率约束,充分利用光伏电站并网逆变器的容量,可发掘光伏的无功支撑能力[23],如式(13)所示。
| $ P_{\mathrm{PV}, i}^{2}+Q_{\mathrm{PV}, i}^{2} \leqslant S_{\mathrm{PV}, i}^{2} $ | (13) |
采用正多边形近似[24]对式(13)进行线性化,以提高计算效率。近似程度随边数增加而增加,但更多的边数需要更多的变量及约束条件。此处使用Big-M法推导出一种线性化近似模型用于替代式(13)所包含的有效区域,在φ1≤30°的范围内,近似程度优于常见的正十二边形近似,且增加的变量和约束较少。约束如下:
| $ \left\{\begin{array}{l} S_{\mathrm{PV}, i} \cos \varphi_{1}-P_{\mathrm{PV}, i} \leqslant\left(1-\mu_{i}\right) M_{1} \\ Q_{\mathrm{PV}, i}+\left(P_{\mathrm{PV}, i}-S_{\mathrm{PV}, i}\right) \cot \frac{\varphi_{1}}{2} \leqslant\left(1-\mu_{i}\right) M_{1} \\ Q_{\mathrm{PV}, i}-\left(P_{\mathrm{PV}, i}-S_{\mathrm{PV}, i}\right) \cot \frac{\varphi_{1}}{2} \geqslant-\left(1-\mu_{i}\right) M_{1} \end{array}\right. $ | (14) |
式中:μi为0-1变量,当μi=1时输出无功受容量约束,当μi=0时,输出无功受功率因素限制;M1为一充分大的正数。
接入容量上下限约束。文献[22]给出了不同电压等级下的光伏参考接入容量范围。依据实际需求,设置接入容量下限可避免光伏电站过度分散接入,可在一定程度上降低运行管理难度。同时,由于安装场地等限制,存在接入容量上限。该约束属于典型的条件约束,使用Big-M法可对该约束进行等价线性化表示:
| $ \left\{\begin{array}{l} S_{\mathrm{PV}, i}-S_{\mathrm{PV}, i, \text { min }} \leqslant\left(1-\delta_{i}\right) M_{1} \\ S_{\mathrm{PV}, i}-S_{\mathrm{PV}, i, \min } \geqslant-\delta_{i} M_{1} \\ S_{\mathrm{PV}, i} \leqslant\left(1-\delta_{i}\right) M_{1} \\ 0 \leqslant S_{\mathrm{PV}, i} \leqslant S_{\mathrm{PV}, i, \text { max }} \end{array}\right. $ | (15) |
式中:δi为0-1变量,δi=1表示如果容量达不到接入容量下限就不接入光伏,δi=0表示如果容量达到接入容量下限,光伏接入容量应在容量上下限之间;SPV, i, min、SPV, i, max分别为接入容量下限和上限。
目标函数为网损最优时,网损计算如下:
| $ \gamma=\sum\limits_{t=1}^{N} \sum\limits_{i, j \in E} r_{i j} L_{i j, t} $ | (16) |
式中:γ为网损;E为节点集合。得到的最优模型设为模型1,即:
| $ \left\{ \begin{array}{l} \begin{aligned} & \min \gamma \\ & \text { s.t. 式(1)- 式(12) } \\ & \quad \text { 式(14)、式(15) } \end{aligned} \end{array} \right. $ | (17) |
建立直接以接入容量最大为目标的评估模型作为模型1的对比模型,目标函数如下:
| $ \max S_{\text {host }} $ | (18) |
当目标函数为总接入容量Shost最大时,不符合文献[20]所提的目标函数是电流的增函数这一必要条件,将二阶锥松弛应用于模型会导致计算结果发散,须采用线性化潮流约束模型。当采用忽略网损的线性化潮流约束[9]时,可将式(6)替换为以下形式:
| $ \left\{\begin{array}{l} P_{\mathrm{PV}, i}-P_{\mathrm{D}, i}=\sum\limits_{k} P_{i k}-\sum\limits_{j} P_{j i} \\ Q_{\mathrm{PV}, i}-Q_{\mathrm{D}, i}=\sum\limits_{k} Q_{i k}-\sum\limits_{j} Q_{j i} \\ v_{i}-v_{j}=2\left(r_{i j} P_{i j}+x_{i j} Q_{i j}\right) \end{array}\right. $ | (19) |
设得到的模型为模型2,最终模型可表示为:
| $ \left\{ \begin{array}{l} \begin{aligned} & \max S_{\text {host }} \\ & \text { s.t. 式(1)一式(5) } \\ & \quad \text { 式(7)一式(12)、式(14)、式(15)、式(19) } \end{aligned} \end{array} \right. $ | (20) |
将在算例中对2种模型所得结果在总接入容量、各节点接入容量和电压幅值等方面进行对比。
2 光伏接入容量确定假设光伏投资方可以承受一定的弃光风险,以追求利润最大为目标。推导光伏投资方收益与总接入容量及弃光率的差分关系,将其中的关键部分定义为风险因子,利用风险因子求解利润最大时的总接入容量,并通过回代策略,确定各备选接入点的接入容量。
2.1 利用风险因子估算总接入容量设光伏投资方获得的利润为W:
| $ W=C_{2} A S_{\text {host }}(1-\eta)-C_{1} S_{\text {host }} $ | (21) |
其中:
| $ A=\left(\sum\limits_{i=1}^{M} \sum\limits_{t=1}^{N} \alpha_{i, t} S_{\mathrm{PV}, i}\right) / S_{\mathrm{host}} $ | (22) |
式中:C1为单位容量投资成本;C2为合同电价;η为设定的光伏弃光阈值η0下的实际弃光率。
求W对Shost的导数,结果如下:
| $ \frac{\mathrm{d} W}{\mathrm{~d} S_{\text {host }}}=\left(C_{2} A-C_{1}\right)-C_{2} A\left(\eta+\frac{\mathrm{d} \eta}{\mathrm{d} S_{\text {host }}} S_{\text {host }}\right) $ | (23) |
在目标函数不变,且其他约束条件相同的情况下,接入容量增加,实际弃光率增加。弃光发生意味着运行受到约束限制,再次增加接入容量不会减少约束的限制。W对Shost的导数是单调非减少的,当其等于0时,W达到最大值。
在式(23)中,由于η与Shost所对应的解析表达式无法获得,导致 η对Shost的导数也无法直接获得。但通过对评估模型进行求解,可以得到任意确定的η0下对应的η与Shost。采用差分方式,可通过有限次迭代和插值近似,求得W的近似最大值。将式(23)中第二个括号的部分写为差分形式,并将其定义为风险因子,表示为λ:
| $ \lambda=\eta+\frac{\Delta \eta}{\Delta S_{\text {host }}} S_{\text {host }} $ | (24) |
设最优风险因子为λ0,其值为:
| $ \lambda_{0}=\left(C_{2} A-C_{1}\right) /\left(C_{2} A\right) $ | (25) |
当λ趋近于λ0时,收益达到极值。
使用λ估算光伏总接入容量的步骤如下:(1) 设置初始弃光阈值为0,将其代入模型,对模型进行求解,得到初始接入容量。(2) 以固定增量增加弃光阈值,对模型进行求解,计算风险因子。(3) 判断风险因子是否超过最优风险因子,如果没有超过,返回步骤(2),如果超过,进入步骤(4)。(4) 依据风险因子和总接入容量以及弃光率的一一对应关系,使用插值算法估算利润达到最大值时的总接入容量So。图 1为估算流程。

|
图 1 光伏总接入容量估算流程 Fig. 1 Flow chart of PV hosting capacity estimation |
在估算利润最大时的光伏总接入容量前,总接入容量和各节点处的接入容量均为变量。利用风险因子插值估算得到利润最大时的总光伏接入容量后,总接入容量不再变化。同时,尽管插值估算得到了利润最大时的总光伏接入容量的近似值,但没有得到对应的各备选节点处的光伏接入容量,须再次利用模型计算对应的各备选节点处的光伏接入容量。在进行求解的时候,相当于在模型中增加了约束,即:
| $ S_{\text {host }}=S_{\mathrm{o}} $ | (26) |
在求解前须对原模型做一定的修改。以模型1为例,此时模型为:
| $ \left\{\begin{array}{l} \min \gamma \\ \text { s.t. } \;\text { 式(1)-式(12) } \\ \quad \text { 式(14)、式(15)、式(26) } \end{array}\right. $ | (27) |
对模型进行求解可得到各备选节点处的光伏接入容量。
2.3 三相不平衡情况下的接入容量确定由于存在不对称负荷和不对称线路参数,不存在三相完全平衡的配电网系统。随着三相不平衡程度的增加,线路损耗和压降不断增加。当三相负荷不平衡较为严重时,仍以三相平衡为条件计算,可能得出和实际出入较大的计算结果。
在三相不平衡情况下,应仿照三相平衡时的计算流程,对每一相支路进行单独计算,并得出光伏接入点在每一相的接入容量。由于三相不平衡,独立计算得到的各相的光伏接入容量可能并不一致。文献[25]指出光伏系统以非全相方式并入配电网可能会加剧配电网三相不平衡。为避免加剧三相不平衡,此处假设光伏系统以全相方式接入配电网。为保证光伏全相运行,取各相独立计算得到的光伏接入容量的最小值的3倍为各光伏接入点的实际光伏接入容量。
3 算例验证为验证所提HC评估方法确定总接入容量和各备选节点接入容量的有效性,在改进的IEEE 33节点配电网模型中进行仿真分析。使用Gurobi 8.1.1教育版对模型进行求解,设置求解器优化间隙阈值为0.1%,仿真用时共约70 min。
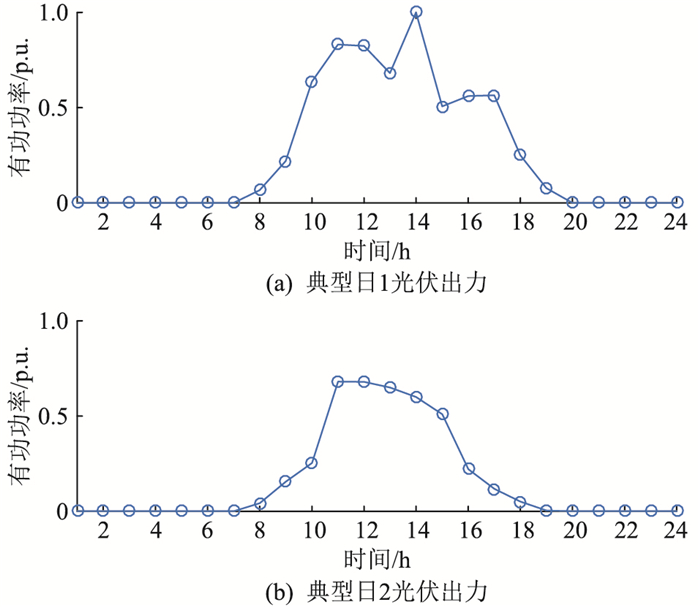
3.1 算例描述使用的IEEE 33节点配电网模型的阻抗和峰值负荷以及基本结构等信息可见文献[26]。假设主联络线上节点2—节点18均满足接入光伏的基本条件,备选节点共17个。选取澳大利亚(DKASC)光伏公开数据集中某两日数据,以典型日峰值功率为基准,对各时刻光伏出力进行标幺处理,结果如图 2所示。
|
图 2 典型日光伏有功出力 Fig. 2 The active output of PV in typical days |
以我国西北某地10 kV配电网年内峰值负荷为基准,对配电网内的典型日负荷进行标幺处理。利用标幺数据,点乘IEEE 33节点系统峰值负荷,用于模拟IEEE 33节点系统典型日中各节点负荷数据。系统总有功负荷如图 3所示。

|
图 3 典型日总有功负荷 Fig. 3 The total active load in typical days |
光伏功率因数大于等于0.95,无功连续可调,节点电压幅值偏差允许范围为±7%,关口处不允许功率反送。参考文献[27],取光伏的日均投资成本为1.298元/kW,上网电价为0.313元/(kW ·h)。
3.2 计算结果及分析首先通过潮流计算得到未接入光伏时系统在典型日内的总网损,为0.533 2 MW ·h。为分析容量下限对接入容量的影响,设定弃光阈值为0,分别将容量下限设置为0和0.2 MV ·A,对模型1进行求解,得到各备选接入点的接入容量如图 4所示。

|
图 4 备选节点光伏接入容量 Fig. 4 Capacity of PV in alternative nodes |
当接入容量下限为0时,总接入容量为0.859 3 MV ·A,在节点6—节点18均有光伏接入。按接入容量的大小进行排序,前四位的节点分别为节点6、8、7、14,对应的容量分别为0.429 8、0.083 5、0.074 4、0.069 3 MV ·A。节点10接入容量最小,为0.014 6 MV ·A。系统总网损为0.409 0 MW ·h,较无光伏接入情况,下降约23.3%。当接入容量下限为0.2 MV ·A时,总接入容量为0.859 4 MV ·A,分布在节点6、8、14,接入容量分别为0.442 9、0.200 0、0.216 5 MV ·A。系统总网损为0.410 0 MW ·h。接入容量下限为0时的网损相比接入容量下限为0.2 MV ·A时的网损值降低并不明显,但接入容量下限设置为0导致接入容量分散在各个备选节点,且大部分接入点接入容量偏小。接入容量下限由0调整到0.2 MV ·A,实际接入点数目由13个减少为3个。计算结果表明:接入容量下限对接入点位置有较大影响。
为与典型的以接入容量最大为目标的评估模型进行对比,设置弃光阈值为0,接入容量下限设置为0.2 MV ·A,对模型2进行求解。计算得到接入容量为0.855 5 MV ·A,接入位置为单一的节点18。模型1和模型2在典型日1的电压幅值分别如图 5和图 6所示。

|
图 5 模型1在典型日1的电压幅值 Fig. 5 Voltage magnitude in typical day 1 calculated by model 1 |

|
图 6 模型2在典型日1的电压幅值 Fig. 6 Voltage magnitude in typical day 1 calculated by model 2 |
由图 5和图 6可以看到:在无光伏出力时刻,主干支路上,随着负荷节点远离首节点,节点电压幅值不断降低。光伏接入后,由于提供了有功功率,光伏接入节点及附近节点的电压幅值有所提高。使用模型1得到的电压幅值最大值为1.005 p.u.,使用模型2得到的电压幅值最大值为1.052 p.u.,在14 h电压幅值最高。由于模型1的实际接入点个数为3个,即节点6、8、14,而模型2的实际接入点个数为1个,所以模型1的电压幅值较为平缓。
为求最大利润时的总光伏接入容量,设置迭代过程中弃光阈值的固定增量为0.5%,初始弃光阈值为0。弃光阈值与总接入容量及风险因子的计算结果如表 1所示。
|
|
表 1 不同η下的计算结果 Table 1 Calculation results under different values of η |
由表 1可以看到:当弃光阈值由0增加到2.0%时,总接入容量由0.859 4 MV ·A增加到1.036 4 MV ·A,增长率约为20.6%。从网损来看,尽管随着弃光阈值的增加,网损不断下降,但下降幅度较小。
随着总接入容量的不断增加,风险因子不断增加。根据式(25)可得到最优风险因子为0.185 6,在0.163 1和0.242 3之间,通过插值估算得到利润最大时对应的弃光率为1.65%,接入容量为1.020 3 MV ·A。将插值估算结果回代入评估模型得到在节点6接入容量为0.592 5 MV ·A,节点8接入容量为0.200 0 MV ·A,节点14接入容量为0.227 8 MV ·A。
为分析三相不平衡对光伏接入容量的影响,设置各节点三相负荷总和保持不变,各节点负荷均不平衡,不平衡度为10%。为体现一般性,设置部分节点a相负荷偏低,部分节点b相负荷偏低,部分节点c相负荷偏低,具体比例设置如下:节点2—节点10的各相负荷的比例为0.9 ∶1.0 ∶1.1,节点11—节点18的各相负荷的比例为1.0 ∶0.9 ∶1.1,节点19—节点33的各相负荷的比例为1.1 ∶0.9 ∶1.0。设置弃光阈值为0,各相光伏接入容量下限为0.066 7 MV ·A,对各相进行独立计算,计算结果如图 7所示。

|
图 7 各相备选节点接入容量 Fig. 7 Capacity of PV in alternative nodes at three phases |
由图 7可以看到:节点6处b相接入容量最小,为0.129 1 MV ·A;节点8处三相所得结果一致,为0.066 7 MV ·A;节点14处依旧为b相接入容量最小,为0.070 7 MV ·A。依据三相独立计算结果,得到三相不平衡情况下的总接入容量为0.799 4 MV ·A。三相不平衡情况下得到的总接入容量为三相平衡假设下总接入容量的93.02%,下降了约7%。
尽管各节点三相负荷不平衡度均为10%,但由于各节点并非总是某一固定相负荷偏低,系统总的负荷不平衡度要小于10%,依据负荷数据计算得到系统的总负荷不平衡度约为5.8%,可知总容量的下降比例在总负荷不平衡度和单一节点负荷不平衡度之间。当总负荷不平衡度和单一节点负荷不平衡度均较小时,可假设三相平衡,否则通过对各相进行单独计算确定光伏接入容量。
4 结语文中引入弃光约束,建立了配电网光伏HC模型。在模型框架下,通过利润与接入容量的差分关系,确定了总接入容量,并通过回代策略实现各备选节点的接入容量确定。在改进的IEEE 33节点系统中进行验证,得到以下结论:
(1) 对评估模型进行计算,可以实现接入位置和接入容量的合理选择,有效降低系统网损。限制接入容量下限,可以在网损增加不明显的同时,减少实际接入点个数, 避免光伏的过度分散接入。
(2) 相对于无弃光的情况,接受一定程度的弃光,可获得更大的接入容量。通过合理设置弃光阈值,在考虑网损的前提下,可实现收益最大化。
(3) 三相不平衡对光伏接入容量有重要的影响。对各相进行独立计算,可实现三相不平衡情况下光伏容量的确定。
所提方法存在以下不足:所提方法依赖于有限的典型日数据,无法对整个光伏生命周期内的场景进行计算。如何在保证一定精度的前提下提高计算效率,将是下一步工作的重点。
| [1] |
彭生江, 陆军, 张中丹, 等. 光伏接入对电网的影响研究[J]. 电力系统保护与控制, 2021, 49(5): 157-164. PENG Shengjiang, LU Jun, ZHANG Zhongdan, et al. Research on the influence of photovoltaic access on a power grid[J]. Power System Protection and Control, 2021, 49(5): 157-164. (  0) 0) |
| [2] |
卓振宇, 张宁, 谢小荣, 等. 高比例可再生能源电力系统关键技术及发展挑战[J]. 电力系统自动化, 2021, 45(9): 171-191. ZHUO Zhenyu, ZHANG Ning, XIE Xiaorong, et al. Key technologies and developing challenges of power system with high proportion of renewable energy[J]. Automation of Electric Power Systems, 2021, 45(9): 171-191. (  0) 0) |
| [3] |
宋建平, 王颖, 许寅. 光伏接入配电网的优化策略研究及影响分析[J]. 供用电, 2022, 39(5): 25-32. SONG Jianping, WANG Ying, XU Yin. Research on optimization strategy and impact analysis of photovoltaic generation integrated to distribution network[J]. Distribution & Utilization, 2022, 39(5): 25-32. (  0) 0) |
| [4] |
贺国伟, 肖峻, 曹加胜. 考虑分布式光伏消纳的大型城市配电网规划实践[J]. 供用电, 2021, 38(10): 26-34. HE Guowei, XIAO Jun, CAO Jiasheng. Planning practice of large urban distribution network considering distributed photovoltaic consumption[J]. Distribution & Utilization, 2021, 38(10): 26-34. (  0) 0) |
| [5] |
ISMAEL S M, ABDEL ALEEM S H E, ABDELAZIZ A Y, et al. State-of-the-art of hosting capacity in modern power systems with distributed generation[J]. Renewable Energy, 2019, 130: 1002-1020. DOI:10.1016/j.renene.2018.07.008 (  0) 0) |
| [6] |
BOLLEN M H J. Integration of distributed generation in the power system[M]. Hoboken, NJ: Wiley, 2011.
(  0) 0) |
| [7] |
ABIDEEN M Z U, ELLABBAN O, AL-FAGIH L. A review of the tools and methods for distribution networks' hosting capacity calculation[J]. Energies, 2020, 13(11): 2758. DOI:10.3390/en13112758 (  0) 0) |
| [8] |
董逸超, 王守相, 闫秉科. 配电网分布式电源接纳能力评估方法与提升技术研究综述[J]. 电网技术, 2019, 43(7): 2258-2266. DONG Yichao, WANG Shouxiang, YAN Bingke. Review on evaluation methods and improvement techniques of DG hosting capacity in distribution network[J]. Power System Technology, 2019, 43(7): 2258-2266. (  0) 0) |
| [9] |
XU X, LI J Y, XU Z, et al. Enhancing photovoltaic hosting capacity-A stochastic approach to optimal planning of static var compensator devices in distribution networks[J]. Applied Energy, 2019, 238: 952-962. (  0) 0) |
| [10] |
陈睿彬, 陆玲霞, 包哲静, 等. 电池储能系统参与用户侧削峰填谷的鲁棒优化调度策略[J]. 电力建设, 2022, 43(10): 66-76. CHEN Ruibin, LU Lingxia, BAO Zhejing, et al. Robust optimal dispatch strategy for battery energy storage system participating in user-side peak load shifting[J]. Electric Power Construction, 2022, 43(10): 66-76. (  0) 0) |
| [11] |
张诗杭. 高渗透率光伏并网消纳能力研究[D]. 北京: 华北电力大学, 2021. ZHANG Shihang. Research on the ability of high permeability photovoltaic grid connection[D]. Beijing: North China Electric Power University, 2021. (  0) 0) |
| [12] |
ALTURKI M, KHODAEI A, PAASO A, et al. Optimization-based distribution grid hosting capacity calculations[J]. Applied Energy, 2018, 219: 350-360. (  0) 0) |
| [13] |
YUAN J Y, WENG Y, TAN C W. Determining maximum hosting capacity for PV systems in distribution grids[J]. International Journal of Electrical Power & Energy Systems, 2022, 135: 107342. (  0) 0) |
| [14] |
丁明, 方慧, 毕锐, 等. 基于集群划分的配电网分布式光伏与储能选址定容规划[J]. 中国电机工程学报, 2019, 39(8): 2187-2201, 2. DING Ming, FANG Hui, BI Rui, et al. Optimal siting and sizing of distributed PV-storage in distribution network based on cluster partition[J]. Proceedings of the CSEE, 2019, 39(8): 2187-2201, 2. (  0) 0) |
| [15] |
朱豪. 基于双层规划理论的主动配电网分布式电源优化配置[D]. 西安: 西安石油大学, 2021. ZHU Hao. Optimal configuration of distributed generation in active distribution network based on bi-level programming theory[D]. Xi'an: Xi'an Shiyou University, 2021. (  0) 0) |
| [16] |
LAKSHMI S, GANGULY S. Simultaneous optimisation of photovoltaic hosting capacity and energy loss of radial distribution networks with open unified power quality conditioner allocation[J]. IET Renewable Power Generation, 2018, 12(12): 1382-1389. (  0) 0) |
| [17] |
许鸣吉, 沈磊, 李胜, 等. 计及综合因素的光伏接入配电网优选研究[J]. 电力工程技术, 2021, 40(2): 46-52. XU Mingji, SHEN Lei, LI Sheng, et al. Optimization of photovoltaic access distribution network considering comperhensive factors[J]. Electric Power Engineering Technology, 2021, 40(2): 46-52. (  0) 0) |
| [18] |
刘科研, 盛万兴, 马晓晨, 等. 基于多种群遗传算法的分布式光伏接入配电网规划研究[J]. 太阳能学报, 2021, 42(6): 146-155. LIU Keyan, SHENG Wanxing, MA Xiaochen, et al. Planning research of distributed photovoltaic source access distribution network based on multi-population genetic algorithm[J]. Acta Energiae Solaris Sinica, 2021, 42(6): 146-155. (  0) 0) |
| [19] |
CHEN Y J, CHEN X M, WU Z L, et al. Coordinated optimization of distribution system reconfiguration and reactive power based on mixed integer convex programming[C]//2018 International Conference on Power System Technology (POWERCON). Guangzhou, China. IEEE, 2019: 2015-2020.
(  0) 0) |
| [20] |
FARIVAR M, LOW S H. Branch flow model: relaxations and convexification—part Ⅰ[J]. IEEE Transactions on Power Systems, 2013, 28(3): 2554-2564. (  0) 0) |
| [21] |
国家质量监督检验检疫总局, 中国国家标准化管理委员会. 电能质量供电电压偏差: GB/T 12325—2008[S]. 北京: 中国标准出版社, 2009. General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China, Standardization Administration of the People's Republic of China. Power quality-deviation of supply voltage: GB/T 12325-2008[S]. Beijing: Standards Press of China, 2009. (  0) 0) |
| [22] |
薛振宇, 益西措姆, 李敬如, 等. 扶贫光伏发电典型接入方式及经济效益评估[J]. 供用电, 2019, 36(4): 79-85. XUE Zhenyu, Yixicuomu, LI Jingru, et al. The typical access mode and economic benefit evaluation of photovoltaic generation for poverty alleviation[J]. Distribution & Utilization, 2019, 36(4): 79-85. (  0) 0) |
| [23] |
王强, 顾乔根, 孙仲民, 等. 计及出力波动的光伏电站无功支撑能力评估[J]. 电力工程技术, 2020, 39(2): 29-34. WANG Qiang, GU Qiaogen, SUN Zhongmin, et al. The evaluation of reactive power support capacity of photovoltaic power station considering output fluctuation[J]. Electric Power Engineering Technology, 2020, 39(2): 29-34. (  0) 0) |
| [24] |
徐晴. 配电网中分布式电源最大准入容量研究[D]. 南京: 东南大学, 2019. XU Qing. Distributed generation hosting capacity assessment method for distribution systems[D]. Nanjing: Southeast University, 2019. (  0) 0) |
| [25] |
邱革非, 杨昊天, 何超, 等. 基于二阶锥松弛的三相不平衡配电网最优潮流研究[J]. 电机与控制应用, 2022, 49(12): 34-40, 59. QIU Gefei, YANG Haotian, HE Chao, et al. Research on opti mal power flow in three-phase unbalanced distribution network based on second-order cone relaxation[J]. Electric Machines & Control Application, 2022, 49(12): 34-40, 59. (  0) 0) |
| [26] |
王守相, 王成山. 现代配电系统分析[M]. 2版. 北京: 高等教育出版社, 2014. WANG Shouxiang, WANG Chengshan. Analysis of modern distribution system[M]. 2nd ed. Beijing: Higher Education Press, 2014. (  0) 0) |
| [27] |
张运洲, 陈宁, 黄碧斌, 等. 基于系统成本的新能源等效上网电价计算方法及应用[J]. 中国电力, 2022, 55(2): 1-8. ZHANG Yunzhou, CHEN Ning, HUANG Bibin, et al. Methodology for calculating VRE equivalent feed-in tariff based on system cost and its application[J]. Electric Power, 2022, 55(2): 1-8. (  0) 0) |
2. School of Artificial Intelligence, Hebei University of Technology, Tianjin 300130, China;
3. Experimental Training Center, Hebei University of Technology, Tianjin 300401, China
 2023, Vol. 42
2023, Vol. 42


 张家安(1975),男,博士,讲师,研究方向为新能源发电系统及智能化控制技术(E-mail:
张家安(1975),男,博士,讲师,研究方向为新能源发电系统及智能化控制技术(E-mail: