文章编号: 2096-3203(2023)06-0161-09 中图分类号: TM64
随着风电渗透率的提高,电力系统的频率稳定面临着严峻挑战[1]。双馈风机作为目前的主流风力发电机,通过电力电子设备接入电力系统,其转子转速与电网频率解耦,不具备传统同步发电机的频率主动支撑能力,系统调频能力显著下降,频率特性恶化[2-3]。因此,双馈风机参与系统调频是当前迫切的需求。
根据调频能量来源,风机的频率控制策略主要分为转子动能控制、功率备用控制和附加储能系统控制[4]。转子动能控制在最大功率点跟踪(maximum power point tracking, MPPT)控制模式下,引入频率相关控制回路,利用转子快速吞吐动能的能力改变风机出力,参与系统调频[5-6]。而功率备用控制通过超速控制或桨距角控制使风机减载运行,储备一定的功率用以调频,相比于转子动能控制,其风能利用效率降低,且桨距角的频繁动作会造成机械磨损,减少机组寿命[7-9]。附加储能系统控制则是通过储能系统吸收和释放能量,辅助风电调频,然而额外的储能设备会增加运行成本,不利于风电场的经济运行[10]。因此,风机的转子动能控制是当前的研究热点。
转子动能控制策略包括下垂控制[11-13]和虚拟惯量控制[14-16]。下垂控制以频率偏差为输入信号,输出与频率偏差呈比例关系的功率增量,在频率最低点附近进行较强支撑。虚拟惯量控制输出正比于频率变化率(rate of change of frequency, ROCOF)的有功增量,以抑制频率的快速跌落。由于虚拟惯量控制对频率的支撑能力随ROCOF减小而减小,甚至在频率反弹后阻碍频率恢复[17],因此有研究将下垂控制和虚拟惯量控制结合使用,进一步提高风机调频能力,该方式被称为综合惯性控制[18-20]。然而,已有研究大多将频率控制系数视为常数,难以适应风速变化。频率控制系数过大会导致风机转速过低,触发转速保护,使风机强制退出调频,引发频率二次跌落;而系数过小则会限制风机的调频能力。对此,文献[21]采用试错法获取不同风速下的频率控制系数,但缺乏理论支撑,可靠性有待商榷。文献[22-23]提出变系数频率控制策略,根据转子转速调整风机下垂系数,但对不同扰动场景下风机调频能力的挖掘仍有不足。文献[24]计及风速与最大功率缺额,通过离线整定和在线匹配的方法确定风机的下垂系数,但并未考虑到频率调整时不同阶段对调频系数的差异化需求。文献[25]将下垂系数设置为与转速和频率偏差耦合的函数,提高了风机改善频率最低点的能力,但扰动初期频率偏差较小,不能及时响应,对频率跌落速度的改善有限。文献[26]提出非线性频率控制策略,以减小系统频率偏差为目标,建立风电参与调频的仿射非线性系统模型并求解非线性最优控制率,进一步提高其调频能力。综上所述,目前研究较少兼顾频率响应特性和风机自身运行状态,且不同扰动场景下的风机调频能力尚未被充分挖掘。
基于此,文中提出一种改进的风机自适应下垂控制策略,结合ROCOF和转子动能构建自适应下垂控制。首先,考虑负荷扰动对系统频率调节的影响,根据系统频率恶化程度划分ROCOF区间,通过Butterworth函数建立下垂系数与ROCOF的耦合关系,提升风机对频率的响应速度,充分挖掘风机对电网频率的支撑能力。其次,在下垂系数中引入转速影响因子,限制风机过度响应,确保风机转速稳定,避免机组转速保护动作引起频率二次跌落。最后,在MTALAB/Simulink搭建了系统仿真模型,通过仿真对比验证了所提策略的有效性和优越性。
1 风机辅助调频原理 1.1 风机运行特性风机将捕获的风能转化为旋转元件的机械能,从而驱动发电机发电。忽略机械摩擦损耗,输入的机械功率Pm可表达为:
| $P_{\mathrm{m}}=\frac{1}{2} \rho \pi R^2 v^3 C_{\mathrm{p}}(\lambda, \beta)$ | (1) |
式中:ρ为空气密度;R为风机叶桨半径;v为风速;Cp(λ, β)为风能捕获系数,由叶尖速比λ和桨距角β决定,其计算如式(2)所示。
| $\left\{\begin{array}{l}C_{\mathrm{p}}(\lambda, \beta)=0.5176\left(\frac{116}{\lambda_{\mathrm{i}}}-0.4 \beta-5\right) \mathrm{e}^{-\frac{21}{\lambda_{\mathrm{i}}}}+0.0068 \lambda \\ \lambda=\omega_{\mathrm{r}} R / v\end{array}\right.$ | (2) |
| $\frac{1}{\lambda_{\mathrm{i}}}=\frac{1}{\lambda+0.08 \beta}-\frac{0.035}{\beta^3+1}$ | (3) |
式中:ωr为风机的转子转速。
为捕获最大风能,风机在正常工况下处于MPPT运行模式,运行曲线如图 1所示。其中,ωmin为切入转速,即风机的转速最小限值;ωbase为MPPT区的风机转速最大限值;ωmax为风机的最大转速;Pmax为风机的最大输出功率。当风机运行在启动区、恒转速区和恒功率区时,处于保护状态,不参与调频[27]。因此,文中主要讨论风机运行在MPPT区时的情况,其有功参考值PMPPT为:
| $P_{\mathrm{MPPT}}=K_{\mathrm{opt}} \omega_{\mathrm{r}}^3 \quad \omega_{\min } \leqslant \omega_{\mathrm{r}}<\omega_{\text {base }}$ | (4) |

|
图 1 风机运行曲线 Fig. 1 Operating curve of wind turbine |
其中:
| $K_{\mathrm{opt}}=\frac{1}{2} \rho \pi \frac{R^5}{\lambda_{\mathrm{opt}}^3} C_{\mathrm{p}}\left(\lambda_{\mathrm{opt}}, 0\right)$ | (5) |
式中:Kopt为MPPT系数,此处取0.422 5[27];λopt为最佳叶尖速比。
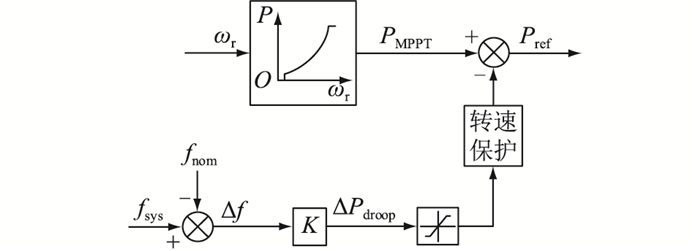
1.2 下垂控制风机的下垂控制原理如图 2所示,在常规MPPT控制的基础上,引入一个与系统频率偏差成正比的有功出力增量,模拟传统同步发电机的一次调频。当系统频率跌落时,风机通过下垂控制释放转子动能,参与系统调频。在传统下垂控制中,下垂系数通常设置为固定值,其有功参考值Pref为:
| $P_{\text {ref }}=P_{\mathrm{MPPT}}-\Delta P_{\text {droop }}$ | (6) |
| $\Delta P_{\text {droop }}=K \Delta f$ | (7) |
| $\Delta f=f_{\mathrm{sys}}-f_{\mathrm{nom}}$ | (8) |
|
图 2 风机传统下垂控制 Fig. 2 Conventional droop control of wind turbine |
式中:ΔPdroop为下垂控制回路的有功出力增量;K为下垂系数;Δf为频率偏差量;fsys为系统实际频率;fnom为系统标称频率。
由于固定的下垂系数,传统下垂控制在频率最低点才能提供较大频率支撑,无法及时响应频率的初期变化[28]。且为确保转子动能较小时风机的安全性,固定系数通常设置较为保守,无法充分挖掘风机调频能力。因此,文中综合考虑ROCOF和转子动能,提出改进的自适应下垂控制,充分利用转子动能参与调频,同时确保风机转速稳定。
2 改进的自适应下垂控制 2.1 基于ROCOF的频率响应区间划分根据文献[29],系统频率响应模型为:
| $\Delta f=\frac{R_{\mathrm{eq}} \omega_{\mathrm{n}}^2}{D_{\mathrm{eq}} R_{\mathrm{eq}}+K_{\mathrm{m}}} \times \frac{\left(1+T_{\mathrm{RT}} s\right) \Delta P_{\mathrm{d}}}{s^2+2 \zeta \omega_{\mathrm{n}} s+\omega_{\mathrm{n}}^2}$ | (9) |
式中:Req为系统的等值调差系数;ωn为振荡角频率;Deq为系统等效阻尼系数;Km为机械功率增益;TRT为机组再热时间常数;ΔPd为系统扰动功率;ζ为阻尼比。
对式(9)进行拉普拉斯反变换,可得系统频率偏差的时域表达式为:
| $\Delta f(t)=\frac{R_{\text {eq }} \Delta P_{\mathrm{d}}}{D_{\text {eq }} R_{\text {eq }}+1}\left(1+\alpha \mathrm{e}^{-\zeta \omega_{\mathrm{n}} t} \sin \left(\omega_{\mathrm{d}} t+\varphi\right)\right)$ | (10) |
式中:α、φ为公式推导过程中产生的系数;ωd为阻尼角频率。
根据式(10)可知,系统扰动发生后的准稳态频率偏差Δfst表达式为:
| $\Delta f_{\mathrm{st}}=\lim\limits_{t \rightarrow \infty} \Delta f(t)=\frac{R_{\mathrm{eq}} \Delta P_{\mathrm{d}}}{D_{\mathrm{eq}} R_{\mathrm{eq}}+1}$ | (11) |
因此ROCOF可以描述为[29]:
| $\frac{\mathrm{d} \Delta f(t)}{\mathrm{d} t}=-\frac{R_{\mathrm{eq}} \Delta P_{\mathrm{d}}}{D_{\text {eq }} R_{\text {eq }}+1} \alpha \omega_{\mathrm{n}} \mathrm{e}^{-\zeta \omega_{\mathrm{n}} t} \sin \left(\omega_{\mathrm{d}} t+\varphi_1\right)$ | (12) |
式中:φ1为公式推导过程中产生的系数。
由式(10)—式(12)分析可知,当系统发生扰动时,电网频率偏差及ROCOF与ΔPd呈正比,即ΔPd越大,ROCOF和频率偏差越大,准稳态频率偏差Δfst也越大。因此,根据Δfst的大小可以判断系统扰动程度。
由于DeqReq数量级较小,假设稳态时系统的功率不平衡量全部由同步机承担,根据式(11)可得其同步机的有功出力增量ΔPG[19]为:
| $\Delta P_{\mathrm{G}}=-\frac{\Delta f_{\mathrm{st}}}{R_{\mathrm{eq}}}$ | (13) |
设置系统准稳态频率偏差Δfst的阈值为Fst。在系统频率偏差为Fst时,对应的同步机最大有功出力ΔPG,max即为系统的临界功率不平衡量:
| $\Delta P_{\mathrm{unb}, \max }=\Delta P_{\mathrm{G}, \max }=-F_{\mathrm{st}} / R_{\mathrm{eq}}$ | (14) |
其中,Fst通常取为电力系统正常条件下的频率偏差限值0.2~0.5 Hz[30]。
系统扰动程度可以由准稳态频率偏差Δfst反映,然而Δfst为滞后标准,因此利用其与ROCOF的对应关系,将ROCOF划分区间。由系统等效转子运动方程可知,当系统功率不平衡量为ΔPunb时,初始ROCOF为:
| $\left.\frac{\mathrm{d} f}{\mathrm{~d} t}\right|_{t=t_0}=-\frac{\Delta P_{\mathrm{unb}}}{2 H_{\mathrm{eq}}}$ | (15) |
式中:Heq为系统的等值惯性常数;t0为初始时间。
将式(14)代入式(15),得到ΔPunb, max对应的初始频率变化f′st:
| $f_{\mathrm{st}}^{\prime}=-\frac{\Delta P_{\mathrm{unb}, \max }}{2 H_{\mathrm{eq}}}=-\frac{F_{\mathrm{st}}}{2 H_{\mathrm{eq}} R_{\mathrm{eq}}}$ | (16) |
根据系统扰动程度,可将ROCOF划分为3个区间,如图 3和表 1所示。图 3给出了系统功率缺额下的典型频率响应曲线。其中,Δfnadir为系统最大频率偏差;A点为故障前的系统频率稳态运行点;B点为故障后系统频率最低点;C点为故障后的系统频率准稳态运行点。

|
图 3 基于ROCOF区间划分的典型频率响应曲线 Fig. 3 Typical frequency response curve based on ROCOF interval division |
|
|
表 1 ROCOF区间划分 Table 1 Interval division of ROCOF |
根据上述分析,系统发生扰动后的频率动态可以分为区间1、区间2和区间3。针对不同的频率动态区间,采用不同的下垂系数策略。
(1) 区间1:采用较大的下垂系数,充分利用转子动能在短时间内为系统提供功率支撑,阻止频率快速跌落。
(2) 区间2:下垂系数随ROCOF减小而减小,在提高频率最低点的同时防止风机过度释放转子动能。
(3) 区间3:频率开始恢复,此时将下垂系数设置较小,保留转子动能以应对后续突发状况。
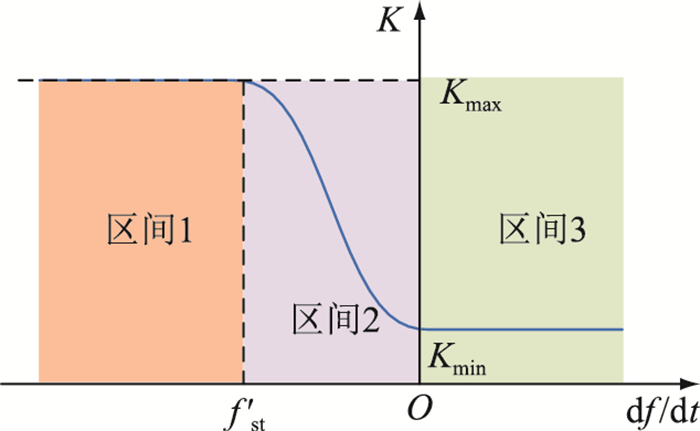
为避免风机有功出力突变给系统频率带来的二次冲击,同时减少风机内部零件的疲劳磨损,文中采用Butterworth函数来满足下垂系数的平滑变化。Butterworth型下垂系数曲线如图 4所示,所建立的下垂系数与ROCOF的耦合关系为:
| $K=\left\{\begin{array}{l}K_{\max } \mathrm{d} f / \mathrm{d} t<f_{\mathrm{st}}^{\prime} \\ \left(K_{\max }-K_{\min }\right) /\left[1+\left(\frac{f_{\mathrm{st}}^{\prime}}{\mathrm{d} f / \mathrm{d} t}-1\right)^2\right]+K_{\min } \\ \qquad \qquad \qquad \quad f_{\mathrm{st}}^{\prime} \leqslant \mathrm{d} f / \mathrm{d} t<0 \\ K_{\min } \mathrm{d} f / \mathrm{d} t \geqslant 0\end{array}\right.$ | (17) |
|
图 4 Butterworth型下垂系数曲线 Fig. 4 Butterworth-type droop coefficient curve |
式中:Kmax、Kmin分别为下垂系数K的上限值与下限值,均为常数。
2.3 转速影响因子为避免触发风机转速保护动作带来的频率二次跌落问题,在所提自适应下垂控制中引入转速影响因子,限制低转速风机的有功出力。
当风机转速为ωr时,转子中可释放的动能为:
| $\Delta E=\frac{1}{2} J\left(\omega_{\mathrm{r}}^2-\omega_{\min }^2\right)$ | (18) |
式中:J为风机的等效转动惯量。
定义转速影响因子η为:
| $\eta=\sqrt{\frac{\omega_{\mathrm{r}}^2-\omega_{\min }^2}{\omega_{\text {base }}^2-\omega_{\min }^2}}$ | (19) |
其中,η∈[0, 1],η随转速ωr减小而减小。通过调整风机有功出力,防止转子失速。
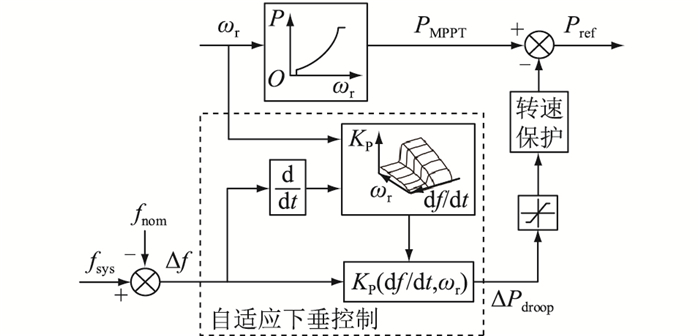
2.4 计及ROCOF与转子动能的下垂控制策略所提自适应下垂控制策略原理如图 5所示,在频率测量环节中采用了低通滤波器,以消除测量信号中的高频噪声。在稳态条件下,风机运行在MPPT模式;而当系统发生频率偏移时,则根据ROCOF和转子转速调整下垂系数,一旦频率偏差越过设定的死区,下垂控制根据频率偏差Δf和自适应下垂系数KP(df/dt, ωr)给出调频功率增量,释放转子动能来支撑系统频率。
|
图 5 计及ROCOF与转子动能的自适应下垂控制策略 Fig. 5 Adaptive droop control strategy based on ROCOF and rotor kinetic energy |
下垂控制回路的有功出力增量ΔPdroop的表达式为:
| $\Delta P_{\text {droop }}=K_{\mathrm{P}}\left(\mathrm{d} f / \mathrm{d} t, \omega_{\mathrm{r}}\right) \Delta f$ | (20) |
结合式(17)和式(19),KP可表述为:
| $K_{\mathrm{P}}=\left\{\begin{array}{l}\eta K_{\max } \mathrm{d} f / \mathrm{d} t<f_{\mathrm{st}}^{\prime} \\ \eta\left(K_{\max }-K_{\min }\right) /\left[1+\left(\frac{f_{\mathrm{st}}^{\prime}}{\mathrm{d} f / \mathrm{d} t}-1\right)^2\right]+ \\ \qquad \;\; \qquad \eta K_{\min } \quad f_{\mathrm{st}}^{\prime} \leqslant \mathrm{d} f / \mathrm{d} t<0 \\ \eta K_{\min } \mathrm{d} f / \mathrm{d} t \geqslant 0\end{array}\right.$ | (21) |
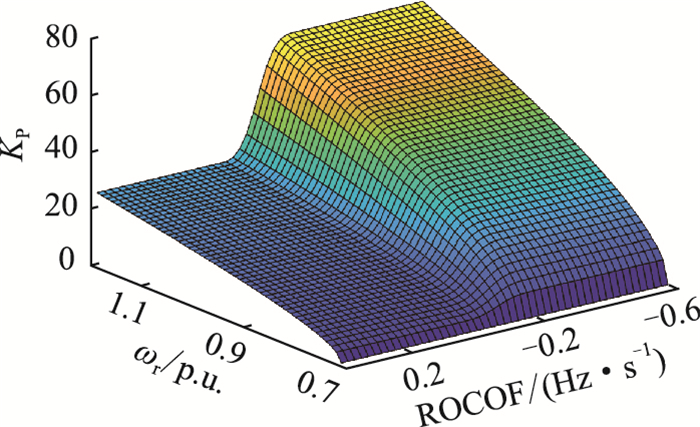
扰动发生后,下垂系数KP根据系统频率的动态响应与风机的转子运行状态灵活调整,其特性如图 6所示。区间1的频率偏差较小,而ROCOF绝对值较大,此时KP取较大值,使得风机迅速响应频率变化,释放转子动能来支撑系统频率。随着频率偏差逐渐增大,且ROCOF绝对值减小,频率进入区间2。此时,风机释放转子动能参与调频,转速逐渐减小,KP随ROCOF与转速减小而减小,使得风机持续参与调频,同时避免风机过度释放转子动能,导致频率二次跌落。当系统频率越过最低点后进入区间3时,ROCOF变为正数,此时KP仅随转速减小而减小,保留转子动能,以应对后续扰动。
|
图 6 下垂系数与转子转速和ROCOF的相关性 Fig. 6 Correlation of droop coefficient with rotor speed and ROCOF |
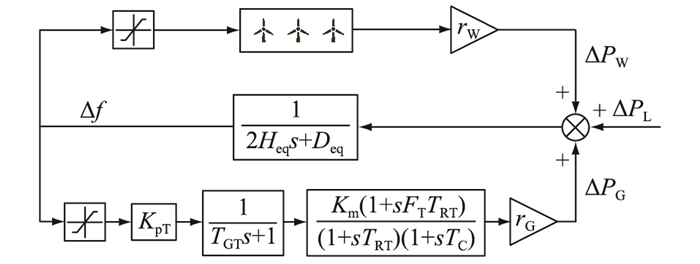
为验证文中所提自适应下垂控制策略的有效性,在MTALAB/Simulink软件中搭建了如图 7所示的仿真系统模型,其中ΔPL、ΔPW分别为负荷和风电机组的有功变化量。系统包含一个140 MW的火电厂和一个60 MW的风电场,其中风电场由40台1.5 MW的双馈风机组成,系统基本参数见表 2。
|
图 7 风火调频系统模型 Fig. 7 Wind-thermal frequency regulation system model |
|
|
表 2 仿真系统基本参数 Table 2 Parameters of simulation system |
同时,为验证所提策略的有效性,考虑4种不同策略。(1) 策略1:MPPT控制,风机不参与调频。(2) 策略2:固定系数的综合惯性控制[18]。(3) 策略3:变系数下垂控制,下垂系数仅由转子转速确定[31]。(4) 策略4:文中提出的计及ROCOF与转子动能的自适应下垂控制策略。
3.2 调频效果仿真分析 3.2.1 不同负荷扰动下的调频效果对比为分析负荷扰动对风机调频效果的影响,分别选取负荷突增5%和10%的情况进行仿真,风速均设定为8.5 m/s。
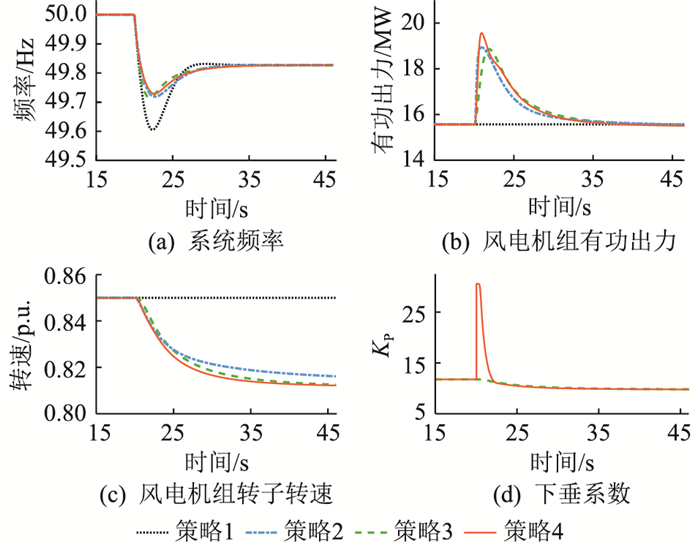
场景1:8.5 m/s的恒风速下,系统负荷在20 s时突增5%,仿真结果如图 8和表 3所示。
|
图 8 场景1的仿真结果 Fig. 8 Simulation results for case 1 |
|
|
表 3 场景1中不同策略的调频效果对比 Table 3 Comparison of frequency regulation effect of different strategies for case 1 |
由图 8(a)和表 3可知,策略4在改善频率最低点、减缓频率下降速度方面效果最佳。由图 8(b)可知,策略2和策略4可以快速响应系统频率变化,增加有功出力,减缓频率跌落速度;而策略3响应较慢,对频率跌落的改善较小。结合图 8(c)中策略3和策略4的转速收敛到同样大小可知,在释放相同转子动能的情况下,策略4的调节效果更好。这是因为在频率跌落后,策略4的下垂系数与ROCOF耦合,扰动发生后其下垂系数立刻增大,随后在ROCOF和转子转速的共同影响下收敛到较小值,防止转子失速;而策略3的下垂系数只随转子动能的释放逐渐减小,如图 8(d)所示。
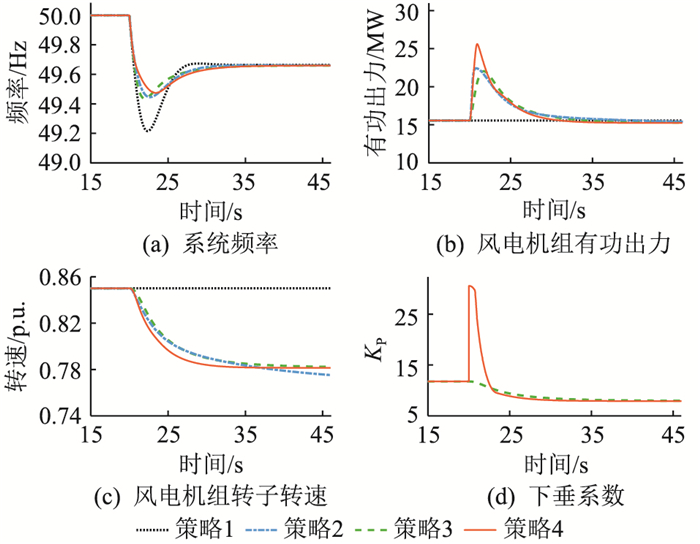
场景2:8.5 m/s的恒风速下,系统负荷在20 s时突增10%,仿真结果如图 9和表 4所示。
|
图 9 场景2的仿真结果 Fig. 9 Simulation results for case 2 |
|
|
表 4 场景2中不同策略的调频效果对比 Table 4 Comparison of frequency regulation effect of different strategies for case 2 |
由图 9(a)和表 4可知,在大负荷扰动的影响下系统频率进一步恶化。与其他策略相比,策略4的频率最低点最高,频率跌落速度最慢。由图 9(b)可知,扰动发生后,策略2与策略4迅速增大了风机有功出力,但策略4短时内增发功率更大,所以其对频率跌落的抑制效果更佳。结合图 9(c)可知,策略4的转速收敛值比策略2更大,因此策略4能以更少的转子动能达到更佳的调频效果。这是因为策略4的下垂系数会随转速的减小收敛到一个较小值,防止风机过度释放转子动能,如图 9(d)所示。
对比场景1和场景2的仿真结果可以看出,在负荷突增5%和10%的情况下,相比于风机不参与调频的策略1,策略4分别将频率最低点提升了0.12 Hz和0.25 Hz,频率最低点的到达时间分别延后了0.3 s和1.0 s。显然,策略4在不同负荷扰动下均能有效改善系统频率响应特性,且随着负荷扰动量的增大,其改善效果更为明显。
3.2.2 不同风速下的调频效果对比风机的调频能力取决于其转子存储的动能,考虑到不同风速会影响风机的转子动能,下面将风速设置为11 m/s,进一步验证所提策略的有效性。
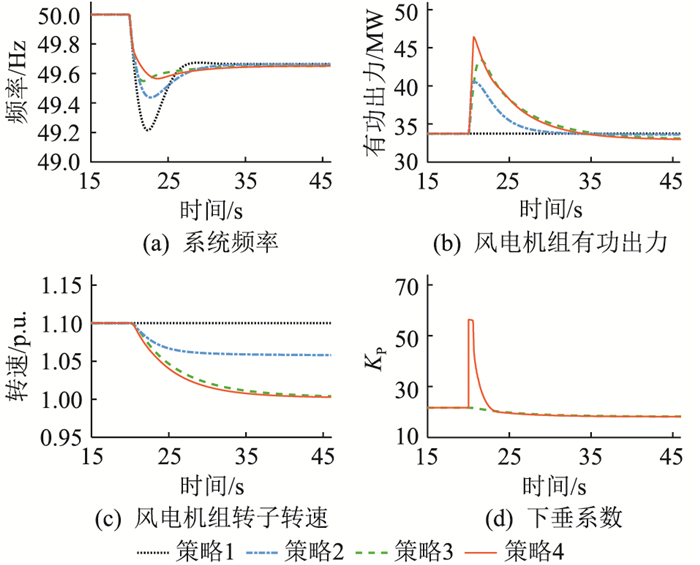
场景3:11 m/s的恒风速下,系统负荷在20 s时突增10%,仿真结果如图 10和表 5所示。
|
图 10 场景3的仿真结果 Fig. 10 Simulation results for case 3 |
|
|
表 5 场景3中不同策略的调频效果对比 Table 5 Comparison of frequency regulation effect of different strategies for case 3 |
由图 10(a)和表 5可知,高风速下策略3和策略4对频率最低点的改善效果更明显,而策略1和策略2的系统频率响应特性并没有变化。这是因为策略2的固定系数不受转速影响,为保证风机在低转速下能够稳定运行,通常不能设定太高,所以在高转速区间无法充分利用转子动能参与调频;而策略3与策略4的下垂系数与转速耦合,在高风速下能有效提高转子动能的利用率。然而,策略3的响应速度并没有得到提升,且策略4的频率最低点到达时间延后了1.2 s,比场景2的跌落速度更慢。由图 10(b)和(c)可知,策略4在频率跌落初期迅速释放转子动能,增大有功出力。与策略3相比,策略4有效阻止了系统频率的过快跌落。
综合场景2和场景3的仿真结果可知,在8.5 m/s和11 m/s的风速下,策略4将频率最低点分别提升至49.47 Hz和49.57 Hz,频率最低点的到达时间分别延后了1.0 s和1.2 s。显然,对比其他策略,策略4在不同风速下的调节性能均为最佳,且随着风速的增大,其调节效果有所提升。
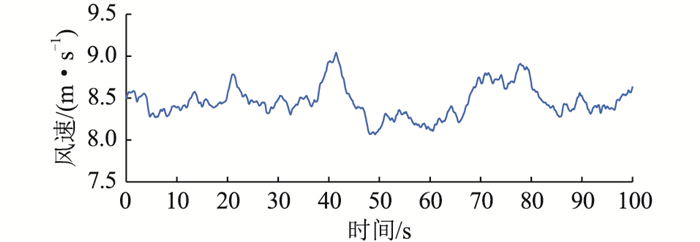
3.2.3 连续扰动下的调频效果分析为验证所提策略在实际运行中的有效性,利用白噪声序列模拟随机风速[32],如图 11所示。
|
图 11 随机风速 Fig. 11 Random wind speed |
设置系统负荷在20 s时突增10%,在40 s时再增5%。仿真结果见图 12和表 6。结合图 12(a)和表 6可知,相比于策略2和策略3,策略4在负荷一次扰动后对频率最低点和频率跌落速度的改善效果更大。在负荷二次扰动后,策略2对系统频率最低点的改善作用最为明显,但在55.5 s时出现了明显的二次跌落,最低点跌落至49.29 Hz,甚至低于策略1。由图 12(b)、(c)可以看出,在遭遇扰动后,策略2快速响应频率变化,但转速下降过快,在55.2 s时触发转速保护,风机退出调频。策略3虽然将转速维持在允许范围内,但其响应速度较慢,对频率跌落速度的改善效果不佳。而策略4的短时增发功率最大,并能及时降低有功出力,使转速收敛在允许范围内。因此,策略4具有更好的调节效果。

|
图 12 随机风速下连续扰动的仿真结果 Fig. 12 Simulation results with continuous disturbance under random wind speed |
|
|
表 6 连续扰动下不同策略的调频效果对比 Table 6 Comparison of frequency regulation effect of different strategies under continuous disturbance |
文中考虑风机自身运行状态和系统频率响应特性,提出了一种改进的双馈风机自适应下垂控制策略。该策略根据ROCOF和转子转速动态调整风机下垂系数参与一次调频,提高了下垂控制响应速度和系统频率最低点,充分发挥了转子动能对系统频率的支撑作用,同时能防止风机转子失速,避免系统频率二次跌落。仿真结果表明,在不同扰动场景下,所提策略的调频性能要优于传统策略,能有效利用转子动能改善频率响应特性,提高系统的频率稳定性。
由于实际电网各节点的频率变化不一致,具有时空分布特性,后续将考虑频率时空分布下的风机控制问题。
| [1] |
刘翔宇, 李晓明, 朱介北, 等. 新型电力系统的频率响应模型综述及展望[J]. 南方电网技术, 2022, 16(10): 38-47. LIU Xiangyu, LI Xiaoming, ZHU Jiebei, et al. Review and prospect on frequency response models of new power system[J]. Southern Power System Technology, 2022, 16(10): 38-47. (  0) 0) |
| [2] |
汪梦军, 郭剑波, 马士聪, 等. 新能源电力系统暂态频率稳定分析与调频控制方法综述[J]. 中国电机工程学报, 2023, 43(5): 1672-1694. WANG Mengjun, GUO Jianbo, MA Shicong, et al. Review of transient frequency stability analysis and frequency regulation control methods for renewable power systems[J]. Proceedings of the CSEE, 2023, 43(5): 1672-1694. (  0) 0) |
| [3] |
刘洪波, 彭晓宇, 张崇, 等. 风电参与电力系统调频控制策略综述[J]. 电力自动化设备, 2021, 41(11): 81-92. LIU Hongbo, PENG Xiaoyu, ZHANG Chong, et al. Overview of wind power participating in frequency regulation control strategy for power system[J]. Electric PowerAutomation Equipment, 2021, 41(11): 81-92. (  0) 0) |
| [4] |
张旭, 陈云龙, 岳帅, 等. 风电参与电力系统调频技术研究的回顾与展望[J]. 电网技术, 2018, 42(6): 1793-1803. ZHANG Xu, CHEN Yunlong, YUE Shuai, et al. Retrospect and prospect of research on frequency regulation technology of power system by wind power[J]. Power System Technology, 2018, 42(6): 1793-1803. (  0) 0) |
| [5] |
孙铭, 徐飞, 陈磊, 等. 利用转子动能的风机辅助频率控制最优策略[J]. 中国电机工程学报, 2021, 41(2): 506-514. SUN Ming, XU Fei, CHEN Lei, et al. Optimal auxiliary frequency control strategy of wind turbine generator utilizing rotor kinetic energy[J]. Proceedings of the CSEE, 2021, 41(2): 506-514. (  0) 0) |
| [6] |
李少林, 王伟胜, 张兴, 等. 风力发电对系统频率影响及虚拟惯量综合控制[J]. 电力系统自动化, 2019, 43(15): 64-70. LI Shaolin, WANG Weisheng, ZHANG Xing, et al. Impact of wind power on power system frequency and combined virtual inertia control[J]. Automation of Electric Power Systems, 2019, 43(15): 64-70. (  0) 0) |
| [7] |
何廷一, 孙领, 李胜男, 等. 考虑风速差异的风电场减载方案与一次调频策略[J]. 电力建设, 2022, 43(7): 139-148. HE Tingyi, SUN Ling, LI Shengnan, et al. Research on deloading scheme and primary frequency regulation strategy of wind farm considering wind speed difference[J]. Electric Power Construction, 2022, 43(7): 139-148. (  0) 0) |
| [8] |
穆钢, 蔡婷婷, 严干贵, 等. 双馈风电机组参与持续调频的双向功率约束及其影响[J]. 电工技术学报, 2019, 34(8): 1750-1759. MU Gang, CAI Tingting, YAN Gangui, et al. Bidirectional power constraints and influence of doubly fed induction generator participating in continuous frequency regulation[J]. Transactions of China Electrotechnical Society, 2019, 34(8): 1750-1759. (  0) 0) |
| [9] |
MAHISH P, PRADHAN A K. Distributed synchronized control in grid integrated wind farms to improve primary frequency regulation[J]. IEEE Transactions on Power Systems, 2020, 35(1): 362-373. DOI:10.1109/TPWRS.2019.2928394 (  0) 0) |
| [10] |
徐晓颖, 吴继平, 滕贤亮, 等. 带频率-电压死区的VSC-HVDC系统一次调频控制策略[J]. 电力工程技术, 2020, 39(3): 8-14. XU Xiaoying, WU Jiping, TENG Xianliang, et al. Primary frequency modulation control strategy for VSC-HVDC system with frequency-voltage dead zone[J]. Electric Power Engineering Technology, 2020, 39(3): 8-14. (  0) 0) |
| [11] |
YANG D J, JIN Z Y, ZHENG T Y, et al. An adaptive droop control strategy with smooth rotor speed recovery capability for type Ⅲ wind turbine generators[J]. International Journal of Electrical Power & Energy Systems, 2022, 135: 107532. (  0) 0) |
| [12] |
CHOI S, KANG Y C, KIM K H, et al. A frequency-responsive power-smoothing scheme of a doubly-fed induction generator for enhancing the energy-absorbing capability[J]. International Journal of Electrical Power & Energy Systems, 2021, 131: 107053. (  0) 0) |
| [13] |
全锐, 潘文霞, 刘明洋. 基于低阶频率响应模型的双馈风电机组下垂系数修正方法[J]. 电力系统自动化, 2018, 42(1): 68-73, 90. QUAN Rui, PAN Wenxia, LIU Mingyang. Modification method for droop coefficient of DFIG based on low-order system frequency response model[J]. Automation of Electric Power Systems, 2018, 42(1): 68-73, 90. (  0) 0) |
| [14] |
乔颖, 郭晓茜, 鲁宗相, 等. 考虑系统频率二次跌落的风电机组辅助调频参数确定方法[J]. 电网技术, 2020, 44(3): 807-815. QIAO Ying, GUO Xiaoqian, LU Zongxiang, et al. Parameter setting of auxiliary frequency regulation of wind turbines considering secondary frequency drop[J]. Power System Technology, 2020, 44(3): 807-815. (  0) 0) |
| [15] |
姚玉永, 张立臣, 穆勇, 等. 基于自适应虚拟电机策略的微电网储能控制研究[J]. 供用电, 2022, 39(7): 84-92. YAO Yuyong, ZHANG Lichen, MU Yong, et al. Research on energy storage control in microgrid based on adaptive virtual machine strategy[J]. Distribution & Utilization, 2022, 39(7): 84-92. (  0) 0) |
| [16] |
边晓燕, 张菁娴, 丁炀, 等. 基于DFIG虚拟惯量的微电网双维自适应动态频率优化控制[J]. 高电压技术, 2020, 46(5): 1476-1485. BIAN Xiaoyan, ZHANG Jingxian, DING Yang, et al. Double layer adaptive dynamic frequency optimization control of microgrid based on DFIG virtual inertia[J]. High Voltage Engineering, 2020, 46(5): 1476-1485. (  0) 0) |
| [17] |
马智慧, 李欣然, 谭庄熙, 等. 考虑储能调频死区的一次调频控制方法[J]. 电工技术学报, 2019, 34(10): 2102-2115. MA Zhihui, LI Xinran, TAN Zhuangxi, et al. Integrated control of primary frequency regulation considering dead band of energy storage[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2102-2115. (  0) 0) |
| [18] |
SUN M, MIN Y, CHEN L, et al. Optimal auxiliary frequency control of wind turbine generators and coordination with synchronous generators[J]. CSEE Journal of Power and Energy Systems, 2020, 7(1): 78-85. (  0) 0) |
| [19] |
ZENG X Y, LIU T Q, WANG S L, et al. Comprehensive coordinated control strategy of PMSG-based wind turbine for providing frequency regulation services[J]. IEEE Access, 2019, 7: 63944-63953. (  0) 0) |
| [20] |
单煜, 汪震, 周昌平, 等. 基于分段频率变化率的风电机组一次调频控制策略[J]. 电力系统自动化, 2022, 46(11): 19-26. SHAN Yu, WANG Zhen, ZHOU Changping, et al. Control strategy of primary frequency regulation for wind turbine based on segmented rate of change of frequency[J]. Automation of Electric Power Systems, 2022, 46(11): 19-26. (  0) 0) |
| [21] |
赵晶晶, 吕雪, 符杨, 等. 基于可变系数的双馈风机虚拟惯量与超速控制协调的风光柴微电网频率调节技术[J]. 电工技术学报, 2015, 30(5): 59-68. ZHAO Jingjing, LYU Xue, FU Yang, et al. Frequency regulation of the wind/photovoltaic/diesel microgrid based on DFIG cooperative strategy with variable coefficients between virtual inertia and over-speed control[J]. Transactions of China Electrotechnical Society, 2015, 30(5): 59-68. (  0) 0) |
| [22] |
LEE J, MULJADI E, SRENSEN P, et al. Releasable kinetic energy-based inertial control of a DFIG wind power plant[J]. IEEE Transactions on Sustainable Energy, 2016, 7(1): 279-288. (  0) 0) |
| [23] |
KIM Y, KANG M, MULJADI E, et al. Power smoothing of a variable-speed wind turbine generator in association with the rotor-speed-dependent gain[J]. IEEE Transactions on Sustainable Energy, 2017, 8(3): 990-999. (  0) 0) |
| [24] |
王同森, 程雪坤. 计及转速限值的双馈风机变下垂系数控制策略[J]. 电力系统保护与控制, 2021, 49(9): 29-36. WANG Tongsen, CHENG Xuekun. Variable droop coefficient control strategy of a DFIG considering rotor speed limit[J]. Power System Protection and Control, 2021, 49(9): 29-36. (  0) 0) |
| [25] |
杨德健, 许益恩, 高洪超, 等. 计及转速平滑恢复的双馈风电机组自适应频率控制策略[J]. 电力系统保护与控制, 2022, 50(6): 172-179. YANG Dejian, XU Yien, GAO Hongchao, et al. Self-adaptive frequency control scheme of a doubly-fed induction generator with smooth rotor speed recovery[J]. Power System Protection and Control, 2022, 50(6): 172-179. (  0) 0) |
| [26] |
聂永辉, 刘家僮, 孙斌, 等. 基于转子动能释放的风电并网系统非线性频率控制策略研究[J/OL]. 中国电机工程学报, 2022: 1-11[2022-10-28]. https://kns.cnki.net/kcms/detail/11.2107.TM.20221027.1139.009.html. NIE Yonghui, LIU Jiatong, SUN Bin, et al. Research on nonlinear frequency control strategy of wind power grid connected system based on rotor kinetic energy release[J/OL]. Proceedings of the CSEE, 2022: 1-11[2022-10-28]. https://kns.cnki.net/kcms/detail/11.2107.TM.20221027.1139.009.html. (  0) 0) |
| [27] |
LIU H, WANG P, ZHAO T Y, et al. A group-based droop control strategy considering pitch angle protection to deloaded wind farms[J]. Energies, 2022, 15(8): 2722. (  0) 0) |
| [28] |
张军六, 李佳朋, 唐震, 等. 基于本地测量的高比例新能源电力系统不平衡功率估算与附加功率控制策略[J]. 电力科学与技术学报, 2022, 37(3): 50-60. ZHANG Junliu, LI Jiapeng, TANG Zhen, et al. Local measurement based unbalanced active power estimation and supplementary power modulation for power systems with high proportions of renewable energy[J]. Journal of Electric Power Science and Technology, 2022, 37(3): 50-60. (  0) 0) |
| [29] |
SHI Q X, LI F X, CUI H T. Analytical method to aggregate multi-machine SFR model with applications in power system dynamic studies[J]. IEEE Transactions on Power Systems, 2018, 33(6): 6355-6367. (  0) 0) |
| [30] |
国家质量监督检验检疫总局, 中国国家标准化管理委员会. 电能质量电力系统频率偏差: GB/T 15945—2008[S]. 北京: 中国标准出版社, 2008. General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China, Standardization Administration of the People's Republic of China. Power quality—fequency deviation for power system: GB/T 15945-2008[S]. Beijing: Standards Press of China, 2008. (  0) 0) |
| [31] |
LEE J, JANG G, MULJADI E, et al. Stable short-term frequency support using adaptive gains for a DFIG-based wind power plant[J]. IEEE Transactions on Energy Conversion, 2016, 31(3): 1068-1079. (  0) 0) |
| [32] |
席磊, 金澄心, 李彦营, 等. 基于信息松弛的多态能源协调控制方法研究[J]. 电力系统保护与控制, 2023, 51(9): 1-12. XI Lei, JIN Chengxin, LI Yanying, et al. A polymorphic energy-coordinated control strategy based on information relaxation[J]. Power System Protection and Control, 2023, 51(9): 1-12. (  0) 0) |
 2023, Vol. 42
2023, Vol. 42


 ,
,  刘辉(1978),男,博士,教授,研究方向为电力系统稳定与控制、能源需求侧响应等(E-mail:
刘辉(1978),男,博士,教授,研究方向为电力系统稳定与控制、能源需求侧响应等(E-mail: