文章编号: 2096-3203(2023)06-0022-10 中图分类号: TM61
2. 清华大学能源与动力工程系,北京 100084
近年来,我国风电[1]、光伏[2]等新能源装机和发电量均实现了快速增长[3-4],大规模新能源接入电网增加了系统应对新能源出力变化的灵活性需求, 配置储能是提升新能源电力系统灵活性的重要措施之一。新能源与储能规划可在源头上维持电力系统供需平衡,为保障系统安全可靠运行提供基础。新能源规划和储能配置都须计及系统时序特性。进行新能源和储能联合优化规划有利于充分考虑新能源的出力特性,使规划结果更为合理可靠[5]。
针对新能源与储能联合规划问题,已有学者进行了相关研究。文献[6]基于碳减排目标建立了新能源和储能规划模型;文献[7]基于新能源多阶段规划模型得到不同新能源配额场景下的储能规划方案;文献[8-10]提出一种考虑新能源出力不确定性的风光储微电网储能容量联合优化方法;文献[11-12]基于典型日方法建立了微电网风光储双层规划模型;文献[13]提出源-荷匹配的风光储容量配比优化方法。以上研究表明了进行新能源与储能联合规划是高比例新能源电力系统经济、可靠发展的重要基础,但通常都是基于某一区域或系统进行新能源与储能规划,对多区域新能源与储能联合规划考虑较少。
新能源与储能联合规划模型为典型的混合整数规划(mixed integer programming,MIP)模型[14],具有高维数的特点[15-17],这类模型通常难以直接用于大区域复杂电网的中长期规划研究。因此,亟须从减小源储联合规划MIP模型规模方面来降低模型的求解难度。一些学者采用人工智能算法进行规划模型的寻优求解。文献[18]建立基于差异进化算法的新能源规划模型;文献[19]提出基于神经网络算法的新能源电力系统容量优化规划方法;文献[20]基于多准则决策分析方法得到不同条件下的风光储容量配置比例。这些算法在一定程度上取得了较好效果,但存在过于依赖初始值和寻优路径、局部搜索能力弱、在局部极值附近早熟收敛等问题。
新能源与储能联合规划通常将MIP模型转换为混合整数线性规划(mixed integer linear programming,MILP)模型以便于求解。针对MILP模型,现阶段多采用分支定界法[21]或割平面法[22]求解,然而这些方法仍需要较长计算时间[23]。分解协调技术[24]被广泛用于提高MIP问题的求解速度,基于拉格朗日松弛的分解法[25]是目前常用的一种分解协调技术,适用于目标函数中包含多决策变量的优化问题求解。
基于以上分析,文中对多区域风光储联合优化规划问题进行研究。首先,考虑新能源出力随机性,建立基于中长期时序电力平衡的多区域风光储联合规划模型。其次,提出基于区域分解协调的分层优化方法,将多区域风光储联合规划模型分解为两层问题,其中下层问题以最小化综合成本为目标,确定各子区域内电源和储能的配置容量;上层问题根据下层问题给定的容量规划方案,求解新能源消纳最大化问题,确定各子区域电源运行情况。两层问题相互迭代,协调得到各区域风光储最优容量。最后,算例分析验证了所提模型和方法的合理性及有效性。
1 多区域风光储联合优化规划数学模型 1.1 目标函数电源规划的主要任务是在满足负荷需求和各种技术经济指标条件下确定电源类型和规模,使规划期内系统能可靠供电且投资经济合理。因此电源规划方案应满足安全性和经济性要求。此外,为提高新能源利用率,还须考虑新能源消纳。因此,文中考虑经济性最优为目标,在约束中计及可靠性和新能源消纳约束。
由于电源规划一般涉及多类电源工程项目,其各自的使用寿命和投产年限通常不同,因此一般采用等年值法处理该问题。风光储联合优化规划模型考虑系统经济性最优,目标函数为系统综合成本最小。计及新能源出力场景及概率,则目标函数为:
| $ \min N=E\left(\sum\limits_{j \in \varPhi_{0}} p_{j}\left(N_{\mathrm{t}, j}+N_{\mathrm{y}, j}+N_{\mathrm{y}, j}^{\prime}\right)\right) $ | (1) |
式中:E(·)为随机场景期望结果;Φ0为新能源出力随机场景集合;pj为场景j的概率;N为综合成本,包含投资费用等年值Nt、年固定运行费用Ny、年可变运行费用N′y。
| $ N_{\mathrm{t}, j}=\sum\limits_{n \in N_{\mathrm{m} }i \in \varPhi_{1}} B_{i} N_{i, n, j} C_{i, n} \varTheta\left(\vartheta, Y_{i}\right) $ | (2) |
| $ N_{\mathrm{y}, j}=\sum\limits_{n \in N_{\mathrm{m}}} \sum\limits_{i \in \varPhi_{1}} \rho_{i} B_{i} N_{i, n, j} C_{i, n} $ | (3) |
| $ N_{\mathrm{y}, j}^{\prime}=\sum\limits_{n \in N_{\mathrm{m}}}\left(\sum\limits_{i \in \varPhi_{1} \cup \varPhi_{2}} \alpha_{\mathrm{co}} B_{\mathrm{co}} N_{i, n, j} E_{i, n, j}+\mu_{l} E_{l, n, j}\right) $ | (4) |
式中:下标n为区域;Nm为区域集合;下标i为电厂类型;Φ1、Φ2分别为待选和已有电厂集合,包含Φg、Φh、Φw、Φpv、Φs,分别为火电、水电、风电、光伏和储能集合;下标l为周期;Ni, n, j为机组台数;Ci, n为单机容量;Bi为单位造价;Yi为机组年限;
| $ \varTheta\left(\vartheta, Y_{i}\right)=\frac{\vartheta(1+\vartheta)^{Y_{i}}}{(1+\vartheta)^{Y_{i}}-1} $ | (5) |
不同于传统规划仅计及电量平衡或典型日电力平衡,文中在风光储联合规划时计及年度时序电力平衡,可保证规划结果的可靠性。
(1) 时序电力平衡约束。
| $ \sum\limits_{i \in \varPhi_{1} \cup \varPhi_{2} \cup \varPhi_{l}} p_{i, j}(t)=D(t)+D_{l, j}(t) $ | (6) |
式中:Φl为联络线集合;pi, j(t)、D(t)分别为电源出力、负荷;t为时刻;Dl, j(t)为场景j中第l个周期的可调负荷,为负值时表示向下调整负荷。
建立可调整负荷数学模型,其主要思想是:在一定周期内,一部分负荷用电功率可进行上、下调节,且控制周期内负荷总用电量不变。其具体形式分别如下:
| $ \left\{\begin{array}{l} 0 \leqslant D_{l, j, \text { up }}(t) \leqslant \bar{D}_{\text {up }} \\ 0 \leqslant D_{l, j \text {, down }}(t) \leqslant \bar{D}_{\text {down }} \end{array} \quad \forall t\right. $ | (7) |
| $ 0 \leqslant \int\limits_{t \in T_{l}} D_{l, j, \text { up }}(t) \mathrm{d} t \leqslant Q_{l} $ | (8) |
| $ \int\limits_{t \in T_{l}} D_{l, j, \text { up }}(t) \mathrm{d} t=\int\limits_{t \in T_{l}} D_{l, j, \text { down }}(t) \mathrm{d} t $ | (9) |
| $ \left\{\begin{array}{l} D_{l, j}(t)=D_{l, j \text {, up }}(t) \quad D_{l, j}(t) \geqslant 0 \\ \left|D_{l, j}(t)\right|=D_{l, j, \text { down }}(t) \quad D_{l, j}(t)<0 \end{array}\right. $ | (10) |
式中:Dl, j, up(t)、Dl, j, down(t)分别为负荷上、下调整功率;Dup、Ddown分别为负荷上、下调整功率最大值,通常可取最大负荷的5%;Ql为调整周期内负荷调整电量上限;Tl为负荷调整周期,由于负荷具有日变化周期特性,因此Tl可取1 d。
(2) 电量平衡约束。
| $ \sum\limits_{i \in \varPhi_{1} \cup \varPhi_{2} \cup \varPhi_{l}} \sum\limits_{t \in T} p_{i, j}(t)=E_{\text {all }}+\sum\limits_{i \in \varPhi_{1} \cup \varPhi_{2}} E_{i, j}^{\prime} $ | (11) |
式中:Eall为总电量;E′i, j为弃电量;T为规划点时段。
(3) 联络线功率约束。
| $ \underline{p}_{i} \leqslant p_{i, j}(t) \leqslant \bar{p}_{i} \quad i \in \varPhi_{l} ; \forall t $ | (12) |
式中:
(4) 电源约束。
新能源出力约束具体形式为:
| $ 0 \leqslant p_{i, j}(t) \leqslant N_{i, j} C_{i} P_{i, j}(t) \quad i \in \varPhi_{\mathrm{w}} \cup \varPhi_{\mathrm{pv}} $ | (13) |
式中:Pi, j(t)为新能源出力随机场景序列;Ni, j为新能源机组台数;Ci为新能源机组单机容量。
水电出力取决于河流流量,出力约束为:
| $ \underline{P}_{i} \leqslant p_{i, j}(t) \leqslant \bar{P}_{i} \quad i \in \varPhi_{\mathrm{h}} ; \forall t $ | (14) |
式中:Pi、Pi分别为机组出力的上、下限。
火电约束为:
| $ \left\{\begin{array}{l} \underline{P}_{i} \leqslant Z_{i, j}(t) p_{i, j}(t) \leqslant \bar{P}_{i} \\ p_{i, j}(t+\Delta t)-p_{i, j}(t) \leqslant P_{i, \text { up }} \\ p_{i, j}(t)-p_{i, j}(t+\Delta t) \leqslant P_{i, \text { down }} \\ u_{i, j}(t)+\sum\limits_{h=1}^{H_{\text {on }}} v_{i, j}(t+h) \leqslant 1 \\ v_{i, j}(t)+\sum\limits_{h=1}^{H_{\text {off }}} u_{i, j}(t+h) \leqslant 1 \\ Z_{i, j}(t)-Z_{i, j}(t-\Delta t)+ \\ \;\;\;\;v_{i, j}(t)-v_{i, j}(t)=0 \end{array}\right. \quad i \in \varPhi_{\mathrm{g}} ; \forall t $ | (15) |
式中:Pi, up、Pi, down分别为机组向上、下爬坡率;ui, j(t)、vi, j(t)为二进制变量,分别表示机组启、停机状态;Δt为爬坡时间间隔;Zi, j(t)为二进制变量,表示机组运行状态;Hon、Hoff分别为机组最小启、停机时间;h为启/停机时间间隔。
储能电池约束为:
| $ \left\{\begin{array}{l} E_{i, j}(t+\Delta t)=E_{i, j}(t)+u_{i, j}^{+}(t) \times \\ \quad \eta_{i}^{+} p_{i, j}^{+}(t) \Delta t-u_{i, j}^{-}(t) \frac{1}{\eta_{i}^{-}} \times \\ \quad p_{i, j}^{-}(t) \Delta t-\alpha_{i} E_{i, j}(t) \\ \underline{E}_{i} \leqslant E_{i, j}(t) \leqslant h_{i} C_{i} \\ 0 \leqslant p_{i, j}^{+}(t) \leqslant C_{i} \\ 0 \leqslant p_{i, j}^{-}(t) \leqslant C_{i} \\ 0 \leqslant u_{i, j}^{+}(t)+u_{i, j}^{-}(t) \leqslant 1 \\ \left|E_{i, j}(t+\Delta t)-E_{i, j}(t)\right| \leqslant \bar{E}_{\mathrm{s}} \\ h_{i} \leqslant \bar{H} \end{array} \quad i \in \varPhi_{\mathrm{s}} ; \forall t\right. $ | (16) |
式中:Ei, j(t)为电量;pi, j+、pi, j-分别为充、放电功率;ηi+、ηi-分别为充、放电效率;αi为自放电率;ui, j+、ui, j-分别为充、放电状态;Ei为电量下限;Es为荷电状态限值;hi为储能时长;H为最大时长。
(5) 备用约束。
| $ \sum\limits_{i \in \varPhi_{1} \cup \varPhi_{2}} v_{i} N_{i, j} C_{i} \geqslant \alpha_{\mathrm{D}} \bar{D} $ | (17) |
式中:υi为电源备用系数;αD为系统备用系数;D为最大负荷。
(6) 新能源电量占比约束。
| $ \sum\limits_{i \in \varPhi_{\mathrm{w}} \cup \varPhi_{\mathrm{pv}}} N_{i, j} E_{i, j} \geqslant \rho_{\mathrm{E}} E_{\text {all }} $ | (18) |
式中:ρE为新能源电量占比率。
此外,新能源弃电量约束是指导储能配置的重要因素之一,其约束形式为:
| $ \sum\limits_{i \in \varPhi_{\mathrm{w}} \cup \varPhi_{\mathrm{pv}}} p_{i, j}(t) \geqslant\left(1-\eta_{\mathrm{r}}\right) \sum\limits_{i \in \varPhi_{\mathrm{w}} \cup \varPhi_{\mathrm{pv}}} \sum\limits_{t \in T} N_{i, j} C_{i} p_{i, j}(t) $ | (19) |
式中:ηr为新能源弃电率。
2 基于区域分解协调的规划模型分层优化方法多区域风光储联合优化规划模型是一个多分区、多电源、多变量的高维数复杂规划问题,求解非常耗时甚至无解,须采用合适的方法进行处理。区域分解法是计算机领域的一种并行算法,其本质是将问题的计算域分解为若干子域分别求解再进行综合的一种数值计算方法。该方法便于在各子域中运用适应其特点的模型和参数,使总体解更符合实际,并有利于采用并行算法,加快运算速度。文中基于区域分解思想,提出基于区域分解协调的风光储联合规划模型分层优化方法。
基于电力系统主要的受限断面(主变、单条输电线或多条输电线组成的广义传输线)对大规模系统进行区域划分,将其分为Nm个独立子区域和Nl条传输线,对应规划模型可分为分区层和协调层两层结构。在分区层,各区域可基于第1章风光储联合规划模型进行源储容量配置;在协调层,可实现区域间传输线的交互功率优化计算,避免各子区域源储独立规划时可能出现的余电区域或缺电区域。
拉格朗日松弛法已在求解多电源机组组合以及联合规划方面得到广泛应用,文中拟采用基于拉格朗日松弛的分解法来求解多区域风光储联合优化规划模型。
2.1 基于拉格朗日松弛的分解法基于拉格朗日对偶松弛的分解协调过程[26]如下。
(1) 将原大规模复杂优化问题min f(x)分解为J个子问题,则原问题的目标函数可用各子问题目标函数之和来表示,具体形式为:
| $ \left\{\begin{array}{cl} \min & f(x)=\sum\limits_{k=1}^{K} f_{k}\left(x_{k}\right) \\ \text { s.t. } & v_{k}\left(x_{k}\right) \geqslant 0 \\ & p_{k, 1}\left(x_{k}\right)=0 \\ & p_{k, 2}(x)=0 \end{array}\right. $ | (20) |
式中:f(x)为原问题目标函数;fk(xk)为子问题k的目标函数;vk(xk)为仅与子问题k内部参数相关的不等式约束;pk, 1(xk)为仅与子问题k内部参数相关的等式约束;pk, 2(x)为各子问题与外界耦合的复杂约束。
(2) 依据拉格朗日对偶松弛理论,引入松弛乘子λ,将具有耦合关系的约束pj, 2(x)松弛到目标函数中,构造拉格朗日函数L(x, λ)。
(3) 将原问题目标函数f(x)等效为
(4) 分别构造对偶函数μ(λ)和对偶问题
(5) 对拉格朗日乘子λ和边界条件进行协调,首先将乘子λ传递给各子问题,计算子问题得到相应变量xj,再根据所得xj更新乘子λ,不断迭代直至得到全局最优结果。
(6) 选取合适迭代方法和步长对拉格朗日乘子进行迭代。
(7) 计算拉格朗日松弛对偶间隙,判断对偶间隙是否满足收敛条件,若满足,则完成计算;若不满足,则继续进行迭代计算直至满足收敛条件。
2.2 基于分解协调的分层优化方法通过分析所构建的多区域风光储联合优化规划模型结构,发现所提模型是一个以综合成本最小为目标的单目标规划模型,约束条件众多。基于拉格朗日对偶松弛理论思想,将新能源电量占比约束式(18)松弛至目标函数式(1)中,得到松弛问题目标函数如下:
| $ \min \left(N+\lambda\left(\rho_{\mathrm{E}} E_{\mathrm{all}}-\sum\limits_{i \in \varPhi_{w} \cup \varPhi_{\mathrm{pv}}} N_{i, j} E_{i, j}\right)\right) $ | (21) |
式(21)为线性公式,可将综合成本和新能源消纳量解耦,因此原多区域风光储联合规划问题可以分为上下两层问题。下层问题目标为求解各区域风光储联合优化规划模型,确定各区域内电源和储能的配置容量。上层问题根据下层问题给定的投资决策容量方案,求解包含传输线功率交换约束的新能源消纳最大化问题,以确定各区域电源运行情况,并将这些运行状态返回至下层问题中。通过上下两层问题之间的迭代求解,得到使目标函数最优的电源和储能投资方案。
下层优化模型为各区域风光储联合规划模型,其目标函数与原问题目标函数相同,为最小化系统综合成本。约束条件包含式(6)—式(11)、式(13)—式(17)、式(19)。
上层问题为新能源消纳最大模型,由式(21)松弛后的上层问题目标函数形式如下:
| $ \min \tilde{N}_{2}=\lambda\left(\rho_{E} E_{\mathrm{all}}-\sum\limits_{i \in \varPhi_{\mathrm{w}} \cup \varPhi_{\mathrm{pv}}} N_{i, j} E_{i, j}\right) $ | (22) |
由于式(22)中第一项为固定值,可以省去该项,原问题即变为最小化新能源电量的负值。为便于理解和符合数学建模的思想,将其转为最大化新能源电量,因此原最小化问题可转化为最大化问题。转化后的上层问题目标函数形式如下:
| $ \max N_{2}=\lambda \sum\limits_{i \in \varPhi_{w} \cup \varPhi_{\mathrm{pv}}} N_{i, j} E_{i, j} $ | (23) |
约束条件包含式(6)—式(17)、式(19)。
拉格朗日松弛后的对偶函数如下:
| $ q(\lambda)=\min N-\lambda \sum\limits_{i \in \varPhi_{\mathbb{w}} \cup \varPhi_{\mathrm{pv}}} N_{i, j} E_{i, j} $ | (24) |
对偶函数式(24)须满足原问题所有约束条件。
依据拉格朗日对偶松弛理论,得到对偶问题如下:
| $ g(\lambda)=\max\limits _{\lambda} q(\lambda) $ | (25) |
对于拉格朗日乘子λ,按照如下方式进行迭代更新:
| $ \lambda_{k+1}=\lambda_{k}+\alpha_{k} g_{k} $ | (26) |
式中:k为迭代次数;αk、gk分别为第k次迭代的步长和次梯度方向,其选取公式如下。
| $ 0<\alpha_{k} <\frac{2\left(q^{*}-q\left(\lambda_{k}\right)\right)}{\left\|g_{k}\right\|^{2}} $ | (27) |
| $ g_{k} =\sum\limits_{i \in \varPhi_{\mathrm{w}} \cup \varPhi_{\mathrm{pv}}} N_{i} E_{i} $ | (28) |
这里需要注意的是,次梯度选取公式不唯一,这里只给出基于耦合约束的一种常见方式。
对于原规划问题和对偶问题的一组可行解(Ci, α, λ),须计算其绝对对偶间隙GL,计算公式如下:
| $ G_{\mathrm{L}}=N\left(\bar{C}_{i}, \bar{\alpha}\right)-g(\bar{\lambda}) $ | (29) |
根据对偶最优定理,当对偶间隙GL=0时,可行解(Ci, α, λ)为原问题和对偶问题的最优解;若GL≠0,则须对乘子λ继续进行迭代直至寻到最优解。但实际中对偶间隙很难达到0,因此文中判断收敛依据改为对偶间隙小于给定精度ε,若满足,则算法收敛,认为该可行解即为最优解。
基于拉格朗日对偶松弛的分解协调算法具体步骤为:
(1) 输入模型所需基础数据,如测试系统的已有机组数据、待规划机组数据、新能源归一化历史出力序列、负荷序列等规划数据。
(2) 根据新能源归一化历史出力和待规划机组成本初值,构建随机场景集。
(3) 设置拉格朗日迭代次数初始值为0,根据工程需求设置合适的拉格朗日乘子初值和求解间隙。
(4) 选择一组场景,求解下层各分区优化问题,判断下层问题是否有解,若无解提示该问题不可求解,调整边界条件重新计算;反之,得到子区域风光储优化容量。
(5) 将步骤(4)中下层问题求解得到的风光储投资决策传入上层问题作为优化边界,求解上层问题,得到各分区各电源出力和拉格朗日乘子。
(6) 将步骤(5)中所得风光储投资决策和拉格朗日乘子带入原问题和对偶问题中分别计算求解。
(7) 判断原问题和对偶问题的差距是否达到了求解间隙,若是则停止求解,迭代结束,输出该问题的目标函数和各决策变量值;反之更新拉格朗日乘子,继续迭代。
(8) 判断是否遍历随机场景集,若是则输出最优解;反之继续计算其余场景集结果,直至得到最终结果。
应用于文中所提模型的拉格朗日分解协调算法流程如图 1所示。

|
图 1 基于拉格朗日对偶松弛的规划模型求解流程 Fig. 1 Solution process of planning model based on Lagrangian pairwise relaxation |
为验证所提多区域风光储联合优化规划模型以及基于区域分解协调的分层优化方法的合理性及有效性,以我国某省级电网为测试系统进行分析,研究2030年的风光储优化规划问题。电网聚合结构示意如图 2所示,分为电网1—5共5个区域,该省级电网通过区域电网1与外省电网G和电网N相连,电网中电源类型主要包括火电、水电、风电和光伏。火电机组煤耗、标煤价格、排放系数参见文献[27-31]。

|
图 2 某省级电网等效聚合结构示意 Fig. 2 Schematic diagram of equivalent aggregation structure of a provincial power grid |
规划期内待选电源为风电和光伏,待选储能装置为储能电池。新能源年限电率上限设为10%,可调节负荷限值为年最大负荷的5%,负荷电量调整平衡周期取1 d,新能源电量占比设为45%。分解协调算法迭代总次数设为50,拉格朗日乘子λ初值设为0,求解间隙ε设为10-4。
3.2 算例分析 3.2.1 规划结果分析(1) 不同求解方法所得结果分析。为了验证所提基于区域分解协调的分层优化方法的性能,设置了对比方法对同一规划模型进行求解,并对2种求解方法所得风光储联合规划结果进行分析。
对比方法:集中求解方法,即直接采用求解器求解第1章所提规划模型,不考虑分解协调技术。
文中方法:分层优化方法,即采用基于区域分解协调的分层优化方法。
2种方法计算结果如表 1所示,文中方法的MILP规模为最大下层问题的规模,计算时间为所有场景平均计算时间。具体各区域电源和储能规划容量如图 3所示。
|
|
表 1 不同规划方法规划结果对比 Table 1 Comparison of planning results of different planning methods |
|
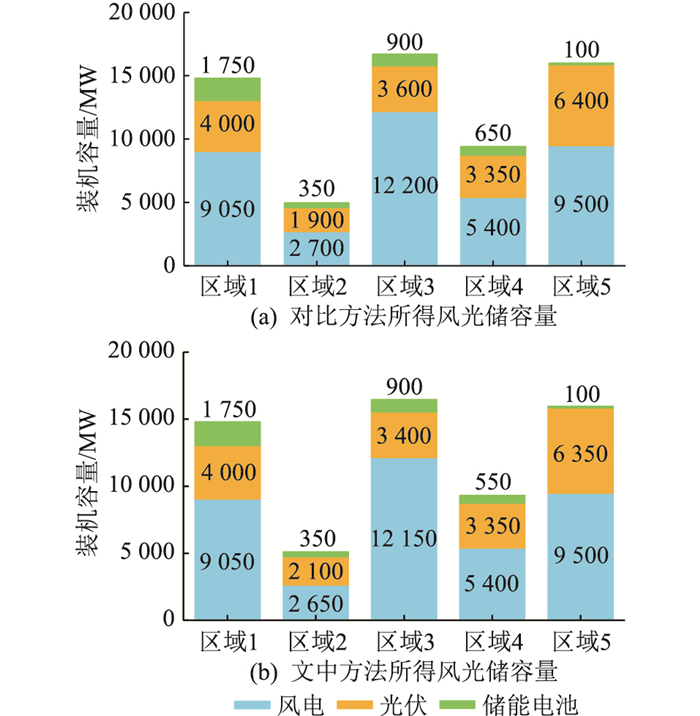
图 3 不同方法下各区域电源和储能规划容量 Fig. 3 Planned capacity of power supply and energy storage in different regions under different methods |
由表 1和图 3可以看出,文中所提求解方法与单层求解方法所得规划结果几乎一致,所有结果相对误差均小于0.5%,证明了所提求解方法的正确性。2种方法所得结果差异突出表现在计算效率方面,基于文中提出的规划模型及求解方法,平均每个场景在3 h之内可得出该省级电网电源规划方案,较对比方法的计算时间减少70.61%,大幅提高了求解效率,这主要是因为问题的求解规模不同。从表 1中可看出文中方法MILP问题节点、行、列数相比对比方法分别减少72.10%、38.41%和0.30%,求解2个MILP问题时分别迭代了17 259次和3 311次,表明文中方法可有效降低规划问题维数,减少MILP求解时的迭代次数。
总的来说,针对前述算例测试系统,文中所提基于区域分解协调的分层优化方法可以在较短时间内得到较为精确的风光储能规划方案,在大规模复杂系统的优化求解中具有明显提升计算效率的优势。
(2) 所提求解方法的收敛性分析。在求解优化问题时,判断一个求解方法能否得到最优解的依据之一是其计算结果可收敛。为了验证文中所采用的基于区域分解协调的求解算法可以收敛到全局最优解,对分解协调算法求解模型时的收敛过程进行分析,图 4为迭代过程中规划结果收敛曲线。

|
图 4 规划结果收敛过程曲线 Fig. 4 Planning result convergence process curves |
由图 4可以看出,在迭代过程中,风电总容量和储能总容量略有增加,光伏总容量有所下降。这主要是由于系统为满足负荷需求,投建新能源时倾向于选择资源更优的风电(利用小时数更高)。而随着新能源容量的增加,新能源弃电增加,系统须提供更多的灵活性来应对新能源大量接入带来的不利影响,因此储能电池容量也呈增长趋势。当拉格朗日迭代次数为14时,风光储容量达到收敛标准。新能源消纳电量随着迭代次数的增加呈上升趋势,其收敛趋势与风储容量的收敛趋势相吻合。系统总成本整体呈下降趋势,表明所有子区域主体以目标成本数值最小为演变方向,但也会出现部分主体目标成本数值增大的情况,这是主体与主体之间存在竞争关系所导致的。
总之,基于文中所提模型,系统目标函数能够收敛,新能源装机容量也能达到收敛标准,因此,所提算法可以在一定的误差要求和有限的迭代次数内收敛到全局最优解,满足工程实际的需求。
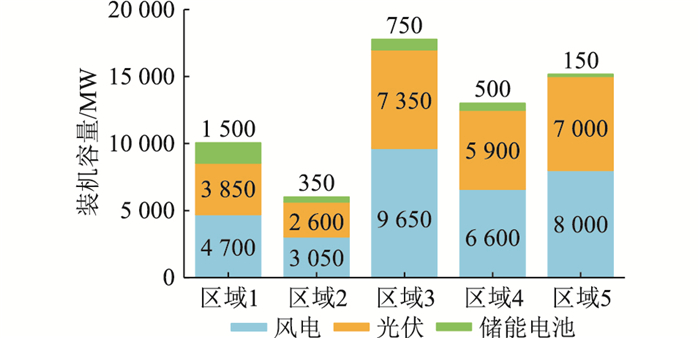
(3) 不同场景所得结果分析。为验证文中所提多区域风光储联合规划模型的合理性,设置对比场景进行比较分析,对比场景中不考虑区域间联络线断面约束。2个案例的规划结果见表 2,对比场景的各区域电源和储能规划容量如图 5所示,文中场景的各区域规划结果如图 3(b)所示。
|
|
表 2 不同场景所得规划结果 Table 2 Planning results for different scenarios |
|
图 5 对比场景的规划结果 Fig. 5 Planning results for comparison scenario |
从表 2中可以看出,不考虑联络线断面约束时,风电容量为光伏容量的1.2倍。而在文中场景中,各子区域在新能源消纳最大的主问题框架下保证子区域的电力电量平衡,风电容量增加了6 750 MW,光伏容量减少了7 500 MW,储能电池功率增加了400 MW,风电容量为光伏容量的2.02倍。从经济性方面看,文中场景综合成本增加了2.53%;从弃电率方面看,文中场景所得新能源弃电率为5.86%,而对比场景弃电率仅为1.26%。
(4) 随机因素对规划结果的影响。新能源随机出力对风光储联合规划结果具有重要影响,须在规划模型中加以考虑。文中分别以60组随机场景为输入求解规划模型,得到各组序列下的风光储最优容量以及综合成本,如图 6所示。图中蓝色柱状图为60组随机场景下所得结果的概率分布;红色曲线为概率分布的拟合结果,用来表示概率分布的形状。可以看出,所有场景下风电装机容量、光伏装机容量、储能电池功率容量以及系统综合成本的收敛结果分别为38 750 MW、19 200 MW、3 650 MW以及4 501.52亿元,所有场景的计算结果均服从正态分布。文中所提模型可以应对新能源随机出力,适用于不同随机场景下的源储规划分析。

|
图 6 多组新能源随机场景的规划结果 Fig. 6 Planning results for multiple sets of renewable energy stochastic scenarios |
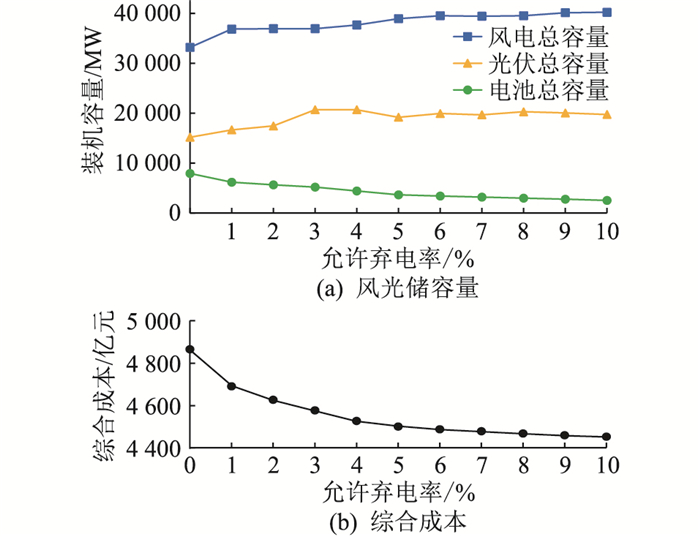
新能源弃电率约束是新能源与储能规划的一个重要约束条件,分析新能源允许弃电率对风光储联合规划模型的影响。假定系统新能源电量占比为45%,不同新能源允许弃电率下的规划结果如图 7所示。
|
图 7 新能源允许弃电率对规划结果的影响 Fig. 7 Impact of renewable energy allowable curtailment rates on planning results |
由图 7可以看出,随着系统新能源允许弃电率的增加,风、光容量整体呈先上升后趋于平缓的趋势,储能电池容量呈下降趋势。这主要是因为在新能源电量占比恒定的条件下,系统新能源配置容量会维持在一定水平,在弃电率较小尤其是为0时,系统需要足额消纳新能源电量,此时新能源容量较小,且需要大量储能电池提供灵活性支撑;而随着允许弃电率的增加,新能源容量呈小幅上升趋势,从图 7中可以看出,风电总装机在弃电率达到6%后趋于稳定值40 000 MW,光伏总装机在弃电率达到3%后趋于稳定值20 000 MW。综合成本随着允许弃电率的增加呈先下降后趋于平稳的趋势。在允许弃电率为0时,由于系统须全额消纳新能源电量,灵活性需求很高,导致常规电源出力较高,系统运行成本和碳排放成本较高,因此系统综合成本较高。随着允许弃电率的增加,系统灵活性需求降低,此时虽然系统投资成本小幅增高,但系统运行成本和碳排放成本降低,综合成本呈降低趋势。当允许弃电率达到6%时,综合成本趋于稳定值4 500亿元。
4 结论风光储联合规划是促进新能源消纳的重要措施之一,针对多区域风光储联合优化规划及求解问题,文中建立多区域风光储联合规划模型,并提出基于区域分解协调的分层优化方法。主要结论如下:
(1) 建立基于中长期时序电力平衡的多区域风光储联合优化规划模型,模型考虑经济性最优,并计及新能源出力长时间尺度特性和随机性。在模型中进一步约束火电机组状态变量以缩减变量规模,可降低规划问题维数。
(2) 提出基于区域分解协调的分层优化方法,将风光储联合规划模型分解为上下两层问题并进行迭代协调,得到风光储最优规划方案。
(3) 相比集中式求解方法,文中所提方法可大幅缩短计算时间,在大规模复杂系统的优化计算中具有明显提升计算效率的优势。
| [1] |
国家能源局. 2019年风电并网运行情况[Z]. 2020. National Energy Administration. Grid connected operation of wind power in 2019[Z]. 2020. (  0) 0) |
| [2] |
刘颖, 唐夏菲, 蔡晔, 等. 考虑省间交易与源荷互动协调的新能源消纳机制[J]. 电力系统及其自动化学报, 2022, 34(2): 16-22. LIU Ying, TANG Xiafei, CAI Ye, et al. Renewable energy consumption mechanism considering the coordination of inter-provincial transactions and source-load interaction[J]. Proceedings of the CSU-EPSA, 2022, 34(2): 16-22. (  0) 0) |
| [3] |
国家能源局. 2019年光伏发电并网运行情况[Z]. 2020. National Energy Administration. Grid connected operation of pho tovoltaic power generation in 2019[Z]. 2020. (  0) 0) |
| [4] |
水电水利规划设计总院. 中国可再生能源发展报告2019[R]. 2020. General Institute of Hydropower Planning and Design. China renewable energy development report 2019[R]. 2020. (  0) 0) |
| [5] |
程浩忠. 电力系统规划[M]. 2版. 北京: 中国电力出版社, 2014. CHENG Haozhong. Power system planning[M]. 2nd ed. Beijing: China Electric Power Press, 2014. (  0) 0) |
| [6] |
PALMINTIER B S, WEBSTER M D. Impact of operational flexibility on electricity generation planning with renewable and carbon targets[J]. IEEE Transactions on Sustainable Energy, 2016, 7(2): 672-684. DOI:10.1109/TSTE.2015.2498640 (  0) 0) |
| [7] |
ABDINA F, ZIO E. An integrated framework for operational flexibility assessment in multi-period power system planning with renewable energy production[J]. Applied Energy, 2018, 222: 898-914. DOI:10.1016/j.apenergy.2018.04.009 (  0) 0) |
| [8] |
谢鹏, 蔡泽祥, 刘平, 等. 考虑多时间尺度不确定性耦合影响的风光储微电网系统储能容量协同优化[J]. 中国电机工程学报, 2019, 39(24): 7126-7136, 7486. XIE Peng, CAI Zexiang, LIU Ping, et al. Cooperative optimization of energy storage capacity for renewable and storage involved microgrids considering multi time scale uncertainty coupling influence[J]. Proceedings of the CSEE, 2019, 39(24): 7126-7136, 7486. (  0) 0) |
| [9] |
孔飘红, 蒋正威, 杨力强, 等. 基于风氢耦合的氢储能系统参与电力市场机制与风险量化模型设计[J]. 供用电, 2022, 39(1): 31-39. KONG Piaohong, JIANG Zhengwei, YANG Liqiang, et al. Mechanism and risk quantification model design of hydrogen storage system participation in power market[J]. Distribution & Utilization, 2022, 39(1): 31-39. (  0) 0) |
| [10] |
李洁, 孙宏宇, 许椿凯, 等. 参与新型电力系统需求响应的分布式储能资源管理与策略研究[J]. 供用电, 2022, 39(2): 29-35. LI Jie, SUN Hongyu, XU Chunkai, et al. Research on distributed energy storage resource management and strategy participating in demand response of new power systems[J]. Distribution & Utilization, 2022, 39(2): 29-35. (  0) 0) |
| [11] |
郭力, 杨书强, 刘一欣, 等. 风光储微电网容量规划中的典型日选取方法[J]. 中国电机工程学报, 2020, 40(8): 2468-2479. GUO Li, YANG Shuqiang, LIU Yixin, et al. Typical day selection method for capacity planning of microgrid with wind turbine-photovoltaic and energy storage[J]. Proceedings of the CSEE, 2020, 40(8): 2468-2479. (  0) 0) |
| [12] |
姜爱华, 钱朝飞, 黄银燕, 等. 计及含氢多储能与电价型需求响应的能量枢纽日前经济调度[J]. 供用电, 2022, 39(3): 82-91. JIANG Aihua, Qian Chaofei, HUANG Yinyan, et al. The day-ahead economic dispatch of the energy hub for wind power accommodation considering hydrogen storage and price-based demand response[J]. Distribution & Utilization, 2022, 39(3): 82-91. (  0) 0) |
| [13] |
李湃, 方保民, 祁太元, 等. 基于源-荷匹配的区域电网风/光/储容量配比优化方法[J]. 中国电力, 2022, 55(1): 46-54. LI Pai, FANG Baomin, QI Taiyuan, et al. Capacity proportion optimization of wind, solar power and battery energy storage system for regional power grid based on source-load matching[J]. Electric Power, 2022, 55(1): 46-54. (  0) 0) |
| [14] |
随权, 林湘宁, 童宁, 等. 基于改进两阶段鲁棒优化的主动配电网经济调度[J]. 中国电机工程学报, 2020, 40(7): 2166-2179, 2396. SUI Quan, LIN Xiangning, TONG Ning, et al. Economic dispatch of active distribution network based on improved two-stage robust optimization[J]. Proceedings of the CSEE, 2020, 40(7): 2166-2179, 2396. (  0) 0) |
| [15] |
刘天琪, 曾红, 何川, 等. 考虑电转气设备和风电场协同扩建的气电互联综合能源系统规划[J]. 电力自动化设备, 2019, 39(8): 144-151. LIU Tianqi, ZENG Hong, HE Chuan, et al. Planning of integrated gas and electricity system considering coordinated expansion of power-to-gas facilities and wind farms[J]. Electric Power Automation Equipment, 2019, 39(8): 144-151. (  0) 0) |
| [16] |
黄彦彰, 周宇昊, 郑文广, 等. 产业园区新型多能联供综合能源服务研究[J]. 发电技术, 2021, 42(6): 734-740. HUANG Yanzhang, ZHOU Yuhao, ZHENG Wenguang, et al. Research on new integrated energy system with multi-power combined supply of industrial parks[J]. Power Generation Technology, 2021, 42(6): 734-740. (  0) 0) |
| [17] |
高垚楠, 陈海峰, 王建永. 一种新型CO2工质冷热电联供系统的热力性分析[J]. 发电技术, 2022, 43(1): 131-138. GAO Yaonan, CHEN Haifeng, WANG Jianyong. Thermodynamic analysis of a new combined cooling, heating and power system using CO2 working fluid[J]. Power Generation Technology, 2022, 43(1): 131-138. (  0) 0) |
| [18] |
KOLTSAKLIS N E, GEORGIADIS M C. A multi-period, multi-regional generation expansion planning model incorporating unit commitment constraints[J]. Applied Energy, 2015, 158: 310-331. (  0) 0) |
| [19] |
SAFARI M, SARVI M. Optimal load sharing strategy for a wind/ diesel/battery hybrid power system based on imperialist competitive neural network algorithm[J]. IET Renewable Power Generation, 2014, 8(8): 937-946. (  0) 0) |
| [20] |
ALSAYED M, CACCIATO M, SCARCELLA G, et al. Multicriteria optimal sizing of photovoltaic-wind turbine grid connected systems[J]. IEEE Transactions on Energy Conversion, 2013, 28(2): 370-379. (  0) 0) |
| [21] |
王健, 程春田, 申建建, 等. 水电站群优化调度非线性全局优化方法[J]. 中国电机工程学报, 2018, 38(17): 5107-5117, 5307. WANG Jian, CHENG Chuntian, SHEN Jianjian, et al. A branch-and-bound based global optimization method for deterministic hydropower operation[J]. Proceedings of the CSEE, 2018, 38(17): 5107-5117, 5307. (  0) 0) |
| [22] |
LU M L, QIAO L B, FENG D W, et al. Mini-batch cutting plane method for regularized risk minimization[J]. Frontiers of Information Technology & Electronic Engineering, 2019, 20(11): 1551-1563. (  0) 0) |
| [23] |
崔全胜, 白晓民, 董伟杰, 等. 用户侧综合能源系统规划运行联合优化[J]. 中国电机工程学报, 2019, 39(17): 4967-4981, 5279. CUI Quansheng, BAI Xiaomin, DONG Weijie, et al. Joint optimization of planning and operation in user-side multi-energy systems[J]. Proceedings of the CSEE, 2019, 39(17): 4967-4981, 5279. (  0) 0) |
| [24] |
张玲, 陈思捷, 严正, 等. 基于区块链共识机制的多区域最优潮流分布式算法[J]. 中国电机工程学报, 2020, 40(20): 6433-6442. ZHANG Ling, CHEN Sijie, YAN Zheng, et al. Distributed multi-area optimal power flow algorithm based on blockchain consensus mechanism[J]. Proceedings of the CSEE, 2020, 40(20): 6433-6442. (  0) 0) |
| [25] |
WU X, LIANG K X, HAN X A. Renewable energy output tracking control algorithm based on the temperature control load state-queuing model[J]. Applied Sciences, 2018, 8(7): 1099. (  0) 0) |
| [26] |
罗天, 汪可友, 李国杰, 等. 基于拉格朗日对偶松弛的多区域柔性直流互联电网无功优化[J]. 电力系统自动化, 2019, 43(11): 68-76. LUO Tian, WANG Keyou, LI Guojie, et al. Reactive power optimization in multi-area VSC-HVDC interconnected power grids based on Lagrangian dual relaxation[J]. Automation of Electric Power Systems, 2019, 43(11): 68-76. (  0) 0) |
| [27] |
朱法华, 王玉山, 徐振, 等. 中国电力行业碳达峰、碳中和的发展路径研究[J]. 电力科技与环保, 2021, 37(3): 9-16. ZHU Fahua, WANG Yushan, XU Zhen, et al. Research on the development path of carbon peak and carbon neutrality in China's Power Industry[J]. Electric Power Technology and Environmental Protection, 2021, 37(3): 9-16. (  0) 0) |
| [28] |
王皓, 艾芊, 甘霖, 等. 基于多场景随机规划和MPC的冷热电联合系统协同优化[J]. 电力系统自动化, 2018, 42(13): 51-58. WANG Hao, AI Qian, GAN Lin, et al. Collaborative optimization of combined cooling heating and power system based on multi-scenario stochastic programming and model predictive control[J]. Automation of Electric Power Systems, 2018, 42(13): 51-58. (  0) 0) |
| [29] |
杨晓辉, 张柳芳, 吴龙杰, 等. 含考虑IDR的冷热电联供微网的主动配电网经济优化调度[J]. 电力系统保护与控制, 2022, 50(3): 19-28. YANG Xiaohui, ZHANG Liufang, WU Longjie, et al. Economic optimal dispatch of an active distribution network with combined cooling, heating andpower microgrids considering integrated demand response[J]. Power System Protection and Control, 2022, 50(3): 19-28. (  0) 0) |
| [30] |
吴引航, 阳婷, 戴晓娟, 等. 含大规模水电的电力现货市场出清及价格机制研究[J]. 浙江电力, 2021, 40(12): 54-60. WU Yinhang, YANG Ting, DAI Xiaojuan, et al. Study of clearing and price mechanism of electricity spot market including large-scale hydropower[J]. Zhejiang Electric Power, 2021, 40(12): 54-60. (  0) 0) |
| [31] |
李坚, 吴亮红, 张红强, 等. 基于排序交叉优化算法的冷热电联供微电网经济调度[J]. 电力系统保护与控制, 2021, 49(18): 137-145. LI Jian, WU Lianghong, ZHANG Hongqiang, et al. Microgrid economic dispatch of combined cooling, heating and power based on a rank pair learning crisscross optimization algorithm[J]. Power System Protection and Control, 2021, 49(18): 137-145. (  0) 0) |
2. Department of Energy and Power Engineering, Tsinghua University, Beijing 100084, China
 2023, Vol. 42
2023, Vol. 42


 史昭娣(1991),女,博士,助理研究员,从事新型电力系统源网荷储协同规划工作(E-mail:
史昭娣(1991),女,博士,助理研究员,从事新型电力系统源网荷储协同规划工作(E-mail: