文章编号: 2096-3203(2023)06-0052-12 中图分类号: TM72
2. 国网江苏省电力有限公司经济技术研究院,江苏 南京 210008;
3. 国网江苏省电力有限公司,江苏 南京 210024
随着整县光伏政策[1]与《“十四五”现代能源体系规划》的颁布与实施,中国配电网的分布式光伏并网数量加速增长[2]。由于光伏发电系统存在日内发电功率不均的特性,配备高比例分布式光伏的配电网会出现间歇性电压越限的问题,严重影响了配电网的安全运行[3],因此研究含高比例分布式光伏配电网的电压控制策略具有重要意义。
传统配电网所采用的变压器分接头调压与电容器组调压属于电压离散调节[4],单次动作成本高而不能频繁动作,无法解决由高比例分布式光伏功率倒送导致的频繁电压越限问题。而光伏系统的逆变器存在预设冗余容量,可以用于无功调压[5],并且随着光储一体化的推进,分布式光伏发电与储能的灵活调压能力亟待有效挖掘。相比于传统方法,利用基于光伏逆变器与基于储能的调压方法具有建设运营成本较低的优势[6],可以避免高昂的电网改造成本,在网架复杂、线路众多的低压配电网中有更高的应用价值。
配电网系统电压控制策略主要分为3类:集中式策略、就地式策略与分布式策略。常规配电网通过配电管理系统对各组件进行集中式控制,但随着越来越多的光伏发电机组与分布式储能模块陆续接入到配电网中,配电管理系统依据现有的数据通信能力与运算能力很难应对分散且众多的光伏发电机组与分布式储能模块[7]。虽然文献[8-9]在计算复杂度与数据维度方面对集中式控制进行了优化,但海量的数据传输仍不可避免地会产生高昂的通信成本。
就地式策略虽无需通信,运算均在本地完成,结构安全可靠[10],但无法调用其他节点资源,使得配电网调压能力无法得到充分释放,且就地控制易对本地节点设备过度调用,缩短设备的使用寿命[11],从而抬高调压成本,经济效果不佳。分布式控制既能避免对控制中心的依赖,又能做到全局的优化控制。文献[12]基于局部通信,利用分布式算法实现与集中式相近的控制效果;文献[13]通过相邻节点耦合变量交互运算,使全局无功功率优化在各个智能体自身优化过程中得以实现;文献[14-16]利用分布式优化算法得到与集中式优化方法相当的储能功率调度与电压支撑效果;文献[17]通过在一致性算法中考虑增量成本策略设计,使其具有类似集中式控制的经济调度能力。
基于一致性算法的分布式控制策略通过相邻控制器的点对点通信,实现全局信息在每个控制器上共享,具有通信成本低、计算速度快的优点[18],在日益复杂的光伏配电网中发挥愈加重要的作用[19-20]。文献[18]基于一致性算法,提出一种针对主动配电网区域自治的优化调度算法,有效降低了配电网的分布式电源运行成本。文献[21]提出一种以光伏逆变器无功功率为一致性变量的分布式控制策略,但该策略仅对分布式能源的无功输出进行了调控。文献[22]将逆变器无功控制与储能的有功控制分为两阶段,分别将无功利用率与荷电状态(state of charge,SOC)作为一致性变量,但忽视了不同节点间电压灵敏度对单位调压成本的影响,经济性不佳。文献[23]基于电压-价格灵敏度对调压设备进行排序,降低了单位调压成本,但是忽略了优先节点持续高负荷输出而产生的设备寿命损耗成本。
综上所述,文中基于一致性算法提出一种计及设备寿命损耗成本的分布式控制策略。在建立储能与逆变器的寿命损耗模型的基础上,构建了光伏逆变器与储能的寿命损耗成本模型,使光伏逆变器和储能寿命损耗与调压经济性得以兼顾。并结合电压灵敏度,以单位调压成本参数作为一致性变量进行分布式控制,保证了控制的高效性与经济性。最后,通过MATLAB搭建IEEE 33节点系统,仿真结果表明了所述方法能有效抑制电压越限,降低调压成本。
1 光伏逆变器与储能调压机理 1.1 电压越限及调压机理分析传统的配电网采用闭环设计、开环运行的标准设计,是一个辐射状网络,潮流由变电站单方向流向负荷,电压也沿远离变电站方向单向降低。但随着可再生能源的不断发展,光伏渗透率大大提高;又由于日内光伏发电功率与负荷功率存在错峰情况,当配电网含高比例光伏时发电功率易在午间超过并网点负荷功率,从而出现功率倒送并抬升光伏并网节点的电压,引起电压越限问题。
图 1为一条简化的配电网线路。由于配电网的电压等级较低,故配电线路的充电电容、线路互感和漏电抗可以忽略。图 1中,N为节点序号;VN为节点N处电压;PN、QN分别为从节点N-1流向节点N的有功与无功功率;PNL、QNL分别为节点N负荷的有功与无功功率;PNBSS、QNBSS分别为节点N储能与配电网交互的有功和无功功率,功率可正可负;PNPV、QNPV分别为节点N的分布式光伏输出的有功与无功功率,QNPV不影响PNPV的输出;RN、XN分别为节点N-1与节点N间的电阻和电抗。
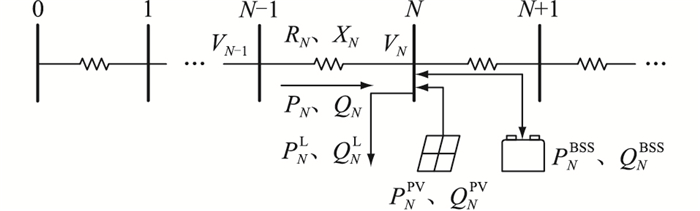
|
图 1 简化配电网馈线 Fig. 1 Simplified distribution network feeder |
节点间的功率关系为:
| $ \left\{\begin{array}{l} P_N-P_{N+1}=P_N^{\mathrm{BSS}}+P_N^{\mathrm{PV}}-P_N^{\mathrm{L}} \\ Q_N-Q_{N+1}=Q_N^{\mathrm{BSS}}+Q_N^{\mathrm{PV}}-Q_N^{\mathrm{L}} \end{array}\right. $ | (1) |
根据DistFlow潮流方程,节点间电压的关系可表示为:
| $ V_{N-1}-V_N=\frac{P_N R_N+Q_N X_N}{U_N}+\mathrm{j} \frac{P_N R_N-Q_N X_N}{U_N} $ | (2) |
式中:VN-1为节点N-1处电压。对其求电压幅值并忽略式中远小于其他项的高次项得到:
| $ V_{N-1}^2=V_N^2+2\left(P_N R_N+Q_N X_N\right) $ | (3) |
对节点N上游所有节点对应的式进行叠加可得:
| $ V_N^2=V_0^2-2 \sum\limits_{i=1}^N\left(P_i R_i+Q_i X_i\right) $ | (4) |
式中:i为节点N前的第i个节点;V0为线路始端电压。由式(4)可知,当光伏发电功率与负荷功率的差值足够大时,就会使电压高于前一节点,当该节点前累计功率差为正时,就会使该节点电压高于接入点电压。因此针对光伏并网引起功率倒送而导致的线路过电压问题,在不影响负荷与光伏有功输出的前提下,可以通过减小PN的反向流动或者增加QN的正向流动的方式解决。在配电网中,RN与XN相差不大,所以有功调压与无功调压具有同等重要的地位。考虑到光伏系统发电收益问题,不缩减其有功功率的输出,而由储能对节点有功进行调节。同时光伏逆变器容量一般会大于光伏额定容量,所以可以在不影响光伏有功功率输出的前提下进行无功调节。即可以通过调节PNBSS与QNPV来抑制电压越限。
| $ \Delta V_N=\left[\begin{array}{ll} S_{i, j}^{\mathrm{V}-\mathrm{P}} & S_{i, j}^{\mathrm{V}-\mathrm{Q}} \end{array}\right]\left[\begin{array}{c} \Delta P_N^{\mathrm{BSS}} \\ \Delta Q_N^{\mathrm{PV}} \end{array}\right] $ | (5) |
式中: ΔVN、ΔPNBSS、ΔQNPV分别为节点N处电压、储能有功与逆变器无功的变化量;Si, jV-P、Si, jV-Q分别为节点i对节点j的有功与无功电压灵敏度系数,与线路阻抗紧密相关[24]。
1.2 电压灵敏度计算电压灵敏度是量化不同节点有功及无功功率调压效果的重要依据,但其计算需要全网实时功率,所以传统灵敏度计算一般在具有全网潮流信息的集中式控制服务器中进行。为使电压灵敏度可用于分布式控制策略,文中基于配电网线路阻抗对电压灵敏度进行了近似计算。
根据式(4)进行移项分解可得:
| $ V_N=V_0-\frac{2\left(\Delta P_N \sum\limits_{i=1}^N R_i+\Delta Q_N \sum\limits_{i=1}^N X_i\right)}{V_N+V_0} $ | (6) |
式中:ΔPN、ΔQN分别为从节点N-1流向节点N的有功与无功功率的变化量。
因为配电网节点电压幅值接近,故用V0代替VN进行计算,得到由节点N处的功率变化导致的电压变化量:
| $ \Delta V_N=\frac{\Delta P_N \sum\limits_{i=1}^N R_i+\Delta Q_N \sum\limits_{i=1}^N X_i}{V_0} $ | (7) |
从而得到仅与阻抗有关的近似电压灵敏度的计算公式:
| $ \left[\begin{array}{ll} S_{i, j}^{\mathrm{V}-\mathrm{P}} & S_{i, j}^{\mathrm{V}-\mathrm{Q}} \end{array}\right]=\left\{ \begin{array}{l} \frac{1}{{{V_0}}}\left[ {\sum\limits_{h = 1}^i {{R_h}} \quad \sum\limits_{h = 1}^i {{X_h}} } \right]\quad i \le j\\ \frac{1}{{{V_0}}}\left[ {\sum\limits_{h = 1}^j {{R_h}} \quad \sum\limits_{h = 1}^j {{X_h}} } \right]\quad i > j \end{array} \right. $ | (8) |
式(8)避免了电压灵敏度迭代计算,为后续各节点分布式计算单位调压成本提供了依据。
2 单位调压成本模型 2.1 储能单位调压成本储能的单位功率成本与其实际使用状态密切相关。储能功率成本包括3个部分:初期的装机成本、持续运维成本以及充放电损耗成本。储能不合理的频繁充放电、高功率充放电以及深度放电都会缩短储能的寿命,从而增加系统的调压成本。因此,须详细分析储能的充放电功率及充放电深度对其寿命的影响,并建立相应的寿命量化模型,以获取准确可靠的动态单位功率成本,从而更有效地进行储能调压控制。
2.1.1 储能损耗成本模型储能电池使用寿命与放电深度、功率以及循环次数均密切相关,而电池无法在额定条件下长期运行,所以实际评估成本时用标称寿命并不准确。由于电池实际使用寿命计算须考虑在非标条件下的随机充放电过程,因此以其为依据对电池的寿命损耗进行准确测算。文献[25]建立电池累积损伤寿命模型,模型通过电池参数计算电池的总有效放电量ΓR:
| $ \mathit{\Gamma}_{\mathrm{R}}=L_{\mathrm{R}} D_{\mathrm{R}} C_{\mathrm{R}} $ | (9) |
式中:LR为额定工作状态下电池的循环使用次数;DR为电池额定放电深度;CR为电池额定容量。
电池寿命在不规则、不同放电深度的充放电下的损失程度可等价于式(10)。
| $ d_k^{\mathrm{eff}}=\eta_k^{\mathrm{c}} \eta_k^{\mathrm{d}} d_k^{\mathrm{a}} $ | (10) |
式中:dkeff为第k次放电时的额定等效放电能量;ηkc为第k次不放电时的电流比系数;ηkd为第k次放电时的循环寿命比系数;dka为第k次放电时的实际放电能量。
由于并网逆变器保证了端电压基本保持恒定,储能功率与电流的变化基本一致,所以功率比可以用电流比等效,ηkc可表示为:
| $ \eta_k^{\mathrm{c}}=\frac{I_{\mathrm{R}}}{I_k^{\mathrm{ES}}}=\frac{P_{\mathrm{R}}}{P_k^{\mathrm{ES}, \mathrm{dis}}} $ | (11) |
式中:IR为额定放电电流;PR为额定功率;IkES为第k次放电时的实际放电电流;PkES, dis为第k次放电时的实际放电功率。
| $ \eta_k^{\mathrm{d}}=\frac{L_{\mathrm{R}}}{L_k^{\mathrm{ES}}} $ | (12) |
式中:LkES为第k次放电状态下对应的实际可循环次数,可利用第k次放电时放电深度DkES计算。
| $ L_k^{\mathrm{ES}}=\eta^{\mathrm{ES}, 0}\left(D_k^{\mathrm{ES}}\right)^{-\eta^{\mathrm{ES}, 1}} \mathrm{e}^{-\eta^{\mathrm{ES}, 2} D_k^{\mathrm{ES}}} $ | (13) |
式中:ηES, 0、ηES, 1、ηES, 2为拟合系数,均大于0。此参数拟合方法同样适用于除磷酸铁锂电池外的其他化学电池,拟合参数一般由电池生产商提供,或者由机构实验获得。
基于上述计算过程可得第k次不规则放电过程的电池寿命损耗成本ckloss:
| $ c_k^{\text {loss }}=\frac{d_k^{\text {eff }}}{\mathit{\Gamma}_{\mathrm{R}}} C_{\mathrm{BSS}}^{\text {cape }} $ | (14) |
式中:CBSScape为电池的初始投资成本。
2.1.2 储能单位调压成本模型储能第k次不规则放电有功调压单位功率成本ckBSS可表示为:
| $ c_k^{\mathrm{BSS}}=\frac{d_k^{\mathrm{eff}}}{\mathit{\Gamma}_{\mathrm{R}}} C_{\mathrm{BSS}}^{\mathrm{cape}}+C_{\mathrm{BSS}}^{\mathrm{M}}+C_{\mathrm{BSS}}^{\mathrm{Ploss}} $ | (15) |
式中:CBSSM为储能单位功率维护成本;CBSSPloss为单位功率产生的有功损耗成本。
从而可以得到节点i处的储能对节点j处的电压控制的单位有功调压成本Si, jV-C, P的计算公式:
| $ S_{i, j}^{\mathrm{V}-\mathrm{C}, \mathrm{P}}=\frac{c_k^{\mathrm{BSS}}}{\Delta V_j}=\frac{c_k^{\mathrm{BSS}}}{S_{i, j}^{\mathrm{V}-\mathrm{P}} \Delta P_{\mathrm{ESS}}} $ | (16) |
式中:ΔVj为节点j调压前后的电压变化量;ΔPESS为储能因调压需求注入的有功功率。
图 2为储能有功单位成本与功率及SOC的关系曲面。由图 2可知,电池的SOC与充放功率对电池的单位功率成本影响显著。当储能在高SOC值时进行大功率充电以及在低SOC值进行大功率放电都会引起单位功率成本的指数抬升。此时从经济性角度出发,以单位调压成本作为一致性变量便可减少在这种极大损耗电池寿命的工况下充放电,并倾向于由SOC值更适宜或储能容量更大的储能单元提供输出,从而尽量避免储能进入此种工况。
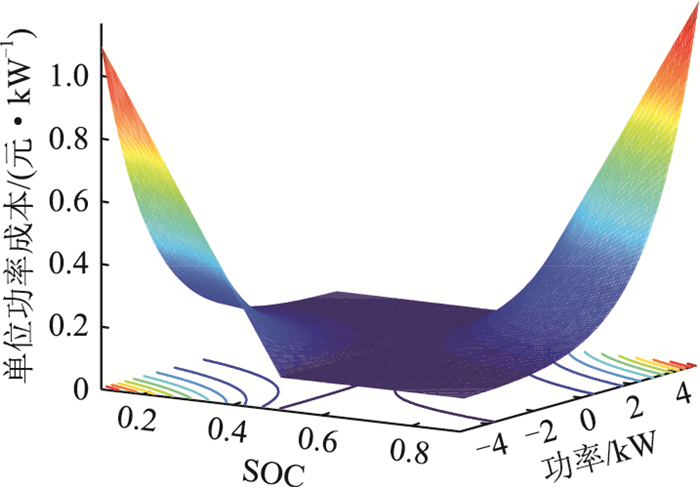
|
图 2 储能有功单位成本与功率及SOC的关系 Fig. 2 The unit cost of active power energy storage varies with the change of power and SOC |
光伏逆变器可以在不追加投资的情况下向配电网提供无功功率,但逆变器进行无功功率调压而产生的成本常常被忽视。无功功率输出会对逆变器部件产生较大的热应力[26],特别是电容等容易在热功率循环中加速老化的组件。此特性使得逆变器产生额外损耗,从而减少了逆变器的寿命,同时更大的功率会使逆变器产生更大的功率损耗。
2.2.1 光伏逆变器损耗成本模型考虑到电容器是影响逆变器设备寿命的重要组件,将电容器作为逆变器的寿命基准[27],参考电容器正常工况下的寿命公式,可以得到无功功率注入寿命减少量LR为:
| $ L_{\mathrm{R}}=O_{\mathrm{L}}^{\mathrm{P}}-O_{\mathrm{L}}^{\mathrm{Q}}=\nu\left(\theta_k-2^{\lambda_k-\mu Q^2}\right) $ | (17) |
式中:OLP、OLQ分别为逆变器仅输出有功和无功时电容器的工作寿命;Q为逆变器输出无功功率;λk、θk、μ、ν由第k次逆变器功率输出时电容器组与逆变器工作参数推算得到,可参考文献[11]。
当逆变器用于提供无功功率时,由于逆变器寿命缩短,导致PV的均衡电力成本增加。为了将LR整合到无功成本值中,须量化逆变器寿命损耗的效果。在这种情况下,需要基于光伏系统的均衡电力成本,均衡电力成本增加值LI对于不同的值LR以近似为:
| $ L_{\mathrm{I}}=\frac{\eta^{\mathrm{LI}, \mathrm{A} 1} L_{\mathrm{R}}+\eta^{\mathrm{LI}, \mathrm{A} 0}}{L_{\mathrm{R}}^2+\eta^{\mathrm{LI}, \mathrm{B} 1} L_{\mathrm{R}}+\eta^{\mathrm{LI}, \mathrm{B} 0}} $ | (18) |
式中:ηLI, A0、ηLI, A1、ηLI, B0、ηLI, B1为常数,根据不同型号逆变器确定。
由于逆变器寿命缩短导致的第k次光伏逆变器无功调压单位成本ckQPV, LR计算如下:
| $ c_k^{\mathrm{QPV}, \mathrm{LR}}=L_{\mathrm{I}} / Q_k^{\mathrm{PV}} $ | (19) |
式中:QkPV为第k次光伏逆变器输出的无功功率。为了简化计算可将ckQPV, LR用式(19)拟合为二次函数形式:
| $ c_k^{\mathrm{QPV}, \mathrm{LR}}=\eta^{\mathrm{LR}, 0}+\eta^{\mathrm{LR}, 1} Q_k^{\mathrm{PV}}+\eta^{\mathrm{LR}, 2}\left(Q_k^{\mathrm{PV}}\right)^2 $ | (20) |
式中:ηLR, 0、ηLR, 1、ηLR, 2分别为二阶函数拟合得到的零阶、一阶、二阶麦克劳林级数。
2.2.2 逆变器单位调压成本模型因此储能第k次不规则放电有功调压单位总成本ckINV可表示为:
| $ c_k^{\mathrm{INV}}=c_k^{\mathrm{QPV}, \mathrm{LR}}+c_{\mathrm{INV}}^{\mathrm{M}}+c_{\mathrm{INV}}^{\mathrm{Ploss}} $ | (21) |
式中:cINVM为光伏逆变器单位功率维护成本;cINVPloss为光伏逆变器每单位功率产生的有功损耗成本。
从而可以得到节点i处逆变器对节点j处节点调压的无功单位调压成本Si, jV-C, Q的计算公式:
| $ S_{i, j}^{\mathrm{V}-\mathrm{C}, \mathrm{Q}}=\frac{c_k^{\mathrm{INV}}}{\Delta V_j}=\frac{c_k^{\mathrm{INV}}}{S_{i, j}^{\mathrm{V}-\mathrm{Q}} \Delta Q_{\mathrm{INV}}} $ | (22) |
式中:ΔQINV为逆变器因调压需求注入的无功功率。
图 3为100 kvar无功输出能力的光伏逆变器输出的单位无功功率成本对应输出无功功率的变化曲线。相比于空载运行状态,满负荷无功输出的成本提高超过10倍,因此在利用光伏逆变器调压时要充分考虑输出功率对成本的影响。虽然储能在单位功率成本上数倍于逆变器,但考虑到电压灵敏度的影响,不同节点处的储能单位调压成本仍会低于其他节点的逆变器调压成本。
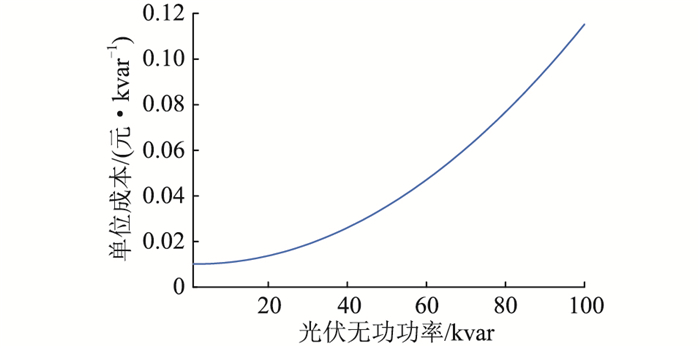
|
图 3 逆变器单位无功功率成本与输出无功功率关系 Fig. 3 Relationship between unit reactive power cost and output reactive power of inverter |
一致性问题源于二十世纪六十年代的管理科学和统计学,在计算机领域具有很长的历史并奠定了分布式计算的基础。所谓一致即指多智能体在某一个状态量上趋于相等,而一致性算法则表征智能体之间信息传递的规则[27]。
设智能体之间信息传递的网络为拓扑图G=(W,E),其中W为一个有限的非空元素集合,称为顶点或节点;E为节点对组成的边的集合。如果任意不同的节点对之间有一条路径,则图被连通。设A=[ai, j]为图G的邻接矩阵,其中非对角线值为顶点到顶点之间的边数和,其数学表达式[28]为:
| $ a_{i, j}= \begin{cases}1 & \left(w_i, w_j\right) \in E \\ 0 & \text { 其他 }\end{cases} $ | (23) |
式中:wi、wj为W的元素。则图G的度矩阵D=diag(d1 d2 … dn)可利用A计算:
| $ d_i=\sum\limits_{j \neq i} a_{i, j} $ | (24) |
文中使用的一致性算法通过网络在相邻节点间进行信息相互传输,更新各节点的状态变量,其网络拓扑为简单图,即不包含图环路或多边的无权无向图。随着迭代计算的进行,节点的状态变量逐渐趋于相同,当所有节点的状态变量差值收敛于一定范围内时,则称系统收敛。此时平均一致性算法可以描述为:
| $ x_i(l+1)=\sum\limits_{j \in W} z_{i, j} x_j(l) $ | (25) |
式中:xi(l)为节点i第l次迭代时的状态变量;zi, j为节点i到节点j状态转移系数。
| $ z_{i, j}= \begin{cases}\frac{1}{1+d_i} \;\; j=i \\ \frac{1}{1+d_i} \;\; j \neq i ;(i, j) \;\;\in \varepsilon \\ 0 \quad j \neq i ;(i, j) \;\;\notin \varepsilon\end{cases} $ | (26) |
式中:ε⊆W×W,为通信路径的集合;(i, j)∈ε表示节点i与节点j之间存在通信链路。
对于连通无向图网络,分布式算法可以使所有初始值渐近收敛到平均一致。
3.2 分布式电压控制模型采用基于一致性算法的分布式控制,须保证网络节点电压在允许范围内:
| $ V_{\min } <V_{i, t}<V_{\max } $ | (27) |
式中:Vi, t为t时刻节点i的电压;Vmax、Vmin分别为电压上限和下限。
为了充分降低调压成本,使电压调节任务按单位效果调节成本分配,文中选定单位调压成本SV-C为一致性变量,此时配电网储能与光伏逆变器调压总成本Ccost为:
| $ C_{\text {cost }}=\sum\limits_{i \in W}\left(P_i c^{\mathrm{BSS}}+Q_i c^{\mathrm{INV}}\right)=\Delta V S^{\mathrm{V}-\mathrm{C}} $ | (28) |
式中:ΔV为需要调节的电压幅值。
调压总成本最小等价于单位调压成本最小,即:
| $ \min C_{\operatorname{cost}} \Leftrightarrow \min S^{\mathrm{V}-\mathrm{C}} $ | (29) |
StV-C为t时刻调压幅值与总成本的比值为:
| $ S_t^{\mathrm{V}-\mathrm{C}}=\frac{C_{\mathrm{cost}, t}}{\Delta V_t} $ | (30) |
式中:Ccost, t为t时刻的调压总成本。主导节点的单位调压成本SV-CND, t根据其量测电压进行更新。在光伏出力的高峰时段,如主导节点电压高于电压上限Vmax,则主导节点电压低于电压上限前,SV-CND, t会单调增加;在负荷需求的高峰时段,如主导节点电压低于电压下限Vmin,则主导节点电压高于电压下限前,SV-CND, t会单调增加;在其他时间段,如电压不出现越限,则在未电压越限或降为0前,SV-CND, t会单调减少。主导节点的单位调压成本SV-CND, t的计算如下:
| $ \begin{array}{c} & S_{N_{\mathrm{D}}, t}^{\mathrm{V}-\mathrm{C}}(k)= \\ & \left\{\begin{array}{l} S_{N_{\mathrm{D}}, t}^{\mathrm{V}-\mathrm{C}}(k-1)+\alpha\left(V_{N_{\mathrm{D}}, t}(k)-V_{\max }\right) \quad V_{N_{\mathrm{D}}, t}(k)>V_{\max } \\ S_{N_{\mathrm{D}}, t}^{\mathrm{V}-\mathrm{C}}(k-1)-\beta \quad S_{N_{\mathrm{D}}, t}^{\mathrm{V}-\mathrm{C}} \geqslant 0 ; V_{\text {min }} \leqslant V_{N_{\mathrm{D}}, t}(k) \leqslant V_{\max } \\ S_{N_{\mathrm{D}}, t}^{\mathrm{V}-\mathrm{C}}(k-1)+\alpha\left(V_{N_{\mathrm{D}}, t}(k)-V_{\text {min }}\right) \quad V_{N_{\mathrm{D}}, t}(k) <V_{\text {min }} \end{array}\right. \end{array} $ | (31) |
式中:SV-CND,t为t时刻主导节点的单位调压成本系数;VND, t为t时刻主导节点ND的电压;α为调节控制方法迭代精度的参数(文中取值为1);β为单位调压成本系数回调参数。
| $ \beta= \begin{cases}\alpha\left(V_{\max }-V_{N_{\mathrm{D}}, t}(k)\right) & V_{N_{\mathrm{D}}, t}(k) \geqslant V_* \\ \alpha\left(V_{N_{\mathrm{D}}, t}(k)-V_{\text {min }}\right) & V_{N_{\mathrm{D}}, t}(k) <V_*\end{cases} $ | (32) |
式中:V*为配电网额定电压值。根据式(25)所示的一致性算法,网络中各节点的单位调节成本变量根据式(33)进行更新。
| $ \begin{gathered} S_t^{\mathrm{V}-\mathrm{C}}(k)=\sum\limits_{j \in W} z_{i, j} S_t^{\mathrm{V}-\mathrm{C}}(k-1)= \\ \sum\limits_{j \in W, j \neq N_{\mathrm{D}}} z_{i, j} S_t^{\mathrm{V}-\mathrm{C}}(k-1)+z_{i, N_{\mathrm{D}}} S_{N_{\mathrm{D}}, t}^{\mathrm{V}-\mathrm{C}}(k-1) \end{gathered} $ | (33) |
通过上述过程即可确定在解决配点网络主导节点电压越限时所需的单位调压成本SV-C。然后,配电网各节点上光伏逆变器的控制器与储能根据本地服务器上的单位调压成本模型计算得到t时刻各自点所需输出的功率值。
逆变器根据单位调节成本变量调节在t时刻需要输出的无功功率Qi, t为:
| $ \begin{array}{c} {Q_{i, t}} = \\ \left\{ \begin{array}{c} \frac{{\sqrt {{{\left( {{\eta ^{{\rm{LR}}, 1\;}}} \right)}^2} - 4{\eta ^{{\rm{LR}}, 2\;}}\left( {{\eta ^{{\rm{LR}}, 0}} - c_k^{{\rm{QPV}}, {\rm{LR\;\;}}}} \right)} - {\eta ^{{\rm{LR}}, 1}}}}{{2{\eta ^{{\rm{LR\;}}, 2}}}}\\ {V_{{N_{\rm{D}}}, t}} \ge {V_{\min }}\\ \frac{{ - \sqrt {{{\left( {{\eta ^{{\rm{LR}}, 1\;}}} \right)}^2\;} - 4{\eta ^{{\rm{LR}}, 2\;\;}}\left( {{\eta ^{{\rm{LR}}, 0\;\;}} - c_k^{{\rm{QPV}}, {\rm{LR\;\;}}}} \right)} + {\eta ^{{\rm{LR}}, 1}}}}{{2{\eta ^{{\rm{LR}}, 2}}}}\\ {V_{{N_{\rm{D}}}, t}} < {V_{\min }} \end{array} \right. \end{array} $ | (34) |
| $ c_k^{\mathrm{QPV}, \mathrm{LR}}=S_{i, j}^{\mathrm{V}-\mathrm{Q}}\left(S_t^{\mathrm{V}-\mathrm{C}}-c_{\mathrm{INV}}^{\mathrm{M}}-c_{\mathrm{INV}}^{\mathrm{Ploss}}\right) $ | (35) |
式中:ckQPV, LR≥0,当单位调压成本低于维护成本时则取0。
此外,光伏逆变器须满足功率与功率因素约束:
| $ -Q_{\mathrm{PV}, i}^{\max } \leqslant Q_{i, t} \leqslant Q_{\mathrm{PV}, i}^{\max }q $ | (36) |
| $ \cos \varphi_{y_{\mathrm{PV}}} \in[-1, -0.9] \cup[0.9, 1] \quad y_{\mathrm{PV}} \in \mathit{\Theta}_{\mathrm{PV}} $ | (37) |
式中:QPV, imax为节点i光伏逆变器允许输出最大无功功率; φyPV为光伏并网点yPV的功率因数角;ΘPV为接入光伏的节点集合。
储能根据单位调节成本变量调节在t时刻需要输出的有功功率为:
| $P_{\mathrm{ESS}, i, t}=\left\{\begin{array}{l} \sqrt{\frac{\mathit{\Gamma}_{\mathrm{R}}\left(C_{\mathrm{BSS}}^{\mathrm{M}}+C_{\mathrm{BSS}}^{\mathrm{Ploss}}\right)}{S_i^{\mathrm{V}-\mathrm{P}} S_t^{\mathrm{V}-\mathrm{C}} \mathit{\Gamma}_{\mathrm{R}}-\eta_i^{\mathrm{d}} C_{\mathrm{BSS}, i}^{\text {cape }} \Delta t}} \quad V_{N_{\mathrm{D}}, t} \geqslant V_{\max } \\ -\sqrt{\frac{\mathit{\Gamma}_{\mathrm{R}}\left(C_{\mathrm{BSS}}^{\mathrm{M}}+C_{\mathrm{BSS}}^{\mathrm{Ploss}}\right)}{S_i^{\mathrm{V}-\mathrm{P}} S_t^{\mathrm{V}-\mathrm{C}} \mathit{\Gamma}_{\mathrm{R}}-\eta_i^{\mathrm{d}} C_{\mathrm{BSS}, i}^{\text {cape }} \Delta t}} \quad V_{N_{\mathrm{D}}, t}<V_{\min } \end{array}\right. $ | (38) |
式中:PBSS, i, t为t时刻节点i储能的有功功率,当PBSS, i, t>0时表示储能从电网接收电能;CBSS, icape为节点i储能的容量;Δt为控制时间间隔。
因此,下一个时刻储能的SOC为:
| $ S_{y_{\mathrm{BSS}}, t+1}=S_{y_{\mathrm{BSS}}, t}+\Delta S_{y_{\mathrm{BSS}, t}} \quad y_{\mathrm{BSS}} \in \mathit{\Theta}_{\mathrm{BSS}} $ | (39) |
式中:SyBSS, t为储能并网点yBSS的SOC值;ΘBSS为接入储能节点集合。储能还须满足功率及SOC约束:
| $ \underline{S} \leqslant S_{y_{\mathrm{BSS}, t}} \leqslant \bar{S} \quad y_{\mathrm{BSS}} \in \mathit{\Theta}_{\mathrm{BSS}} $ | (40) |
| $ -P_{\mathrm{BSS}, y_{\mathrm{BSS}}}^{\mathrm{rated}} \leqslant P_{\mathrm{BSS}, y_{\mathrm{BSS}}, t} \leqslant P_{\mathrm{BSS}, y_{\mathrm{BSS}}}^{\mathrm{rated}} \quad y_{\mathrm{BSS}} \in \mathit{\Theta}_{\mathrm{BSS}} $ | (41) |
式中:$\underline{S}、\bar{S}$分别为储能SOC的下限和上限;PBSS, yBSSrated为节点yBSS储能的额定有功功率。
由此通过单位调节成本得到了最优调压效果的储能有功与光伏逆变器无功输出方案。
3.3 控制流程文中提出一种计及光伏逆变器与储能电池寿命损耗成本的分布式电压控制策略,以单位调压成本作为一致性参数, 以经济性为目标协调控制逆变器无功输出和储能有功输出。t时刻分布式功率控制算法的流程如图 4所示,具体如下。
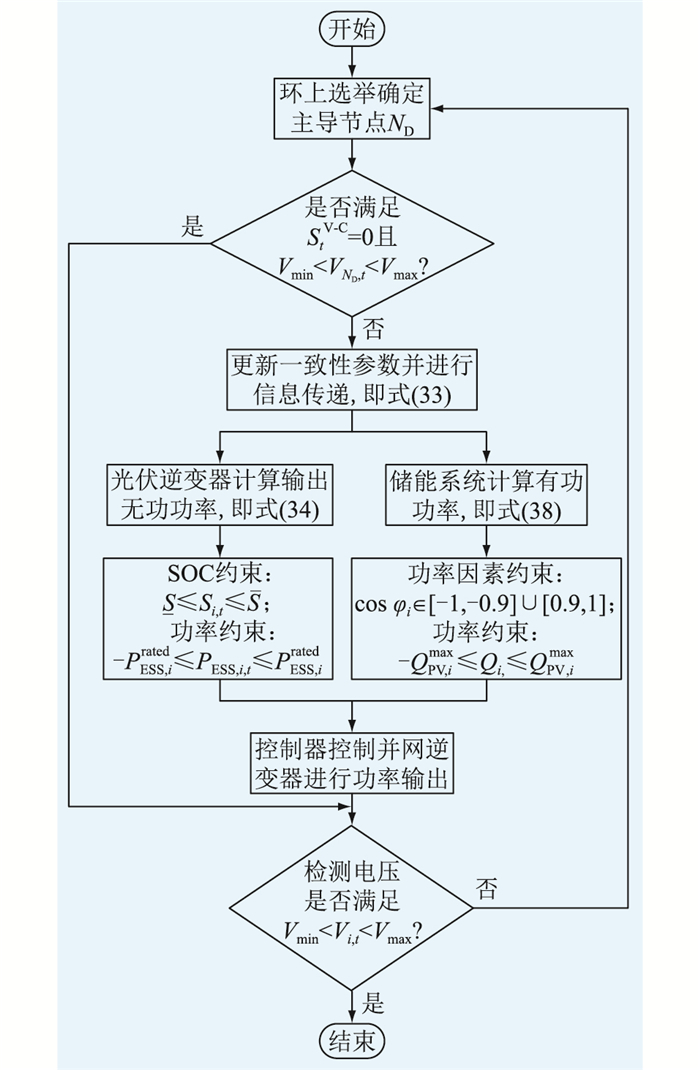
|
图 4 控制策略流程 Fig. 4 Flow chart of control strategy |
(1) 确定主导节点ND。首先t时刻进行节点电压检测,如果有节点检测到电压越限,则触发环上选举算法,进行异步环leader选举,重新选择主导节点。检测到电压越限的处理器P发送一个含节点电压信息msg(自己的标识符)到左邻;当其他节点处理器接收一个msg时,检验收到的msg并更新记载值然后转发msg;当某处理器收到一个含有自身标识符的msg,则此处理器节点确定为主导节点,并向周围发送终止msg。如果主导节点电压未越限且单位调压成本StV-C为0,则直接对所有节点电压进行检测,均未越限则结束控制。
(2) 更新单位调压成本StV-C。确定好主导节点后,主导节点根据电压越限值对单位调压成本StV-C进行迭代计算;计算完毕后单位调压成本通过通信网络传递到网络中的各个逆变器与储能的本地服务器中;各逆变器与储能根据分布式控制模型以及单位调压成本模型计算无功与有功输出功率值;控制器根据计算值控制各自并网逆变器功率输出,直至主导节点电压不再越限;系统重新检测电压越限,确定主导节点,直至所有节点电压不越限。
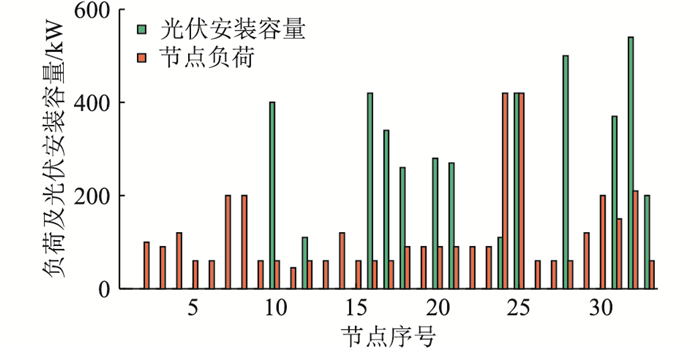
4 算例分析 4.1 算例背景为验证文中所提策略的有效性及其在配电网中应用的可行性,将IEEE 33节点配电系统[29-31]作为算例,利用MATLAB进行仿真分析,对所提策略的有效性进行验证。该系统含有33个节点,基准电压和基准容量分别为VBase=12.66 kV、SBase=10 MV ·A。光伏安装点与安装容量以及各节点负荷峰值容量如图 5所示,这里逆变器具备Volt/Var控制功能,容量为光伏安装容量的1.1倍,逆变器经变压器直接接入配电网,且发出功率优先满足本地负荷。分布式储能与光伏在相同节点接入,储能接入容量为所在节点接入光伏在额定功率下发电4 h电量的15%。
|
图 5 光伏的安装容量与节点的峰值负荷功率 Fig. 5 The installed capacity of PV and the peak load power of each node |
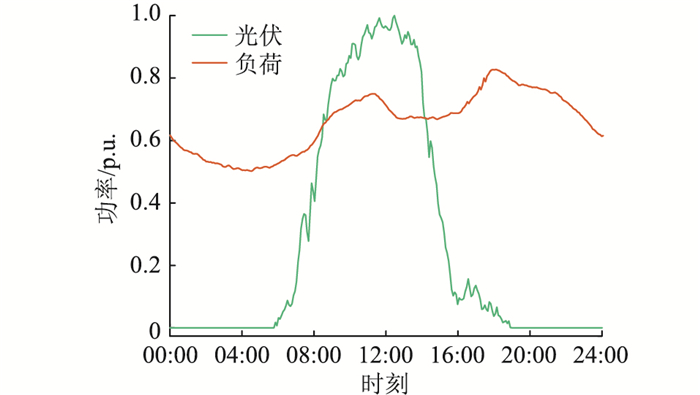
配电网结构与光储分布示意如图 6所示。系统总负荷和光伏总有功输出功率一天24 h的变化情况如图 7所示。该配电网系统的分布式光伏渗透率[32-34]为113.6%,且一级电压控制系统已根据日前调度利用有载调压器与电容器完成初步调压动作。为解决光伏午间急剧功率倒送引起的暂态电压越限问题,文中设计了光储分布式调压策略对电压越限进行抑制,避免有载调压器与电容器的多次动作。

|
图 6 配电网结构与光储分布示意 Fig. 6 Schematic diagram of distribution network structure and optical storage distribution |
|
图 7 系统内总光伏和负荷典型日的功率 Fig. 7 Power of total PV and load on a typical day in the system |
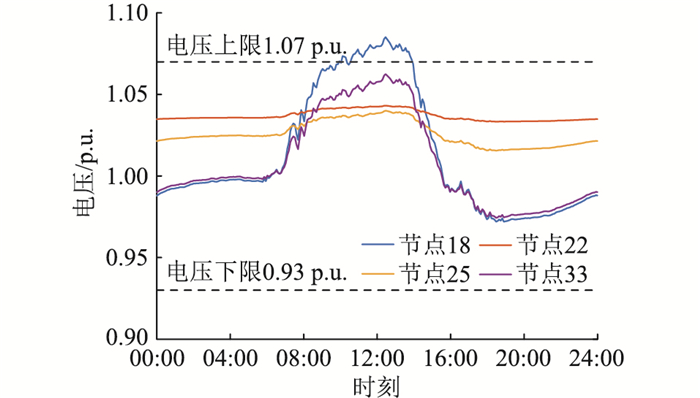
通过仿真计算,若配电网不具备调压控制能力,系统关键节点日内的电压曲线如图 8所示,所选关键节点为配电网4条支路的末端节点。结合图 8可知,系统电压抬升效果与线路倒送功率成正比,且在09:55—13:50期间,18节点电压持续越限,最大越限幅度达到1.085,此外节点13—17也出现不同程度的过电压。其他支路节点由于到首端的阻抗距离较小而电压并未越限,且阻抗距离越小电压波动越小,所以文中将电压越限最严重的18节点作为主要观察节点。
|
图 8 无控制时末节点电压 Fig. 8 Terminal node voltage without control |
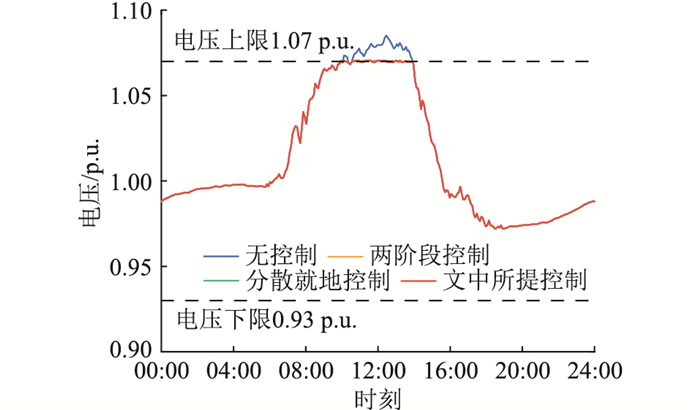
文中主要考察所提基于单位调压成本的控制策略对电压越限的控制效果及该策略下的电压调节成本,并与另外2种分布式控制策略进行比较。一种是常规的先调用无功后调用有功的分散就地式控制策略;另一种是基于逆变器无功利用率与储能SOC一致的两阶段控制策略[22](后续简称为两阶段控制)。
图 9为不同控制策略下的18节点电压曲线,可见,3种控制策略均调用光伏逆变器与储能调压,使配电网电压越限得到有效抑制,在调节能力允许的情况下,其控制效果的主要区别在于控制成本。
|
图 9 不同控制策略下的18节点电压 Fig. 9 18-node voltages under different control strategies |
文中设计的控制策略以经济性为目标调动各节点的逆变器与储能参与调压。根据第1章分析可知,相邻节点的电压灵敏度以及实际电压接近,在文中所提控制策略下具有相似的调压结果,所以选取了越限支路的关键节点(16、18)、中间节点(10)和其他支路有调压能力的末节点(21、25、33)作为代表进行分析。由于越限时间段外调用的功率均为0,所以选取09:00—15:00存在电压越限的时段进行分析。
图 10为文中设计控制策略下关键节点控制效果。由图 10可见,配电网节点过电压过程中出现3次峰值,第一次电压峰值较小,系统中仅节点18电压越限,此时节点10、16、18的逆变器均参与调压,输出的功率值随着距离越限点的阻抗距离缩小而增大,且18节点也未因是本地节点而满负荷工作;与此同时,其他支路节点的逆变器由于对电压越限点的电压灵敏度不高且单位调压成本较大而并未动作。
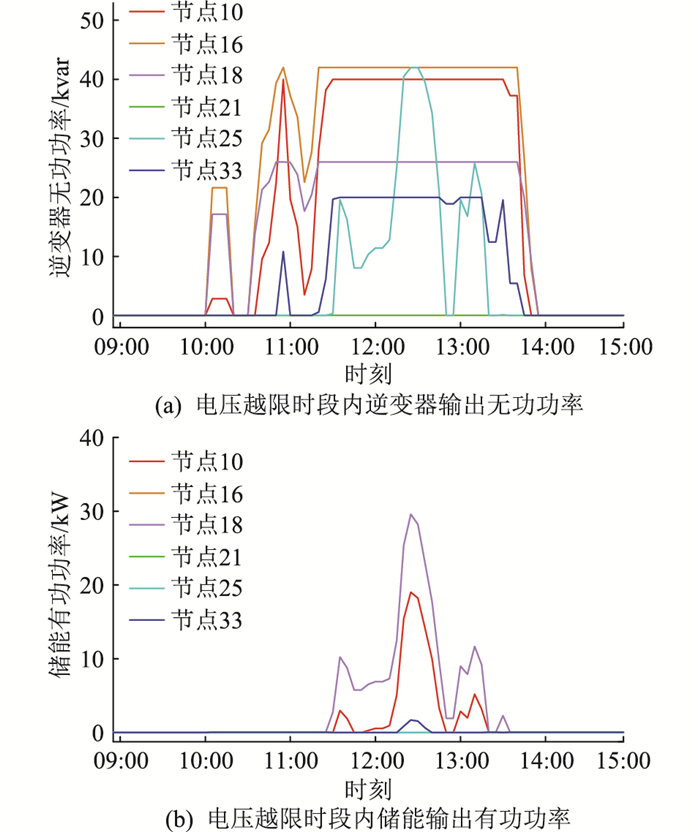
|
图 10 文中设计控制策略下关键节点控制结果 Fig. 10 Control results of key nodes under control strategy designed in this paper |
第二次电压峰值时,电压越限更大,节点10、16、18的逆变器向配电网注入大量无功,期间均出现短暂饱和,节点10也由于更大装机容量使输出功率反超电压灵敏度更大的节点16;同时节点33的逆变器在越限较大的时段内也参与了调压,但2次电压越限值均未超过0.015 p.u.,所以除节点18外各节点储能均未投入调压。第三次过电压值远高于前2次过电压,节点25的逆变器也切入使用,并且此前一直未投入使用的其他节点储能也参与了调压。节点18为主导节点,节点16距离主导节点近且容量大,所以这2个节点的储能都进行了大功率输出;而距离主导节点远的节点10与33由于电压灵敏度小,同调压效果下单位调压成本更高,因此输出功率相对较小。
图 11为累计总成本与单位调压成本的变化趋势。在整个电压调节过程中逆变器无功调压成本占比始终高于储能有功调压占比,逆变器调压成本占总成本为74.7%。由第3章可知储能存在最低单位功率成本,而从11:25开始当单位调压成本连续超过储能单位运维成本0.1元时,各节点储能陆续切入使用;12:20后成本低的光伏逆变器可调功率使用殆尽,此后单位调压成本才大幅提高,使得其他节点储能能够投入调压,累计成本也因此大幅抬高,以保证调压的效果。单位调压成本总体的变化曲线与电压越限曲线趋势相同,但受到节点间电压灵敏度离散的影响,单位调压成本总体的波动更大。
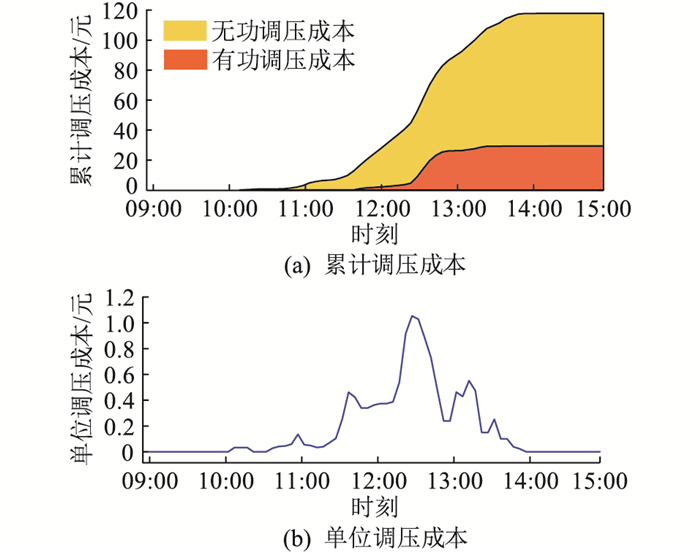
|
图 11 累计总成本与单位调压成本 Fig. 11 Cumulative total cost and unit regulating cost |
文中设计策略通过对不同节点间储能与逆变器进行合理的调压功率分配以达到经济性最优的效果。图 12为3种策略下有功、无功的功率输出对比。由图 12可见,分散就地控制方法仅调用了节点16—18的储能与逆变器进行调压,而另一种两阶段电压控制方法调用了所有节点的储能与逆变器进行调压。文中所提控制策略虽也调用了大部分节点的储能与逆变器进行调压,但相比基于利用率的两阶段方法,文中策略的功率分配兼顾了不同设备的调压成本与不同节点的电压灵敏度。虽然逆变器调压的成本相对更低,但即使全部额定功率输出也无法满足抑制电压越限的需求,所以须协调控制有功与无功的输出。
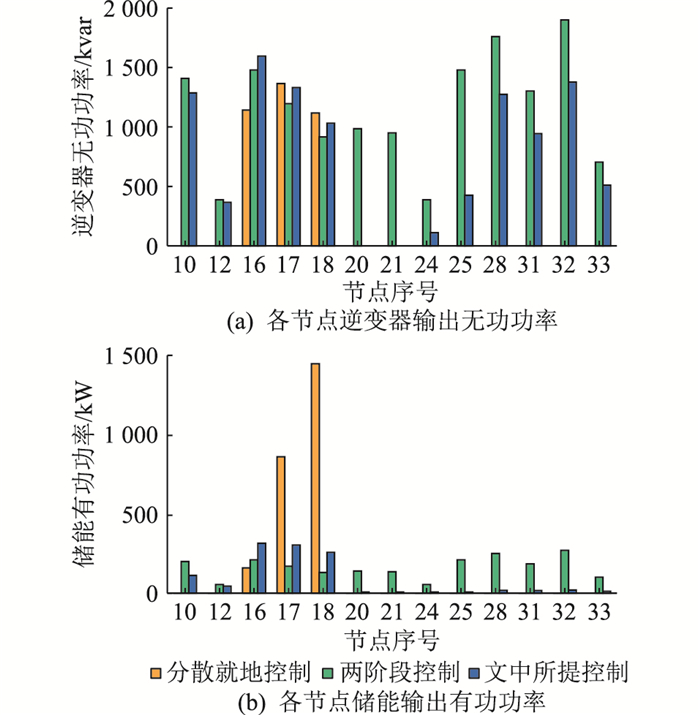
|
图 12 3种策略下的控制结果对比 Fig. 12 Comparison of control results under three strategies |
在逆变器控制方面,考虑到输出功率越高使用寿命损耗越大的特性,文中所提控制策略汲取了两阶段控制的优势,将无功需求较均匀地分配给各个逆变器,使电压灵敏度较高的节点储能与逆变器更多参与调压,且缺额主要由电压灵敏度更高的节点处的储能来补足,避免了逆变器平均单位功率成本的提高。
在储能控制方面,由于电压越限时优先调用逆变器进行调压,所以储能的有功调压需求量相对较少,主要调用电压灵敏度高、在电压越限节点附近的储能进行调压,兼顾储能SOC上升导致的成本增加,相比分散就地式控制调用了更多节点的储能,又同时相比于两阶段控制策略少调用了82 kW的有功功率,从而充分降低的调压成本。
通过将单位调压成本作为一致性算法的一致性参数,文中所提控制策略在成本上控制效果明显优于其他策略。从图 13所示的不同控制策略的累计调压成本可以看出,虽然3种控制成本的累计曲线趋势基本相同,但文中所提控制策略的单位调压成本始终低于其他策略,差距随时间积累,文中所提控制策略在总成本上具有明显优势。
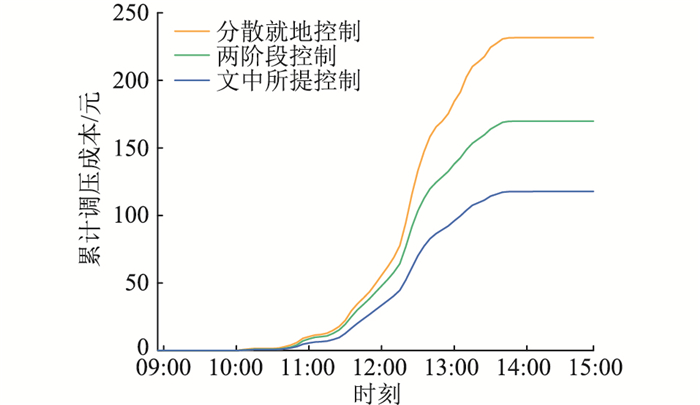
|
图 13 3种控制策略下的累计调压成本 Fig. 13 Cumulative regulation cost under three control strategies |
表 1对比了3种控制策略的调压效果,可以看出,文中所提控制策略具有显著的成本优势。相较于分散就地控制,文中所提控制策略更多调用相邻节点无功代替本地有功,使单位有功成本与单位无功成本相较于分散就地式控制分别减小了67.2%与1.9%,有功调压总量减小了54.4%,无功调压总量增加了183.1%,从而使最终总成本下降了48.9%。而相较于两阶段控制,文中所提控制策略利用电压-价格灵敏度权衡调压效果与成本,使得单位有功成本与单位无功成本相较于两阶段控制分别增加了14.3%、6.2%,有功、无功调压总量分别下降了46.6%、30.9%,从而使最终总成本下降了30.3%。
|
|
表 1 不同策略参数对比 Table 1 Comparison of different strategy parameters |
在运行效率方面,由于文中所提控制策略含有非线性计算,所以平均单次迭代时间要长于分散就地控制与两阶段控制。但文中所提控制基于单位调压成本,并利用电压灵敏度推得各个节点功率输出值,使算法在迭代计算时可以沿更大梯度方向收敛。最终文中所提控制策略下24 h调压程序累计执行时间同比分散就地控制、两阶段控制分别增加了73.9%和8.1%,与两阶段控制效率相当,即文中所提控制策略在增加有限运算量的基础上可以获得相比其他控制方法更大的经济优势。
5 结论文中针对高比例光伏接入配电网导致的电压越限问题,提出了一种计及设备寿命损耗成本的分布式电压控制策略,并与分散就地控制策略以及基于逆变器无功利用率与储能SOC一致的两阶段控制策略进行了仿真对比,得出以下结论:
(1) 文中所提控制策略能有效调控配电网中各节点光伏逆变器与储能的功率输出,解决由于分布式光伏功率倒送导致的电压越限问题。
(2) 该控制策略相比其他控制策略推导了设备的寿命损耗成本,使配电网获得经济性的同时避免了调压出力集中在部分节点的问题,减少了设备的寿命损耗。
(3) 该策略以单位调压成本作为一致性变量,在相同调压效果下,以成本最低的功率调控方式对电压越限进行抑制,总调压成本低于其他策略,经济性更佳。
致谢
本文得到国网江苏省电力有限公司科技项目“配置储能的高渗透分布式光伏主动支撑技术研究”(J2022017)、江苏省研究生科研与实践创新计划项目(KYCX23_1768)资助,谨此致谢!
| [1] |
国家能源局. 《关于报送整县(市、区)屋顶分布式光伏开发试点方案的通知》[EB/OL]. [2023-03-20]. http://gdsolar.org/dongtaiinfo_1879.html. National Energy Administration. Notice on submitting the county (city, district) roof distributed photovoltaic development pilot program[EB/OL]. [2023-03-20]. http://gdsolar.org/dongtaiinfo_1879.html. (  0) 0) |
| [2] |
李建林, 方知进, 谭宇良, 等. 电化学储能系统在整县制屋顶光伏中应用前景分析[J]. 太阳能学报, 2022, 43(4): 1-12. LI Jianlin, FANG Zhijin, TAN Yuliang, et al. Application prospect analysis of electrochemical energy storage technology in county-wide rooftop photovoltaic system[J]. Acta Energiae Solaris Sinica, 2022, 43(4): 1-12. DOI:10.19912/j.0254-0096.tynxb.2022-0084 (  0) 0) |
| [3] |
李建林, 袁晓冬, 郁正纲, 等. 利用储能系统提升电网电能质量研究综述[J]. 电力系统自动化, 2019, 43(8): 15-24. LI Jianlin, YUAN Xiaodong, YU Zhenggang, et al. Comments on power quality enhancement research for power grid by energy storage system[J]. Automation of Electric Power Systems, 2019, 43(8): 15-24. (  0) 0) |
| [4] |
SUN X Z, QIU J, YI Y, et al. Cost-effective coordinated voltage control in active distribution networks with photovoltaics and mobile energy storage systems[J]. IEEE Transactions on Sustainable Energy, 2022, 13(1): 501-513. DOI:10.1109/TSTE.2021.3118404 (  0) 0) |
| [5] |
RESHIKESHAN S S M, MATTHIESEN S L, ILLINDALA M S, et al. Autonomous voltage regulation by distributed PV inverters with minimal inter-node interference[J]. IEEE Transactions on Industry Applications, 2021, 57(3): 2058-2066. DOI:10.1109/TIA.2021.3064911 (  0) 0) |
| [6] |
WANG L C, BAI F F, YAN R F, et al. Real-time coordinated voltage control of PV inverters and energy storage for weak networks with high PV penetration[J]. IEEE Transactions on Power Systems, 2018, 33(3): 3383-3395. DOI:10.1109/TPWRS.2018.2789897 (  0) 0) |
| [7] |
YU P, WAN C, SONG Y H, et al. Distributed control of multi-energy storage systems for voltage regulation in distribution networks: a back-and-forth communication framework[J]. IEEE Transactions on Smart Grid, 2021, 12(3): 1964-1977. DOI:10.1109/TSG.2020.3026930 (  0) 0) |
| [8] |
KRYONIDIS G C, KONTIS E O, CHRYSOCHOS A I, et al. A coordinated droop control strategy for overvoltage mitigation in active distribution networks[J]. IEEE Transactions on Smart Grid, 2018, 9(5): 5260-5270. DOI:10.1109/TSG.2017.2685686 (  0) 0) |
| [9] |
LI J Q, CHEN J, ZHANG W, et al. Bi-level dispatching strategy for HESS in distribution networks with high PV penetration considering voltage regulation and price arbitrage[C]//2018 IEEE Power & Energy Society General Meeting (PESGM). Portland, OR, USA. IEEE, 2018: 1-5.
(  0) 0) |
| [10] |
HU Y, LIU W Y, WANG W Z. A two-layer volt-var control method in rural distribution networks considering utilization of photovoltaic power[J]. IEEE Access, 2020, 8: 118417-18425. DOI:10.1109/ACCESS.2020.3003426 (  0) 0) |
| [11] |
GANDHI O, RODRÍGUEZ-GALLEGOS C D, GORLA N B Y, et al. Reactive power cost from PV inverters considering inverter lifetime assessment[J]. IEEE Transactions on Sustainable Energy, 2019, 10(2): 738-747. DOI:10.1109/TSTE.2018.2846544 (  0) 0) |
| [12] |
TANG Z Y, HILL D J, LIU T. Fast distributed reactive power control for voltage regulation in distribution networks[J]. IEEE Transactions on Power Systems, 2019, 34(1): 802-805. DOI:10.1109/TPWRD.2018.2868158 (  0) 0) |
| [13] |
JU Y T, ZHANG Z F, WU W C, et al. A bi-level consensus ADMM-based fully distributed inverter-based volt/var control method for active distribution networks[J]. IEEE Transactions on Power Systems, 2022, 37(1): 476-487. DOI:10.1109/TPWRS.2021.3097798 (  0) 0) |
| [14] |
王枭, 何怡刚, 马恒瑞, 等. 考虑规模化储能的配电网电压分布式控制[J]. 电力自动化设备, 2022, 42(2): 25-30, 55. WANG Xiao, HE Yigang, MA Hengrui, et al. Distributed voltage control of distribution network considering large-scale energy storage[J]. Electric Power Automation Equipment, 2022, 42(2): 25-30, 55. DOI:10.16081/j.epae.202111012 (  0) 0) |
| [15] |
鲁鹏, 田浩, 武伟鸣, 等. 需求侧能量枢纽和储能协同提升风电消纳和平抑负荷峰谷模型[J]. 电力科学与技术学报, 2021, 36(1): 42-51. LU Peng, TIAN Hao, WU Weiming, et al. Demand side energy hub and energy storage cooperate to smooth peak and valley and improve wind power consumption model[J]. Journal of Electric Power Science and Technology, 2021, 36(1): 42-51. (  0) 0) |
| [16] |
孔顺飞, 胡志坚, 谢仕炜, 等. 考虑分布式储能与电动汽车充电网络的配电网多目标规划[J]. 电力科学与技术学报, 2021, 36(1): 106-116. KONG Shunfei, HU Zhijian, XIE Shiwei, et al. Multi-objective planning of distribution network considering distributed energy storage and electric vehicle charging network[J]. Journal of Electric Power Science and Technology, 2021, 36(1): 106-116. (  0) 0) |
| [17] |
李梓瑄, 包宇庆, 宋梦, 等. 计及开关寿命损耗的温控负荷分布式控制策略[J]. 电力工程技术, 2022, 41(4): 75-82. LI Zixuan, BAO Yuqing, SONG Meng, et al. Distributed control strategy of temperature control loads considering switch life loss[J]. Electric Power Engineering Technology, 2022, 41(4): 75-82. (  0) 0) |
| [18] |
蒲天骄, 刘威, 陈乃仕, 等. 基于一致性算法的主动配电网分布式优化调度[J]. 中国电机工程学报, 2017, 37(6): 1579-1590. PU Tianjiao, LIU Wei, CHEN Naishi, et al. Distributed optimal dispatching of active distribution network based on consensus algorithm[J]. Proceedings of the CSEE, 2017, 37(6): 1579-1590. (  0) 0) |
| [19] |
陈刚, 包宇庆, 张金龙, 等. 计及寿命损耗成本的储能单元分布式协同控制策略[J]. 电网技术, 2018, 42(5): 1495-1501. CHEN Gang, BAO Yuqing, ZHANG Jinlong, et al. Distributedcooperative control strategy for energy storage units considering life loss cost[J]. Power System Technology, 2018, 42(5): 1495-1501. (  0) 0) |
| [20] |
张新民, 郭铭海, 林亚培, 等. 考虑灵活性的含分布式光伏配电网双层优化调度方法[J]. 电力科学与技术学报, 2021, 36(3): 56-66. ZHANG Xinmin, GUO Minghai, LIN Yapei, et al. A bilayer optimal dispatch approach for distribution networks with distributed photovoltaic considering the flexibility[J]. Journal of Electric Power Science and Technology, 2021, 36(3): 56-66. (  0) 0) |
| [21] |
GERDROODBARI Y Z, RAZZAGHI R, SHAHNIA F. Improving voltage regulation and unbalance in distribution networks using peer-to-peer data sharing between single-phase PV inverters[J]. IEEE Transactions on Power Delivery, 2022, 37(4): 2629-2639. (  0) 0) |
| [22] |
张博, 唐巍, 蔡永翔, 等. 基于一致性算法的户用光伏逆变器和储能分布式控制策略[J]. 电力系统自动化, 2020, 44(2): 86-94. ZHANG Bo, TANG Wei, CAI Yongxiang, et al. Distributed control strategy of residential photovoltaic inverter and energy storage based on consensus algorithm[J]. Automation of Electric Power Systems, 2020, 44(2): 86-94. (  0) 0) |
| [23] |
WANG P F, LIANG D H, YI J L, et al. Integrating electrical energy storage into coordinated voltage control schemes for distribution networks[J]. IEEE Transactions on Smart Grid, 2014, 5(2): 1018-1032. (  0) 0) |
| [24] |
刘星, 陈众, 陈李杰, 等. 含高渗透率光伏的配电网就地-分布式电压控制[J]. 电力电容器与无功补偿, 2021, 42(6): 268-275. LIU Xing, CHEN Zhong, CHEN Lijie, et al. Local-distributed voltage control in distribution networks with high permeability of PVs[J]. Power Capacitor & Reactive Power Compensation, 2021, 42(6): 268-275. (  0) 0) |
| [25] |
ZHANG Y X, XU Y, YANG H M, et al. Optimal whole-life-cycle planning of battery energy storage for multi-functional services in power systems[J]. IEEE Transactions on Sustainable Energy, 2020, 11(4): 2077-2086. (  0) 0) |
| [26] |
DAS A, GUPTA Y, ANAND S, et al. Temperature droop-based dynamic reactive power sharing technique to improve the lifetime of power electronic converter[J]. IEEE Transactions on Power Electronics, 2022, 37(5): 5245-5255. (  0) 0) |
| [27] |
NAINA P M, SWARUP K S. Double-consensus-based distributed energy management in a virtual power plant[J]. IEEE Transactions on Industry Applications, 2022, 58(6): 7047-7056. (  0) 0) |
| [28] |
SHI G D, XIA W G, JOHANSSON K H. Convergence of max-min consensus algorithms[J]. Automatica, 2015, 62: 11-17. (  0) 0) |
| [29] |
詹红霞, 肖竣文, 邓小勇, 等. 计及柔性负荷的高比例风光渗透下配电网孤岛划分策略[J]. 电力工程技术, 2022, 41(4): 108-116. ZHAN Hongxia, XIAO Junwen, DENG Xiaoyong, et al. Islanding strategy for distribution network with high proportion of wind/photovoltaic penetration considering flexible load[J]. Electric Power Engineering Technology, 2022, 41(4): 108-116. (  0) 0) |
| [30] |
申洪涛, 刘宝铭, 任鹏, 等. 基于辨识解耦的含高渗透分布式光伏用户集群基线负荷估计方法[J]. 电力系统保护与控制, 2022, 50(3): 164-173. SHEN Hongtao, LIU Baoming, REN Peng, et al. Aggregated baseline load estimation method under high distributed photovoltaic penetration based on identification and decoupling[J]. Power System Protection and Control, 2022, 50(3): 164-173. (  0) 0) |
| [31] |
王中, 黎丽丽, 李振华, 等. 考虑新能源渗透的电网频率概率分布研究[J]. 电力系统保护与控制, 2021, 49(20): 65-73. WANG Zhong, LI Lili, LI Zhenhua, et al. The evolution characteristics of power grid frequency probability distribution[J]. Power System Protection and Control, 2021, 49(20): 65-73. (  0) 0) |
| [32] |
姚宏民, 杜欣慧, 李廷钧, 等. 光伏高渗透率下配网消纳能力模拟及电压控制策略研究[J]. 电网技术, 2019, 43(2): 462-469. YAO Hongmin, DU Xinhui, LI Tingjun, et al. Simulation of consumption capacity and voltage control strategy of distribution network with high penetration of photovoltaics[J]. Power System Technology, 2019, 43(2): 462-469. (  0) 0) |
| [33] |
帅挽澜, 朱自伟, 李雪萌, 等. 考虑风电消纳的综合能源系统"源-网-荷-储"协同优化运行[J]. 电力系统保护与控制, 2021, 49(19): 18-26. SHUAI Wanlan, ZHU Ziwei, LI Xuemeng, et al. "Source-network-load-storage" coordinated optimization operation for an integrated energy system considering wind power consumption[J]. Power System Protection and Control, 2021, 49(19): 18-26. (  0) 0) |
| [34] |
董炜, 华文, 王冠中, 等. 基于快速核学习的新能源高渗透电网频率风险评估[J]. 浙江电力, 2022, 41(4): 1-6. DONG Wei, HUA Wen, WANG Guanzhong, et al. Frequency risk assessment for power grid with high-penetration renewable integration based on fast kernel learning[J]. Zhejiang Electric Power, 2022, 41(4): 1-6. (  0) 0) |
2. State Grid Jiangsu Electric Power Co., Ltd. Economic and Technological Research Institute, Nanjing 210008, China;
3. State Grid Jiangsu Electric Power Co., Ltd., Nanjing 210024, China
 2023, Vol. 42
2023, Vol. 42


 姚璐勤(1998), 男, 硕士在读, 研究方向为新能源发电及并网技术(E-mail:
姚璐勤(1998), 男, 硕士在读, 研究方向为新能源发电及并网技术(E-mail: