文章编号: 2096-3203(2023)06-0083-08 中图分类号: TM615
目前国家大力提倡构建清洁低碳的环境友好型能源体系,提升清洁能源利用水平,进一步提高电力系统运行效率。屋顶光伏发电作为一种清洁电力,不仅可以促进节能减排,而且不占用现有土地,充分利用闲置的建筑屋顶资源,同时还可以就地消纳,具有多种推广优势。国家能源局日前下发《关于报送整县(市、区)屋顶分布式光伏开发试点方案的通知》,加快了大规模屋顶光伏的发展进程[1-3]。
不同于集中式的地面光伏电站,屋顶光伏发电须考虑与建筑屋顶之间的配合,以及如何安全运行。因此,目前的相关文献主要集中于分布式屋顶光伏发电系统在前期评估、设计、施工、验收及运维等各个阶段的技术研究[4-6],而针对大规模屋顶光伏规划项目经济性方面的研究相对较少。文献[7]对考虑建设距离的远方集中式光伏电站和就地的分布式光伏发电系统的经济性进行比较,建立了包含发电、输电、配电整个过程的光伏系统效率与成本的计算模型;文献[8]分析了包含电价、政府补贴、初投资成本、利率、组件安装形式等影响屋顶光伏发电系统经济性的因素,建立了各因素在不同变化趋势下的屋顶光伏经济性模型;文献[9]引入效益指标对分布式光伏发电项目平准化成本模型进行改进,并利用改进模型对比不同太阳资源地区、不同折现率、不同电价及补贴等情况下的分布式光伏项目的经济性;文献[10-12]则基于光伏补贴政策和分时电价政策建立了分布式光伏发电的经济性评价模型,以期为政府相关政策的完善和精准实施提供理论依据。
随着补贴政策的取消和电价政策的改变,现有文献中的经济性分析模型已无法适应未来屋顶光伏项目的规划。同时全国碳交易市场[13-17]正式启动上线,旨在通过市场手段助力能源转型,大大促进了清洁光伏产业的发展。光伏发电可以减少碳排放,从而获得碳指标,用户可以通过参与碳交易将碳指标转变为经济收益,而已有文献中并没有相关研究。并且在未来较长一段时间内,随着减排目标的提升和碳资产体系的完善[18-20],碳价将持续上涨,因此考虑大规模屋顶光伏项目参与碳交易市场的经济收益十分必要。
若定量地研究碳交易收益,则需要对未来碳交易价格进行预测。目前,国内外文献中用于价格预测的数理模型主要有两大类。一是通过单一模型进行预测,文献[21]利用已实现波动率异质自回归模型(heterogeneous autoregressive model of realized volatility,HAR-RV)动态预测欧洲气候交易所期货合约的第二阶段碳期货价格;文献[22]通过网络搜索变量,运用动态条件相关系数混频数据抽样(dynamic conditional correlation-mixed data sampling,DCC-MIDAS)模型对我国碳价进行预测;文献[23]分别利用广义自回归条件异方差(generalized autoregressive conditional heteroskedasticity,GARCH)模型、k-最近邻模型和隐含波动率对碳期权价格进行预测,比较了3种预测方法的优劣。二是通过组合不同频率、类型模型的方法进行预测,文献[24]提出了一种将遗传算法(genetic algorithm,GA)、经验模式分解(empirical mode decomposition,EMD)和人工神经网络(artificial neural network,ANN) 相结合的多尺度集成预测模型,验证了该模型相比单一模型的优越性;文献[25-27]提出了基于自回归移动平均(auto-regressive and moving average,ARMA)模型和GARCH模型的ARMA-GARCH模型、马尔科夫区制转移单变量自回归模型和基于交叉验证的支持向量机(cross validation and support vector machine,CV-SVM)模型等组合模型,将碳价及其收益率预测进行精细化、复杂化处理。已有相关文献中多采用比较高级、复杂的单一或组合预测模型,提高预测精度和模型鲁棒性,但也大大增加了预测过程的复杂性,而未见对典型的、简易的预测方法加以改进和发展,提高精确度的同时也便于推广运用。
针对以上问题,文中研究参与碳交易市场的大规模屋顶光伏的经济性。主要工作和贡献如下:(1) 研究大规模屋顶光伏项目参与碳交易市场的途径和方法,为项目开发提供指导;(2) 结合全寿命周期的屋顶光伏发电模型,引入碳交易收益建立经济性分析模型;(3) 对传统的灰色预测GM(1, 1)模型进行改进,实现对未来碳交易市场交易价格的预测,从而探究屋顶光伏项目建设的经济性以及碳交易对投资回报的影响。
1 大规模屋顶光伏项目参与碳交易市场机制我国碳交易市场的交易标的由中国碳排放配额(Chinese emission allowance,CEA)以及中国核证自愿减排量(Chinese certified emission reduction,CCER)两部分组成。全国碳交易市场的第一个履约周期在2021年结束,而国家也正在积极筹备重新启动CCER项目的备案和减排量的签发。屋顶光伏若为履约企业资产,则可根据企业自身履约的盈缺情况将其碳排放指标直接进行碳交易,否则可通过申请成为CCER开发项目参与到碳交易市场,从而获得除发电以外的收益。
CCER是指中国在清洁发展机制(clean development mechanism,CDM)中经核证的减排量,依据《碳排放权交易管理暂行条例》,国家鼓励企业、事业单位在我国境内实施可再生能源、林业碳汇、甲烷利用等项目进行自愿减排核证。根据国家发改委制定的《温室气体自愿减排交易管理暂行办法》,在国家自愿减排交易登记簿备案自愿减排项目的减排量,用于抵消碳排放。国内外机构、企业、团体和个人均可参与温室气体自愿减排量交易。目前国家发改委公示CCER审定项目已累计超2 000个,合计备案减排量5 293万t,其中风电、光伏项目占多数[28]。
CCER是一种抵消机制,《全国碳排放权交易管理办法(试行)》中规定了CCER抵消比例不得超过5%,而根据未来碳中和目标所带来的碳配额抵消的潜在需求,未来碳交易市场对CCER的需求会大增[29-30]。当前,在CCER整体呈现供不应求的情况下,CCER挂牌价格呈不断上涨趋势。2021年12月复旦碳价指数显示,CCER交易价格在40元/t左右,而2022年8月北京碳交易试点的CCER价格已突破80元/t,同时欧盟碳交易价格最高已突破100欧元/t。引入CCER交易及抵消机制是一条兼具生态、经济效益的途径,是对碳交易市场的重要补充,尤为利好可再生能源项目,很多企业正在加速布局,且涉及多个减排行业,应用前景十分广阔。
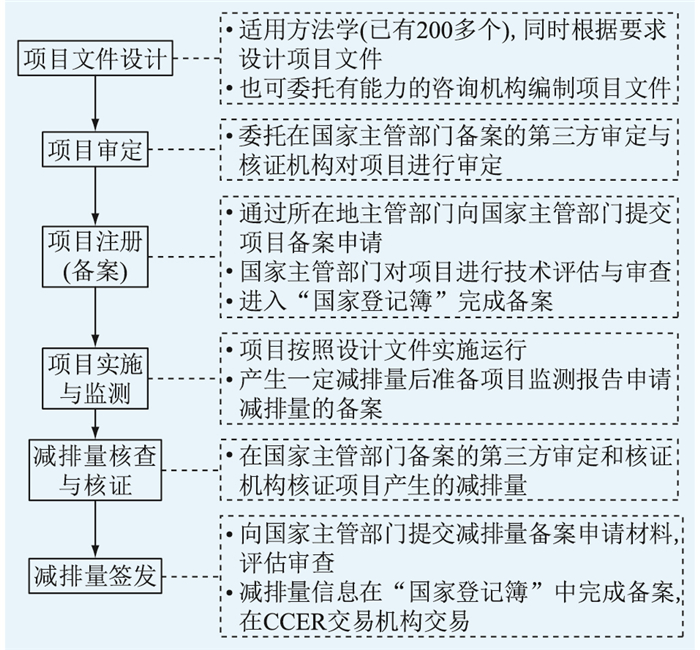
大规模屋顶光伏项目可根据自身条件申请成为CCER开发项目,从而参与到碳交易市场。开发流程在很大程度上沿袭了CDM项目的框架和思路,主要包括项目文件设计、项目审定、项目备案、项目实施与监测、减排量核查与核证、减排量签发6个步骤。具体流程如图 1所示。
|
图 1 CCER项目的开发流程 Fig. 1 Development process of CCER project |
关于CCER碳核算方面,不同行业项目有对应的减排方法学。与当前电力系统碳排放计量及核算方法相同,新能源发电项目的碳减排量等于其发电量替代该区域电网内火电厂生产同等发电量所产生的CO2排放量[31],即排放因子法。因此,屋顶光伏发电的碳核算CCER额度可以表示为:
| $ Q_{\text {ccer }}=E_{\mathrm{pv}} F_{\text {grid }} $ | (1) |
式中:Epv为光伏发电量;Fgrid为光伏项目所在区域的电网电量边际排放因子。
所获得的碳指标可通过协议转让、单向竞价等交易方式,在全国碳排放权交易系统上进行交易,从而转变为经济收益。
2 考虑碳交易的屋顶光伏经济性模型 2.1 光伏发电出力模型光伏组件的输出功率与其实际接收到的太阳辐照度S和表面温度T有关,同时受光伏组件转换效率η1以及光伏发电系统效率(综合考虑逆变器效率、线损等)η2的影响[32]。实际发电过程中,光照强度、温度、湿度、风速等因素是实时变化的。在认定光伏组件上的太阳辐照度和温度均匀、最大功率点跟踪性能良好、光伏板倾斜角设计最佳的情况下,光伏发电系统的输出功率Ppv可用式(2)进行估算。
| $ P_{\mathrm{pv}}=\eta_1 \eta_2 P_{\text {ref }}\left[1+\alpha\left(T-T_{\text {ref }}\right)\right] \frac{S}{S_{\text {ref }}} $ | (2) |
式中:Pref为标准条件下的光伏组件发电功率;α为光伏组件最大功率温度系数;Tref为参考光伏组件表面温度,Tref=25 ℃;Sref为参考太阳辐照度,Sref=1 000 W/m2。
其中,光伏组件的实际电池温度要高于组件背板温度,可以用式(3)计算光伏组件的实际温度。
| $ T=T_{\text {back }}+\frac{S}{1 \;000} \Delta T $ | (3) |
式中:Tback为光伏组件的背板温度;ΔT为太阳辐照度为1 000 W/m2时光伏组件电池温度与背板温度之差,ΔT≈3 ℃。
因此,光伏项目的初始年发电量Epv0可以用式(4)计算得到。
| $ \begin{gathered} E_{\mathrm{pv} 0}= \\ \int_0^{8\;760} \eta_1 \eta_2 P_{\text {ref }}\left[1+\alpha\left(T_{\text {back }}+\frac{S}{1\;000} \Delta T-T_{\text {ref }}\right)\right] \frac{S}{S_{\text {ref }}} \mathrm{d} t_1 \end{gathered} $ | (4) |
式中:t1为发电时间。
此外,光伏项目寿命周期(一般为25 a)内,全过程发电模型还须考虑光伏组件的衰减率。第1年光伏组件衰减率为2%,此后第2~25年光伏衰减率为0.5%,即随着时间的推移,光伏组件衰减后的效率值η1为:
| $ \eta_1=\left\{\begin{array}{l} 0.98 \quad y=1 \\ 0.98-0.005(y-1) \quad 2 \leqslant y \leqslant 25 \end{array}\right. $ | (5) |
式中:y为项目运行的年份。
因此,项目第y年的发电量为:
| $ E_{\mathrm{pv}}(y)=\eta_1 E_{\mathrm{pv} 0} $ | (6) |
光伏发电项目的成本Cpv主要包括项目初始投资成本Cini和运维成本Com。
| $ C_{\mathrm{pv}}=C_{\mathrm{ini}}+C_{\mathrm{om}} $ | (7) |
项目初始投资成本包含咨询设计、设备采购、施工建设等,光伏设计、采购、施工(engineering procurement construction, EPC)总包价格一般与装机规模成正比。
| $ C_{\mathrm{ini}}=k_{\mathrm{epc}} W_{\mathrm{pv}} $ | (8) |
式中:kepc为中标的光伏EPC总承包单价;Wpv为光伏的装机容量。
项目的运维成本主要包括运行期间的电站管理、组件清洗、组件支架及基础维护、设备计划性检修、设备预防性试验等,不同地区的运维成本存在一定差异。
| $ C_{\mathrm{om}}=k_{\mathrm{om}} W_{\mathrm{pv}} $ | (9) |
式中:kom为拟中标的光伏运维单价。
2.3 光伏发电收益模型大规模屋顶光伏发电项目一般是“自发自用、余电上网”,因此以往的屋顶光伏发电收益主要来源于两部分:(1) 自发自用电量Eown对应的节约电费收益Lown;(2) 余量上网电量Esale对应的售电收益Lsale。随着碳交易市场的开放,屋顶光伏发电还可以通过CCER交易获得收益Lcarbon。
(1) 自发自用节约电费收益:
| $ L_{\text {own }}=\iota_{\text {buy }} E_{\text {own }} $ | (10) |
式中:ιbuy为从电网购电的平均用电电价。
(2) 余量上网售电收益:
| $ L_{\text {sale }}=\iota_{\text {sale }} E_{\text {sale }} $ | (11) |
式中:ιsale为该光伏项目上网售电电价。
2.4 光伏发电残值模型光伏发电项目寿命周期结束以后还存在一定的残值Lrv,主要是设备的处理,一般与初始投资成正比[33]。
| $ L_{\mathrm{rv}}=r_{\mathrm{rv}} C_{\mathrm{ini}} $ | (12) |
式中:rrv为光伏项目净残值率。
2.5 碳交易收益模型光伏发电所带来的碳指标可以通过碳交易变现为经济收益,因此除电费收益以外,还须考虑碳交易收益。假如大规模屋顶光伏CCER项目每年参与碳交易,每次交易当年碳核算额度,则寿命周期内参与碳交易市场的收益为:
| $ L_{\text {carbon }}=\sum\limits_{y=1}^{25} \iota_y Q_y $ | (13) |
式中:ιy为第y年交易的成交单价;Qy为第y年交易的CCER碳额成交量。
2.6 光伏发电投资模型考虑到资金的时间成本,光伏发电项目投资分析时,须以加权平均资金成本为折现率来计算项目净现值[34]。25 a寿命周期内,光伏项目的累计净现值Lpv计算如下:
| $ \begin{gathered} L_{\mathrm{pv}}(Y)= \\ \left\{\begin{array}{c} \sum\limits_{y=1}^Y \frac{L_{\mathrm{own}}(y)+L_{\mathrm{sale}}(y)-C_{\mathrm{om}}(y)+\iota_y Q_y}{(1+r)^y}-C_{\mathrm{ini}} \\ 1 \leqslant Y \leqslant 24 \\ \sum\limits_{y=1}^Y \frac{L_{\mathrm{own}}(y)+L_{\mathrm{sale}}(y)-C_{\mathrm{om}}(y)+\iota_y Q_y}{(1+r)^y}+ \\ \frac{L_{\mathrm{rv}}}{(1+r)^{25}}-C_{\mathrm{ini}} \quad Y=25 \end{array}\right. \end{gathered} $ | (14) |
式中:Y为项目结算时的运行年份;r为折现率。当Lpv(25)=0时,折现率则表示内部收益率。
3 基于改进GM(1, 1)模型的碳价预测相较于已有研究,文中构建的光伏发电经济性模型的主要区别是引入大规模屋顶光伏CCER项目参与碳交易市场获得的收益部分。为了定量计算这部分收益,需要对未来一段周期内的碳交易价格进行预测,因此文中提出一种基于差分阈值滤波法的改进灰色预测GM(1, 1)模型。相较于其他预测模型,灰色预测模型的特点是可以通过稀疏的、不完全的样本信息,利用微分方程充分挖掘系统的本质,由无规律的原始数据得到规律性较强的生成序列,精度高、运算简便、易于检验[35-36],能够较好地适用于我国碳排放市场成立时间尚短、历史数据少、序列的完整性及可靠性低的现状。
关于数列预测的一个变量、一阶微分的GM(1, 1)模型是目前使用最广泛的灰色预测模型。GM(1, 1)模型是基于随机的原始时间序列经时间累加而形成的新的时间序列,该序列所呈现的规律可用一阶线性微分方程的解来逼近[37]。由于灰色预测GM(1, 1)模型的精度与初始序列的光滑度有关,因此文中采用差分阈值滤波法对GM(1, 1)模型的初始序列进行处理,达到提升初始序列光滑度的效果,进而提高GM(1, 1)模型的预测精度。
基于改进GM(1, 1)模型的碳交易价格预测方法流程如下。
(1) 差分阈值滤波法数据处理。设原始序列为:
| $ X_{0, \text { ini }}=\left(x_0(1), x_0(2), \cdots, x_0(m)\right) $ | (15) |
采用一阶差分处理整个有序序列,得出增量序列X′0, ini,再计算出原来序列的标准差sd,去掉增量序列中大于两倍sd的点,得到光滑度提升后的原始序列:
| $ X_0=\left(x_0(1), x_0(2), \cdots, x_0(n)\right) \quad n \leqslant m $ | (16) |
进一步得到X0的1次累加生成序列X1:
| $ X_1=\left(x_1(1), x_1(2), \cdots, x_1(n)\right) $ | (17) |
| $ x_1(k)=\sum\limits_{i=1}^k x_0(i) \quad i=1, 2, \cdots, n $ | (18) |
(2) 数据检验。对序列X0进行检验,以验证建立GM(1, 1)模型的可行性。计算序列X0的级比:
| $ \lambda_i=x_0(i-1) / x_0(i) \quad i=1, 2, \cdots, n $ | (19) |
若满足λi∈(e-2/(n+1), e2/(n+1)),则序列X0可以用于建立GM(1, 1)模型进行灰色预测。若不满足,则须对序列X0进行适当的变换处理,比如作平移变换:
| $ y_0(i)=x_0(i)+c \quad i=1, 2, \cdots, n $ | (20) |
式中:y0(i)为x0(i)经平移变换后的子序列;c为常数。取常数c使得所有级比都落在可容覆盖区间内。
(3) 建立GM(1, 1)模型。以通过检验后的序列X0建立GM(1, 1)灰微分方程:
| $ \left\{\begin{array}{l} x_0(i)+a z_1(i)=b \\ z_1(i)=0.5 x_1(i)+0.5 x_1(i+1) \end{array} \quad i=1, 2, \cdots, n\right. $ | (21) |
用回归分析求得发展参数a和灰作用量b。将变量i=2, 3, …, n视为连续变量t,则相应白化模型为:
| $ \frac{\mathrm{d} x_1(t)}{\mathrm{d} t}+a x_1(t)=b $ | (22) |
求解得:
| $ x_1(t)=\left(x_0(1)-\frac{b}{a}\right) \mathrm{e}^{-a(t-1)}+\frac{b}{a} $ | (23) |
即得时间响应式为:
| $ \begin{aligned} \hat{x}_1(i+1) & =\left(x_0(1)-\frac{b}{a}\right) \mathrm{e}^{-a i}+\frac{b}{a} \\ i & =1, 2, \cdots, n-1 \end{aligned} $ | (24) |
从而得到预测值为:
| $ \hat{x}_0(i+1)=\hat{x}_1(i+1)-\hat{x}_1(i) \quad i=1, 2, \cdots, n-1 $ | (25) |
(4) 检验预测值。可用残差验证法验证预测值的精度,计算相对残差ε(i)。
| $ \varepsilon(i)=\frac{x_0(i)-\hat{x}_0(i)}{x_0(i)} \quad i=1, 2, \cdots, n $ | (26) |
|ε(i)|越小说明精度越高,|ε(i)| < 0.1时具有较好的效果。
4 算例分析以北京某110 kV工业用户10 MWp屋顶光伏规划项目为例,应用所提模型进行经济性分析。由于该工业用户生产负荷很大,光伏发电将全部就地消纳。根据项目坐标从Meteonorm 7.3库中下载气象数据,并由PVsyst仿真得到在最佳倾斜角情况下首年交流侧发电量为1 080万kW ·h,其他参数见表 1。假设项目全寿命周期内各参数保持不变,不计贷款及税费等因素。
|
|
表 1 项目参数 Table 1 Item parameters |
由于全国碳交易市场的启动时间较短,在此选取北京碳交易试点市场的历史成交价数据进行碳价预测。基于改进前、后GM(1, 1)模型的2016年—2021年平均碳价预测及验证评价如表 2所示。
|
|
表 2 基于改进前、后模型的碳价预测评价 Table 2 Carbon price forecast evaluation based on the unimproved model and the improved model |
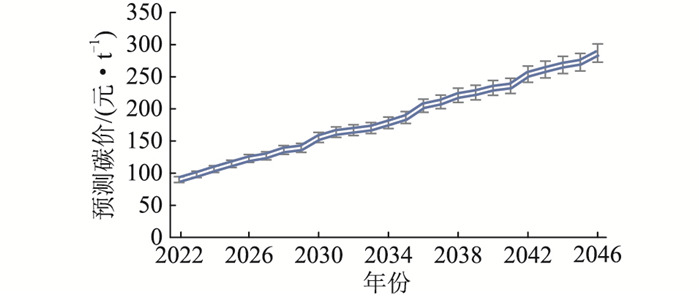
从历史数据的预测和检验结果来看,基于改进前、后GM(1, 1)预测模型的相对残差都小于10%,但改进后的预测结果整体的相对残差范围更小、精度更高,显示了基于文中所提改进GM(1, 1)模型的碳价预测方法具有较高的可信度。因此可以应用该方法对北京碳交易市场的未来碳价进行预测,预测结果如图 2所示。结果显示该项目的碳交易市场成交价总体呈持续上升趋势,验证了碳交易市场价格具有广阔的发展前景。
|
图 2 未来25 a碳价预测 Fig. 2 Carbon price forecast for the next 25 years |
进一步地,由于预测是基于历史数据,而过去几年的碳价是一直抬升的,因此预测结果是持续升高的。但碳交易市场的不断壮大以及减排成本的提升推动技术不断发展,预测碳价会伴随“碳中和”拐点的到来而趋于饱和。大部分发达国家实现碳中和的目标是2050年,而我国是2060年,所以我国碳交易价格预计会在2060年前后趋于饱和。文中所提改进GM(1, 1)模型在预测的同时也在检验,届时对于饱和趋势同样具有适用性。
另一方面,由于目前CCER项目具有稀缺性,而拥有过剩碳配额的企业出于对未来不确定性的考虑,普遍出现惜售现象,因此目前CCER碳指标交易价格具有一定的优势。但随着CCER项目申报工作的大范围开放以及碳交易市场的饱和,预计CCER交易价格会跟随碳配额价格趋势变化。
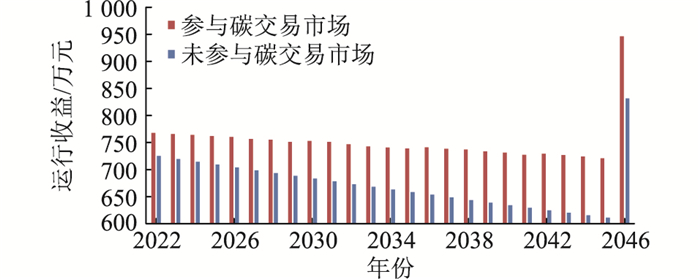
4.2 考虑参与碳交易市场的项目经济性分析在光伏发电全部消纳的情况下计算考虑参与碳交易市场的大规模屋顶光伏项目的运行收益,并与未考虑参与碳交易市场时的情况进行对比分析,如图 3及表 3所示。
|
图 3 全寿命周期运行收益 Fig. 3 Operating revenue over the life cycle |
|
|
表 3 项目经济性计算对比 Table 3 Economic calculation comparison of the project |
由结果可知,考虑参与碳交易市场的大规模屋顶光伏项目与未参与碳交易市场的情形相比,总投资收益、年投资回报率、内部收益率均有明显增长,其中内部收益率由14.99%提高至17.96%,同比提升了2.97%,验证了参与碳交易市场的大规模屋顶光伏项目具有较好的经济性。
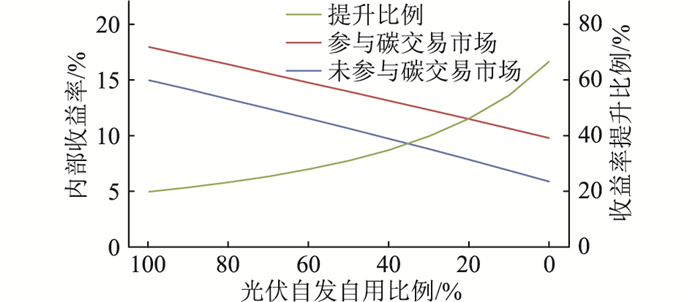
4.3 灵敏度分析进一步地,对屋顶光伏项目在不同自发自用比例情况下参与碳交易对项目收益率的灵敏度进行分析,如图 4所示。
|
图 4 收益率灵敏度分析 Fig. 4 Sensitivity analysis of yield |
由图 4可知,屋顶光伏发电项目在不同的自发自用比例下,参与碳交易市场对项目经济性的影响程度差异较大。其中,当光伏发电量全部自发自用时,电费收益最佳,此时碳交易收益对项目收益率影响相对最小,提升了17.96%。然而,随着光伏发电的自发自用比例降低,碳交易收益对项目收益率的影响升高,当电量全部上网售电时,电费收益最差,碳交易使得项目收益率由5.88%提升至9.79%,同比大幅提高了3.91%。
总体而言,参与碳交易市场能够显著提升屋顶光伏项目的经济性,是在不同自发自用比例的应用场景下对投资内部收益率的保障,是光伏后补贴时代通过市场手段获得额外收益的有效途径,在未来的项目规划中应着重考虑。
5 结语在碳交易市场快速发展以及大力鼓励清洁能源发电的背景下,研究屋顶光伏发电模型,并提出了一种考虑参与碳交易市场的大规模屋顶光伏经济性模型。同时,对传统的GM(1, 1)灰色预测模型进行改进,实现对未来碳交易市场交易价格的预测,进而分析参与碳交易市场对屋顶光伏经济性的影响。结果显示考虑参与碳交易市场的大规模屋顶光伏具有较为显著的经济性提升。文中研究了屋顶光伏发电项目适应新时代发展趋势的盈利模式,对未来新能源发电项目以及新型电力系统建设具有一定的借鉴意义。在后续研究中,将结合碳交易市场机制的发展,进一步考虑参与碳交易市场的交易策略,以寻求碳交易收益最大化。
| [1] |
张敏, 刘进, 林江刚, 等. "双碳"背景下屋顶分布式光伏开发环境效益分析[J]. 能源研究与利用, 2021(6): 37-41. ZHANG Min, LIU Jin, LIN Jianggang, et al. Environmental benefit analysis of roof distributed photovoltaic development under the background of "double carbon"[J]. Energy Research & Utilization, 2021(6): 37-41. DOI:10.3969/j.issn.1001-5523.2021.06.008 (  0) 0) |
| [2] |
陈皓勇. "双碳"目标下的电能价值分析与市场机制设计[J]. 发电技术, 2021, 42(2): 141-150. CHEN Haoyong. Electricity value analysis and market mechanism design under carbon-neutral goal[J]. Power Generation Technology, 2021, 42(2): 141-150. (  0) 0) |
| [3] |
陈兵, 徐瑞, 徐春雷, 等. 规模化储能分区聚合有功调度控制技术研究[J]. 电力工程技术, 2021, 40(3): 35-41. CHEN Bing, XU Rui, XU Chunlei, et al. Large-scale energy storage aggregation active power dispatching and control in subarea division of power grid[J]. Electric Power Engineering Technology, 2021, 40(3): 35-41. (  0) 0) |
| [4] |
陈少伟, 林坤杰, 陈碧琳. 分布式光伏发电系统的谐波源机理模型[J]. 浙江电力, 2022, 41(8): 57-64. CHEN Shaowei, LIN Kunjie, CHEN Bilin. Harmonic source mechanism model of distributed photovoltaic power generation system[J]. Zhejiang Electric Power, 2022, 41(8): 57-64. (  0) 0) |
| [5] |
申翔. 建筑屋顶光伏发电系统的研究与应用[D]. 南宁: 广西大学, 2021. SHEN Xiang. Research and application of building roof photovoltaic power generation system[D]. Nanning: Guangxi University, 2021. (  0) 0) |
| [6] |
江林. 屋顶并网分布式光伏发电技术方案应用探讨[J]. 电工技术, 2018(11): 139-141. JIANG Lin. Investigation on application of rooftop grid-connected distributed photovoltaic generation technology scheme[J]. Electric Engineering, 2018(11): 139-141. DOI:10.3969/j.issn.1002-1388.2018.11.052 (  0) 0) |
| [7] |
王康达, 张保会. 远方集中式与就地分布式光伏供电经济性比较[J]. 电力系统自动化, 2017, 41(16): 179-186. WANG Kangda, ZHANG Baohui. Economy comparison of distant ground photovoltaic stations and distributed photovoltaic stations[J]. Automation of Electric Power Systems, 2017, 41(16): 179-186. DOI:10.7500/AEPS20161104004 (  0) 0) |
| [8] |
蔡逸斌. 长沙市居住建筑分布式光伏应用经济性分析研究[D]. 长沙: 湖南大学, 2018. CAI Yibin. Study on economic efficiency of distributed PV system in Changsha[D]. Changsha: Hunan University, 2018. (  0) 0) |
| [9] |
杨昌辉, 石瑞智. 我国分布式光伏发电项目经济效益评价研究: 基于区域层面不同电价情景的分析[J]. 价格理论与实践, 2021(12): 167-171. YANG Changhui, SHI Ruizhi. Study on the evaluation of economic benefits of distributed photovoltaic power generation projects in China—analysis based on different tariff scenarios at regional level[J]. Price: Theory & Practice, 2021(12): 167-171. (  0) 0) |
| [10] |
李陆苗, 周鹏, 李整军, 等. 考虑分时电价与光伏出力关系的分布式光伏投资决策研究[J/OL]. 中国管理科学: 1-10[2022-04-14]. https://doi.org/10.16381/j.cnki.issn1003-207x.2021.0486. LI Lumiao, ZHOU Peng, LI Zhengjun, et al. The joint impact of time-of-use pricing and intermittent generation on solar photovoltaic investment for manufacturing firm[J/OL]. Chinese Journal of Management Science: 1-10[2022-04-14]. https://doi.org/10.16381/j.cnki.issn1003-207x.2021.0486. (  0) 0) |
| [11] |
杨智. A公司分布式光伏发电项目投资可行性研究[D]. 郑州: 郑州大学, 2018. YANG Zhi. Research on the A company' investment feasibility of distributed photovoltaic power generation project[D]. Zhengzhou: Zhengzhou University, 2018. (  0) 0) |
| [12] |
刘进军, 高林朝, 张香萍, 等. 基于EPC模式分布式光伏发电技术经济分析[J]. 河南科学, 2021, 39(11): 1738-1745. LIU Jinjun, GAO Linchao, ZHANG Xiangping, et al. Technical and economic analysis of distributed photovoltaic power generation based on EPC mode[J]. Henan Science, 2021, 39(11): 1738-1745. DOI:10.3969/j.issn.1004-3918.2021.11.004 (  0) 0) |
| [13] |
蓝虹, 陈雅函. 碳交易市场发展及其制度体系的构建[J]. 改革, 2022(1): 57-67. LAN Hong, CHEN Yahan. Development and system construction of carbon trading market[J]. Reform, 2022(1): 57-67. (  0) 0) |
| [14] |
朱磊, 梁壮, 谢俊, 等. 全国统一碳市场对电力行业减排的影响分析[J]. 环境经济研究, 2019, 4(2): 28-43. ZHU Lei, LIANG Zhuang, XIE Jun, et al. Analysis of the impact of national carbon market on emission reduction in power industry in China[J]. Journal of Environmental Economics, 2019, 4(2): 28-43. (  0) 0) |
| [15] |
HINTERMANN B. Pass-through of CO2 emission costs to hourly electricity prices in Germany[J]. Journal of the Association of Environmental and Resource Economists, 2016, 3(4): 857-89. DOI:10.1086/688486 (  0) 0) |
| [16] |
王一, 吴洁璇, 王浩浩, 等. 碳排放权市场与中长期电力市场交互作用影响分析[J]. 电力系统及其自动化学报, 2020, 32(10): 44-54. WANG Yi, WU Jiexuan, WANG Haohao, et al. Analysis of interactions between carbon emission trading market and medium-and long-term electricity market[J]. Proceedings of the CSU-EPSA, 2020, 32(10): 44-54. (  0) 0) |
| [17] |
贾德香, 柳占杰, 高骞, 等. 计及碳-电一体化交易的虚拟电厂竞价策略[J]. 电力科学与技术学报, 2021, 36(2): 89-97. JIA Dexiang, LIU Zhanjie, GAO Qian, et al. Bidding strategy of the virtual power plant based on the consideration of carbon-electricity integration trading in auxiliary service market[J]. Journal of Electric Power Science and Technology, 2021, 36(2): 89-97. (  0) 0) |
| [18] |
贾彦, 刘申燕. 依托全国碳排放权交易市场加快打造国际碳金融中心[J]. 产权导刊, 2022(2): 22-27. JIA Yan, LIU Shenyan. Relying on the national carbon emission trading market to accelerate the construction of an international carbon financial center[J]. Property Rights Guide, 2022(2): 22-27. (  0) 0) |
| [19] |
彭晓洁, 钟永馨. 碳排放权交易价格的影响因素及策略研究[J]. 价格月刊, 2021(12): 25-31. PENG Xiaojie, ZHONG Yongxin. Research on influencing factors and strategies of carbon emission trading price[J]. Prices Monthly, 2021(12): 25-31. (  0) 0) |
| [20] |
王海燕, 李怡璇. "双碳"目标下碳金融的发展现状及发展策略[J]. 商业观察, 2022(8): 17-19. WANG Haiyan, LI Yixuan. Development status and strategies of carbon finance under the target of "double carbon"[J]. Business Observation, 2022(8): 17-19. (  0) 0) |
| [21] |
CHEVALLIER J, SÉVI B. On the realized volatility of the ECX CO2 emissions 2008 futures contract: distribution, dynamics and forecasting[J]. Annals of Finance, 2011, 7(1): 1-29. (  0) 0) |
| [22] |
蔡文娟. 基于谷歌趋势的碳价波动性及预测研究[J]. 对外经贸, 2020(1): 31-34. CAI Wenjuan. Study on the volatility and forecast of carbon price based on google trends[J]. Foreign Economic Relations & Trade, 2020(1): 31-34. (  0) 0) |
| [23] |
BYUN S J, CHO H. Forecasting carbon futures volatility: the predictive power of GARCH models with energy volatilities[J]. Energy Economics, 2013, 40(2): 207-221. (  0) 0) |
| [24] |
ZHU B Z. A novel multiscale ensemble carbon price prediction model integrating empirical mode decomposition, genetic algorithm and artificial neural network[J]. Energies, 2012, 5(2): 355-370. (  0) 0) |
| [25] |
范莉莉, 刘璐. 基于ARMA-GARCH模型的中国碳价收益率波动分析[J]. 经济界, 2020(5): 25-32. FAN Lili, LIU Lu. Analysis on the fluctuation of carbon price return rate in China based on ARMA-GARCH model[J]. Economic Affairs, 2020(5): 25-32. (  0) 0) |
| [26] |
杨通录, 邓晓卫, 栾震, 等. 基于MS-AR模型的碳排放权交易价格波动性研究: 以湖北碳排放权交易中心为例[J]. 绿色科技, 2019(10): 280-282, 285. YANG Tonglu, DENG Xiaowei, LUAN Zhen, et al. Research on price volatility of carbon emissions trading based on MS-AR model—taking Hubei carbon emission trading center as the research object[J]. Journal of Green Science and Technology, 2019(10): 280-282, 285. (  0) 0) |
| [27] |
鞠可一, 戈棨琛, 周德群, 等. 中国碳交易市场碳价波动分析[J]. 江苏科技大学学报(自然科学版), 2019, 33(1): 78-86. JU Keyi, GE Qichen, ZHOU Dequn, et al. Analysis of carbon price fluctuation in China carbon trading market[J]. Journal of Jiangsu University of Science and Technology (Natural Science Edition), 2019, 33(1): 78-86. (  0) 0) |
| [28] |
2022年5月碳排放权交易市场动态[J]. 造纸信息, 2022(6): 18-20. Market dynamics of carbon emission trading in May 2022[J]. China Paper Newsletters, 2022(6): 18-20. (  0) 0) |
| [29] |
YIN W, ZHU Z Y, KIRKULAK-ULUDAG B, et al. The determinants of green credit and its impact on the performance of Chinese banks[J]. Journal of Cleaner Production, 2020, 124991. (  0) 0) |
| [30] |
陈星星. 中国碳排放权交易市场: 成效、现实与策略[J]. 东南学术, 2022(4): 167-177. CHEN Xingxing. China's carbon emission trading market: effectiveness, reality and strategy[J]. Southeast Academic Research, 2022(4): 167-177. (  0) 0) |
| [31] |
张跃. 基于自愿减排机制的光伏项目投资评价研究[D]. 天津: 天津大学, 2018. ZHANG Yue. Research on investment evaluation of China's photovoltaic project based on Chinese certified emission reduction mechanism[D]. Tianjin: Tianjin University, 2018. (  0) 0) |
| [32] |
黄盛娟, 唐荣, 唐立军. 光伏组件功率衰减分析研究[J]. 太阳能, 2015(6): 21-25. HUANG Shengjuan, TANG Rong, TANG Lijun. Study on power attenuation analysis of photovoltaic module[J]. Solar Energy, 2015(6): 21-25. (  0) 0) |
| [33] |
王怀斌, 胡芳, 刘伊雯. 光伏阵列倾角与土地成本双因素影响下的光伏发电项目经济性分析研究[J]. 太阳能, 2022(8): 19-26. WANG Huaibin, HU Fang, LIU Yiwen. Economic analysis and research of PV power generation project under the influence of PV array inclination angle and land cost[J]. Solar Energy, 2022(8): 19-26. (  0) 0) |
| [34] |
毛剑, 杨勇平, 侯宏娟, 等. 太阳能辅助燃煤发电技术经济分析[J]. 中国电机工程学报, 2015, 35(6): 1406-1412. MAO Jian, YANG Yongping, HOU Hongjuan, et al. Techno-economic analysis of solar thermal aided coal-fired power plants[J]. Proceedings of the CSEE, 2015, 35(6): 1406-1412. (  0) 0) |
| [35] |
彭武元, 陈思宇. 中国碳排放试点市场碳交易价格分析及预测[J]. 技术经济, 2020, 39(3): 102-110. PENG Wuyuan, CHEN Siyu. Analysis and forecast of carbon trading price in China's carbon emission pilot market[J]. Journal of Technology Economics, 2020, 39(3): 102-110. (  0) 0) |
| [36] |
刘思峰. 灰色系统理论及其应用[M]. 8版. 北京: 科学出版社, 2017. LIU Sifeng. Grey system theory and its application[M]. 8th ed. Beijing: Science Press, 2017. (  0) 0) |
| [37] |
李梦婉, 沙秀艳. 基于GM(1, 1)灰色预测模型的改进与应用[J]. 计算机工程与应用, 2016, 52(4): 24-30. LI Mengwan, SHA Xiuyan. Application of improved GM(1, 1) grey prediction model[J]. Computer Engineering and Applications, 2016, 52(4): 24-30. (  0) 0) |
 2023, Vol. 42
2023, Vol. 42


 周鹏(1980),男,学士,工程师,从事电力系统继电保护研究调试工作(E-mail:
周鹏(1980),男,学士,工程师,从事电力系统继电保护研究调试工作(E-mail: