文章编号: 2096-3203(2023)05-0138-10 中图分类号: TM743
2. 南洋理工大学电气工程学院, 新加坡 639798
短期电力负荷预测是电力系统规划、用电、调度等方面的重要基础工作。由于电能需求的实时性以及电能难以大量储存的特点,维持电能的供需平衡十分重要,因此准确、合理的负荷预测能为电力系统的优化调度、安全运行与合理定价等决策提供关键的数据支撑[1],且能有效提高经济效益,促进电能消纳。
目前主流的预测方法主要分为两大类:一类是统计方法,如线性回归法、指数平滑法、自回归移动平均法等,这类方法原理简单,容易实现,但当样本数据较为复杂时,预测效果一般;另一类是人工智能算法,包括支持向量机(support vector machine,SVM)、人工神经网络(artificial neural network,ANN)等传统人工智能方法,但这些方法对时间序列的处理效果较差,在对较长时间序列进行预测时效果不理想。人工智能算法还包括如今逐渐兴起的现代人工智能算法,其中的深度学习方法可以有效解决以上问题。
主流的深度学习方法主要有卷积神经网络(convolutional neural networks,CNN)[2]、长短期记忆(long short-term memory,LSTM)网络等。CNN主要被用于计算机视觉[3]、自然语言处理等方面[2],而以LSTM为代表的现代循环神经网络(recurrent neural network,RNN)在被用于负荷预测时,可以对负荷数据的抽象特征进行提取以减少数据的复杂度[4],达到兼顾负荷数据的时序性与非线性因素的效果[5]。文献[6]基于双向LSTM建立了短期负荷预测模型,对新能源电网负荷进行预测;文献[7]建立了基于LSTM的递归神经网络,对不同用电群体分别进行预测。但当输入特征含有非连续的离散数据时,LSTM的预测精度会受到影响[8],并且使用单一模型预测也会产生泛化性不佳的问题。
针对处理离散数据精度会受到影响的问题,第一,可以通过引入注意力机制进行处理。文献[9]提出了一种基于残差网络、LSTM和注意力机制的多任务学习模型,实现了对共享特征不同程度的关注。文献[10]提出了一种基于注意力机制的LSTM网络(LSTM network with attention mechanism, Attention-LSTM)模型,在4种不同类型的负荷场景下进行实验,验证了该模型的有效性。第二,可以使用新的编码方式进行解决。在目前的预测任务中,大多使用独热编码处理离散数据,但当离散数据较多时,输入特征维数会过高[11],从而导致收敛速度减慢,预测精度降低,而均值编码可以有效解决这些问题,提高预测性能。
针对使用单一模型进行预测具有泛化性不佳的问题,集成学习方法可以集成多个决策树模型进行预测,以此提高泛化能力。文献[12]提出了一种基于随机森林(random forest,RF)的负荷预测方法。文献[13]利用极限梯度提升树(extreme gradient boosting,XGBoost)建立了预测模型,并对多种信息进行融合,之后进行预测。但决策树属于学习能力较弱的模型,并且也缺乏对时间序列的处理能力,因此一些学者提出了组合预测的方法。文献[14]提出了基于CNN与LSTM的预测模型,但预测环节依旧是LSTM单独完成。文献[15]提出了一种基于XGBoost与LSTM的组合预测模型,但对于指定的负荷序列仍然使用单个方法进行预测。
近年来,集成学习中的Stacking方法逐渐兴起。Stacking由于其特殊的模型结构,可以通过交叉验证的方法同时训练多个模型[16-17],相较于一般的组合模型有更好的预测性能与更强的泛化能力。文献[18]提出了一种基于多模型融合的Stacking集成学习预测方法,取得了良好的预测效果,但LSTM只是被用于训练基学习器,没有充分发挥其处理时间序列的优势。
针对处理离散数据方面的问题以及泛化性不佳的问题,文中提出一种基于Attention-LSTM与Stacking多模型集成的短期负荷预测方法。该方法在数据处理方面,采用均值编码处理离散数据;在特征提取方面,使用Attention-LSTM充分提取负荷数据的特征,然后将处理后的序列与其他的输入特征组成新的特征向量;在预测模型方面,采用Stacking集成学习预测模型,通过集成多个模型进行训练,得到最终的预测结果。所提方法可以兼顾三者优势,取得较好的预测效果。
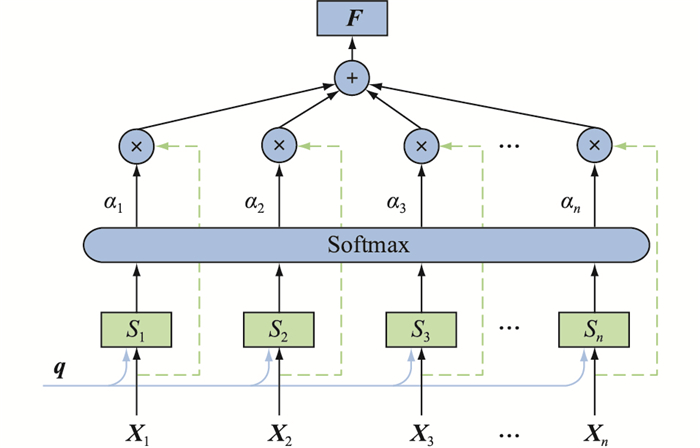
1 模型原理 1.1 注意力机制注意力机制是一种通过模拟人类大脑处理信息的方式[19],近些年逐渐被用于深度学习领域。借鉴人脑的注意力机制,使模型聚焦于更为重要的特征信息,在模型训练时为其分配更大的权重比例,而对于相对不重要的信息则分配较小的权重,以此降低对次要信息的敏感度,从而在模型计算能力有限的情况下提高模型对数据的处理能力。注意力机制的计算过程如图 1所示。具体过程可分为如下三步。
|
图 1 注意力机制的计算过程 Fig. 1 The calculation process of the attention mechanism |
(1) 计算注意力分数Si。图 1中,X=(X1,X2,…,Xn)为输入向量;q为查询向量。通过注意力评分函数来计算每个输入向量与查询向量的相关性,最常用的评分函数为点积函数,其公式为:
| $S_i=\boldsymbol{X}_i^{\mathrm{T}} \boldsymbol{q}$ | (1) |
(2) 计算注意力分布权重αi。使用Softmax函数将注意力分数Si归一化到[0, 1]范围内。
| $\alpha_i=\operatorname{Softmax}\left(S_i\right)=\exp \left(S_i\right) /\sum\limits_{i=1}^n \exp \left(S_i\right)$ | (2) |
(3) 计算最终的注意力输出向量F。根据注意力分布权重αi,对输入数据进行加权平均,得到最终的输出。
| $\boldsymbol{F}=\sum\limits_{i=1}^n \alpha_i \boldsymbol{X}_i$ | (3) |
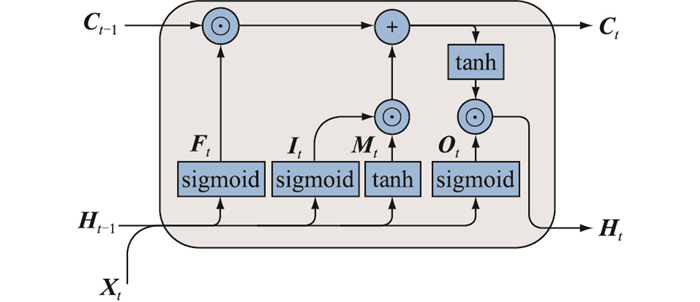
LSTM网络模型是在传统的RNN基础上进行改进,可以缓解RNN中由于连续矩阵乘积导致的梯度消失或梯度爆炸问题[20],是如今应用最为广泛的一种现代RNN模型。LSTM网络在RNN的基础上引入了记忆元,能较好地处理过去的信息[21],且为了控制记忆元,采用状态门来调节各记忆元的输出,其网络结构如图 2所示。
|
图 2 LSTM网络结构 Fig. 2 LSTM network structure |
图 2中各部分的计算公式如下。
| $\boldsymbol{I}_t=f\left(\boldsymbol{X}_t \boldsymbol{W}_{\mathrm{xi}}+\boldsymbol{H}_{t-1} \boldsymbol{W}_{\mathrm{hi}}+\boldsymbol{b}_{\mathrm{i}}\right)$ | (4) |
| $\boldsymbol{F}_t=f\left(\boldsymbol{X}_t \boldsymbol{W}_{\mathrm{xf}}+\boldsymbol{H}_{t-1} \boldsymbol{W}_{\mathrm{hf}}+\boldsymbol{b}_{\mathrm{f}}\right)$ | (5) |
| $\boldsymbol{O}_t=f\left(\boldsymbol{X}_t \boldsymbol{W}_{\mathrm{xo}}+\boldsymbol{H}_{t-1} \boldsymbol{W}_{\mathrm{ho}}+\boldsymbol{b}_{\mathrm{o}}\right)$ | (6) |
| $\boldsymbol{M}_t=\tanh \left(\boldsymbol{X}_t \boldsymbol{W}_{\mathrm{xm}}+\boldsymbol{H}_{t-1} \boldsymbol{W}_{\mathrm{hm}}+\boldsymbol{b}_{\mathrm{m}}\right)$ | (7) |
| $\boldsymbol{C}_t=\boldsymbol{F}_t \odot \boldsymbol{C}_{t-1}+\boldsymbol{I}_t \odot \boldsymbol{M}_t$ | (8) |
| $\boldsymbol{H}_t=\boldsymbol{O}_t \odot \tanh \left(\boldsymbol{C}_t\right)$ | (9) |
式中:It、Ft、Ot、Mt分别为输入门、遗忘门、输出门和候选记忆单元;Xt、Ct、Ht分别为t时刻的输入、记忆元输出与隐状态;Wxi、Wxf、Wxo、Wxm和Whi、Whf、Who、Whm分别为与Xt和Ht-1相乘的权重矩阵;bi、bf、bo、bm为权重偏置;f(·)为sigmoid函数;⊙表示哈达玛积,即2个同阶矩阵对应矩阵元素相乘。
由式(8)可知,t时刻的记忆元输出Ct主要受Ct-1与Mt两部分影响,It控制采用Mt中的新数据数量,Ft控制保留在记忆元Ct-1中的旧数据数量,以此达到兼顾当前与过去数据的目的。
1.3 Stacking多模型融合方法Stacking是一种融合多个学习器训练模型的方法,其基本思想为:使用原始的训练数据来训练数个基学习器,再将基学习器的输出组成一个新的数据集来训练元学习器。基于Stacking的多模型融合方法通过组合多个预测模型来获得更加优越的预测性能,同时也使得模型具有良好的泛化性能[22]。目前应用比较普遍的Stacking集成学习模型原理如图 3所示。

|
图 3 Stacking集成学习模型原理 Fig. 3 Principle of Stacking ensemble learning model |
由图 3可知,该模型共有2层,第一层由N个不同的基学习器组成,第二层由一个元学习器构成。基于Stacking多模型融合的预测流程如下。
(1) 划分数据集。先将原始数据集划分为训练集D与测试集Dt,再将训练集D分为N个子数据集,记为D1、D2、…、DN。
(2) 训练第一层模型。设D(-j)=D-Dj,D(-j)、Dj分别为第j个方法Aj训练所用的训练集与验证集。以交叉验证的方法对第一层模型进行训练,给定N个不同的训练方法,训练得出基学习器Ln,其中n=1, 2, …, N。
(3) 生成新的数据集。设Zn为基学习器Ln输出的预测结果,在交叉验证结束后,可以将N个预测结果组合成新的数据集,即:
| $\boldsymbol{D}^{\prime}=\left\{\boldsymbol{Z}_1, \boldsymbol{Z}_2, \cdots, \boldsymbol{Z}_N, \boldsymbol{D}_t\right\}$ | (10) |
将原始的数据集替换为D′,进行下一层训练。
(4) 训练第二层模型。将第一层模型输出的全新数据集D′作为第二层模型的输入,再通过第二层的预测方法A′来训练元学习器L′,进而得出最终的预测结果。
2 基于Attention-LSTM与Stacking的融合预测模型LSTM神经网络可以通过门控记忆元较好地处理负荷特征,相较于传统的机器学习方法,能更好地处理时间序列,充分地利用历史负荷数据提取负荷数据中的特征。但LSTM网络同样具有一定的局限性,一是在处理离散数据时,由于离散数据不能用时间序列表示,门控记忆元对其处理效果较差,从而导致收敛速度变慢,精度也受到影响;二是使用单一模型进行预测时,由于负荷预测问题的假设空间很大,有限的样本会存在多个假设与训练集相同的情况,从而导致模型泛化性不佳的问题[16]。
针对问题一,文中在LSTM网络的基础上引入注意力机制,使得模型在训练时更加聚焦于对负荷变化影响较大的关键信息,为其分配更大的权重,以此对负荷数据进行特征提取;然后采用均值编码处理离散数据,将处理过的数据重新组合成新的数据集再进行预测。针对问题二,将新的数据集输入到基于Stacking的多模型集成学习模型中进行预测,可以充分发挥各个子模型的优势,增强整体模型的泛化性,进而提高预测精度。
文中提出的基于Attention-LSTM与Stacking的融合预测模型分为四部分,包括原始数据处理、特征提取层、Stacking预测模型与预测结果评估,下面将分别进行介绍。
2.1 原始数据处理 2.1.1 均值编码原始数据既包含例如温度、负荷的连续序列数据,又包含例如节假日、星期的离散数据。在离散数据的处理方式中,独热编码由于其原理简单、容易实现,应用最为广泛。但这种编码方式假设了一个扁平的特征空间,忽略了标签之间的内在联系,而且会使得输入特征的维数过高,对模型的训练效果产生负面影响。而目标编码可以将目标嵌入低维空间,在保持精度的同时提高收敛速度[23]。将数据集中的每个离散数据都用该类别的平均目标值代替即可实现目标编码,因此目标编码也被称为均值编码。例如,对于数据集中表示节假日的离散数据,对数据集中所有工作日与节假日中的负荷数据分别取平均值,用二者各自的平均值来代替该离散数据,以此实现用连续的时间序列来表示离散数据。
综上,文中采用均值编码来代替传统的独热编码,以此处理数据集中的离散数据。
2.1.2 数据标准化将经过均值编码处理后离散数据与原始数据集中的序列数据进行整合,再对整合后的序列数据进行标准化处理。文中采用的标准化方法为Z-score标准化,即:
| $z_i=\left(x_i-\mu\right) /\sigma$ | (11) |
式中:zi为标准化处理后的样本数据;xi为原始样本数据;μ为所有样本数据的均值;σ为所有样本数据的标准差。经过Z-score标准化处理后,样本数据符合均值为0,标准差为1的正态分布,提高了数据的可比性,使得模型能更好地对数据进行处理与训练,加快收敛速度。
在对原始数据进行标准化处理后,将负荷数据提取出来,再对其进行单独处理。
2.2 Attention-LSTM特征提取层一般的LSTM神经网络分为输入层、中间层与输出层。数据从输入层输入到模型中,经过多个中间层对模型进行训练以提取特征,最后通过输出层输出最后的预测结果。文中利用LSTM网络提取负荷数据的特征,而预测由后续的Stacking模型完成,因此LSTM网络不需要输出层。将最后一层隐藏层的输出数据提取出来,即可得到经过特征提取的负荷数据。使用Attention-LSTM进行特征提取的步骤如下。
首先,将经过标准化处理的负荷数据输入到多层LSTM网络中进行训练,在训练过程中,使用适应性矩估计(adaptive moment estimate,Adam)算法对模型参数进行优化。该算法是一种基于一阶梯度的随机目标函数优化算法,在训练过程中可以不断迭代、更新网络参数。相较于其他优化算法,Adam算法具有易于实现、计算效率高、内存要求小的优势[24-25]。
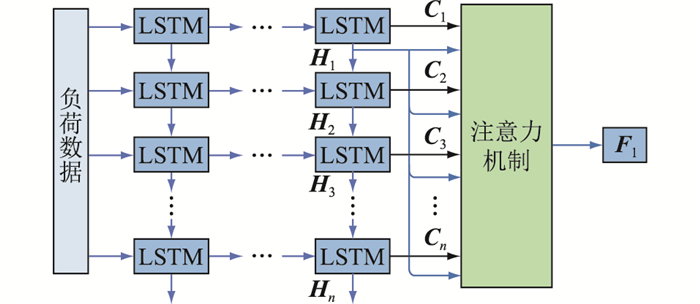
然后,将最后一层LSTM隐藏层的隐状态与输出分别记为H=(H1, H2, …, Hn)与C=(C1, C2, …, Cn)。将输出C作为注意力机制层的输入向量,隐状态H作为查询向量,对每一个隐状态分别计算注意力值。Attention-LSTM特征提取层的结构如图 4所示。
|
图 4 Attention-LSTM特征提取层的结构 Fig. 4 Structure of Attention-LSTM feature extraction layer |
以计算图 4中H1的注意力值为例,其计算公式如下:
| $S_{i, 1}=\boldsymbol{C}_i^{\mathrm{T}} \boldsymbol{H}_1$ | (12) |
| $\alpha_{i, 1}=\exp \left(S_{i, 1}\right) /\sum\limits_{i=1}^n \exp \left(S_{i, 1}\right)$ | (13) |
式中:Si,1为LSTM网络输出与隐状态H1的点积注意力分数;αi, 1为各个LSTM神经元输出的注意力分布权重;F1为模型最终的输出。对最后一层LSTM隐藏层的所有隐状态分别计算注意力输出向量,最终得到输出序列F1、F2、…、Fn,即为经过特征提取的负荷数据。
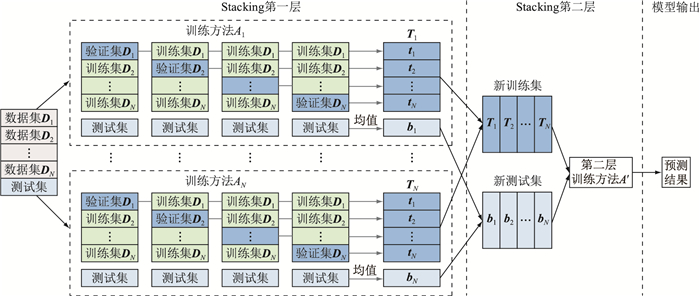
2.3 Stacking预测模型将通过Attention-LSTM提取过特征的负荷数据、经过均值编码处理过的离散数据以及其他如温度、电价等连续数据整合到一起,并将其分为N个大小相同的子数据集与1个测试集,一同作为Stacking模型的输入数据,其模型结构如图 5所示。
|
图 5 Stacking预测模型结构 Fig. 5 Stacking forecasting model structure |
选择合适的N个训练方法后,将整合的数据输入到Stacking第一层预测模型中。以训练方法A1为例,通过交叉验证的方法对基学习器进行训练,获得D1、D2、…、DN共计N组验证集的预测值,记为t1、t2、…、tN,以及N组测试集的预测值。将N组验证集的预测值进行组合,得到T1=(t1, t2, …, tN),同时将N组测试集的预测值取平均,得到一组预测值b1。
同理,对训练方法A2—AN重复上述步骤,最终可以训练得到每个基学习器的预测值(T1, T2, …, TN)与测试集的预测值(b1, b2, …, bN)。因此,每次的训练集都会与原始数据不同,扩大了数据集的规模,也有效提高了模型的泛化能力。
2.3.2 Stacking第二层预测模型Stacking第二层预测模型中包含一个训练方法A′,将第一层基学习器的预测值(T1, T2, …, TN)作为训练集,第一层得到的测试集的预测值(b1, b2, …, bN)作为测试集,使用方法A′来训练元学习器,得到最终的预测结果。
2.4 预测结果评估将最终得出的预测结果进行反归一化,再对预测结果进行评估。文中选取3个评估指标来评估模型预测的性能,分别为相对均方根误差(root mean square error,RMSE)、平均绝对百分比误差(mean absolute percentage error,MAPE)与预测精度,分别记为yRMSE、yMAPE、ySCORE,其计算公式如下:
| $y_{\mathrm{RMSE}}=\sqrt{\frac{1}{k} \sum\limits_{i=1}^k\left(y_i-\hat{y}_i\right)^2}$ | (15) |
| $y_{\mathrm{MAPE}}=\frac{1}{k} \sum\limits_{i=1}^k\left|\frac{y_i-\hat{y}_i}{y_i}\right| \times 100 \%$ | (16) |
| $y_{\mathrm{SCORE}}=\left(1-\frac{1}{k} \sum\limits_{i=1}^k \frac{\left|y_i-\hat{y}_i\right|}{y_{i \max }-y_{i \min }}\right) \times 100 \%$ | (17) |
式中:k为预测数据的个数;yi为负荷实际值;
文中使用的数据集为2014年全球能源预测竞赛中所用数据[26]与西班牙某地的数据集[27],二者数据采样间隔时间都为1 h。前者包括某地2006年—2014年之间的负荷数据与温度数据,记为数据集1,选用负荷、温度、时刻、星期与节假日作为输入数据;后者包括西班牙某地2016年—2018年的负荷数据与电价数据,记为数据集2,选用负荷、电价、时刻、星期与节假日作为输入数据。算例分析中均按照4 ∶1的比例划分训练集与测试集。为保证实验结果的准确性,每种模型均进行5次实验,最后取预测精度排在中位数的预测结果进行后续的分析与对比。
实验的硬件平台为Intel Core i7-11700 CPU与NVDIA GeForce GTX 1650 GPU,在Python3.9中完成相关程序的编写,使用Keras深度学习库中的Tensorflow框架实现相关功能。
3.1 Stacking框架下的方法选择首先需要对Stacking框架下的两层训练方法进行选择,选择标准如下:
(1) 就基学习器的预测效果而言,预测性能较好的方法有助于提高模型整体预测效果,故应当在Stacking的第一层选择预测精度较高的方法来训练基学习器。
(2) 就基学习器的数量而言,基学习器过少难以实现各训练方法互补,过多则会使模型冗余,使得模型变得更加复杂,甚至可能降低预测性能[28]。通常选择3~5个不同的模型方法对Stacking第一层的基学习器进行训练。
(3) 就基学习器的差异性而言,应选择原理差异较大的方法来训练基学习器。从不同的角度来训练数据,可以最大程度地综合不同方法的优越性能,以此进一步提升预测性能[29]。
(4) 就模型的泛化能力而言,应当在模型的第二层选择泛化能力较强的模型来训练元学习器,以改善第一层训练结果所产生的预测偏差[18]。
分别采用RF、梯度提升决策树(gradient boosting decision tree,GBDT)、XGBoost、轻量级梯度提升机(light gradient boosting machine,LightGBM)、SVM、自适应增强算法(adaptive boosting,Adaboost)与K近邻(K-nearest neighbor,KNN)对数据集1中2006年的第一季度负荷进行预测,并根据预测结果选择Stacking框架下的预测方法,各方法的预测指标如表 1所示,可知前5种模型的预测精度均高于96%,yMAPE可保持在2%左右且yRMSE可保持在80 MW以内,各参数相较于Adaboost与KNN这2种模型明显更优,故选择前5种模型训练Stacking框架下的学习器。
|
|
表 1 各模型单独预测的各项指标 Table 1 Metrics predicted by each model individually |
对于Stacking第二层的训练方法,LightGBM在保证预测精度的同时又可以减少内存占用[8],并且其预测精度在5种模型中是最高的,因此选择该方法训练元学习器。对于Stacking第一层的训练方法,为防止同一模型对数据的重复训练而产生过拟合,不选用LightGBM。对于其他4种模型,GBDT与XGBoost是基于Boosting的集成学习模型,而XGBoost是在GBDT的基础上优化过的模型;RF是基于Bagging的集成学习模型;SVM是一种非线性的学习模型,可以用于解决小样本的回归问题。为选择基学习器的训练方法,须对这4种模型的预测误差进行相关性分析。文中采用Pearson系数分析各模型的相关程度,二维向量的Pearson系数Pxy计算公式如下:
| $P_{x y}=\frac{\sum\limits_{m=1}^M\left(x_{1, m}-\bar{x}_1\right)\left(x_{2, m}-\bar{x}_2\right)}{\sqrt{\sum\limits_{m=1}^M\left(x_{1, m}-\bar{x}_1\right)^2} \sqrt{\sum\limits_{m=1}^M\left(x_{2, m}-\bar{x}_2\right)^2}}$ | (18) |
式中:M为向量长度;x1, m、x2, m分别为2个向量中的元素;x1、x2分别为2个向量中元素的平均值。Pxy的值在-1~1之间,当Pxy的绝对值越接近于1时,说明2个向量之间的相关性越强;反之,Pxy的绝对值越接近于0时,相关性越弱[18]。
根据式(18)计算4种模型预测误差的相关性,计算结果如图 6所示。可见,XGBoost与GBDT的误差相关系数为0.971,误差相似度最高,这说明二者原理类似,与前文分析一致。故为避免相似方法的重复训练,不将这2种方法一同加入Stacking模型第一层训练基学习器。

|
图 6 4种模型的误差相关性分析 Fig. 6 Error correlation analysis of four models |
为确定二者之中更加优越的模型,对XGBoost与GBDT进一步进行实验对比。将4种模型以不同的形式进行组合,作为Stacking第一层基学习器的训练方法。不同组合方式的预测指标如表 2所示。
|
|
表 2 不同组合形式下Stacking模型的各项指标 Table 2 Metrics of the Stacking model under different combinations |
由表 2可知,XGBoost-SVM-RF组合方法相较于后两者,yRMSE分别减少了9 MW、0.21 MW,yMAPE分别减少了0.31%、0.02%,预测精度ySCORE分别提升了0.56%、0.02%。说明将XGBoost与其他2种模型进行组合相较于GBDT的组合预测效果更好,因此XGBoost的预测性能更加优越。而将4种模型一同加入Stacking模型第一层训练基学习器,会造成模型冗余,预测效果反而出现小幅度下降。
综上所述,文中采用XGBoost、SVM与RF 3种模型训练Stacking的第一层基学习器,采用LightGBM模型训练第二层的元学习器。
3.2 预测结果分析为验证Attention-LSTM-Stacking模型(后文简称AL-Stacking模型)的预测性能,将此模型与门控学习单元(gate recurrent unit,GRU)、LightGBM和SVM这3种基于不同原理的模型进行对比。
采用数据集1、2进行实验,AL-Stacking模型的参数见表 3,对比实验模型的参数见表 4。
|
|
表 3 AL-Stacking模型中的参数汇总 Table 3 Summary of parameters in AL-Stacking model |
|
|
表 4 对比模型中的参数汇总 Table 4 Summary of parameters in compare models |
在进行对比实验之前,需要先对2个数据集的连续数据进行相关性分析,以此观察其他连续数据与负荷数据的相关性,从而确定LSTM网络层需要提取的数据特征。序列数据的相关性计算仍采用Pearson系数。经计算,数据集1中的温度数据与负荷数据的Pearson系数为0.042,二者基本无关;数据集2中的电价数据与负荷数据的Pearson系数为0.566,二者呈中等程度相关。温度数据和电价数据与负荷数据都没有较强的相关性,因此不需要进行特征提取。而离散数据经过均值编码处理后,变成了周期性变化的时间序列,其变化规律已经固定,无须过多处理。因此,LSTM网络层只需要对负荷数据进行特征提取。
对于数据集1,选择2006年第四季度的数据进行实验;对于数据集2,选择2016年第一季度的数据进行实验,实验结果汇总如表 5所示。
|
|
表 5 各数据集的各项预测指标汇总 Table 5 Summary of the predicted parameters for each dataset |
由表 5可以看出,在2个不同的数据集下,AL-Stacking模型的各个预测指标相较于其他3种模型均有不同程度的改善:在数据集1中,yRMSE分别减少了27.33 MW、23.49 MW、63.5 MW,yMAPE分别减少了0.51%、0.49%、1.63%,预测精度ySCORE分别提高了0.7%、0.67%、2.28%;在数据集2中,yRMSE分别减少了225.95 MW、257.43 MW、409.51 MW,yMAPE分别减少了0.62%、0.67%、1.16%,预测精度ySCORE分别提高了0.99%、1.05%、1.88%。综上所述,在2个数据集的实验中,AL-Stacking模型相较于其他对比模型,具有更好的预测效果。
图 7为2个数据集下的预测结果对比。可以看出,2个数据集的负荷数据呈现出不同的变化趋势,而实验所用的4种模型都能较好地拟合出负荷数据的变化趋势。但在负荷波动较大的峰谷时刻,3种对比实验模型均出现了不同程度的负荷波动,相比之下,AL-Stacking模型在负荷的峰谷时刻误差较小,整体的预测效果更加准确,证明了模型性能的优越性,且其能在不同的数据集中都取得较好的预测效果,证明了模型具有较强的泛化能力。

|
图 7 2个数据集下的预测结果 Fig. 7 Forecast results for two datasets |
为进一步探究预测结果是否平稳,需要考察单点的预测效果。计算各模型在单个预测点的相对误差,从而观察每个预测点的预测精度与整体预测值序列的波动程度,相对误差yR的计算公式如下:
| $y_{\mathrm{R}}=\left|\frac{y_i-\hat{y}_i}{y_i}\right| \times 100 \%$ | (19) |
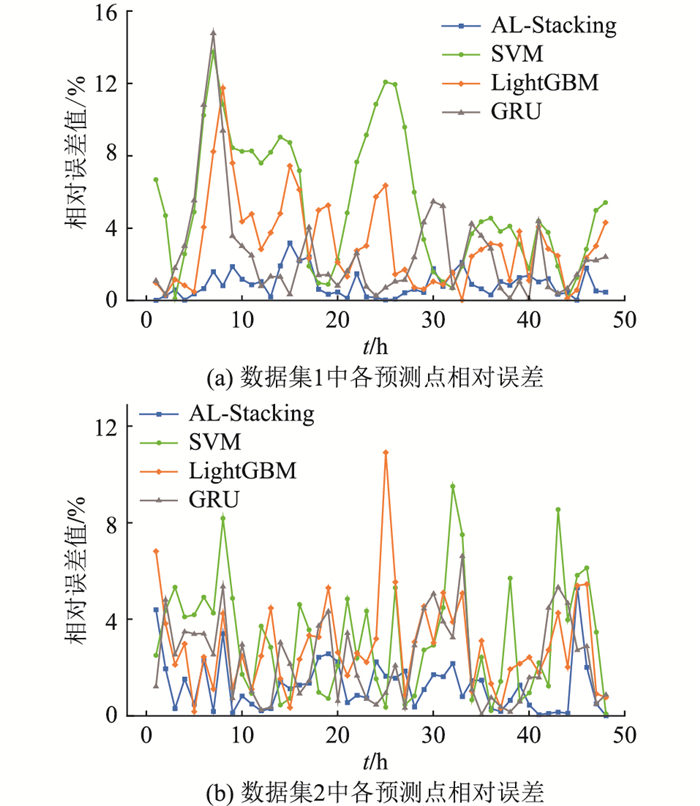
对图 7中各模型单点的相对预测误差分别进行计算,结果如图 8所示。对于数据集1,用于实验的各模型单点的相对预测误差可以保持在16%以内,而AL-Stacking模型在各预测点的相对预测误差都可以保持在3%以内;对于数据集2,各模型单点的相对预测误差可以保持在12%以内,而AL-Stacking模型在各预测点的相对预测误差可以基本稳定在3%左右。就准确性而言,AL-Stacking模型的单点预测效果相较于其他预测模型更为精确;就稳定性而言,各预测模型单点的相对预测误差随着时间的推移会有不同程度的波动,但AL-Stacking模型的预测误差波动相对较小,更加稳定。
|
图 8 2个数据集下各预测点的相对误差 Fig. 8 The relative error of each forecast point in two datasets |
为验证AL-Stacking模型的各个部分均对预测结果有改进意义,对模型进行灵敏度分析。采用数据集2中2016年第一季度的数据进行消融实验,实验结果见表 6。其中实验A表示未采用Stacking预测框架进行预测,其他实验组别以此类推。
|
|
表 6 消融实验结果汇总 Table 6 Summary of ablation experiment results |
对比表 6的实验结果可知,实验E的预测精度比实验D高,说明LSTM网络特征提取层可以有效地提取负荷特征,提升预测性能;实验E的预测精度比实验B高,说明引入注意力机制的LSTM网络特征提取层提取负荷特征的效果更佳,相较于单独的LSTM网络可以进一步提升预测性能;实验E的预测精度比实验C高,说明均值编码相较于独热编码可以降低输入特征的维数,提升预测精度,与前文的理论分析一致;实验E的预测精度比实验A高,说明Stacking集成学习框架可以集成多个模型进行预测,提升模型的整体预测效果。
由此可见,文中所提模型的4个改进部分均可使实验的预测效果得到一定的提升,将各部分整合后的预测模型可以达到最优的预测效果。
4 结论文中提出了一种Attention-LSTM与Stacking多模型集成的负荷预测方法,兼顾了Attention-LSTM能更好地处理时间序列数据中的非线性因素的优点,以及Stacking集成学习方法融合多个子模型共同进行预测从而增强泛化性的优点,并采用均值编码实现了输入数据的降维,使得整体模型具有优越的预测性能。与GRU、LightGBM、SVM 3种方法在2个数据集下对比预测效果,结果表明,文中提出的方法在2个不同数据集下的预测精度都超过了98%,相较于其他方法更为精确,评估所用的2种预测误差相较于其他方法有明显的下降,短期预测的预测时效可超过两周,整体预测效果更好。最后通过消融实验验证了文中模型的各个改进部分均可使预测效果提升,改进后模型的预测效果可以达到最优。
在今后的工作中,可以考虑更多的负荷影响因素,例如降水量、湿度等。此外,还可以对基于Stacking的预测框架进行改善,加入更多的预测模型,或者使用多层Stacking模型进行预测。
| [1] |
王平飞. 基于时间序列的卷积LSTM电力负荷预测研究[D]. 成都: 四川大学, 2021. WANG Pingfei. Research on power load prediction based on time series convolution LSTM[D]. Chengdu: Sichuan University, 2021. (  0) 0) |
| [2] |
王业, 崔玉, 陆兆沿, 等. 基于CNN图像识别算法的保护装置智能巡视技术[J]. 电力工程技术, 2022, 41(6): 252-257. WANG Ye, CUI Yu, LU Zhaoyan, et al. Intelligent inspection technology of protection device based on convolution neural network image recognition algorithm[J]. Electric Power Engineering Technology, 2022, 41(6): 252-257. (  0) 0) |
| [3] |
白浩, 齐林海, 王红. 融合知识图谱与卷积神经网络的电压暂降分类识别[J]. 电力信息与通信技术, 2021, 19(11): 131-139. BAI Hao, QI Linhai, WANG Hong. Classification and recognition of voltage sag based on knowledge graph and convolution neural network[J]. Electric Power Information and Communication Technology, 2021, 19(11): 131-139. (  0) 0) |
| [4] |
朱继忠, 董瀚江, 李盛林, 等. 数据驱动的综合能源系统负荷预测综述[J]. 中国电机工程学报, 2021, 41(23): 7905-7924. ZHU Jizhong, DONG Hanjiang, LI Shenglin, et al. Review of data-driven load forecasting for integrated energy system[J]. Proceedings of the CSEE, 2021, 41(23): 7905-7924. (  0) 0) |
| [5] |
王增平, 赵兵, 纪维佳, 等. 基于GRU-NN模型的短期负荷预测方法[J]. 电力系统自动化, 2019, 43(5): 53-58. WANG Zengping, ZHAO Bing, JI Weijia, et al. Short-term load forecasting method based on GRU-NN model[J]. Automation of Electric Power Systems, 2019, 43(5): 53-58. (  0) 0) |
| [6] |
杨龙, 吴红斌, 丁明, 等. 新能源电网中考虑特征选择的Bi-LSTM网络短期负荷预测[J]. 电力系统自动化, 2021, 45(3): 166-173. YANG Long, WU Hongbin, DING Ming, et al. Short-term load forecasting in renewable energy grid based on Bi-directional long short-term memory network considering feature selection[J]. Automation of Electric Power Systems, 2021, 45(3): 166-173. (  0) 0) |
| [7] |
KONG W C, DONG Z Y, JIA Y W, et al. Short-term residential load forecasting based on LSTM recurrent neural network[J]. IEEE Transactions on Smart Grid, 2019, 10(1): 841-851. (  0) 0) |
| [8] |
陈纬楠, 胡志坚, 岳菁鹏, 等. 基于长短期记忆网络和LightGBM组合模型的短期负荷预测[J]. 电力系统自动化, 2021, 45(4): 91-97. CHEN Weinan, HU Zhijian, YUE Jingpeng, et al. Short-term load prediction based on combined model of long short-term memory network and light gradient boosting machine[J]. Automation of Electric Power Systems, 2021, 45(4): 91-97. (  0) 0) |
| [9] |
王琛, 王颖, 郑涛, 等. 基于ResNet-LSTM网络和注意力机制的综合能源系统多元负荷预测[J]. 电工技术学报, 2022, 37(7): 1789-1799. WANG Chen, WANG Ying, ZHENG Tao, et al. Multi-energy load forecasting in integrated energy system based on ResNet-LSTM network and attention mechanism[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1789-1799. (  0) 0) |
| [10] |
LIN Z F, CHENG L L, HUANG G H. Electricity consumption prediction based on LSTM with attention mechanism[J]. IEEJ Transactions on Electrical and Electronic Engineering, 2020, 15(4): 556-562. (  0) 0) |
| [11] |
KLIMO M, LUKÁCP, TARÁBEK P. Deep neural networks classification via binary error-detecting output codes[J]. Applied Sciences, 2021, 11(8): 3563. (  0) 0) |
| [12] |
吴潇雨, 和敬涵, 张沛, 等. 基于灰色投影改进随机森林算法的电力系统短期负荷预测[J]. 电力系统自动化, 2015, 39(12): 50-55. WU Xiaoyu, HE Jinghan, ZHANG Pei, et al. Power system short-term load forecasting based on improved random forest with grey relation projection[J]. Automation of Electric Power Systems, 2015, 39(12): 50-55. (  0) 0) |
| [13] |
LI G Y, LI W, TIAN X L, et al. Short-term electricity load forecasting based on the XGBoost algorithm[J]. Smart Grid, 2017, 7(4): 274-285. (  0) 0) |
| [14] |
唐戈, 余一平, 秦川, 等. 基于CNN-LSTM分位数回归的母线负荷日前区间预测[J]. 电力工程技术, 2021, 40(4): 123-129. TANG Ge, YU Yiping, QIN Chuan, et al. Day-ahead interval prediction of bus load based on CNN-LSTM quantile regression[J]. Electric Power Engineering Technology, 2021, 40(4): 123-129. (  0) 0) |
| [15] |
赵齐昌. 基于XGBoost-LSTM组合模型的电力负荷预测研究[D]. 汉中: 陕西理工大学, 2022. ZHAO Qichang. Research on power load forecasting based on XGBoost-LSTM combined model[D]. Hanzhong: Shaanxi University of Technology, 2022. (  0) 0) |
| [16] |
谭真奇. 基于Stacking集成学习的负荷预测方法研究[D]. 贵阳: 贵州大学, 2021. TAN Zhenqi. Research on load forecasting method based on Stacking integrated learning[D]. Guiyang: Guizhou University, 2021. (  0) 0) |
| [17] |
朱文广, 李映雪, 杨为群, 等. 基于K-折交叉验证和Stacking融合的短期负荷预测[J]. 电力科学与技术学报, 2021, 36(1): 87-95. ZHU Wenguang, LI Yingxue, YANG Weiqun, et al. Short-term load forecasting based on the K-fold cross validation and stacking ensemble[J]. Journal of Electric Power Science and Technology, 2021, 36(1): 87-95. (  0) 0) |
| [18] |
史佳琪, 张建华. 基于多模型融合Stacking集成学习方式的负荷预测方法[J]. 中国电机工程学报, 2019, 39(14): 4032-4042. SHI Jiaqi, ZHANG Jianhua. Load forecasting based on multi-model by Stacking ensemble learning[J]. Proceedings of the CSEE, 2019, 39(14): 4032-4042. (  0) 0) |
| [19] |
任建吉, 位慧慧, 邹卓霖, 等. 基于CNN-BiLSTM-Attention的超短期电力负荷预测[J]. 电力系统保护与控制, 2022, 50(8): 108-116. REN Jianji, WEI Huihui, ZOU Zhuolin, et al. Ultra-short-term power load forecasting based on CNN-BiLSTM-Attention[J]. Power System Protection and Control, 2022, 50(8): 108-116. (  0) 0) |
| [20] |
徐玉婷, 田世明, 陈宋宋, 等. 基于LSTM的居民负荷预测及其可调节潜力分析[J]. 电力信息与通信技术, 2023, 21(5): 1-8. XU Yuting, TIAN Shiming, CHEN Songsong, et al. Resident load forecasting based on LSTM and its adjustable potential analysis[J]. Electric Power Information and Communication Technology, 2023, 21(5): 1-8. (  0) 0) |
| [21] |
胡威, 张新燕, 李振恩, 等. 基于优化的VMD-mRMR-LSTM模型的短期负荷预测[J]. 电力系统保护与控制, 2022, 50(1): 88-97. HU Wei, ZHANG Xinyan, LI Zhen'en, et al. Short-term load forecasting based on an optimized VMD-mRMR-LSTM model[J]. Power System Protection and Control, 2022, 50(1): 88-97. (  0) 0) |
| [22] |
KARDANI N, ZHOU A N, NAZEM M, et al. Improved prediction of slope stability using a hybrid stacking ensemble method based on finite element analysis and field data[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2021, 13(1): 188-201. (  0) 0) |
| [23] |
RODRÍGUEZ P, BAUTISTA M A, GONZÀLEZ J, et al. Beyond one-hot encoding: lower dimensional target embedding[J]. Image and Vision Computing, 2018, 75: 21-31. (  0) 0) |
| [24] |
ZHOU Y F, ZHANG M C, ZHU J L, et al. A randomized block-coordinate Adam online learning optimization algorithm[J]. Neural Computing and Applications, 2020, 32(16): 12671-12684. (  0) 0) |
| [25] |
于华楠, 阮筱颖, 王鹤. 基于改进堆叠去噪自动编码器的电能质量扰动分类方法[J]. 电力信息与通信技术, 2021, 19(9): 1-7. YU Huanan, RUAN Xiaoying, WANG He. Power quality disturbance classification method based on improved stacked denoising autoencoders[J]. Electric Power Information and Communication Technology, 2021, 19(9): 1-7. (  0) 0) |
| [26] |
HONG T, PINSON P, FAN S, et al. Probabilistic energy forecasting: global energy forecasting competition 2014 and beyond[J]. International Journal of Forecasting, 2016, 32(3): 896-913. (  0) 0) |
| [27] |
HUANG S C, ZHANG J, HE Y, et al. Short-term load forecasting based on the CEEMDAN-sample entropy-BPNN-transformer[J]. Energies, 2022, 15(10): 3659. (  0) 0) |
| [28] |
刘波, 秦川, 鞠平, 等. 基于XGBoost与Stacking模型融合的短期母线负荷预测[J]. 电力自动化设备, 2020, 40(3): 147-153. LIU Bo, QIN Chuan, JU Ping, et al. Short-term bus load forecasting based on XGBoost and Stacking model fusion[J]. Electric Power Automation Equipment, 2020, 40(3): 147-153. (  0) 0) |
| [29] |
石颖. 基于数据挖掘的用户负荷曲线分析与负荷预测技术研究[D]. 广州: 华南理工大学, 2021. SHI Ying. Electrical load profile analysis and load forecasting technology based on data mining[D]. Guangzhou: South China University of Technology, 2021. (  0) 0) |
2. School of Electrical Engineering, Nanyang Technological University, Singapore 639798, Singapore
 2023, Vol. 42
2023, Vol. 42


 朱继忠(1966), 男, 博士, 教授, IEEE Fellow, 中国电机工程学会外籍会士, IET Fellow, 研究方向为综合智慧能源系统优化运行与控制、电网安全经济运行、新能源及其应用、智能电网及需求侧响应、智慧楼宇负荷及用户系统等(E-mail:
朱继忠(1966), 男, 博士, 教授, IEEE Fellow, 中国电机工程学会外籍会士, IET Fellow, 研究方向为综合智慧能源系统优化运行与控制、电网安全经济运行、新能源及其应用、智能电网及需求侧响应、智慧楼宇负荷及用户系统等(E-mail: