文章编号: 2096-3203(2023)05-0010-10 中图分类号: TM282
干式变压器具有防火防爆特性良好、抗短路能力强、体积小、安装费用低等优点,随着城市用电负荷的增加,具有良好的应用前景[1-2]。干式变压器在长期运行过程中受到电、热、机械等应力的共同作用,可能导致内部铁心、绕组等部件发生松动变形,并发展成严重事故[3-4]。因此,检测干式变压器的机械状态对提高低压配电网的可靠性、保障电力系统的安全可靠运行十分重要[5-7]。
干式变压器的振动信号主要来源于因磁致伸缩和硅钢片叠片间吸引力产生的铁心振动,以及因洛伦兹力产生的绕组振动[8-9]。电源质量、运行环境的改变及产生故障和缺陷等因素均会改变变压器的运行状况,使变压器内部铁心和绕组的磁场、电场和受力变化,导致振动信号变化[10-14]。在常用的变压器机械故障检测方法中,振动信号分析法因与系统无直接电联系、易于实现在线检测、能灵敏地反映铁心和绕组的机械状态而广受关注[15-17]。
近年来,国内外学者针对干式变压器振动机理及机械状态检测方法进行了大量研究[18-19]。祝丽花等建立了考虑铁心磁致伸缩效应的三维磁-机械强耦合数值模型,较准确地计算了干式变压器铁心振动位移及铁心周围声场分布,通过实验验证了铁心100 Hz振动信号与电压平方成正比,发现铁心振动幅值随电压升高增大明显,占干式变压器本体振动的主要部分[20-21]。陆昕等通过有限元仿真,得出干式变压器铁心、绕组和上端排线位置振动较明显的结论,实验测得干式变压器振动信号的频率集中在400 Hz以内,且振动集中在工频倍频处[22]。罗世豪、金潇等通过采集干式变压器在铁心松动、绕组变形等典型缺陷下的声纹或噪声信号进行特征分析,实现了不同故障状态的识别,但识别结果易受变压器结构和环境因素的干扰[23-24]。Manohar等将振动传感器粘合在铁心、正常绕组和模拟短路故障的绕组上,分析各测点在空载及不同负载状态下振动信号频率分布,发现铁心振动与负载条件无关,200 Hz频率分量可以作为绕组局部短路故障的特征值[25]。钟星鸣在干式变压器上、下夹件和侧面安装了加速度传感器,分析对比了空载和不同负载工况下的振动信号特性,发现绕组振动对变压器整体振动的贡献较小[26]。现有研究大多通过实验测量铁心和绕组振动对干式变压器振动贡献的大小,铁心振动可以通过变压器空载状态下的振动信号测得,但负载时绕组的振动总是通过夹件、垫块等固体连接件受到铁心振动的影响,因此,文中采用有限元仿真的方法,进一步探究铁心和绕组单独振动的强度大小及其对干式变压器振动的贡献。
实际应用中,高剑锋设计了一套基于振动信号频域特征值的干式变压器状态监测系统,但其对干式变压器振动信号特征的分析不够充分,监测系统选取的特征值过于单一[27]。冯忠奎等也研制了一套基于振动信号的干式变压器故障检测系统,但该系统中振动传感器安装在变压器外绝缘伸缩支架上,所测振动信号受到支架振动特性的影响[28]。
为进一步研究针对干式变压器典型机械故障的诊断方法,文中采用仿真与实验相结合的方法,以SCB11-100/10干式变压器为研究对象,对干式变压器铁心和绕组的振动规律和信号分布进行仿真分析。文中搭建了干式变压器振动信号采集实验平台,通过实验探究不同工况下干式变压器的振动信号特征和变化规律,分析提取其中能表征干式变压器机械故障的特征量。
1 干式变压器振动仿真文中构建了SCB11-100/10干式变压器有限元仿真模型。干式变压器铁心和绕组振动频率为电压频率的2倍,即工频电压作用下的振动频率主要为100 Hz,因此,通过100 Hz频域仿真,分析干式变压器铁心和绕组的电磁力分布及振动特性。
1.1 三维变压器模型实验所用SCB11-100/10干式变压器的主要参数如表 1所示。
|
|
表 1 干式变压器主要参数 Table 1 Main parameters of dry-type transformer |
实际变压器结构较复杂,为减小仿真运算量,从以下方面对变压器几何模型进行简化:
(1) 干式变压器铁心硅钢片经环氧树脂浇注固化,硅钢片叠片间气隙很小,铁心振动主要来自磁致伸缩效应,因此将铁心视为一个整体,忽略硅钢片之间的相互影响。
(2) 实际变压器的低压绕组由32层铜箔轧制而成,高压绕组经环氧树脂浇注形成一体化结构,振动一体性较好,因此将低压绕组、高压绕组分别等效为一个整体。
(3) 将铁心和绕组截面等效为圆形,铁心和绕组高度与变压器实际尺寸一致。
(4) 忽略夹件、垫块、冷却装置等结构,通过在铁心下表面和高低压绕组上下面分别设置固定约束来模拟夹件、垫块对铁心和绕组的固定作用。
简化后的干式变压器仿真模型如图 1所示。
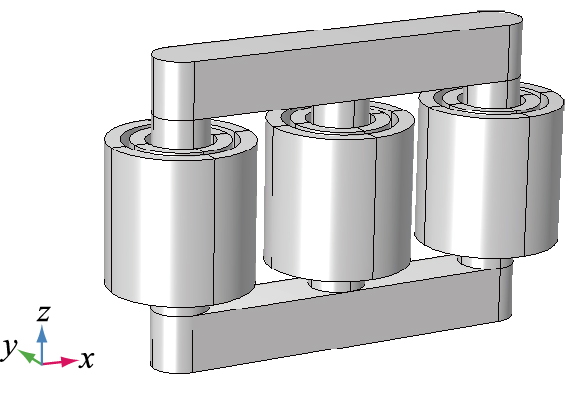
|
图 1 简化仿真模型 Fig. 1 Simplified simulation model |
正弦激励下,电压与磁通的关系为:
| $ U_0=4.44 f N B S $ | (1) |
式中:U0为空载电压;f为电压频率;N为高压绕组匝数;S为铁心截面积;B为相应铁心截面积的铁心磁通密度。
在电压幅值、频率与绕组匝数不变的条件下,铁心中的磁通大小取决于截面积大小。模型等效过程中,在变压器各结构相对距离不变的前提下,将铁心和绕组横截面等效为圆形,等效后模型中铁心和绕组截面积与实际结构存在一定差异。因此,为保证仿真结果与实际的一致性,引入截面修正系数k对仿真中与截面积有关的量进行修正。
| $ k=S_0 / S_1 $ | (2) |
式中:S0为铁心实际截面积,S0=0.019 m2;S1为等效模型的铁心截面积,S1=0.007 9 m2。计算得到模型的截面修正系数k=2.4。
将式(1)与式(2)结合,得到考虑截面积修正后的实际磁通-电压关系为:
| $ B_0=\frac{U_0}{4.44 f N S_0}=\frac{U_0}{4.44 f N k S_1} $ | (3) |
式中:B0为实际磁通。通过对与截面积有关的参量进行修正,使仿真计算时相关参数与实际结构一致,从而保证仿真所得结果的准确性。
1.2 铁心振动仿真结果分析干式变压器铁心的磁致伸缩效应主要由励磁电流引起,即为空载状态下流过绕组的电流,因此,通过空载仿真探究变压器在铁心磁致伸缩效应下的振动信号分布。在变压器的高压侧施加额定电压,低压侧设为开路,以A相为电压相位基准,B、C相电压依次滞后120°,得到空载下铁心的磁通密度分布,如图 2所示。
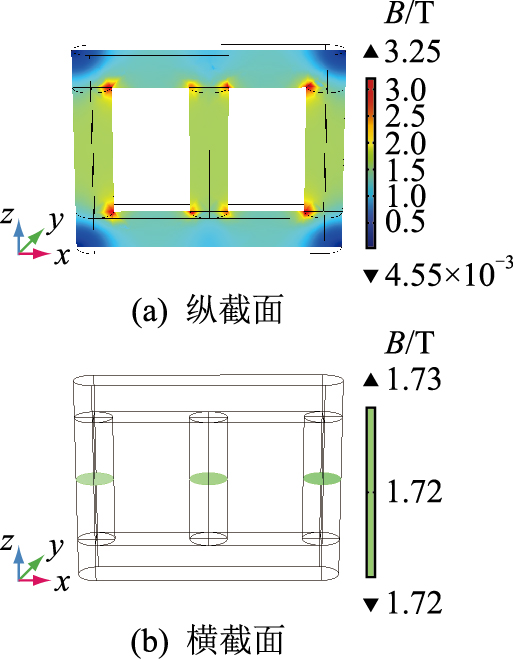
|
图 2 铁心磁通密度模 Fig. 2 Core magnetic flux density |
图 2(a)为空载状态下变压器铁心的整体磁通密度分布,其中铁心窗四角的磁通密度模较大,可能是因为网格剖分在此处有奇点。图 2(b)为三相铁心柱中心处的磁通密度,三相铁心横截面的磁通密度模大小均为1.72 T。
将表 1所列的变压器相关参数代入式(1),计算得到铁心横截面的磁感应强度大小为1.71 T,与仿真结果几乎一致,相对误差仅为0.06%,验证了仿真模型的准确性。
铁心表面X、Y、Z三个方向的振动加速度幅值分布如图 3所示。
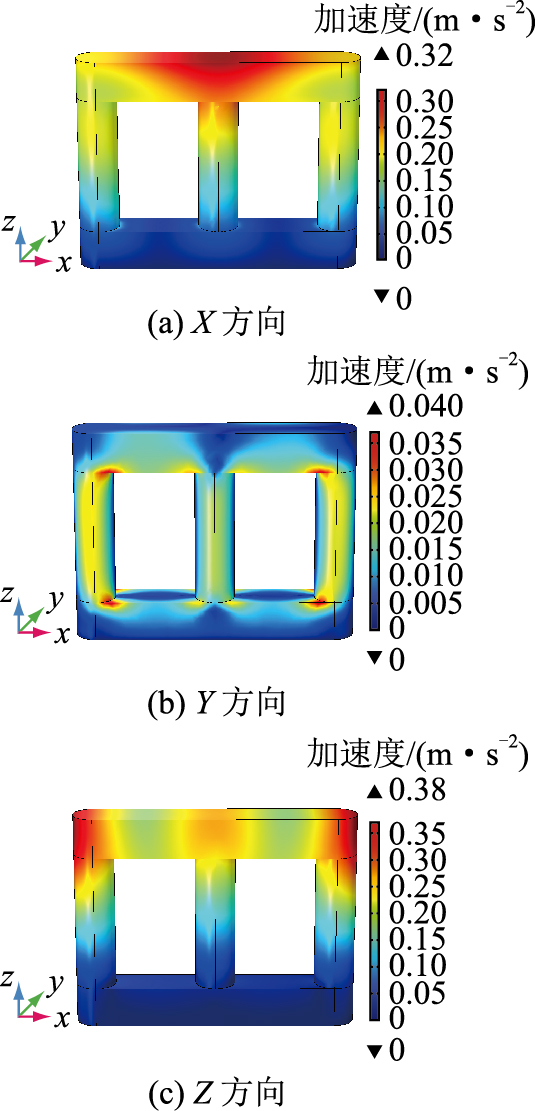
|
图 3 振动加速度幅值分布 Fig. 3 Vibration acceleration amplitude distribution |
铁心磁通主要在XZ平面内流通,磁致伸缩应变的方向和磁场强度的方向相同。由图 3所示仿真结果可见,铁心在X、Z方向的振动加速度幅值较大。其中,X方向振动加速度幅值在铁轭B相对应位置达到最大,最大值为0.32 m/s2;Z方向加速度幅值最大分布在铁轭A、C两相对应位置,最大值为0.38 m/s2,由于B相比A、C两相在Z方向上受到铁轭的约束更强,所以B相在Z方向上加速度幅值较小。铁心Y方向磁通较少,图 3(b)中Y方向的加速度幅值总体较小,最大仅为0.04 m/s2。由于铁心下表面设置了固定约束,所以仿真时铁心下半部分的振动加速度较小。
由图 3可知,铁心上表面振动较为强烈,可以选择在铁心上表面安装振动信号传感器,进行振动信号的测量。
1.3 绕组振动仿真结果分析通过在高低压绕组中分别施加方向相反的额定电流,模拟正常工况下干式变压器的绕组振动规律。以A相为电流相位基准,B、C相依次滞后120°。在固体力学模块添加洛伦兹力贡献的体载荷来模拟绕组所受电磁力作用。仿真得到干式变压器高低压绕组的漏磁通分布,如图 4所示。

|
图 4 磁通密度模分布 Fig. 4 Magnetic flux density distribution |
由图 4可知,由于高低压绕组的电流方向相反,变压器的轴向磁场集中分布于同相高压绕组内侧和低压绕组外侧之间的区域,仿真得到的磁通密度模最大为0.03 T,且轴向方向上在绕组中间部分磁通密度模较大;高压绕组外侧和低压绕组内侧磁场相互抵消,磁通密度模较小;径向磁场在高、低压绕组上、下两端达到最大,绕组端部磁通密度模较明显。仿真结果与理论分析一致。
由于仿真所用模型的高低压绕组结构为二维轴对称结构,X、Y方向上绕组受力分布规律相同,因此可将X、Y方向上的仿真结果相结合,得到绕组的径向结果。高低压绕组的径向和轴向所受洛伦兹力如图 5所示。
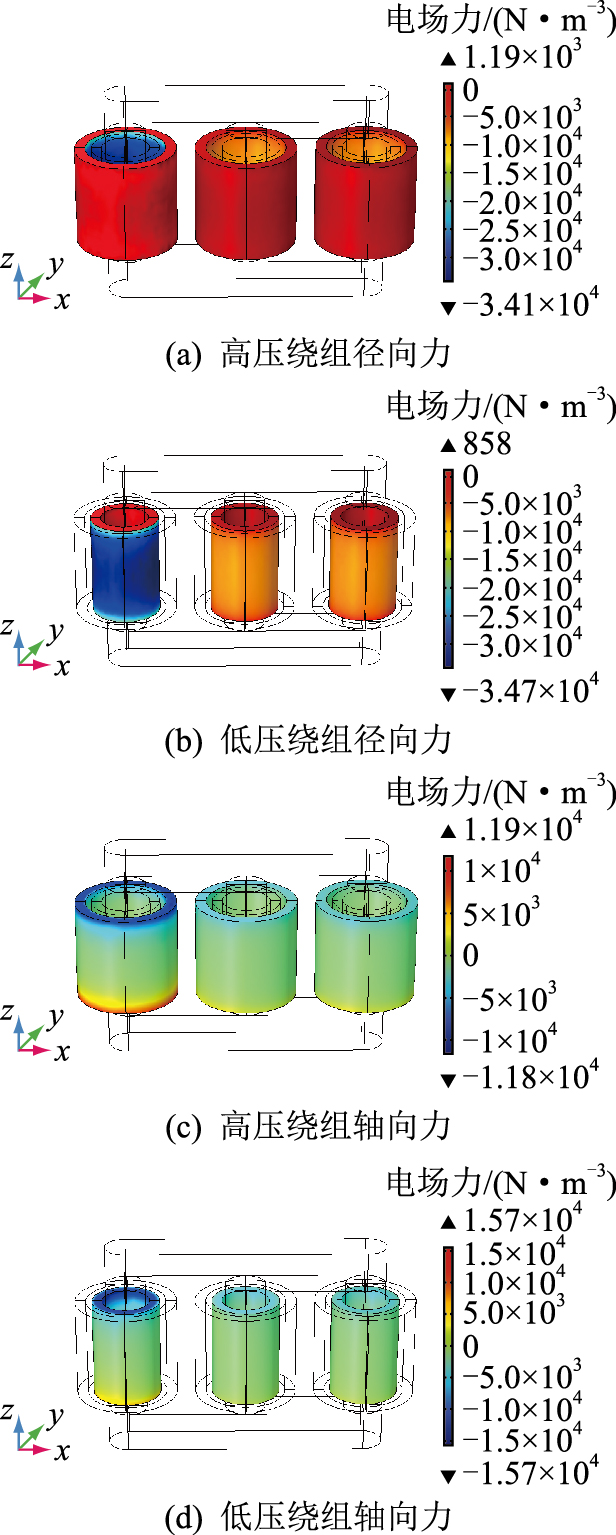
|
图 5 绕组受洛伦兹力分布 Fig. 5 Lorentz force distribution of windings |
图 5中,三相绕组的受力分布与仿真施加条件有关。图中A相绕组所受径向、轴向力较大,B、C相绕组受力较小,这是由于该时刻A相电流最大,所以受力最大;B、C两相电流分别超前、滞后A相120°,电流有效值减半,所以B、C两相受力较小。
结合图 4、图 5分析可知,图 4中绕组的轴向磁通分布主要集中在高、低压绕组的相邻表面,图 5(a)、(b)中高压绕组内侧和低压绕组外侧所受径向电场力最为集中,二者分布规律相同。其中,高压绕组所受径向电场力的最大值为3.41×104 N/m3,方向沿径向向外;低压绕组所受径向电场力的最大值为3.47×104 N/m3,方向沿径向指向轴心。
由于径向磁通主要分布在绕组端部,所以图 5(c)、(d)中,高、低压绕组上、下两端所受轴向力较大。同一绕组上、下两端所受轴向力大小相等、方向相反。其中,高压绕组轴向受力最大值为1.19×104 N/m3;低压绕组轴向受力最大值为1.57×104 N/m3。从数值可以看出,绕组所受轴向洛伦兹力的最大值小于绕组所受径向洛伦兹力的最大值。
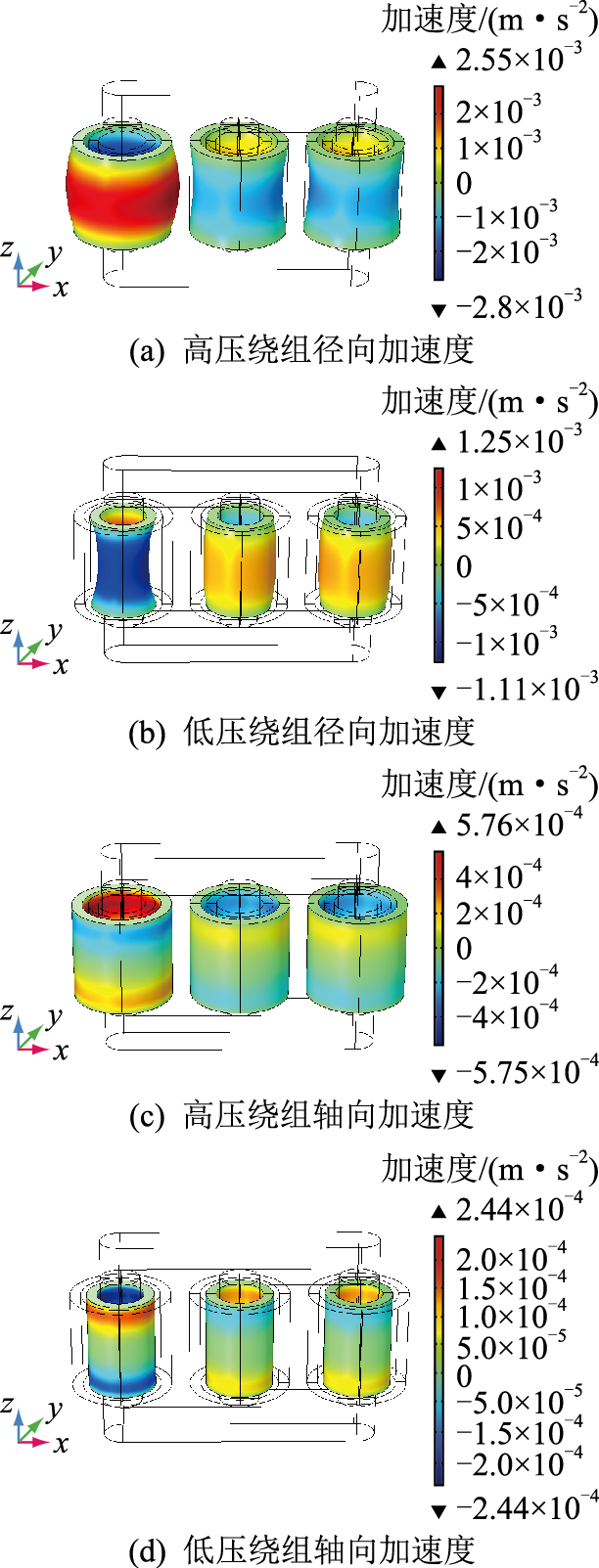
高、低压绕组的径向和轴向振动加速度分布如图 6所示。
|
图 6 绕组振动加速度分布 Fig. 6 Vibration acceleration distribution of windings |
图 6中,高、低压绕组的振动加速度大小及方向与其所受电场力有关。结合图 5、图 6分析,图 5中绕组所受径向力主要集中在高压绕组内侧和低压绕组外侧,由于绕组是固体实心结构,因此图 6中在电场力的作用下同一绕组内外侧共同运动,且运动方向与图 5中电场力方向一致。
由于绕组轴向上中间段径向洛伦兹力大,所以中间段径向加速度较大;绕组轴向力主要集中在绕组两端,所以轴向加速度主要集中在靠近绕组端部区域。轴向的受力和加速度分布略有区别是由于在绕组上、下表面设置了固定约束以模拟垫块的紧固作用,因此绕组端部所受轴向力最大,而加速度最大值出现在接近端部附近,但绕组的轴向受力分布与其轴向加速度的总体分布一致。
1.4 铁心和绕组振动对比根据1.2节和1.3节的干式变压器铁心、绕组振动仿真结果,分析正常工况下铁心、绕组对干式变压器整体振动的贡献。
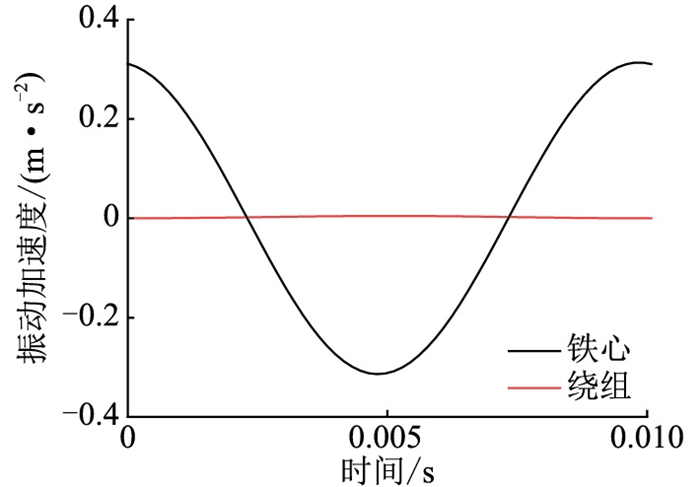
选取A相铁心柱上表面中点为铁心振动信号测点,A相高压绕组外表面中间高度处为绕组振动信号测点。对铁心、绕组A相测点的振动结果进行动态数据拓展,比较一个工频周期内二者振动加速度信号的大小,结果如图 7所示。
|
图 7 铁心、绕组振动加速度贡献 Fig. 7 Vibration acceleration contribution of the core and winding |
图 7中,铁心和绕组的振动加速度均为100 Hz的周期变化,其中铁心振动加速度的最大值为0.31 m/s2,绕组振动加速度的最大值为0.002 3 m/s2,各时刻中绕组的加速度振幅均远小于铁心,二者振幅相差2个数量级,所以图中绕组振动几乎呈一条直线。
绕组上、下端固定约束的设置会对绕组振动加速度仿真结果产生一定影响,但仿真结果总体跟实际吻合:干式变压器的容量相对较小、额定工况下绕组流过的负载电流和所受洛伦兹力较小。此外,由于高压绕组经环氧树脂浇注成一个整体,结构的一体性较好,因此干式变压器的绕组振动较小,正常运行过程中的振动主要来源于由磁致伸缩产生的铁心振动。因此,在后续实验中,只考虑不同工况下的干式变压器铁心振动变化规律。
2 铁心紧固与松动故障振动信号实验搭建SCB11-100/10干式变压器振动信号采集实验平台,对干式变压器铁心紧固及松动状态下的振动信号进行采集。
2.1 实验平台搭建实验所使用的SCB11-100/10干式变压器实际结构为降压变压器,考虑实际运行时产生的压降,低压侧额定电压设计值留有5%裕度。实验中,将降压变压器作升压变压器使用,通过三相调压器向干式变压器的低压侧加压,高压侧空载,升压过程中所产生的铁耗与铜耗远小于降压,不必增加损耗系数。因此,实验过程中施加的最大电压应比低压侧额定电压低5%,即低压侧所加电压最大应不超过380 V,以保证高压侧空载电压不超过额定值。振动信号采集实验平台如图 8所示。

|
图 8 实验平台示意 Fig. 8 Schematic diagram of experiment platform |
通过分压器分压后从A相低压侧采集电压信号作为参考,并将振动传感器安装在铁心上表面进行振动信号的测量,传感器的灵敏度为(10±20%) mV/(m ·s-2),可测的振动信号频带范围为10~20 000 Hz。振动传感器的输出信号经信号处理电路进行滤波和放大后,与A相电压信号一同通过示波器进行采集和显示。
根据1.2节的铁心振动仿真结果,铁心上表面的振动较为强烈,因此选择振动传感器测点为B相铁心柱上表面的中点对应位置,如图 9所示。

|
图 9 测点分布 Fig. 9 Distribution of measuring points |
为研究干式变压器铁心振动的影响因素和不同工况下的振动信号变化规律,设计如下实验。
首先,以20 V为步长对变压器逐级加压至380 V,研究铁心振动信号随外加电压的变化规律。其次,变压器运行时的铁心振动会使铁心夹件受迫振动,长期作用下可能导致铁心夹件松动,产生异常振动信号,因此改变铁心上夹件的螺栓紧固程度,模拟干式变压器的铁心松动故障,研究铁心松动前后的振动信号变化规律。具体故障设置如图 10所示。

|
图 10 铁心上夹件A相侧螺栓 Fig. 10 Bolt on the clip pieces of A phase |
对实验测得的不同工况下的铁心振动信号进行时域和频域特征分析,并分析铁心松动状态下振动信号变化规律。
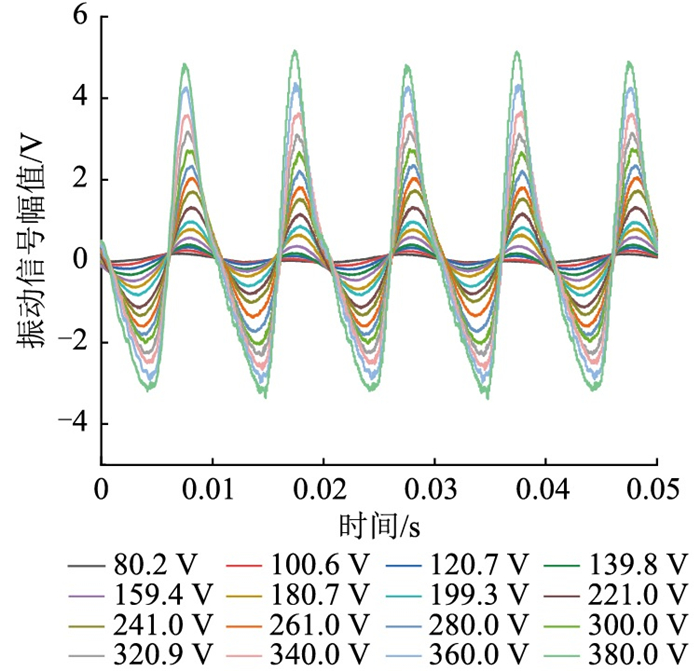
3.1 铁心振动随电压变化分析以20 V为步长对变压器逐级加压至380 V,测量得到不同电压下的铁心振动信号时域波形,如图 11所示。
|
图 11 振动信号波形随电压变化 Fig. 11 Vibration signal values with changed voltage |
图 11中,随着外加电压的增大,振动信号幅值不断增大,波形从正弦逐渐变化为尖顶锯齿形,时域波形出现一定畸变,但振动信号的频率和相位几乎不变。对图 11中不同电压下的振动信号进行频谱分析,得0~500 Hz下的频率分布,如图 12所示。

|
图 12 频率分布随电压变化瀑布 Fig. 12 Waterfall of frequency distribution with changed voltage |
图 12中,不同电压下的主频率分量均为100 Hz。随着外加电压的升高,铁心振动信号快速增大,各频率分量的幅值均随电压升高而增加,且电压较高时高次谐波幅值增长较快。
为进一步研究振动信号随外加电压的变化规律,分别提取图 11中不同电压下时域振动信号的峰值,以电压平方的标幺值为横坐标,得到振动信号峰值随电压平方的变化关系,如图 13所示。图中U为实验中低压侧所加电压大小;UN为低压侧额定电压,UN=400 V。

|
图 13 振动信号峰值和电压平方的关系 Fig. 13 Relationship between vibration peak and squared voltage |
由图 13可见,振动信号峰值与电压平方近似成正比。外加电压较低时,由于励磁电压小,磁场较低,磁致伸缩应变响应较小,因此振动信号也较小。当外加电压为140~340 V时,振动信号峰值随所加电压的平方几乎呈线性关系增长,拟合曲线为:
| $ v_1=5.479\left(U / U_{\mathrm{N}}\right)^2-0.304 $ | (4) |
式中:v1为总振动信号的峰值。
外加电压在140~340 V之间时,铁心处于硅钢片磁化曲线的线性区域,因此磁致伸缩振动也随外加电压的平方呈线性增长。在该线性区域内,应变响应对外磁场比较敏感,微小的磁场增量即可引起较大的应变输出,且随着铁心磁化强度的不断增加,铁心硅钢片接缝处的磁场更为复杂,产生的磁致伸缩应力和电磁力也较大,所以振动信号增长较快,线性增长曲线的斜率较大。
电压加到340 V以后,铁心逐渐进入磁化曲线非线性区域,此时总振动信号峰值增长变快,不再和电压的平方成正比。
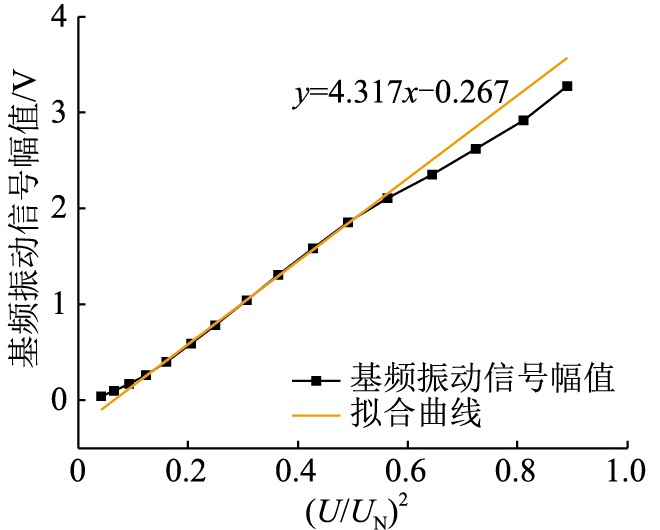
提取振动信号100 Hz基频分量,探究不同电压下100 Hz基频分量幅值随电压平方的变化关系,如图 14所示。
|
图 14 基频振动信号幅值和电压平方的关系 Fig. 14 Relationship between fundamental frequency vibration and squared voltage |
图 14中,基频振动信号幅值随电压平方的变化规律与图 13中整体振动信号的变化规律具有相似性,电压加到140~300 V时,基频振动信号幅值随电压平方呈线性增长,拟合曲线为:
| $ v_2=4.317\left(U / U_{\mathrm{N}}\right)^2-0.267 $ | (5) |
式中: v2为基频振动信号幅值。
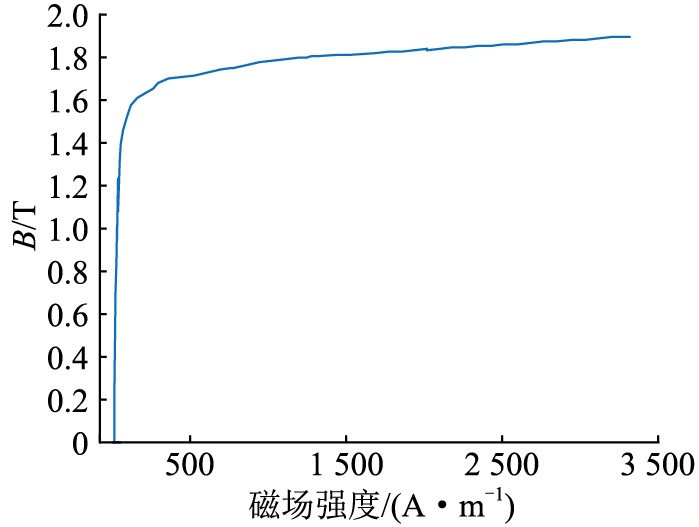
10 kV干式变压器硅钢片磁化曲线如图 15所示。由式(1)推算可得,当外加电压大小分别为140、300、320、340、380 V时,各电压下的铁心磁通密度分别为0.6、1.28、1.37、1.45、1.63 T。由图 15可知,当电压较低时,铁心处于磁化曲线的线性区域,此时振动信号主要由100 Hz基频信号构成,总振动信号随电压平方增大的变化规律与基频信号一致,均为随电压平方近似呈线性关系增长。图 14中,当外加电压达到300 V以上时,铁心已接近硅钢片磁化曲线的非线性区域,此时基频振动信号幅值不再保持线性增长规律,基频振动信号与电压平方逐渐偏离线性关系。
|
图 15 干式变压器硅钢片磁化曲线 Fig. 15 B-H curve of the core of dry-type transformer |
对比图 13和图 14可知,电压加到340 V以后,总振动信号峰值随电压平方增长变快是因为电压较高时高次谐波分量的幅值增长较快。这是因为在铁心逐渐饱和的过程中,由于磁化曲线的非线性,励磁电流波形会发生畸变而呈尖顶波,电流中的谐波含量增加,由此引发磁致伸缩振动信号中高次谐波振动分量快速增长,总振动信号峰值偏离原本的线性曲线。
3.2 铁心松动振动信号特征分析铁心紧固状态变化会对其振动状态产生较大影响,并在其表面的振动信号中有所反映。因此,以铁心上夹件完全松动的极限状态作为对比,探究铁心松动前后振动信号的显著变化特征。
在变压器低压侧加电压至380 V,此时变压器铁心磁通接近额定运行状态,测得铁心紧固时和上夹件完全松动后B相测点在2个工频周期内的时域振动信号波形,如图 16所示。

|
图 16 铁心松动前后振动信号 Fig. 16 Vibration signal of the core before and after the core loosen |
图 16中,铁心紧固及松动状态下的振动信号整体均呈现出100 Hz的周期性,但由于振动信号含有一定的高次谐波分量,导致振动信号的时域波形存在一定畸变。干式变压器铁心夹件松动会导致铁心所受约束力减小,振动增强,对比图 16(a)、(b)可知,铁心松动后,振动信号的峰值明显增大。
对图 16中铁心松动前后的振动信号进行0~1 000 Hz内的频域分布对比,结果如图 17所示。

|
图 17 铁心松动前后振动信号频率分布 Fig. 17 Vibration signal frequency distribution before and after the core loosen |
图 17中,铁心紧固状态下的谐波主要为100 Hz的高次倍频分量,并且振动信号的频率分量主要集中在400 Hz及以下,400 Hz以上的成分占比较少。其中,200 Hz谐波分量的幅值较大,因此导致图 16(a)中的振动信号时域波形出现半个周期内波形不对称的现象。
由于铁心夹件松动导致铁心振动强度的增大,在图 17中,振动信号的50、100、150、200、600 Hz等频率分量的幅值均增加。其中,150、550 Hz分量的振幅变化较明显,可能是由于铁心机械结构的变化使变压器振动固有频率发生了改变,接近150 Hz和550 Hz处存在变压器的固有频率,使该处的振动增强。
将基频振动信号幅值占总振动信号幅值的大小记为基频占比。以400 Hz为分界值,频率高于400 Hz为高倍频信号,低于400 Hz为低倍频信号,定义两者之比为高低频比。将高于50 Hz的50 Hz奇数次倍频的占比记为奇次谐波比,高于100 Hz的50 Hz偶数次倍频的占比记为偶次谐波比,两者的比值为奇偶次谐波比。选取基频占比、高低频比、奇次谐波比、偶次谐波比和奇偶谐波比等特征值对松动状态特征进行分析,结果如表 2所示。
|
|
表 2 振动信号特征值计算 Table 2 Vibration signal eigenvalue calculation |
表 2中,由于铁心松动后振动信号中高次谐波成分的增加,基频振动信号在总信号中的占比减小,高低频比增加。由于铁心松动前后150、550 Hz等50 Hz奇数次倍频分量的幅值变化较大,所以奇次谐波占比和奇偶次谐波比变化明显。铁心松动后,振动信号中的偶次谐波占比减小。但由于高次谐波分量的幅值很小,奇次谐波比、偶次谐波比及奇偶次谐波比的变化率具有较大的随机性,难以作为故障判断的主要依据。因此,以振动信号的基频分量占比变化率作为铁心松动故障的特征值,认为当振动信号中基频分量的占比减少超过10%时,变压器可能发生了铁心松动故障,须及时对变压器进行检修。
由铁心松动前后振动信号的时频域分析可知:铁心紧固时振动信号的基频分量占振动信号的50%以上,振动信号中几乎不含400 Hz以上的高次谐波成分,频率集中在较低频带内;当铁心发生松动后,时域振动信号波形的幅值增大且存在明显畸变,振动信号中高次谐波分量明显增大,振动信号基频分量的占比降低。
此外,铁心振动信号的特征还和变压器运行年限等因素有关。在未存在机械故障的状态下,老化变压器振动信号就会有较高的幅值和高次谐波成分出现。文中采用的是新购置的SCB11-100/10干式变压器,变压器健康状态较好,测得的振动信号分布情况比较理想。
因此,可以通过记录干式变压器在不同工况下的振动信号作为对比的数据库,分析得到正常运行或存在机械故障时的振动信号特征及特征值分布范围,将实时测得的振动信号进行特征值分析对比,进而实现对干式变压器铁心机械状态的诊断。
4 结论文中采用仿真和实验相结合的方法,对干式变压器铁心和绕组的振动信号分布进行仿真分析,通过实验探究了不同工况下干式变压器的振动信号特征及变化规律,并分析提取出了可以表征铁心松动故障的特征量。主要结论如下:
(1) 由于干式变压器容量小,且高压绕组由环氧树脂浇注固化形成一体式结构,因此绕组产生的振动较小,额定工况下干式变压器振动主要来源于铁心的磁致伸缩效应。
(2) 外加电压使铁心磁通处于磁化曲线的线性段时,铁心总振动信号峰值以及基频振动信号幅值都随电压的平方呈线性增长。随着磁化曲线进入非线性段、铁心逐渐饱和,总振动信号峰值因高次谐波的快速增加而增长变快,基频振动信号幅值因铁心饱和而增长变慢。
(3) 铁心松动会导致振动信号的幅值增大,高次谐波含量明显增加。振动信号的基频占比和高低频比可以作为表征铁心机械状态的特征量。
| [1] |
张乾荣, 魏忠正. 环氧树脂浇注干式变压器局部放电的原因分析和管控措施[J]. 变压器, 2021, 58(2): 66-68. ZHANG Qianrong, WEI Zhongzheng. Cause analysis and control measures of partial discharge of epoxy resin cast dry-type transformer[J]. Transformer, 2021, 58(2): 66-68. (  0) 0) |
| [2] |
熊兰, 赵艳龙, 杨子康, 等. 树脂浇注干式变压器温升分析与计算[J]. 高电压技术, 2013, 39(2): 265-271. XIONG Lan, ZHAO Yanlong, YANG Zikang, et al. Temperature rise analysis and calculation of cast resin dry-type transformers[J]. High Voltage Engineering, 2013, 39(2): 265-271. (  0) 0) |
| [3] |
桑静波. 干式变压器的在线故障诊断与寿命预测[D]. 北京: 北京交通大学, 2020. SANG Jingbo. On-line fault diagnosis and life prediction of dry-type transformers[D]. Beijing: Beijing Jiaotong University, 2020. (  0) 0) |
| [4] |
李永建, 闫鑫笑, 张长庚, 等. 基于磁-热-流耦合模型的变压器损耗计算和热点预测[J]. 电工技术学报, 2020, 35(21): 4483-4491. LI Yongjian, YAN Xinxiao, ZHANG Changgeng, et al. Numerical prediction of losses and local overheating in transformer windings based on magnetic-thermal-fluid model[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 4483-4491. (  0) 0) |
| [5] |
邵宇鹰, 王枭, 彭鹏, 等. 基于波束形成算法的干式变压器异响定位装置研制及应用[J]. 高压电器, 2022, 58(5): 187-194. SHAO Yuying, WANG Xiao, PENG Peng, et al. Development and application of abnormal-sound-locating device for dry-type transformer based on beam forming algorithm[J]. High Voltage Apparatus, 2022, 58(5): 187-194. (  0) 0) |
| [6] |
蔡昌万. 机械故障状态下的非晶合金干式变压器振动信号分析方法研究[D]. 赣州: 江西理工大学, 2021. CAI Changwan. Study on vibration signal analysis method of amorphous alloy drytype transformer under mechanical fault state[D]. Ganzhou: Jiangxi University of Science and Technology, 2021. (  0) 0) |
| [7] |
张晓华, 蔡巍, 武宇平, 等. 基于漏磁通的干式变压器匝间故障诊断[J]. 电网与清洁能源, 2021, 37(11): 55-62, 71. ZHANG Xiaohua, CAI Wei, WU Yuping, et al. Inter-turn fault diagnosis of dry-type transformers based on flux leakage[J]. Power System and Clean Energy, 2021, 37(11): 55-62, 71. (  0) 0) |
| [8] |
汲胜昌, 张凡, 师愉航, 等. 基于振动信号的电力变压器机械状态诊断方法研究综述[J]. 高电压技术, 2020, 46(1): 257-272. JI Shengchang, ZHANG Fan, SHI Yuhang, et al. Review on vibration-based mechanical condition monitoring in power transformers[J]. High Voltage Engineering, 2020, 46(1): 257-272. (  0) 0) |
| [9] |
黄敏均. 户内配电变压器低频噪声监测分析与治理[J]. 江苏电机工程, 2011, 30(2): 55-58. HUANG Minjun. Monitoring and treatment of low-frequency noise of indoor distribution transformer[J]. Jiangsu Electrical Engineering, 2011, 30(2): 55-58. (  0) 0) |
| [10] |
朱叶叶, 汲胜昌, 张凡, 等. 电力变压器振动产生机理及影响因素研究[J]. 西安交通大学学报, 2015, 49(6): 115-125. ZHU Yeye, JI Shengchang, ZHANG Fan, et al. Vibration mechanism and influence factors in power transformers[J]. Journal of Xi'an Jiaotong University, 2015, 49(6): 115-125. (  0) 0) |
| [11] |
潘超, 葛佳柔, 刘天舒, 等. 单相变压器首端匝间短路电磁振动特性研究[J]. 电力工程技术, 2019, 38(6): 147-153, 166. PAN Chao, GE Jiarou, LIU Tianshu, et al. The electromagnetic vibration characteristics of the first end of single-phase transformer[J]. Electric Power Engineering Technology, 2019, 38(6): 147-153, 166. (  0) 0) |
| [12] |
余长厅, 黎大健, 汲胜昌, 等. 基于振动噪声及BP神经网络的变压器故障诊断方法研究[J]. 高压电器, 2020, 56(6): 256-261. YU Zhangting, LI Dajian, JI Shengchang, et al. Research on transformer fault diagnosis method based on vibration noise and BP neural network[J]. High Voltage Apparatus, 2020, 56(6): 256-261. (  0) 0) |
| [13] |
何文林, 郑一鸣. 基于振动检测的变压器绕组机械稳定性评估[J]. 浙江电力, 2022, 41(7): 57-62. HE Wenlin, ZHENG Yiming. Evaluation on mechanical stability of transformer windings based on vibration detection[J]. Zhejiang Electric Power, 2022, 41(7): 57-62. (  0) 0) |
| [14] |
蔡文方, 聂玲, 应光耀, 等. 振动分析法在变压器故障诊断及隐患治理中的应用[J]. 浙江电力, 2022, 41(2): 53-59. CAI Wenfang, NIE Ling, YING Guangyao, et al. Application of vibration analysis in transformer fault diagnosis and hidden peril management[J]. Zhejiang Electric Power, 2022, 41(2): 53-59. (  0) 0) |
| [15] |
张琛, 熊庆, 汲胜昌, 等. 基于压电材料的变压器振动能量收集装置研究[J]. 电力工程技术, 2021, 40(6): 173-178. ZHANG Chen, XIONG Qing, JI Shengchang, et al. Vibration energy harvesting device for transformer based on piezoelectric material[J]. Electric Power Engineering Technology, 2021, 40(6): 173-178. (  0) 0) |
| [16] |
HONG K X, HUANG H, ZHOU J P, et al. A method of real-time fault diagnosis for power transformers based on vibration analysis[J]. Measurement Science and Technology, 2015, 26(11): 115011. (  0) 0) |
| [17] |
赵莉华, 丰遥, 谢荣斌, 等. 基于交叉小波的变压器振动信号幅频特征量提取方法[J]. 高电压技术, 2019, 45(2): 505-511. ZHAO Lihua, FENG Yao, XIE Rongbin, et al. Amplitude and frequency feature extraction for transformer vibration based on cross-wavelet transform[J]. High Voltage Engineering, 2019, 45(2): 505-511. (  0) 0) |
| [18] |
ZOU D X, QIAN G C, ZHANG X J, et al. Multi-physical field simulation of winding vibration characteristics of dry-type transformer[C]//2020 IEEE International Conference on Ap plied Superconductivity and Electromagnetic Devices (ASEMD). Tianjin, China. IEEE, 2020: 1-2.
(  0) 0) |
| [19] |
何源. 故障状态下干式变压器铁心的振动研究[D]. 天津: 河北工业大学, 2020. HE Yuan. Research on vibration of dry-type transformer core in fault state[D]. Tianjin: Hebei University of Technology, 2020. (  0) 0) |
| [20] |
祝丽花, 杨庆新, 闫荣格, 等. 考虑磁致伸缩效应电力变压器振动噪声的研究[J]. 电工技术学报, 2013, 28(4): 1-6, 19. ZHU Lihua, YANG Qingxin, YAN Rongge, et al. Research on vibration and noise of power transformer cores including magnetostriction effects[J]. Transactions of China Electrotechnical Society, 2013, 28(4): 1-6, 19. (  0) 0) |
| [21] |
祝丽花, 王斌, 刘松, 等. 不同负载对干式变压器电磁振动的影响分析[J]. 电工技术学报, 2018, 33(7): 1599-1606. ZHU Lihua, WANG Bin, LIU Song, et al. Research on electromagnetic vibration of dry type transformer under different types of load[J]. Transactions of China Electrotechnical Society, 2018, 33(7): 1599-1606. (  0) 0) |
| [22] |
陆昕, 周雄, 钱帅伟, 等. 干式变压器有限元仿真模型的电磁和振动分析[J]. 应用声学, 2020, 39(4): 638-646. LU Xin, ZHOU Xiong, QIAN Shuaiwei, et al. Electromagnetic and vibration analysis of dry transformer finite element simulation model[J]. Journal of Applied Acoustics, 2020, 39(4): 638-646. (  0) 0) |
| [23] |
罗世豪. 基于声纹的干式变压器典型缺陷识别研究[D]. 北京: 华北电力大学, 2021. LUO Shihao. Research on typical defects recognition of dry-type transformer based on voiceprint[D]. Beijing: North China Electric Power University, 2021. (  0) 0) |
| [24] |
金潇. 基于声信号的配电变压器故障诊断方法研究[D]. 武汉: 武汉大学, 2017. JIN Xiao. Research on fault diagnosis method for distribution transformer based on acoustic signal[D]. Wuhan: Wuhan University, 2021. (  0) 0) |
| [25] |
MANOHAR S S, SUBRAMANIAM A, BAGHERI M, et al. Transformer winding fault diagnosis by vibration monitoring[C]//2018 Condition Monitoring and Diagnosis (CMD). Perth, WA, Australia. IEEE, 2018: 1-6.
(  0) 0) |
| [26] |
钟星鸣. 干式变压器的振动和噪声研究[D]. 广州: 华南理工大学, 2010. ZHONG Xingming. Research on vibration and noise of dry-type transformer[D]. Guangzhou: South China University of Technology, 2010. (  0) 0) |
| [27] |
高剑锋. 用振动分析法评估干式变压器状态的研究[J]. 安徽科技, 2022(2): 50-52. GAO Jianfeng. Study on evaluating the condition of dry-type transformer by vibration analysis method[J]. Anhui Science & Technology, 2022(2): 50-52. (  0) 0) |
| [28] |
冯忠奎, 刘广, 崔炎, 等. 基于振动信号的干式变压器状态监测与故障诊断系统研究[J]. 电子测试, 2022, 36(12): 111-113. FENG Zhongkui, LIU Guang, CUI Yan, et al. Research on state monitoring and fault diagnosis system of dry transformer based on vibration signal[J]. Electronic Test, 2022, 36(12): 111-113. (  0) 0) |
 2023, Vol. 42
2023, Vol. 42


 李沂新(2001), 女, 硕士在读, 研究方向为干式变压器故障诊断(E-mail:
李沂新(2001), 女, 硕士在读, 研究方向为干式变压器故障诊断(E-mail: