文章编号: 2096-3203(2023)05-0148-10 中图分类号: TM72
模块化多电平换流器(modular multilevel converter, MMC)具有易扩展、开关损耗小和输出波形质量好等优点,在柔性直流输电领域得到了广泛应用[1-5]。在提高对架空线路频发的直流短路故障防御性方面,相比全桥型MMC,全桥-半桥混合型MMC具备较低的构建成本、较高的运行效率及良好的直流故障穿越能力[6-7],并被用于昆柳龙柔性直流输电工程[8]。
为提高极端天气下输电系统的运行可靠性,混合型MMC可运行于低直流电压工况[9]。此外,为提升器件利用率[10-11]、降低子模块电容值及提高设备功率密度[12-13],可通过增加全桥子模块(full bridge sub-module, FBSM)配比,使混合型MMC工作于交流升压工况。因此,高调制比运行工况是混合型MMC典型运行场景之一。
工程中,MMC子模块电容的重量和体积均占子模块的50%以上,成本占1/3[14]。为此,国内外学者对MMC子模块电容的优化开展了大量研究工作,先后提出基于二倍频环流注入[15-16]、三次谐波共模电压注入[17-18]及改变运行调制比[19]的电容优化方法。其优化机理为:在满足换流器传输功率需求下,通过改变桥臂输出电压或桥臂电流主动控制桥臂瞬时功率,以减小电压纹波幅值,进而降低电容需求。电容电压波动率与电容值密切相关,为进
一步降低子模块电容值,文献[20-21]提出基于高电容电压波动率的电容优化方法。该方法考虑开关器件的电压应力约束,在维持子模块电容电压最大值不变的前提下,通过降低子模块电容电压的直流分量及增大电压波动率,实现电容值的优化。文献[22-23]综合环流注入、三次谐波共模电压注入及运行调制比的设计实现子模块电容值的进一步优化。
对于高调制比混合型MMC,一般通过对所有子模块一起排序实现电容电压的均衡[18-19],两类子模块电容充放电行为存在强耦合,其电压的直流分量及波动分量均存在差异。然而,现有混合型MMC电容优化方法未充分考虑该耦合特性,存在半桥子模块(half bridge sub-module, HBSM)电容电压波动率小的不足,难以实现其电容值的优化。
针对上述问题,文中提出可实现FBSM、HBSM电容电压动态特性准确调节的模组解耦控制方法;进一步,通过对全桥及半桥模组平均开关函数的优化设计,大幅减小了HBSM的电容需求。文中所提电容优化方法不仅可调节FBSM、HBSM电容电压的直流分量及纹波分量,还能有效降低高调制比运行工况下混合型MMC的重量、体积及成本。
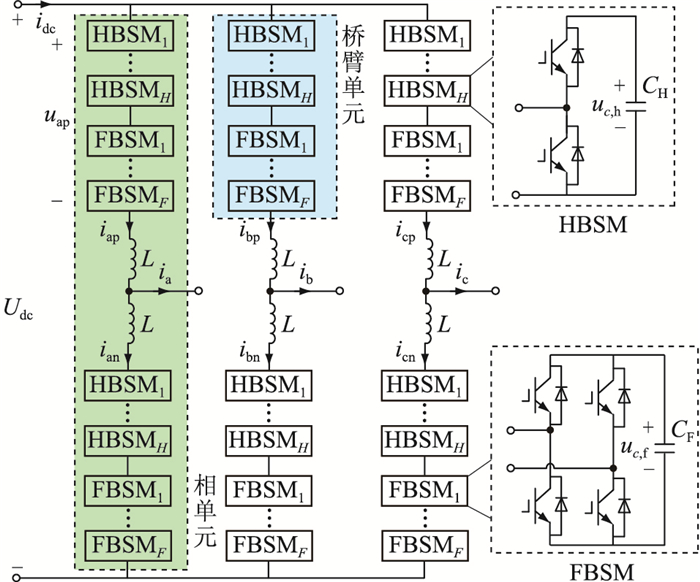
1 混合型MMC子模块电容电压波动分析 1.1 混合型MMC的工作原理混合型MMC的拓扑如图 1所示,每个桥臂包含H个HBSM、F个FBSM及1个桥臂电抗器L。其中,Udc、idc分别为直流侧电压和电流;ia、ib、ic为交流侧三相电流;uap、iap分别为A相上桥臂输出电压和电流;ibp、icp分别为B、C相上桥臂电流;CF、CH分别为FBSM和HBSM的电容;uc, f、uc, h分别为FBSM和HBSM动态电容电压;ian、ibn、icn分别为A、B、C相下桥臂电流。
|
图 1 混合型MMC拓扑 Fig. 1 Hybrid MMC topology |
忽略环流抑制器输出电压,uapref、iap可表示为:
| $\left\{\begin{array}{l}u_{\text {apref }}=\frac{1}{2} U_{\mathrm{dc}}-u_{\mathrm{a}} \sin \omega t \\ i_{\text {ap }}=\frac{1}{3} i_{\mathrm{dc}}+\frac{1}{2} i_{\mathrm{a}} \sin (\omega t-\varphi)\end{array}\right.$ | (1) |
式中:uapref为A相上桥臂输出电压的指令值;ua为A相相电压;ω为基频角频率;φ为功率因数角。
定义调制比m如下:
| $m=\frac{2 u_{\mathrm{a}}}{U_{\mathrm{dc}}}$ | (2) |
由于FBSM具有输出负电平的能力,所以混合型MMC可以在m>1时稳定运行,即实现高调制比运行。当m < 1时,FBSM工作在半桥模式。桥臂输出电压指令恒大于0,两类子模块统一排序进行投切。FBSM、HBSM电容电压波动率相同。
通过增加FBSM配比,换流器可运行于交流升压工况[12]。此时,两类子模块工作差异性显著。为实现电容电压的均衡,当桥臂输出电压指令为正时,对所有子模块排序进行投切,当桥臂输出电压指令为负时,仅对FBSM进行排序投切[18-19]。两类子模块充放电行为存在耦合, 电容电压波动率存在差异。文中综合考虑实现高调制比和直流故障穿越能力,选取全桥-半桥2 ∶1的方案[10-12]。
1.2 高调制比下子模块电容电压纹波分析为更好分析两类子模块电压纹波间的差异性,假设不同FBSM、HBSM间电容电压动态特性一致,将桥臂等效为全桥及半桥2个模组。
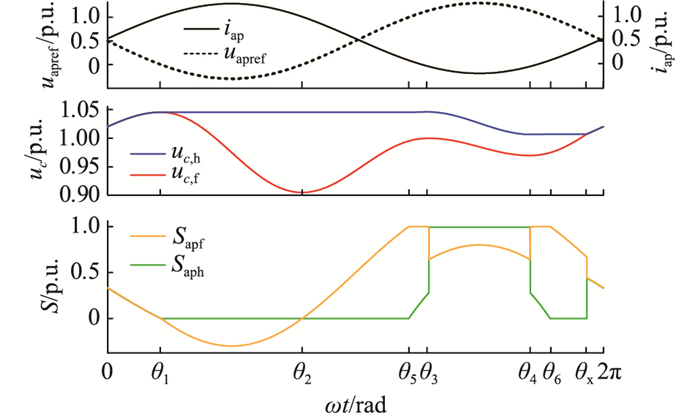
根据桥臂输出电压指令及桥臂电流的正负,可逐区间分析FBSM、HBSM电容的充放电过程,计算FBSM、HBSM电容电压波动率[12]。为简化分析,假设CF=CH。如图 2所示,根据FBSM电容电压波动最大值Δuc, fmax出现的区间,可以分为3种情况。其中,uc为子模块电容电压。对uapref、iap、uc进行归一化处理,其基准值分别为udc、

|
图 2 FBSM、HBSM电容电压纹波 Fig. 2 Capacitor voltage ripples of FBSMs and HBSMs |
图 2中,θ1、θ2为uapref的过零点角度,θ3、θ4为iap的过零点角度,θ5、θ6为uapref等于FUC的角度。可利用式(1)中uapref及iap离线计算θ1—θ6[13],不会增加控制器的运算量。以下简要分析电容充放电过程。
以θ1为起始点,在区间[θ1, θ2),uc, f、uc, h满足:
| $\left\{\begin{array}{l}u_{c, \mathrm{f}}=0+\frac{1}{C_{\mathrm{F}}} \int_{\theta_1}^{\omega t} S_{\text {apf }} i_{\text {ap }} \mathrm{d}(\omega t) \\ u_{c, \mathrm{~h}}=0\end{array} \quad \omega t \in\left[\theta_1, \theta_2\right)\right.$ | (3) |
式中:Sapf为全桥模组平均开关函数。
| $S_{\text {apf }}=u_{\text {apref }} /\left(F U_C\right) \quad \omega t \in\left[\theta_1, \theta_2\right)$ | (4) |
然后FBSM优先充电,定义两类子模块电压相等的角度为θx,根据θx位置与Δuc, fmax出现的区间可分为如下3种情况。
(1) θ2 < θx≤θ3,Δuc, fmax出现在区间[θ3, θ4]。uc, f与uc, h在[θx, θ1+2π]内满足:
| $\begin{array} {c} \left\{\begin{array}{l}u_{c, \mathrm{f}}=u_{c, \mathrm{f}}\left(\theta_1\right)+\frac{1}{C_{\mathrm{F}}} \int_{\theta_{\mathrm{x}}}^{\omega t} S_{\text {apf }} i_{\text {ap }} \mathrm{d}(\omega t) \\ u_{c, \mathrm{~h}}=u_{c, \mathrm{f}}\left(\theta_1\right)+\frac{1}{C_{\mathrm{H}}} \int_{\theta_{\mathrm{x}}}^{\omega t} S_{\text {aph }} i_{\text {ap }} \mathrm{d}(\omega t)\end{array}\right. \\ \omega t \in\left[\theta_{\mathrm{x}}, \theta_1+2 \pi\right] \\ \end{array}$ | (5) |
式中:Saph为半桥模组平均开关函数。
| $S_{\text {aph }}=S_{\text {apf }}=u_{\text {apref }} /\left(H U_C+F U_C\right)$ | (6) |
如图 2(a)所示,FBSM电容电压波动最大值Δuc, fmax与HBSM电容电压波动最大值Δuc, hmax相等且满足:
| $\Delta u_{c, \mathrm{fmax}}=\Delta u_{c, \text { hmax }}=\frac{1}{C_{\mathrm{F}}}\left|\int_{\theta_3}^{\theta_4} S_{\text {apf }} i_{\text {ap }} \mathrm{d}(\omega t)\right|$ | (7) |
(2) θ4 < θx < θ1+2π,Δuc, fmax出现在区间[θ4, θ1+2π]。由于uc, h(θ3)>uc, f(θ3),在区间[θ3, θ4]内,HBSM将优先放电。由于该区间内的uapref>HUC,根据排序均压算法,Saph应满足:
| $S_{\text {aph }}=\left\{\begin{array}{l}1 \quad \omega t \in\left[\theta_3, \theta_4\right) \\ \left(u_{\text {apref }}-F U_C\right) /\left(H U_C\right) \quad \omega t \in\left[\theta_4, \theta_6\right) \\ 0 \quad \omega t \in\left[\theta_6, \theta_{\mathrm{x}}\right) \\ u_{\text {apref }} /\left(H U_C+F U_C\right) \quad \omega t \in\left[\theta_{\mathrm{x}}, \theta_1+2 \pi\right]\end{array}\right.$ | (8) |
为满足uapref需求,Sapf可表示为:
| $S_{\text {apf }}=\left(u_{\text {apref }}-S_{\text {aph }} H U_C\right) /\left(F U_C\right)$ | (9) |
此时,Δuc, hmax依旧满足式(7),而Δuc, fmax出现在图 2(b)所示的区间[θ4, θ1+2π],可表示为:
| $\Delta u_{c, \text { fmax }}=\frac{1}{C_{\mathrm{F}}} \int_{\theta_4}^{2 \pi+\theta_1} S_{\text {apf }} i_{\text {ap }} \mathrm{d}(\omega t)$ | (10) |
(3) θ4 < θx < θ1+2π,Δuc, fmax出现在区间[θ1, θ2]。类似,可推导出Saph及Sapf仍分别满足式(8)、式(9),且Δuc, hmax依旧满足式(7)。Δuc, fmax在图 2(c)所示的区间[θ1, θ2],其值可表示为:
| $\Delta u_{c, \text { fmax }}=\frac{1}{C_{\mathrm{F}}}\left|\int_{\theta_1}^{\theta_2} S_{\text {apf }} i_{\text {ap }} \mathrm{d}(\omega t)\right|$ | (11) |
根据式(7)、式(10)及式(11),FBSM、HBSM平均电容电压波动率可分别表示为εF、εH,如式(12)所示。
| $\left\{\begin{array}{l}\varepsilon_{\mathrm{F}}=\Delta u_{c, \mathrm{fmax}} /\left(2 U_C\right) \\ \varepsilon_{\mathrm{H}}=\Delta u_{c, \mathrm{hmax}} /\left(2 U_C\right)\end{array}\right.$ | (12) |
对于大容量的MMC,无论是应用于高压直流输电还是交流电网异步互联,换流器的功率因数一般较大[19],但考虑换流器可能存在发出无功功率较大的工况,因此文中将功率因数的分析计算范围选为0.54≤cos φ≤1。
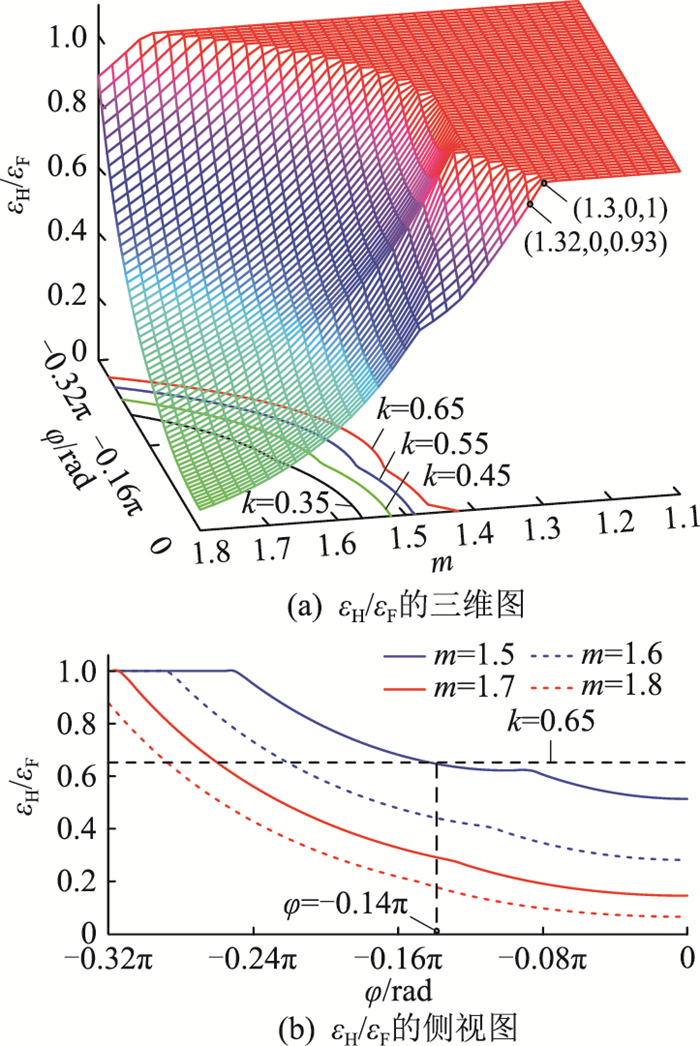
以全桥-半桥2 ∶1的混合型MMC为例,图 3为HBSM与FBSM平均电容电压波动率比值εH/εF与调制比m及功率因数角φ间的关系。其中,φ的取值范围为-0.32π≤φ≤0(0.54≤cos φ≤1);m的取值范围为1.1≤m≤1.8[12, 24];k=εH/εF。
|
图 3 不同m及φ对应的εH/εF Fig. 3 εH/εF with different m and φ |
由图 3可知:
(1) 当1.1≤m≤1.3且0.54≤cos φ≤1时,FBSM、HBSM电容电压波动率相等,即εH/εF=1;
(2) 当1.3 < m≤1.325且cos φ=1时,FBSM、HBSM电容电压波动率出现差异,即εH≤εF;
(3) 当1.3 < m≤1.8,0.54≤cos φ≤1且εH/εF≠1时,对于确定的φ值,εH/εF随着m的增大而减小;
(4) 当1.5≤m≤1.8且0.9≤cos φ≤1时,εH/εF < 0.65,即HBSM平均电容电压波动率较小。
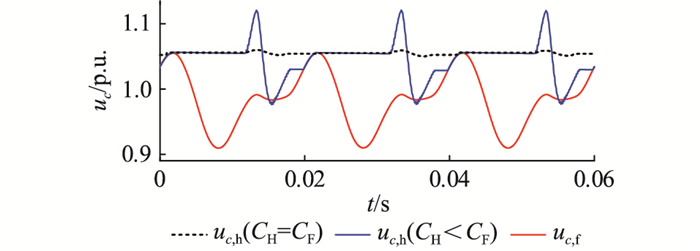
2 基于模组解耦的混合型MMC子模块电容优化对于εH < εF的运行区域,降低CH可增加HBSM电容电压波动率。但受排序均压算法的影响,直接降低CH会增加HBSM电容电压的最大值。以逆变器为例,图 4为cos φ=1且m=1.8的A相上桥臂两类子模块的电容电压波形,其中,εF=7%。可发现由于两类子模块电容电压直流分量的差异,降低CH后,uc, hmax大于1.1 p.u.,会增加器件电压应力。
|
图 4 传统排序算法下的FBSM、HBSM电容电压波形 Fig. 4 HBSMs′ and FBSMs′ capacitor voltages waves of traditional sorting algorithm |
针对兼顾HBSM电容电压波动率及避免HBSM器件承受高压应力的问题,文中提出全桥及半桥模组的直接解耦控制。其原理是根据稳态下的桥臂输出电压指令及桥臂电流,按照现有排序均压算法计算半桥及全桥模组的平均开关函数。
由于投切过程不涉及两类子模块电容电压瞬时值的比较,上述方法可消除图 4中两类子模块电容电压直流分量的差异,进而防止开关器件承受过压应力。同时,由于两类子模块充放电动作与现有排序均压算法相同,文中称为直接解耦控制。
以图 2(c)中电压纹波类型为例,图 5为直接解耦下全/半桥模组平均开关函数。其中,对uapref、iap、uc同图 2进行归一化处理;对Sapf、Saph分别进行归一化处理,其基准值分别为FUC、HUC。可利用MATLAB定积分与零点求解函数对FBSM、HBSM电容的充放电能量进行计算求得θx。根据排序均压算法,得到Saph如式(13)所示,对应Sapf仍满足式(9)。该计算可线下进行,不会增加在线控制的运算量。通过控制两类子模块电容电压直流分量,可防止器件承受过电压应力。
|
图 5 基于直接解耦的全/半桥模组平均开关函数 Fig. 5 Sapf and Saph with direct coupling control |
| $\begin{array} {c} S_{\text {aph }}= \\ \left\{\begin{array}{l}0 \quad \omega t \in\left[\theta_1, \theta_5\right) \cup\left[\theta_6, \theta_{\mathrm{x}}\right) \\ \left(u_{\text {apref }}-F U_C\right) /\left(H U_C\right) \quad \omega t \in\left[\theta_5, \theta_3\right) \cup\left[\theta_4, \theta_6\right) \\ 1 \quad \omega t \in\left[\theta_3, \theta_4\right) \\ u_{\text {apref }} /\left(H U_C+F U_C\right) \quad \omega t \in\left[\theta_{\mathrm{x}}, \theta_1+2 \pi\right]\end{array}\right. \end{array}$ | (13) |
相比现有排序均压控制,直接解耦控制虽可实现两类子模块电容电压直流分量的调节,但未能对电压波形进行构建,这导致在某些工况下HBSM电容存在进一步优化空间。为此,本节提出模组解耦优化控制,在保证HBSM电容电压最大值不增加的前提下,通过灵活改变Saph,减小HBSM的充放电能量,以进一步降低CH。
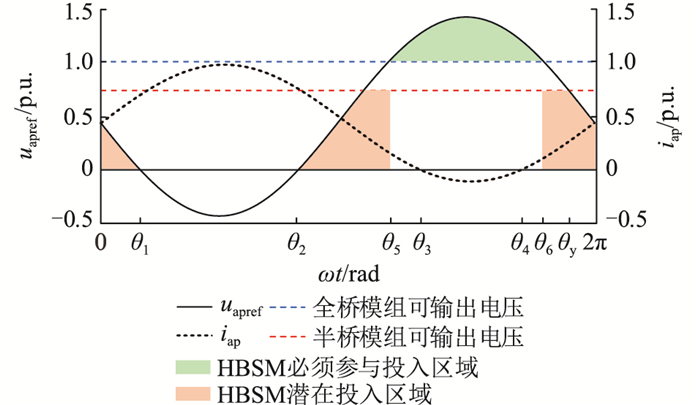
图 6为稳态下的桥臂输出电压指令、桥臂电流及全/半桥模组可输出电压,θy为HBSM在θ6后起始投入的角度。当uapref为负时,FBSM投入;当uapref大于FUC时,为满足桥臂输出电压指令值,HBSM必须投入。该区间内可灵活分配半桥模组及全桥模组输出电压指令。
|
图 6 全/半桥模组投入区域 Fig. 6 The input area of the full/half bridge module |
相同电容电压波动率下,HBSM一个基频周期内充、放电能量峰值越小对应的电容需求越小[12]。因此,可通过降低半桥模组的充、放电能量降低其电容需求。通过分析发现,在桥臂电流为负的区间内,当半桥模组输出电压指令为桥臂输出电压指令减去FUC时,HBSM电容值最小。此时,半桥模组的平均开关函数可表示为:
| $S_{\text {aph }}=\frac{u_{\text {apref }}-F U_C}{H U_C} \quad \omega t \in\left[\theta_5, \theta_6\right)$ | (14) |
相应的,HBSM能量的变化值WCH可表示为:
| $\begin{gathered}W_{\mathrm{CH}}=\frac{1}{H}\left|\int_{\theta_5}^{\theta_6}\left(u_{\text {apref }}-F U_C\right) i_{\text {ap }} \mathrm{d}(\omega t)\right| \\ \omega t \in\left[\theta_5, \theta_6\right)\end{gathered}$ | (15) |
为保证电容电压平衡,HBSM在一个周期内的能量净变化值应为0。为便于计算与分析,文中选取全桥模组输出电压指令与半桥模组输出电压指令的比值为F/H。此时,Saph可表示为:
| $S_{\text {aph }}=\frac{u_{\text {apref }}}{N U_C} \quad \omega t \in\left[\theta_{\mathrm{y}}, \theta_1+2 \pi\right]$ | (16) |
式中:N为桥臂子模块个数,即N=F+H。相应地,HBSM能量变化值可表示为:
| $\begin{gathered}W_{\mathrm{CH}}=\frac{1}{H} \int_{\theta_{\mathrm{y}}}^{\theta_1+2 \pi} \frac{H}{N} u_{\text {apref }} i_{\text {ap }} \mathrm{d}(\omega t) \\ \omega t \in\left[\theta_{\mathrm{y}}, \theta_1+2 \pi\right]\end{gathered}$ | (17) |
其中,变量θy可利用MATLAB的求零点函数对式(15)、式(17)联立求解得到。此过程仍可通过线下计算求得。
其余时间半桥模组旁路,只有全桥模组投入。因此,一个基频周期内Saph为:
| ${{S}_{\text{aph }}}=\left\{ \begin{array}{*{35}{l}} \frac{{{u}_{\text{apref }}}-F{{U}_{C}}}{H{{U}_{C}}}\ \ \ \omega t\in \left[ {{\theta }_{5}}, {{\theta }_{6}} \right) \\ 0\ \ \ \omega t\in \left[ {{\theta }_{1}}, {{\theta }_{5}} \right)\cup \left[ {{\theta }_{6}}, {{\theta }_{\text{y}}} \right) \\ \frac{u_{\text{apref }}}{N{{U}_{C}}}\ \ \ \omega t\in \left[ {{\theta }_{\text{y}}}, 2\pi +{{\theta }_{1}} \right] \\ \end{array} \right.$ | (18) |
一个基频周期内,HBSM能量变化的最大值为:
| $\begin{gathered}W_{\text {CHmax }}=\frac{1}{H}\left|\int_{\theta_3}^{\theta_4}\left(u_{\text {apref }}-F U_C\right) i_{\text {ap }} \mathrm{d}(\omega t)\right| \\ \omega t \in\left[\theta_3, \theta_4\right)\end{gathered}$ | (19) |
Sapf仍满足式(9),FBSM能量变化最大值为:
| $\begin{gathered}W_{\text {CFmax }}= \\ \max \left\{\left|\int_{\theta_1}^{\theta_2} S_{\text {apf }} U_C i_{\text {ap }} \mathrm{d}(\omega t)\right|, \left|\int_{\theta_2}^{\theta_3} S_{\text {apf }} U_C i_{\text {ap }} \mathrm{d}(\omega t)\right|, \right. \\ \left.\left|\int_{\theta_3}^{\theta_4} S_{\text {apf }} U_C i_{\text {ap }} \mathrm{d}(\omega t)\right|, \left|\int_{\theta_4}^{\theta_1+2 \pi} S_{\text {apf }} U_C i_{\text {ap }} \mathrm{d}(\omega t)\right|\right\}\end{gathered}$ | (20) |
电容CH、CF为:
| $\left\{\begin{array}{l}C_{\mathrm{H}}=\frac{W_{\mathrm{CH} \max }}{2 \varepsilon U_C^2} \\ C_{\mathrm{F}}=\frac{W_{\mathrm{CF} \max }}{2 \varepsilon U_C^2}\end{array}\right.$ | (21) |
将式(19)、式(20)代入式(21)可得优化后的CH、CF。该计算方法使用给定的m和φ,因此测量环节不会导致误差。针对不同的工况,可根据上述计算方法得到相应的数据,方便在实际应用中查找。
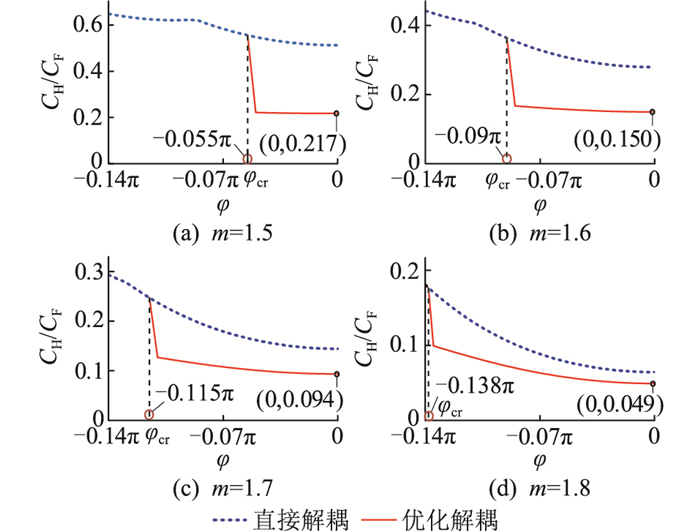
图 7为不同m和φ下HBSM电容值的优化效果。其中,纵坐标为解耦控制后的CH与CF的比值(传统设计中的FBSM、HBSM电容相等)。定义解耦优化后FBSM电容电压波动率恰好等于传统控制下FBSM电容电压波动率的功率因数角为临界功率因数角φcr。图 7中,在φcr处发生越变的原因是采用解耦优化后的模组平均开关函数较大降低了HBSM能量变化最大值,进而使得在临界点处HBSM电容值的变化较大。当φ≤φcr时,在该区间内采用直接解耦,HBSM电容值降低;当φ>φcr时,采用解耦优化后的模组平均开关函数不会影响εF,且能够在直接解耦的基础上进一步降低HBSM电容值。
|
图 7 不同m下HBSM电容值优化 Fig. 7 Optimization of HBSMs′ capacitance under different m |
从图 7中可以看出,当m确定时,φ越大优化后的HBSM电容值越小;当φ确定时,m越大优化后的HBSM电容值越小。
3 模组解耦控制策略 3.1 基于HBSM电容电压闭环反馈的二次调节首先,根据半桥模组平均开关函数和桥臂电流,计算出各桥臂HBSM的电容电压纹波。以A相上桥臂为例,HBSM的电容电压纹波为:
| $\begin{array}{c} \tilde{u}_{\text {chref }}= \\ \left\{\begin{array}{l}0 \quad \omega t \in\left[\theta_1, \theta_5\right) \\ \frac{1}{C_{\mathrm{H}}} \int_{\theta_5}^{\omega t} \frac{u_{\text {apref }}-F U_C}{H U_C} i_{\text {ap }} d(\omega t) \quad \omega t \in\left[\theta_5, \theta_6\right) \\ \tilde{u}_{\text {chref }}\left(\theta_6\right) \quad \omega t \in\left[\theta_6, \theta_{\mathrm{y}}\right) \\ \tilde{u}_{\text {chref }}\left(\theta_6\right)+\frac{1}{C_{\mathrm{H}}} \int_{\theta_{\mathrm{y}}}^{\omega t} \frac{u_{\text {apref }}}{N U_C} i_{\text {ap }} \mathrm{d}(\omega t) \\ \qquad \qquad \omega t \in\left[\theta_{\mathrm{y}}, \theta_1+2 \pi\right]\end{array}\right. \end{array}$ | (22) |
对式(22)进行快速傅里叶变换分析,得到HBSM电容电压纹波的直流分量,进而得到HBSM电容电压指令为:
| $u_{\text {apch, ref }}=U_C-\tilde{u}_{\text {chref, dc }}+\tilde{u}_{\text {chref }}$ | (23) |
式中:
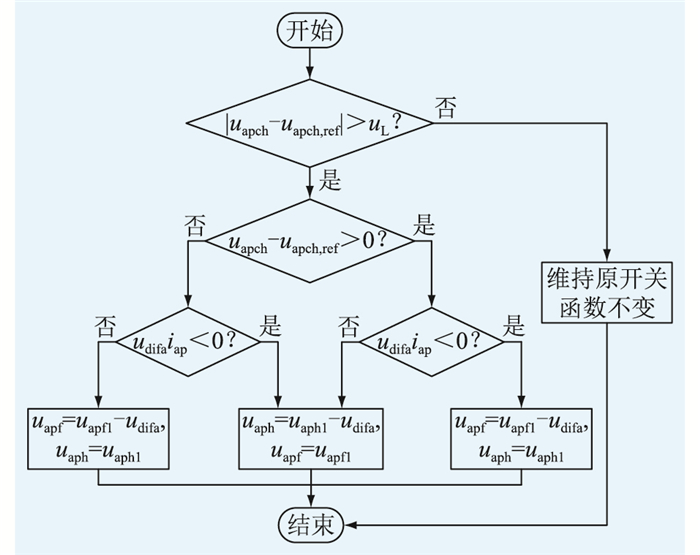
文中以二倍频输出电压指令为例,对全桥及半桥模组的输出电压指令进行二次调节,图 8为A相上桥臂的二次调节流程。其中,uapch、uapch, ref分别为HBSM实际电容电压和HBSM给定电容电压;udifa为A相二倍频输出电压;uapf1、uaph1分别为二次调节前全桥及半桥模组输出电压;uapf、uaph分别为二次调节后全桥及半桥模组输出电压。为防止模组电压指令值的频繁变化,增加开关频率,定义HBSM电容电压容许偏差为uL。判断HBSM实际电容电压与HBSM给定电容电压的差值是否大于uL,若不大于uL,说明偏差在允许范围内,保持二倍频电压分配方式不变;若大于uL,根据实际电容电压的大小进一步改变二倍频电压分配方式。
|
图 8 基于HBSM电容电压闭环反馈的二次调节流程 Fig. 8 Flow chart of secondary regulation based on HBSM capacitor voltage closed-loop feedback |
以桥臂电流与二倍频电压的乘积的正负作为判别二倍频电压对子模块电容充放电的依据。若HBSM需要放电,则将属于放电时刻的二倍频电压分配给HBSM或将属于充电时刻的二倍频电压分配给FBSM;若HBSM需要充电,则将属于充电时刻的二倍频电压分配给HBSM或将属于放电时刻的二倍频电压分配给FBSM。需要注意的是,若二次调节后的模组输出电压大于其输出电压能力,则将超过最大输出电压的部分分配给另一类模组。
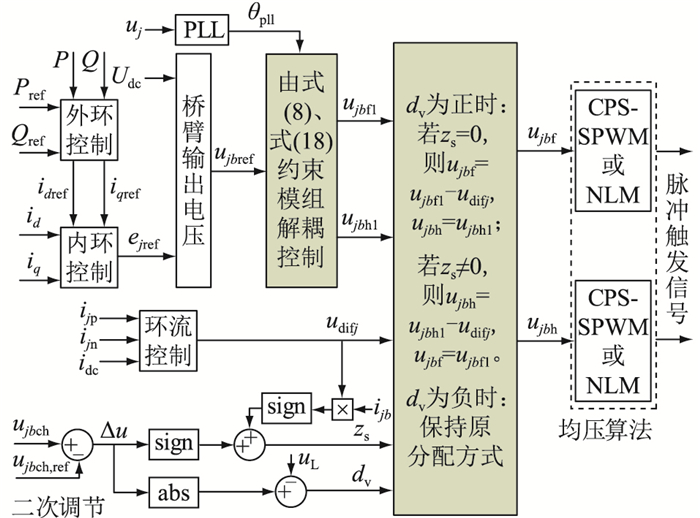
3.2 基于稳态量的全/半桥独立投切策略图 9为基于模组解耦的混合型MMC控制系统框图,包含电压及电流双闭环控制、基于比例谐振(proportional resonance,PR)的二倍频环流控制、基于模组平均开关函数的解耦控制以及基于HBSM电容电压闭环反馈的二次调节控制。其中,P、Q分别为实际有功和无功功率;Pref、Qref分别为给定有功和无功功率;id、iq分别为d轴和q轴实际电流;idref、iqref分别为d轴和q轴给定电流;udifj为j相二倍频输出电压;ujbch、ujbch, ref分别为HBSM实际电容电压和HBSM给定电容电压;ujbf1、ujbh1分别为二次调节前全桥和半桥模组输出电压指令;uj为相电压;ujbf、ujbh分别为二次调节后全桥和半桥模组输出电压指令;j=a, b, c,为A、B、C三相;b=p, n,为上、下桥臂。根据输出的内电势指令ejref以及直流侧额定电压Udc计算桥臂输出电压的指令ujbref。由锁相环(phase locked loop, PLL)提供的相位θpll以及根据式(9)、式(18)计算得到的全桥模组与半桥模组的平均开关函数,得到全桥模组与半桥模组输出电压的指令。环流控制的udifj与桥臂电流ijb相乘输入到sign函数(符号函数:输入为负时,输出-1;输入为正时,输出1;输入为0时,输出0),ujbch与ujbch, ref相减得到Δu输入到sign函数,将上述sign函数的2个输出量相加得到zs,Δu经abs函数(绝对值函数:输出为输入的绝对值)与uL相减得到dv。dv为正时,对模组输出电压指令进行二次调节,再根据zs是否等于0,判断分配的方式,得到最终的模组输出电压指令。然后经过载波相移正弦脉宽调制(carrier phase shifted sinusoidal pulse-width modulation,CPS-SPWM)或最近电平逼近调制(nearest level modulation,NLM)后得到脉冲触发信号。
|
图 9 解耦控制的混合型MMC控制系统 Fig. 9 System of hybrid MMC control with decoupling control |
混合型MMC工作在高调制比工况时,两类子模块输出电压差异性明显,这可能会导致全/半桥电容电压不均衡,出现模组持续充、放电的现象[13, 25]。为避免此问题,文中提出基于HBSM电容电压闭环反馈的二次调节控制。
4 仿真验证为验证所提出的子模块电容优化方法有效性,基于MATLAB/Simulink搭建了单端混合型MMC的仿真模型,仿真参数参考文献[18],并在其基础上进行相应修改,如表 1所示。调制方式参考文献[25-26]。传统控制的HBSM与FBSM电容值C按照FBSM电容电压波动率εF=7%设计;解耦优化的HBSM与FBSM电容值按照优化后FBSM、HBSM电容电压波动率εF=7%设计;考虑到子模块电容电压实际值的一致性,在仿真中将二次调节的容许偏差uL设置为0。
|
|
表 1 混合型MMC仿真参数 Table 1 Hybrid MMC simulation parameters |
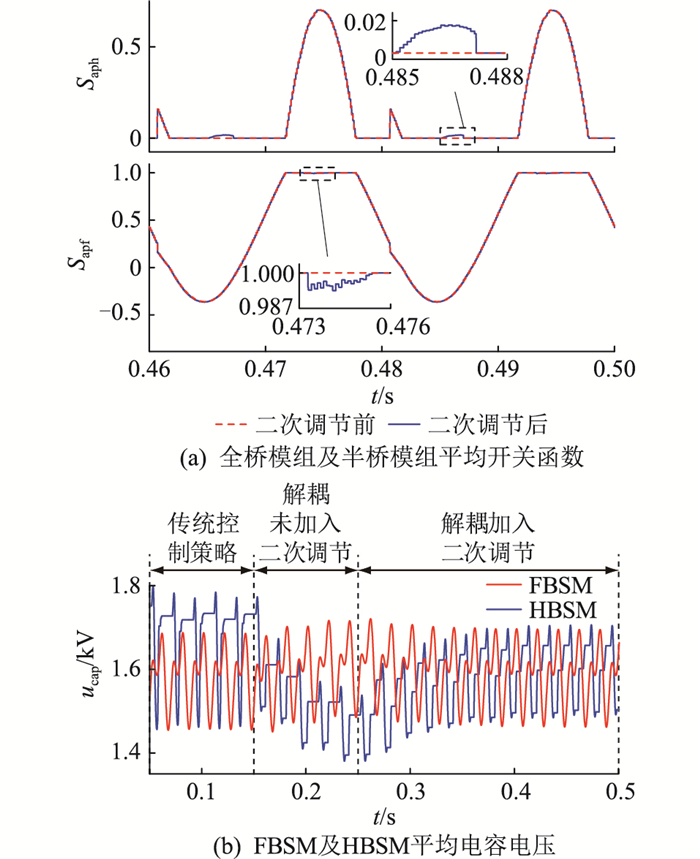
为验证文中所提优化方法中二次调节的效果,以m=1.7为例,对混合型MMC二次调节投入前后的A相上桥臂子模块平均电容电压ucap波形进行分析,如图 10所示。
|
图 10 m=1.7混合型MMC仿真波形 Fig. 10 Hybrid MMC simulation waveforms with m=1.7 |
从图 10(a)中可以看出,二次调节后的全桥及半桥模组全投入和全旁路的区间减小,会影响器件的开关损耗。选取器件ABB 5SNA 1500E330300进行计算[27],换流器总损耗仅增加2.276%,对总损耗影响较小。
从图 10(b)中可以看出,在未投入二次调节的区间,FBSM与HBSM的电容电压不均衡,有发散的趋势;在投入二次调节后,HBSM电容电压开始跟随二次调节控制中HBSM电容电压指令值,并逐渐达到稳态。结合图 10(a)中的全桥及半桥模组的平均开关函数可以看出,二次调节对全桥及半桥模组的开关函数进行了微调,实现了模组间的均压。
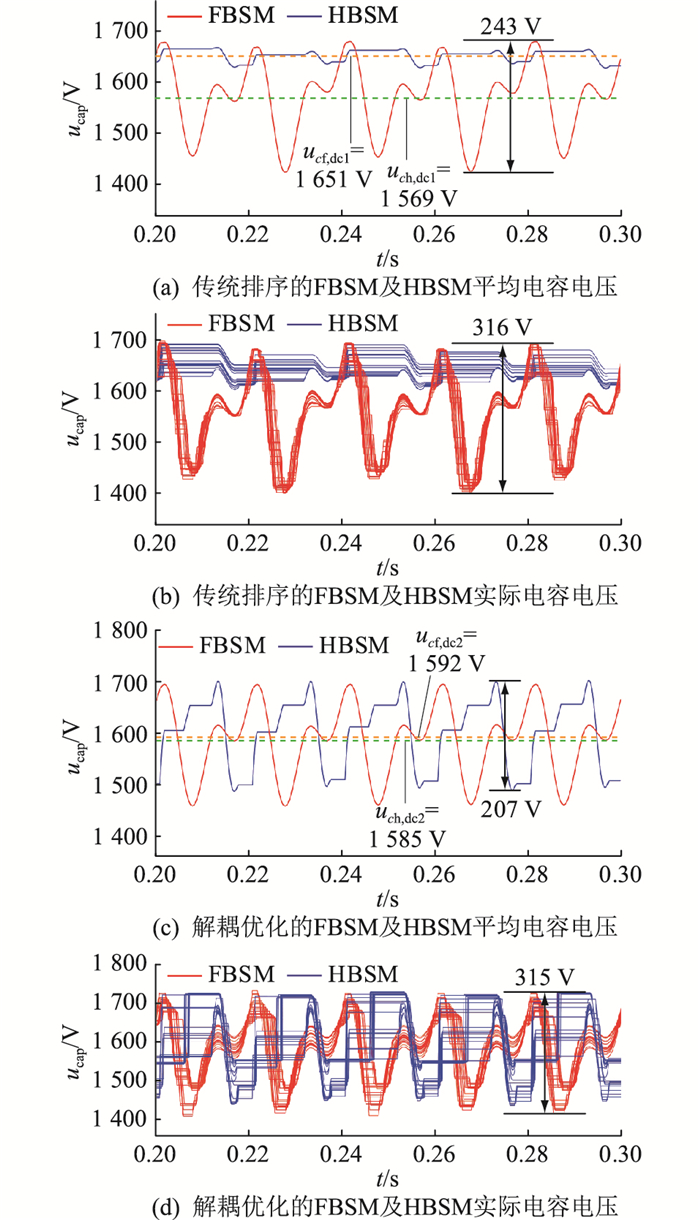
为更直观地体现文中所提优化方法的效果,以m=1.7为例,混合型MMC传统排序和解耦优化的FBSM与HBSM平均电容电压和实际电容电压如图 11所示。
|
图 11 m=1.7传统排序与解耦优化的子模块电容电压 Fig. 11 The capacitor voltage of sub-module traditional sequencing and decoupling optimization with m=1.7 |
图 11中,ucf, dc1、uch, dc1分别为传统排序下的FBSM及HBSM电容电压的直流分量;ucf, dc2、uch, dc2分别为解耦优化的FBSM及HBSM电容电压的直流分量。由图 11(a)可以看出,传统排序下Δuc, fmax=243 V,εF=7.6%,与设计值基本一致,但FBSM与HBSM电容电压的直流分量差值为82 V,差异较大。由图 11(c)可以看出,解耦优化后Δuc, fmax与Δuc, hmax基本一致为207 V,εH=6.5%,且FBSM与HBSM电容电压直流分量差值仅为7 V,差异较小。由于子模块电容电压间的差异性,实际模组电容电压的波动率会大于电容电压平均值的波动率,如图 11(b)、图 11(d)所示。传统排序和解耦优化的Δuc, fmax分别为316 V和315 V,实际模组电容电压波动率分别为9.9%和9.8%,其子模块电容电压波动均在允许范围之内。
综上,文中提出的优化方法在降低HBSM电容值的同时保证了FBSM与HBSM电容电压的波动率和直流分量。解耦优化后HBSM电容值为传统排序下HBSM电容值的9.4%,与图 7(c)中计算结果基本一致。
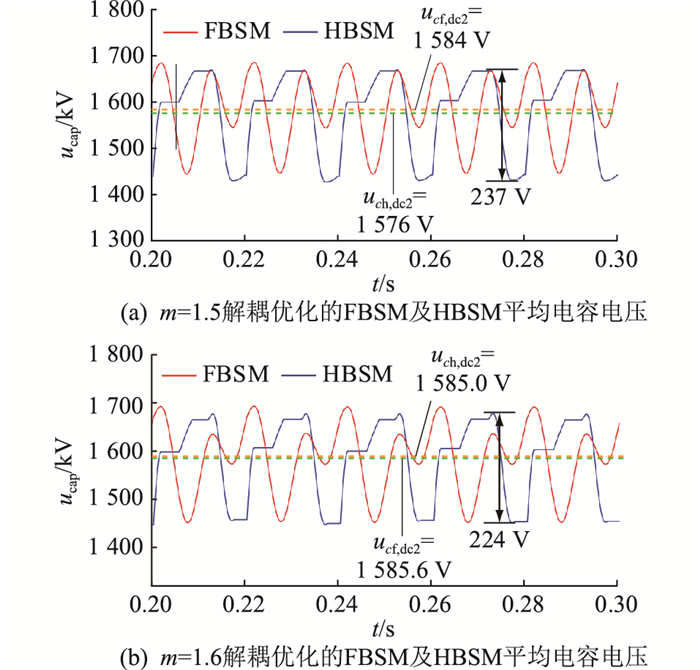
为更好地验证文中所提方法的普适性,分别对m=1.5和m=1.6进行仿真验证,仿真波形如图 12所示。相比表 1中的仿真参数,仅子模块电容参数变动,当m=1.5时,CF=4.597 mF、CH=0.999 mF;当m=1.6时,CF=5.633 mF、CH=0.844 mF。
|
图 12 m=1.5与m=1.6解耦优化的子模块平均电容电压波形 Fig. 12 Decoupled optimized sub-module average capacitor voltage waveform with m=1.5 and m=1.6 |
从图 12中可以看出,解耦优化后的FBSM与HBSM电容电压的波动率基本一致。当m=1.5时Δuc, hmax=237 V,εH=7.4%;当m=1.6时Δuc, hmax=224 V,εH=7.0%。FBSM与HBSM电容电压的直流分量差异较小,得到了有效的控制。
为验证2.2节所分析的电容优化效果与运行调制比间的规律,对单位功率因数下的不同调制比工况进行仿真。除子模块电容值外,其他仿真参数见表 1。其中,HBSM与FBSM电容值均按照解耦优化后εH=εF=7%设计。解耦优化的仿真结果见表 2。
|
|
表 2 不同调制比下的解耦优化仿真结果 Table 2 Simulation results decoupling optimization under different m |
表 2中εH为优化后HBSM平均电容电压的波动率;CH/CF为优化后的HBSM电容值与传统排序下子模块电容值的比值,优化效果与图 7中的理论计算值基本一致。从表中可看出,解耦优化有效的降低了HBSM电容值;当功率因数一定时,m越大解耦优化的效果越好。
5 结论针对高调制比混合型MMC电容电压波动率小的问题,文中提出模组解耦控制,在不影响HBSM电容电压最大值的前提下,降低其电容值,仿真结果验证了所提方法的可行性和有效性。文中主要结论如下:
(1) 当1.5≤m≤1.8,0.9≤cos φ≤1时,εH/εF < 0.65,此时HBSM电容电压波动率较小。
(2) 提出可实现HBSM充放电能量最小的模组平均开关函数设计原则,在固定HBSM电压波动率下,可有效降低其电容值;且对于单位功率因数,调制比越大,所提方法的优化效果越显著。
(3) 解耦控制策略可对FBSM、HBSM的充放电进行独立控制,可实现子模块电容电压直流分量及电压纹波的准确控制。
| [1] |
鲁晓军, 林卫星, 向往, 等. 基于模块化多电平换流器的直流电网小信号建模[J]. 中国电机工程学报, 2018, 38(4): 1143-1156, 1292. LU Xiaojun, LIN Weixing, XIANG Wang, et al. Small signal modeling of MMC-based DC grid[J]. Proceedings of the CSEE, 2018, 38(4): 1143-1156, 1292. (  0) 0) |
| [2] |
白志红, 周玉虎. 模块化多电平换流器的载波层叠脉宽调制策略分析与改进[J]. 电力系统自动化, 2018, 42(21): 139-144. BAI Zhihong, ZHOU Yuhu. Analysis and improvement on carrier level-shifted pulse width modulation strategy for modular multilevel converter[J]. Automation of Electric Power Systems, 2018, 42(21): 139-144. (  0) 0) |
| [3] |
陈武晖, 吴明哲, 张军, 等. 模块化多电平换流器电磁暂态模型研究综述[J]. 电网技术, 2020, 44(12): 4755-4765. CHEN Wuhui, WU Mingzhe, ZHANG Jun, et al. Review of electromagnetic transient modeling of modular multilevel converters[J]. Power System Technology, 2020, 44(12): 4755-4765. (  0) 0) |
| [4] |
随顺科, 任铁强, 邹强, 等. 连接风电系统的柔性直流电网MMC在线投入分析与验证[J]. 供用电, 2022, 39(11): 26-31. SUI Shunke, REN Tieqiang, ZOU Qiang, et al. On-line input analysis and verification of flexible DC network MMC connected to wind power system[J]. Distribution & Utilization, 2022, 39(11): 26-31. (  0) 0) |
| [5] |
朱海勇, 吴小丹, 董云龙, 等. 考虑延时补偿的配电网柔直网侧谐波电流抑制策略[J]. 浙江电力, 2021, 40(11): 78-84. ZHU Haiyong, WU Xiaodan, DONG Yunlong, et al. Harmonic current suppression strategy of MMC-MVDC considering delay compensation[J]. Zhejiang Electric Power, 2021, 40(11): 78-84. (  0) 0) |
| [6] |
罗永捷, 蒲羿, 宋勇辉, 等. 混合型模块化多电平换流器启动冲击电流特性分析及控制策略[J]. 电工技术学报, 2020, 35(S1): 49-59. LUO Yongjie, PU Yi, SONG Yonghui, et al. The inrush current characteristics and control strategies of hybrid modular multilevel converter systems during start-up processes[J]. Transactions of China Electrotechnical Society, 2020, 35(S1): 49-59. (  0) 0) |
| [7] |
王泽青, 夏成军, 赖胜杰, 等. 混合型MMC非闭锁型直流故障穿越的故障等效模型[J]. 电力工程技术, 2023, 42(2): 103-111. WANG Zeqing, XIA Chengjun, LAI Shengjie, et al. Fault equivalent model for non-blocking DC fault ride-through of hybrid MMC[J]. Electric Power Engineering Technology, 2023, 42(2): 103-111. (  0) 0) |
| [8] |
付超, 邱建, 李诗旸, 等. 昆柳龙多端直流稳定控制策略设计及系统构建[J]. 南方电网技术, 2022, 16(1): 33-40. FU Chao, QIU Jian, LI Shiyang, et al. Stability control strategy and system design for Kunliulong multi-terminal HVDC transmission[J]. Southern Power System Technology, 2022, 16(1): 33-40. (  0) 0) |
| [9] |
ZHANG Y Q, ZHANG J Z, DENG F J, et al. Voltage balancing control of hybrid MMC under over-modulation situations with optimal circulating current injection[J]. International Journal of Electrical Power & Energy Systems, 2022, 140: 108053. (  0) 0) |
| [10] |
JUDGE P D, CHAFFEY G, MERLIN M M C, et al. Dimensioning and modulation index selection for the hybrid modular multilevel converter[J]. IEEE Transactions on Power Electronics, 2017, 33(5): 3837-3851. (  0) 0) |
| [11] |
SHENG J, YANG H Y, LI C S, et al. Active thermal control for hybrid modular multilevel converter under overmodulation operation[J]. IEEE Transactions on Power Electronics, 2020, 35(4): 4242-4255. (  0) 0) |
| [12] |
林艺哲, 林磊, 徐晨. 稳态负电平输出下的混合型MMC设计方法[J]. 中国电机工程学报, 2018, 38(14): 4202-4211, 4326. LIN Yizhe, LIN Lei, XU Chen. A design method of hybrid modular multilevel converter with negative output in steady state[J]. Proceedings of the CSEE, 2018, 38(14): 4202-4211, 4326. (  0) 0) |
| [13] |
LU M Z, HU J B, ZENG R, et al. Imbalance mechanism and balanced control of capacitor voltage for a hybrid modular multilevel converter[J]. IEEE Transactions on Power Electronics, 2018, 33(7): 5686-5696. (  0) 0) |
| [14] |
李钰, 陆锋, 樊强, 等. 不平衡电网电压下的MMC子模块电压波动抑制方法[J]. 电力系统自动化, 2020, 44(4): 91-100. LI Yu, LU Feng, FAN Qiang, et al. Suppression method for voltage fluctuation of sub-module in multilevel modular converter with unbalanced power grid voltage[J]. Automation of Electric Power Systems, 2020, 44(4): 91-100. (  0) 0) |
| [15] |
施恩泽, 吴学智, 荆龙, 等. 网压不平衡下环流注入对模块化多电平换流器的影响分析[J]. 电工技术学报, 2018, 33(16): 3719-3731. SHI Enze, WU Xuezhi, JING Long, et al. Analysis of the impact on modular multilevel converter with circulating current injection under unbalanced grid voltage[J]. Transactions of China Electrotechnical Society, 2018, 33(16): 3719-3731. (  0) 0) |
| [16] |
ZHAO C, LEI M, HU Y, et al. Energy storage requirement optimization of hybrid modular multilevel converter with circulating current injection[J]. IEEE Transactions on Industrial Electronics, 2019, 66(9): 6637-6648. (  0) 0) |
| [17] |
孟经伟, 周月宾, 张楠, 等. 低电容用量高纹波MMC的三次谐波电压注入方法[J]. 电工电能新技术, 2021, 40(2): 1-8. MENG Jingwei, ZHOU Yuebin, ZHANG Nan, et al. A third-order harmonic injection method for low-capacitance modular multilevel converters with high ripples[J]. Advanced Technology of Electrical Engineering and Energy, 2021, 40(2): 1-8. (  0) 0) |
| [18] |
陆锋, 李钰, 樊强, 等. 混合MMC电容电压波动差异机理及抑制策略[J]. 电力系统自动化, 2019, 43(17): 92-101. LU Feng, LI Yu, FAN Qiang, et al. Mechanism and suppression strategy of capacitor voltage fluctuation difference in hybrid multilevel modular converter[J]. Automation of Electric Power Systems, 2019, 43(17): 92-101. (  0) 0) |
| [19] |
赵聪, 李耀华, 李子欣, 等. 混合型模块化多电平变流器电容优化设计[J]. 中国电机工程学报, 2017, 37(19): 5717-5729, 5849. ZHAO Cong, LI Yaohua, LI Zixin, et al. Capacitance optimization design of hybrid modular multilevel converter[J]. Proceedings of the CSEE, 2017, 37(19): 5717-5729, 5849. (  0) 0) |
| [20] |
杨文博, 宋强, 刘文华, 等. 降低模块化多电平换流器子模块电容值的控制方法[J]. 电力系统自动化, 2015, 39(16): 86-94. YANG Wenbo, SONG Qiang, LIU Wenhua, et al. A control strategy for reducing submodule capacitance value of modular multilevel converter[J]. Automation of Electric Power Systems, 2015, 39(16): 86-94. (  0) 0) |
| [21] |
ILVES K, ANTONOPOULOS A, HARNEFORS L, et al. Capacitor voltage ripple shaping in modular multilevel converters allowing for operating region extension[C]//IECON 2011-37th Annual Conference of the IEEE Industrial Electronics Society. Melbourne, VIC, Australia. IEEE, 2012: 4403-4408.
(  0) 0) |
| [22] |
董鹏, 蔡旭, 吕敬. 大幅减小子模块电容容值的MMC优化方法[J]. 中国电机工程学报, 2018, 38(18): 5369-5380. DONG Peng, CAI Xu, LYU Jing. Optimized method of MMC for greatly reducing the capacitance of the submodules[J]. Proceedings of the CSEE, 2018, 38(18): 5369-5380. (  0) 0) |
| [23] |
韩啸, 李睿. 一种MMC子模块电容电压波动最小化容值优化方法[J]. 电源学报, 2021, 19(3): 40-51. HAN Xiao, LI Rui. Capacitance optimization method for minimizing submodule capacitor voltage fluctuation of modular multilevel converter[J]. Journal of Power Supply, 2021, 19(3): 40-51. (  0) 0) |
| [24] |
李冠宏, 路茂增, 边敦新, 等. 基于三次谐波电压注入的扩展混合型MMC运行区域的控制方法. 电测与仪表: 1-9. http://kns.cnki.net/kcms/detail/23.1202.TH.20210604.1727.004.html. LI Guanhong, LU Maozeng, BIAN Dunxin, et al. Third harmonic voltage injection based control method with expanding the operation area of hybrid MMC. Electrical Measurement and Instrumentation: 1-9. http://kns.cnki.net/kc-ms/detail/23.1202.TH.20210604.1727.004.html. (  0) 0) |
| [25] |
LI Z X, GAO F Q, XU F, et al. Power module capacitor voltage balancing method for a ±350 kV/1000 MW modular multilevel converter[J]. IEEE Transactions on Power Electronics, 2016, 31(6): 3977-3984. (  0) 0) |
| [26] |
罗永捷, 李耀华, 李子欣, 等. 适用于高压大容量MMC-HVDC系统的改进低开关频率均压控制策略[J]. 中国电机工程学报, 2017, 37(5): 1341-1351. LUO Yongjie, LI Yaohua, LI Zixin, et al. An improved reduced switching frequency voltage balancing control strategy for bulk power MMC-HVDC systems[J]. Proceedings of the CSEE, 2017, 37(5): 1341-1351. (  0) 0) |
| [27] |
赵宇含, 王鑫, 赵成勇, 等. 半桥-全桥子模块混合型MMC的换流阀损耗分析方法[J]. 电网技术, 2021, 45(7): 2847-2856. ZHAO Yuhan, WANG Xin, ZHAO Chengyong, et al. Converter valve loss analysis based on half bridge-full bridge sub-module hybrid MMC[J]. Power System Technology, 2021, 45(7): 2847-2856. (  0) 0) |
 2023, Vol. 42
2023, Vol. 42



 孙标(1997), 男, 硕士在读, 研究方向为电力电子、模块化多电平换流器(E-mail:
孙标(1997), 男, 硕士在读, 研究方向为电力电子、模块化多电平换流器(E-mail: