文章编号: 2096-3203(2023)05-0158-09 中图分类号: TM715
为了构建清洁、低碳、安全、高效的现代能源体系[1],综合能源系统(integrated energy system, IES)应运而生。IES以电力系统为核心,通过其系统内部的各种能源设备实现了冷、热、电、气等多种能源之间的协调规划和互补互济,提高了能源的利用效率[2-3],是我国现代能源体系的重要组成部分。相比于单独的能源系统和单一负荷,IES中多元负荷之间具有复杂的耦合关系以及更多的不确定性因素[4],负荷预测又是能源协调规划的首要前提,这对负荷预测的准确性、实时性以及可靠性提出了更高的要求,因此IES多元负荷预测成为近年来的研究热点。
近年来国内外学者们研究并提出了较多的IES多元负荷预测方法,传统的时间序列方法和回归分析法等随着深度学习的快速发展而逐步被取代[5]。基于循环神经网络(recurrent neural networks,RNN)的长短时记忆(long short-term memory,LSTM)网络[6-9]及其变体双向长短时记忆(bi-directional long short-term memory,BiLSTM)网络[10-13]和门控循环单元(gated recurrent unit,GRU)[14]是目前最为常用的方法,还有在此基础上的各种改进预测模型,如文献[15]通过引入注意力机制对LSTM的隐含层进行赋权,从而提出一种改进的LSTM多元负荷预测模型,提高了训练的速度和预测精度。这些方法在预测精度上都有较大的提升,但预测过程都是单一负荷预测的叠加,对于多元负荷之间的耦合关系考虑不全面。不同于传统的电力负荷预测,IES多元负荷预测不仅要考虑各个负荷复杂的耦合关系,而且要保证各类负荷预测的实时性。多任务学习(multi task learning,MTL)通过共享层使各子任务能够获取彼此之间的隐含信息,提高了模型泛化能力,且降低了预测模型的复杂度,因此MTL在多元负荷预测方面有较好的应用价值。文献[16-19]都采用了MTL的方式实现多元负荷的联合预测,能够通过共享层获取负荷之间的耦合关系,预测效果较好,并且各自都采用了不同的方式以进一步提高预测的精度。但在MTL模型搭建中均采用了LSTM作为共享层,在数据量较大的情况下,模型的训练时间很长,会影响预测的实时性。
在多元负荷预测的特征选取方面,部分研究考虑影响因素的全面性而尽可能挖掘所有因素作为输入特征,但会导致一些无关因素输入预测模型,反而影响了预测的精度;部分研究对各影响因素进行相关性分析以选取最为相关的因素作为输入特征,如文献[20-22]均采用相关性分析的方式来选择输入特征,但实际IES中多元负荷和各影响因素之间并不完全是线性关系,且相关系数的应用有严格的条件约束,对于不同实际IES来说应用起来较为困难,通过相关性分析得到的各因素与负荷之间的相关程度可能有所偏差,进而影响最终的预测精度。
针对以上问题,结合现有的研究基础,文中提出一种基于极限梯度提升(extreme gradient boosting,XGBoost)与MTL的IES冷热电多元负荷预测模型。旨在利用XGBoost特征重要排序的方法来选取模型输入特征,降低预测模型的复杂度以及提升模型的适用性;以GRU共享MTL的方式获取多元负荷耦合信息,从而在提升预测精度的同时缩短训练时间,进一步提高模型的应用价值。
1 XGBoost特征重要度排序提升(Boosting)算法的思想是将许多弱分类器集成在一起,形成一个强分类器。XGBoost是Boosting算法的一种,将许多分类回归树模型集成在一起,形成一个很强的分类器。相比于梯度提升决策树(gradient boosting decision tree,GBDT),XGboost力争把速度和效率发挥到极致,从而适用于更大范围。
XGBoost作为机器学习中应用较为广泛的算法,可以对特征重要性进行排序来选取特征,以解决由于冗余特征而导致的建模过程变慢、模型预测精度降低的问题[23]。XGBoost能够计算原始特征变量数据中每个特征的重要性得分,一般来说,重要性得分可以衡量特征在模型构建中的价值。一个特征的属性越多地被用来在模型中构建决策树,其重要性就相对越高。
设有一组数据集:D={(x1, y1), (x2, y2), …, (xn, yn)}, 并假设一棵决策树的模型为
(1) 在GBDT的基础上进行改进,在损失函数中加入正则化项。其目标函数如下:
| $F_{\mathrm{obj}}=\sum\limits_{i=1}^n L\left(y_i, \hat{y}_i\right)+\sum\limits_{k=1}^K \varOmega\left(f\left(\boldsymbol{x}_k\right)\right)$ | (1) |
式中:Fobj为决策树的目标函数。等式右边第一项表示整个强学习器的损失函数,第二项表示在这些强学习器中k个相对的弱学习器的复杂度,具体计算公式如下。
| $\left\{\begin{array}{l}L\left(y_i, \hat{y}_i\right)=\frac{1}{2} \sum\limits_{i=1}^n\left(\hat{y}_i-y_i\right)^2 \\ \varOmega\left(f\left(\boldsymbol{x}_k\right)\right)=\gamma T+\frac{1}{2} \lambda\|\boldsymbol{\omega}\|^2\end{array}\right.$ | (2) |
式中:λ、γ为超参数; T为所设决策树的总叶子节点数; ω为所有叶子节点通过决策树模型输出的预测值组成的特征向量。
(2) Boosting算法使用的是加法模型,强学习器的预测值就等于当前树预测值与前一棵树的预测值的和,所以将目标函数转化为前t-1次加上t次的目标函数。
(3) 对目标函数进行二阶泰勒展开,得到关于特征向量的一元二次函数并进行求导,得到目标函数极值点也就是最优解。
(4) 通过最优解定义出分裂的增益。
(5) 根据贪心准则遍历所有特征可能的分裂点计算出增益值,选取增益值最大的特征进行分裂。分裂完成则决策树模型构建完成[18]。
某一特征j在第k棵决策树中的重要度可以用式(3)计算。
| $\hat{J}_j^2(k)=\sum\limits_{t=1}^{T-1} \hat{i}_t^2 I\left(v_t=j\right)$ | (3) |
式中:
| $\hat{J}_j^2=\frac{1}{M} \sum\limits_{k=1}^M \hat{J}_j^2(k)$ | (4) |
文中所提XGBoost-GRU-MTL模型如图 1所示。首先,对实际的IES冷热电负荷以及各不确定因素进行数据预处理,将冷热电负荷直接作为模型输入,而对各个不确定因素进行XGBoost重要度排序,得到各因素对于IES各类负荷的贡献度,通过贡献度筛选出真正影响各类负荷的影响因素并与冷热电负荷共同作为输入;然后基于MTL的硬共享机制和GRU搭建多元负荷预测模型,通过GRU共享层来挖掘多元负荷间的耦合信息;最后基于该预测模型对冷热电负荷进行联合预测,得到冷热电负荷的预测结果。
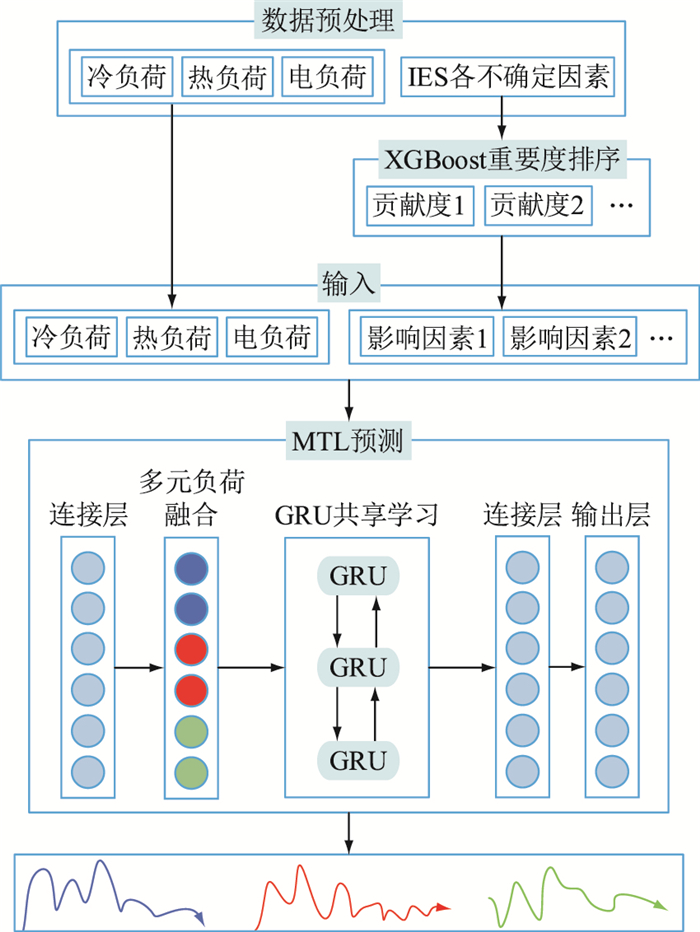
|
图 1 多元负荷预测模型总体框架 Fig. 1 General framework for multivariate load forecasting models |
RNN是一种常见的时序问题的处理方式,但是在解决时序问题中很可能出现梯度爆炸或者梯度消失。LSTM的出现解决了RNN存在的这些问题,被广泛用于时序预测等问题[24],然而LSTM的3个门的控制信息导致特征参数较多,收敛较慢,训练时间较长[25-27]。GRU是LSTM神经网络的一种变体,用更新门和重置门来替代LSTM的3个门的作用,更新门用于保持时间序列的同步,重置门用于控制当前信息和记忆信息传递的数据量,因此GRU在结构上更为简单,训练样本较少,更容易实现。文中采用了GRU作为MTL的共享层,目的在于降低整个多元负荷预测模型的复杂程度并大大减少训练时间,使之更加适用于实际IES的负荷预测,以便做出更加实时的调度和控制。GRU结构见图 2。
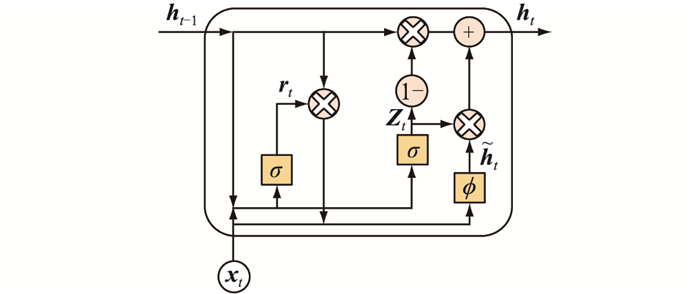
|
图 2 GRU结构 Fig. 2 Structure of GRU |
GRU中ht的计算公式为:
| $\boldsymbol{r}_t=\sigma\left(\boldsymbol{W}_{\mathrm{r}} \boldsymbol{h}_{t-1}+\boldsymbol{U}_{\mathrm{r}} \boldsymbol{x}_t\right)$ | (5) |
| $\boldsymbol{Z}_t=\sigma\left(\boldsymbol{W}_\mathrm{z} \boldsymbol{h}_{t-1}+\boldsymbol{U}_\mathrm{z} \boldsymbol{x}_t\right)$ | (6) |
| $\tilde{\boldsymbol{h}}_{\mathrm{t}}=\phi\left(\boldsymbol{W}_{\mathrm{h}}\left(\boldsymbol{r}_t \boldsymbol{h}_{t-1}\right)+\boldsymbol{U}_{\mathrm{h}} \boldsymbol{x}_t\right)$ | (7) |
| $\boldsymbol{h}_t=\left(1-\boldsymbol{Z}_t\right) \boldsymbol{h}_{t-1}+\boldsymbol{Z}_t \tilde{\boldsymbol{h}}_t$ | (8) |
式中:xt为输入;rt、Zt分别为重置门和更新门的输出;ht-1为上一时刻状态向量;
IES多元负荷预测并不是各种单一类型负荷预测的简单叠加,分别建模独立预测的方式并不合适,而应考虑多元负荷之间的耦合机理,挖掘彼此之间更多的隐含信息,从而使多元负荷预测不失实际意义。MTL是一种联合多个任务同时学习来增加模型表示和泛化能力的一种方式,其任务之间共享优化学习引起的参数正则化相比普通训练模型拟合的正则化有着先天性的优势[28]。
各子任务在共享机制上主要有软共享机制和硬共享机制。图 3简单描述了这2种共享机制,图 3(a)为软共享机制方式,各子任务的特征参数不同,在进行共享学习前首先要经过合适的正则化处理才能实现各子任务的信息共享,适用于相关性较弱的子任务;而图 3(b)所示硬共享机制通过共享层实现各子任务的共享学习,共享的特征参数相同,适用于有一定相关性的子任务。MTL的硬共享机制能够考虑到多元负荷之间耦合关系的本质就在于共享表示层,使得任务之间相互影响,在预测目标之间相关性较高的情况下,参数共享层不会带来太大的损失,而且能够加强参数共享,多个目标的模型可以联合训练,减小模型的参数规模,防止模型过拟合。因此,对于IES来说,多元负荷之间具有复杂的耦合关系且有较多不确定因素,参数众多且冷热电各子任务联系较为紧密,更适合采用硬共享机制来搭建模型,拟合效果较好且具有更好的泛化能力。因此,文中采用硬共享机制构建IES多元负荷预测模型。
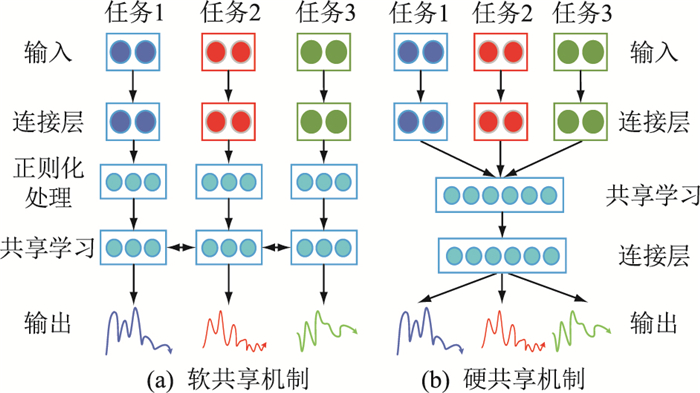
|
图 3 共享机制 Fig. 3 Sharing mechanism |
文中以上海某综合能源站作为研究对象,能源站采用先进的燃气冷热电三联供供能技术,燃气内燃机组的发电通过主变升压接入35 kV开关站,通过电网分配负责区域电力供应,同时燃气内燃机组排出的高温烟气(360 ℃)和高温冷却水(95 ℃)进入烟气热水型溴化锂机组,实现制冷和采暖供应。数据集包含2021年1月—2021年12月的冷热电负荷数据,数据采样率为1 h,即每天包含24组数据。气象数据来源于国家气象局,气象站点也对应于该能源站的地理位置,气象数据中有18个影响因素,包括气压、海平面气压、最高气压、最低气压、风力、最大风速、极大风速、2分钟平均风速、极大风速的风向、2分钟平均风速的风向、最大风速的风向、温度/气温、最高气温、最低气温、体感温度、相对湿度、最小相对湿度和降水量,时间间隔同样为1 h。对正常工作日和休息日进行对比分析,另外考虑了日类型信息,0代表休息日,1代表工作日。
3.1 数据预处理首先采用Z-Score公式计算出数据点到总体均值的距离Z,公式如下:
| $Z=\frac{x-\mu}{v}$ | (9) |
式中:x为数据点的数值;μ为总体数据的均值;υ为总体数据的标准差。将Z过大的点剔除并使用均值填充的方法将所有数据填充完整。为了保证硬共享机制各子任务之间参数的一致性以及方便进行对比,将预处理之后的冷热电负荷数据都统一归算到MW;其次考虑到其他输入特征的量纲问题的影响,将冷热电负荷以及各气象数据进行归一化处理以方便输入。因为后面评价指标中用到了平均绝对百分比误差(mean absolute percentage error,MAPE),当预测值与最小值接近时,若采用传统的归一化计算则会导致归一化后的值接近于0,从而产生较大的MAPE值,所以将传统归一化计算式进行转化,计算式为:
| $Z=\frac{x_i-x_{i, \min }}{x_{i, \max }-x_{i, \min }}+1$ | (10) |
式中:xi为各输入特征量归一化前的数据;xi, min、xi, max分别为xi对应的最小值和最大值。
为了保证预测值能够反映实际的IES中各类负荷真实的物理意义,最后使用反归一化对预测值进行处理以还原其量纲。反归一化的计算式为:
| $x_i=Z\left(x_{i, \max }-x_{i, \min }\right)+x_{i, \min }$ | (11) |
以XGBoost重要度排序的方法得到18个气象条件以及日类型信息对冷热电负荷各自的贡献度,前6位的影响因素一致,同时也印证了该IES中冷热电负荷之间有着紧密的耦合关系。这6个因素对于冷热电负荷的贡献度之和分别为0.979、0.949、0.984,其余因素几乎对负荷没有贡献度,将这些因素剔除后表示成并列柱状图,如图 4所示。
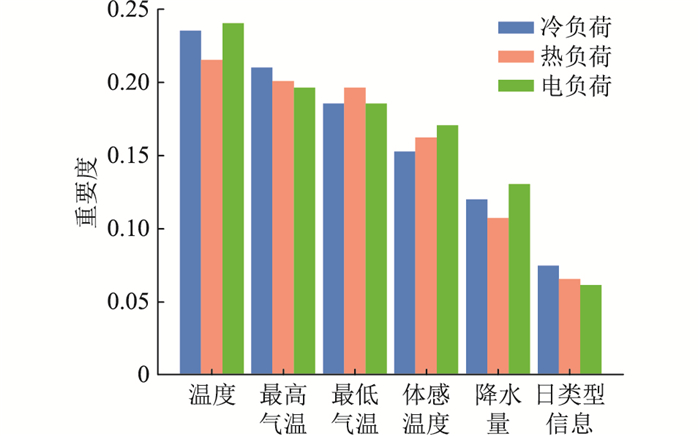
|
图 4 XGBoost重要度排序 Fig. 4 Importance ranking of XGBoost |
将贡献度最高的6个影响因素作为输入特征对负荷预测起到修正作用,再加上预测日t时刻前10个时间尺度的负荷,输出未来预测日t时刻的冷热电负荷,时间尺度为1 h。
3.3 模型构建及超参数设置文中以Python作为编程语言,在TensorFlow和Keras框架下搭建多元负荷预测模型,训练集、测试集和验证集的比例分别为70%、15%、15%,冷热电负荷3个子任务的权重分别为0.3、0.3、0.4。因为深度学习模型的训练需要大量的时间,采用离线训练与在线测试相结合的方式,在离线训练阶段训练预测模型的输入特征与输出之间的关系,在线测试阶段将当前时刻的各特征输入训练好的GRU-MTL预测模型获得预测结果进行验证。
文中在离线训练构建模型的过程中主要考虑了以下5个方面:
(1) 通过反复训练找到合适的共享GRU层数、GRU各层神经元的个数、融合层的层数以及学习率和最大迭代次数。
(2) 将训练集的各特征向量作为输入,对应的负荷预测值作为输出,训练该模型直至学习率衰减到最小预设值。
(3) 计算模型输出的预测值与实际值的误差,采用Adam优化算法,依据均方根误差(root mean square error, RMSE)损失函数自上而下优化网络参数。
(4) 选择均方根误差ERMSE、平均绝对百分比误差EMAPE作为评价指标对模型性能进行评价。
| $E_{\mathrm{RMSE}}=\sqrt{\frac{1}{n}\left[\omega_i \sum\limits_{i=1}^n\left(y_i-y_i^{\prime}\right)^2\right]}$ | (12) |
| $E_{\mathrm{MAPE}}=\frac{1}{n}\left(\omega_i \sum\limits_{i=1}^n \frac{\left|y_i-y_i^{\prime}\right|}{y_i}\right) \times 100 \%$ | (13) |
式中:n为样本数据个数;ωi为权重;yi为冷热电负荷实际值;
(5) 离线训练结果分析。目前深度学习超参数的选取主要还是依据训练学习的效果来确定,为此进行了关键超参数的敏感性分析。
3.3.1 共享GRU层数分析共享GRU层数对模型预测效果和训练时间的影响,具体如表 1所示,采用冷热电负荷预测的EMAPE值来说明预测的精度。当GRU层数大于4时预测精度开始降低,在精度相差不大的情况下,3层相比4层训练时间显著减少,且相比于2层,3层的预测精度提升较大,所以文中选取共享GRU层数为3。
|
|
表 1 共享GRU层数对模型的影响 Table 1 Impact of shared GRU layers on the model |
分析GRU层神经元个数对模型参数数量、训练时间以及预测精度的影响,具体如表 2所示。当神经元个数为64时训练时间较短且预测精度较高,神经元个数继续增多训练时间大幅增加且精度几乎没有提升,所以文中选择GRU层神经元个数为64。
|
|
表 2 GRU层神经元个数对模型的影响 Table 2 Impact of the number of neurons in the GRU layer on the model |
分析最大迭代次数对模型训练时间以及预测精度的影响,具体如表 3所示。当迭代次数为250左右时拟合效果已达到最佳,继续增加迭代次数会造成过拟合而降低预测精度、增加训练时间,所以文中选择最大迭代次数为250。
|
|
表 3 最大迭代次数对模型的影响 Table 3 Impact of the maximum number of iterations on the model |
根据模型训练阶段得到的主要超参数设置如表 4所示。
|
|
表 4 超参数设置情况 Table 4 Hyperparameter setting |
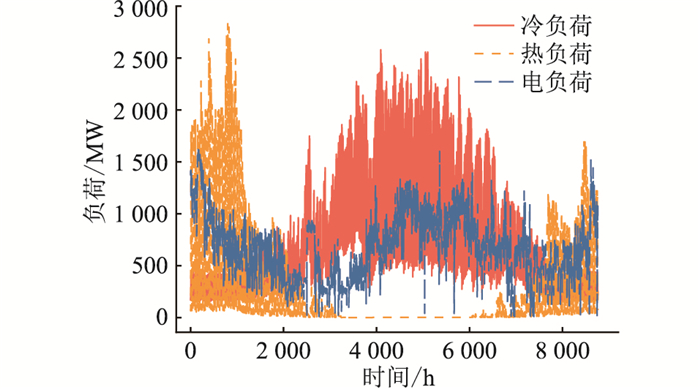
该综合能源站全年实际运行情况如图 5所示。可以明显看到夏季主要供冷而停止供热,冬季主要供热而供冷较少,所以文中分别对夏季典型日和冬季典型日进行对比分析,结果更符合该IES的实际情况。选定该能源站7月16日、7月17日作为夏季典型日,1月15日、1月16日作为冬季典型日进行测试和对比分析。
|
图 5 综合能源站全年运行情况 Fig. 5 Full year operation of integrated energy stations |
为了验证文中所提出的XGBoost-GRU-MTL多元负荷预测模型的优势、引入XGBoost特征重要度排序进行特征选取是否对最终的预测起到正向的修正作用以及在构建模型过程中采用MTL理论是否适合该综合能源站的实际情况,对比模型选择为:(1) 单任务LSTM对冷热电负荷的分别预测;(2) 目前MTL常用的LSTM-MTL联合预测;(3) 文中所提出的模型,考虑XGBoost特征重要度排序,基于GRU-MTL对3种负荷的联合预测。
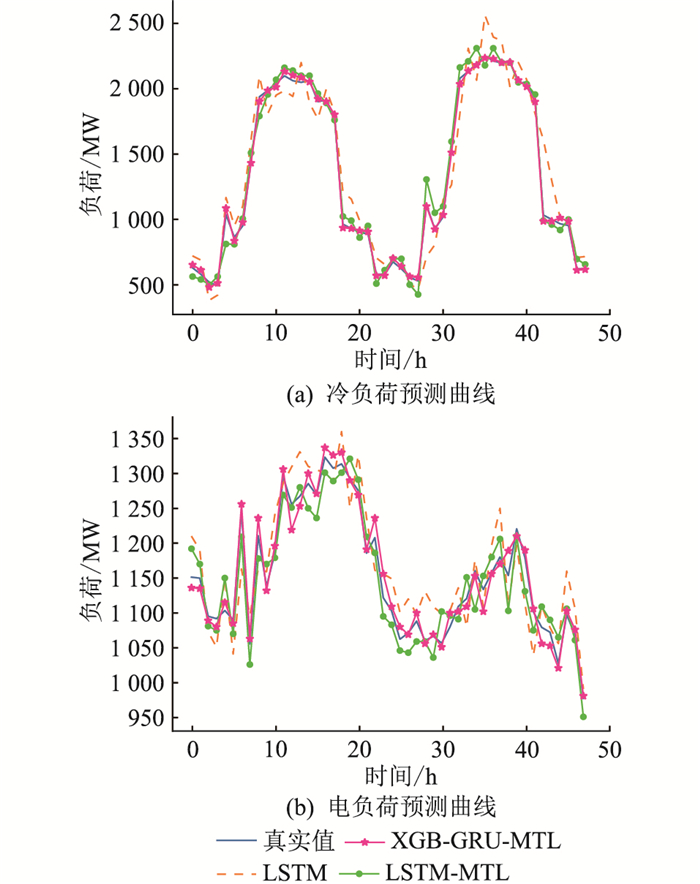
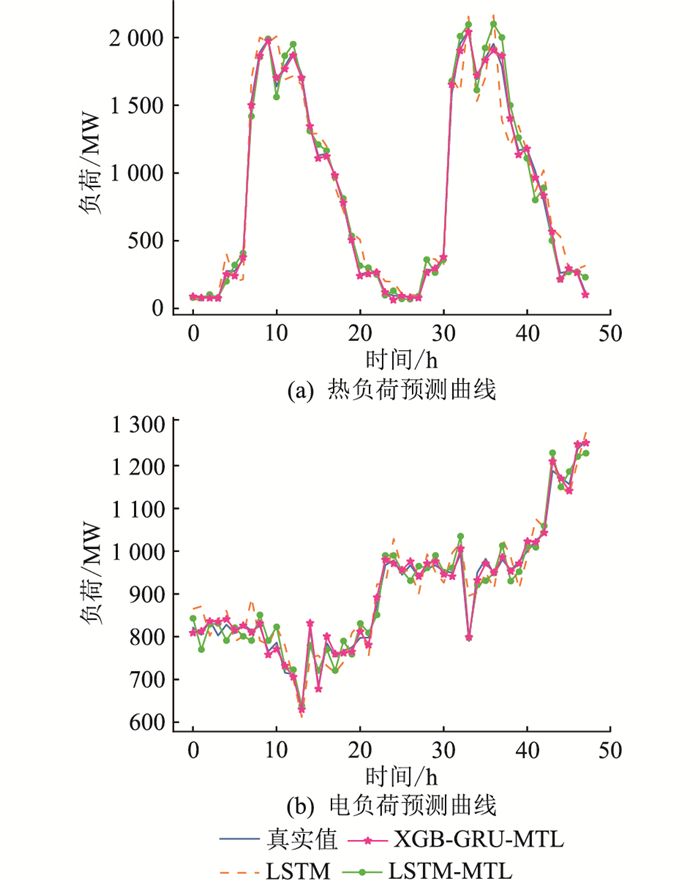
夏季典型日和冬季典型日的负荷预测曲线分别如图 6和图 7所示。从最直观的角度来看,文中所提模型与实际负荷曲线的贴合度最好, 预测精度最高。表 5、表 6分别为夏季典型日和冬季典型日的评价指标对比,具体对比分析如下。
|
图 6 夏季典型日负荷预测曲线 Fig. 6 Load forecast curves in typical summer days |
|
图 7 冬季典型日负荷预测曲线 Fig. 7 Load forecast curves in typical winter days |
|
|
表 5 夏季典型日评价指标对比 Table 5 Comparison of evaluation indicators in typical summer days |
|
|
表 6 冬季典型日评价指标对比 Table 6 Comparison of evaluation indicators in typical winter days |
(1) 对于电负荷的预测,在夏季典型日,相较于单一LSTM预测,2种MTL预测模型在预测精度上的MAPE值由3.48%分别降低到了2.19%和1.07%,而冬季典型日则由4.36%分别降低到了2.55%和1.12%。无论是夏季典型日还是冬季典型日,电负荷变化范围小,负荷在一个集中的区间内波动,且波动较为剧烈,普通的单一任务预测模型LSTM虽然在总体的预测精度上能够得到较为理想的预测结果,但是对于负荷的这种剧烈波动,单任务预测相对保守,通过一个相对平均的预测来获得理想的预测结果,而从预测曲线的变化上看,变化趋势与实际负荷变化相差较大,因此单任务预测对于多元负荷的分别预测不能够适应现代IES负荷的剧烈波动。而后2种MTL预测模型通过多种负荷之间共享的辅助信息互相学习,能够较好地适应IES这种负荷的剧烈波动,符合实际IES中负荷的变化趋势,在预测的精度上也有较好的提升,能够更好地提前预知实际IES中的负荷变化以便指导生产。
(2) 在夏季典型日冷负荷及冬季典型日热负荷的预测上,相较于单一LSTM预测,MTL联合预测冷负荷MAPE值由12.56%分别降低到了6.01%和2.02%,热负荷MAPE值由26.00%分别降低到了12.19%和4.97%。这是由于负荷变化跨度大,波峰波谷相差巨大,传统单任务预测模型LSTM保守的预测策略难以实现这样跨度的预测,其误差被拉大,精度已无法满足实际要求,而后2种MTL预测模型精度提升明显,且负荷变化范围越大,提升越明显。
3.4.2 XGBoost重要度排序对于负荷预测的影响对比后2种MTL联合预测模型,考虑XGBoost重要度排序对特征进行选取的方法,在夏季典型日,冷负荷MAPE值由6.01%降低到了2.02%,电负荷MAPE值由2.19%降低到了1.07%;在冬季典型日,热负荷MAPE值由12.19%降低到了4.97%,电负荷MAPE值由2.55%降低到了1.12%。这是由于通过贡献度选取真正对负荷预测有贡献的特征使这些因素发挥了其对于负荷预测该有的修正作用,同时提升了各子任务之间共享信息的效用,在波峰、波谷及负荷变化剧烈的时刻提升更明显。文中所提XGBoost特征重要度排序方法提升了模型最终预测精度,且不确定因素越多,该方法的提升空间越大。
3.4.3 不同模型在训练时间和预测时间上的对比对比表 7中各模型的训练时间和预测时间,单任务模型是对于各类负荷预测的简单叠加,训练时间和预测时间均为MTL联合预测的2倍多,数据量越大这种差距就越明显;文中所提模型使用GRU作为共享层简化了整个模型的复杂度,而且在进行XGBoost重要度排序选择输入特征之后,特征参数减少使得训练时间也有较显著的降低,因此该模型对于实际IES多元负荷的联合预测实用性较好。
|
|
表 7 模型所需时间对比 Table 7 Comparison of time required by models |
文中提出一种XGBoost-GRU-MTL模型用于对IES进行多元负荷预测,并采用上海某综合能源站的实际运行数据进行了应用分析和验证,得到的主要结论如下:
(1) 目前IES中各类负荷之间存在较为密切的关系,MTL联合预测能够通过共享层获取更多信息,在实际IES中负荷波动剧烈和负荷变化范围大等问题的解决上效用明显,单一负荷预测的简单叠加已经不能满足现代IES多元负荷预测的要求。
(2) 随着IES的快速发展,影响多元负荷预测的因素越来越多,若不考虑各因素对负荷的实际效用反而会影响其该有的修正作用。将XGBoost重要度排序的方法应用于特征选取,不仅提高了预测精度、缩短了训练时间,而且相比于传统的相关性分析选取特征的方式具有更好的适用性。
在IES的负荷影响因素方面,文中主要考虑了该能源站的气象条件、日类型信息等时序类因素,对于区域规划布局、建筑设计特性等空间类因素对IES负荷的影响考虑不足,在今后的研究中可以更加深入地考虑空间类因素对于负荷预测的影响,以实现IES多元负荷预测精度的进一步提高,追求更好的适用性。
| [1] |
陈胜, 卫志农, 顾伟, 等. 碳中和目标下的能源系统转型与变革: 多能流协同技术[J]. 电力自动化设备, 2021, 41(9): 3-12. CHEN Sheng, WEI Zhinong, GU Wei, et al. Carbon neutral oriented transition and revolution of energy systems: multi-energy flow coordination technology[J]. Electric Power Automation Equipment, 2021, 41(9): 3-12. (  0) 0) |
| [2] |
朱继忠, 董瀚江, 李盛林, 等. 数据驱动的综合能源系统负荷预测综述[J]. 中国电机工程学报, 2021, 41(23): 7905-7924. ZHU Jizhong, DONG Hanjiang, LI Shenglin, et al. Review of data-driven load forecasting for integrated energy system[J]. Proceedings of the CSEE, 2021, 41(23): 7905-7924. DOI:10.13334/j.0258-8013.pcsee.202337 (  0) 0) |
| [3] |
吕岩, 潘毅群, 刘海静, 等. 冷热负荷预测在区域供能项目中的应用——以上海西虹桥1号能源站为例[J]. 全球能源互联网, 2021, 4(2): 197-203. LYU Yan, PAN Yiqun, LIU Haijing, et al. Application of cooling and heating load prediction for district energy supply: a case in West Hongqiao 1# energy station[J]. Journal of Global Energy Interconnection, 2021, 4(2): 197-203. (  0) 0) |
| [4] |
WANG Y L, WANG Y D, HUANG Y J, et al. Optimal scheduling of the regional integrated energy system considering economy and environment[J]. IEEE Transactions on Sustainable Energy, 2019, 10(4): 1939-1949. DOI:10.1109/TSTE.2018.2876498 (  0) 0) |
| [5] |
ZHAO Z Q, ZHENG P, XU S T, et al. Object detection with deep learning: a review[J]. IEEE Transactions on Neural Networks and Learning Systems, 2019, 30(11): 3212-3232. DOI:10.1109/TNNLS.2018.2876865 (  0) 0) |
| [6] |
WANG Y, GAN D H, SUN M Y, et al. Probabilistic individual load forecasting using pinball loss guided LSTM[J]. Applied Energy, 2019, 235: 10-20. DOI:10.1016/j.apenergy.2018.10.078 (  0) 0) |
| [7] |
张宇帆, 艾芊, 林琳, 等. 基于深度长短时记忆网络的区域级超短期负荷预测方法[J]. 电网技术, 2019, 43(6): 1884-1892. ZHANG Yufan, AI Qian, LIN Lin, et al. A very short-term load forecasting method based on deep LSTM RNN at zone level[J]. Power System Technology, 2019, 43(6): 1884-1892. DOI:10.13335/j.1000-3673.pst.2018.2101 (  0) 0) |
| [8] |
LIU E J, WANG Y X, HUANG Y Z. Short-term forecast of multi-load of electrical heating and cooling in regional integrated energy system based on deep LSTM RNN[C]//2020 IEEE 4th Conference on Energy Internet and Energy System Integration (EI2). Wuhan, China. IEEE, 2021: 2994-2998.
(  0) 0) |
| [9] |
WANG B, ZHANG L M, MA H R, et al. Parallel LSTM-based regional integrated energy system multienergy source-load information interactive energy prediction[J]. Complexity, 2019, 2019: 7414318. (  0) 0) |
| [10] |
WU K H, WU J A, FENG L A, et al. An attention-based CNN-LSTM-BiLSTM model for short-term electric load forecasting in integrated energy system[J]. International Transactions on Electrical Energy Systems, 2021, 31(1): e12637. (  0) 0) |
| [11] |
陈锦鹏, 胡志坚, 陈纬楠, 等. 二次模态分解组合DBiLSTM-MLR的综合能源系统负荷预测[J]. 电力系统自动化, 2021, 45(13): 85-94. CHEN Jinpeng, HU Zhijian, CHEN Weinan, et al. Load prediction of integrated energy system based on combination of quadratic modal decomposition and deep bidirectional long short-term memory and multiple linear regression[J]. Automation of Electric Power Systems, 2021, 45(13): 85-94. (  0) 0) |
| [12] |
李睿智, 刘念, 延肖何. 基于势博弈的综合能源系统用户能量管理优化方法[J]. 电力科学与技术学报, 2021, 36(1): 21-31. LI Ruizhi, LIU Nian, YAN Xiaohe. An optimization method for user energy management of integrated energy system based on potential game[J]. Journal of Electric Power Science and Technology, 2021, 36(1): 21-31. (  0) 0) |
| [13] |
朱文广, 李映雪, 杨为群, 等. 基于K-折交叉验证和Stacking融合的短期负荷预测[J]. 电力科学与技术学报, 2021, 36(1): 87-95. ZHU Wenguang, LI Yingxue, YANG Weiqun, et al. Short-term load forecasting based on the K-fold cross-validation and Stacking ensemble[J]. Journal of Electric Power Science and Technology, 2021, 36(1): 87-95. (  0) 0) |
| [14] |
WANG X, WANG S X, ZHAO Q Y, et al. A multi-energy load prediction model based on deep multi-task learning and ensemble approach for regional integrated energy systems[J]. International Journal of Electrical Power & Energy Systems, 2021, 126: 106583. (  0) 0) |
| [15] |
田浩含, 张智晟, 于道林. 基于改进LSTM的区域综合能源系统多元负荷短期预测研究[J]. 电力系统及其自动化学报, 2021, 33(9): 130-137. TIAN Haohan, ZHANG Zhisheng, YU Daolin. Research on multi-load short-term forecasting of regional integrated energy system based on improved LSTM[J]. Proceedings of the CSU-EPSA, 2021, 33(9): 130-137. (  0) 0) |
| [16] |
孙庆凯, 王小君, 张义志, 等. 基于LSTM和多任务学习的综合能源系统多元负荷预测[J]. 电力系统自动化, 2021, 45(5): 63-70. SUN Qingkai, WANG Xiaojun, ZHANG Yizhi, et al. Multiple load prediction of integrated energy system based on long short-term memory and multi-task learning[J]. Automation of Electric Power Systems, 2021, 45(5): 63-70. (  0) 0) |
| [17] |
吕忠麟, 顾洁, 孟璐. 基于耦合特征与多任务学习的综合能源系统短期负荷预测[J]. 电力系统自动化, 2022, 46(11): 58-66. LYU Zhonglin, GU Jie, MENG Lu. Short-term load forecasting for integrated energy system based on coupling features and multi-task learning[J]. Automation of Electric Power Systems, 2022, 46(11): 58-66. (  0) 0) |
| [18] |
史佳琪, 谭涛, 郭经, 等. 基于深度结构多任务学习的园区型综合能源系统多元负荷预测[J]. 电网技术, 2018, 42(3): 698-707. SHI Jiaqi, TAN Tao, GUO Jing, et al. Multi-task learning based on deep architecture for various types of load forecasting in regional energy system integration[J]. Power System Technology, 2018, 42(3): 698-707. (  0) 0) |
| [19] |
马天男, 王超, 彭丽霖, 等. 计及需求响应和深度结构多任务学习的电力系统短期负荷预测[J]. 电测与仪表, 2019, 56(16): 50-60. MA Tiannan, WANG Chao, PENG Lilin, et al. Short-term load forecasting of power system considering demand response and multi-task learning based on deep structure[J]. Electrical Measurement & Instrumentation, 2019, 56(16): 50-60. (  0) 0) |
| [20] |
胡伟, 杨梓俊, 王瑾然, 等. 园区综合能源系统日前多目标优化调度[J]. 电力科学与技术学报, 2021, 36(1): 13-20. HU Wei, YANG Zijun, WANG Jinran, et al. Multi-objective optimal scheduling of integrated energy system in the industry park[J]. Journal of Electric Power Science and Technology, 2021, 36(1): 13-20. (  0) 0) |
| [21] |
吴晨, 姚菁, 薛贵元, 等. 基于MMoE多任务学习和长短时记忆网络的综合能源系统负荷预测[J]. 电力自动化设备, 2022, 42(7): 33-39. WU Chen, YAO Jing, XUE Guiyuan, et al. Load forecasting of integrated energy system based on MMoE multi-task learning and LSTM[J]. Electric Power Automation Equipment, 2022, 42(7): 33-39. (  0) 0) |
| [22] |
鲁斌, 霍泽健, 俞敏. 基于LSTNet-Skip的综合能源系统多元负荷超短期预测[J]. 中国电机工程学报, 2023, 43(6): 2273-2283. LU Bin, HUO Zejian, YU Min, et al. LSTNet-Skip-based multivariate load ultra-short-term forecasting for integrated energy systems[J]. Proceedings of the CSEE, 2023, 43(6): 2273-2283. (  0) 0) |
| [23] |
CHEN C, ZHANG Q M, YU B, et al. Improving protein-protein interactions prediction accuracy using XGBoost feature selection and stacked ensemble classifier[J]. Computers in Biology and Medicine, 2020, 123: 103899. (  0) 0) |
| [24] |
陆继翔, 张琪培, 杨志宏, 等. 基于CNN-LSTM混合神经网络模型的短期负荷预测方法[J]. 电力系统自动化, 2019, 43(8): 131-137. LU Jixiang, ZHANG Qipei, YANG Zhihong, et al. Short-term load forecasting method based on CNN-LSTM hybrid neural network model[J]. Automation of Electric Power Systems, 2019, 43(8): 131-137. (  0) 0) |
| [25] |
赵兵, 王增平, 纪维佳, 等. 基于注意力机制的CNN-GRU短期电力负荷预测方法[J]. 电网技术, 2019, 43(12): 4370-4376. ZHAO Bing, WANG Zengping, JI Weijia, et al. A short-term power load forecasting method based on attention mechanism of CNN-GRU[J]. Power System Technology, 2019, 43(12): 4370-4376. (  0) 0) |
| [26] |
邓带雨, 李坚, 张真源, 等. 基于EEMD-GRU-MLR的短期电力负荷预测[J]. 电网技术, 2020, 44(2): 593-602. DENG Daiyu, LI Jian, ZHANG Zhenyuan, et al. Short-term electric load forecasting based on EEMD-GRU-MLR[J]. Power System Technology, 2020, 44(2): 593-602. (  0) 0) |
| [27] |
朱伟, 孙运全, 钱尧, 等. 基于CEEMD-GRU模型的短期电力负荷预测方法[J]. 电测与仪表, 2023, 60(1): 16-22. ZHU Wei, SUN Yunquan, QIAN Yao, et al. Short-term electric load forecasting method based on CEEMD-GRU model[J]. Electrical Measurement and Instrumentation, 2023, 60(1): 16-22. (  0) 0) |
| [28] |
李亚. 多任务学习的研究[D]. 合肥: 中国科学技术大学, 2018. LI Ya. Research on multi-task learning[D]. Hefei: University of Science and Technology of China, 2018. (  0) 0) |
 2023, Vol. 42
2023, Vol. 42


 马传杰(1997), 男, 硕士在读, 研究方向为综合能源系统多元负荷预测、智能发电等(E-mail:
马传杰(1997), 男, 硕士在读, 研究方向为综合能源系统多元负荷预测、智能发电等(E-mail: