文章编号: 2096-3203(2023)05-0177-08 中图分类号: TM711
随着越来越多的敏感负荷接入电网,用户对电压暂降愈加关注,准确定位暂降源有助于快速排除故障以及划分故障责任,提高供电可靠性[1]。考虑到我国配电网自动化程度普遍不高,配电自动化监控终端无法覆盖所有的线路节点。因此,基于少量电压测量装置的精确定位对配电自动化水平不高地区的暂降源精确定位具有重要意义[2-3]。
传统基于单一测点信息判断暂降源相对于监测点上下游关系的电压暂降源定位方法主要有基于扰动能量与扰动功率[4-5]、基于电压和电流测量[6]、基于等效阻抗实部极性[7]、基于系统参量斜率[8],但这些方法只能判断出电压暂降源位于监测点的上游或下游,不能确定其在全网中的具体位置[9]。基于综合判据和智能算法虽然可以精确定位故障点[10-11],但存在计算过程复杂、工程可行性低等缺点。
同步相量测量装置(phasor measurement unit,PMU)基于全球定位系统(global positioning system,GPS)或北斗卫星系统的标准时钟信号进行电网实时监测,在输电网和配电网中得到了成功应用[12-14]。文献[15]基于PMU的检测信息进行故障分析与处理,从而达到定位目的。文献[16]对基于配电网同步相量测量装置(synchrophasor measurement unit for distribution network,D-PMU)的中压配电网精确故障定位技术的发展前景和关键技术进行分析与讨论,并给出PMU在智能电网中的精确定位方法。出于经济性考虑,在配电网每个节点安装PMU是不现实的。文献[17]提出一种基于有限PMU实现单故障和多故障定位的配电网故障定位方法。文献[18]提出一种基于PMU边缘终端的智能电网台区相间短路故障定位方法。文献[19]提出基于有限微型同步相量测量装置(micro-phasor measurement unit, μPMU)实现全网配电网故障定位的方法,利用各节点的全局相量信息来准确定位故障区段。文献[20]利用较少的μPMU和电压测量装置实现了故障的定位,但要实现较高的定位精度需要大量计算。
文中提出一种基于μPMU和二分搜索法的辐射状配电网电压暂降源精确定位方法。首先,以一个8节点辐射状配电网为例,对电路分层方法和装置配置策略进行叙述。接着,根据装设μPMU的分层电路计算暂降源电流,并将此电流注入各母线,计算末端母线虚拟电压变化量与实测电压变化量的误差,选取每个分层电路中误差最小的母线为候选母线,找出包含所有候选母线的分层电路,在该分层电路中比较所有候选母线注入暂降源电流时末端母线的误差大小,误差最小值对应的候选母线为暂降源邻近母线。然后,基于二分法搜索法思想在暂降源邻近母线相邻区段中点设置虚拟母线,比较暂降源电流注入虚拟母线时末端母线的误差大小,缩小定位区间,实现暂降源的精确定位。最后,在MATLAB中利用IEEE 33节点模型对文中定位方法进行了验证,结果表明该方法对辐射状配电网的不同类型、不同位置的电压暂降源定位精度高且具有较强抗干扰能力。
1 基于μPMU的电压暂降源邻近母线确定引起电压暂降的暂降源主要分为三大类:由电缆损坏、雷电、设备故障等各种原因引起的短路故障,变压器投切及大型感性电动机启动等[21-22]。以上暂降源出现时,系统中部分支路电流会突然增大,大电流使系统等效阻抗分压变大,进而导致公共连接点(point of common coupling, PCC)处电压骤降。
1.1 配电网分层模型与μPMU配置策略对于一个含有h条末端母线的辐射状配电网,将其分为h个分层电路,各分层电路由变压器总线与末端母线之间的串联阻抗组成。检测装置的配置原则如下:需要2个μPMU,分别安装在变压器二次侧出线母线处和任意一条末端母线处;在其他h-1个末端母线处,只要安装普通检测装置即可,如电压互感器、故障录波器等。
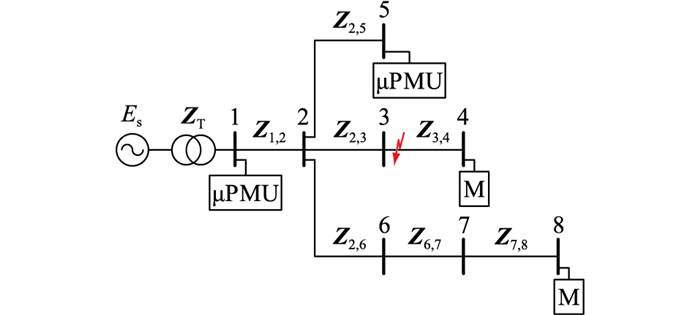
为了更好地描述分层方法和后续电压暂降源定位的思路,建立如图 1所示的8节点配电网模型。其中母线1和母线5安装μPMU,母线4和母线8安装普通电压幅值检测装置M,暂降源位于区段3—4之间且靠近母线3处。
|
图 1 8节点配电网示意 Fig. 1 Schematic diagram of 8-node distribution network |
图 1中,Es为三相电源;ZT为变压器三相阻抗;Zx, y为线路三相阻抗,下标x、y分别为该线路阻抗左、右两端母线编号。
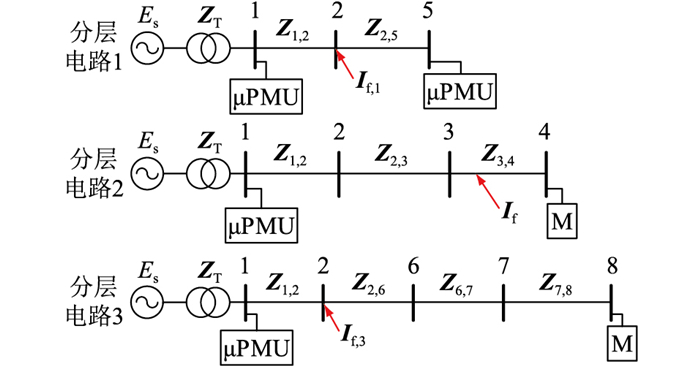
在暂降源定位过程中,首先对配电网进行分层。图 1所示配电网可分为3个分层电路,见图 2。
|
图 2 分层电路示意 Fig. 2 Schematic diagram of layered circuit |
当电压暂降发生的时候,配电网所有母线电压都会受到暂降源的影响。图 2中,当暂降源在母线3—4之间时,暂降源引起的大电流If,即暂降源电流通过公共母线2流入到分层电路1和分层电路3中,如图 2中If,1和If,3所示,即每个分层电路母线的电压暂降都与If有关。
1.2 暂降源电流的计算要计算暂降源电流,就要检测出暂降前和暂降期间电压的幅值和相位。因此,必须通过装有μPMU的分层电路计算暂降源电流。对于图 1所示的配电网,用图 2中的分层电路1计算暂降源电流。暂降源电流通过公共母线2流入分层电路1中,母线5上的μPMU测量到暂降前与暂降期间电压,相减得到电压变化量ΔV5如式(1)所示。
| $ \Delta \boldsymbol{V}_5=\left[\begin{array}{c} V_5^{\mathrm{a}, \mathrm{pf}}-V_5^{\mathrm{a}, \mathrm{df}} \\ V_5^{\mathrm{b}, \mathrm{pf}}-V_5^{\mathrm{b}, \mathrm{df}} \\ V_5^{\mathrm{c}, \mathrm{pf}}-V_5^{\mathrm{c}, \mathrm{df}} \end{array}\right]_{3 \times 1} $ | (1) |
式中:
| $ \left[\begin{array}{l} \boldsymbol{I}_1 \\ \boldsymbol{I}_5 \end{array}\right]_{6 \times 1}=\left[\begin{array}{cc} \boldsymbol{Z}_{\mathrm{T}} & \boldsymbol{Z}_{\mathrm{T}} \\ \boldsymbol{Z}_{\mathrm{T}} & \boldsymbol{Z}_{\mathrm{T}}+\boldsymbol{Z}_{1, 2}+\boldsymbol{Z}_{2, 5} \end{array}\right]_{6 \times 6}^{-1} \times\left[\begin{array}{l} \Delta \boldsymbol{V}_1 \\ \Delta \boldsymbol{V}_5 \end{array}\right]_{6 \times 1} $ | (2) |
将式(2)中求得的虚拟注入电流I1和I5相加,就得到了暂降源电流If[23]。
| $ \boldsymbol{I}_{\mathrm{f}}=\boldsymbol{I}_1+\boldsymbol{I}_5 $ | (3) |
求得暂降源电流If后,对于各分层电路分别假设暂降源电流注入各个母线节点,计算末端母线电压变化量并与实测的末端母线电压变化量求误差,通过分析各母线产生的误差大小确定暂降源邻近母线。
对于分层电路1,假设暂降源在母线1处,则暂降源电流从母线1流入分层电路1,末端母线5上的电压变化量ΔV5, 1, 1可以通过式(4)求出。ΔVm, n, i为暂降源电流从分层电路i母线n流入时,母线m的电压变化量。类似地,再假设暂降源分别位于母线2和母线5,将暂降源电流分别注入母线2和母线5,利用式(5)和式(6)可以计算出末端母线上的电压变化量ΔV5, 2, 1和ΔV5, 5, 1, 分别如式(5)、式(6)所示。
| $ \begin{array}{c} {\left[\Delta \boldsymbol{V}_{5, 1, 1}\right]_{3 \times 1}=} \\ {\left[\begin{array}{lll} \boldsymbol{Z}_{\mathrm{T}} & \boldsymbol{Z}_{\mathrm{T}}+\boldsymbol{Z}_{1, 2} & \boldsymbol{Z}_{\mathrm{T}}+\boldsymbol{Z}_{1, 2}+\boldsymbol{Z}_{2, 5} \end{array}\right]_{3 \times 9} \times\left[\begin{array}{c} \boldsymbol{I}_{\mathrm{f}} \\ \mathit{\pmb{0}} \\ \mathit{\pmb{0}} \end{array}\right]_{9 \times 1}} \end{array} $ | (4) |
| $ \begin{array}{c} {\left[\Delta \boldsymbol{V}_{5, 2, 1}\right]_{3 \times 1}=} \\ {\left[\begin{array}{lll} \boldsymbol{Z}_{\mathrm{T}} & \boldsymbol{Z}_{\mathrm{T}}+\boldsymbol{Z}_{1, 2} & \boldsymbol{Z}_{\mathrm{T}}+\boldsymbol{Z}_{1, 2}+\boldsymbol{Z}_{2, 5} \end{array}\right]_{3 \times 9} \times\left[\begin{array}{c} \mathit{\pmb{0}} \\ \boldsymbol{I}_{\mathrm{f}} \\ \mathit{\pmb{0}} \end{array}\right]_{9 \times 1}} \end{array} $ | (5) |
| $ \begin{array}{c} {\left[\Delta \boldsymbol{V}_{5, 5, 1}\right]_{3 \times 1}=} \\ {\left[\begin{array}{lll} \boldsymbol{Z}_{\mathrm{T}} & \boldsymbol{Z}_{\mathrm{T}}+\boldsymbol{Z}_{1, 2} & \boldsymbol{Z}_{\mathrm{T}}+\boldsymbol{Z}_{1, 2}+\boldsymbol{Z}_{2, 5} \end{array}\right]_{3 \times 9} \times\left[\begin{array}{c} \mathit{\pmb{0}} \\ \mathit{\pmb{0}} \\ \boldsymbol{I}_{\mathrm{f}} \end{array}\right]_{9 \times 1}} \end{array} $ | (6) |
若真实的暂降源不在上述假设的母线处, 则末端母线5处计算所得
| $ \left[\begin{array}{c} \boldsymbol{E}_{5, 1, 1} \\ \boldsymbol{E}_{5, 2, 1} \\ \boldsymbol{E}_{5, 5, 1} \end{array}\right]_{9 \times 1}=\left[\begin{array}{c} \left|\Delta \boldsymbol{V}_5-\Delta \boldsymbol{V}_{5, 1, 1}\right| \\ \left|\Delta \boldsymbol{V}_5-\Delta \boldsymbol{V}_{5, 2, 1}\right| \\ \left|\Delta \boldsymbol{V}_5-\Delta \boldsymbol{V}_{5, 5, 1}\right| \end{array}\right]_{9 \times 1} $ | (7) |
类似地,重复式(4)—式(7),得到分层电路2和3的末端母线实测值与计算值的误差如式(8)和式(9)所示,然后求出各三相绝对值之和,进而确定各分层电路的候选母线。
| $ \left[\begin{array}{l} \boldsymbol{E}_{4, 1, 2} \\ \boldsymbol{E}_{4, 2, 2} \\ \boldsymbol{E}_{4, 3, 2} \\ \boldsymbol{E}_{4, 4, 2} \end{array}\right]_{12 \times 1}=\left[\begin{array}{c} \left|\Delta \boldsymbol{V}_4-\Delta \boldsymbol{V}_{4, 1, 2}\right| \\ \left|\Delta \boldsymbol{V}_4-\Delta \boldsymbol{V}_{4, 2, 2}\right| \\ \left|\Delta \boldsymbol{V}_4-\Delta \boldsymbol{V}_{4, 3, 2}\right| \\ \left|\Delta \boldsymbol{V}_4-\Delta \boldsymbol{V}_{4, 4, 2}\right| \end{array}\right]_{12 \times 1} $ | (8) |
| $ \left[\begin{array}{l} \boldsymbol{E}_{8, 1, 3} \\ \boldsymbol{E}_{8, 2, 3} \\ \boldsymbol{E}_{8, 6, 3} \\ \boldsymbol{E}_{8, 7, 3} \\ \boldsymbol{E}_{8, 8, 3} \end{array}\right]_{15 \times 1}=\left[\begin{array}{c} \left|\Delta \boldsymbol{V}_8-\Delta \boldsymbol{V}_{8, 1, 3}\right| \\ \left|\Delta \boldsymbol{V}_8-\Delta \boldsymbol{V}_{8, 2, 3}\right| \\ \left|\Delta \boldsymbol{V}_8-\Delta \boldsymbol{V}_{8, 6, 3}\right| \\ \left|\Delta \boldsymbol{V}_8-\Delta \boldsymbol{V}_{8, 7, 3}\right| \\ \left|\Delta \boldsymbol{V}_8-\Delta \boldsymbol{V}_{8, 8, 3}\right| \end{array}\right]_{15 \times 1} $ | (9) |
每个分层电路误差最小的母线最接近暂降源,对于图 1所示配电网来说,当暂降源位于区段3—4之间靠近母线3时,分层电路2中母线3误差最小,最接近暂降源,母线3将会被选为分层电路2的候选母线。而分层电路1和3不包含暂降源,则与分层电路2相连的公共母线2误差最小最接近暂降源,因此母线2将会被选为分层电路1和3的候选母线。综上,图 1所示配电网的暂降源邻近母线的候选母线为母线3和公共母线2。
对于一个辐射状网络,暂降源电流通过公共母线从暂降源所在分层电路流入其他分层电路,所以对于不包含暂降源的分层电路,其与暂降源所在分层电路相连的公共母线距离暂降源最近,该公共母线被选为候选母线,也就是说所有候选母线均在暂降源所在的分层电路中。
为进一步确定离暂降源最近的母线,即确定电压暂降源邻近母线,须找到一个包含所有候选母线的分层电路。在该分层电路中比较暂降源电流注入所有候选母线时末端母线的误差大小,误差最小值对应的候选母线即为暂降源邻近母线。
对于图 1所示配电网来说,分层电路2同时包含母线2和母线3,由式(8)可知候选母线3注入暂降源电流时末端母线的误差小于候选母线2,所以母线3是整个配电网的暂降源邻近母线。
2 基于二分搜索法的电压暂降源精确定位二分搜索法也称折半搜索法,每次搜索都可以使搜索区段的范围缩小一半,计算量小,能够快速逼近暂降源,且满足高精度要求。文中精确定位采用二分搜索法的思想,不断缩小暂降源搜索区间,直到满足定位精度要求。
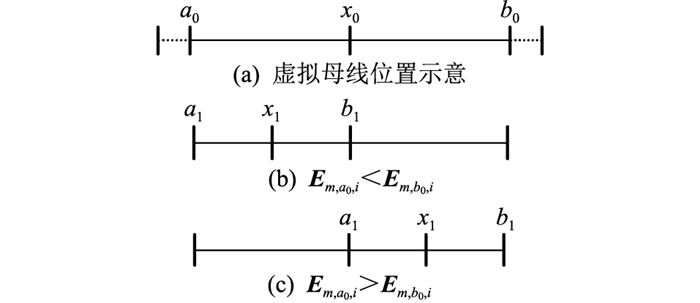
确定暂降源邻近母线后,在暂降源邻近母线的上、下游区段中点设置虚拟母线a0和母线b0。如果暂降源邻近母线只有上游区段,则虚拟母线a0和b0位于上游区段的中点和暂降源邻近母线处。同理,如果暂降源邻近母线只有下游区段,则虚拟母线a0和b0位于暂降源邻近母线和下游区段的中点处。x0为母线a0和母线b0的中点,如图 3(a)所示。
|
图 3 二分搜索法精确定位原理 Fig. 3 Binary search method of accurate positioning principle |
确定搜索区段
按照与第一轮搜索相同的步骤继续进行搜索,经过k次搜索后,满足式(10)定位精度要求即可停止搜索。
| $ \left|L_{a_k, b_k}\right| \leqslant \lambda $ | (10) |
式中:丨Lak, bk丨为母线ak与母线bk之间线路长度;λ为满足定位精度的误差长度。取ak和bk中点xk认为是电压暂降源的精确位置。
当暂降源邻近母线是公共母线时,暂降源邻近母线所在的分层电路就不止一个,若直接在多个分层电路中进行二分搜索,不仅计算量大,而且可能会得到错误的结果。因此,须设置虚拟母线寻找新的且只存在于唯一分层电路中的暂降源邻近母线,进而确定唯一包含暂降源的搜索区段,提高搜索效率。
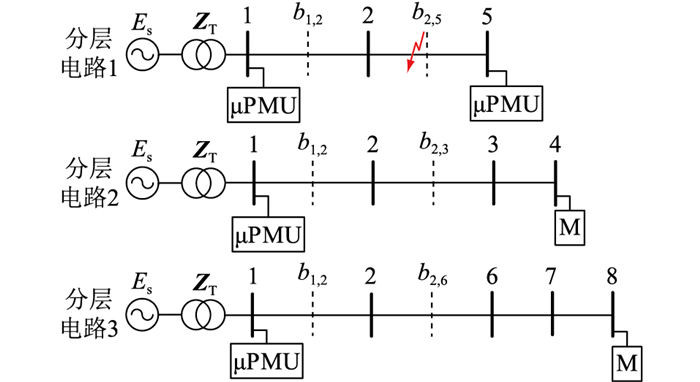
当真实的暂降源位于母线2—5之间靠近中点处,如图 4所示,求得的暂降源邻近母线是公共母线2时,暂降源邻近母线存在于3个分层电路中。此时,在母线2相邻上、下游区段中点设置虚拟母线b1, 2、b2, 5、b2, 3与b2, 6。将暂降源电流注入各虚拟母线和公共母线2,比较末端母线的误差大小,得到各分层电路新的候选母线为虚拟母线b2, 5和公共母线2,接着在分层电路1中比较暂降源电流注入母线b2, 5和母线2时末端母线的误差大小,判断得出母线b2, 5是新的暂降源邻近母线。若求得的暂降源邻近母线仍是公共母线,在公共母线和虚拟母线的中点设置新的虚拟母线,将暂降源电流注入新的虚拟母线和公共母线,比较末端母线的误差大小,寻找新的暂降源邻近母线,直到新的暂降源邻近母线不是公共母线为止。这样就确定了唯一包含暂降源邻近母线的分层电路,进而可以通过二分搜索法进行精确定位。
|
图 4 虚拟母线设置示意 Fig. 4 Schematic diagram of virtual bus setting |
由于阻抗矩阵的精确度会对文中方法的定位准确性造成影响,为了保证方法的实用性,在工程实际中需要对线路阻抗参数不准确的线路进行识别及参数校正。阻抗矩阵参数校正方法可参考文献[24],以此提高文中方法暂降源定位的准确性。
采用式(11)计算暂降源的定位精度δ。
| $ \delta=\left[1-\left(D_{\mathrm{f}}-D_{\mathrm{p}}\right)\right] \times 100 \% $ | (11) |
式中:Df为暂降源位置;Dp为定位位置。
基于μPMU和二分搜索法的电压暂降源精确定位流程如图 5所示。
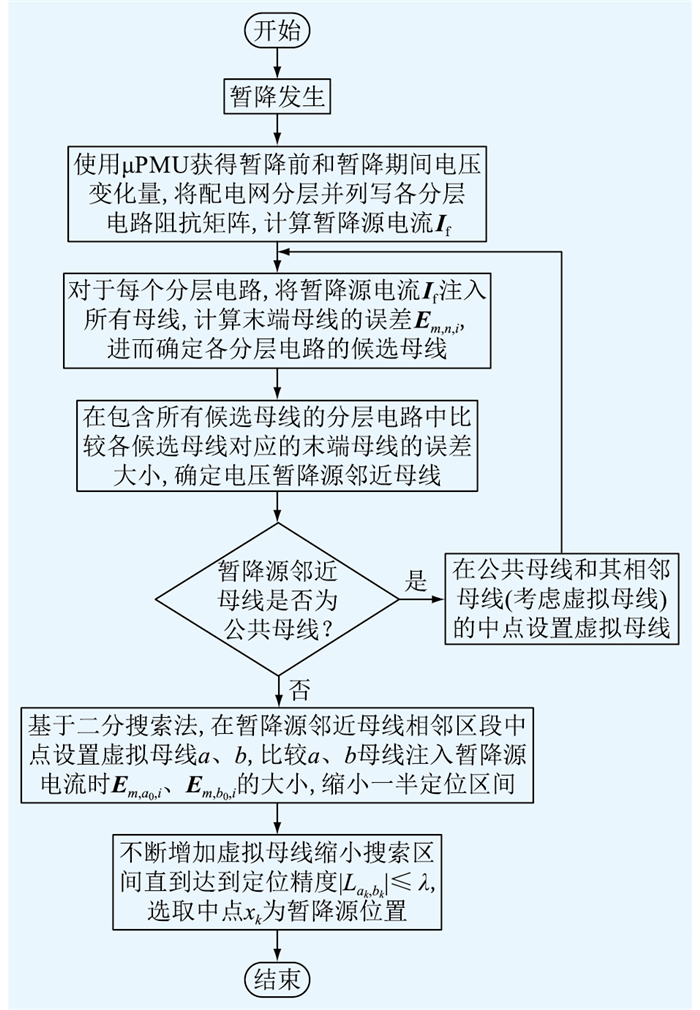
|
图 5 电压暂降源精确定位流程 Fig. 5 Precise location process of voltage sag sources |
为验证文中提出的电压暂降源定位方法,在MATLAB中搭建IEEE 33节点仿真模型。IEEE 33节点模型为辐射状网络,有33个母线节点,根节点(母线1)电压为12.66 kV,变压器容量为10 MV ·A。在母线1和母线33配置μPMU,末端母线18、22和25配置普通电压检测装置M。IEEE 33节点模型和检测装置的配置见图 6,模型参数参考文献[25]。
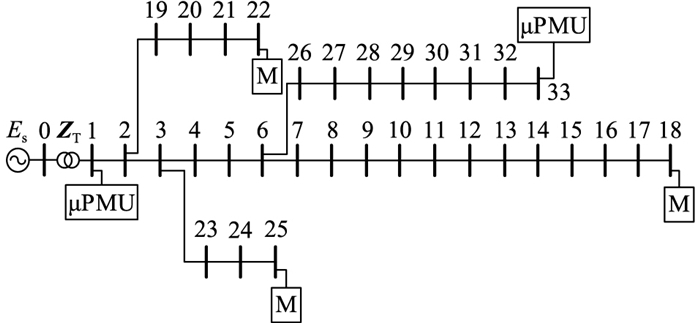
|
图 6 IEEE 33节点配电系统 Fig. 6 IEEE 33-node distribution system |
在区段7—8上距7节点20%(Df=0.2)的位置设置三相短路。按照文中方法,首先将标准模型分为4个分层电路,如图 7所示。以A相为例,分层电路2上2个μPMU测得母线1电压变化量为1 086.32-j319.61 V和母线33上的电压变化量995.68-j229.90 V,普通检测装置测得母线22、18和25上的电压变化量分别为1 233 V、6 338.5 V和2 137 V,将母线1和母线33的电压变化量和阻抗矩阵的逆相乘得暂降源电流为843.12-j639.99 A,然后依次将暂降源电流注入各母线,根据末端母线的误差大小确定每个分层电路的候选母线,进而得到暂降源邻近母线,并采用二分法进行暂降源精确定位。定位误差区间设为10-4,即精确定位搜索区段长度的0.1%。
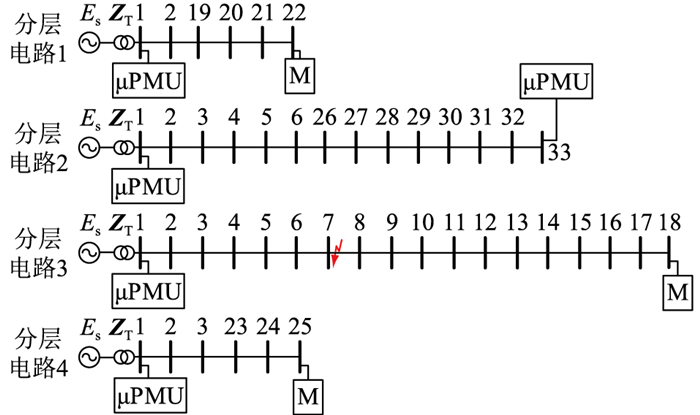
|
图 7 IEEE 33节点分层电路示意 Fig. 7 Schematic diagram of an IEEE 33-node layered circuit |
当三相短路发生时,各分层电路末端母线误差的计算结果如图 8所示,其中横坐标为各分层电路的母线,纵坐标为对应的末端母线暂降前、后电压变化量的计算值与实测值的误差大小。
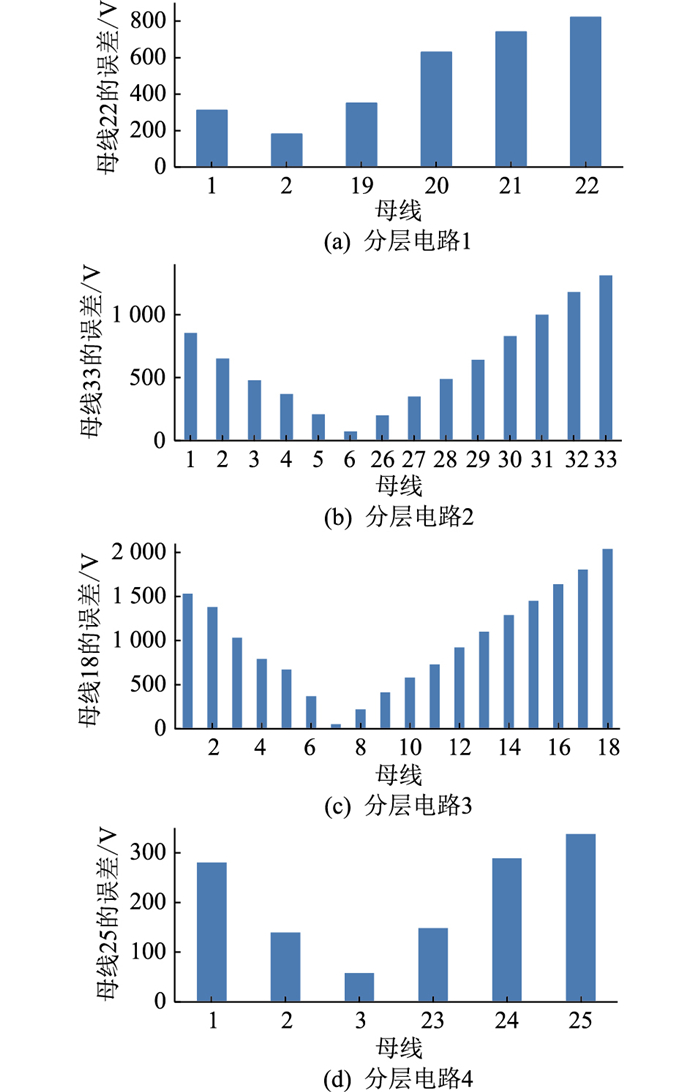
|
图 8 各分层电路末端母线误差计算结果 Fig. 8 Eerror calculation results of the terminal bus of each layered circuit |
由图 8计算误差可知,4个分层电路的候选母线分别是母线2、母线6、母线7和母线3。在分层电路3中比较4条候选母线注入暂降源电流时末端母线的误差,由图 8(c)可知母线7对应的误差最小,所以母线7是整个配电网的暂降源邻近母线。
3.1.2 暂降源精确定位在找到暂降源邻近母线7后,由于母线7不属于公共母线,接下来直接用二分搜索法进行精确定位。经过11轮搜索后,搜索区段的长度小于10-4,达到了精确定位的误差要求。取第11轮搜索区间的中点7.199 7作为暂降源位置,即暂降源位于区段7—8上,到母线7的距离为19.97%区段长度。定位位置Dp=0.199 7,定位精度为99.97%。
3.2 不同暂降源条件下的定位结果为验证该方法对不同位置、不同类型以及不同噪声环境下电压暂降源的定位效果,设置不同类型和有噪声的暂降源进行定位。
3.2.1 不同类型暂降源不同位置的定位结果对IEEE 33节点模型进行改造,在区段23—24和区段28—29处接入变压器T和感应电动机IM,控制启动和投入时间均为0.1 s。在区段1—2、15—16、17—18和20—21距区段首节点30%和70%区段长度处分别设置单相接地短路(LG)、两相接地短路(LLG)、两相相间短路(LL)和三相短路(LLL)。定位结果如表 1所示,可见文中方法对短路故障、感应电动机启动和变压器投入不同类型不同位置的电压暂降源均有较高的定位精度。
|
|
表 1 不同暂降源不同位置的定位结果 Table 1 Location results of different voltage sag sources at different locations |
在距公共母线6左右两侧30%处设置不同类型的暂降源,定位效果如表 2所示,其中b5, 6和b6, 7为区段5—6和6—7的中点处的虚拟母线。定位结果表明文中方法在暂降源邻近母线是公共母线时能够寻找出新的暂降源邻近母线,根据新的暂降源邻近母线确定暂降源所在分层电路,实现电压暂降源的精确定位。
|
|
表 2 暂降源位于公共母线附近的定位结果 Table 2 Location results of voltage sag source near the common bus |
在实际应用中,现场环境不可避免地会对μPMU产生影响。在μPMU采集相量数据时,添加不同程度的噪声,暂降源设置在区段28—29距首节点30%区段长度处,暂降源类型为两相接地短路故障和单相接地短路故障,定位结果如表 3所示。在噪声环境下,文中方法定位的精度有所下降,但在20 dB噪声环境下,定位精度仍然不低于95.18%,说明文中方法具有较好的抗干扰能力。
|
|
表 3 不同噪声环境下的定位结果 Table 3 Location results under different noise environments |
在该算法中暂降源电流是基于电压变化量计算的,暂降前和暂降期间均包含分布式电源提供的电压,与无分布式电源时相比,求解得到的电压变化量不变。因此有无分布式电源不改变暂降源电流的求解结果,且有无分布式电源不影响对配电网的分层,不影响暂降源精确定位的结果。
在母线25、33、12处安装额定功率为4.5 MV ·A光伏发电系统,发电出力分别控制在额定功率的70%、65%、50%,接地电阻设置为100 Ω,并与文献[15]中同一位置、同一暂降源类型下的定位结果进行比较,结果见表 4。文献[15]是基于PMU的检测信息进行故障分析与处理,从而达到定位目的。
|
|
表 4 定位结果比较 Table 4 Comparison of location results |
比较结果显示,在含有分布式电源的情况下,在常见的短路故障暂降源定位误差比较中,文中针对配电网的暂降源定位算法定位误差更小,且所需要的PMU数量更少。
4 结语文中提出一种基于μPMU和二分搜索法的电压暂降源精确定位方法,针对辐射状配电网的电压暂降源定位,只需要2个μPMU和少量的普通电压测量装置,获取到少数母线的电压变化量,就可以确定暂降源邻近母线,进而运用二分搜索法进行暂降源的精确定位。该方法不仅可以进行故障引起的暂降源定位,对变压器投切和感应电机启动暂降源的定位同样适用。在IEEE 33节点模型中的验证结果表明,文中所提方法可以对线路不同位置、不同类型的电压暂降源实现准确定位,定位精度高,并且具有较强的抗干扰能力。
| [1] |
阚力丰, 李华强, 李春海. 基于供需协调的电压暂降综合治理策略[J]. 电力系统及其自动化学报, 2018, 30(6): 90-95. KAN Lifeng, LI Huaqiang, LI Chunhai. Comprehensive management strategy for voltage sags based on coordination of supply and demand[J]. Proceedings of the CSU-EPSA, 2018, 30(6): 90-95. (  0) 0) |
| [2] |
颜景斌, 夏赛, 王飞, 等. 基于改进遗传算法的有源配电网故障定位分析[J]. 电力系统及其自动化学报, 2019, 31(6): 107-112. YAN Jingbin, XIA Sai, WANG Fei, et al. Analysis of fault location for active distribution network based on improved genetic algorithm[J]. Proceedings of the CSU-EPSA, 2019, 31(6): 107-112. DOI:10.3969/j.issn.1003-8930.2019.06.017 (  0) 0) |
| [3] |
辛峰, 尤向阳, 葛笑寒, 等. 基于空间相量模型的三相电压暂降扰动特征提取与分类[J]. 电力系统保护与控制, 2022, 50(8): 59-64. XIN Feng, YOU Xiangyang, GE Xiaohan, et al. Feature extraction and classification of three-phase voltage dips based on a space phasor model[J]. Power System Protection and Control, 2022, 50(8): 59-64. (  0) 0) |
| [4] |
鲁涛, 吕干云, 贾德香, 等. 基于直流扰动功率的直流配电网电压暂降源定位[J]. 电工电气, 2020(6): 1-4, 46. LU Tao, LYU Ganyun, JIA Dexiang, et al. Voltage sag source location of DC distribution network based on DC disturbance power[J]. Electrotechnics Electric, 2020(6): 1-4, 46. DOI:10.3969/j.issn.1007-3175.2020.06.001 (  0) 0) |
| [5] |
胡安平, 陶以彬, 庄俊, 等. 基于扰动无功功率的电压暂降源定位[J]. 科学技术与工程, 2020, 20(30): 12415-12422. HU Anping, TAO Yibin, ZHUANG Jun, et al. Voltage sag location based on disturbance reactive power[J]. Science Technology and Engineering, 2020, 20(30): 12415-12422. DOI:10.3969/j.issn.1671-1815.2020.30.023 (  0) 0) |
| [6] |
MOHAMMADI Y, LEBORGNE R C. Improved DR and CBM me thods for finding relative location of voltage sag source at the PCC of distributed energy resources[J]. International Journal of Electrical Power & Energy Systems, 2020, 117: 105664. (  0) 0) |
| [7] |
FILHO J L, DA SILVA BORGES F A, DE ANDRADE LIRA RABELO R, et al. Methods for voltage sag source location by cluster aqlgorithm and decision rule labeling with a comparative approach of K-means and DBSCAN clustering algorithms[C]//2020 5th International Conference on Smart and Sustainable Technologies (SpliTech). Split, Croatia. IEEE, 2020: 1-8.
(  0) 0) |
| [8] |
LI C, TAYJASANANT T, XU W, et al. Method for voltage-sag-source detection by investigating slope of the system trajectory[J]. IEE Proceedings-Generation, Transmission and Distribution, 2003, 150(3): 367. DOI:10.1049/ip-gtd:20030214 (  0) 0) |
| [9] |
陈汝斯, 林涛, 毕如玉, 等. 基于有限量测数据的主动配电网电压暂降源精确定位策略[J]. 电工技术学报, 2019, 34(S1): 312-320. CHEN Rusi, LIN Tao, BI Ruyu, et al. Strategy to precisely locate voltage sag source in active distribution grid with data measured by limited power quality observations[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 312-320. DOI:10.19595/j.cnki.1000-6753.tces.180695 (  0) 0) |
| [10] |
赵乔, 王增平, 董文娜, 等. 基于免疫二进制粒子群优化算法的配电网故障定位方法研究[J]. 电力系统保护与控制, 2020, 48(20): 83-89. ZHAO Qiao, WANG Zengping, DONG Wenna, et al. Research on fault location in a distribution network based on an immune binary particle swarm algorithm[J]. Power System Protection and Control, 2020, 48(20): 83-89. (  0) 0) |
| [11] |
朱占春, 潘宗俊, 唐金锐, 等. 基于单端暂态能量谱相似性的配电网故障区段定位新方法[J]. 电力科学与技术学报, 2021, 36(2): 180-191. ZHU Zhanchun, PAN Zongjun, TANG Jinrui, et al. A novel fault location method for power distribution systems using energy spectrum similarity analysis of single-terminal transient waveform[J]. Journal of Electric Power Science and Technology, 2021, 36(2): 180-191. (  0) 0) |
| [12] |
USMAN M U, FARUQUE M O. Validation of a PMU-based fault location identification method for smart distribution network with photovoltaics using real-time data[J]. IET Generation, Transmission & Distribution, 2018, 12(21): 5824-5833. (  0) 0) |
| [13] |
ZHANG Y, WANG J H, LIU J Z. Attack identification and correction for PMU GPS spoofing in unbalanced distribution systems[J]. IEEE Transactions on Smart Grid, 2020, 11(1): 762-773. DOI:10.1109/TSG.2019.2937554 (  0) 0) |
| [14] |
刘海泳, 代佰华, 朱洪防, 等. 考虑敏感区域的电压暂降监测装置优化配置[J]. 电力工程技术, 2022, 41(2): 90-96. LIU Haiyong, DAI Baihua, ZHU Hongfang, et al. Optimal configuration of voltage sag monitors considering sensitive areas[J]. Electric Power Engineering Technology, 2022, 41(2): 90-96. (  0) 0) |
| [15] |
陶维青, 肖松庆, 秦明辉, 等. 含有限PMU的主动配电网故障定位[J]. 太阳能学报, 2022, 43(4): 112-120. TAO Weiqing, XIAO Songqing, QIN Minghui, et al. Fault location of active distribution network with limited PMU[J]. Acta Energiae Solaris Sinica, 2022, 43(4): 112-120. (  0) 0) |
| [16] |
于力, 焦在滨, 王晓鹏, 等. 基于PMU的中压配电网精确故障定位方法及关键技术[J]. 电力系统自动化, 2020, 44(18): 30-38. YU Li, JIAO Zaibin, WANG Xiaopeng, et al. Accurate fault location scheme and key technology of medium-voltage distribution network with synchrophasor measurement units[J]. Automation of Electric Power Systems, 2020, 44(18): 30-38. (  0) 0) |
| [17] |
杨睿, 高红均, 刘俊勇. 基于有限PMU配置的配电网故障定位[J]. 电力自动化设备, 2022, 42(4): 138-145. YANG Rui, GAO Hongjun, LIU Junyong. Distribution network fault location based on limited PMU configuration[J]. Electric Power Automation Equipment, 2022, 42(4): 138-145. (  0) 0) |
| [18] |
葛磊蛟, 刘航旭, 顾志成, 等. 基于PMU边缘终端的智能配电网台区相间短路故障定位方法[J]. 湖北电力, 2021, 45(4): 8-15. GE Leijiao, LIU Hangxu, GU Zhicheng, et al. Location method of inter-phase short circuit fault in station area of smart distribution network based on PMU edge terminal[J]. Hubei Electric Power, 2021, 45(4): 8-15. (  0) 0) |
| [19] |
张健磊, 高湛军, 王志远, 等. 基于有限μPMU的主动配电网故障定位方法[J]. 电网技术, 2020, 44(7): 2722-2731. ZHANG Jianlei, GAO Zhanjun, WANG Zhiyuan, et al. Fault location method for active distribution based on finite μPMU[J]. Power System Technology, 2020, 44(7): 2722-2731. (  0) 0) |
| [20] |
BUZO R F, BARRADAS H M, LEÃO F B. A new method for fault location in distribution networks based on voltage sag measurements[J]. IEEE Transactions on Power Delivery, 2021, 36(2): 651-662. (  0) 0) |
| [21] |
汪颖, 陈春林, 肖先勇. 电压暂降源异质堆叠集成学习识别法[J]. 电力系统保护与控制, 2021, 49(15): 1-8. WANG Ying, CHEN Chunlin, XIAO Xianyong. Heterogeneous stacking integrated learning identification method for voltage sag sources[J]. Power System Protection and Control, 2021, 49(15): 1-8. (  0) 0) |
| [22] |
沙浩源, 郑建勇, 梅飞, 等. 基于轨迹特征关键点匹配的电压暂降同源数据精确检测算法[J]. 电力系统自动化, 2022, 46(6): 109-116. SHA Haoyuan, ZHENG Jianyong, MEI Fei, et al. Accurate detection algorithm for homologous voltage sag data based on matching of feature key points for trajectories[J]. Automation of Electric Power Systems, 2022, 46(6): 109-116. (  0) 0) |
| [23] |
贾科, 董雄鹰, 李论, 等. 基于稀疏电压幅值量测的配电网故障测距[J]. 电网技术, 2020, 44(3): 835-845. JIA Ke, DONG Xiongying, LI Lun, et al. Fault location for distribution network based on transient sparse voltage amplitude measurement[J]. Power System Technology, 2020, 44(3): 835-845. (  0) 0) |
| [24] |
宋哲. 基于微型PMU的配电网故障定位方法研究[D]. 济南: 山东大学, 2019. SONG Zhe. Research on fault location method of distribution network based on μPMU[D]. Jinan: Shandong University, 2019. (  0) 0) |
| [25] |
MAJIDI M, ARABALI A, ETEZADI-AMOLI M. Fault location in distribution networks by compressive sensing[J]. IEEE Transactions on Power Delivery, 2015, 30(4): 1761-1769. (  0) 0) |
 2023, Vol. 42
2023, Vol. 42


 马莉(1974),女,博士,副教授,研究方向为电能质量、供电安全和配电自动化(E-mail:
马莉(1974),女,博士,副教授,研究方向为电能质量、供电安全和配电自动化(E-mail: