文章编号: 2096-3203(2023)04-0002-11 中图分类号: TM912
锂离子电池具有高能量密度、高功率密度和长循环寿命的特性,已经被广泛应用在纯电动汽车中[1-3]。为了充分发挥电池的性能,需要采用电池管理系统(battery management system, BMS)对电池进行精细管理[4-7]。其中,准确估计电池剩余放电电量(remaining discharge capacity, RDC)有利于提高用户对电动汽车的续航信心,降低驾驶者的“里程焦虑”[8-9]。
为了提高电池RDC的估计精度,精确的电池模型非常重要[10]。典型的电化学机理模型是Doyle提出的伪二维(pseudo two dimension, P2D)模型。P2D模型用偏微分方程描述内部的机理反应,模型精度高,但计算成本较高,不适合直接用于BMS在线计算[11]。等效电路模型(equivalent circuit model, ECM)用电路元件来模拟电池电压的极化和驰豫行为[12-14],计算量较小,但缺乏内部机理反应的信息,模型精度较低,尤其是在低荷电状态(state of charge,SOC)区域电压仿真误差急剧增加[15-16]。为了提高低SOC区域的模型精度,考虑锂离子固相扩散过程,根据表面SOC和平均SOC之间的差异,可以开发出电化学机理的扩展等效电路模型(extended equivalent circuit model,EECM)[17]。但是,现有的ECM和EECM不能匹配不同电流倍率下的电池容量差异导致的开路电压的变化,因此不能反映不同电流下低SOC区域电压快速下降的差异特性。准确模拟不同电流倍率下的电池端电压模型对于RDC的估计十分重要[18-19]。文献[20]建立了电池电压与容量之间的模型,估算可变电流下铅酸电池的可用容量。文献[21]对不同放电电流下的截止SOC进行标定,提出经验模型,基于安时积分法来确定不同电流倍率下的电池剩余放电时间。但目前研究均未考虑针对不同电流倍率下的电池内部机理进行建模,须进行大量的校准工作[22-23]。
为了提高不同电流倍率下的模型精度,须改进EECM。文中在考虑平均SOC和表面SOC差异的基础上,利用容量增量(incremental capacity,IC)曲线获取电池内部反应信息,通过能斯特方程构造附加反应的容量-开路电压曲线,进一步修正开路电压,从而提高电压仿真精度。BMS会基于模型端电压的预测值来判定电池是否达到放电电压截止下限。改进的EECM通过降低端电压的仿真误差来提高截止条件判断的准确性,从而进一步提升RDC预测的精确度。
1 电池实验文中研究对象为商用棱柱形锂离子电池,正极材料为LiNixCoyMn1-x-yO2, 负极材料为石墨。参考容量为37 A·h,该容量作为放电倍率(current rate, C-rate)的基准容量值。
首先,对该款电池进行了不同倍率的恒流放电实验。电池以1/3 C恒流充电至上截止电压4.2 V,然后恒压充电,直到充电电流降至1/20 C。之后电池以不同的倍率放电至下截止电压2.8 V,使电池完全放电。实际的纯电动汽车持续放电电流通常小于1 C,因此实验中所选择的放电倍率包括1/20 C、1/10 C、1/5 C、1/3 C、2/5 C、1/2 C和1 C。
其次,通过复合脉冲特性(hybrid pulse power characteristic,HPPC)测试获取电池的开路电压和内阻特性。HPPC测试中将电池调整到目标SOC值,然后施加电流脉冲获取电池的极化及驰豫电压,用于电池模型参数的辨识。同时在不同的SOC下进行电化学阻抗谱(electrochemical impedance spectroscopy,EIS)测试,以全面获取电池的内阻特性。此外,为了得到电池内部正极和负极的电压曲线,拆解该电池,并将该电池的正极和负极制作成以锂金属为参考电极的纽扣电池。以1/15 C的电流对纽扣电池进行充放电,测量其电压曲线。
所有电池实验均在25 ℃的恒温箱内进行,充放电测试通过DIGATRON制造的UBT 100-020-8型电池测试台架完成,该测试台架的电流测试范围为-100 A~100 A,电压范围为0 V~20 V,电压的测量精度为1 mV。
据电池厂家的说明书,电池的标准容量QST,即常温下的1 C放电容量,约为39.21 A ·h。文中,电池的标准容量用于定义电池的SOC和计算不同放电倍率下的相对容量。如图 1所示,电池放电的容量随放电倍率的变化而变化,对于1 C以下的电流倍率,电池放电容量随放电倍率的增大而减小,在1/20 C的电流下,电池容量为42.22 A ·h,是标准容量的108%。
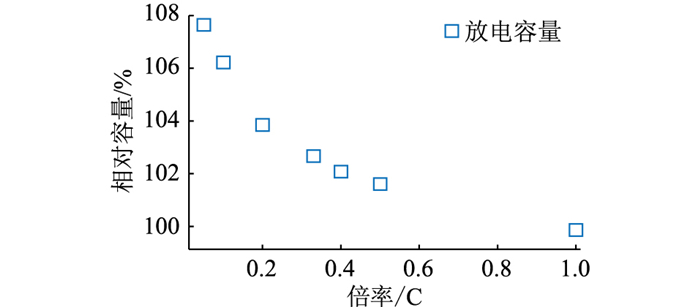
|
图 1 不同倍率下电池放电容量 Fig. 1 Battery discharge capacity at different rates |
测试得到电池不同倍率下的放电曲线,如图 2所示。放电曲线可以划分为3个区间:第一个区间为放电容量0 A ·h~15 A ·h,电压平稳下降;第二个区间为放电容量20 A ·h~40 A ·h,存在一个电压平台;第三个区间为放电末期,存在一个电压快速下降区域。如图 2(b)所示,在低倍率下,电池电压在快速下降前,存在一个小的电压平台,且随着放电倍率增加,此电压平台逐渐消失,1 C放电工况下,不存在此电压平台。为了准确模拟电池的放电电压并估计电池当前状态,必须开发准确的电池模型。
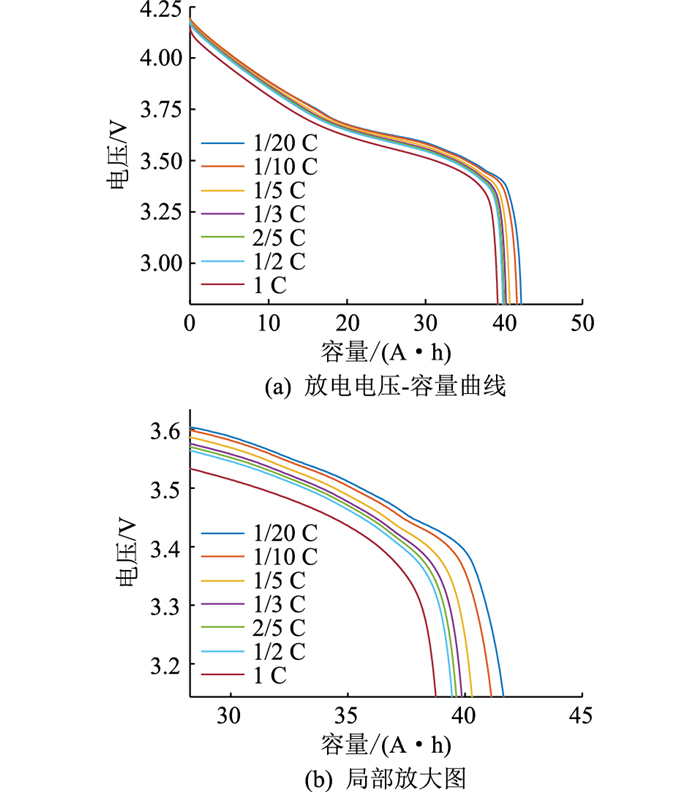
|
图 2 不同倍率放电电压-容量曲线对比 Fig. 2 Comparison of discharge voltage-capacity curves at different rates |
常见的ECM包括Rint模型、一阶RC模型等,如图 3所示。其中Rint模型由恒压源E和欧姆阻抗R组成,恒压源E代表了电池的开路电压,是电池SOC的函数。而一阶RC模型则包括由恒压源E、欧姆内阻R0、极化内阻R1和电容C1并联组成的RC电路。Rint模型较简单,易于计算;一阶RC模型较复杂,可以比较精确地仿真电池的瞬态特性。
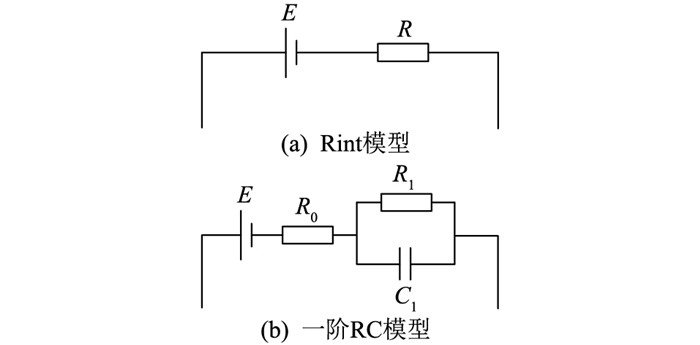
|
图 3 ECM示意 Fig. 3 Schematic diagram of ECMs |
电池模型参数可以利用HPPC测试得到的电流和电压脉冲数据,通过粒子群优化(particle swarm optimization, PSO)算法使模型电压仿真值与实验值的均方根误差(root mean square error, RMSE)最小来获取。辨识得到的一阶RC模型参数包括欧姆内阻R0、极化内阻R1以及RC环节时间常数τ1,参数辨识结果详见图 4。
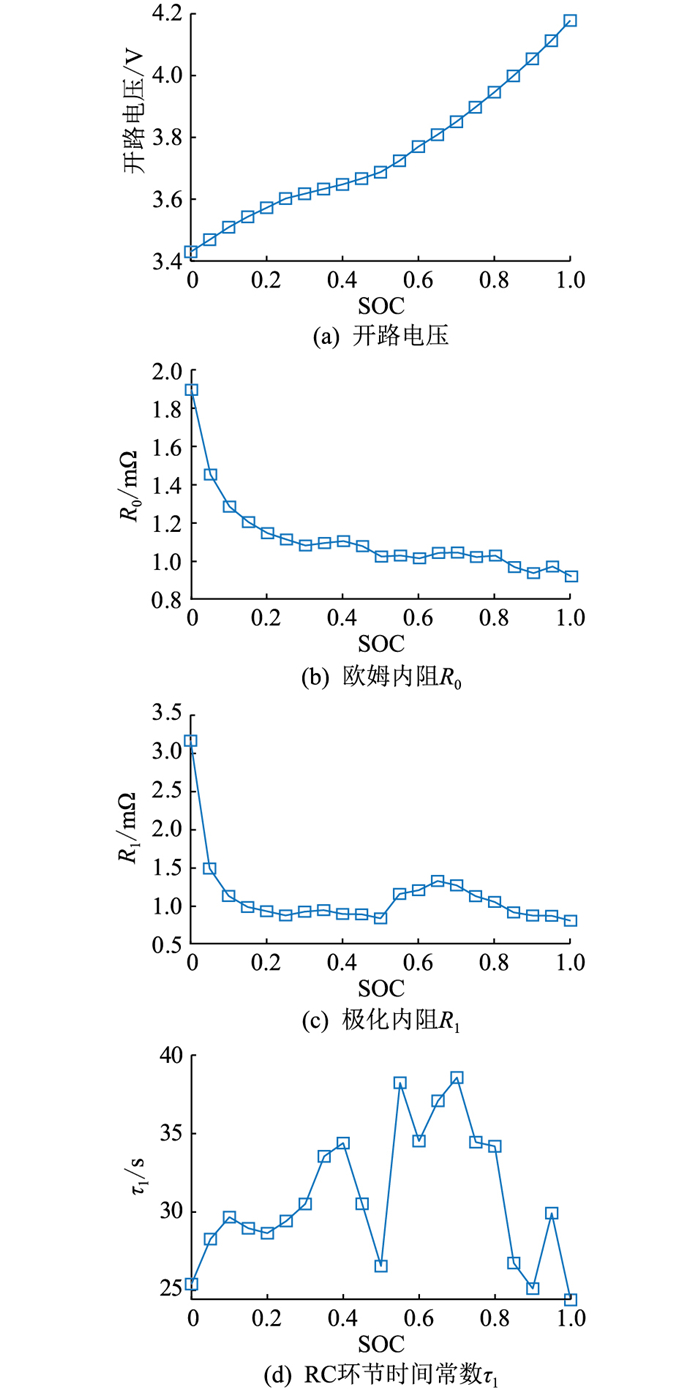
|
图 4 ECM参数辨识结果 Fig. 4 Identification results of ECM parameters |
各参数均为电池SOC的函数,因此,对于电池SOC的定义尤为重要。电池的SOC值z定义为电池特定温度与特定倍率下的可用放电电量QRDC与总放电电量QST的比值,如式(1)所示。对于文中所测试的电池,倍率为1 C,温度为室温,即25 ℃。
| $ z=Q_{\mathrm{RDC}} / Q_{\mathrm{ST}} $ | (1) |
在该定义下,电池的SOC不随工作条件的变化而变化,不同的温度、不同的放电倍率不会影响SOC的值。电池的SOC被考虑为电池的一个内部状态,与电池内部的锂离子浓度分布情况直接相关。在该定义下,电池的SOC可能为负值,例如电池以很小的倍率持续放电,会放出比1 C放电更多的电量,这种情况下,在放电末期电池的SOC就会为负值。
对于Rint模型,开路电压取值与图 4(a)相同,在恒流充放电工况下,内阻R的计算为:
| $ R=R_0+R_1 $ | (2) |
Rint模型和一阶RC模型对1 C放电的端电压仿真结果对比如图 5所示。Rint模型与一阶RC模型的仿真结果几乎完全相同。在放电初始阶段,一阶RC模型可以较为精确地仿真电池的瞬态过程。随着电池放电时间增加,一阶RC模型中的RC环节迅速饱和,模型输出结果与Rint模型输出结果趋于相同。文中对电池模型的分析面向放电的全过程,因此采用相对简单的Rint模型进行分析与比较。式(3)为Rint模型的端电压计算公式。
| $ U_k=E\left(z_k\right)+I\left(R_0\left(z_k\right)+R_1\left(z_k\right)\right) $ | (3) |
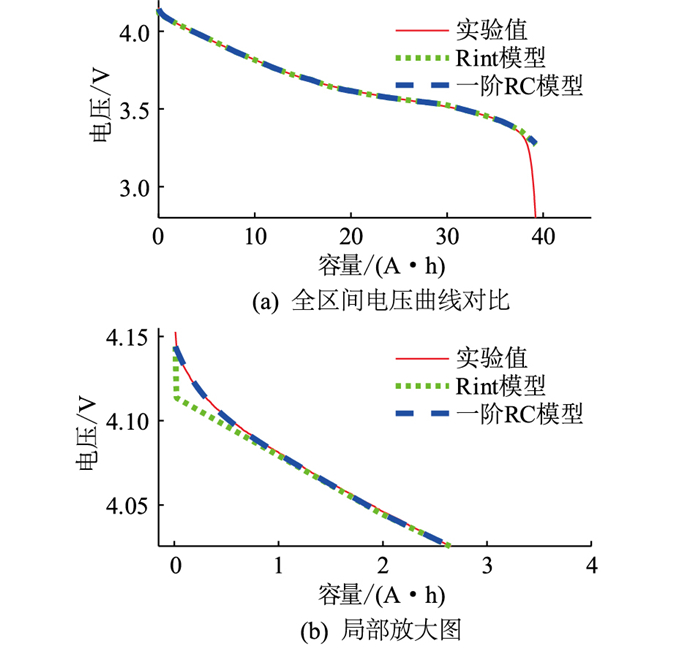
|
图 5 1 C放电下不同ECM仿真结果对比 Fig. 5 Comparison of simulation results of different ECMs for 1 C discharge |
式中:Uk为电池k时刻的端电压;I为流经电池的电流;E(zk)为根据电池k时刻SOC值确定的开路电压;zk为电池k时刻的SOC值。
图 6对比了不同放电倍率下Rint模型端电压仿真结果,图 7为仿真误差。分析可知,在中高SOC区域,ECM具有较高的仿真精度,存在±10 mV误差。但在放电末端,真实测量到的电压快速下降,而模型仿真不能体现这种变化,电压仿真误差快速增加。实际上,基于ECM的特性,在不同倍率下电池可以放出的电量相同,无法有效获得不同倍率下的电池可用电量,所以,须进一步优化和改进ECM。
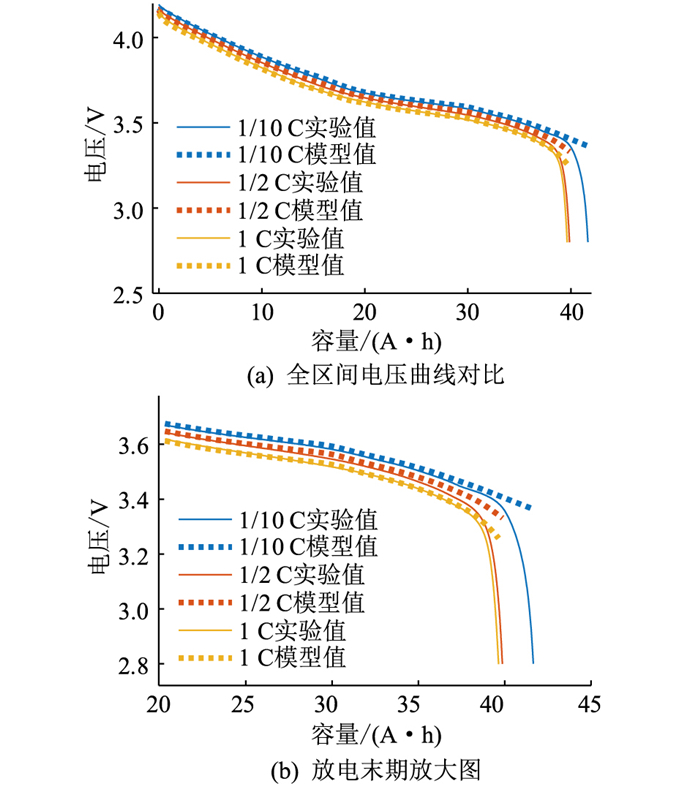
|
图 6 ECM在不同倍率下的仿真结果 Fig. 6 Simulation results of ECM at different rates |
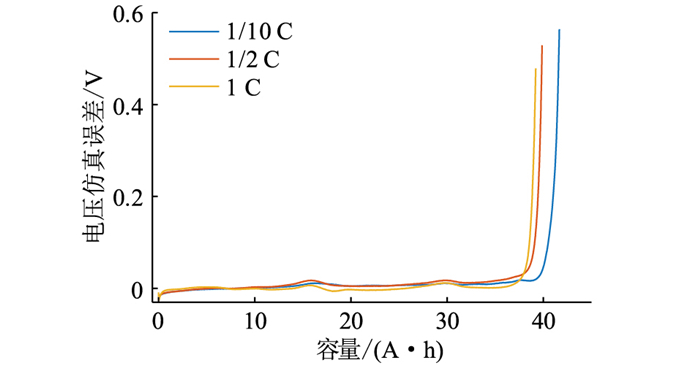
|
图 7 ECM在不同倍率下的端电压仿真误差 Fig. 7 The terminal voltage simulation error of ECM at different rates |
为了提高ECM精度,须深入电池内部机理,基于电池内部机理改进电池模型,提高电池模型精度。根据P2D机理模型,在电池充电和放电过程中,电池内部正负极颗粒表面发生锂离子的嵌入和脱嵌反应,如图 8所示。图中c+、c-分别为正极、负极锂离子的浓度;r为正负极活性材料颗粒的半径。
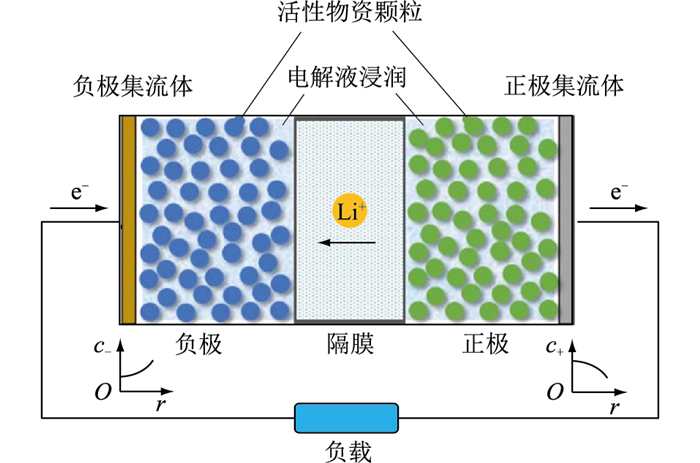
|
图 8 锂离子电池内部工作示意 Fig. 8 Schematic diagram of the internal structure of lithium-ion batteries |
在固相颗粒中存在锂离子的扩散过程,遵循菲克定律。菲克第一定律如式(4)所示,该定律描述了在浓差驱动下的锂离子固相扩散通量正比于扩散系数和浓度对位置的导数。菲克第二定律如式(5)所示,描述了锂离子浓度对时间的导数与浓度对半径的二阶导数成正比。锂离子的扩散会导致颗粒的表面锂离子浓度与颗粒的平均锂离子浓度存在差异。基于电池的P2D机理模型,电池的SOC值z代表颗粒中的平均锂离子浓度,然而电池的开路电压由电池的表面锂离子浓度决定。基于此机理,提出EECM[17],EECM中电池开路电压由电池的表面SOC决定,表面SOC与平均SOC的差异用一阶惯性环节进行描述,如式(6)所示。
| $ J=-D_{\mathrm{s}} \frac{\partial c}{\partial L} $ | (4) |
| $ \frac{\partial c}{\partial t}=\frac{1}{r^2} \times \frac{\partial}{\partial r}\left(D_{\mathrm{s}} r^2 \frac{\partial c}{\partial r}\right) $ | (5) |
| $ z_{k, \text { surf }}-z_k=\lambda I\left(1-\mathrm{e}^{-t / \tau}\right) $ | (6) |
式中:J为扩散通量;Ds为扩散系数;c为锂离子的浓度;L为锂离子处于电池体系内的位置;zk, surf为k时刻活性颗粒表面SOC值;λ为比例系数;I为电流;t为锂离子扩散时间;τ为表面到颗粒内部的锂离子浓度扩散的时间常数。利用PSO算法根据端电压RMSE最小的优化目标对模型参数进行辨识,辨识结果为λ=0.001 1,τ=2 000。
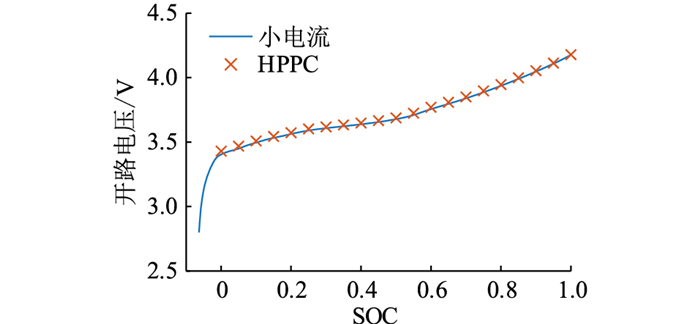
EECM中,电池的开路电压非常重要,电池的表面SOC可能到达负值,因此传统HPPC测试得到的结果不能用在EECM中。考虑电池小倍率充放电工况,如1/20 C放电工况下,放电电流非常小,内阻导致的压降也较小,其电压曲线与开路电压曲线非常接近,因此,采用1/20 C放电曲线作为电池的近似开路电压曲线。通过1/20 C小电流放电得到的开路电压与HPPC测试得到的开路电压对比如图 9所示,2种方法获得的开路电压曲线基本完全相同。采用HPPC测试得到的开路电压仅为20个离散的采样点,且SOC均大于0;而采用1/20 C恒流放电得到的开路电压曲线可以体现SOC小于0时的开路电压值,且获得的开路电压曲线为连续的曲线,可以更好地仿真电池的特性。
|
图 9 开路电压对比 Fig. 9 Comparison of open circuit voltages |
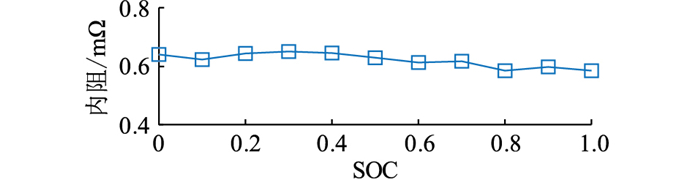
电池的内阻特性也非常重要,在传统ECM中,电池的内阻是关于电池SOC的函数,通过大量的实验标定不同SOC下的内阻数值,建立内阻的插值表格。电池的内阻通常认为是关于电池的温度、SOC的复杂函数,这从本质上无法直接与电池的机理相联系。从EECM的角度出发,电池内部由于固相扩散导致的极化过电势,可以通过引入表面SOC以考察颗粒的固相扩散过程的影响。而电池其他部分的内阻,主要包括由于液相的电导率、集流体的电导率、液相的扩散、电荷转移阻抗等导致的电池内阻,在不同SOC下近似不变。电池的EIS测试也可以验证,通过交流阻抗测试得到的不同SOC下的电池高频欧姆阻抗基本不变,在建模时可以将欧姆内阻考虑为一个常数,EIS测试得到内阻值如图 10所示。
|
图 10 EIS测试的欧姆内阻 Fig. 10 Ohmic resistance tested by EIS |
EECM模型的端电压计算公式如下:
| $ U_k=E\left(z_{k, \text { surf }}\right)+I R_{\mathrm{e}} $ | (7) |
式中:E(zk, surf)为根据表面SOC值确定的开路电压;Re为电池内阻值,是与SOC无关的常数值。
为了补偿使用小电流开路电压-SOC曲线所带来的潜在误差,修正式(7)可得:
| $ U_k=E\left(z_{k, \text { surf }}\right)+\left(I-I_{1 / 20 \mathrm{C}}\right) R_{\mathrm{e}} $ | (8) |
式中:I1/20C为以1/20 C放电的电流值。
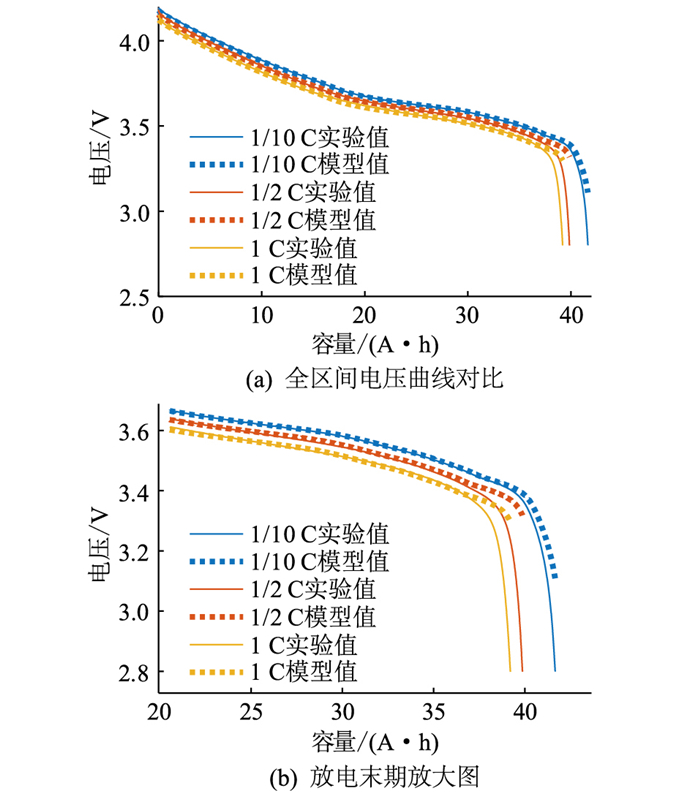
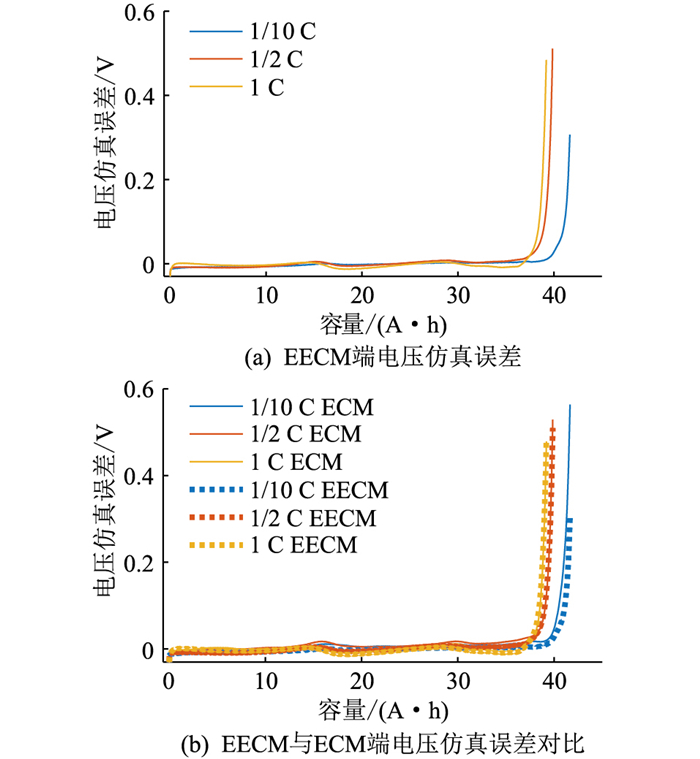
图 11为EECM在不同电流倍率下端电压仿真结果与实验结果对比,图 12为EECM端电压仿真误差以及EECM与ECM端电压仿真误差对比。2.2节所使用的EECM相比于原始的ECM更加简单,并未通过大量的实验标定不同SOC下的阻抗,电池的内阻仅仅考虑为常数项。而EECM的仿真结果仍能较好地描述电池的电压特性,与实验结果非常接近,大部分时间内仿真模型结果误差在±10 mV左右。对于1/10 C放电工况,一定程度上仍然能够体现出电池在放电末期的电压迅速降低过程。但对于较大的放电电流工况,EECM不能很好地描述电池在放电末期的电压快速降低的特性。
|
图 11 EECM在不同倍率下的仿真结果 Fig. 11 Simulation results of EECM at different rates |
|
图 12 EECM在不同倍率下的端电压仿真误差 Fig. 12 The terminal voltage simulation error of EECM at different rates |
为了更好地仿真电池在不同倍率下的电压变化,须改进EECM。实际上,根据EECM,由式(6)可知电池平均SOC和表面SOC之差与放电电流成正比,则电池的总可用容量也应该与放电电流成正比。然而根据图 2所示,放电容量显然与放电电流倍率不成正比,因此,EECM无法准确描述大电流倍率下的电池性能。为进一步改进EECM,须分析电池电压曲线内蕴含的机理特性。
IC分析法是一种被广泛应用的电池静态电压曲线分析方法[24-28]。从IC曲线,即电池容量对电压的导数曲线,可以得到电池更多的内在信息,可用于发现锂离子电池在运行过程中的内部反应机理和老化机理。IC曲线中的峰代表原始放电电压曲线中的平台区,与相变过程直接相关。
图 13(a)为电池在不同倍率下计算得到的IC曲线,IC曲线利用Savitzky-Golay滤波器进行平滑。由于流过电池的电流不同,内阻导致的压降也不同,因此不同放电倍率下IC曲线的峰的位置也不同。为了实现IC曲线归一化的对比,使用电流值与内阻的乘积进行峰值修正,修正内阻为1.6 mΩ,平移修正后的IC曲线如图 13(b)所示。随着流过电池的电流增加,IC曲线逐渐变得平滑,同时在电压区间3.5 V~4.2 V内,不同倍率下的IC曲线形状相似。该结果表明,在3.5 V~4.2 V内,不同倍率放电电压曲线均遵循EECM所描述的电池机理。该结论可以通过图 14所示的不同倍率下以3.5 V为截止电压的电池容量与倍率的关系进行验证。将电池的放电截止电压设置为3.5 V,电池的放电容量与放电倍率基本符合线性关系,该特点与EECM的出发点是相互契合的。然而,在3.43 V左右,IC曲线上存在一个峰,且峰值随着电流的增加单调减小,该峰与图 2所示的在电压快速下降区域之前的小电压平台相关联。
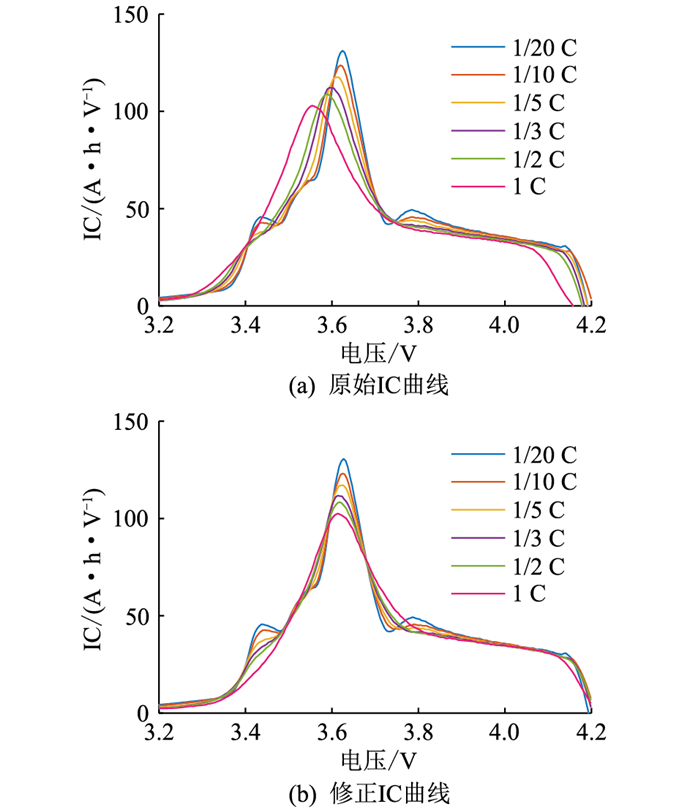
|
图 13 不同倍率的IC曲线对比 Fig. 13 Comparison of IC curves at different rates |
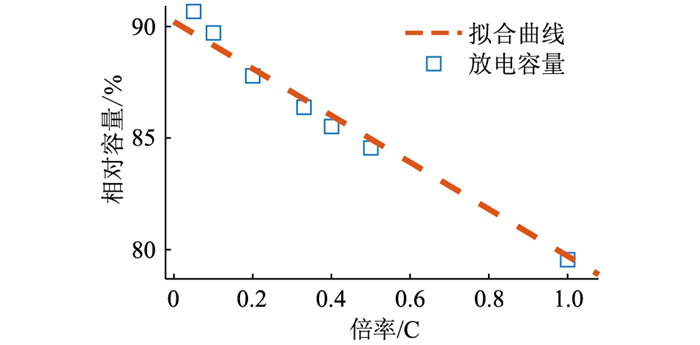
|
图 14 不同倍率下以3.5 V为放电截止电压的电池相对容量 Fig. 14 The relative capacity of the battery under the condition of 3.5 V discharge cutoff voltage at different rates |
IC曲线分析的结果表明,在电池内部,小倍率放电情况下存在一个电化学反应,且随着倍率增加,该反应会逐渐消失。对该电池进行拆解,将其正负极极片取出,并与锂片制作成为纽扣电池,进行小倍率充放电实验,从而分别测量得到正负极材料的电压特性曲线。
测试得到的电池正极与负极电压特性曲线如图 15所示。电池的正极电压特性曲线非常平滑,没有任何额外的电压平台;而电池的负极电压特性曲线在0.2 V存在一个明显的小电压平台。负极的电压平台对应于图 1中全电池小倍率下在电压迅速下降前的电压平台,以及图 13中IC曲线上3.43 V左右出现的峰。
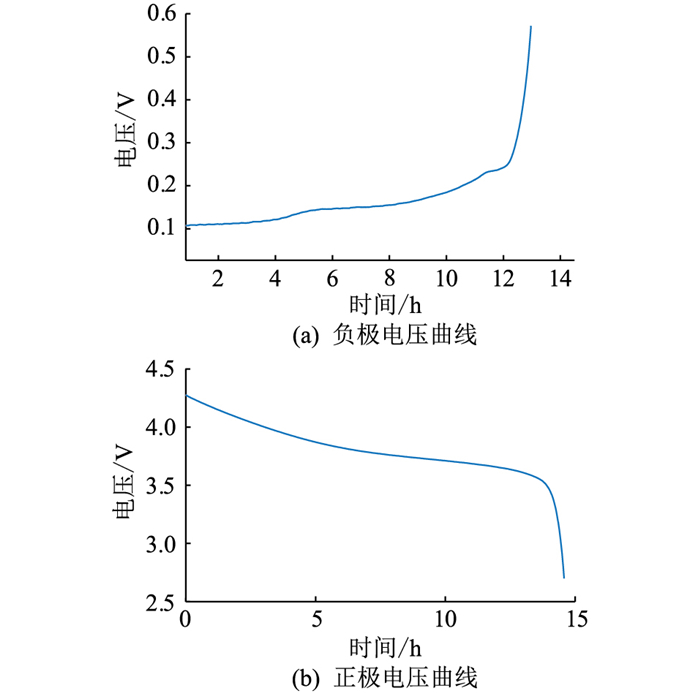
|
图 15 电池正负极电压曲线 Fig. 15 Battery positive and negative voltage curves |
然而,在EECM中考虑正极和负极的电势,会导致电池模型非常复杂,计算量较大。因此,将电池的这一电压平台考虑为与放电倍率相关的附加反应。对于一个典型的锂嵌入/嵌出反应,化学势遵循能斯特方程,如式(9)所示。
| $ E=E_0+\frac{R_{\mathrm{q}} T}{n F} \ln \left(\frac{X-x}{x}\right) $ | (9) |
式中:E0为对应于该反应的参考电势;Rq为摩尔气体常数;T为温度;n为参与该附加反应实际转移的电子数目;F为法拉第常数;X为参与该反应需要消耗的总电量;x为参与该反应已消耗的电量。
令
| $ x=X /\left(1+\exp \left(\frac{E-E_0}{k}\right)\right) $ | (10) |
式中:k为能斯特斜率。
假设电池进行正常的充放电反应消耗的电量为q1,进行该附加反应时,电池消耗的电量为q2,电量与开路电压E之间存在的函数关系为f,则:
| $ q_1=f_1(E) $ | (11) |
| $ q_2=f_2(E) $ | (12) |
由于1 C放电的IC曲线中并没有该附加反应的峰值,以1 C的放电电流为基准,可以得到电量-开路电压的q1-E曲线。而小于1 C倍率的放电IC曲线中存在该附加反应的峰值,消耗电量为q2。f2符合能斯特方程,根据式(10)可以得到q2-E曲线,其中X为1.9,E0为3.43,k为0.018,则总容量-开路电压关系为:
| $ q=q_1+g(I) q_2=f(E) $ | (13) |
式中:g(I)为电流倍率的函数,电流倍率越大该值就越小,表明该附加反应所消耗的电量就越小。
根据式(13),求其反函数就可得到考虑附加反应下的开路电压-总容量之间的函数关系曲线,即:
| $ E=f^{-1}(q) $ | (14) |
改进EECM的开路电压值根据图 16所示流程计算,而其余电路部分与EECM相同,其端电压计算公式为式(15)。在不同放电倍率下,将g(I)设置为优化参数,利用PSO算法使端电压仿真值和实验值的RMSE最小,从而确定g(I)的取值。之后将电流作为自变量与得到的优化参数值进行线性拟合,两者的相关性系数为0.992 5,具有较好的线性关系,最终得到g(I)的函数表达如式(16)所示。
| $ U_{\mathrm{est}}=E+\left(I-I_{1 / 20 \mathrm{C}}\right) R_{\mathrm{e}} $ | (15) |
| $ g(I)=-0.04246 \times \frac{I}{Q_{\mathrm{ST}}}+0.06531 $ | (16) |
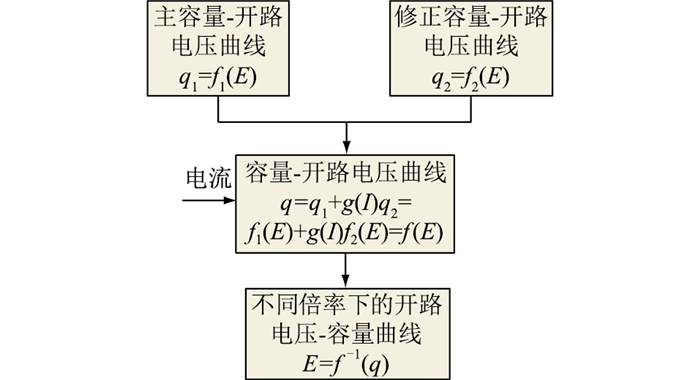
|
图 16 改进EECM开路电压计算流程 Fig. 16 Improved EECM open circuit voltage calculation process |
式中:Uest为改进EECM的端电压仿真值。
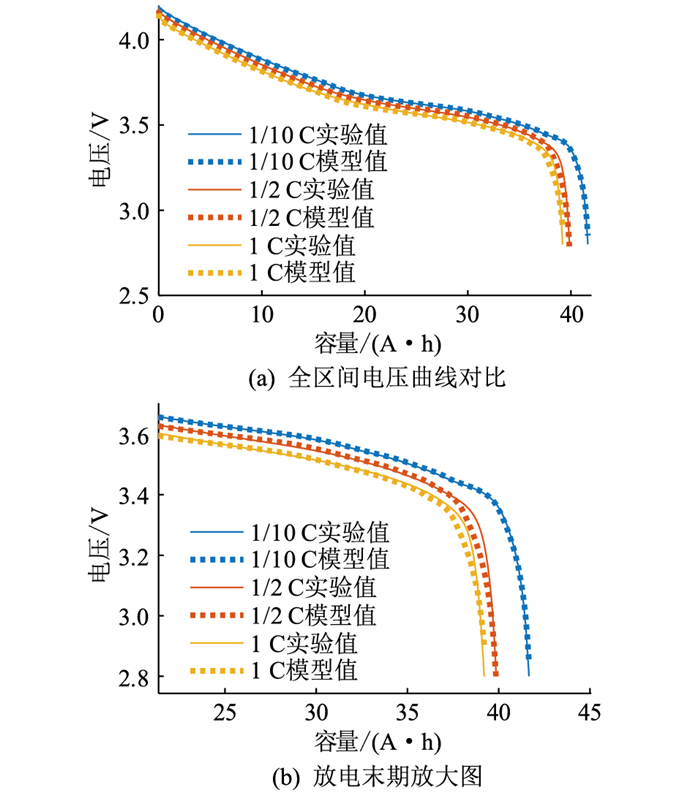
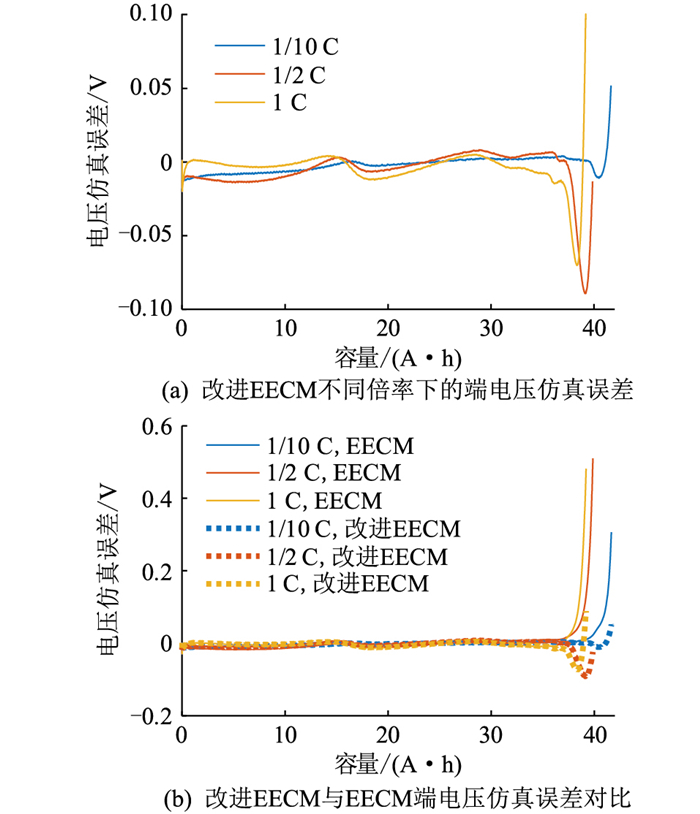
改进EECM在不同倍率下的仿真结果见图 17,仿真误差见图 18(a),改进EECM与ECM的端电压仿真误差对比见图 18(b)。改进EECM可以较好地仿真电池的端电压尤其是在放电末端的变化,能够体现出电压的快速下降, 端电压末端仿真误差相较于ECM和EECM大幅下降。改进EECM可以在全SOC区域精确地描述电池的电压特性。
|
图 17 改进EECM在不同倍率下的仿真结果 Fig. 17 Simulation results of improved EECM at different rates |
|
图 18 改进EECM在不同倍率下的端电压仿真误差 Fig. 18 The terminal voltage simulation error of improved EECM at different rates |
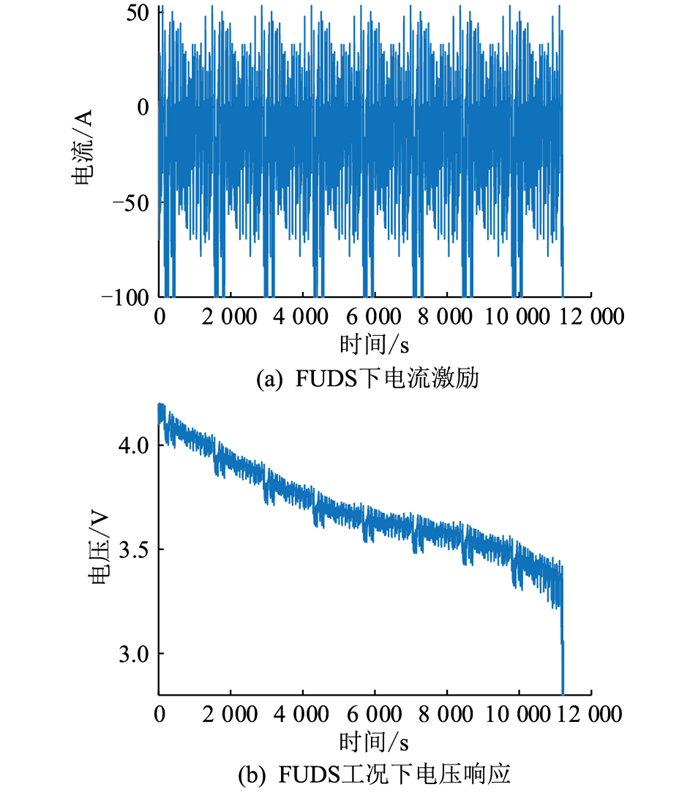
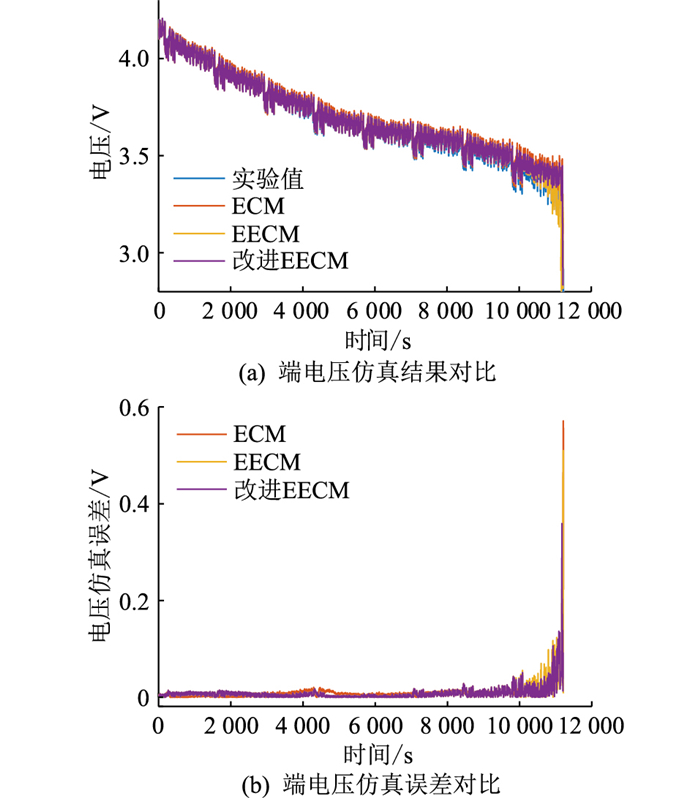
改进EECM亦可增加RC环节,用于仿真动态工况下的电池行为,对实验电池进行了美国联邦城市运行工况(federal urban driving schedule, FUDS)实验。FUDS的实验电流电压曲线如图 19所示。不同模型在FUDS工况下的误差对比如图 20所示,最大误差与RMSE对比如表 1和表 2所示。
|
图 19 FUDS下电流电压曲线 Fig. 19 Current and voltage curves under FUDS |
|
图 20 FUDS下不同电池模型仿真结果对比 Fig. 20 Comparison of simulation results of different battery models under FUDS |
|
|
表 1 不同模型的端电压仿真误差最大值 Table 1 Maximum simulation error of terminal voltage for different models |
|
|
表 2 不同模型的端电压仿真RMSE值 Table 2 Simulation RMSE value of terminal voltage for different models |
分析可知,所提出的改进EECM在动态工况下同样可以较好地描述电池特性,端电压仿真精度优于ECM和EECM,尤其在低SOC情况下可以更好地描述电池的电压快速下降过程。
3 电池RDC估计考虑到所提出的改进EECM可以有效提高模型精度,准确描述电池在放电末期的电压快速下降过程,因此可以将该模型用于BMS,优化相关算法结果。针对RDC估计问题,改进EECM可以提高估计精度,基于改进EECM的电池RDC估计流程如图 21所示。主要根据电池的当前状态,估计电池未来的电流情况,输入电池模型预测电池未来的电压序列,进而依据电池的放电截止条件,计算电池RDC[29-30]。
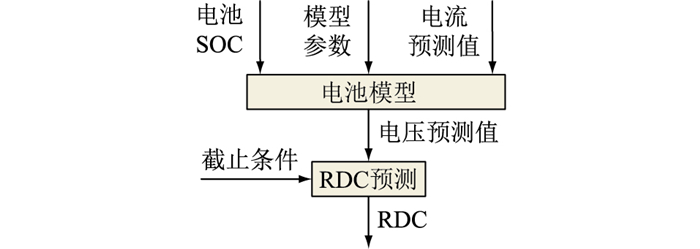
|
图 21 电池RDC预测 Fig. 21 Battery RDC prediction |
对于电池RDC估计,首先,要精确获得电池的当前状态参数与模型参量,可以通过电池参数辨识方法与状态估计方法获得;其次,要可靠预测电池未来的电流变化,通常基于电池的历史工况来进行预测;进而可以利用电池模型预测电池未来的电压,获得电池RDC,电池模型端电压的准确预测是RDC估计的核心问题。图 22为电池在不同SOC与不同倍率下的电池RDC的参考值。
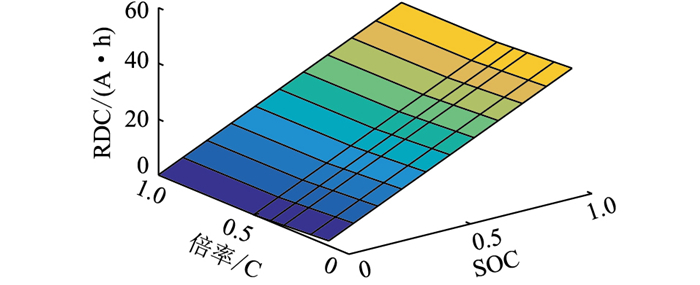
|
图 22 不同SOC和倍率下的RDC Fig. 22 RDC under different SOC values and C-rates |
基于ECM、EECM和改进的EECM估计5%SOC时不同倍率下电池RDC,对比如图 23所示。RDC与放电倍率存在较大的相关性,倍率越大,RDC越小。对于ECM,RDC估计结果几乎不随放电电流变化而变化,电流升高,RDC估计结果仅有轻微的降低,导致在较大倍率的情况下,RDC估计误差存在较大的偏差。例如在1 C工况下,电池实际RDC仅为2 A ·h左右,然而基于ECM,估计得到的电池RDC有5 A ·h。该估计结果可能会导致电池过度放电,影响电池寿命和安全性。采用EECM,结果可以得到较大的改善,随着倍率的增加,RDC估计结果线性降低,不过估计值仍然存在明显的偏差。而采用文中所提出的改进EECM,电池在不同倍率下的电压仿真误差更小,电池RDC估计结果精确性提高, 且改进EECM计算量低,因此有潜力在实际BMS中进行在线计算和应用。
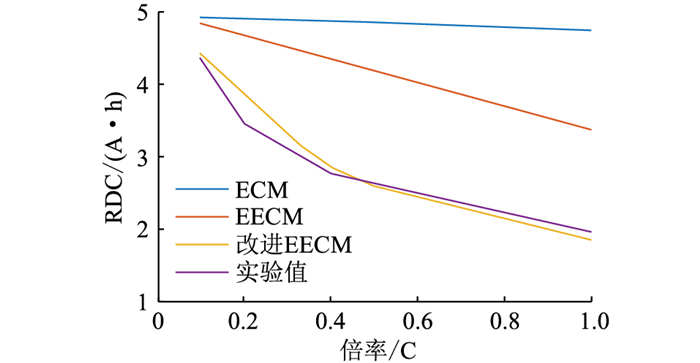
|
图 23 5%SOC下不同模型的电池RDC预测结果比较 Fig. 23 Comparison of the battery RDC prediction results with different models under 5%SOC |
文中提出一种改进EECM,并与传统ECM和EECM在各种电流工况下的端电压仿真误差进行对比。结果表明,电池容量随放电电流的变化而变化。传统ECM不能模拟这种现象,而EECM可以描述3.5 V以上电压区域的电压变化,但在电池电压快速下降区域显示出巨大的误差,因此也不适用于低SOC区域的电池RDC估计。基于内部机理,考虑了电池表面SOC以及在不同电流下的附加反应,修正了开路电压-容量曲线,提出一种改进EECM,该模型在全SOC区间放电过程中具有高精度,可应用于实际BMS中,进行在线仿真和电池管理, 提高RDC估计精度。
但电池中存在不同的电化学反应,在未来的研究中,为了进一步提高模型精度和可解释性,将分别对正极和负极的电位进行建模,以更好地分析整个电池的电压曲线。
| [1] |
WANG Y J, TIAN J Q, SUN Z D, et al. A comprehensive review of battery modeling and state estimation approaches for advanced battery management systems[J]. Renewable and Sustainable Energy Reviews, 2020, 131: 110015. DOI:10.1016/j.rser.2020.110015 (  0) 0) |
| [2] |
HU X S, FENG F, LIU K L, et al. State estimation for advanced battery management: key challenges and future trends[J]. Renewable and Sustainable Energy Reviews, 2019, 114: 109334. DOI:10.1016/j.rser.2019.109334 (  0) 0) |
| [3] |
申永鹏, 孙嵩楠, 刘东奇, 等. 车载混合储能系统Symlets小波变换能量管理方法[J]. 电力系统保护与控制, 2022, 50(6): 74-81. SHEN Yongpeng, SUN Songnan, LIU Dongqi, et al. Symlets wavelet transform energy management method for a vehicle-mounted hybrid energy storage system[J]. Power System Protection and Control, 2022, 50(6): 74-81. (  0) 0) |
| [4] |
LIU K L, LI K, PENG Q, et al. A brief review on key technologies in the battery management system of electric vehicles[J]. Frontiers of Mechanical Engineering, 2019, 14(1): 47-64. DOI:10.1007/s11465-018-0516-8 (  0) 0) |
| [5] |
蔡涛, 张钊诚, 袁奥特, 等. 锂离子电池储能安全管理中的机器学习方法综述[J]. 电力系统保护与控制, 2022, 50(24): 178-187. CAI Tao, ZHANG Zhaocheng, YUAN Aote, et al. Review of machine learning for safety management of li-ion battery energy storage[J]. Power System Protection and Control, 2022, 50(24): 178-187. (  0) 0) |
| [6] |
杜生鑫, 金阳. 锂离子电池储能舱风冷散热数值模拟与优化[J]. 电力工程技术, 2022, 41(6): 58-64. DU Shengxin, JIN Yang. Numerical simulation and optimization of air cooling heat dissipation of lithium-ion battery storage cabin[J]. Electric Power Engineering Technology, 2022, 41(6): 58-64. (  0) 0) |
| [7] |
吕超, 张爽, 朱世怀, 等. 储能锂离子电池包强制风冷系统热仿真分析与优化[J]. 电力系统保护与控制, 2021, 49(12): 48-55. LYU Chao, ZHANG Shuang, ZHU Shihuai, et al. Thermal simulation analysis and optimization of forced air cooling system for energy storage lithium-ion battery pack[J]. Power System Protection and Control, 2021, 49(12): 48-55. (  0) 0) |
| [8] |
LAI X, HUANG Y F, GU H H, et al. Remaining discharge energy estimation for lithium-ion batteries based on future load prediction considering temperature and ageing effects[J]. Energy, 2022, 238: 121754. DOI:10.1016/j.energy.2021.121754 (  0) 0) |
| [9] |
夏向阳, 邓子豪, 张嘉诚, 等. 基于动力锂离子电池健康状态的全寿命周期优化充电策略[J]. 电力科学与技术学报, 2022, 37(6): 17-24. XIA Xiangyang, DENG Zihao, ZHANG Jiacheng, et al. Life cycle optimal charging strategy based on the SOH of power lithium ion battery[J]. Journal of Electric Power Science and Technology, 2022, 37(6): 17-24. (  0) 0) |
| [10] |
HUA X, ZHANG C, OFFER G. Finding a better fit for lithium ion batteries: a simple, novel, load dependent, modified equivalent circuit model and parameterization method[J]. Journal of Power Sources, 2021, 484: 229117. DOI:10.1016/j.jpowsour.2020.229117 (  0) 0) |
| [11] |
XU L, LIN X K, XIE Y, et al. Enabling high-fidelity electrochemical P2D modeling of lithium-ion batteries via fast and non-destructive parameter identification[J]. Energy Storage Materials, 2022, 45: 952-968. (  0) 0) |
| [12] |
NEMES R, CIORNEI S, RUBA M, et al. Modeling and simulation of first-order li-Ion battery cell with experimental validation[C]//2019 8th International Conference on Modern Power Systems (MPS). Cluj-Napoca, Cluj, Romania. IEEE, 2019: 1-6.
(  0) 0) |
| [13] |
TRAN M K, MEVAWALA A, PANCHAL S, et al. Effect of integrating the hysteresis component to the equivalent circuit model of Lithium-ion battery for dynamic and non-dynamic applications[J]. Journal of Energy Storage, 2020, 32: 101785. (  0) 0) |
| [14] |
BAIRWA B L, PAREEK K, HAMPANNAVAR S K. Investigation on lithium ion battery equivalent circuit models for dynamic load profiles[J]. Energy Storage, 2021, 3(2): e231. (  0) 0) |
| [15] |
NOURA N, BOULON L, JEMEÏ S. A review of battery state of health estimation methods: hybrid electric vehicle challenges[J]. World Electric Vehicle Journal, 2020, 11(4): 66. (  0) 0) |
| [16] |
ZHANG C, ALLAFI W, DINH Q, et al. Online estimation of battery equivalent circuit model parameters and state of charge using decoupled least squares technique[J]. Energy, 2018, 142: 678-688. (  0) 0) |
| [17] |
OUYANG M G, LIU G M, LU L G, et al. Enhancing the estimation accuracy in low state-of-charge area: a novel onboard battery model through surface state of charge determination[J]. Journal of Power Sources, 2014, 270: 221-237. (  0) 0) |
| [18] |
BALASINGAM B, AHMED M, PATTIPATI K. Battery management systems—challenges and some solutions[J]. Energies, 2020, 13(11): 2825. (  0) 0) |
| [19] |
TRAN M K, MATHEW M, JANHUNEN S, et al. A comprehensive equivalent circuit model for lithium-ion batteries, incorporating the effects of state of health, state of charge, and temperature on model parameters[J]. Journal of Energy Storage, 2021, 43: 103252. (  0) 0) |
| [20] |
SHEN W X, CHAN C C, LO E W C, et al. Estimation of battery available capacity under variable discharge currents[J]. Journal of Power Sources, 2002, 103(2): 180-187. (  0) 0) |
| [21] |
DOERFFEL D, ABU SHARKH S. A critical review of using the Peukert equation for determining the remaining capacity of lead-acid and lithium-ion batteries[J]. Journal of Power Sources, 2006, 155(2): 395-400. (  0) 0) |
| [22] |
ZHENG Y J, GAO W K, HAN X B, et al. An accurate parameters extraction method for a novel on-board battery model considering electrochemical properties[J]. Journal of Energy Storage, 2019, 24: 100745. (  0) 0) |
| [23] |
LI Z Y, SHI X H, SHI M Y, et al. Investigation on the impact of the HPPC profile on the battery ECM parameters' offline identification[C]//2020 Asia Energy and Electrical Engineering Symposium (AEEES). Chengdu, China. IEEE, 2020: 753-757.
(  0) 0) |
| [24] |
JIANG B, DAI H F, WEI X Z. Incremental capacity analysis based adaptive capacity estimation for lithium-ion battery considering charging condition[J]. Applied Energy, 2020, 269: 115074. (  0) 0) |
| [25] |
AIELLO O. Electromagnetic susceptibility of battery management systems' ICs for electric vehicles: experimental study[J]. Electronics, 2020, 9(3): 510. (  0) 0) |
| [26] |
LI X Y, YUAN C G, LI X H, et al. State of health estimation for Li-ion battery using incremental capacity analysis and Gaussian process regression[J]. Energy, 2020, 190: 116467. (  0) 0) |
| [27] |
CHANG C, WANG Q Y, JIANG J C, et al. Lithium-ion battery state of health estimation using the incremental capacity and wavelet neural networks with genetic algorithm[J]. Journal of Energy Storage, 2021, 38: 102570. (  0) 0) |
| [28] |
SHE C Q, WANG Z P, SUN F C, et al. Battery aging assessment for real-world electric buses based on incremental capacity analysis and radial basis function neural network[J]. IEEE Transactions on Industrial Informatics, 2020, 16(5): 3345-3354. (  0) 0) |
| [29] |
XIONG R, ZHANG Y Z, HE H W, et al. A double-scale, particle-filtering, energy state prediction algorithm for lithium-ion batteries[J]. IEEE Transactions on Industrial Electronics, 2018, 65(2): 1526-1538. (  0) 0) |
| [30] |
CHEN Y J, YANG X L, LUO D, et al. Remaining available energy prediction for lithium-ion batteries considering electrothermal effect and energy conversion efficiency[J]. Journal of Energy Storage, 2021, 40: 102728. (  0) 0) |
 2023, Vol. 42
2023, Vol. 42


 张志行(1998),男,硕士在读,研究方向为电池管理(E-mail:
张志行(1998),男,硕士在读,研究方向为电池管理(E-mail: