文章编号: 2096-3203(2023)04-0167-08 中图分类号: TM63
2. 江苏金智科技股份有限公司,江苏 南京 211100
目前,电网中大量应用的动态数据采集设备为同步相量测量装置(phasor measurement unit,PMU)[1]。PMU量测在电力系统内部状态切换时可能产生跳变的事件数据,也会因互感器误差、PMU设备故障、时间同步异常、通信系统中断等诸多因素[2]产生异常跳变,即量测值中出现异常数据。智能电网的电网安全评估、预防控制和运行分析均以准确的电力系统状态估计为基础,若量测值中存在误差较大的异常数据,将导致系统状态估计准确度降低,影响系统实时监测及控制[3-7]。而基于异常数据所作的决策判断可能威胁到整个电网安全。因此,为保障电网安全可靠运行,研究PMU异常数据及其辨识方法有重要意义。
国内外学者已经针对PMU异常数据辨识方法展开了深入研究[8-15]。文献[12]提出了一种基于谱聚类的PMU异常数据检测算法,采用决策树方法分辨出事件数据,再通过谱聚类进行正常数据与异常数据的辨识,但其决策依赖异常数据维持的时间长度定义,易将事件数据误辨识为异常数据;文献[13]提出了基于核心微簇与离群微簇的异常数据辨识算法,先在线更新潜在核心微簇和离群微簇,再通过基于密度的噪声应用空间聚类(density-based spatial clustering of applications with noise, DBSCAN) 算法重新对所有微簇进行离线聚类,更新核心微簇,算法复杂度较高;文献[14]提出了一种基于PMU和数据采集与监视控制系统的单一点互校核算法,其准确率高,速度较快;文献[15]提出了一种基于多维特征向量和阈值的异常数据辨识算法。上述算法应用时都要先训练模式分类器再进行异常数据区分,无法实现在线更新,应用难度大。
为了降低辨识算法的复杂度,可以采用流聚类[16-18]算法进行数据的在线训练和聚类。该算法通过提取有效的聚类特征(cluster feature, CF),动态地对数据进行聚类分析,依据少量的特征数据集存储对新数据进行快速处理和分类,因此具有良好的在线更新和实时应用特性,适用于连续采集等具有大数据特征的应用场景。目前,尚未有相关工作将流聚类算法应用于PMU异常数据辨识。
信息熵[19]是信息论的基本概念,可描述信息源各可能事件发生的不确定性。采用信息熵对PMU量测值进行筛选,可以减少训练集的样本数以用于配电网安全态势感知要素分析[20]。文献[21]通过小波熵对故障状态下的电气量相角特征进行分析,从而获得准确的故障元件。信息熵同样也可用于聚类算法以获得更加准确的分类结果。文献[22]将信息熵作为加权依据,在聚类过程中弱化低质量的簇,使聚类结果更加准确;文献[23]将信息熵应用于混合数据类型的聚类算法研究中,以确定不同数据类型的数据权重;文献[24]在计算聚类距离时引入信息熵对距离进行加权,提升了分类的准确性。文献[25]提出了样本稳定性的概念,利用信息熵描述二元信源的确定性,优先筛选稳定性高的样本簇,提升后续的聚类准确度。综上所述,信息熵用于流聚类主要是从度量和聚类距离方面对聚类进行良性的干预,使算法更为准确。
文中基于信息熵理论,研究PMU事件数据和异常数据描述,定义PMU异常数据判别熵(PMU abnormal data identification entropy, PADIE),提出基于信息熵的PMU异常数据和事件数据描述和辨识框架;将PADIE与流聚类算法相结合,提出基于流聚类的在线PMU异常数据辨识算法。该算法实现了对异常数据与事件数据的在线、准确、实时辨识。基于文中理论研究所实现的变电站PMU数据校核装置可以在站内实时、就地完成PMU异常数据识别,改进了传统PMU数据上送主站后要从海量数据中依赖多源数据校核识别出异常数据的方法,提升了PMU异常数据识别的实时性,降低了运算量,为变电站内保护、测控各装置准确实时应用PMU数据提供了更好的技术支撑。
1 基于信息熵的PMU异常数据辨识框架PMU事件数据是指由于电力系统内部状态切换导致的PMU量测值跳变;PMU异常数据是指电力系统内部状态并未发生变化,而是由于数据采集误差、通信异常等导致的PMU量测值跳变。
1.1 PMU异常数据和事件数据定义文中参考了文献[12]和[15]中对异常数据的定义。异常数据在偏离正常值后会回到正常值,即其值围绕正常值上下波动;事件数据在偏离正常值后不会回到正常值或需要较长时间再回到正常值。
定义α为偏离因子;ta为发生数据偏离前的时刻,Pta为该时刻的PMU数据;tb为发生数据偏离后恢复到正常数据的时刻,Ptb为该时刻的PMU数据;Pt为t时刻(ta < t < tb)跳变过程中的PMU数据;Pta、Pt、Ptb分别为ta、t和tb时刻的正常值;te为事件判断时长阈值。当Pt满足式(1)时为异常数据。
| $ \left\{\begin{array}{l} \left|P_{t_{\mathrm{a}}}-\bar{P}_{t_{\mathrm{a}}}\right| / \bar{P}_{t_{\mathrm{a}}} \leqslant \alpha \\ \left|P_t-\bar{P}_t\right| / \bar{P}_t>\alpha \quad t_{\mathrm{a}} <t<t_{\mathrm{b}} \\ \left|P_{t_{\mathrm{b}}}-\bar{P}_{t_{\mathrm{b}}}\right| / \bar{P}_{t_{\mathrm{b}}} \leqslant \alpha \\ t_{\mathrm{b}}-t_{\mathrm{a}} \leqslant t_{\mathrm{e}} \end{array}\right. $ | (1) |
事件数据的特性满足:
| $ \left\{\begin{array}{l} \left|P_{t_{\mathrm{a}}}-\bar{P}_{t_{\mathrm{a}}}\right| / \bar{P}_{t_{\mathrm{a}}} \leqslant \alpha \\ \left|P_t-\bar{P}_t\right| / \bar{P}_t>\alpha \quad t_{\mathrm{a}} <t<t_{\mathrm{b}} \\ \left|P_{t_{\mathrm{b}}}-\bar{P}_{t_{\mathrm{b}}}\right| / \bar{P}_{t_{\mathrm{b}}}>\alpha \\ t_{\mathrm{b}}-t_{\mathrm{a}}>t_{\mathrm{e}} \end{array}\right. $ | (2) |
由式(2)可知,当发生数据偏离正常值后超过te时间仍未恢复到正常值时,该数据为事件数据。
1.2 PMU异常数据判别信息熵定义信息熵用于描述事件发生的不确定性,定义如式(3)所示。
| $ H(D)=-\sum\limits_{i=1}^n P\left(C_i\right) \log _2\left(P\left(C_i\right)\right) $ | (3) |
式中:D为整个数据集;H(D)为数据集D的信息熵;n为数据集D中的类别个数;Ci为数据集D中第i个分类;P(Ci)为数据集D中第i个分类的占比。
在异常数据辨识中引入信息熵的概念,定义PADIE,用于描述一段数据中出现异常数据后的数据不确定度。首先对PMU数据的信息进行定义。定义一个样本C如下:
| $ C=\left\{P_1, P_2, \cdots, P_N\right\} $ | (4) |
式中:P1—PN为PMU数据;N为样本中数据的个数。假如该样本中存在c个异常数据,定义pc为样本中异常数据的占比,如式(5)所示。
| $ p_c=c / N $ | (5) |
定义1-pc为样本中正常数据的占比。基于PMU数据信息pc和1-pc,采用信息熵公式构造样本C的PADIE值Z(C):
| $ Z(C)=-k_1 p_c \log _2\left(p_c\right)-k_2\left(1-p_c\right) \log _2\left(1-p_c\right) $ | (6) |
式中:k1、k2为权重系数。
1.3 基于PMU异常数据判别信息熵的辨识框架PADIE反映了PMU数据异常的不确定性。按照事件判断时长阈值te内PMU数据点的数量进行样本C的选取。
假如k1和k2取值相同:
(1) 当pc=0.5时,跳变数据与正常数据比例相同,PMU数据源的不确定度最大。
(2) 当pc < 0.5时,pc越接近0,Z(C)越接近0,样本C的不确定度越小;当pc为0时,不确定度为0,样本C中均为正常数据。
(3) 当pc>0.5时,pc越接近1,Z(C)越接近0,样本C的不确定度越小;当pc为1时,不确定度为0,样本C中数据偏离持续时间超过了te,所以样本C中均为事件数据。
因此,结合pc与Z(C)可对数据进行正常数据、异常数据与事件数据的判断。定义连续的样本C1、C2、…、Ci, 对应的异常数据占比为pc1、pc2、…、pci, 信息熵为Z(C1)、Z(C2)、…、Z(Ci)。
当Z(Ci)=0时,若pci=0,则样本Ci均为正常数据;若pci=1,则样本Ci均为事件数据。当Z(Ci)>0时,若下一个样本Ci+1的Z(Ci+1)=0且pc(i+1)=1,即样本Ci+1为事件数据,则说明事件是在样本Ci的时间内发生的,所以Ci中的跳变值也为事件数据,否则Ci中的跳变值为异常数据。
2 异常数据辨识算法文中将PADIE值作为度量,结合流聚类算法实现PMU异常数据辨识。流聚类算法通过对数据序列迭代处理,不断更新CF,并对不断更新的窗口数据进行迭代聚类,从而实现对连续数据流的快速聚类。与传统聚类方法相比,流聚类方法更适用于动态扩展的数据集,其通过CF维护和窗口定义降低了聚类处理的计算性能要求,且不再需要存储全部样本数据,提升了算法的实时性。
2.1 PMU异常数据判别信息熵计算PADIE计算中首先要找出PMU数据中的跳变值。按照式(1)和式(2)计算跳变值时,Pt采用滑窗求取均值的方式计算。假设滑窗的样本数量为m,则在t时刻Pt的计算公式如式(7)和式(8)所示,其中k为权重系数。式(8)用于设置数据点的上下限。
| $ \bar{P}_t=\left(m \bar{P}_{t-1}-Q_{t-m}+Q_t\right) / m $ | (7) |
| $ Q_t= \begin{cases}P_t\;\;\;\;\;\;\;\;-k \alpha \leqslant \left(P_t-\bar{P}_{t-1}\right) / \bar{P}_{t-1} \leqslant k \alpha \\ \bar{P}_{t-1}(1-k \alpha) \;\;\;\; \left(P_t-\bar{P}_{t-1}\right) / \bar{P}_{t-1} <-k \alpha \\ \bar{P}_{t-1}(1+k \alpha) \;\;\;\; \left(P_t-\bar{P}_{t-1}\right) / \bar{P}_{t-1}>-k \alpha\end{cases} $ | (8) |
得到正常值后,根据式(1)—式(6)即可完成对PMU异常数据判别信息熵的计算。
2.2 目标函数定义聚类的优化准则为组内距离最小化,组间距离最大化。以信息熵为CF,对样本及对应的簇内、簇间距离进行定义,定义如下。
将聚类特征簇作为数据集D进行信息熵的计算。设Ci、Cj为聚类特征簇D中的2个样本,对应的信息熵指标分别为Z(Ci)、Z(Cj),反映2个样本内数据类型的不确定度,两者之间的距离可定义为:
| $ L\left(C_i, C_j\right)=\left|Z\left(C_i\right)-Z\left(C_j\right)\right| $ | (9) |
簇D的质心Z0为:
| $ \bar{Z}_0=\sum\limits_{i=1}^N Z\left(C_i\right) / N $ | (10) |
任意样本Ci到簇D的距离定义为样本Ci到簇的质心的距离:
| $ L\left(C_i, D\right)=\left|Z\left(C_i\right)-\bar{Z}_0\right| $ | (11) |
设Nm、Nn分别为2个聚类特征簇Dm和Dn的样本个数,簇Dm和簇Dn之间的距离定义为:
| $ L\left(D_m, D_n\right)=\left[\frac{\sum\limits_{i=1}^{N_m} \sum\limits_{j=1}^{N_n}\left(Z\left(C_i\right)-Z\left(C_j\right)\right)^2}{N_m N_n}\right]^{\frac{1}{2}} $ | (12) |
若存在样本空间
| $ \left\{ {\begin{array}{*{20}{l}} {\min \sum\limits_{i = 1}^M {\sum\limits_{ j = 1, \atop j \in {D_i}}^{{N_i}} {\left| {Z\left( {{C_j}} \right) - {{\bar Z}_{0, i}}} \right|} } }\\ {\max \sum\limits_{\begin{array}{*{20}{c}} {1 \le m, n \le M, }\\ {m \ne n} \end{array}}^M L \left( {{D_m}, {D_n}} \right)} \end{array}} \right. $ | (13) |
式中:Z0, i为簇Di的质心;Ni为簇Di的样本个数。
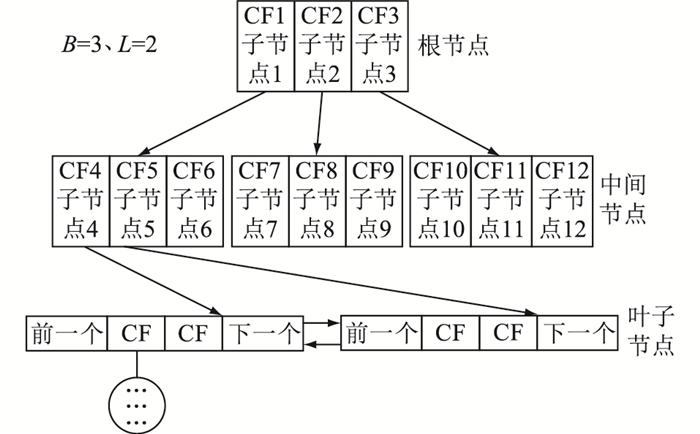
2.3 基于BIRCH的PMU异常数据辨识算法文中采用利用层次方法的平衡迭代规约和聚类(balanced iterative reducing and clustering using hierarchies,BIRCH)[18]算法实现流聚类。对数据建立分层结构CF树,其中每个节点包含一组CF。这些CF包含了描述数据集中一组点的充分统计信息以及子节点指向的CF的所有信息。该CF树的规模由参数B(每个中间节点最大的CF数)、L(每个叶子节点最大的CF数)、T(每个CF的聚类半径)决定。具体CF树的结构如图 1所示。
|
图 1 CF树 Fig. 1 CF tree |
CF结构是一个三元组(N, SLS, SSS),用于存储一组点的充分统计信息,其中SLS为N个样本特征维度的向量和;SSS为N个样本特征维度的平方和。CF三元组满足线性关系,因此可以高效地更新CF树。每插入一个样本时,从根开始向下遍历当前树,计算与新样本最近的叶子CF,新样本到簇的距离以及簇间的距离通过式(11)和式(12)进行计算。找到合适的叶子CF后,基于CF树中三元组的线性可加特性,可快速更新CF值,完成实时在线聚类。
完成聚类后,每个样本可以根据聚类结果实现对正常数据、异常数据与事件数据的辨识。
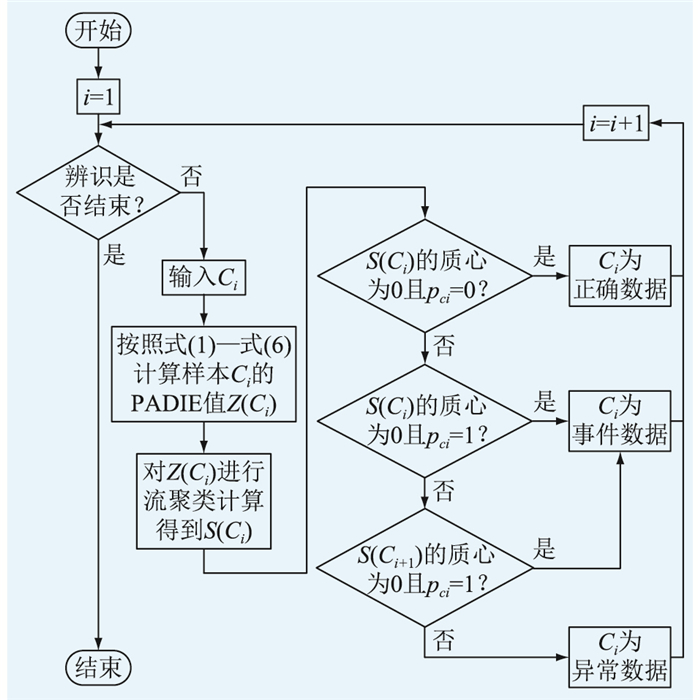
基于流聚类的PMU异常数据辨识的具体流程如图 2所示。以样本Ci= Pi1, Pi2, …, PiN为例,首先计算样本的PADIE值Z(Ci),然后计算样本的CF,再按照BIRCH参数B、L、T进行聚类,得到其聚类的类别标识S(Ci),最后根据聚类结果完成对正常数据、异常数据与事件数据的辨识。
|
图 2 基于流聚类的PMU异常数据辨识流程 Fig. 2 Flow chart of PMU abnormal data identification based on stream clustering |
文中采用站域多态数据融合测控原型系统实现基于流聚类的PMU异常数据辨识算法。中央处理器(central processing unit,CPU)采用Intel Core i7-8665U处理器(主频1.9 GHz),其通过以太网口按照GB/T 26865.2协议接收同步相量数据集中器的PMU数据,然后进行异常数据辨识。
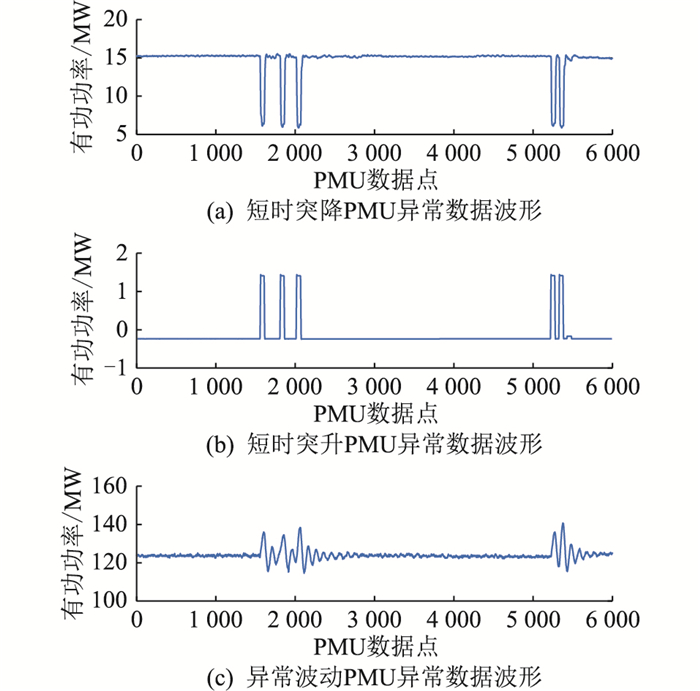
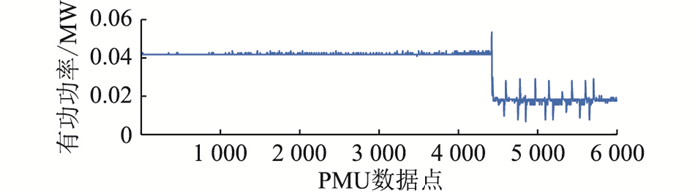
3.1 异常数据辨识实验某变电站的PMU数据的传输频率为100点/s,每个波形持续时间为60 s,每个波形总计6 000个点。对43个采集对象的282万个PMU采集数据进行统计分析,选取图 3与图 4为典型波形进行说明。图 3为采样传感器受到干扰后引起PMU数据异常突变与波动的典型波形,图 4为典型的由负荷切换引起的事件数据波形。
|
图 3 现场采集的PMU异常数据波形 Fig. 3 Abnormal data waveforms of PMU collected on site |
|
图 4 现场采集的PMU事件数据波形 Fig. 4 Event data waveform of PMU collected on site |
图 3异常数据特征为:短时突降,维持片刻,随后恢复;短时突升,维持片刻,随后恢复;数据异常波动。图 4事件数据特性为:偏离正常值后不再返回。
针对以上PMU数据样本,采用基于流聚类的PMU异常数据辨识算法,其参数取值如下:式(1)和式(2)中的te取1 s,α取0.05,即正常数据的偏差不超过±5%,α的取值与实际应用中被辨识数据的正常波动范围有关;式(4)中的N取100;式(6)的k1和k2均取30,因为文中同时关注正常数据与异常数据,如果取k1>k2,则正常数据的比例对信息熵影响更大,因此k1和k2的取值原则是根据应用对正常数据和异常数据的关注程度取值,两者幅值大小只影响聚类时半径的取值;式(7)中的m取300,即以3 s为窗口计算参考正常值,如果增大m,则滑窗数据更为平滑,但响应速度更慢,因此m的取值原则是根据辨识数据的变化速率与应用的响应速度要求取值;式(8)中的k取1,即正常值计算时上下限偏差为±5%。BIRCH算法中B取3,L取2,半径T取0.5。由于pc为0.5时信息熵达到峰值,对pc取中间值0.25时,计算pc(即0.25与0.24)的信息熵的差值为0.487,所以在半径T取0.5时,pc≤0.25的样本都会单独分为一类,而pc>0.25的样本则会逐渐合并。
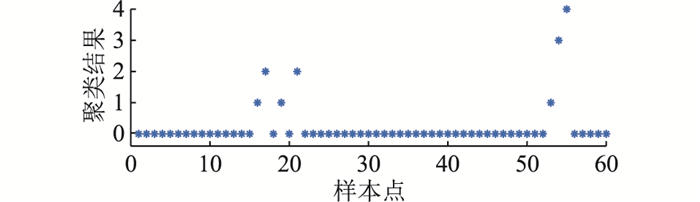
对图 3中3种典型PMU异常数据波形进行归一化处理后,得到异常数据辨识结果,如图 5—图 7所示,纵坐标“聚类结果”是指各样本的信息熵通过流聚类分类后的类别编号,其中类别0是质心为0,即Z(Ci)为0的点,其他类别是Z(Ci)大于0的点。按照1.3节,可通过Z(Ci)与pci对正常数据、异常数据与事件数据进行判别。
|
图 5 短时突降辨识结果 Fig. 5 Identification results of short-time sudden drop |
|
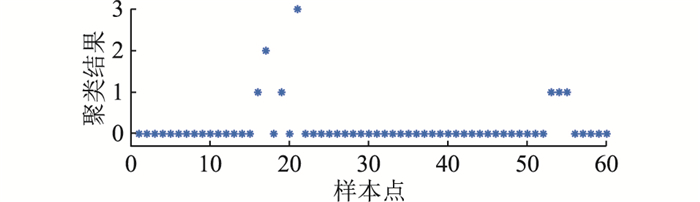
图 6 短时突升辨识结果 Fig. 6 Identification results of short-time sudden rise |
|
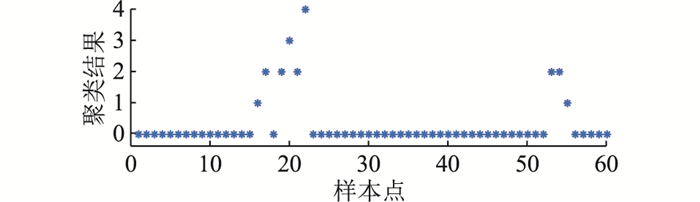
图 7 数据波动辨识结果 Fig. 7 Identification results of data fluctuation |
图 5—图 7的聚类结果中未出现聚类类别为0且pc为1的事件数据样本,可知图中聚类类别不为0的样本中的跳变值均为异常数据。
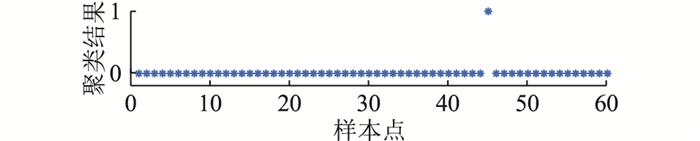
对图 4的PMU事件数据波形进行归一化处理后,得到的异常数据辨识结果如图 8所示。
|
图 8 事件数据辨识结果 Fig. 8 Identification results of event data |
图 8中样本1~44的聚类类别均为0,且pc为0,因此均为正常数据;样本46~60的聚类类别均为0,且pc为1,因此均为事件数据;由于样本45聚类类别为1,但样本46为事件数据,说明事件是在样本45的时间内发生,所以样本45中的跳变值为事件数据。
基于流聚类的异常数据辨识结果如表 1所示。辨识结果中“0”为正常数据,“1”为异常数据,“2”为事件数据。该方法对以上样本的异常数据和事件数据的辨识准确率为100%。
|
|
表 1 基于流聚类的异常数据辨识结果 Table 1 Identification results of abnormal data based on stream clustering |
原型系统中基于流聚类的异常数据辨识算法由x86架构Intel Core i7-8665U实现。由于pc为0或1时进行信息熵计算均无须计算对数,因此按照计算最复杂情况,即0 < pc < 1时统计计算耗时与算法总耗时。信息熵计算包括加减600次,乘法7次,除法1次,对数2次,比较300次;流聚类计算包括加减10次,乘法2次,除法2次,平方1次,比较5次;共计时钟周期1 147个,耗时604 ns,实测计算耗时692 μs。
实验结果表明,对于每个10 ms PMU数据通过692 μs的时间即可计算完成,满足实时性要求。1 min 6 000个PMU数据作为1组实验数据,从282万个PMU数据中提取异常数据18组,事件数据85组,经文中算法辨识后,异常数据辨识准确率为100%。对比某变电站2022年采集实际数据的波动特性与文献[15]中其他同行所获取的2015年的实际数据,发现其波动特性基本一致。可见在电网运行数据波动特征不发生剧烈变化的前提下,文中算法具有较好的适用性。
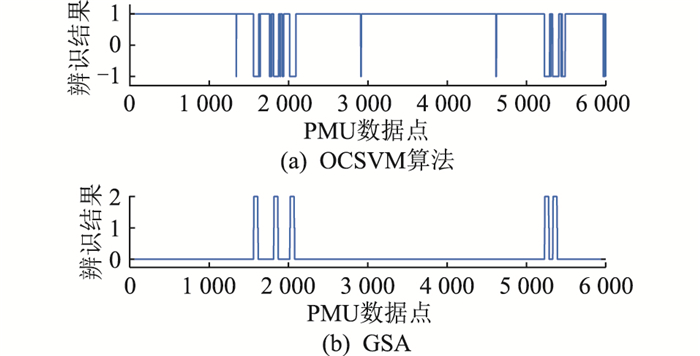
3.2 同类算法对比采用一类支持向量机[26](one-class support vector machine,OCSVM)算法与间隙统计算法[27](gap statistic algorithm,GSA)对PMU异常数据进行辨识。OCSVM算法设置为:使用高斯核,训练数据的异常点比例为0.01,训练停止的公差标准为0.001。辨识结果为1表明PMU数据点为正常数据,辨识结果为-1表明PMU数据点为异常数据。GSA设置聚类参数k的遍历范围为1~10。辨识结果为0表明PMU数据点为正常数据,为其他值表明PMU数据点为异常数据。对图 3中的异常数据波形进行归一化处理,采用2种算法所得的辨识结果如图 9—图 11所示。
|
图 9 OCSVM算法和GSA的短时突降辨识结果 Fig. 9 Identification results of short-time sudden drop using OCSVM algorithm and GSA |
|
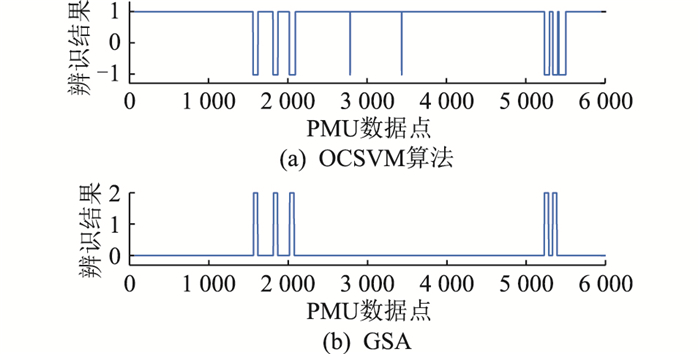
图 10 OCSVM算法和GSA的短时突升辨识结果 Fig. 10 Identification results of short-time sudden rise using OCSVM algorithm and GSA |
|
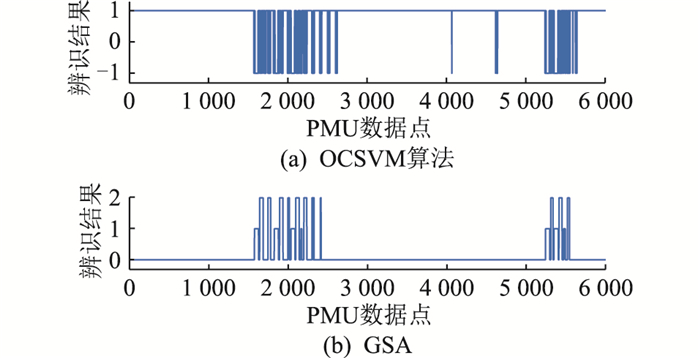
图 11 OCSVM算法和GSA的数据波动辨识结果 Fig. 11 Identification results of data fluctuation using OCSVM algorithm and GSA |
文中算法与OCSVM算法和GSA的比较结果如表 2所示。其中P1为异常数据辨识率;P2为误辨识率。P1和P2的计算分别见式(14)、式(15)。
| $ P_1=n_{\mathrm{f}} / N_{\mathrm{f}} $ | (14) |
| $ P_2=n_{\mathrm{t}} / N_{\mathrm{t}} $ | (15) |
|
|
表 2 与同类算法辨识指标的比较 Table 2 Comparison of identification indexes with similar algorithms |
式中:nf为辨识出的异常数据点数;Nf为异常数据总数;nt为将正常数据误辨识为异常数据的点数;Nt为正常数据总数。
文中18组异常数据中短时突降、短时突升和数据波动3种异常数据类型占比为7 ∶8 ∶3,与文献[15]中的统计数据相当,将3种异常数据类型的辨识结果按照发生比率加权后得到OCSVM算法的P1=96.54%、P2=2.21%;GSA的P1=84.26%、P2=0.91%;文中算法的P1=100%、P2=0。
根据以上实验结果可知,OCSVM算法辨识耗时较低,但是辨识准确度不够:部分样本辨识时P1指标能达到100%,但P2指标不稳定,异常波动样本辨识的P1和P2指标均较差。GSA耗时长,辨识准确度不够:部分样本辨识时P2指标能达到0,但P1指标较差,异常波动样本辨识的P1指标虽然达到100%,但P2指标较差。文中算法对于不同样本类型均实现了P1指标达到100%,P2指标达到0的辨识效果,且可实现事件数据与异常数据的区分。文中算法的最大耗时也仅比OCSVM算法大4.4%。
4 结语文中针对PMU异常数据辨识问题,从信息熵理论出发,研究提出PADIE定义和基于该信息熵的PMU异常数据辨识框架。将PADIE和流聚类算法结合,提出一种基于流聚类的PMU异常数据辨识算法。结合原型实现,对从实际运行电网中所获取的PMU量测值数据集进行了所提出辨识算法的实验,实验结果表明文中算法的辨识率和误辨识率均优于同类算法。
文中研究可为今后PMU异常数据的修正、异常数据溯源与智能告警等应用提供参考。如何优化异常数据信息熵的聚类效果和进一步对异常数据进行修复、溯源和告警,是未来要继续研究的方向。
| [1] |
黄子蒙, 余娟, 向明旭, 等. 基于改进动态时间弯曲的PMU频率异常检测及类型识别[J]. 电力系统自动化, 2022, 46(24): 104-112. HUANG Zimeng, YU Juan, XIANG Mingxu, et al. Frequency anomaly detection and type identification of PMU based on improved dynamic time warping[J]. Automation of Electric Power Systems, 2022, 46(24): 104-112. (  0) 0) |
| [2] |
徐飞阳, 薛安成, 常乃超, 等. 电力系统同步相量异常数据检测与修复研究现状与展望[J]. 中国电机工程学报, 2021, 41(20): 6869-6886. XU Feiyang, XUE Ancheng, CHANG Naichao, et al. Research status and prospects of detection, correction and recovery for abnormal synchrophasor data in power system[J]. Proceedings of the CSEE, 2021, 41(20): 6869-6886. (  0) 0) |
| [3] |
周婧怡, 李红娇. 针对PMU测量的虚假数据注入攻击检测方法[J]. 信息网络安全, 2022, 22(5): 75-83. ZHOU Jingyi, LI Hongjiao. False data injection attack detection method against PMU measurements[J]. Netinfo Security, 2022, 22(5): 75-83. (  0) 0) |
| [4] |
常鹏, 吴泽群, 孙文仲, 等. 基于PMU优化部署的电网CPS线下攻击保护[J]. 智慧电力, 2021, 49(6): 60-66. CHANG Peng, WU Zequn, SUN Wenzhong, et al. Offline attack protection of power grid CPS based on PMU optimized deployment[J]. Smart Power, 2021, 49(6): 60-66. (  0) 0) |
| [5] |
王海波, 吴升涛, 周文海, 等. 基于不同量测数据融合的配电网状态估计研究[J]. 机电信息, 2023(4): 12-16. WANG Haibo, WU Shengtao, ZHOU Wenhai, et al. Research on distribution network state estimation based on different measurement data fusion[J]. Mechanical and Electrical Information, 2023(4): 12-16. (  0) 0) |
| [6] |
CUI M J, WANG J H, TAN J, et al. A novel event detection method using PMU data with high precision[J]. IEEE Transactions on Power Systems, 2019, 34(1): 454-466. (  0) 0) |
| [7] |
曹鹏, 刘敏, 杭鲁庆. 基于改进磷虾群算法的配电网PMU优化配置研究[J]. 电网与清洁能源, 2022, 38(4): 61-67. CAO Peng, LIU Min, HANG Luqing. Research on PMU optimal configuration of distribution networks based on improved krill herd algorithm[J]. Power System and Clean Energy, 2022, 38(4): 61-67. (  0) 0) |
| [8] |
王磊. 配电网同步相量与电能质量同步监测一体机[D]. 济南: 山东大学, 2018. WANG Lei. Integrated machine for synchronous phasor and power quality monitoring of distribution network[D]. Jinan: Shandong University, 2018. (  0) 0) |
| [9] |
朱志敏. 基于Linux的广域测量系统相量数据集中器的研发[D]. 合肥: 合肥工业大学, 2019. ZHU Zhimin. Research and development of phasor data concentrator for wide-area measurement system based on Linux[D]. Hefei: Hefei University of Technology, 2019. (  0) 0) |
| [10] |
IDEHEN I, OVERBYE T J. PMU time error detection using second-order phase angle derivative measurements[C]//2019 IEEE Texas Power and Energy Conference (TPEC). College Station, TX, USA. IEEE, 2019: 1-6.
(  0) 0) |
| [11] |
张江南, 雷江龙, 贺勇, 等. 基于PMU误差校正的输电线路参数在线辨识方法[J]. 电力系统保护与控制, 2022, 50(19): 130-137. ZHANG Jiangnan, LEI Jianglong, HE Yong, et al. Transmission line parameter identification method based on PMU error correction[J]. Power System Protection and Control, 2022, 50(19): 130-137. (  0) 0) |
| [12] |
YANG Z W, LIU H, BI T S, et al. Bad data detection algorithm for PMU based on spectral clustering[J]. Journal of Modern Power Systems and Clean Energy, 2020, 8(3): 473-483. (  0) 0) |
| [13] |
CAO F, ESTERT M, QIAN W N, et al. Density-based clustering over an evolving data stream with noise[C]//Proceedings of the 2006 SIAM International Conference on Data Mining. Philadelphia, PA: Society for Industrial and Applied Mathematics, 2006.
(  0) 0) |
| [14] |
刘雯静, 杨军, 袁文, 等. 一种基于PMU和SCADA单节点互校核的前端数据辨识框架[J]. 电力系统保护与控制, 2020, 48(8): 1-9. LIU Wenjing, YANG Jun, YUAN Wen, et al. A front-end data identification framework based on single-node mutual checking between PMU and SCADA[J]. Power System Protection and Control, 2020, 48(8): 1-9. (  0) 0) |
| [15] |
万楚林, 陈皓勇, 郭曼兰. 基于模式识别的WAMS有功功率错误数据处理[J]. 电网技术, 2017, 41(3): 922-930. WAN Chulin, CHEN Haoyong, GUO Manlan. Wrong active power data identification and correction for WAMS based on pattern recognition[J]. Power System Technology, 2017, 41(3): 922-930. (  0) 0) |
| [16] |
BEZDEK J C, KELLER J M. Streaming data analysis: cluster ing or classification?[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2021, 51(1): 91-102. (  0) 0) |
| [17] |
CARNEIN M, TRAUTMANN H. Optimizing data stream representation: an extensive survey on stream clustering algorithms[J]. Business & Information Systems Engineering, 2019, 61(3): 277-297. (  0) 0) |
| [18] |
ZHANG T, RAMAKRISHNAN R, LIVNY M. BIRCH: an efficient data clustering method for very large databases[J]. ACM SIGMOD Conference, 1996. (  0) 0) |
| [19] |
SHANNON C E. A mathematical theory of communication[J]. The Bell System Technical Journal, 1948, 27(3): 379-423. (  0) 0) |
| [20] |
田书欣, 李昆鹏, 魏书荣, 等. 基于同步相量测量装置的配电网安全态势感知方法[J]. 中国电机工程学报, 2021, 41(2): 617-632. TIAN Shuxin, LI Kunpeng, WEI Shurong, et al. Security situation awareness approach for distribution network based on synchronous phasor measurement unit[J]. Proceedings of the CSEE, 2021, 41(2): 617-632. (  0) 0) |
| [21] |
杨欢. 基于WAMS/SCADA数据的配电网故障分析方法[D]. 沈阳: 东北大学, 2018. YANG Huan. Fault analysis method of distribution network based on WAMS/SCADA data[D]. Shenyang: Northeastern University, 2018. (  0) 0) |
| [22] |
邵长龙, 孙统风, 丁世飞. 基于信息熵加权的聚类集成算法[J]. 南京大学学报(自然科学), 2021, 57(2): 189-196. SHAO Changlong, SUN Tongfeng, DING Shifei. Ensemble clustering based on information entropy weighted[J]. Journal of Nanjing University (Natural Science), 2021, 57(2): 189-196. (  0) 0) |
| [23] |
崔文秀. 基于信息熵定义属性权重的混合数据聚类算法研究[D]. 太原: 山西大学, 2021. CUI Wenxiu. Research on mixed data clustering algorithm based on information entropy to define attribute weight[D]. Taiyuan: Shanxi University, 2021. (  0) 0) |
| [24] |
张安勤, 吴蕊, 张挺. 基于信息熵的异常检测算法[J]. 上海电力大学学报, 2020, 36(4): 386-390. ZHANG Anqin, WU Rui, ZHANG Ting. Anomaly detection algorithm based on information entropy[J]. Journal of Shanghai University of Electric Power, 2020, 36(4): 386-390. (  0) 0) |
| [25] |
李飞江, 钱宇华, 王婕婷, 等. 基于样本稳定性的聚类方法[J]. 中国科学: 信息科学, 2020, 50(8): 1239-1254. LI Feijiang, QIAN Yuhua, WANG Jieting, et al. Clustering method based on sample's stability[J]. Scientia Sinica (Informa- tionis), 2020, 50(8): 1239-1254. (  0) 0) |
| [26] |
闫梦秋, 杨轶俊, 赵舫. 基于改进OCSVM的智能变电站数据流异常检测方法研究[J]. 电力系统保护与控制, 2022, 50(6): 100-106. YAN Mengqiu, YANG Yijun, ZHAO Fang. A data stream anomaly detection method based on an improved OCSVM smart substation[J]. Power System Protection and Control, 2022, 50(6): 100-106. (  0) 0) |
| [27] |
BRODINOVÁ Š, FILZMOSER P, ORTNER T, et al. Robust and sparse k-means clustering for high-dimensional data[J]. Advances in Data Analysis and Classification, 2019, 13(4): 905-932. (  0) 0) |
2. Wiscom System Co., Ltd., Nanjing 211100, China
 2023, Vol. 42
2023, Vol. 42


 邓小玉(1975),女,学士,高级工程师,从事电力系统及自动化工作(E-mail:
邓小玉(1975),女,学士,高级工程师,从事电力系统及自动化工作(E-mail: