文章编号: 2096-3203(2023)04-0141-08 中图分类号: TM614
2. 浙江医学电子与数字健康重点实验室,浙江 嘉兴 314001;
3. 江苏金风软件技术有限公司,江苏 无锡 214000
随着碳达峰和碳中和目标的提出,大规模发展新能源已成为世界范围内的共识[1]。作为重要的绿色资源,风电的发展尤为迅速,但也带来大量的运维成本[2-3]。风电机组和风电场配置的运行监测和数据采集系统可以积累大量的运行数据,这些风电大数据常被用于状态监测、风功率预测[4-6]和风功率曲线建模等。然而,风电机组的工作环境极其恶劣,导致风电大数据中往往包含大量异常数据。异常数据的存在将使风电智能运维的效果大打折扣,因此,对风电大数据进行异常识别和清洗成为一项重要的工作。
风功率数据作为风力发电运行的核心数据,对其进行有效的异常识别和清洗引起国内外学者的广泛关注[7]。目前,针对风电机组风功率的异常数据识别研究较为普遍,大体可以分为三种方法:第一种异常识别算法是基于统计规律,如3sigma[8]、四分位、方差[9]和方差变化率[10]等方法来识别异常数据,其仅在离散型和堆积型数据之一有明显优势;第二种异常识别算法是基于各个数据点之间的距离和密度来识别异常数据,常用算法有基于距离的局部离群因子(local outlier factor, LOF)算法、k-means和基于密度的噪声应用空间聚类(density-based spatial clus tering of applications with noise, DBSCAN)算法等,其异常识别速度慢,参数设置困难;第三种异常数据识别算法是基于风功率曲线的数据模型[11],常用的算法有Copula函数[12]等,其对大量异常值识别效果不佳。此外,文献[13]提出一种基于Thompson tau-四分位的风电功率异常数据识别方法,但容易造成正常数据误识别现象。文献[14-15]利用图像分割和边缘检测等图像处理技术识别风电机组的异常数据,但需要专家经验构建标准的风功率曲线。文献[16]利用风机机组原理对异常数据识别,结合四分位法清洗叶尖速比和风功率散点。文献[17]针对风功率曲线的不同异常数据类型,提出相应的异常数据清洗算法。
然而,风电场内部往往拥有数十台独立运行的风电机组,受风电机组地理位置和高度差异性的影响,叠加各风电机组之间的聚合效应,风电场的风功率数据分布相对于单台风电机组更加复杂和混乱,故对风电场风功率异常数据识别的难度更大。目前,针对风电场风功率数据的异常检测工作相对较少。文献[18]利用四分位法对风电场的输出功率异常数据进行识别,但当异常数据比例较大时,清洗效果不好。文献[19]提出利用四分位和k-means组合的方法去识别风电场风功率的异常数据,其中四分位法用来识别离散型异常数据,k-means用来识别堆积型异常数据,但清洗结果受k的取值影响比较大。文献[20]分析风电场在弃风限电情况下的时序数据,提出分段判定方法识别,但爬坡率阈值的选取直接影响限风数据的识别效果。文献[21]利用LOF对风电场的风功率异常数据进行识别,但在大量堆积型异常点情况下,LOF算法的异常识别效果有待提高。文献[22]基于Copula理论,提出一种基于概率风电场功率曲线和典型异常值特征的异常值识别方法,但大量异常值会对联合概率密度函数的拟合产生影响。文献[23]提出一种基于DBSCAN的半监督异常检测方法,利用有限量的标记数据来监督指导风电场异常数据的检测过程,但识别密度较高的堆积型数据能力较差。文献[24]提出四分位-DBSCAN的异常识别方法,四分位法被用于剔除稀疏异常点,DBSCAN被用于剔除堆积型异常点,但因每个风速区间共享相同的DBSCAN参数值,致使不同风速区间的清洗效果有待进一步优化。特别需要指出,对风电场风功率异常数据进行识别并有效清洗,有助于提高风电场功率预测精度,提升电网安全稳定和经济运行水平。
针对传统的基于方差相关的异常识别算法存在人为设置阈值过程漫长和整个风速区间采用固定阈值效果不佳等问题,文中提出基于方差变化率判据-四分位的组合方法实现风电场风功率异常数据的识别。通过该方法的研究,证明了组合方法更加有利于风电异常数据识别的观点。文中首先对5个风电场的运行数据质量进行简要分析,并对1号风电场的风功率异常数据分布和产生机理进行阐述;其次利用规则对风电场的风功率数据进行预处理,识别明显异常的数据点;接着利用方差变化率判据识别风功率曲线上下两侧的堆积型异常数据点;再利用四分位法识别剩余的离散型异常数据点;最后,通过宁夏风电场的实际算例验证所提异常数据识别方法的优越性和通用性。
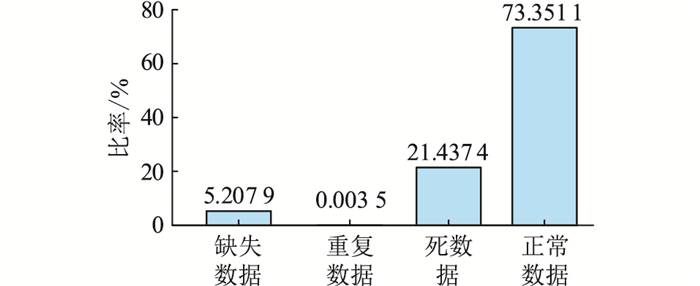
1 风电场站运行数据分析由于停机检修、弃风限电和风电机组发生故障等原因,风电场的运行大数据不可避免地存在着数据重复、数据缺失和数据异常等问题。文中以宁夏不同区域的5个风电场为研究对象,针对2020年的实际运行功率数据开展异常数据识别研究。图 1给出了5个风电场功率数据质量总体分析结果,由图可见缺失数据和死数据(长时间不变的物理量)平均所占比率分别达到5.21%和21.44%,而正常数据平均所占比率仅为73.35%。因此有必要对风电场开展功率数据异常识别工作。
|
图 1 风电场运行数据质量分析 Fig. 1 Quality analysis of wind farm data |
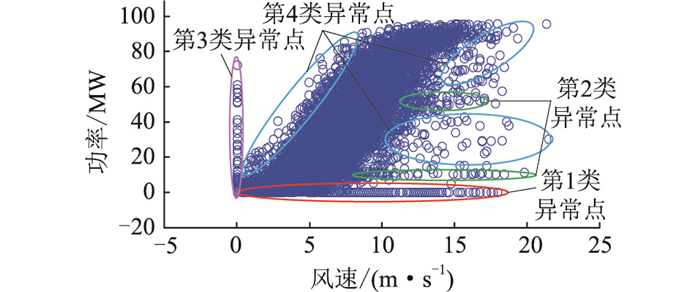
图 2为1号风电场的风功率散点图,考虑到1号风电场由33台同型号风电机组组成且轮毂高度均为80 m,故采用风电场测风塔80 m高度的风速数据和风电场实际输出功率绘制图 2。
|
图 2 1号风电场风功率散点 Fig. 2 Wind power scatter of wind farm No.1 |
由图 2可知,1号风电场风功率曲线中存在大量的离散型和堆积型异常数据点。根据异常数据点的形态分布和产生机理,可将异常数据可分为四类。
(1) 停机数据点。停机数据点一般分布在曲线最底部,易形成大量堆积点。其主要特征为:风速大于或者等于0,而风电的实际运行功率一般小于或者等于某阈值(阈值通常选取5 kW),偶尔会出现负功率现象。分析其原因主要有计划检修而停机、极端气候、风电机组故障、通信系统故障和测量装置故障等。
(2) 弃风限电数据点。该数据点一般分布在曲线中部的堆积数据点,其主要特征为:风速大于0且发生变化,而实际风功率在连续1~2 h内,基本维持在一个恒定功率值附近。分析其主要原因有:本地负荷或者计划调度功率远小于风电场站实际可发功率,只有进行弃风限电才能保证电网的调峰调频;同时网架结构的输出能力不足也会引发弃风限电。
(3) 曲线左上部的堆积型数据点。该数据点的主要特征为:风速为0,而风电的实际运行功率大于0。其产生的主要原因有风速仪异常或者通信系统
故障。
(4) 曲线周围的其他异常数据点。该数据点一般分布在曲线的周围,离散或者堆积出现。其主要特征为:一般无规律,离曲线距离较远或者密度较低。其产生的原因主要有通信系统故障、测量装置故障和极端气候。
2 风功率的异常数据识别算法基于风电场运行数据质量和风功率散点图的异常数据分布与形成原理分析,文中提出一种结合风功率方差变化率判据和四分位法的风电场风功率异常数据识别算法,主要步骤包括物理规则预处理、风功率方差变化率判据法、四分位法三个处理过程。其中,物理规则用于剔除一些明显异常的数据点,风功率方差变化率判据法针对大量的堆积型异常数据进行识别,四分位法对剩余的离散型异常数据进行识别。
2.1 物理规则的数据预处理考虑原始的风电场风功率数据集会存在缺失值和重复值。对缺失值的识别,一般判断数据是否含有NaN。针对缺失值,可根据缺失值占总数据比例的大小选择处理方法,若缺失值占比较大,一般通过均值和三次样条插值对数据进行填充;若缺失值所占比例较小,通常会直接删除缺失值所在行的数据。对于重复值的识别,一般判断前后数据是否保持一致。针对重复值,一般只保留最后一组数据。
在识别并处理缺失值和重复值之后,首先寻找风速v < 0的数据位置,删除含有负风速的数据行。然后,寻找风速大于0,但功率小于接近0的某个值(该值一般取5 kW),将该数据点标记为停机点并删除;其次,寻找功率大于0,但风速却小于接近0的某个值(一般取0.5 m/s),将其标记为风速仪异常点并剔除;最后将风速大于切出风速或功率大于风电场站额定功率的数据点进行剔除。
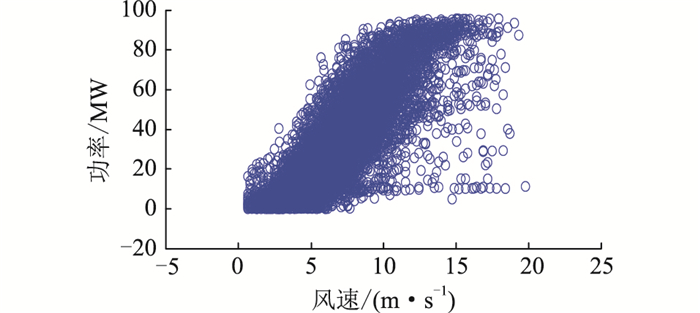
对图 2所示的1号风电场的原始风功率数据,经过删除缺失值、保留最后一组重复值和删除负风速数据行等预处理后,利用物理规则剔除停机点和风速仪异常点等明显异常数据点,得到如图 3所示的预处理结果。图 3中还存在大量的离散型和堆积型的异常数据点,还应进一步利用其他算法对异常数据进行识别和清洗。
|
图 3 基于物理规则的异常数据识别 Fig. 3 Physical rules based identification of abnormal data |
在数理统计中,若数据分布存在大量的堆积型异常数据点,统计量中的均值、方差、标准差、方差变化率和标准差变化率会发生突变。文中以风功率的方差变化率作为区分正常数据点和异常数据点的依据,当方差变化率小于阈值,数据点标记为正常值;而当方差变化率大于阈值,数据点标记为异常值。
利用风功率方差变化率判据识别异常数据的流程如下:首先,对经预处理后的风电场风功率数据集U按照风速区间划分数据子集,风速区间的划分间距一般取0.5 m/s,如式(1)所示。
| $ U=\{U(1), U(2), \cdots, U(m)\} $ | (1) |
式中:m=1, 2, …, W,其中W为风速总分区个数。
记某一个风速区间内的样本集合U(m),其表达如式(2)所示。
| $ U(m)=\left\{\left(v_1, p_1\right), \cdots, \left(v_i, p_i\right), \cdots, \left(v_n, p_n\right)\right\} $ | (2) |
式中:n为风速区间内的样本总数;vi为第i个数据样本的风速;pi为第i个数据样本的功率。
然后,针对每个子风速区间的功率数据,按照功率顺序从大到小排序,使得功率满足式(3)。
| $ p_{i+1}<p_i $ | (3) |
接着计算滑动差,实质是先计算风速每个区间内各个功率点的方差si,如式(4)所示。
| $ s_i=\frac{\sum\limits_{j=1}^i\left(p_j-\bar{p}_i\right)^2}{i} $ | (4) |
式中:pj为第j个数据样本点的功率值;pi为i个数据样本点的功率的平均值。
pi与该数据样本点之前所有功率数据的离散程度可以利用si来评估。在此基础上,方差一次变化率ki可用来判断方差是否发生明显变化,如式(5)所示。
| $ k_i=\frac{\left|s_i-s_{i-1}\right|}{d} \quad i=2, 3, \cdots, n $ | (5) |
式中:d为风速区间的划分间距。
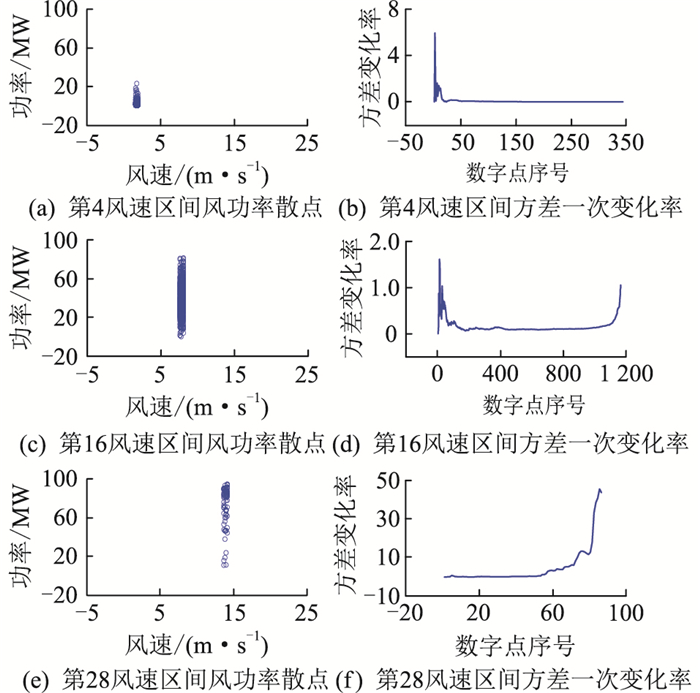
将图 3的风功率数据分为低、中、高三个风速段,低风速段风速为0~6 m/s,中风速段风速为6~12 m/s,高风速段风速为12~20 m/s。取风速区间的划分间距为0.5 m/s,得到如图 4所示的不同风速区间风功率散点图和方差变化率曲线,图中第4、第16、第28风速区间分别对应低、中和高风速段。
|
图 4 不同风速区间的风功率及其方差变化率 Fig. 4 Wind power and variance change rate at different wind speed regions |
在图 4(a)中,第4风速区间风功率散点图的异常点在功率集合的上侧,当数据点序号在0—20,其对应的方差一次变化率先增加再减小直至趋于0。而当数据点序号在20—343,其对应的方差一次变化率基本保持在0.1以下。在图 4(b)中,第16风速区间风功率散点图的异常点在功率集合的上侧和下侧;当数据点序号在0—200,其对应的方差一次变化率先增加至1.6,再减小至0.1。当数据点序号在200—1 000,其对应的方差一次变化率基本维持0.1附近,当数据点序号在1 000—1 156,其对应的方差一次变化率从0.1增加至1.0。在图 4(c)中,第28风速区间风功率散点图的异常点在功率集合的下侧,当数据点序号在0—50,其对应的方差一次变化率基本维持在1.0以下,而当数据点序号在50—86,其对应的方差变化率从0.47增加至44。
通过上述对风电场的低、中和高风速段的风功率方差一次变化率的分析,可以人为地计算每个风功率数据点所对应的ki,并设置合适的方差变化率阈值kv。通过对ki和kv进行比较,可以识别出第m个风速区间内风功率数据中的正常值Un(m)和异常值Ul(m),如式(6)和式(7)所示。
| $ U_{\mathrm{n}}(m)=\left\{\left(x_i, y_i\right) \mid\left(x_i, y_i\right) \in U(m), k_i \leqslant k_{\mathrm{v}}\right\} $ | (6) |
| $ U_1(m)=\left\{\left(x_i, y_i\right) \mid\left(x_i, y_i\right) \in U(m), k_i>k_v\right\} $ | (7) |
最后,按照上述操作流程,对风电场每个风速子区间的正常数据和异常数据处理结果进行归类整理,可以得到整个风电场站总的正常数据集Vn和异常数据集Vl,如式(8)和式(9)所示。
| $ V_{\mathrm{n}}=\left\{U_{\mathrm{n}}(1), U_{\mathrm{n}}(2), \cdots, U_{\mathrm{n}}(N)\right\} $ | (8) |
| $ V_1=\left\{U_1(1), U_1(2), \cdots, U_1(W-N)\right\} $ | (9) |
式中:N为正常区间数。
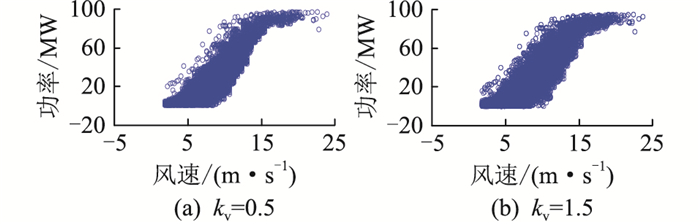
在基于物理规则对原始数据处理的基础上,利用风功率方差变化率判据对风功率异常数据的识别结果如图 5所示。相比图 3的基于物理规则的识别结果,基于方差变化率判据的异常数据识别方法清洗了风功率曲线下方的大部分异常数据和风功率曲线上方的小部分异常数据。
|
图 5 基于方差变化率的异常数据识别 Fig. 5 Anomaly data identification based on variance change rate |
图 5(a)和5(b)分别是方差变化率阈值kv=0.5和kv=1.5情况下的识别结果。在图 5(a)中,风功率曲线上方仅存在少数异常点,但风功率曲线的下方存在过度识别;在图 5(b)中,风功率曲线下部的异常点基本被完全识别,但风功率曲线上方的异常效果不及图 5(a)。
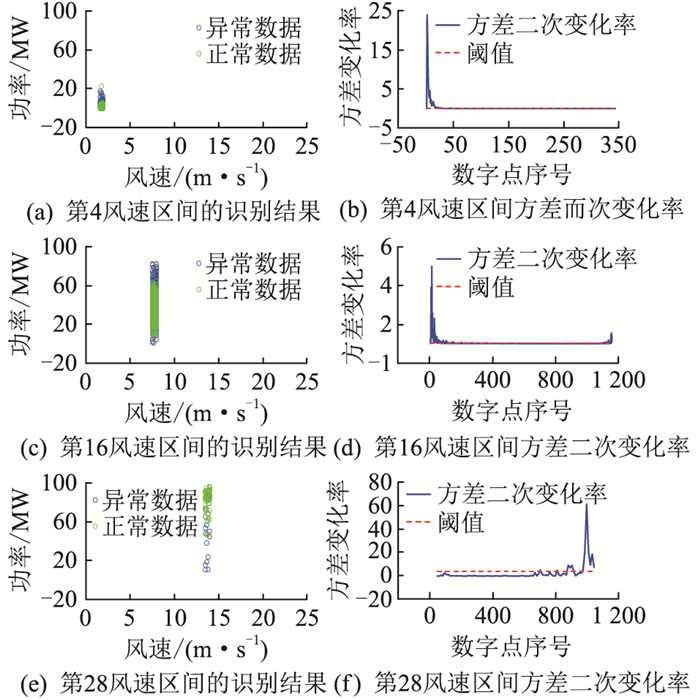
考虑人为选取风功率方差变化率阈值的过程较为漫长,且整个风速区间采用固定阈值效果不佳,因此文中进一步对方差变化率取差分,图 4中3个风速区间所对应的方差二次变化率如图 6所示,风功率方差二次变化率曲线平缓部分对应风功率正常点,而风功率方差二次变化率曲线非平稳区段对应风功率异常点。为了识别风功率异常点,文中利用箱型图(四分位法的原理),根据每个风速区间的风功率数据整体分布来识别出风功率方差二次变化率曲线非平稳区段。值得一提的是,文中只将方差二次变化率hi大于箱型图的外限hv所对应的数据识别为异常数据,因此可得式(10)。
|
图 6 风功率方差二次变化率曲线及异常识别结果 Fig. 6 Wind power variance quadratic change rate curve and anomaly identification result |
| $ U_{\mathrm{n}}(m)=\left\{\left(x_i, y_i\right) \mid\left(x_i, y_i\right) \in U(m), h_i \leqslant h_{\mathrm{v}}\right\} $ | (10) |
图 6(a)、6(c)和6(e)中的红色虚线是箱型图自动选取的方差二次变换率阈值,可见该方法能够较好地将各个风速区间的风功率方差二次变化率曲线平缓段和非平稳段区分出来。图 6(b)、6(d)和6(f)是利用箱型图自动选取的阈值对各个风速区间的识别结果,可见对堆积型异常点识别效果较好。
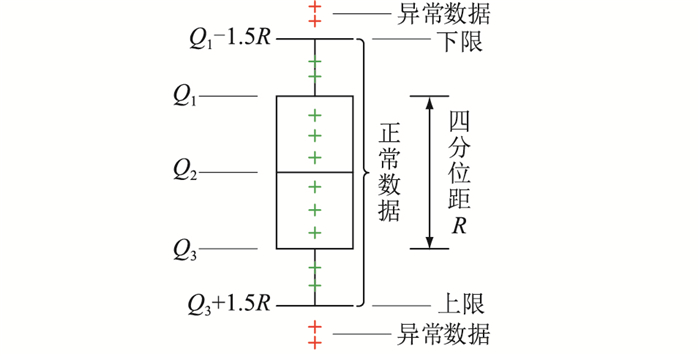
2.3 四分位法在对风电场的风功率数据进行物理规则预处理和方差变化率判据处理之后,可利用四分位法对剩余的风功率数据集进一步处理。如图 7所示四分位法的原理,将按照升序进行排列的数据样本X={x1, x2, …, xn}进行四分位法异常识别,流程如下:首先计算第一四分位数Q1和第三四分位数Q3;然后计算Q3与Q1之差作为四分位距R;近一步计算四分位的上限Fu和下限Fl,其中Fu为Q3与1.5R之和,Fl为Q1与1.5R之差;最后,四分位法把X处于[Fl, Fu]之间的数据识别为正常数据,而把X处于[Fl, Fu]之外的数据识别为异常数据。
|
图 7 四分位法示意 Fig. 7 Schematic diagram of the quartile method |
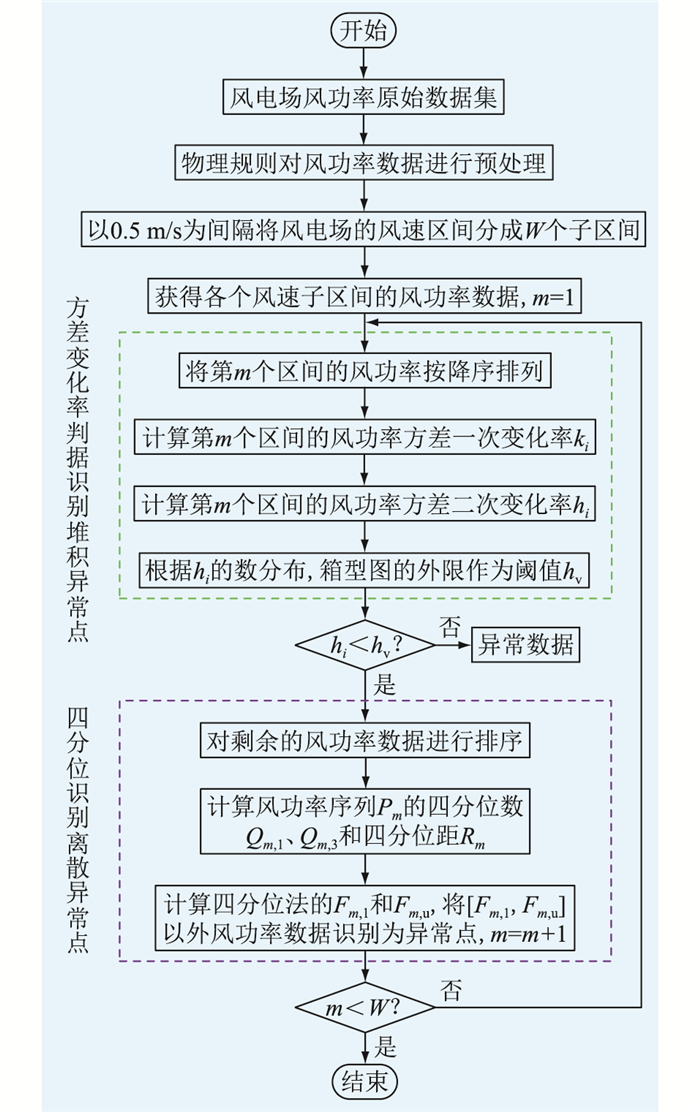
经过对风功率方差变化率判据法及四分位法进行异常值识别过程分析,建立基于风功率方差变化率判据-四分位法进行风电场风功率异常数据识别。其详细流程如图 8所示,输入的风电场风功率数据经过物理规则处理后,将风速数据按照从小到大顺序排序,并将最小风速与最大风速之间的数据按某区间宽度(通常取0.5 m/s)等分成若干个风速区间;然后依次对每个风速区间的功率数据利用风功率方差变化率判据法识别出堆积异常点,利用四分位法识别离散异常点;重复风功率方差变化率判据法和四分位法的步骤,直到识别出整个风电场的风功率异常数据点。
|
图 8 风电场风功率异常数据识别流程 Fig. 8 Flow chart of wind power anomaly data identification in wind farm |
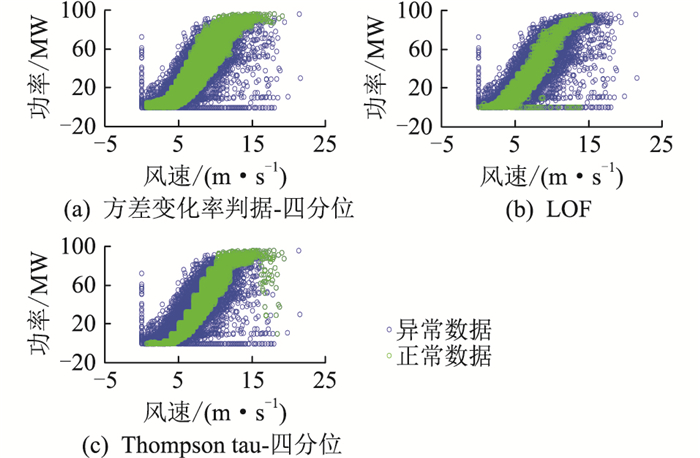
考虑所提的风功率方差变化率判据的异常数据识别算法可以有效自动识别出大部分堆积型异常数据点,而四分位法的异常数据识别算法可以有效自动识别出大部分离散型异常数据点,因此将两种方法进行组合。组合算法对1号风电场的识别效果如图 9所示,图中蓝色的风功率数据点为识别出异常数据点,而绿色的风功率数据点为正常数据点,图 9(a)是方差变化率判据-四分位的识别效果,可见基于方差变化率判据-四分位基本对经过物理规则预处理后风功率数据的异常数据高效识别,说明所提算法可以有效识别风电场的离散型和堆积型异常数据点。为了说明文中所提算法对风电场风功率数据识别的优越性,对1号风电场的数据集采用基于LOF和Thompson tau-四分位算法进行异常数据识别,异常识别结果如图 9(b)和9(c)所示。考虑方差变化率判据-四分位法对异常数据的识别率36.33%,故LOF的样本中异常点的比例设为35%,选择的领域点个数为20。对比图 9(a)与图 9(b),在原始数据总量和异常数据识别率近似的情况下,LOF算法对堆积型数据的识别效果不佳。图 9(c)是基于Thompson tau-四分位对1号风电场的识别效果,其在风功率曲线上侧存在过识别,而在风功率曲线的尾部存在离散型数据未有效识别。
|
图 9 1号风电场风功率的异常数据识别 Fig. 9 Anomaly data identification of wind power at wind farm No.1 |
为了有效量化风功率数据异常识别的效果,常采用均方根误差来表征风功率曲线建模时的误差,并对比异常数据剔除前后的误差大小[24, 28]。风功率的均方根误差eRMSE,如式(11)所示。
| $ e_{\mathrm{RMSE}}=\sqrt{\frac{1}{M} \sum\limits_{i=1}^M\left(\hat{p}_i-p_i\right)^2} $ | (11) |
式中:M为功率数据的个数;
异常识别率定义为异常剔除的数据量与剔除前数据点数量之比[28],如式(12)所示。
| $ \gamma=\frac{N_{\mathrm{b}}-N_{\mathrm{a}}}{N_{\mathrm{b}}} \times 100 \% $ | (12) |
式中:Nb为异常剔除之前数据点的数量;Na为异常剔除之后数据点的数量。
对比各种识别算法的效果如表 1所示,各种算法都是基于MATLAB 2021a和台式机(Intel(R) Core(TM) i9-10900K CPU @ 3.70GHz 16GB RAM)上运行实现的,表中耗时为连续运行10次算法的平均时间。LOF识别算法耗时最长,Thompson tau-四分位法的识别率最高,大量正常数据被误识别,方差变化率判据-四分位的识别算法耗时最短。对于一个好的异常识别算法,其所对应的风功率曲线建模的均方根误差eRMSE和异常识别率γ应尽可能小[28]。综合从异常识别率、均方根误差和耗时等角度去对比无操作、LOF、Thompson tau-四分位和方差变化率判据-四分位等异常识别算法,文中所提的算法不论从定性还是定量的角度,其异常数据识别的性能皆优于其他几种异常识别算法。
|
|
表 1 不同算法的识别效果对比 Table 1 Comparison of identify effects of different algorithms |
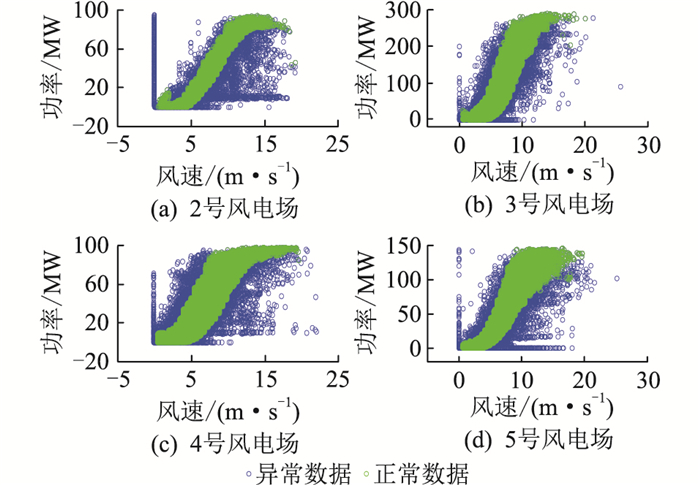
为了进一步验证文中所提算法的有效性,对其他4个风电场的风功率数据进行异常数据识别,识别结果如图 10所示。
|
图 10 2号、3号、4号和5号风电场的数据识别效果 Fig. 10 Identification effect of wind farm No.2, 3, 4, 5 |
4个风电场皆实现了风功率数据的正常数据和异常数据的有效区分。4个风电场的风功率数据的数据分布、异常数据占比和异常数据形态都不一致,而识别结果却皆与理想的风功率曲线相似,说明此方法针对不同风电场均有效。
4 结论文中针对风电场的风功率运行数据,先利用物理规则对数据集进行预处理,剔除一些明显异常的数据点。在此基础上,利用风功率方差变化率判据和四分位的组合方法来自动识别剩余的堆积型和离散型异常数据点,主要结论如下:
(1) 所提出的基于方差变化率判据-四分位的风功率异常数据识别算法可以同时识别风电场的停机、弃风限电、风功率曲线左上方的堆积型和周围的其他离散型等异常点。
(2) 基于方差变化率判据-四分位法的风功率异常数据识别算法的异常数据识别效果优于已有LOF和Thompson tau-四分位方案,同时通过多个风电场的应用验证了所提方法的有效性。
(3) 所提的基于方差变化率判据-四分位的风功率异常识别算法利用箱型图自动选取每个风速子区间的判据阈值,克服了人为设置阈值过程漫长和整个风速区间采用固定阈值效果不佳等问题。
在文中风电场风功率异常数据识别的基础上,下一步着重研究风电场风功率数据异常数据清洗算法,对缺失数据和误剔除数据进行高效重构研究。
| [1] |
姚钢, 杨浩猛, 周荔丹, 等. 大容量海上风电机组发展现状及关键技术[J]. 电力系统自动化, 2021, 45(21): 33-47. YAO Gang, YANG Haomeng, ZHOU Lidan, et al. Development status and key technologies of large-capacity offshore wind turbines[J]. Automation of Electric Power Systems, 2021, 45(21): 33-47. (  0) 0) |
| [2] |
向东, 陈松, 季益俊, 等. 智能化含风电配电网多目标协同调度模型[J]. 电网与清洁能源, 2022, 38(7): 127-133, 140. XIANG Dong, CHEN Song, JI Yijun, et al. An intelligent multi-objective collaborative dispatching model for distribution networks containing wind power[J]. Power System and Clean Energy, 2022, 38(7): 127-133, 140. (  0) 0) |
| [3] |
禹海峰, 黄婧杰, 蒋诗谣, 等. 计及储能使用年寿命的风电场整体性储能配置[J]. 电力科学与技术学报, 2022, 37(4): 152-160. YU Haifeng, HUANG Jingjie, JIANG Shiyao, et al. The overall energy storage configuration of wind farms considering the service life of electric energy storage[J]. Journal of Electric Power Science and Technology, 2022, 37(4): 152-160. (  0) 0) |
| [4] |
孙蓉, 李强, 罗海峰, 等. 基于自适应移动平滑与时间卷积网络误差修正的风电功率预测[J]. 全球能源互联网, 2022, 5(1): 11-22. SUN Rong, LI Qiang, LUO Haifeng, et al. Wind power forecasting based on error correction using adaptive moving smoothing and time convolution network[J]. Journal of Global Energy Interconnection, 2022, 5(1): 11-22. (  0) 0) |
| [5] |
SHI W H, QU J X, WANG W S. Wind power operation capacity credit assessment considering energy storage[J]. Global Energy Interconnection, 2022, 5(1): 1-8. DOI:10.1016/j.gloei.2022.04.001 (  0) 0) |
| [6] |
CONG Z H, YU Y C, LI L Y, et al. Wind power time series simulation model based on typical daily output processes and Markov algorithm[J]. Global Energy Interconnection, 2022, 5(1): 44-54. DOI:10.1016/j.gloei.2022.04.004 (  0) 0) |
| [7] |
武佳卉, 邵振国, 杨少华, 等. 数据清洗在新能源功率预测中的研究综述和展望[J]. 电气技术, 2020, 21(11): 1-6. WU Jiahui, SHAO Zhenguo, YANG Shaohua, et al. Review and prospect of data cleaning in renewable energy power prediction[J]. Electrical Engineering, 2020, 21(11): 1-6. DOI:10.3969/j.issn.1673-3800.2020.11.002 (  0) 0) |
| [8] |
OUYANG T H, KUSIAK A, HE Y S. Modeling wind-turbine power curve: a data partitioning and mining approach[J]. Renewable Energy, 2017, 102: 1-8. DOI:10.1016/j.renene.2016.10.032 (  0) 0) |
| [9] |
杨茂, 杨春霖, 杨琼琼, 等. 计及风向信息的风电功率异常数据识别研究[J]. 太阳能学报, 2019, 40(11): 3265-3272. YANG Mao, YANG Chunlin, YANG Qiongqiong, et al. Study on data recognition of wind power abnormality considering wind direction information[J]. Acta Energiae Solaris Sinica, 2019, 40(11): 3265-3272. (  0) 0) |
| [10] |
SHEN X J, FU X J, ZHOU C C. A combined algorithm for cleaning abnormal data of wind turbine power curve based on change point grouping algorithm and quartile algorithm[J]. IEEE Transactions on Sustainable Energy, 2019, 10(1): 46-54. (  0) 0) |
| [11] |
WANG Y, HU Q H, LI L H, et al. Approaches to wind power curve modeling: a review and discussion[J]. Renewable and Sustainable Energy Reviews, 2019, 116: 109422. (  0) 0) |
| [12] |
马然, 栗文义, 齐咏生. 风电机组健康状态预测中异常数据在线清洗[J]. 电工技术学报, 2021, 36(10): 2127-2139. MA Ran, LI Wenyi, QI Yongsheng. Online cleaning of abnormal data for the prediction of wind turbine health condition[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2127-2139. (  0) 0) |
| [13] |
邹同华, 高云鹏, 伊慧娟, 等. 基于Thompson tau-四分位和多点插值的风电功率异常数据处理[J]. 电力系统自动化, 2020, 44(15): 156-162. ZOU Tonghua, GAO Yunpeng, YI Huijuan, et al. Processing of wind power abnormal data based on Thompson tau-quartile and multi-point interpolation[J]. Automation of Electric Power Systems, 2020, 44(15): 156-162. (  0) 0) |
| [14] |
LONG H, SANG L W, WU Z J, et al. Image-based abnormal data detection and cleaning algorithm via wind power curve[J]. IEEE Transactions on Sustainable Energy, 2020, 11(2): 938-946. (  0) 0) |
| [15] |
WANG Z J, WANG L, HUANG C. A fast abnormal data cleaning algorithm for performance evaluation of wind turbine[J]. IEEE Transactions on Instrumentation and Measurement, 2021, 70: 1-12. (  0) 0) |
| [16] |
梅勇, 李霄, 胡在春, 等. 基于风电机组控制原理的风功率数据识别与清洗方法[J]. 动力工程学报, 2021, 41(4): 316-322, 329. MEI Yong, LI Xiao, HU Zaichun, et al. Identification and cleaning of wind power data methods based on control principle of wind turbine generator system[J]. Journal of Chinese Society of Power Engineering, 2021, 41(4): 316-322, 329. (  0) 0) |
| [17] |
LUO Z H, FANG C Y, LIU C L, et al. Method for cleaning abnormal data of wind turbine power curve based on density clustering and boundary extraction[J]. IEEE Transactions on Sustainable Energy, 2022, 13(2): 1147-1159. (  0) 0) |
| [18] |
朱倩雯, 叶林, 赵永宁, 等. 风电场输出功率异常数据识别与重构方法研究[J]. 电力系统保护与控制, 2015, 43(3): 38-45. ZHU Qianwen, YE Lin, ZHAO Yongning, et al. Methods for elimination and reconstruction of abnormal power data in wind farms[J]. Power System Protection and Control, 2015, 43(3): 38-45. (  0) 0) |
| [19] |
赵永宁, 叶林, 朱倩雯. 风电场弃风异常数据簇的特征及处理方法[J]. 电力系统自动化, 2014, 38(21): 39-46. ZHAO Yongning, YE Lin, ZHU Qianwen. Characteristics and processing method of abnormal data clusters caused by wind curtailments in wind farms[J]. Automation of Electric Power Systems, 2014, 38(21): 39-46. (  0) 0) |
| [20] |
张东英, 李伟花, 刘燕华, 等. 风电场有功功率异常运行数据重构方法[J]. 电力系统自动化, 2014, 38(5): 14-18, 24. ZHANG Dongying, LI Weihua, LIU Yanhua, et al. Reconstruction method of active power historical operating data for wind farm[J]. Automation of Electric Power Systems, 2014, 38(5): 14-18, 24. (  0) 0) |
| [21] |
ZHENG L, HU W, MIN Y. Raw wind data preprocessing: a data-mining approach[J]. IEEE Transactions on Sustainable Energy, 2015, 6(1): 11-19. (  0) 0) |
| [22] |
YE X, LU Z X, QIAO Y, et al. Identification and correction of outliers in wind farm time series power data[J]. IEEE Transactions on Power Systems, 2016, 31(6): 4197-4205. (  0) 0) |
| [23] |
ZHOU Y F, HU W, MIN Y, et al. A semi-supervised anomaly detection method for wind farm power data preprocessing[C]//2017 IEEE Power & Energy Society General Meeting. Chicago, IL, USA. IEEE, 2018: 1-5.
(  0) 0) |
| [24] |
ZHAO Y N, YE L, WANG W S, et al. Data-driven correction approach to refine power curve of wind farm under wind curtailment[J]. IEEE Transactions on Sustainable Energy, 2018, 9(1): 95-105. (  0) 0) |
2. Key Laboratory of Medical Electronics and Digital Health of Zhejiang Province, Jiaxing 314001, China;
3. Jiangsu Goldwind Software & Technology Co., Ltd., Wuxi 214000, China
 2023, Vol. 42
2023, Vol. 42


 吴永斌(1995),男,博士在读,研究方向为永磁同步电机和高压断路器故障诊断、风功率异常数据识别与清洗、新能源惯量阻尼控制等;
吴永斌(1995),男,博士在读,研究方向为永磁同步电机和高压断路器故障诊断、风功率异常数据识别与清洗、新能源惯量阻尼控制等;