文章编号: 2096-3203(2023)04-0133-08 中图分类号: TM73
2. 国网浙江省电力有限公司温州供电公司,浙江 温州 325000;
3. 东南大学电气工程学院,江苏 南京 210096
随着电力系统向清洁低碳转型,以风电、光伏为代表的新能源得到了大力发展,在电网中所占比例越来越高[1-4]。为解决新能源高渗透率下存在的弃风弃光[5]现象,在传统机组的基础上,须充分调动需求侧资源[6-7],提高电网的消纳能力。空调负荷调度方式灵活、可调控性强[8],是可利用的重要需求侧资源。
直接负荷控制(direct load control,DLC)是空调负荷参与需求侧调节的主要方式[9]。文献[10]概述了空调负荷参与DLC的基本要求,并提出了一个通用优化框架,在降低馈线负载量的基础上,最大程度减少对用户热舒适性的影响。文献[11]提出了一种基于空调等温控负荷开关状态的控制策略,以实现连续调节储备。文献[12]基于集群空调负荷的虚拟储能特性和储能容量,提出了联合系统出力跟踪策略,以消纳风电资源。文献[13]提出了一种考虑时间约束的空调控制策略,并设计了群组削峰算法。上述文献在对空调负荷进行调控时,都是将预设的温度区间作为空调负荷的启停约束,但用户的热舒适度不只受到室内温度的影响,还受到其他环境因素和人体因素的影响[14],仅考虑室内温度难以衡量用户真实的热舒适体验。丹麦的Fanger教授提出了热舒适度模型,从环境因素和人体因素2个维度出发,综合量化了用户的热舒适感受。
目前,在空调调控过程中考虑热舒适度模型的研究较少。文献[15]提出了一种基于热舒适度模型的DLC策略,以最小化空调机组功率和甩负荷指令之间的偏差值。文献[16]在文献[15]的基础上,将热舒适度指标建模为目标函数的惩罚项,并提出了一种在调度周期内最大化可中断容量的DLC模型。文献[17]从发电侧和用户侧分别提出了不同的控制策略,发电侧以追踪误差最小为目标函数,用户侧以热舒适不满意度最小为目标函数,从而在功率跟踪误差和人体热舒适之间取得平衡。上述文献为文中研究热舒适度模型提供了理论和技术基础,但文献[15-17]只考虑了一种人群的热舒适性,没有兼顾用户群体的多样性。不同用户群体之间的热忍受能力存在差异,对热舒适温度区间的要求不同,若统一调度,会直接影响用户参与响应的积极性[18]。
针对上述问题,文中引进热舒适度模型,量化调度过程中用户的热舒适体验。根据热舒适度模型中的人体参数,通过聚类的方式划分出具有不同热忍受能力特征的用户群体。在此基础上,提出基于用户差异化热舒适度的空调DLC策略,以每类用户群体的舒适阈值作为空调的启停约束。最后通过算例验证可知,文中所提策略与传统策略相比,能在确保消纳任务完成的基础上挖掘每类人群的调度潜力,让热忍受能力强的用户多出力,热忍受能力弱的用户少出力,且确保每类人群的热舒适性。
1 热舒适度模型和空调模型 1.1 热舒适度模型在空调调度过程中,用户的热舒适体验是需要考虑的重要因素。以往研究大多基于经验预设用户的热舒适温度区间,但这无法反映用户真实的热舒适度情况[19]。文中引进热舒适度模型,综合了环境参数和人体参数,通过计算预测平均投票值(pre dicted mean vote,PMV)和预测不满意度百分比(pre dicted percent dissatisfied,PPD)来准确刻画用户的热舒适体验。
PMV包含了4个独立的环境参数(室内温度、平均辐射温度、空气流动速度、空气湿度)和2个独立的人体参数(人体能量代谢率、服装热阻)。PMV代表了绝大多数人在同一环境下的冷热体验[20],其计算公式为:
| $ \begin{gathered} f_{\mathrm{PMV}}=\left(0.303 \mathrm{e}^{-0.036 M}+0.028\right)\{(M-W)- \\ 3.05 \times 10^{-3}\left[5733-6.99(M-W)-p_{\mathrm{a}}\right]- \\ 0.42(M-W-58.15)-1.7 \times 10^{-5} M\left(5867-p_{\mathrm{a}}\right)- \\ 0.0014 M\left(34-t_{\text {in }}\right)-3.96 \times 10^{-8} f_{\mathrm{cl}}\left[\left(t_{\mathrm{cl}}+273\right)^4-\right. \\ \left.\left.\left(\bar{t}_{\mathrm{r}}+273\right)^4\right]-f_{\mathrm{cl}} h_{\mathrm{c}}\left(t_{\mathrm{cl}}-t_{\mathrm{in}}\right)\right\} \end{gathered} $ | (1) |
式中:fPMV为PMV函数的取值; M为人体能量代谢率,与人体活动程度有关; W为人体活动产生的机械功; pa为环境的水蒸气压力,是相对湿度φ和室内温度tin的函数; fcl为着装系数,是服装热阻Icl的函数; tr为平均辐射温度; hc为对流换热系数,是室内温度tin、服装表面温度tcl和空气流速var的函数。tcl、fcl、pa、hc的计算如式(2)—式(5)所示。
| $ \begin{gathered} t_{\mathrm{cl}}=35.7-0.028(M-W)- \\ I_{\mathrm{cl}}\left\{3.96 \times 10^{-8} f_{\mathrm{cl}}\left[\left(t_{\mathrm{cl}}+273\right)^4-\right.\right. \\ \left.\left.\left(\bar{t}_{\mathrm{r}}+273\right)^4\right]+f_{\mathrm{cl}} h_{\mathrm{c}}\left(t_{\mathrm{cl}}-t_{\mathrm{in}}\right)\right\} \end{gathered} $ | (2) |
| $ f_{\mathrm{cl}}=\left\{\begin{array}{l} 1+1.29 I_{\mathrm{cl}} \quad I_{\mathrm{cl}} \leqslant 0.078 \\ 1.05+0.645 I_{\mathrm{cl}} \quad I_{\mathrm{cl}}>0.078 \end{array}\right. $ | (3) |
| $ p_{\mathrm{a}}=\varphi \times 10 \mathrm{e}^{16.653\;6-4\;030.183 /\left(t_{\mathrm{in}}+235\right)} $ | (4) |
| $ \begin{gathered} h_{\mathrm{c}}= \\ \left\{\begin{array}{l} 2.38\left|t_{\mathrm{cl}}-t_{\mathrm{in}}\right|^{0.25} 2.38\left|t_{\mathrm{cl}}-t_{\mathrm{in}}\right|^{0.25}>12.1 \sqrt{v_{\mathrm{ar}}} \\ 12.1 \sqrt{v_{\mathrm{ar}}} \quad 2.38\left|t_{\mathrm{cl}}-t_{\mathrm{in}}\right|^{0.25} \leqslant 12.1 \sqrt{v_{\mathrm{ar}}} \end{array}\right. \end{gathered} $ | (5) |
由于用户个体间存在差异,对冷热感觉并不完全相同,因此PPD参数被提出,用来表示人体对当前环境温度不满意的百分数,即热舒适不满意程度。PPD计算公式为:
| $ f_{\mathrm{PPD}}=100-95 \mathrm{e}^{-\left(0.033\;53 f_{\mathrm{PMV}}^4+0.217\;9 f_{\mathrm{PMV}}^2\right)} $ | (6) |
式中:fPPD为PPD函数的取值。由式(6)可知,当fPMV=0时,fPPD取最小值5%。即在最适宜的热环境下,人体的热舒适不满意度依然有5%。
1.2 空调热动力学模型空调负荷通过开关动作,使所属系统的室内温度稳定在预期的范围内。由空调开关状态引起的室内温度变化过程可用一阶常微分方程模拟[21-22]:
| $ \dot{T}_{\text {in }}(t)=\frac{1}{C_{\mathrm{th}} R_{\mathrm{th}}}\left(T_{\text {out }}(t)-T_{\mathrm{in}}(t)-s(t) R_{\mathrm{th}} P_{\text {rate }}\right) $ | (7) |
式中:Cth、Rth分别为空调负荷的等效热容和等效阻抗; Tin(t)为t时段的室内温度; Tout(t)为t时段的室外温度; Prate为空调的额定功率值;s(t)为t时段空调的开关状态,s(t)=0说明t时段空调处于关闭状态,该时段室内温度会升高,s(t)=1说明t时段空调处于开启状态,该时段室内温度会降低。
若空调机组由N个空调组成的,则空调机组的功率计算公式为:
| $ P^{\text {rate }, \mathrm{G}}(t)=\sum\limits_{n=1}^N \frac{1}{\gamma_n} P_{\text {rate }, n} $ | (8) |
式中:Prate, G(t)为t时段该机组的实际功率值;γn为第n个空调的性能系数; Prate, n为第n个空调的额定功率值。
2 人群划分 2.1 用户差异化的PPD聚类方法用户能量代谢率和服装热阻的不同, 会导致其热忍受能力存在差异。故文中基于PPD中的独立人体参数,将具有相似热忍受能力特征的用户聚集成新的用户群,再对其进行调度。
夏季夜晚,用户一般是处于休闲放松的状态。人体参数的取值[16-19]如表 1所示。人体能量代谢率M的取值范围为[40.74,69.84] W/m2,服装热阻Icl的取值范围为[0.1,0.5] clo。人体活动程度越剧烈,M值就越大; 服装越厚重,Icl值就越大。
|
|
表 1 人体参数的取值 Table 1 The values of human body parameters |
假设在调度区域内,有I个空调用户,I值足够大。同一调度区域的用户所处环境相似,故将除室内温度以外的独立环境参数赋值为夏季典型日的常数值。随机生成在表 1范围内的[Mi, (Icl)i]数组,用于表示第i个用户的人体特性(i∈[1, I])。由式(1)和式(6)可知,当M值和Icl值发生变化时,fPPD最小时的室内温度值ta也会不同,故须求解每个[Mi, (Icl)i]数组对应的(ta)i。在得到各用户最适宜的室内温度值(ta)i后,将各用户的室内温度值设为(ta)i+m,为使fPPD值变化幅度更大,m取值为2。计算此时各用户的fPPD值, 形成[Mi, (Icl)i, (fPPD)i]数组。
在相同的温度变化下,热忍受能力强的用户对温度变化不敏感,fPPD值会较小;热忍受能力弱的用户对温度变化敏感,fPPD值会较大。通过对[Mi, (Icl)i, (fPPD)i]中的fPPD值聚类,便可完成对用户群体的划分。K-means算法作为无监督的聚类算法,有实现便捷、聚类效果良好等优点。可使用K-means算法达到对用户划分的目的,具体的算法流程如图 1所示。

|
图 1 K-means聚类流程 Fig. 1 Flow chart of K-means clustering |
人群划分结果如图 2所示,用户被划分为具有不同热忍受能力特征的5类群体,即A类—E类。fPPD值越小说明该类人群对温度变化越不敏感,热忍受能力越强。故A类人群的热忍受能力是最强的,而E类人群的热忍受能力是最弱的,即由A到E,热忍受能力由强到弱。

|
图 2 人群划分结果 Fig. 2 Group division results |
选取每类最接近质心的三维数组,将数组中的M值和Icl值作为该类人群的人体参数代表值。表 2反映的是每类人群的热舒适特征,从表 2中可以看出,热忍受能力越强的用户群体,M值和Icl值就越大。这是因为人体活动程度越剧烈,代谢越快,人体产生的热量就越多;服装越厚重,储热能力就越好,此时人体对于环境的自适应能力越强,对温度变化越不敏感。但也是产热和储热的缘故,热忍受能力越强的用户群体在最适宜状态下要求的室内温度值也越小。
|
|
表 2 人群特征分析 Table 2 Analysis of population characteristic |
在第2章的基础上,文中提出一种基于用户差异化热舒适度的空调DLC策略。在微网系统中,负荷聚合商通过通信网络将风电装置、空调负荷和其他负荷进行连接。负荷聚合商在获取需要消纳的风电资源信息后,会下达指令给空调负荷和其他负荷。空调负荷和其他负荷将共同出力,消纳系统中的风电资源。微网调度结构示意如图 3所示。

|
图 3 微网调度结构 Fig. 3 Microgrid scheduling structure |
目标函数:
| $ \min f=\sum\limits_{t=1}^T\left|P_{\mathrm{ac}}(t)+P_{\text {other }}(t)-P_{\mathrm{w}}(t)\right| $ | (9) |
式中:Pac(t)为t时段空调负荷的出力功率值;Pother(t)为t时段除空调以外其他负荷的出力功率值;Pw(t) 为t时段风电装置的出力功率值;T为总时段数。若空调负荷用户可被划分为L类群体,每类群体含有J台空调机组,则t时段空调负荷的功率计算公式如下:
| $ P_{\mathrm{ac}}(t)=\sum\limits_{l=1}^L \sum\limits_{j=1}^J s_{j, l}(t) P_{j, l}^{\mathrm{rate}, \mathrm{G}} $ | (10) |
式中:j为空调机组编号; l为用户群体编号; sj, l(t)为第l类人群中第j台机组在t时段的开关状态; Pj, lrate, G为第l类人群中第j台机组的实际功率值。
空调负荷在调度过程中须满足以下约束。
(1) 功率平衡约束。
| $ P_{\text {tie }}(t)=P_{\mathrm{ac}}(t)+P_{\text {other }}(t)-P_{\mathrm{w}}(t) $ | (11) |
式中:Ptie(t)为t时段联络线上的功率值。联络线是微网与上级电网进行能量交换的通道,其分布的功率值应为微网系统中空调负荷和其他负荷出力值与风电出力值之差。
(2) PPD开关约束。
| $ s_{j, l}(t)= \begin{cases}0 \quad f_{j, l}^{\mathrm{PPD}}(t-\theta) \geqslant f_{\text {limit }}^{\mathrm{PPD}} \text { 且 } f_{j, l}^{\mathrm{PMV}}(t-\theta)<0 \\ 1 \quad f_{j, l}^{\mathrm{PPD}}(t-\theta) \geqslant f_{\text {limit }}^{\mathrm{PPD}} \text { 且 } f_{j, l}^{\mathrm{PMV}}(t-\theta) \geqslant 0 \\ s_{j, l}(t) \quad f_{j, l}^{\mathrm{PPD}}(t-\theta)<f_{\text {limit }}^{\mathrm{PPD}}\end{cases} $ | (12) |
式中: θ为无限小的时间长度; fj, lPMV(t-θ)、fj, lPPD(t-θ)分别为第l类人群中第j台机组在t-1时段末的PMV函数值和PPD函数值。式(12)的含义为: 空调机组在t时段的开关状态取决于其t-1时段末的fPPD值。当fPPD值超出阈值flimitPPD且处于较热的状态时,t时段应打开空调机组,进行降温操作;当fPPD值超出阈值flimitPPD且处于较冷的状态时,t时段应关闭空调机组,进行升温操作;当fPPD值处于舒适阈值范围内时,t时段空调机组的开关状态须通过求解目标函数式(9)来获取。在文中,此约束条件从第二个时段开始作用。
(3) 最小运行时间约束。为避免频繁开关造成的机械疲劳问题,对空调负荷的运行时间进行约束。
| $ \tau_{j, l}^{\mathrm{on}}(t) \geqslant \tau_{\min }^{\mathrm{on}} $ | (13) |
式中:τj, lon(t)为第l类人群中第j台机组在t时段的已运行时长;τminon为最小运行时间。τj, lon(t)的计算公式[23]为:
| $ \tau_{j, l}^{\text {on }}(t)=\left(\tau_{j, l}^{\text {on }}(t-1)+s_{j, l}(t) \Delta t\right) s_{j, l}(t) $ | (14) |
式中:Δt为每个时段的时长。
4 算例仿真 4.1 仿真参数设置文中以微网系统为调度背景,对所提策略进行仿真验证。可供调度的空调用户由2.2节中的5类人群组成,每类人群包含15台空调机组,每台空调机组包含100个空调,相同机组内的空调拥有相同的参数值和开关状态。
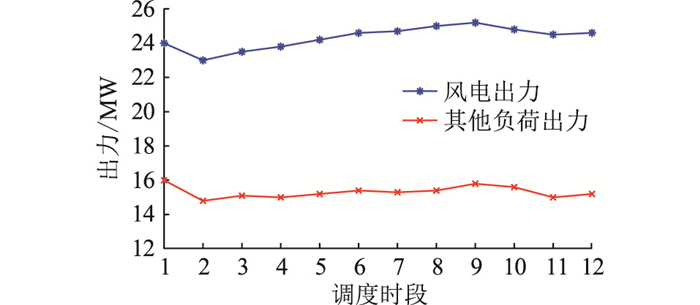
根据文献[24], Cth的取值范围为[0.001 5, 0.006 5] (kW ·h) ·℃-1 ·m-2,1/Rth的取值范围为[0.001, 0.003] (kW ·h) ·℃-1 ·m-2。为对比每类人群的出力情况,设空调额定功率值Prate为5 kW,空调性能系数γ为2.5,最小运行时间τminon为10 min; 根据ISO 7730,舒适阈值fPPDlimit设为30%。空调负荷的总调度时间分为12个时段,每个时段10 min。风电装置和其他负荷在各时段的出力情况见图 4。
|
图 4 风电和其他负荷出力 Fig. 4 Output of wind power and other loads |
文中将传统调度策略作为所提策略的对照策略。传统调度策略通过预设的温度区间,对空调负荷进行启停。根据文献[25], 当温度变化超过3 ℃,人体就会感觉明显的热不适,故将传统调度策略中第l类人群空调机组的运行温度区间设置为[(ta)l-3, (ta)l+3],每类人群的空调机组运行温度区间跨度均为6 ℃。以上2种策略均通过MATLAB的Yamlip工具箱建模,再通过Cplex求解器对模型进行求解。
4.2 仿真结果分析 4.2.1 热舒适度分析在传统调度策略下,每类人群中机组的热舒适情况见表 3,其中t0为调度中热不适总时长;fPPDmax为运行中fPPD的最大值。从表 3中可以看出,A类人群的机组和B类人群的机组在整个调度过程均处于热舒适状态,且热忍受能力最强的A类人群有11台机组热不适程度始终低于20%,热忍受能力较强的B类人群有6台机组热不适程度始终低于20%,故传统调度策略保障了热忍受能力相对较强的人群在调度中的热舒适性。而热忍受能力较弱的D类人群有11台机组在调度过程中热舒适超出了阈值,热不适时间最长达到了49 min(第9台机组),热不适程度最高达到了50.27%(第4台机组);热忍受能力最弱的E类人群有14台机组在调度过程中热舒适超出了阈值,热不适时间最长为81 min(第10台机组),热不适程度最高达到了78.86%(第4台机组)。这说明了传统调度策略无法保障热忍受能力相对较弱的人群在调度中的热舒适性。
|
|
表 3 传统调度策略下机组热舒适情况 Table 3 Thermal comfort of units under traditional scheduling strategy |
在文中所提策略下,每类人群机组的热舒适情况如表 4所示。
|
|
表 4 文中所提策略下机组热舒适情况 Table 4 Thermal comfort of units under strategy proposed in this paper |
从表 4中可以看出,在文中调度策略下仅有7台机组在调度过程中热舒适超出了阈值,每台机组热不适时间均小于5 min,热不适程度最高为33.77%(D类人群第15台机组),其余机组在整个调度过程中均处于热舒适状态。故文中所提策略有效保障了每类人群的热舒适性,空调机组即便在调度过程中超出了舒适阈值,在经过开关动作后,很快又回到了热舒适状态。
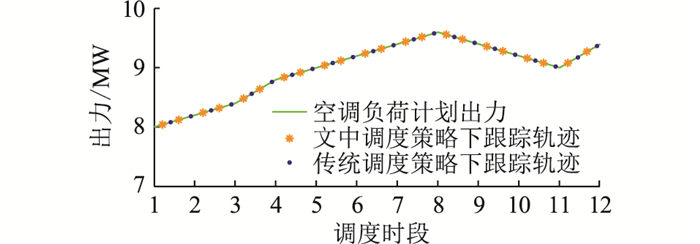
4.2.2 出力分析空调负荷计划以及实际的出力情况如图 5所示。2种策略下人群出力情况如表 5所示。
|
图 5 空调负荷计划及实际出力 Fig. 5 Air-conditioning load planned and actual output |
|
|
表 5 2种策略下人群出力 Table 5 Population output under two strategies |
从图 5中可以看出,在2种策略下,每类人群的空调机组协同运行,均可完成每个调度时段的指定消纳任务。但由表 5可知,2种策略的人群出力情况差异较大。文中调度策略中,热忍受能力越强的用户群体出力值就越大。热忍受能力最强的A类人群总出力值为23 400 kW,比热忍受能力最弱的E类人群多出力了3 800 kW。而在传统调度策略中,人群出力较为平均,并未体现差异性。
当独立人体参数值和其他独立环境参数值确定时,PPD为室内温度的函数。为揭示2种策略下人群出力差异性的原因,将文中调度策略中的PPD约束转化为对应的温度区间约束,如表 6所示。由表 6可知,当文中调度策略的PPD约束转化为温度区间约束后,热忍受能力越强的人群实际可调控的温度区间跨度就越大,故在文中调度策略下,热忍受能力越强的用户群体,出力越多。A、B 2类用户群体热忍受能力相对较强,实际可调控的温度区间跨度要大于传统调度策略的温度区间跨度,故A、B 2类用户群体在文中调度策略下的出力值要大于传统调度策略下的出力值。而D、E这2类热忍受能力相对较弱的用户群体对温度变化较为敏感,实际可调控的温度区间跨度要小于传统调度策略的温度区间跨度,故D、E 2类用户群体在文中调度策略下的出力值要小于传统调度策略下的出力值。在传统调度策略中,因每类人群设置的运行温度区间跨度均为6 ℃,故无法体现出人群出力的差异性。
|
|
表 6 约束转换 Table 6 Constraint transformation |
从机组运行角度来看,图 6和图 7分别反映了2种策略下A类和E类人群中机组运行的情况,其中黑色虚线为PPD约束转化而来的温度区间,也就是热舒适温度区间; 而红色虚线为传统调度策略中预设的温度区间。

|
图 6 2种调度策略下A类人群中机组运行情况 Fig. 6 Operation of class A crowd units under two scheduling strategies |
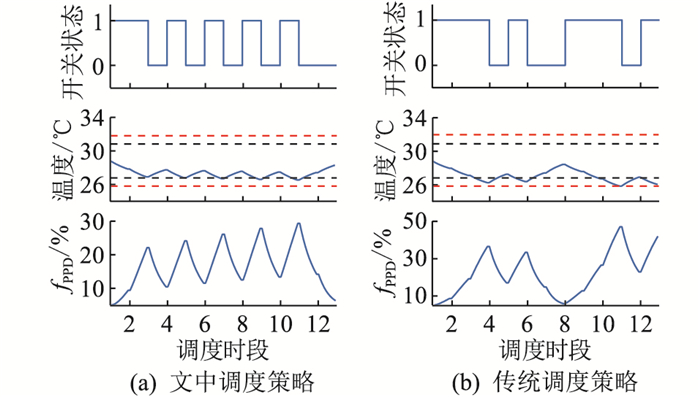
|
图 7 2种调度策略下E类人群中机组运行情况 Fig. 7 Operation of class E crowd units under two scheduling strategies |
传统调度策略无法量化每类人群的热舒适体验,故每类人群中的空调机组运行温度区间跨度均相同。由图 6可知,对于热忍受能力相对较强的用户群体而言,其机组在调度过程中室内温度只要低于红色温度区间下界,就须关闭升温、停止出力,但此时仍处于热舒适温度区间内部。而对于热忍受能力相对较弱的用户群体而言,如图 7所示,其机组在调度过程中室内温度已经超出了热舒适温度区间,但传统调度策略仍对其进行调控,导致其fPPD值超出舒适阈值。由此可知,传统调度策略无法挖掘热忍受能力相对较强的用户群体的调度潜力,且无法保障热忍受能力相对较弱的用户群体的热舒适性。而文中所提策略引入热舒适度模型,量化了每类人群在调度过程中的热舒适体验,增强对热忍受能力强的用户群体的调控力度,降低对热忍受能力弱的用户群体的调控力度,挖掘了每类人群的调度潜力。由图 6可知,在文中调度策略下,A类人群机组多出力了2个调度时段;而由图 7可知,在文中策略下,E类人群机组少出力了2个调度时段。且在调度过程中,2类人群中的机组均未超出舒适阈值,有效保证了其调度过程中的热舒适性。
5 结论文中根据热舒适度模型中的人体参数,将用户划分为具有不同热忍受能力特征的5类群体,并提出基于用户差异化热舒适度的调度策略。得出结论如下:
(1) 在人群划分方面,热忍受能力越强的用户群体,其M值和Icl值越大,最适宜状态下室内温度值越小。
(2) 在热舒适性方面,文中所提策略基本保障了每类人群在调度过程中的热舒适性。
(3) 在消纳效果方面,文中所提策略下的空调负荷在每个调度时段均能完成消纳任务,且热忍受能力越强的用户群体出力越多。
(4) 在调度潜力方面,文中所提策略以每类人群的舒适阈值为空调启停的开关约束,相较于传统策略,挖掘了各类人群的调度潜力。对于热忍受能力强的用户群体,加强对其调控的力度;而对于热忍受能力弱的用户群体,缩短对其的调控时间,确保其热舒适性。
文中所调度的空调负荷是处于同一区域的,故忽略了除室内温度以外的其他独立环境参数的变化。因此讨论在不同环境下差异化用户群体的空调负荷调度问题是今后工作的重点。
致谢
本文得到江苏省研究生实践创新项目(SJCX22_ 0569)资助,谨此致谢!
| [1] |
胡秦然, 丁昊晖, 陈心宜, 等. 美国加州2020年轮流停电事故分析及其对中国电网的启示[J]. 电力系统自动化, 2020, 44(24): 11-18. HU Qinran, DING Haohui, CHEN Xinyi, et al. Analysis on rotating power outage in California, USA in 2020 and its enlightenment to power grid of China[J]. Automation of Electric Power Systems, 2020, 44(24): 11-18. (  0) 0) |
| [2] |
陈维江, 赵国亮. 以新能源为主体的新型电力系统关键技术和装备[J]. 全球能源互联网, 2022, 5(1): 1. CHEN Weijiang, ZHAO Guoliang. Key technology and equipment of new power system based on renewable energy[J]. Journal of Global Energy Interconnection, 2022, 5(1): 1. (  0) 0) |
| [3] |
朱丽萍, 刘文颖, 胡阳, 等. 计及高比例新能源电网分区的输电线路功率双层优化模型[J]. 智慧电力, 2021, 49(7): 9-15. ZHU Liping, LIU Wenying, HU Yang, et al. Transmission line power bi-level optimization model considering high proportion new energy grid partition[J]. Smart Power, 2021, 49(7): 9-15. (  0) 0) |
| [4] |
LIANG H Q, HAN X N, YU H Y, et al. Transmission line fault-cause identification method for large-scale new energy grid connection scenarios[J]. Global Energy Interconnection, 2022, 5(4): 362-374. DOI:10.1016/j.gloei.2022.08.003 (  0) 0) |
| [5] |
李鹏, 王瑞, 冀浩然, 等. 低碳化智能配电网规划研究与展望[J]. 电力系统自动化, 2021, 45(24): 10-21. LI Peng, WANG Rui, JI Haoran, et al. Research and prospect of planning for low-carbon smart distribution network[J]. Automation of Electric Power Systems, 2021, 45(24): 10-21. (  0) 0) |
| [6] |
孙毅, 李泽坤, 许鹏, 等. 异构柔性负荷建模调控关键技术及发展方向研究[J]. 中国电机工程学报, 2019, 39(24): 7146-7158, 7488. SUN Yi, LI Zekun, XU Peng, et al. Research on key technologies and development direction of heterogeneous flexible load modeling and regulation[J]. Proceedings of the CSEE, 2019, 39(24): 7146-7158, 7488. (  0) 0) |
| [7] |
杨鹏, 郁丹, 郭雨涵, 等. 考虑需求侧响应的新能源消纳优化模型研究[J]. 供用电, 2022, 39(11): 79-86. YANG Peng, YU Dan, GUO Yuhan, et al. Optimization model of new energy accommodation considering demand response[J]. Distribution & Utilization, 2022, 39(11): 79-86. (  0) 0) |
| [8] |
杨梓俊, 丁小叶, 陆晓, 等. 面向需求响应的变频空调负荷建模与运行控制[J]. 电力系统保护与控制, 2021, 49(15): 132-140. YANG Zijun, DING Xiaoye, LU Xiao, et al. Inverter air conditioner load modeling and operational control for demand response[J]. Power System Protection and Control, 2021, 49(15): 132-140. (  0) 0) |
| [9] |
杨肖虎, 罗剑波, 郁琛, 等. 适应大规模新能源并网的电力系统备用配置及优化综述[J]. 电力工程技术, 2020, 39(1): 10-20, 63. YANG Xiaohu, LUO Jianbo, YU Chen, et al. Review of power system reserve configuration and optimization for large-scale renewable energy integration[J]. Electric Power Engineering Technology, 2020, 39(1): 10-20, 63. (  0) 0) |
| [10] |
RAMANATHAN B, VITTAL V. A framework for evaluation of advanced direct load control with minimum disruption[J]. IEEE Transactions on Power Systems, 2008, 23(4): 1681-1688. (  0) 0) |
| [11] |
LU N, ZHANG Y. Design considerations of a centralized load controller using thermostatically controlled appliances for continuous regulation reserves[J]. IEEE Transactions on Smart Grid, 2013, 4(2): 914-921. (  0) 0) |
| [12] |
艾欣, 赵阅群, 周树鹏. 空调负荷直接负荷控制虚拟储能特性研究[J]. 中国电机工程学报, 2016, 36(6): 1596-1603. AI Xin, ZHAO Yuequn, ZHOU Shupeng. Study on virtual energy storage features of air conditioning load direct load control[J]. Proceedings of the CSEE, 2016, 36(6): 1596-1603. (  0) 0) |
| [13] |
杨济如, 石坤, 崔秀清, 等. 需求响应下的变频空调群组削峰方法[J]. 电力系统自动化, 2018, 42(24): 44-52. YANG Jiru, SHI Kun, CUI Xiuqing, et al. Peak load reduction method of inverter air-conditioning group under demand response[J]. Automation of Electric Power Systems, 2018, 42(24): 44-52. (  0) 0) |
| [14] |
王志强, 王珊, 张馨月, 等. 计及用户响应行为差异性的区域电采暖负荷特性建模[J]. 电力系统自动化, 2019, 43(7): 67-73. WANG Zhiqiang, WANG Shan, ZHANG Xinyue, et al. Load characteristics modeling of regional electric heating system considering difference of users response behaviors[J]. Automation of Electric Power Systems, 2019, 43(7): 67-73. (  0) 0) |
| [15] |
LUO F J, ZHAO J H, DONG Z Y, et al. Optimal dispatch of air conditioner loads in southern China region by direct load control[J]. IEEE Transactions on Smart Grid, 2016, 7(1): 439-450. (  0) 0) |
| [16] |
GUO W K, ZHENG Y, WEN J H, et al. Peak load reduction by thermostatically controlled load dispatch with thermal comfort model[C]//10th International Conference on Advances in Power System Control, Operation & Management (APSCOM 2015). Hong Kong, China. Institution of Engineering and Technology, 2015: 1-6.
(  0) 0) |
| [17] |
YANG J E, LIU T Y, WANG H B, et al. Optimizing the regulation of aggregated thermostatically controlled loads by jointly considering consumer comfort and tracking error[J]. Energies, 2019, 12(9): 1757. (  0) 0) |
| [18] |
宋梦, 高赐威, 苏卫华. 面向需求响应应用的空调负荷建模及控制[J]. 电力系统自动化, 2016, 40(14): 158-167. SONG Meng, GAO Ciwei, SU Weihua. Modeling and controlling of air-conditioning load for demand response applications[J]. Automation of Electric Power Systems, 2016, 40(14): 158-167. (  0) 0) |
| [19] |
朱承治, 陆帅, 周金辉, 等. 基于电-热分时间尺度平衡的综合能源系统日前经济调度[J]. 电力自动化设备, 2018, 38(6): 138-143, 151. ZHU Chengzhi, LU Shuai, ZHOU Jinhui, et al. Day-ahead economic dispatch of integrated energy system based on electricity and heat balance in different time scales[J]. Electric Power Automation Equipment, 2018, 38(6): 138-143, 151. (  0) 0) |
| [20] |
余洋, 权丽, 贾雨龙, 等. 平抑新能源功率波动的聚合温控负荷改进模型预测控制[J]. 电力自动化设备, 2021, 41(3): 92-99. YU Yang, QUAN Li, JIA Yulong, et al. Improved model predictive control of aggregated thermostatically controlled load for power fluctuation suppression of new energy[J]. Electric Power Automation Equipment, 2021, 41(3): 92-99. (  0) 0) |
| [21] |
HAO H, SANANDAJI B M, POOLLA K, et al. Aggregate flexibility of thermostatically controlled loads[J]. IEEE Transactions on Power Systems, 2015, 30(1): 189-198. (  0) 0) |
| [22] |
BASHASH S, FATHY H K. Modeling and control of aggregate air conditioning loads for robust renewable power management[J]. IEEE Transactions on Control Systems Technology, 2013, 21(4): 1318-1327. (  0) 0) |
| [23] |
王珂, 姚建国, 姚良忠, 等. 电力柔性负荷调度研究综述[J]. 电力系统自动化, 2014, 38(20): 127-135. WANG Ke, YAO Jianguo, YAO Liangzhong, et al. Survey of research on flexible loads scheduling technologies[J]. Automation of Electric Power Systems, 2014, 38(20): 127-135. (  0) 0) |
| [24] |
LUO F J, DONG Z Y, MENG K, et al. An operational planning framework for large-scale thermostatically controlled load dispatch[J]. IEEE Transactions on Industrial Informatics, 2017, 13(1): 217-227. (  0) 0) |
| [25] |
夏一哉, 牛建磊, 赵荣义. 空气流动对热舒适影响的实验研究: 总结与分析[J]. 暖通空调, 2000, 30(3): 41-45. XIA Yizai, NIU Jianlei, ZHAO Rongyi. Effects of air movement on thermal comfort: a literature review[J]. Heating Ventilating & Air Conditioning, 2000, 30(3): 41-45. (  0) 0) |
2. State Grid Wenzhou Power Supply Company of Zhejing Electric Power Co., Ltd., Wenzhou 325000, China;
3. School of Electrical Engineering, Southeast University, Nanjing 210096, China
 2023, Vol. 42
2023, Vol. 42


 张勇(1998),男,硕士在读,研究方向为电力系统调度(E-mail:
张勇(1998),男,硕士在读,研究方向为电力系统调度(E-mail: