文章编号: 2096-3203(2023)04-0175-10 中图分类号: TM341
永磁同步电机(permanent magnet synchronous machine, PMSM)的无差拍预测电流控制(dead-beat predictive current control, DPCC)方法因其响应速度快、计算量少等优点,近年来逐渐成为领域内的研究热点[1-4]。该方法主要基于电机的离散参数模型,通过实时估算电流未来时刻值来给出控制器参考电压指令,并通过空间矢量脉宽调制(space vector pulse width modulation, SVPWM)[5-6]将其转换为相应的开关动指令,从而达到电机电流快速控制的目的。与传统比例积分(proportional integral,PI)控制器相比,该方法具有动态性能高的特点[7],因此该方法在伺服系统、机器人系统等需要快速动作响应的系统中具有很大的应用潜力。
从现有研究来看,一方面,采用DPCC技术可以极大地提高电机电流控制的速度[8];另一方面,由于该方法是一种开环控制方法,电机电气物理参数的准确性对控制性能影响极大,而电机系统中的参数往往是时变、非线性的,因此该方法在应用中的性能大大降低,同时具有稳定性问题[9-10]。针对参数不精确导致的控制鲁棒性问题,国内外已有相关研究,当前方法大都为误差补偿。为增强对参数变化的适应性,文献[11-12]分别提出了一种鲁棒性增强的预测电流控制方法和一种改进控制结构以减小定子电流稳态误差的方法,但这些方法计算量大,占用了较多计算资源、同时会牺牲电流控制环的响应速度。对于电机参数变化超过一定范围导致控制发散的问题,有学者提出采用扰动观测器来进行补偿。文献[13]提出了一种带观测器的扰动补偿的预测控制方法,但观测器会引入额外的噪声,系统的动态性能会受到较大影响。后续研究在此基础上进行了优化,文献[14]采用滞环控制方法对无差拍控制误差进行补偿,但该方法存在控制噪声较大的问题。文献[15-16]基于内模原理进行扰动观测器设计,但内模控制本身也需要较为精确的模型参数,因此实际消除参数误差影响的效果有限。文献[17]采用了卡尔曼滤波方法来观测参数误差带来的扰动量,但该方法涉及到高阶矩阵的反复计算,运算量较大,增加了实现实时性控制的难度。文献[18]则受自抗扰控制(active disturbance rejection control,ADRC)方法的启发,采用扩张状态观测器,代价是增多了控制参数变量,加大了参数整定的难度。文献[19-20]提出了复合预测的无差拍电流跟踪控制来降低参数误差引起的谐波干扰,但本质上只能降低干扰,并没有消除干扰源。
以上方法均基于参数误差补偿的思路,只能降低误差,在参数变化范围过大时也存在发散的问题。因此,文中将不采用参数误差补偿的方法,而从参数校正角度改进无差拍控制。通过结合参数自适应算法,在线进行电机参数自调整,进而修改预测电流控制器的参数,以达到控制器参数与电机参数匹配的效果,从源头上实现完全消除由参数误差导致的控制稳态误差。最后,文中从理论和仿真两方面对比基于误差补偿和基于参数校正方法的优缺点。
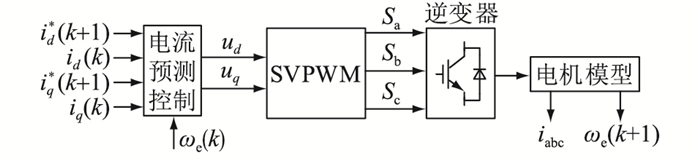
1 无差拍预测电流控制(DPCC) 1.1 无差拍电流控制器原理基本的DPCC方法的控制原理如图 1所示,其中ud、uq分别为d、q轴的电压;id、iq分别为d、q轴的电流;id*、iq*分别为d、q轴反馈电流;ωe为转子电角速度;Sa、Sb、Sc为开关信号;iabc为三相电流。
|
图 1 无差拍电流控制原理 Fig. 1 Control principle of the dead-beat current control |
为方便描述,选择PMSM的dq轴电流作为状态变量,将电机模型转化为状态空间形式,如式(1)所示。
| $ \frac{\mathrm{d} \boldsymbol{i}_{\mathrm{s}}}{\mathrm{d} t}=\boldsymbol{A} \boldsymbol{i}_{\mathrm{s}}+\boldsymbol{B} \boldsymbol{u}+\boldsymbol{D} $ | (1) |
其中:
| $ \boldsymbol{i}_{\mathrm{s}}=\left[\begin{array}{l} i_d \\ i_q \end{array}\right] $ | (2) |
| $ \boldsymbol{u}=\left[\begin{array}{l} u_d \\ u_q \end{array}\right] $ | (3) |
| $ \boldsymbol{A}=\left[\begin{array}{cc} -R_{\mathrm{s}} / L_d & \omega_{\mathrm{e}} \\ -\omega_{\mathrm{e}} & -R_{\mathrm{s}} / L_q \end{array}\right] $ | (4) |
| $ \boldsymbol{B}=\left[\begin{array}{cc} 1 / L_d & 0 \\ 0 & 1 / L_q \end{array}\right] $ | (5) |
| $ \boldsymbol{D}=\left[\begin{array}{c} 0 \\ -\omega_e \psi_{\mathrm{f}} / L_q \end{array}\right] $ | (6) |
式中:Rs为定子电阻;Ld、Lq分别为d、q轴的电感;ψf为转子磁链。
为了实现数字控制器设计,须将连续域中的方程进一步转化为离散域。采用欧拉方法对其离散化后,控制模型如式(7)所示。
| $ \boldsymbol{i}_{\mathrm{s}}(k+1)=\boldsymbol{F i}_{\mathrm{s}}(k)+\boldsymbol{G} \boldsymbol{u}(k)+\boldsymbol{H} $ | (7) |
| $ \boldsymbol{F}=\left[\begin{array}{cc} 1-T_{\mathrm{s}} R_{\mathrm{s}} / L_d & \omega_{\mathrm{e}}(k) T_{\mathrm{s}} \\ -\omega_{\mathrm{e}}(k) T_{\mathrm{s}} & 1-T_{\mathrm{s}} R_{\mathrm{s}} / L_q \end{array}\right] $ | (8) |
| $ \boldsymbol{G}=\left[\begin{array}{cc} T_{\mathrm{s}} / L_d & 0 \\ 0 & T_{\mathrm{s}} / L_q \end{array}\right] $ | (9) |
| $ \boldsymbol{H}=\left[\begin{array}{c} 0 \\ -T_{\mathrm{s}} \omega_{\mathrm{e}}(k) \psi_{\mathrm{f}} / L_q \end{array}\right] $ | (10) |
式中:Ts为控制采样周期。
根据式(7)所示离散控制模型,在每一个控制周期内,可以根据当前时刻(设为k时刻)采样得到的状态信息对下一时刻(k+1时刻)的状态信息进行预测计算。假设参数能够完美匹配,则可以认为k+1时刻电流实际值能完全跟随k时刻的反馈值,即:
| $ \boldsymbol{i}_{\mathrm{s}}^*(k)=\boldsymbol{i}_{\mathrm{s}}(k+1) $ | (11) |
将式(11)代入式(7),可得到控制电压输出表达式为:
| $ \boldsymbol{u}(k)=\boldsymbol{G}^{-1}\left(\boldsymbol{i}_{\mathrm{s}}^*(k)-\boldsymbol{F i}_{\mathrm{s}}(k)-\boldsymbol{H}\right) $ | (12) |
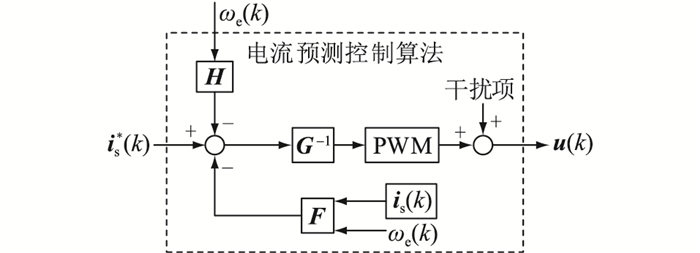
实时的无差拍电流控制结构如图 2所示,其中PWM为脉宽调制技术。假设控制模型的参数与被控对象实际参数完全一致,在每个控制周期内由当前时刻电流值计算得到的下一时刻电压反馈都能瞬时输出,理想状态下将在一个控制周期后完成反馈跟踪,达到较好的控制效果。
|
图 2 实时无差拍电流控制结构 Fig. 2 The real-time dead-beat current control structure |
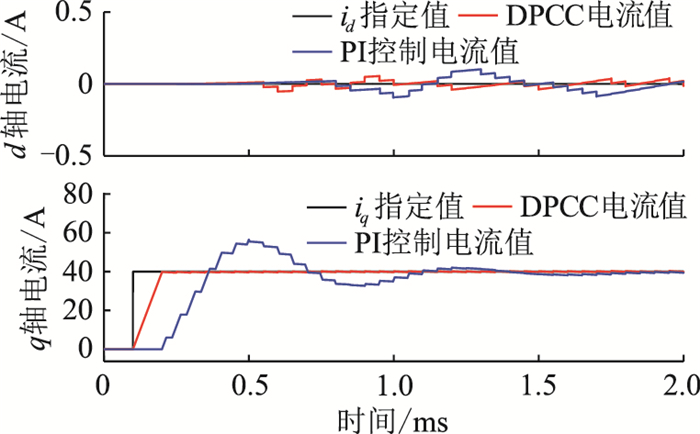
图 3对比了采用无差拍电流控制器和PI电流控制器的控制效果。可以明显看出,PI控制器的调节时间较长,为1.4 ms,而采用无差拍电流控制器大大缩短了控制时间,在一个控制周期(0.1 ms)内就能完成控制过程。
|
图 3 无差拍电流控制器与PI控制器控制效果对比 Fig. 3 The performance comparison of dead-beat current controller and PI controller |
首先,控制器中的计算电压矢量可表示为:
| $ \boldsymbol{u}(k)=\hat{\boldsymbol{G}}^{-1}\left(\boldsymbol{i}_{\mathrm{s}}^*(k)-\hat{\boldsymbol{F}} \boldsymbol{i}_{\mathrm{s}}(k)-\hat{\boldsymbol{H}}\right) $ | (13) |
其中变量上方的“^”表示控制器不精确的参数。在无差拍控制条件下,默认控制器在进入稳态过程后,id(k+1)≈id(k),而iq(k+1)≈iq(k)。进一步,式(13)可以化简为式(14)和式(15)。
| $ \begin{gathered} i_d(k+1)= \\ \frac{\hat{L}_{\mathrm{s}}}{\hat{L}_{\mathrm{s}}-T_{\mathrm{s}} \Delta R_{\mathrm{s}}} i_d^*(k+1)-\frac{\Delta L_{\mathrm{s}}}{\hat{L}_{\mathrm{s}}-T_{\mathrm{s}} \Delta R_{\mathrm{s}}} T_{\mathrm{s}} \omega_{\mathrm{e}}(k) i_q(k) \end{gathered} $ | (14) |
| $ \begin{gathered} i_q(k+1)=\frac{\hat{L}_{\mathrm{s}}}{L_{\mathrm{s} 0}} i_q^*(k+1)+\frac{T_{\mathrm{s}} \Delta R_{\mathrm{s}}-\Delta L_{\mathrm{s}}}{L_{\mathrm{s} 0}} i_q(k)- \\ \frac{\Delta L_{\mathrm{s}}}{L_{\mathrm{s} 0}} T_{\mathrm{s}} \omega_{\mathrm{e}}(k) i_d(k)+\frac{T_{\mathrm{s}}}{L_{s 0}} T_{\mathrm{s}} \Delta \psi_{\mathrm{f}} \omega_{\mathrm{e}}(k) \end{gathered} $ | (15) |
式中:
由式(14)和式(15)可以看出,电机永磁磁链的不匹配只对电流iq的响应有影响,而定子电阻和电感参数的不匹配对电流id和iq的响应都有影响。如果在控制器的设计中不考虑参数不匹配的情况,会影响PMSM的性能。
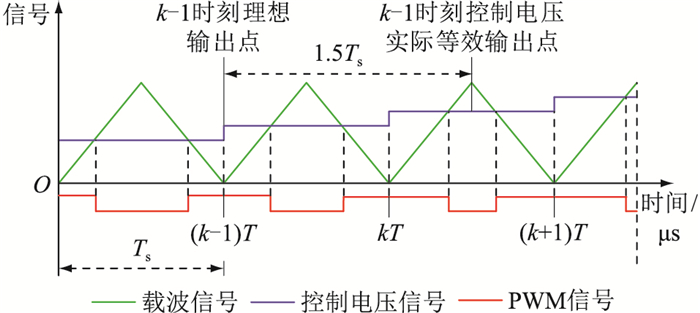
然而,在实际控制中数字控制器系统存在程序计算和PWM更新引起的延时,k时刻计算的电压值存在一个采样周期的延迟。PWM的更新与输出时刻点见图 4,其中T为采样时间;(k-1)T为采样时刻;kT为数字采样时刻;(k+1)T为PWM更新时刻。
|
图 4 数字系统信号时序示意 Fig. 4 Timing schematic of digital system signals |
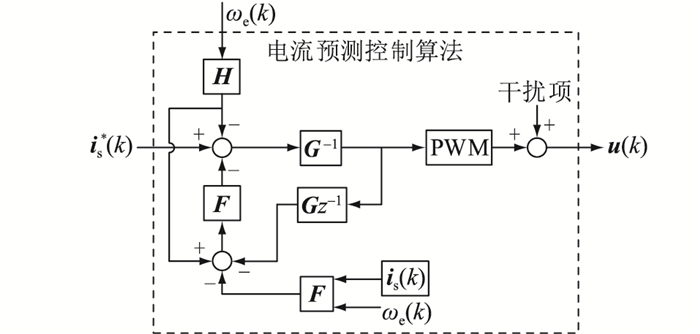
将该数字系统的更新延时考虑进控制环节,假设精确模型参数为G,而控制器采用不精确模型参数
| $ G_{\text {closed-loop }}(z)=\delta \frac{z}{z^2-1+\delta} $ | (16) |
|
图 5 考虑采样延时的无差拍电流控制 Fig. 5 Dead-beat current control considering time delay |
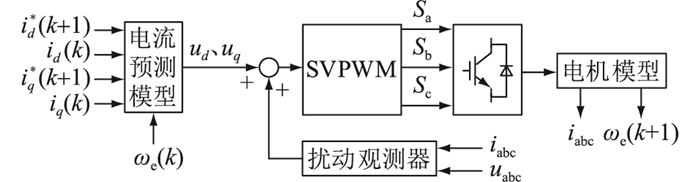
为克服上述模型参数不匹配和数字控制系统采样延时对控制性能的影响,传统方法通过引入带扰动观测器的DPCC算法来对稳态误差进行补偿[14]。该方法通过设计扰动观测器,提前预测出扰动量的大小,再通过前馈补偿的方式对输出电压进行一次修正,从而可以同时对模型参数不匹配和数字采样延时引起的误差起到补偿作用。整个控制部分的系统结构如图 6所示,采用了无差拍电流控制器与扰动前馈补偿并联输出的形式,其中uabc为三相电压。
|
图 6 带扰动观测器的无差拍电流控制结构 Fig. 6 Control structure of dead-beat current controller with disturbance observer |
将扰动观测器的扰动观测结果作为补偿前馈项,施加在控制环输出电压上,以此来补偿参数误差导致的误差电压,进一步弥补参数误差引起的控制动态性能下降。电压最终输出指令ud*(k)、uq*(k)如式(17)所示,其中
| $ \left\{\begin{array}{l} u_d^*(k)=u_d(k)+\hat{f}_d(k+1) \\ u_q^*(k)=u_q(k)+\hat{f}_q(k+1) \end{array}\right. $ | (17) |
第1章中所提方法对误差补偿是有效的,但新增加的扰动观测器会引入额外的动态干扰,而干扰项加在控制环输出通道上会致使电机响应变慢[21-22]。因此,文中基于参数的实时调整来补偿模型参数误差的影响。
电机参数的调整是基于最小二乘原理的参数辨识方法,其计算过程简单,占用计算资源较少,同时可以在输入信号叠加噪声的条件下实现参数的无偏估计[23-27]。
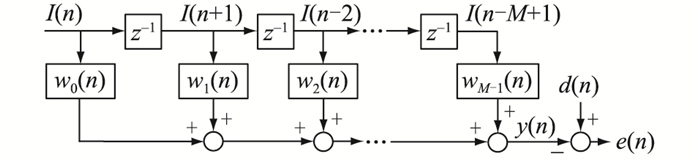
为在每个时刻都能实现最小二乘法的实时更新,通常要从一组给定的初始条件开始,利用新的输入变量中的信息以及过去估计值权重对新估计值进行更新。整个估计系统的实际输出由一个横向滤波器产生[28],如图 7所示,其中M为横向滤波器中的抽头个数;d(n)为指令变量;y(n)为输出变量。横向滤波器的每个节点对应的输入变量可以分别表示为I(n)、I(n-1)、…、I(n-M+1),每个分支的权重由w0(n)、w1(n)、…、wM-1(n)决定输出,则系统输出与期望输出之差e(n)可表示为:
| $ e(n)=d(n)-y(n)=d(n)-\sum\limits_{i=1}^{M-1} w_i(n) I(n-i) $ | (18) |
|
图 7 具有M个抽头的横向滤波器结构 Fig. 7 Structure of transverse filter with M layers |
最小二乘法的基本思想就是使得e(n)在每个时刻取得最小值,该算法将重点聚焦于在有限个观测数据中寻找横向滤波器的最优权重值[29-30]。
为了描述方便,以一个普通的单输入单输出离散信号系统为例,推导最小二乘法的计算过程。通常情况下,普通的单输入单输出离散信号系统可以用差分方程描述:
| $ \sum\limits_{l=1}^N a_l y(k-l)=\sum\limits_{l=1}^N b_l I(k-l)+\xi(k) $ | (19) |
式中:al、bl为滤波器滤波参数,l=1, 2, …, N;I(k)为k时刻观测的输入量;y(k)为k时刻观测的输出量;ξ(k)为测量过程中的噪声。将式(19)的参数归类,可以变换得到:
| $ y(k)=\boldsymbol{h}(k) \boldsymbol{\theta}+\xi(k) $ | (20) |
其中:
| $ \boldsymbol{\theta}=\left[\begin{array}{llllll} a_1 & \cdots & a_N & b_1 & \cdots & b_N \end{array}\right]^{\mathrm{T}} $ | (21) |
| $ \begin{array}{*{20}{c}} \boldsymbol{h}(k)=\\ {\left[ { - y(k - 1) \cdots - y(k - N)I(k - 1) \cdots I(k - N)} \right]} \end{array} $ | (22) |
为得出更通用的结论,将多个形如式(20)的方程放在一个矩阵中描述,可以写为:
| $ \boldsymbol{Y}(k)=\boldsymbol{H}_1(k) \boldsymbol{\theta}(k)+\boldsymbol{E}(k) $ | (23) |
式中:Y(k)=[y(1) y(2) … y(k)]T,为输出矩阵;H1(k)为状态变量矩阵;E(k)为测量噪声矩阵。
一个系统的参数辨识模型如式(23)所示,其求解的问题是在每个时刻寻找合适的参数向量θ,使得系统输出值和采用模型计算的估计值保持最小差距。通常将误差的平方和最小作为评判依据,估计值误差的平方和函数为:
| $ \boldsymbol{J}(\boldsymbol{\theta})=\left(\boldsymbol{Y}-\boldsymbol{H}_1 \boldsymbol{\theta}\right)^{\mathrm{T}}\left(\boldsymbol{Y}-\boldsymbol{H}_1 \boldsymbol{\theta}\right) $ | (24) |
对式(24)求导,根据极值定理,当J(θ)导数取0时,误差平方和函数为0,可得参数估计方程为:
| $ \frac{\partial \boldsymbol{J}(\boldsymbol{\theta})}{\partial \boldsymbol{\theta}}=\frac{\partial\left(\boldsymbol{Y}-\boldsymbol{H}_1 \boldsymbol{\theta}\right)^{\mathrm{T}}\left(\boldsymbol{Y}-\boldsymbol{H}_1 \boldsymbol{\theta}\right)}{\partial \boldsymbol{\theta}}=0 $ | (25) |
| $ \boldsymbol{\theta}(k)=\left(\boldsymbol{H}_1^{\mathrm{T}}(k) \boldsymbol{H}_1(k)\right)^{-1} \boldsymbol{H}_1^{\mathrm{T}}(k) \boldsymbol{Y}(k) $ | (26) |
采用最小二乘法中的递归算式,令P(k)=(H1T(k)H1(k))-1,由式(26)可以进一步推导,整理得出参数估计的一般矩阵形式为:
| $ \left\{\begin{array}{l} \boldsymbol{\theta}(k)=\boldsymbol{\theta}(k-1)+\boldsymbol{K}(k)\left(\boldsymbol{Y}(k)-\boldsymbol{h}^{\mathrm{T}}(k) \boldsymbol{\theta}(k-1)\right) \\ \boldsymbol{K}(k)=\boldsymbol{P}(k-1) \boldsymbol{h}(k)\left(\boldsymbol{h}^{\mathrm{T}}(k) \boldsymbol{P}(k-1) \boldsymbol{h}(k)\right)^{-1} \\ \boldsymbol{P}(k)=\left(\boldsymbol{I}-\boldsymbol{K}(k) \boldsymbol{h}^{\mathrm{T}}(k)\right) \boldsymbol{P}(k-1) \end{array}\right. $ | (27) |
式中:P(k)、K(k)分别为当前时刻的滤波器参数迭代矩阵和滤波器参数矩阵;I为单位矩阵。在每个参数辨识周期实时更新滤波器参数,每当下一时刻获取系统新的状态数据时,都会对前一次所计算的预估结果进行修正,不断进行这种迭代直到系统参数收敛到一定范围为止。借助该递归算法,在很短时间内就能获取被观测对象的准确参数。
2.2 带参数纠正的无差拍控制器设计为提高DPCC方法抗参数失调的性能,消除参数变化引起的稳态误差,提出采用参数辨识算法自动改变电流控制器的增益。该算法将递推最小二乘法内嵌在电流环控制中,在计算电流环之前先对电机参数进行预测。内嵌的参数预测过程如下。
首先,将模型式(20)重写为式(28),将其描述为一般表达式,如式(29)所示。
| $ \begin{gathered} {\left[\begin{array}{c} u_d(k) \\ u_q(k) \end{array}\right]=} \\ {\left[\begin{array}{ccc} i_d(k) & \frac{i_d(k)-i_d(k-1)}{h}-\omega_{\mathrm{e}}(k) i_q(k) & 0 \\ i_q(k) & \omega_{\mathrm{e}}(k) i_d(k)+\frac{i_q(k)-i_q(k-1)}{h} & \omega_{\mathrm{e}}(k) \end{array}\right]\left[\begin{array}{c} R_{\mathrm{s}} \\ L_{\mathrm{s}} \\ \psi_{\mathrm{f}} \end{array}\right]} \end{gathered} $ | (28) |
| $ \boldsymbol{y}(k)=\boldsymbol{h}_1^{\mathrm{T}}(k) \boldsymbol{\theta}_1(k) $ | (29) |
式中:h为传感器测量变量;Ls为定子电感;y(k)=[ud(k) uq(k)]T,为状态空间的输出;h1T(k)为传感器测量变量;θ1(k)=[Rs Ls ψf]T,为时变参数。
由于在整个控制过程中没有精确的值,系统输出的观测值记为
| $ \left\{\begin{array}{l} \hat{\boldsymbol{\theta}}_1(k)= \\ \quad \hat{\boldsymbol{\theta}}_1(k-1)+\boldsymbol{K}(k)\left(\boldsymbol{Y}(k)-\boldsymbol{h}_1^{\mathrm{T}}(k) \hat{\boldsymbol{\theta}}_1(k-1)\right) \\ \boldsymbol{K}(k)= \\ \quad \boldsymbol{P}(k-1) \boldsymbol{h}_1(k)\left(\boldsymbol{h}_1^{\mathrm{T}}(k) \boldsymbol{P}(k-1) \boldsymbol{h}_1(k)+\mu\right)^{-1} \\ \boldsymbol{P}(k)=\frac{1}{\mu}\left(\boldsymbol{I}-\boldsymbol{K}(k) \boldsymbol{h}_1^{\mathrm{T}}(k)\right) \boldsymbol{P}(k-1) \end{array}\right. $ | (30) |
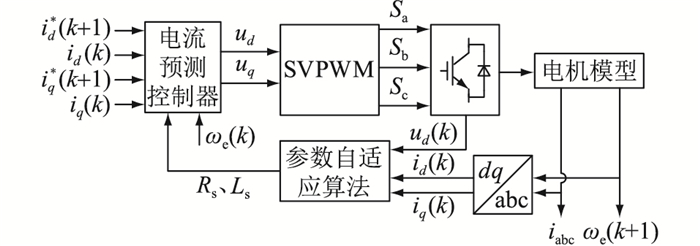
然后,须将电机的参数辨识算法集成到DPCC算法中。加入电机参数自适应算法后的控制结构如图 8所示。实时运行的程序根据前几个时刻的采集值计算得到当前时刻电机参数的精确值,然后通过程序加载实时修改无差拍电流控制器的参数。
|
图 8 带电机参数自适应的系统控制结构 Fig. 8 Control structure of system with adaptive motor parameters |
整个算法的流程如图 9所示。参数辨识程序内嵌在电流环控制中,其计算周期通过设置电流环计数器计数值实现。为了避免控制系统发散的风险,在其中加入以下2个环节:

|
图 9 参数辨识流程 Fig. 9 Flow chart of parameter identification |
(1) 由于电机参数变化速率相比于控制周期非常缓慢,在每个控制周期内的估计过程中可以认为电机参数是固定不变的,因此可以将参数估计的计算周期改为电流控制回路的计算周期(通常为100 μs)的10倍,即1 ms,以此保证参数估计的计算时间足够,同时消除环路控制时延以及避免无差拍电流控制器的参数变化过快导致控制系统不稳定。
(2) 估计参数变化也应限定在一定的范围内。如果估计结果超出范围,则在无差拍电流控制器中修改这些参数时会导致结果发散。通常情况下,造成这种情况的主要原因是计算过程受到测量噪声的影响,因此应在一定程度上放弃和限制估计结果,以保证系统的正常运行。程序中将估计参数限制在标称值的0.1~2.5倍,这意味着限定了参数变化最大允许范围的边界。
3 仿真结果验证为验证无差拍电流控制器的性能,在Simulink中搭建无差拍电流控制模型,采用的参数见表 1。
|
|
表 1 仿真参数 Table 1 Simulation parameters |
首先,对无差拍控制在参数不匹配条件下的影响进行仿真。从稳定域分析可以清楚地看出,控制系统参数的容错极限为0~2倍的真实值,这表明若参数偏离这个范围,控制系统将振荡。此外,参数不匹配即使不引起稳定性问题,也会引入稳态误差。图 10—图 12为在不同参数不匹配条件下,无差拍电流控制的控制效果。
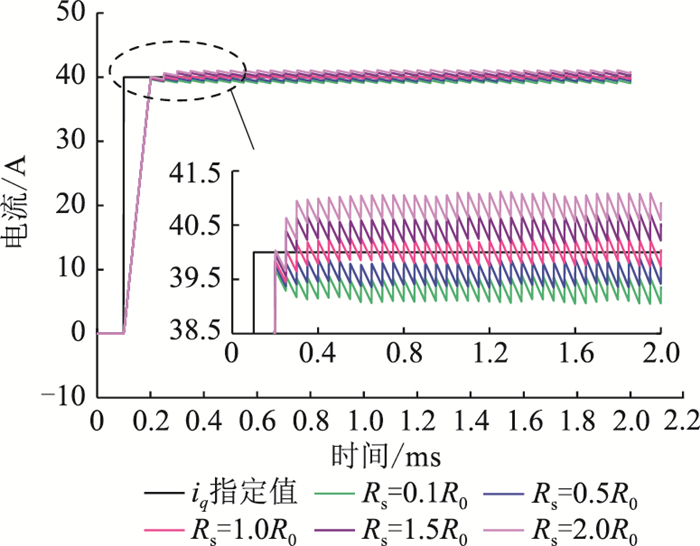
|
图 10 在电阻参数不匹配时q轴电流响应 Fig. 10 q axis current response under resistance value unmatched condition |
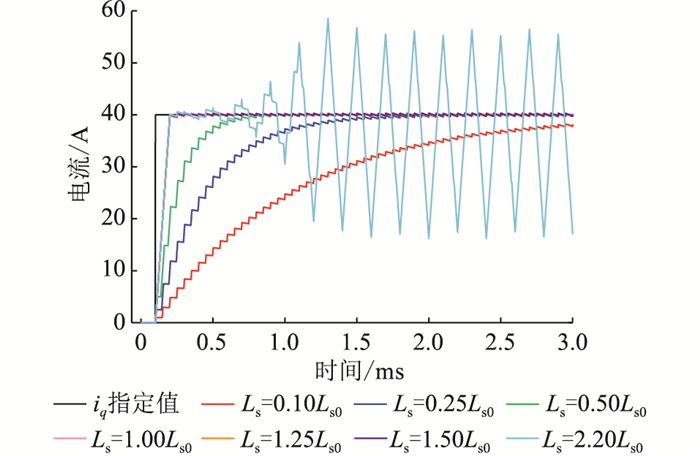
|
图 11 在电感参数不匹配时q轴电流响应 Fig. 11 q axis current response under inductance value unmatched condition |
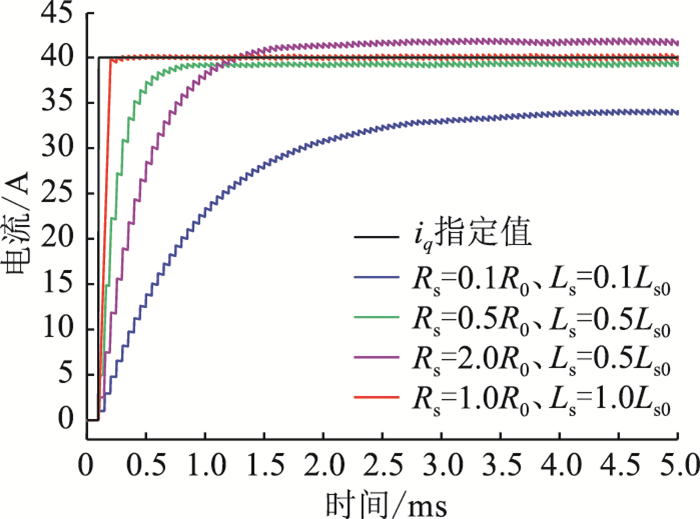
|
图 12 在电感和电阻同时不匹配时q轴电流的响应 Fig. 12 q axis current response under both resistance and inductance value unmatched condition |
从图 10—图 12中可以明显看出,电阻参数变化对电流控制的稳态误差有一定的影响,但由于电阻参数上获得的电压占比较小(7.5%左右),因此其影响并不显著;当电感参数变化时,对电流控制的稳态误差不会产生影响,但却严重影响电流动态响应调节时间,恶化控制效果,当参数误差过大时还会引起控制的发散。仿真结果验证了前述分析,参数不匹配对控制回路动态和稳态特性同时产生了重要影响。
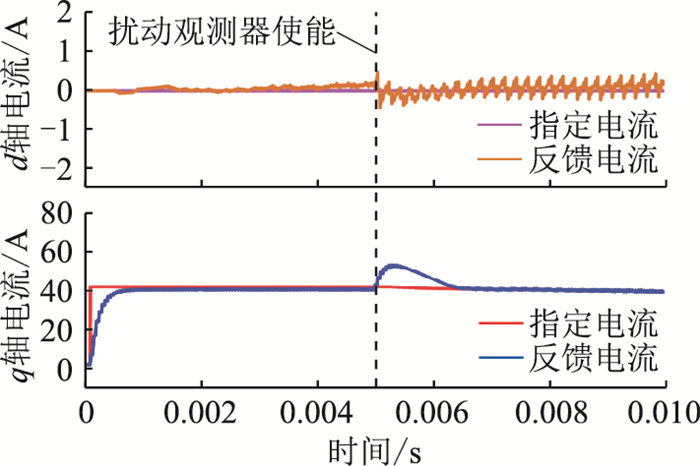
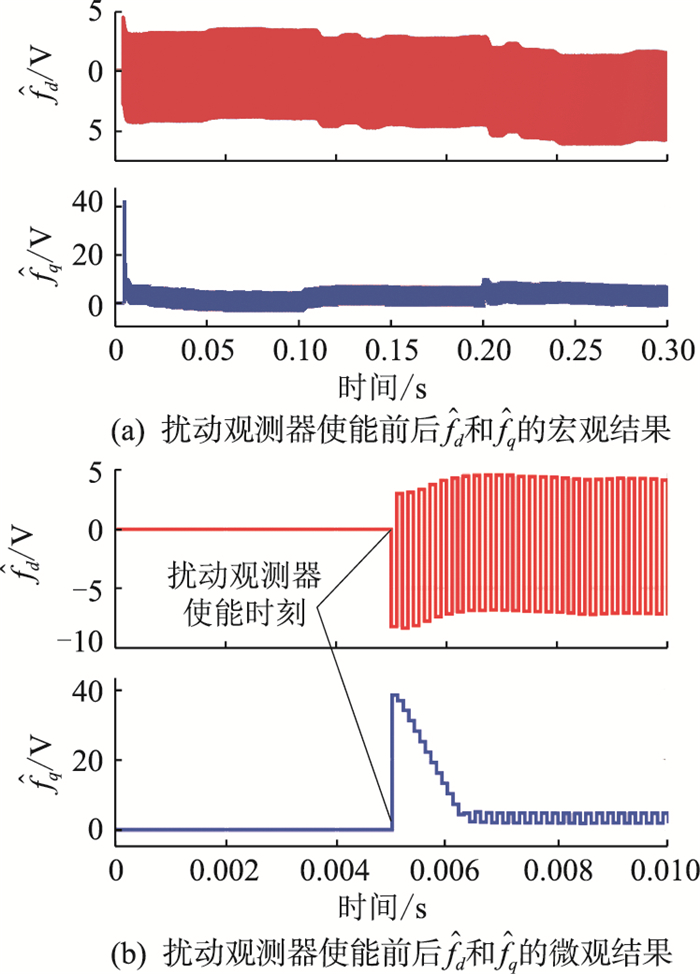
3.2 扰动观测器前馈补偿仿真加入扰动观测器前后电流的变化如图 13所示。仿真中设置了一组不匹配的情况,即在控制器参数设置为Ls=0.5Ls0、Rs=0.1R0的条件下进行仿真。可以看到,在未加入扰动观测器时,电流的动态响应输出和指令值之间存在着稳态误差。在扰动观测器使能以后,经过一个短时间的调整,dq轴下的电流逐渐稳定,且控制的动态误差被完全补偿。这表明在引入前馈控制器后,参数误差带来的控制误差被消除。全程的补偿电压如图 14所示。由于采用了扰动观测器来补偿电压,在扰动观测器使能后,补偿电压呈方波脉冲形式,这也将大大增加最终输出的电流的纹波。
|
图 13 在Ls=0.5Ls0、Rs=0.1R0条件下dq轴电流的动态响应过程 Fig. 13 The response of dq axis current under Ls=0.5Ls0, Rs=0.1R0 |
|
图 14 扰动观测器输出 |
另一组仿真在同样的参数不匹配条件下对比了dq轴电流的阶跃响应,有无扰动观测器前馈补偿的电流阶跃响应效果如图 15所示。可以看出,一方面,扰动观测器加入后系统电流调整过程将不存在稳态误差;另一方面,加入扰动观测器后,整体动态响应速度相对于参数完全匹配的情况大大降低,这是因为扰动观测器前馈自身也存在响应收敛时间,其对整个系统的收敛时间并没有有效改善。

|
图 15 在Ls=0.5Ls0、Rs=0.1R0条件下有无扰动观测器的dq轴电流的阶跃响应过程对比 Fig. 15 Comparison of step response of dq axis current under Ls=0.5Ls0, Rs=0.1R0 with and without disturbance observer |
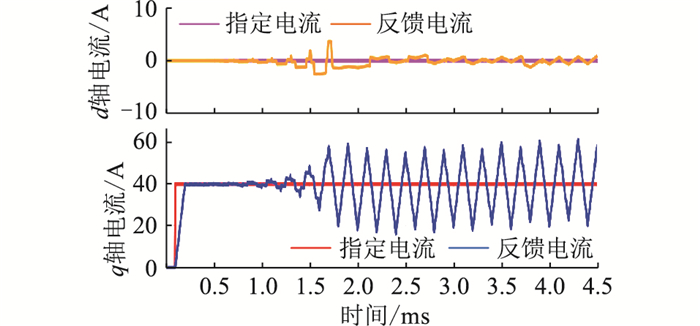
此外,为探究扰动观测器前馈补偿能否改善系统参数稳定域,仿真中设置Ls=2.2Ls0、Rs=0.1R0,其仿真结果如图 16所示。由图 16可知,电流出现了振荡效应,这也意味着扰动观测器前馈电流补偿的方法并不能扩宽系统的参数稳定域。
|
图 16 在Ls=2.2Ls0、Rs=0.1R0条件下dq轴电流的动态响应 Fig. 16 Step response of dq axis current under Ls=2.2Ls0, Rs=0.1R0 |
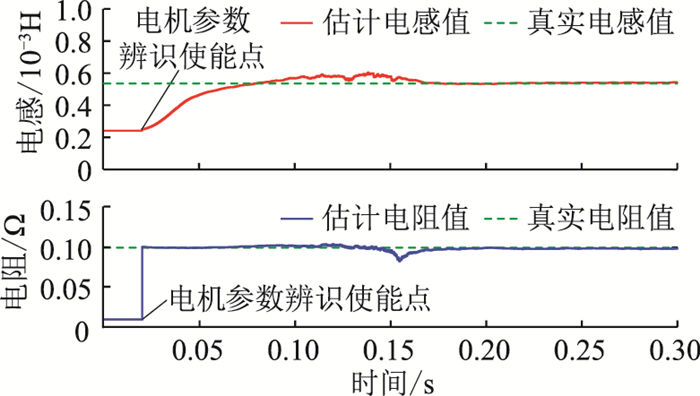
为更清晰地显示结合了参数辨识算法的无差拍电流控制方法的有效性,在无差拍电流控制环路中设置了参数辨识算法的使能时间,即在某一个时刻让参数辨识算法生效。设置辨识算法的实现速度比电流环慢10倍,参数识别结果如图 17所示。
|
图 17 电阻和电感参数辨识过程 Fig. 17 The process of resistance and inductance identification |
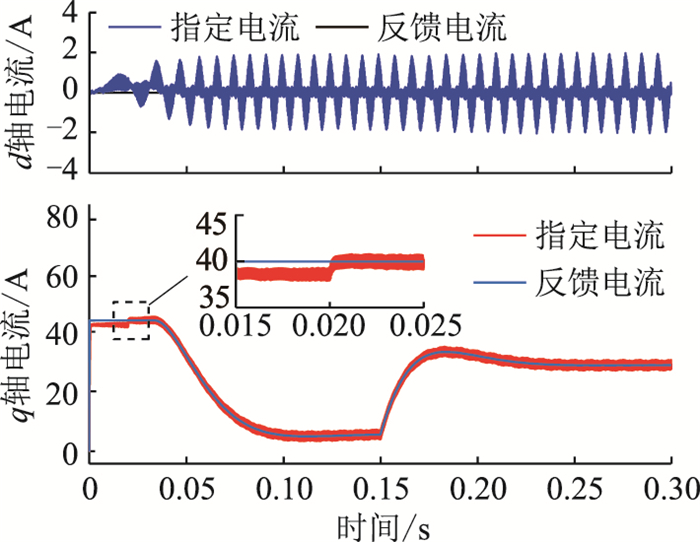
在仿真中,设定Ls=0.56Ls0、Rs=0.1R0,参数辨识算法使能时刻为0.02 s。从图 17中可以看到,随着辨识算法的迭代运算,辨识的电感值和电阻值都逐渐收敛到真实值。0.15 s时对电机进行加载,随着iq电流的上升,在一小段暂态调整时间后,辨识的电机参数仍然跟随真实值。在此过程中,dq轴电流的控制效果如图 18所示。在参数辨识算法实施之前,由于电机实际参数和控制器参数存在误差,可以明显看到电流的稳态误差,但随着参数
|
图 18 dq轴电流在参数辨识算法使能前后的响应结果 Fig. 18 dq axis current response results before and after the parameter identification algorithm enabled |
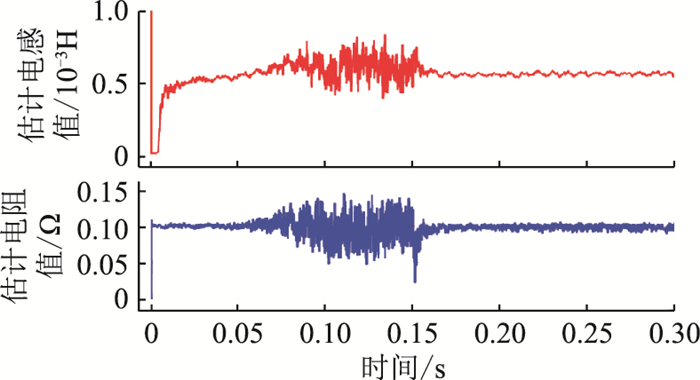
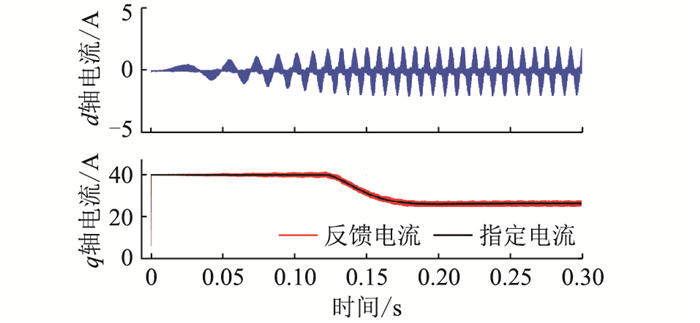
此外,为证明带参数辨识算法彻底摒除了前述参数误差极限的限制,文中进行了另一次仿真。在仿真中,设定控制器参数Ls=2.2Ls0、Rs=0.1R0。此时,在传统的控制方法下,电流处于不稳定区域,如图 11、图 16所示的仿真结果,呈现发散形态。然而,在加入了参数辨识算法后,dq轴下的电流能被稳定跟踪,如图 19、图 20所示。这表明结合了参数辨识算法后的无差拍电流控制将不受上文分析的参数稳定域的限制,鲁棒性更好。
|
图 19 在Ls=2.2Ls0、Rs=0.1R0条件下电机参数辨识 Fig. 19 Motor parameter identification under Ls=2.2Ls0, Rs=0.1R0 |
|
图 20 采用参数辨识算法后在Ls=2.2Ls0、Rs=0.1R0条件下电流响应 Fig. 20 Current response with parameter identification algorithm enabled under Ls=2.2Ls0, Rs=0.1R0 |
文中主要针对电机参数不精确对无差拍控制性能衰减的问题,提出了一种基于参数自适应的PMSM无差拍控制方法。通过分析与仿真,得到的结论如下:
(1) 采用基于最小二乘原理的参数辨识算法调整电机参数,该算法计算过程简单、占用计算资源较少,同时可以在输入信号叠加噪声的条件下实现参数的无偏估计;
(2) 结合了参数辨识算法的无差拍电流控制方法可以有效补偿参数不匹配条件下无差拍电流控制的静态误差和动态误差,相比于扰动观测器,其动态特性改善较为明显;
(3) 由于参数辨识基本得到了电机模型的精确参数,电流控制过程将不受参数稳定域的限制,系统鲁棒性提升更为明显。
| [1] |
WANG X Q, WANG Z, XU Z X, et al. Deadbeat predictive current control-based fault-tolerant scheme for dual three-phase PMSM drives[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(2): 1591-1604. DOI:10.1109/JESTPE.2020.2983691 (  0) 0) |
| [2] |
ZHANG Y C, JIANG T, JIAO J. Model-free predictive current control of a DFIG using an ultra-local model for grid synchronization and power regulation[J]. IEEE Transactions on Energy Conversion, 2020, 35(4): 2269-2280. DOI:10.1109/TEC.2020.3004567 (  0) 0) |
| [3] |
韩钟辉. 永磁同步电机调速系统预测电流控制研究[D]. 徐州: 中国矿业大学, 2019. HAN Zhonghui. Research on the predictive current control of permanent magnet synchronous motor speed control system[D]. Xuzhou: China University of Mining and Technology, 2019. (  0) 0) |
| [4] |
姜哲, 卜飞飞, 潘子昊, 等. 永磁同步电机伺服系统改进型无差拍电流控制算法[J]. 电力工程技术, 2020, 39(6): 177-183. JIANG Zhe, BU Feifei, PAN Zihao, et al. Improved deadbeat current control algorithm for permanent magnet synchronous motor servo system[J]. Electric Power Engineering Technology, 2020, 39(6): 177-183. (  0) 0) |
| [5] |
张永昌, 屈祈延, 杨海涛. 基于空间矢量调制的Vienna整流器无模型预测电流控制[J]. 电工技术学报, 2022, 37(21): 5541-5547. ZHANG Yongchang, QU Qiyan, YANG Haitao. Model free predictive current control of Vienna rectifier based on space vector modulation[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5541-5547. (  0) 0) |
| [6] |
俞沛宙, 王澍, 杨继辉, 等. 基于灰狼优化的永磁同步电机自适应反推鲁棒控制策略[J]. 电力系统保护与控制, 2021, 49(2): 39-46. YU Peizhou, WANG Shu, YANG Jihui, et al. Adaptive backstepping robust control strategy of PMSM based on grey wolf optimization[J]. Power System Protection and Control, 2021, 49(2): 39-46. (  0) 0) |
| [7] |
黄守道, 马河涛, 张其松, 等. 对转永磁同步电机无差拍预测控制[J]. 大电机技术, 2018(5): 25-29. HUANG Shoudao, MA Hetao, ZHANG Qisong, et al. Control of anti-rotary PMSM based on deadbeat predictive control[J]. Large Electric Machine and Hydraulic Turbine, 2018(5): 25-29. (  0) 0) |
| [8] |
郑泽东, 王奎, 李永东, 等. 采用模型预测控制的交流电机电流控制器[J]. 电工技术学报, 2013, 28(11): 118-123. ZHENG Zedong, WANG Kui, LI Yongdong, et al. Current controller for AC motors using model predictive control[J]. Transactions of China Electrotechnical Society, 2013, 28(11): 118-123. (  0) 0) |
| [9] |
张永昌, 高素雨. 考虑延时补偿的永磁同步电机电流预测控制[J]. 电气工程学报, 2016, 11(3): 13-20. ZHANG Yongchang, GAO Suyu. Predictive current control for permanent magnet synchronous motor with delay compensation[J]. Journal of Electrical Engineering, 2016, 11(3): 13-20. (  0) 0) |
| [10] |
荆江平, 余小婵, 刘元. 三相虚拟磁链观测并网逆变器预测技术[J]. 电力科学与技术学报, 2022, 37(6): 157-164. JING Jiangping, YU Xiaochan, LIU Yuan. Three-phase virtual flux linkage observation grid-connected inverter prediction technology[J]. Journal of Electric Power Science and Technology, 2022, 37(6): 157-164. (  0) 0) |
| [11] |
KIM S K. Offset-free one-step ahead state predictor for power electronic applications using robust proportional-integral observer[J]. IEEE Transactions on Industrial Electronics, 2016, 63(3): 1763-1770. DOI:10.1109/TIE.2015.2499170 (  0) 0) |
| [12] |
冯景欢, 夏长亮, 王贺超, 等. 永磁同步电机改进无差拍电流预测控制[J]. 电工电能新技术, 2015, 34(8): 1-6, 31. FENG Jinghuan, XIA Changliang, WANG Hechao, et al. Improved deadbeat predictive current control strategy of permanent magnet synchronous motors[J]. Advanced Technology of Electrical Engineering and Energy, 2015, 34(8): 1-6, 31. (  0) 0) |
| [13] |
BODE G H, LOH P C, NEWMAN M J, et al. An improved robust predictive current regulation algorithm[J]. IEEE Transactions on Industry Applications, 2005, 41(6): 1720-1733. (  0) 0) |
| [14] |
ZHANG X G, HOU B S, MEI Y. Deadbeat predictive current control of permanent-magnet synchronous motors with stator current and disturbance observer[J]. IEEE Transactions on Power Electronics, 2017, 32(5): 3818-3834. (  0) 0) |
| [15] |
尹忠刚, 白聪, 杜超, 等. 基于内模干扰观测器的永磁同步直线电机无差拍电流预测控制方法[J]. 电工技术学报, 2018, 33(24): 5741-5750. YIN Zhonggang, BAI Cong, DU Chao, et al. Deadbeat predictive current control for permanent magnet linear synchronous motor based on internal model disturbance observer[J]. Transactions of China Electrotechnical Society, 2018, 33(24): 5741-5750. (  0) 0) |
| [16] |
WANG F X, ZUO K K, TAO P, et al. High performance model predictive control for PMSM by using stator current mathematical model self-regulation technique[J]. IEEE Transactions on Power Electronics, 2020, 35(12): 13652-13662. (  0) 0) |
| [17] |
李英强, 杨明, 龙江, 等. 基于扩展卡尔曼滤波的永磁同步电机无电流传感器预测控制[J]. 电机与控制应用, 2018, 45(1): 107-113. LI Yingqiang, YANG Ming, LONG Jiang, et al. Current sensorless predictive control based on extended Kalman filter for PMSM drives[J]. Electric Machines & Control Application, 2018, 45(1): 107-113. (  0) 0) |
| [18] |
曾岳南, 曾祥彩, 周斌. 永磁同步电机传动系统电流环非线性自抗扰控制器的设计与稳定性分析[J]. 电工技术学报, 2017, 32(17): 135-143. ZENG Yuenan, ZENG Xiangcai, ZHOU Bin. Nonlinear active disturbance rejection controller design for current loop of PMSM drive system and its stability analysis[J]. Transactions of China Electrotechnical Society, 2017, 32(17): 135-143. (  0) 0) |
| [19] |
樊小利. 永磁同步电机模型预测控制的研究与实现[D]. 成都: 西南交通大学, 2015. FAN Xiaoli. Research and experiment based on model predictive control of the permanent magnet synchronous motor[D]. Chengdu: Southwest Jiaotong University, 2015. (  0) 0) |
| [20] |
韩伟, 王大志, 刘宝成. 基于复合预测的无差拍谐波电流跟踪控制[J]. 仪器仪表学报, 2014, 35(6): 1425-1432. HAN Wei, WANG Dazhi, LIU Baocheng. Dead-beat harmonic current tracking control method based on mixed prediction[J]. Chinese Journal of Scientific Instrument, 2014, 35(6): 1425-1432. (  0) 0) |
| [21] |
孙凯翔, 胡兆稳, 阚超豪, 等. 基于满秩辨识方程的内置式永磁同步电机多参数在线辨识[J]. 电子测量技术, 2018, 41(24): 112-118. SUN Kaixiang, HU Zhaowen, KAN Chaohao, et al. Full rank identification equation based muti-parameter online identification for interior permanent magnet synchronous motors[J]. Electronic Measurement Technology, 2018, 41(24): 112-118. (  0) 0) |
| [22] |
张荣芸, 周成龙, 时培成, 等. 基于自适应积分滑模与扰动观测的多PMSM同步控制[J]. 电力系统保护与控制, 2022, 50(20): 127-138. ZHANG Rongyun, ZHOU Chenglong, SHI Peicheng, et al. Mul ti-PMSM synchronous control based on adaptive integral sliding mode and disturbance observation[J]. Power System Protection and Control, 2022, 50(20): 127-138. (  0) 0) |
| [23] |
齐歌, 李敬业. 基于扰动观测的永磁同步电动机双预测控制研究[J]. 组合机床与自动化加工技术, 2020(12): 85-89. QI Ge, LI Jingye. Research on dual predictive control of permanent magnet synchronous motor based on disturbance observation[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2020(12): 85-89. (  0) 0) |
| [24] |
仝淼, 李好文, 郑岗. 带延迟补偿的PMSM改进无差拍电流预测控制[J]. 电力电子技术, 2020, 54(12): 99-102. TONG Miao, LI Haowen, ZHENG Gang. Improved deadbeat predictive current control for PMSM with delay compensation[J]. Power Electronics, 2020, 54(12): 99-102. (  0) 0) |
| [25] |
吴嘉欣, 张懿, 魏海峰, 等. 永磁同步电机无磁链电流预测控制[J]. 微特电机, 2020, 48(4): 46-49, 59. WU Jiaxin, ZHANG Yi, WEI Haifeng, et al. Flux-free current predictive control of permanent magnet synchronous motor[J]. Small & Special Electrical Machines, 2020, 48(4): 46-49, 59. (  0) 0) |
| [26] |
RAHMAN K M, HITI S. Identification of machine parameters of a synchronous motor[J]. IEEE Transactions on Industry Applications, 2005, 41(2): 557-565. (  0) 0) |
| [27] |
WANG Q W, WANG G L, ZHAO N N, et al. An impedance model-based multiparameter identification method of PMSM for both offline and online conditions[J]. IEEE Transactions on Power Electronics, 2021, 36(1): 727-738. (  0) 0) |
| [28] |
SANDRE-HERNANDEZ O, MORALES-CAPORAL R, RANGEL-MAGDALENO J, et al. Parameter identification of PMSMs using experimental measurements and a PSO algorithm[J]. IEEE Transactions on Instrumentation and Measurement, 2015, 64(8): 2146-2154. (  0) 0) |
| [29] |
DENG W T, XIA C L, YAN Y, et al. Online multiparameter identification of surface-mounted PMSM considering inverter disturbance voltage[J]. IEEE Transactions on Energy Conversion, 2017, 32(1): 202-212. (  0) 0) |
| [30] |
MA X J, BI C. A technology for online parameter identification of permanent magnet synchronous motor[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(3): 237-242. (  0) 0) |
 2023, Vol. 42
2023, Vol. 42


 舒朝君(1962),女,学士,副教授,研究方向为电工新技术(E-mail:
舒朝君(1962),女,学士,副教授,研究方向为电工新技术(E-mail: