文章编号: 2096-3203(2023)03-0196-10 中图分类号: TM351
2. 国网江苏省电力有限公司营销服务中心,江苏 南京 210019;
3. 金陵科技学院机电工程学院, 江苏 南京 211112
内置式电机由于高转矩密度、高功率密度等优点已被广泛应用于电动汽车的驱动电机中[1-6]。其中,内置切向式永磁电机因其相邻磁极相当于并联,可产生“聚磁”效应,利于减小电机体积、提高功率密度,在电动汽车中具有较好的应用前景[7-10]。
磁场的精确计算是进行电机设计、分析电磁性能的必要前提。内置式永磁电机转子结构的复杂度较高,且隔磁桥处存在磁饱和现象,磁场计算难度较大[11]。目前,永磁电机常用的磁场计算方法主要有等效磁路法、有限元法、解析法3种。等效磁路法建模简单,但计算精度较低、使用范围相对较小[12];有限元法通用性较好且计算精度较高,但对计算硬件要求较高,计算量大且速度慢,难以在计算精度和速度上得到良好的折衷[13-14];而解析法以其计算速度快且精度高、可通过表达式体现电机设计参数与电磁性能之间映射关系等优点,成为电机磁场计算的有效手段之一。
在解析法中,子域法是基于麦克斯韦方程组建立不同子域的方程,根据磁场关系列写边界条件进行求解,物理概念清晰[15-18]。该方法可以考虑开槽效应、电枢反应场以及线圈和线圈几何形状间的相互作用,具有较高的计算精度和计算速度[19-21]。子域法通常假设铁芯磁导率为无穷大,而内置式永磁电机隔磁桥处的饱和效应使得传统子域模型方法在此处无法建立边界条件,因此会产生较大计算误差[22]。
近些年来,对子域计算方法的研究也有了一定进展,研究对象从最初的表贴式永磁电机已逐渐发展为更多种结构的电机,并将开槽效应、转子偏心等纳入了研究范围。文献[23-24]分别对双转子结构和内置U型转子结构的永磁电机进行计算,具有充分的可行性和较高的计算精度。文献[25]为避免简化形状的电机产生计算误差,采用边界离散化方法改善传统的子域模型。然而,大多数研究对于内置式电机隔磁桥处的饱和效应都采取了简化假设,这使得内置式电机隔磁桥处的子域计算问题始终未能得到较好解决。
同时,一些考虑饱和效应的半解析法也进入了广大学者的视野。文献[26]提出将转子磁势模型与磁等效电路模型相结合,模拟桥区的复杂饱和,精确计算V型电机的磁场,但这也增加了建模和计算的工作量,计算时间成本高,不利于再进行优化。文献[27]虽然考虑了铁芯饱和现象对轴向漏磁的影响,但子域计算本身已十分复杂,再结合等效磁路法的复杂电路,对计算条件要求较高。文献[28]基于有限元法得到饱和处的磁导率,其计算时间较长,且未从根本解决铁芯饱和的解析计算问题。因此,兼顾计算精度和计算速度的内置式永磁电机计算方法是仍有待国内外学者研究的问题。
针对内置式永磁电机磁场解析建模中隔磁桥处铁芯饱和现象不能计算这一难题,文中提出了一种考虑定子多层绕组结构和转子隔磁桥饱和效应的切向式永磁电机电枢磁密解析计算方法。基于子域解析建模思想,将切向式永磁电机中的隔磁桥用等效气隙替代,通过等磁阻原理计算等效气隙的参数。为保证计算精确度,设定误差判据,对磁场进行循环迭代求解。最后,以切向式永磁电机为计算模型,采用8极9槽和10极12槽两种不同极槽配合的切向式永磁电机建立有限元模型,利用有限元方法对文中所提出的计算方法进行验证。结果表明,该方法可以有效地解决内置式电机隔磁桥饱和现象不能计算的问题,在确保计算速度的前提下,提高了内置式电机磁场计算的准确度,为进一步分析电机的电磁性能奠定了基础。
1 内置切向式转子铁芯隔磁桥等效模型电枢磁场的计算是分析电机带负载磁场的基础,且电枢磁场下的磁密谐波会影响电磁转矩的大小,还会出现振动和噪声等现象,因此文中基于电机在电枢磁场下的气隙磁密进行建模计算。
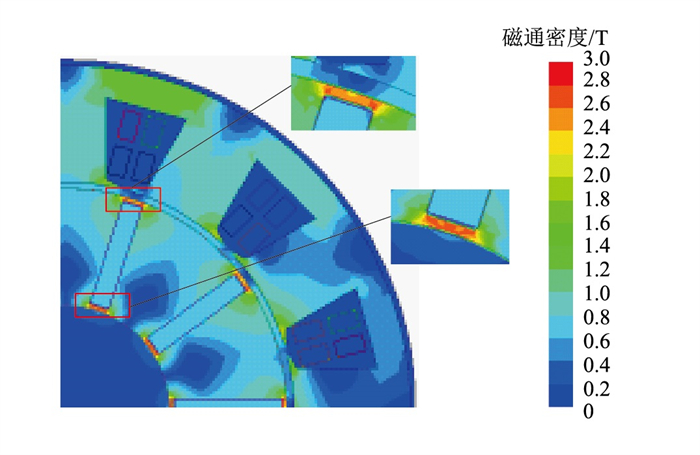
1.1 隔磁桥饱和现象在内置式永磁电机中,为保证转子铁芯具有足够的机械强度,同时避免永磁体的漏磁系数过大而导致其利用率过低,须设置隔磁桥结构,其原理是使隔磁桥处铁芯中的磁通达到饱和以抑制漏磁磁通。以切向式永磁电机为例,其原理如图 1所示。
|
图 1 切向式永磁电机隔磁桥饱和现象 Fig. 1 Spoke-type permanent magnet synchronous machine magnetic bridge saturation phenomenon |
当隔磁桥处铁芯达到饱和后,该处的磁导率降低,磁阻增加,可进一步抑制电机漏磁通的产生。但由于铁芯材料的磁化曲线具有非线性特性,隔磁桥处的磁阻与铁芯的磁导率以及饱和区域的大小有关。当隔磁桥越窄,其饱和程度越高,磁导率越低,而磁阻与磁导率为倒数关系,因此磁阻将越大,漏磁越少;反之,隔磁桥越宽,其饱和程度越低,磁导率越高,磁阻越小,漏磁越大。但考虑到实际电机加工的机械强度有限,不能为了达到较好的抑制漏磁效果而一味地减小隔磁桥处的铁芯面积,因此,隔磁桥饱和现象无法被忽视。
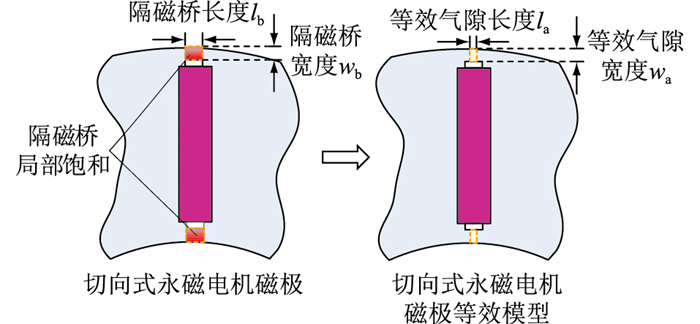
1.2 隔磁桥等效模型子域解析建模方法在处理铁芯磁导率时,假设其磁导率无穷大,即忽略铁芯磁阻,且不计铁芯饱和,以便于建立不同材料之间的边界条件,多用于表贴式永磁电机的磁场解析建模中。然而,内置式永磁电机由于隔磁桥处存在饱和现象,其磁阻增加,磁导率并非无穷大,若按照传统的处理方法对隔磁桥处的铁芯磁导率进行假设将无法准确计算电机内磁场。针对该问题,文中提出一种利用子域模型中虚拟的等效气隙对隔磁桥处饱和铁芯进行磁阻等效的方法,并与子域解析建模方法相结合,以解决隔磁桥处饱和效应带来的解析建模的难题,其等效模型如图 2所示。
|
图 2 隔磁桥等效模型 Fig. 2 Equivalent model of magnetic bridge |
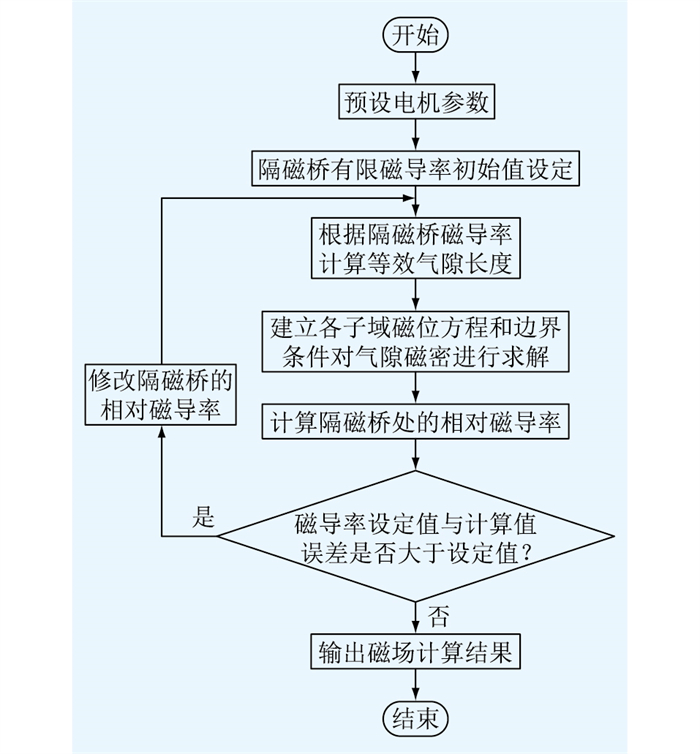
该等效方法的具体步骤如下:首先,在计算中考虑隔磁桥处的饱和影响,将永磁电机转子中的每处隔磁桥分别用虚拟的矩形等效气隙进行等效,等效气隙的宽度wa与隔磁桥的实际宽度wb相同;其次,预估隔磁桥处铁芯的饱和程度,给定隔磁桥处相对磁导率初始值μr0作为循环迭代的初始值,根据隔磁桥处磁阻与等效气隙磁阻相等的原理建立等式la=lb/μr0,计算出能等效模拟原隔磁桥中饱和情况的等效气隙长度la;然后,将其带入磁场的解析计算中,建立各个子域的矢量磁位方程和边界条件,对气隙磁密进行求解;最后,将计算所得的磁密与有限元结果进行比对,若误差大于设定值,则修改隔磁桥处的相对磁导率数值,进行下一次迭代,直至解析计算结果与有限元结果的差值满足要求,输出此时的磁密计算结果。该等效方法的具体流程如图 3所示。
|
图 3 等效气隙法计算流程 Fig. 3 Flow chart of equivalent air gap method |
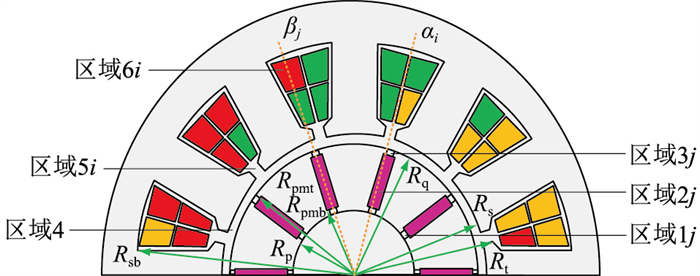
文中所研究的多层绕组切向式永磁电机模型的横截面如图 4所示,将其划分为6个子域:子域1为磁极底部隔磁桥的等效气隙1,子域2为永磁体磁极,子域3为磁极顶部隔磁桥的等效气隙2,子域4为气隙部分,子域5、6分别为槽口和槽身部分。
|
图 4 文中电机模型子域分区 Fig. 4 Subdomain partition of the machine model in this paper |
对极数为PP、槽数为QQ的电机,用变量j表示电机转子区域第j个磁极部分的序号,j=1,2,…,PP;用变量i表示第i个定子槽部分的序号,i=1,2,…,QQ。图 4中,区域1j为转子部分第j个等效气隙1的区域,区域2j为转子部分第j个磁极的区域,区域3j为转子部分第j个等效气隙2的区域,区域5i为定子槽部分第i个槽口的区域,区域6i为定子槽部分第i个槽身的区域。电机模型的结构完全由以下参数决定:βj为第j个磁极中心位置;αi为第i个槽的中心角度,为弧度制;Rp、Rpmb、Rpmt、Rq、Rs分别为转子铁芯外半径、磁极底部隔磁桥外半径、永磁体外半径、磁极顶部隔磁桥外半径及定子铁芯内半径;Rt、Rsb分别为槽身内半径和外半径。
为简化分析,文中进行如下假设[29]。
(1) 不考虑电机的轴向长度,磁密只有径向分量和切向分量。
(2) 永磁体的相对磁导率为1。
(3) 定子和转子铁芯具有无限磁导率,电导率为0。
(4) 忽略电机端部效应。
2.2 电枢绕组电流密度由于多层绕组结构可以减少电枢磁场的低次谐波,增加电机的弱磁性能,因此文中以4层绕组为研究对象进行建模。定子槽身上层绕组区域和下层绕组区域的电流密度函数Ji1、Ji2和Ji3、Ji4如图 5所示, 其中αbs为槽身宽对应的圆心角,采用弧度制。
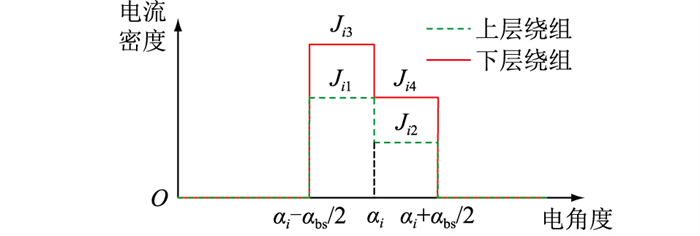
|
图 5 电枢绕组电流密度函数 Fig. 5 Current density function of stator windings |
电流密度Ji1、Ji2和Ji3、Ji4的傅里叶级数表达式为:
| $ {J_{i{\rm{t}}}} = {J_{i{\rm{t}}0}} + \sum\limits_n {{J_{i{\rm{t}}n}}} \cos \left( {{E_n}\left( {\alpha + {\alpha _{{\rm{bs}}}}/2 - {\alpha _i}} \right)} \right) $ | (1) |
| $ {J_{i{\rm{b}}}} = {J_{i{\rm{b}}0}} + \sum\limits_n {{J_{i{\rm{b}}n}}} \cos \left( {{E_n}\left( {\alpha + {\alpha _{{\rm{bs}}}}/2 - {\alpha _i}} \right)} \right) $ | (2) |
其中:
| $ {E_n} = n\frac{\pi }{{{\alpha _{{\rm{bs}}}}}} $ | (3) |
| $ {J_{i{\rm{t}}0}} = \left( {{J_{i1}} + {J_{i2}}} \right)/2 $ | (4) |
| $ {J_{i{\rm{t}}n}} = \frac{2}{{n\pi }}\left( {{J_{i1}} - {J_{i2}}} \right)\sin (n\pi /2) $ | (5) |
| $ {J_{i{\rm{b}}0}} = \left( {{J_{i3}} + {J_{i4}}} \right)/2 $ | (6) |
| $ {J_{i{\rm{b}}n}} = \frac{2}{{n\pi }}\left( {{J_{i3}} - {J_{i4}}} \right)\sin (n\pi /2) $ | (7) |
式中:Jit为第i个定子槽的上层绕组电流密度;Jib为第i个定子槽的下层绕组电流密度;α为任意一点的位置角;n为区域6i的相应谐波次数。在定子槽身上层绕组的电流密度傅里叶展开式中,Jit0取值为Ji1,Jitn取值为Ji2。在定子槽身下层绕组的电流密度傅里叶展开式中,Jib0取值为Ji3,Jibn取值为Ji4。
2.3 磁场基本方程根据磁场的库伦规范,矢量磁位A满足:
| $ \nabla \cdot \mathit{\boldsymbol{A}} = 0 $ | (8) |
磁场是无源场,根据磁场中的高斯定律,磁通密度B是无散度的,而磁场强度H的旋度等于电流密度,即:
| $ \nabla \cdot \mathit{\boldsymbol{B}} = 0 $ | (9) |
| $ \nabla \times \mathit{\boldsymbol{H}} = \mathit{\boldsymbol{J}} $ | (10) |
对于内置式电机,各个区域的B =(Br, Bα, Bz)和H =(Hr, Hα, Hz)通过磁性材料方程耦合,其中Br、Bα、Bz分别为磁通密度B在径向、切向和垂直于二维面z轴方向上分量的幅值;Hr、Hα、Hz分别为磁场强度H在径向、切向和垂直于二维面z轴方向上分量的幅值。
| $ \mathit{\boldsymbol{B}} = {\mu _0}{\mu _{\rm{r}}}\mathit{\boldsymbol{H}} + {\mu _0}\mathit{\boldsymbol{M}} $ | (11) |
式中:μ0为空气磁导率;μr为永磁材料的相对磁导率;M =(Mx, My, 0)为磁化向量,Mx、My分别为M在直角坐标系下x、y轴方向上分量的幅值。
对式(11)进行Nabla算子叉乘运算得:
| $ \nabla \times \mathit{\boldsymbol{B}} = {\mu _0}{\mu _{\rm{r}}}\nabla \times \mathit{\boldsymbol{H}} + {\mu _0}\nabla \times \mathit{\boldsymbol{M}} $ | (12) |
联立式(8)—式(10)、式(12)得到磁场的泊松方程为:
| $ {\nabla ^2}\mathit{\boldsymbol{A}} = - \nabla \times \mathit{\boldsymbol{B}} $ | (13) |
| $ {\nabla ^2}\mathit{\boldsymbol{A}} = - {\mu _0}{\mu _{\rm{r}}}\nabla \times \mathit{\boldsymbol{H}} - {\mu _0}\nabla \times \mathit{\boldsymbol{M}} $ | (14) |
| $ {\nabla ^2}\mathit{\boldsymbol{A}} = - {\mu _0}{\mu _{\rm{r}}}\mathit{\boldsymbol{J}} - {\mu _0}\nabla \times \mathit{\boldsymbol{M}} $ | (15) |
由于在气隙区域4中没有电流,电流密度J =0,且计算电枢磁场时永磁体不考虑励磁作用,磁化向量M =0,因此将式(15)中子域4和子域1、2、3的泊松方程简化为拉普拉斯方程。
| $ {\nabla ^2}\mathit{\boldsymbol{A}} = 0 $ | (16) |
对于电机内的任意一点,在极坐标系下,用r表示该点到电机圆心的半径;Az为该点处的矢量磁位z轴分量。
| $ \frac{{{\partial ^2}{A_z}}}{{\partial {r^2}}} + \frac{1}{r} \times \frac{{\partial {A_z}}}{{\partial r}} + \frac{1}{{{r^2}}} \times \frac{{{\partial ^2}{A_z}}}{{\partial {\alpha ^2}}} = 0 $ | (17) |
根据2.3节中的磁场理论,分别建立6个子域的矢量磁位方程。
(1) 等效气隙区域1j内矢量磁位z轴分量Az1j的通解为:
| $ \begin{array}{c} {A_{z1j}} = \sum\limits_{p = 1}^P {\left[ {{C_{1j}}{{\left( {\frac{r}{{{R_{{\rm{pmb}}}}}}} \right)}^{{L_p}}} + {D_{1j}}{{\left( {\frac{r}{{{R_{\rm{p}}}}}} \right)}^{ - {L_p}}}} \right]} \times \\ \cos \left( {{L_p}\left( {\beta + {\beta _{{\rm{el}}}}/2 - {\beta _j}} \right)} \right) \end{array} $ | (18) |
其中:
| $ {L_p} = p\frac{\pi }{{{\beta _{{\rm{e}}1}}}} $ | (19) |
(2) 永磁体区域2j内矢量磁位z轴分量Az2j的通解为:
| $ \begin{array}{c} {A_{z2j}} = \sum\limits_{v = 1}^V {\left[ {{C_{2j}}{{\left( {\frac{r}{{{R_{{\rm{pmt}}}}}}} \right)}^{{U_v}}} + {D_{2j}}{{\left( {\frac{r}{{{R_{{\rm{pmb}}}}}}} \right)}^{ - {U_v}}}} \right]} \times \\ \cos \left( {{U_v}\left( {\beta + {\beta _{{\rm{pm}}}}/2 - {\beta _j}} \right)} \right) \end{array} $ | (20) |
其中:
| $ {U_v} = v\frac{\pi }{{{\beta _{{\rm{pm}}}}}} $ | (21) |
(3) 等效气隙区域3j内矢量磁位z轴分量Az3j的通解为:
| $ \begin{array}{c} {A_{z3j}} = \sum\limits_{q = 1}^Q {\left[ {{C_{3j}}{{\left( {\frac{r}{{{R_{\rm{q}}}}}} \right)}^{{Y_q}}} + {D_{3j}}{{\left( {\frac{r}{{{R_{{\rm{pmt}}}}}}} \right)}^{ - {Y_q}}}} \right]} \times \\ \cos \left( {{Y_q}\left( {\beta + {\beta _{{\rm{e}}2}}/2 - {\beta _j}} \right)} \right) \end{array} $ | (22) |
其中:
| $ {Y_q} = q\frac{\pi }{{{\beta _{{\rm{e}}2}}}} $ | (23) |
(4) 气隙区域4内矢量磁位z轴分量Az4的通解为:
| $ \begin{array}{c} {A_{z4}} = \sum\limits_{k = 1}^K {\left[ {{A_4}{{\left( {\frac{r}{{{R_{\rm{s}}}}}} \right)}^k} + {B_4}{{\left( {\frac{r}{{{R_{\rm{q}}}}}} \right)}^{ - k}}} \right]} \cos (k\alpha ) + \\ \sum\limits_{k = 1}^K {\left[ {{C_4}{{\left( {\frac{r}{{{R_{\rm{s}}}}}} \right)}^k} + {D_4}{{\left( {\frac{r}{{{R_{\rm{q}}}}}} \right)}^{ - k}}} \right]} \sin (k\alpha ) \end{array} $ | (24) |
(5) 定子槽口区域5i内矢量磁位z轴分量Az5i的通解为:
| $ \begin{array}{c} {A_{z5i}} = \sum\limits_{m = 1}^M {\left[ {{C_{5i}}{{\left( {\frac{r}{{{R_{\rm{t}}}}}} \right)}^{{F_m}}} + {D_{5i}}{{\left( {\frac{r}{{{R_{\rm{s}}}}}} \right)}^{ - {F_m}}}} \right]} \times \\ \cos \left( {{F_m}\left( {\alpha + {\alpha _{{\rm{bo}}}}/2 - {\alpha _i}} \right)} \right) + D\ln r \end{array} $ | (25) |
其中:
| $ {F_m} = m\frac{\pi }{{{\alpha _{{\rm{bo}}}}}} $ | (26) |
(6) 定子槽身区域6i内矢量磁位z轴分量Az6i的通解为:
| $ \begin{array}{c} {A_{z6i}} = \sum\limits_{n = 1}^N {\left[ {{C_{6i}}{{\left( {\frac{r}{{{R_{{\rm{sb}}}}}}} \right)}^{{E_n}}} + {D_{6i}}{{\left( {\frac{r}{{{R_{\rm{t}}}}}} \right)}^{ - {E_n}}}} \right]} \times \\ \cos \left( {{E_n}\left( {\alpha + {\alpha _{{\rm{bs}}}}/2 - {\alpha _i}} \right)} \right) + C\ln r + {A_{\rm{p}}} \end{array} $ | (27) |
式中:p、v、q、k、m、n为相应谐波次数;P、V、Q、K、M、N分别为p、v、q、k、m、n计算过程中取到的最大谐波次数,其中P、V、Q为电机转子部分子域的谐波次数,通常取电机极数PP的整数倍数,K、M、N为电机定子部分子域的谐波次数,通常取电机槽数QQ的整数倍;C1j、D1j、C2j、D2j、C3j、D3j、A4、B4、C4、D4、C5i、D5i、C6i、D6i、C、D、Ap均为待定系数;β为在转子区域内某点处的位置角;βe1为磁极底部隔磁桥等效气隙宽度对应的圆心角;βpm为磁极宽度对应的圆心角;βe2为磁极顶部隔磁桥等效气隙宽度对应的圆心角;αbo为槽口宽对应的圆心角,上述角度均采用弧度制。
2.5 边界条件为确定2.4节所给出的磁位通解中的待定系数,须施加边界条件。在所有相邻两界面的交界处,根据磁位和磁密在相邻界面上应为连续量,建立边界条件。
(1) 转子铁芯与等效气隙1交界处,即r=Rp时,有:
| $ {\left. {\sum\limits_{j = 1}^{{P_{\rm{P}}}} {{B_{1j{\rm{r}}}}} } \right|_{r = {R_{\rm{p}}}}} = 0 $ | (28) |
式中:B1jr为电机在子域1内第j个等效气隙范围内的径向气隙磁通密度。
(2) 等效气隙1与永磁体交界处,即r=Rpmb时,满足:
| $ \begin{array}{c} {\left. {\sum\limits_{j = 1}^{{P_{\rm{P}}}} {{B_{1j\alpha }}} } \right|_{r = {R_{{\rm{pmb}}}}}} = {\left. {\sum\limits_{j = 1}^{{P_{\rm{P}}}} {{B_{2j\alpha }}} } \right|_{r = {R_{{\rm{pmb}}}}}}\\ \theta \in \left( {{\beta _j} - {\beta _{{\rm{pm}}}}/2, {\beta _j} + {\beta _{{\rm{pm}}}}/2} \right) \end{array} $ | (29) |
| $ \begin{array}{c} {\left. {\sum\limits_{j = 1}^{{P_{\rm{P}}}} {{A_{z1j}}} } \right|_{r = {R_{{\rm{pmb}}}}}} = {\left. {\sum\limits_{j = 1}^{{P_{\rm{P}}}} {{A_{z2j}}} } \right|_{r = {R_{{\rm{pmb}}}}}}\\ \theta \in \left( {{\beta _j} - {\beta _{{\rm{e1}}}}/2, {\beta _j} + {\beta _{{\rm{e1}}}}/2} \right) \end{array} $ | (30) |
式中:B1jα、B2jα分别为电机在子域1、2内第j个等效气隙范围内的切向气隙磁通密度;θ为电机内任一点的位置角,当在转子区域内时,θ即为变量β,当在定子区域内时,θ即为变量α。
(3) 永磁体与等效气隙2交界处,即r=Rpmt时,满足:
| $ \begin{array}{l} \left. {\sum\limits_{j = 1}^{{P_{\rm{P}}}} {{B_{2j\alpha }}} } \right|_{r = {R_{{\rm{pmt}}}}} = {\left. {\sum\limits_{j = 1}^{{P_{\rm{P}}}}{{B_{3j\alpha }}} } \right|_{r = {R_{{\rm{pmt}}}}}}\\ \theta \in \left( {{\beta _j} - {\beta _{{\rm{pm}}}}/2, {\beta _j} + {\beta _{{\rm{pm}}}}/2} \right) \end{array} $ | (31) |
| $ \begin{array}{l} {\left. {\sum\limits_{j = 1}^{{P_{\rm{P}}}} {{A_{z3j}}} } \right|_{r = {R_{{\rm{pmt}}}}}} = {\left. {\sum\limits_{j = 1}^{{P_{\rm{P}}}} {{A_{z2j}}} } \right|_{r = {R_{{\rm{pmt}}}}}}\\ \theta \in \left( {{\beta _j} - {\beta _{{\rm{e}}2}}/2, {\beta _j} + {\beta _{{\rm{e}}2}}/2} \right) \end{array} $ | (32) |
式中:B3jα为电机在子域3内第j个等效气隙范围内的切向气隙磁通密度。
(4) 等效气隙2与气隙的交界处,即r=Rq时,满足:
| $ {\left. {\sum\limits_{j = 1}^{{P_{\rm{P}}}} {{B_{3j\alpha }}} } \right|_{r = {R_{\rm{q}}}}} = {\left. {{B_{4\alpha }}} \right|_{r = {R_{\rm{q}}}}}\quad \theta \in (0, 2\pi ) $ | (33) |
| $ \begin{array}{c} {\left. {{A_{z4}}} \right|_{r = {R_{\rm{q}}}}} = {\left. {\sum\limits_{j = 1}^{{P_{\rm{P}}}} {{A_{z3j}}} } \right|_{r = {R_{\rm{q}}}}}\\ \theta \in \left( {{\beta _j} - {\beta _{{\rm{e}}2}}/2, {\beta _j} + {\beta _{{\rm{e}}2}}/2} \right) \end{array} $ | (34) |
式中:B4α为电机在子域4气隙处的磁通密度。
(5) 槽口与气隙交界处,即r=Rs时,满足:
| $ {\left. {\sum\limits_{i = 1}^{{Q_{\rm{Q}}}} {{B_{5i\alpha }}} } \right|_{r = {R_{\rm{s}}}}} = {\left. {{B_{4\alpha }}} \right|_{r = {R_{\rm{s}}}}}\quad \theta \in (0, 2\pi ) $ | (35) |
| $ \begin{array}{c} {\left. {{A_{z4}}} \right|_{r = {R_{\rm{s}}}}} = {\left. {\sum\limits_{i = 1}^{{Q_{\rm{Q}}}} {{A_{z5i}}} } \right|_{r = {R_{\rm{s}}}}}\\ \theta \in \left( {{\alpha _i} - {\alpha _{{\rm{bo}}}}/2, {\alpha _i} + {\alpha _{{\rm{bo}}}}/2} \right) \end{array} $ | (36) |
式中:B5iα为电机在子域5内第i个槽口范围内的切向气隙磁通密度。
(6) 槽口与槽身交界处,即r=Rt时,满足:
| $ \begin{array}{c} {\left. {\sum\limits_{i = 1}^{{Q_{\rm{Q}}}} {{B_{5i\alpha }}} } \right|_{r = {R_{\rm{t}}}}} = {\left. {\sum\limits_{i = 1}^{{Q_{\rm{Q}}}} {{B_{6i\alpha }}} } \right|_{r = {R_{\rm{t}}}}}\\ \theta \in \left( {{\alpha _i} - {\alpha _{{\rm{bs}}}}/2, {\alpha _i} + {\alpha _{{\rm{bs}}}}/2} \right) \end{array} $ | (37) |
| $ \begin{array}{c} {\left. {\sum\limits_{i = 1}^{{Q_{\rm{Q}}}} {{A_{z5i}}} } \right|_{r = {R_{\rm{t}}}}} = {\left. {\sum\limits_{i = 1}^{{Q_{\rm{Q}}}} {{A_{z6i}}} } \right|_{r = {R_{\rm{t}}}}}\\ \theta \in \left( {{\alpha _i} - {\alpha _{{\rm{bo}}}}/2, {\alpha _i} + {\alpha _{{\rm{bo}}}}/2} \right) \end{array} $ | (38) |
式中:B6iα为电机在子域6内第i个槽口范围内的切向气隙磁通密度。
2.6 气隙磁密表达式通过联立矢量磁位的通解方程与边界条件,列写方程式,对未知系数求解。
| $ \mathit{\boldsymbol{B}} = \left( {{B_{\rm{r}}}, {B_\alpha }, {B_z}} \right) = \nabla \times \mathit{\boldsymbol{A}} = \left( {\frac{1}{r} \times \frac{{\partial {A_z}}}{{\partial \alpha }}, - \frac{{\partial {A_z}}}{{\partial r}}, 0} \right) $ | (39) |
通过求解方程组,可得气隙部分径向磁密B4r和切向磁密B4α的表达式分别为:
| $ \begin{array}{c} {B_{4{\rm{r}}}} = \frac{1}{r} \times \frac{{\partial {A_{z4}}}}{{\partial \alpha }} = \\ - \frac{k}{r}\sum\limits_{k = 1}^K {\left[ {{A_4}{{\left( {\frac{r}{{{R_{\rm{s}}}}}} \right)}^k} + {B_4}{{\left( {\frac{r}{{{R_{\rm{q}}}}}} \right)}^{ - k}}} \right]} \sin (k\alpha ) + \\ \frac{k}{r}\sum\limits_{k = 1}^K {\left[ {{C_4}{{\left( {\frac{r}{{{R_{\rm{s}}}}}} \right)}^k} + {D_4}{{\left( {\frac{r}{{{R_{\rm{q}}}}}} \right)}^{ - k}}} \right]} \cos (k\alpha ) \end{array} $ | (40) |
| $ \begin{array}{c} {B_{4\alpha }} = - \frac{{\partial {A_{z4}}}}{{\partial r}} = \\ - \frac{k}{r}\sum\limits_{k = 1}^K {\left[ {{A_4}{{\left( {\frac{r}{{{R_{\rm{s}}}}}} \right)}^k} - {B_4}{{\left( {\frac{r}{{{R_{\rm{q}}}}}} \right)}^{ - k}}} \right]} \cos (k\alpha ) - \\ \frac{k}{r}\sum\limits_{k = 1}^K {\left[ {{C_4}{{\left( {\frac{r}{{{R_{\rm{s}}}}}} \right)}^k} - {D_4}{{\left( {\frac{r}{{{R_{\rm{q}}}}}} \right)}^{ - k}}} \right]} \sin (k\alpha ) \end{array} $ | (41) |
为验证解析计算的有效性,文中以10极12槽和8极9槽两种极槽配合的4台切向式分数槽永磁电机为例进行验证,电机模型如图 6所示。电机Ⅰ为定子绕组Y-△连接的8极9槽电机,电机Ⅱ为定子绕组Y-△连接的10极12槽电机,电机Ⅲ为定子绕组Y-Y连接的8极9槽电机,电机Ⅳ为定子绕组Y-Y连接的10极12槽电机。图中,A、B、C和X、Y、Z为绕组相序,符号“+”、“-”为电流的参考方向,“+”表示流出二维面域,“-”表示流入二维面域。
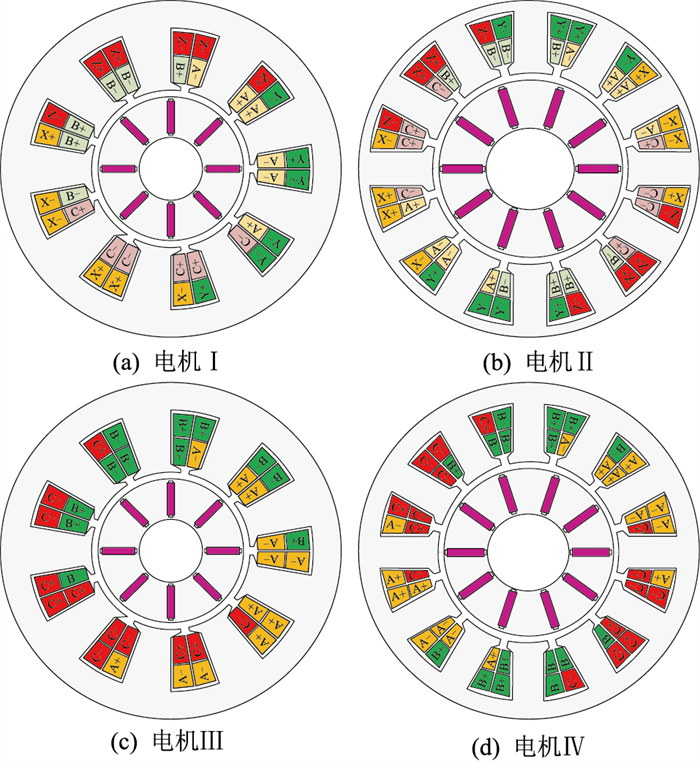
|
图 6 电机模型 Fig. 6 Machine models |
4台电机主要尺寸和参数见表 1,电机的定子采用硅钢片37WW270,转子采用硅钢片50W470,有限元仿真与解析模型中各电机参数及材料均一致。
|
|
表 1 电机的主要参数 Table 1 Main parameters of prototype machines |
由于定子绕组Y-△型连接方式中,△型连接绕组匝数为Y型连接绕组匝数的
文中电机的两处隔磁桥长度lb均为4.5×10-3 mm。根据电机饱和情况,先设定等效气隙部分的初始相对磁导率μr0为20,则子域模型中等效气隙的长度la为2.25×10-4 mm,以此作为子域计算的等效气隙初值,完成对气隙磁密的第一次计算求解。当所求磁密满足误差判据时即可输出结果。
将图 6中4台电机的状态作为各电机有限元仿真t=0 s时刻的起始状态进行仿真,此时转子某一磁极的中心线为水平,转子角度为0 rad。图 7和图 8分别为电机Ⅰ和电机Ⅱ在2种方法下的磁密对比,可见2台电机在文中的解析计算下均具有较高的准确性。
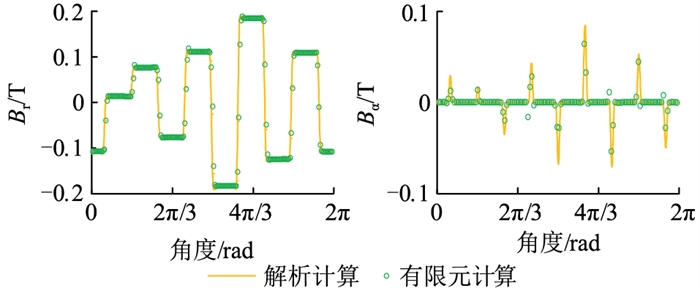
|
图 7 t=0 s时刻电机Ⅰ气隙磁密波形对比 Fig. 7 Air gap flux density comparison of machine Ⅰ at t=0 s |
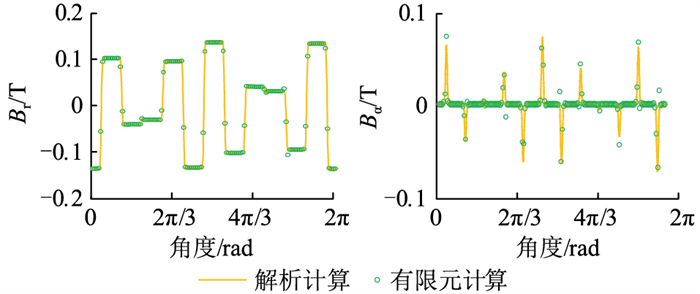
|
图 8 t=0 s时刻电机Ⅱ气隙磁密波形对比 Fig. 8 Air gap flux density comparison of machine Ⅱ at t=0 s |
对8极9槽和10极12槽电机径向气隙磁密分别进行傅里叶分析,如图 9所示,可知8极9槽电机的谐波含量较高。
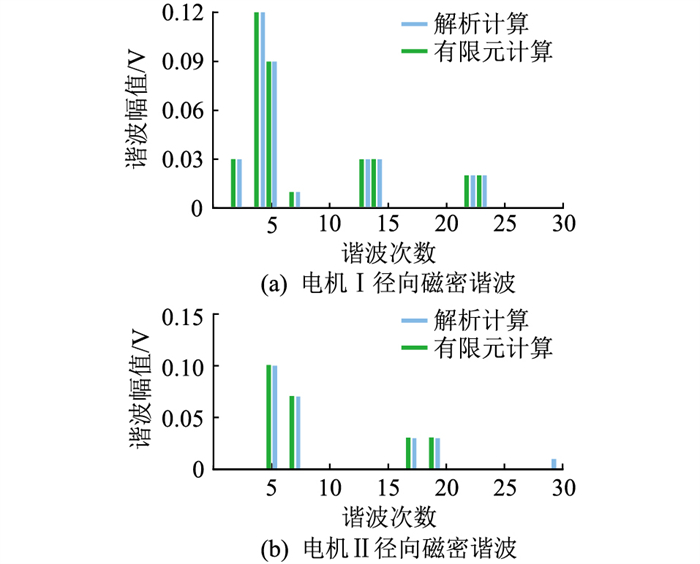
|
图 9 电机Ⅰ、Ⅱ径向磁密谐波分析 Fig. 9 Flux density harmonic analysis of machine Ⅰ and Ⅱ |
文中还对电机Ⅰ、电机Ⅱ在不同时刻下进行2种方法的磁密对比,如图 10、图 11所示,可知,2台电机的磁密波形均拟合较好,增加了文中所提出的解析计算方法的可信度。
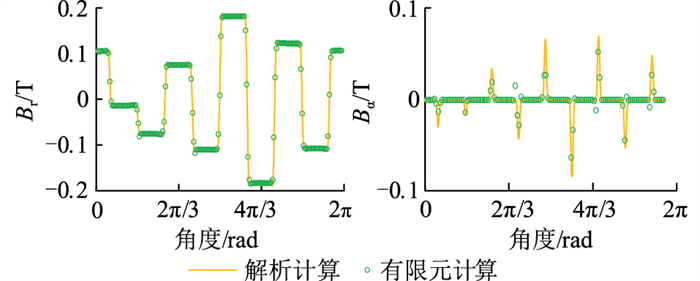
|
图 10 t=5 s时刻电机Ⅰ气隙磁密波形对比 Fig. 10 Air gap flux density comparison of machine Ⅰ at t=5 s |
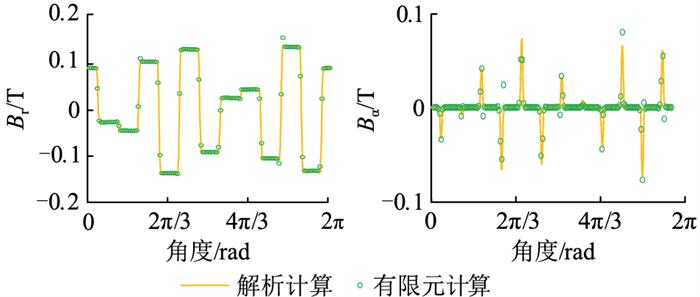
|
图 11 t=5 s时刻电机Ⅱ气隙磁密波形对比 Fig. 11 Air gap flux density comparison of machine Ⅱ at t=5 s |
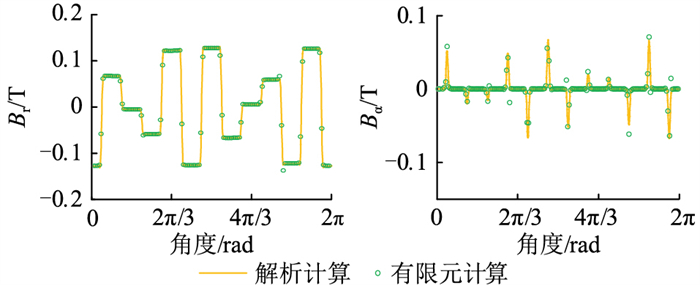
图 12和图 13为电机Ⅲ和电机Ⅳ在2种方法下的磁密对比。由图可得,8极9槽电机和10极12槽电机的磁密波形均拟合较好。
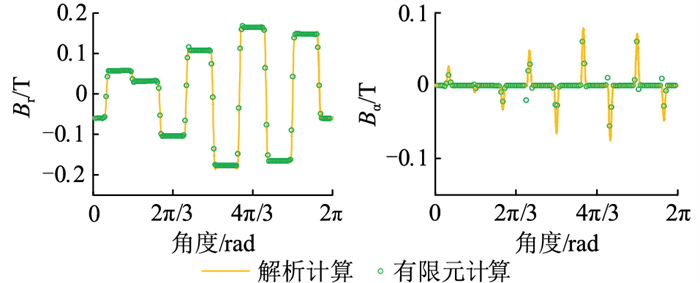
|
图 12 t=0 s时刻电机Ⅲ气隙磁密波形对比 Fig. 12 Air gap flux density comparison of machine Ⅲ at t=0 s |
|
图 13 t=0 s时刻电机Ⅳ气隙磁密波形对比 Fig. 13 Air gap flux density comparison of machine Ⅳ at t=0 s |
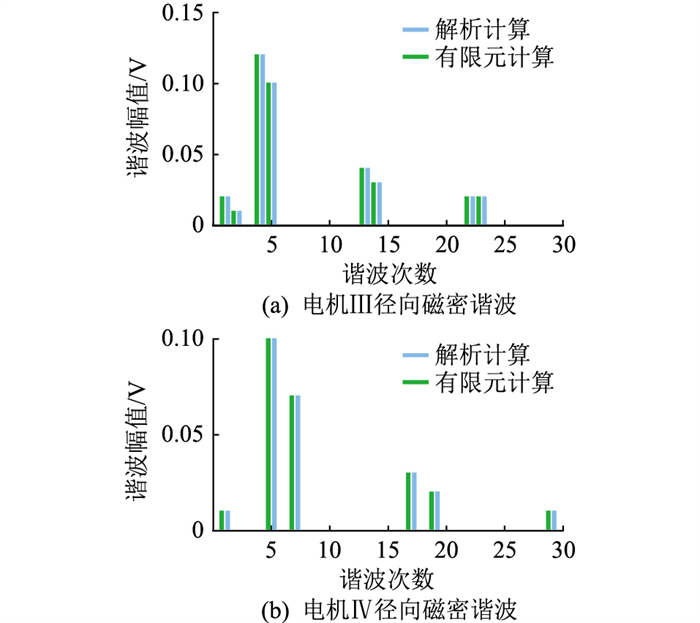
对电机Ⅲ、Ⅳ的径向气隙磁密进行谐波分析,结果如图 14所示。
|
图 14 电机Ⅲ、Ⅳ径向磁密谐波分析 Fig. 14 Flux density harmonic analysis of machine Ⅲ and Ⅳ |
对比图 9和图 14可得,8极9槽定子绕组三相连接可有效减小电机各次谐波,而10极12槽电机定子绕组Y-△连接可以有效减小电机次谐波幅值。
由以上结果可得,基于有限元法的气隙磁密的径向分量和切向分量与解析算法结果基本一致。
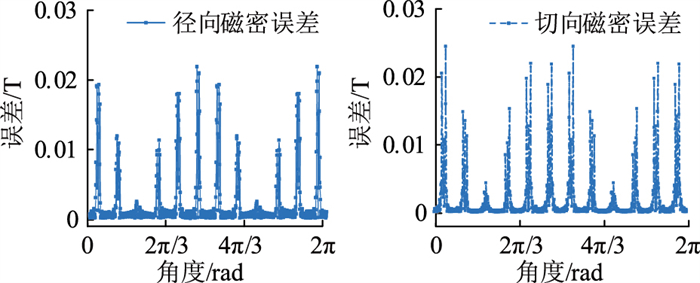
文中的磁密误差计算是对解析法和有限元法在每个步长下的磁密幅值逐点相减求得的误差值。在利用解析法和有限元法计算气隙磁密时,每隔2π/1 000角度计算一个位置处的径向磁密和切向磁密,每个周期一共计算1 000个点,并形成磁密波形图。以电机Ⅱ为例,磁密的解析计算和有限元仿真的绝对误差趋势见图 15。由图 15可知,磁密最大误差多出现在定子铁芯齿部的中线处,该处的磁密幅值较大,因此相对而言该处的误差率并不高。
|
图 15 电机Ⅱ气隙磁密误差 Fig. 15 Air gap flux density error of machine Ⅱ |
计算误差率时,首先将各点处2种方法下的计算值相减,获得该点的绝对误差,再对整个周期内的所有误差进行离散积分,得到全周期的绝对误差计算值。将该误差计算值与有限元计算结果离散积分后的值相比,可得到解析法的计算误差率。具体计算公式如下。
径向磁密误差εr:
| $ {\varepsilon _{\rm{r}}} = \frac{{\sum\limits_{h = 1}^{1000} {\left| {{B_{{\rm{An}}, {\rm{r}}}}(h) - {B_{{\rm{FE}}, {\rm{r}}}}(h)} \right|} \Delta \theta }}{{\sum\limits_{h = 1}^{1000} {\left| {{B_{{\rm{FE}}, {\rm{r}}}}(h)} \right|} \Delta \theta }} \times 100\% $ | (42) |
切向磁密误差εα:
| $ {\varepsilon _\alpha } = \frac{{\sum\limits_{h = 1}^{1000} {\left| {{B_{{\rm{An}}, \alpha }}(h) - {B_{{\rm{FE}}, \alpha }}(h)} \right|} \Delta \theta }}{{\sum\limits_{h = 1}^{1000} {\left| {{B_{{\rm{FE}}, \alpha }}(h)} \right|} \Delta \theta }} \times 100\% $ | (43) |
式中:h为将电机气隙沿圆周方向分成1 000等份后某一段的序号;Δθ为每一段气隙所占的弧度角,即为2π/1 000;BAn, r(h)、BAn, α(h)分别为第h段中解析法计算所得的径向磁密和切向磁密幅值;BFE, r(h)、BFE, α(h)分别为第h段中有限元法计算所得的径向磁密和切向磁密幅值。
经计算,文中径向磁密误差率的计算结果约为6.08%,切向磁密误差率约为4.67%。
在解析法和有限元法下,4台电机的计算时间如表 2所示,可知4台电机的解析法计算时间均远远小于有限元法。所有计算都是在一台计算机上进行的,该计算机采用英特尔酷睿CPU i5-10400F 2.9 GHz处理器,并安装了16 GB RAM。显然,解析法大大节省了计算时间。
|
|
表 2 解析法与有限元法计算时间对比 Table 2 Comparison of calculation time between analytical method and finite element method |
分析表 2可知,子域解析法的计算时间与极槽数有关,极槽数多则划分的子域较多,计算时间较长。而有限元法一般与电机尺寸大小有关,基本不随极槽数变化。
4 结语文中提出了一种考虑定子多层绕组结构和转子隔磁桥饱和效应的子域解析建模方法,并将其应用于切向式永磁电机电枢磁场计算中。首先,为考虑多层绕组结构电枢磁动势的计算,文中将定子槽区域进行了子域划分。然后,为准确解决子域建模时无法计及饱和铁芯有限磁导率的问题,文中利用等效气隙对隔磁桥处的饱和铁芯进行等效,基于矩形等效气隙和隔磁桥处的磁阻相等的原理计算出等效气隙的对应长度,将其代入子域模型中进行计算,并结合铁芯磁化曲线设置计算误差判据,通过迭代循环,获得准确的气隙磁场结果。最后,通过与有限元法的对比,证明了该方法具有较高的计算精度和计算效率。
文中提出的等效气隙子域方法也适用于其他内置式电机隔磁桥处饱和效应的等效计算,但对于结构不规则的电机模型,如V型转子结构,建立模型时仍须对其磁场进行径向和切向上的子域划分以拟合自身结构,因此其子域模型的计算有待进一步的深入研究。
致谢
本文得到江苏省高校自然科学基金面上项目(17KJB470005)资助,谨此致谢!
| [1] |
仉志华, 董浩东, 张昊, 等. 变频软启动永磁同步电机低电压穿越能力评估方法[J]. 电力工程技术, 2022, 41(5): 202-209. ZHANG Zhihua, DONG Haodong, ZHANG Hao, et al. Low voltage ride through capability evaluation method for permanent magnet synchronous motor with variable frequency convertor based softly starting[J]. Electric Power Engineering Technology, 2022, 41(5): 202-209. (  0) 0) |
| [2] |
LIU G H, LIU L, CHEN Q, et al. Torque calculation of five-phase interior permanent magnet machine using improved analytical method[J]. IEEE Transactions on Energy Conversion, 2019, 34(2): 1023-1032. DOI:10.1109/TEC.2018.2880574 (  0) 0) |
| [3] |
王要强, 朱亚昌, 冯玉涛, 等. 永磁同步电机新型趋近律滑模控制策略[J]. 电力自动化设备, 2021, 41(1): 192-198. WANG Yaoqiang, ZHU Yachang, FENG Yutao, et al. New reaching law sliding mode control strategy for permanent magnet synchronous motor[J]. Electric Power Automation Equipment, 2021, 41(1): 192-198. (  0) 0) |
| [4] |
许德智, 黄泊珉, 杨玮林. 神经网络自适应的永磁直线同步电机超扭曲终端滑模控制[J]. 电力系统保护与控制, 2021, 49(13): 64-71. XU Dezhi, HUANG Bomin, YANG Weilin. Neural network adaptive super twist terminal sliding mode control for a permanent magnet linear synchronous motor[J]. Power System Protection and Control, 2021, 49(13): 64-71. DOI:10.19783/j.cnki.pspc.201154 (  0) 0) |
| [5] |
陈浈斐, 邢宁, 马宏忠, 等. 分数槽永磁电机永磁体谐波涡流损耗建模与分析[J]. 电工技术学报, 2022, 37(14): 3514-3527. CHEN Zhenfei, XING Ning, MA Hongzhong, et al. Analytical modeling and analysis of magnet harmonic loss in fractional slot permanent-magnet machines[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3514-3527. (  0) 0) |
| [6] |
张兴华, 童歆渝, 刘伟. 考虑铁芯损耗的内置式永磁同步电机模型参数测量[J]. 电力自动化设备, 2018, 38(3): 194-198, 204. ZHANG Xinghua, TONG Xinyu, LIU Wei. Parameter measurement of interior permanent magnet synchronous motor model considering iron losses[J]. Electric Power Automation Equipment, 2018, 38(3): 194-198, 204. (  0) 0) |
| [7] |
张炳义, 王超, 冯桂宏, 等. 切向结构永磁同步电机漏磁系数分析与计算[J]. 电机与控制学报, 2020, 24(12): 62-69. ZHANG Bingyi, WANG Chao, FENG Guihong, et al. Analysis and calculation of the leakage coefficient of spoke type permanent magnet synchronous motor[J]. Electric Machines and Control, 2020, 24(12): 62-69. (  0) 0) |
| [8] |
LI J, WANG K. A novel spoke-type PM machine employing asymmetric modular consequent-pole rotor[J]. IEEE/ASME Transactions on Mechatronics, 2019, 24(5): 2182-2192. DOI:10.1109/TMECH.2019.2931950 (  0) 0) |
| [9] |
WANG Y, ZHU Z Q, FENG J H, et al. Investigation of unbalanced magnetic force in fractional-slot permanent magnet machines having an odd number of stator slots[J]. IEEE Transactions on Energy Conversion, 2020, 35(4): 1954-1963. DOI:10.1109/TEC.2020.2995803 (  0) 0) |
| [10] |
徐萌, 王艳阳, 高洁, 等. 基于双锁相环的永磁同步电机转子初始位置估算方法[J]. 电力系统保护与控制, 2022, 50(19): 49-57. XU Meng, WANG Yanyang, GAO Jie, et al. Rotor initial position estimation method of PMSM based on a double phase-locked loop[J]. Power System Protection and Control, 2022, 50(19): 49-57. (  0) 0) |
| [11] |
佟文明, 姚颖聪, 李世奇, 等. 考虑磁桥不均匀饱和的内置式永磁同步电机等效磁网络模型[J]. 电工技术学报, 2022, 37(12): 2961-2970. TONG Wenming, YAO Yingcong, LI Shiqi, et al. Equivalent magnetic network model for interior permanent magnet machines considering non-uniform saturation of magnetic bridges[J]. Transactions of China Electrotechnical Society, 2022, 37(12): 2961-2970. (  0) 0) |
| [12] |
YEO H K, LIM D K, JUNG H K. Magnetic equivalent circuit model considering the overhang structure of an interior permanent-magnet machine[J]. IEEE Transactions on Magnetics, 2019, 55(6): 1-4. (  0) 0) |
| [13] |
TARAN N, IONEL D M, RALLABANDI V, et al. An overview of methods and a new three-dimensional FEA and analytical hybrid technique for calculating AC winding losses in PM machines[J]. IEEE Transactions on Industry Applications, 2021, 57(1): 352-362. (  0) 0) |
| [14] |
佟文明, 侯明君, 孙鲁, 等. 基于精确子域模型的带护套转子高速永磁电机转子涡流损耗解析方法[J]. 电工技术学报, 2022, 37(16): 4047-4059. TONG Wenming, HOU Mingjun, SUN Lu, et al. Analytical method of rotor eddy current loss for high-speed surface-mounted permanent magnet motor with rotor retaining sleeve[J]. Transactions of China Electrotechnical Society, 2022, 37(16): 4047-4059. (  0) 0) |
| [15] |
YANG J T, CHEN J H, YANG G L, et al. Accurate calculation of magnetic field of same-pole and same-slot surface-mounted three-phase permanent magnet synchronous motor[J]. IEEE Transactions on Magnetics, 2022, 58(8): 1-10. (  0) 0) |
| [16] |
高锋阳, 齐晓东, 李晓峰, 等. 部分分段Halbach永磁同步电机优化设计[J]. 电工技术学报, 2021, 36(4): 787-800. GAO Fengyang, QI Xiaodong, LI Xiaofeng, et al. Optimization design of partially-segmented Halbach permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2021, 36(4): 787-80. (  0) 0) |
| [17] |
李灏淳, 李立毅, 于吉坤, 等. 多边形转子磁轭永磁同步电机空载气隙磁场解析计算[J]. 中国电机工程学报, 2018, 38(11): 3354-3364. LI Haochun, LI Liyi, YU Jikun, et al. Analytic calculation of no-load air-gap magnetic fields of polygonal rotor magnetic yoke permanent magnet synchronous motors[J]. Proceedings of the CSEE, 2018, 38(11): 3354-3364. (  0) 0) |
| [18] |
LIANG P X, CHAI F, LI Y, et al. Analytical prediction of magnetic field distribution in spoke-type permanent-magnet synchronous machines accounting for bridge saturation and magnet shape[J]. IEEE Transactions on Industrial Electronics, 2017, 64(5): 3479-3488. (  0) 0) |
| [19] |
LIANG P X, CHAI F, YU Y J, et al. Analytical model of a spo-ke-type permanent magnet synchronous in-wheel motor with trapezoid magnet accounting for tooth saturation[J]. IEEE Transactions on Industrial Electronics, 2019, 66(2): 1162-1171. (  0) 0) |
| [20] |
DEVILLERS E, LE BESNERAIS J, LUBIN T, et al. A review of subdomain modeling techniques in electrical machines: performances and applications[C]//2016 XXⅡ International Conference on Electrical Machines (ICEM). Lausanne, Switzerland. IEEE, 2016: 86-92.
(  0) 0) |
| [21] |
崔征山, 周扬忠, 周祎豪. 基于改进子域模型的双绕组无轴承磁通切换电机磁场解析计算[J]. 电机与控制学报, 2022, 26(3): 66-77. CUI Zhengshan, ZHOU Yangzhong, ZHOU Yihao. Analytical calculation of magnetic field of dual-winding bearingless flux-switching permanent magnet motors based on improved subdomain model[J]. Electric Machines and Control, 2022, 26(3): 66-77. (  0) 0) |
| [22] |
WU S, GUO L Y, WANG H M, et al. Analytical calculation for magnetic field in spoke-type permanent magnet machines based on a rotor magnetic potential model[J]. IEEE Transactions on Magnetics, 2022, 58(2): 1-5. (  0) 0) |
| [23] |
GOLOVANOV D, GERADA C. An analytical subdomain model for dual-rotor permanent magnet motor with halbach array[J]. IEEE Transactions on Magnetics, 2019, 55(12): 1-16. (  0) 0) |
| [24] |
HAJDINJAK M, MILJAVEC D. Analytical calculation of the magnetic field distribution in slotless brushless machines with U-shaped interior permanent magnets[J]. IEEE Transactions on Industrial Electronics, 2020, 67(8): 6721-6731. (  0) 0) |
| [25] |
DONG L Y, LI W Y, SHUAI Z J. An improved subdomain model for predicting the magnetic field of a motor containing non-orthogonal boundaries[J]. IEEE Transactions on Energy Conversion, 2022, 37(3): 2048-2057. (  0) 0) |
| [26] |
WU S, SHI T N, GUO L Y, et al. Accurate analytical method for magnetic field calculation of interior PM motors[J]. IEEE Transactions on Energy Conversion, 2021, 36(1): 325-337. (  0) 0) |
| [27] |
KONG X H, HUA Y T, ZHANG Z R, et al. Analytical modeling of high-torque-density spoke-type permanent magnet in-wheel motor accounting for rotor slot and eccentric magnetic pole[J]. IEEE Transactions on Transportation Electrification, 2021, 7(4): 2683-2693. (  0) 0) |
| [28] |
邢庆利, 王玉彬, 杜锌成. 考虑铁心饱和的内置式永磁同步电机气隙磁场解析计算[J]. 电机与控制应用, 2022, 49(1): 39-48. XING Qingli, WANG Yubin, DU Xincheng. Analytical calculation of air-gap magnetic field of interior permanent magnet synchronous motor considering iron core saturation[J]. Electric Machines & Control Application, 2022, 49(1): 39-48. (  0) 0) |
| [29] |
张守首, 郭思源. 考虑分段斜极和磁性槽楔的永磁同步电机磁场解析方法[J]. 电工技术学报, 2019, 34(1): 11-22. ZHANG Shoushou, GUO Siyuan. Analytical magnetic field method of permanent magnet synchronous machine considering step-skewed magnets and magnetic slot wedge[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 11-22. (  0) 0) |
2. State Grid Jiangsu Electric Power Co., Ltd. Marketing Service Center, Nanjing 210019, China;
3. School of Mechanical and Electrical Engineering, Jinling Institute of Technology, Nanjing 211112, China
 2023, Vol. 42
2023, Vol. 42


 陈浈斐(1987),女,博士,副教授,研究方向为电机系统设计与电磁分析(E-mail:
陈浈斐(1987),女,博士,副教授,研究方向为电机系统设计与电磁分析(E-mail: