文章编号: 2096-3203(2023)03-0188-08 中图分类号: TM51
局部放电是指绝缘系统由于局部场强过高,导致部分发生放电但没有完全击穿的一种放电现象,其为高压电气设备绝缘劣化的重要征兆。通过分析局部放电信号的特征来判断局部放电缺陷的类型,有利于有效地监测维护电力设备[1-3]。
局部放电相位分布(phase resolved partial discharge,PRPD)图谱是目前最为主流的一种局部放电分析模式,能清晰地反映放电脉冲相位、放电量和放电频率的分布特征[4-8],因此国内外学者主要通过从中提取特征参数进行局部放电模式识别。文献[9]提取PRPD图谱中陡峭度、偏斜度等8个统计特征作为有效特征值,并结合支持向量机,采用投票方式进行分类;文献[10]提取PRPD图谱灰度图像的分形特征作为识别特征量,选用径向基函数人工神经网络进行分类;文献[11]从灰度图像中提取信息熵、灰度标准差、平均绝对误差等3个统计特征和分维数、广义维数等分形特征作为识别特征量,搭建反向传播神经网络(back propagation neural network,BPNN)对局部放电模式进行识别。然而传统识别方法中特征参数的提取一般依赖于专家经验,提取的特征量有限且具有一定的主观性,因此有学者提出利用深度学习方法对PRPD图谱自主学习数据特征进行局部放电识别,如文献[12]采用卷积神经网络(convolutional neural network,CNN)识别变压器PRPD图谱,验证了该方法相比于人工提取统计特征识别方法有更高的识别准确率;文献[13]搭建深度残差网络(deep residual network,DRN)模型对局部放电灰度图像自适应提取有效特征值,并完成对气体绝缘开关设备(gas insulated switchgear, GIS)中4种典型绝缘缺陷的识别,验证了该方法相比于传统识别方法提取的特征具有更好的区分度,识别效果更好。然而,利用深度学习方法对数据的数量和复杂性有较高要求,目前各学者用来训练深度学习网络的准确数据量有限,模型的泛化性能有待考究[14]。同时,使用单一的图像特征可能会因为轮廓相似导致识别率降低,引入数值化分形特征描述图像的粗糙度可使识别结果更加可靠。
文中提出了一种基于深度学习和多模型融合的局部放电模式识别方法。采集PRPD图谱分别构建4种开关柜典型局部放电缺陷的样本集,引入迁移学习的思想,基于DRN搭建局部放电模式识别模型;为了综合图像特征和数值化分形特征的优势,利用Sugeno模糊积分将DRN和传统识别模型进行融合。在模型性能与识别精度上,将融合识别模型与无迁移学习模型和单一识别模型分别进行对比,结果验证了文中所提融合识别模型的优势。
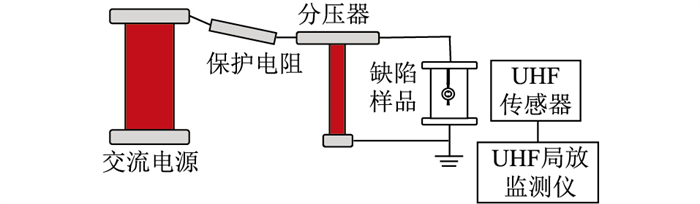
1 缺陷局部放电实验 1.1 局部放电实验平台局部放电实验平台如图 1所示,其主要由交流电源、绝缘缺陷样品和特高频(ultra high frequency,UHF)传感器组成。每次设置1种缺陷样品进行实验,当施加一定电压水平时,缺陷样品将发生局部放电而产生电磁波信号,由UHF传感器对局部放电信号进行采集。实验中采用的UHF传感器检测频带为300~1 500 MHz,平均等效高度为11.5 mm。
|
图 1 局部放电实验平台 Fig. 1 Partial discharge experimental platform |
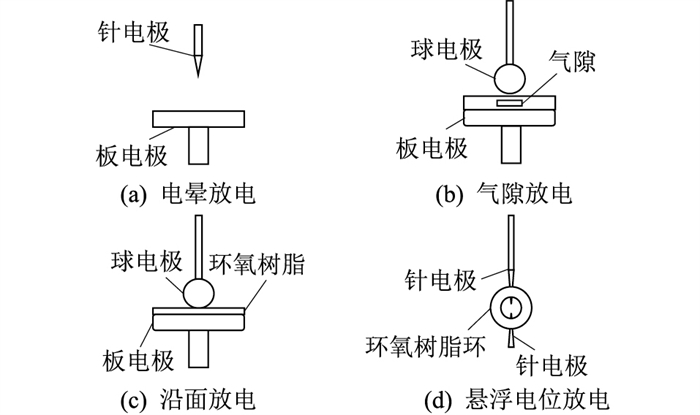
高压开关柜内不同绝缘缺陷产生的局部放电类型众多,主要可分为4类典型局部放电模式[15]:金属尖端处由于电场集中而产生的电晕放电,主要发生在柜内金属导体表面毛刺处;固体绝缘内部杂质由于介电常数较小而产生的气隙放电,主要发生在固体绝缘部位,如支撑绝缘子、电压互感器等处;固体绝缘表面由于脏污而产生的沿面放电,主要发生在支撑绝缘子处;脱落或松散的金属零件处产生的悬浮放电,主要发生在脱落的加固件,如螺钉等处。根据4种典型绝缘缺陷的特点设计了4种局部放电缺陷模型,其结构如图 2所示。
|
图 2 局部放电缺陷模型结构 Fig. 2 Structure of partial discharge defect model |
电晕放电缺陷模型如图 2(a)所示,高压端接铜制针电极,针半径为0.25 mm;接地端接板电极,采用半径为40 mm的光滑铜板,针-板间隙设置为30 mm。气隙放电缺陷模型如图 2(b)所示,高压端接铝制球电极,球半径为30 mm;接地端接铝制板电极,板半径为40 mm,在球电极和板电极中间夹有带气隙的薄片(厚度为2 mm),气隙半径为5 mm(厚度为0.5 mm)。球电极离气隙距离很小,可以保证气隙放电的临界场强比沿面放电低,因此该模型不会产生沿面放电,且从实验测量图谱来看均为典型气隙放电。沿面放电缺陷模型如图 2(c)所示,铝制球电极球半径为15 mm;铝制板电极半径为40 mm;中间环氧树脂圆形薄片半径为45 mm、厚度为2 mm;球电极底端与环氧树脂薄片上表面紧密接触。悬浮电位放电缺陷模型利用环氧树脂环将上、下针电极固定在空中来进行模拟,如图 2(d)所示,上、下电极采用棒半径为1.5 mm、针半径为0.25 mm的铜针,上、下针电极针尖距离设置为3 mm。
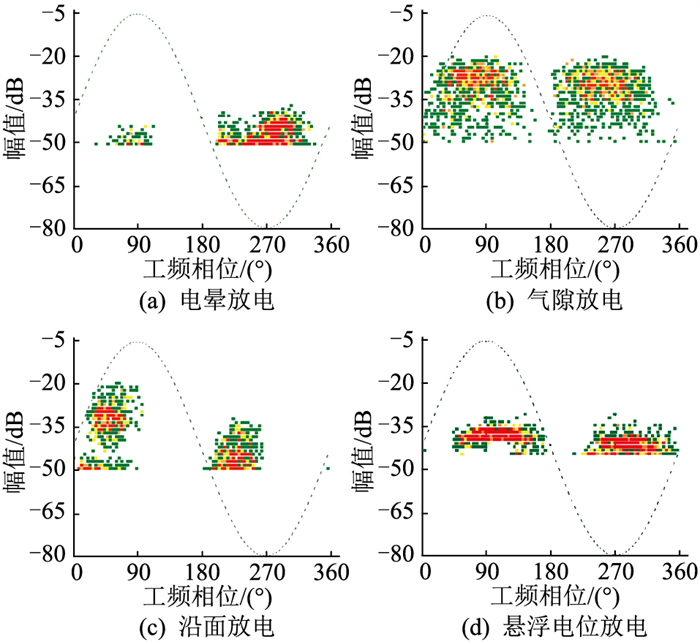
1.3 PRPD图谱分析在实验过程中,采用逐级加压法,在6.5~11.0 kV不同阶升电压下对4种局部放电缺陷的PRPD图谱进行采集,以模拟不同放电阶段及放电程度。不同电压水平下放电图谱主要在放电幅值和频次上存在差异,保证了同类别数据的多样性。为了验证采集图谱的有效性,对图 3所示4种局部放电缺陷的典型图谱进行分析。其中,红、黄、绿3种颜色表示放电频次的多少,绿色表示放电频次在0~20之间,黄色表示放电频次在20~40之间,红色表示放电频次大于40。
|
图 3 UHF采集的PRPD图谱 Fig. 3 PRPD collected by UHF profiles |
不同缺陷的局部放电图谱之间的特征存在明显差异:对于电晕放电图谱,放电点主要集中于工频相位40°~100°和200°~340°区间内,工频正负周期的放电密集程度和幅值分布规律都存在明显差异,在工频相位230°~300°范围内脉冲数量最多,在正半周幅值范围为-55~-45 dB,在负半周幅值范围为-55~-38 dB;对于气隙放电图谱,放电点分布较为分散,在工频相位0°~170°和180°~350°范围内都有放电信号,主要分布在工频相位45°与230°附近,呈向左偏斜趋势,正负半周幅值和分布规律大致相同,在正负半周放电点幅值接近,最大为-28 dB;对于沿面放电图谱,放电信号主要分布在工频相位20°~100°和190°~265°范围内,在正半周幅值范围为-50~-19 dB,在负半周幅值范围为-50~-24 dB,放电信号分布区域近似为三角形;对于悬浮电位放电图谱,放电信号主要分布在工频相位45°~170°和200°~360°范围内,放电点的幅值分布更加密集,其幅值不高且稳定分布在-45~-33 dB之间,放电信号分布区域近似为窄条状分布,表明了悬浮放电的稳定性,多数放电点幅值分布在-37 dB附近。
特征明显的PRPD图谱可以通过经验法判定其局部放电类型。但对于经验难以分辨的PRPD图谱,则须搭建识别准确率高、泛化能力强的模型来自动识别局部放电缺陷。
2 基于深度学习的局部放电模式识别由于现场测量中采集的PRPD图谱受检测设备类型等因素的影响,可能会出现相位、幅值偏移的现象,而DRN对输入图像矩阵具有缩放、平移和扭曲不变性[16]等优点,因此选择DRN搭建迁移学习模型来进行局部放电缺陷的诊断。
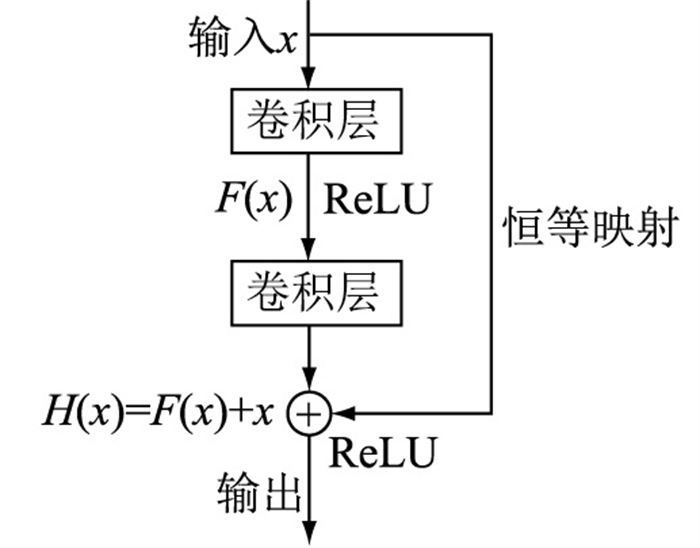
2.1 DRN模型CNN直接将数字图像矩阵作为输入网络,可自主挖掘其中的特征信息,具有一定的鲁棒性,可被用于对局部放电PRPD图谱的识别[17-18]。然而有研究发现,如果网络层数不断加深,其识别准确率不会一直提高,而是呈先上升到饱和再下降,出现“退化现象”[14]。为克服此类问题,文献[19]提出了DRN的概念,其主要思想是在CNN每几层中加入残差学习模块,进行层与层之间的短路连接。其基本结构单元如图 4所示,输入为x,主线经过卷积操作得到的输出为F(x),恒等映射的作用是将输入直接连接到输出,将F(x)与输入相加得到期望特征输出H(x)=F(x)+x,相加后的结果再通过ReLU激活函数进行输出。残差模块相当于将学习目标转化为求残差函数F(x),当F(x)=0时,该卷积层作恒等映射,允许输入信息x通过恒等映射直接传递进入后层网络;当F(x)>0时,卷积层将学习到新的特征信息。
|
图 4 DRN的基本结构单元 Fig. 4 Basic structural unit of DRN |
文中具体选择的DRN模型为ResNet101模型,其详细参数见文献[20],网络结构如图 5所示。ResNet101结构中箭头与其所包含的卷积层共同构成残差学习模块。

|
图 5 ResNet101结构 Fig. 5 ResNet101 structure |
图谱样本以二维向量的方式输入DRN,在通过多重卷积层和池化层后被抽取出相应的特征;将抽取的特征扩展为一维数组并输入全连接层;针对局部放电模式识别问题,选择Softmax分类器作为DRN的输出函数以判定局部放电类型。
2.2 迁移学习与训练过程由于DRN的训练对样本数量和复杂度都有较高要求,因此在小样本学习下并不适用。而迁移学习通过将源域数据迁移到目标任务,可以实现小样本下的有效学习[14]。迁移学习的主要方法有基于特征、共享参数和结构关系的迁移。文中将DRN模型与迁移学习方法相结合,通过共享预训练模型的参数信息,实现从源域大数据集至目标域局部放电缺陷识别任务的迁移。文中提出的基于迁移学习的DRN识别过程如图 6所示。

|
图 6 识别过程 Fig. 6 Identification process |
具体实现步骤如下:
(1) 划分训练集与测试集。基于实验构建PRPD图谱样本集,其中电晕放电163张,气隙放电150张,沿面放电157张,悬浮电位放电168张。从4类典型局部放电缺陷图谱中各随机选取60张,形成总数为240张的测试集。为了增强训练后模型的鲁棒性,其余图谱利用改变亮度、色度等方法扩充形成总数量为4 000的训练集。训练过程中采用双线性插值的方式将图像尺寸调整为224×224×3,利用式(1)对样本数据进行归一化:
| $ {p^*} = \frac{{p - \bar p}}{\delta } $ | (1) |
式中:p*为归一化后的像素值;p为图谱的像素值;p为图谱像素均值;δ为像素值的标准差。
(2) 采用ImageNet图像数据集对DRN模型进行预训练,导入经过ImageNet预训练后的模型原始参数对卷积层和池化层的参数进行初始化,在参数更新过程中将各层参数固定,以避免固定层的参数被修改,保存网络的泛化能力。
(3) 移除预训练DRN顶层结构,仅保留卷积网络,将原网络最后的全连接层和Softmax层分别替换为参数结构为1×1×1 024的全连接层和1×1×4的Softmax层,搭建新全连接层和降维Softmax层分别用于特征提取和输出局部放电类型的识别。
(4) 采用训练集对迁移学习模型进行训练,通过固定层从PRPD图谱中提取出边缘、纹理等公有特性;通过非固定层将公有特性输入到简单网络进行训练;通过Softmax分类器输出局部放电识别类型。DRN的训练目标是最小化损失函数,对于局部放电缺陷分类的识别,采用交叉熵作为损失函数,可表示为:
| $ L = - \frac{1}{m}\sum\limits_{a = 1}^m {\sum\limits_{b = 1}^n {{p_{ab}}} } \ln \left( {{q_{ab}}} \right) $ | (2) |
式中:L为每一次迭代的损失值;m为每次迭代的样本数;n为样本的类别数;pab为样本类别;qab为网络预测输出值。当损失值不再有下降趋势时保存训练模型,得到适用于局部放电缺陷识别的网络模型。
(5) 采用步骤(4)得到的训练模型对测试集进行分类识别,获得对4种局部放电类型的识别准确率。当新的检测图谱输入到网络模型时,可输出相应的识别结果。
3 基于模糊积分的多模型融合方法数值化分形特征具有特征参数少、区分度强的优点,利用其描述图像的粗糙度,可以避免使用单一图像特征时由于轮廓相似致使识别率降低的问题。利用文献[10]介绍的方法提取第2章中构建的图谱样本集的分形特征,将其作为有效特征量。基于经典BPNN搭建局部放电识别模型,设计的BPNN输入层神经元个数为4(对应提取的分形特征个数),输出层神经元个数为4(对应放电类型个数),隐含层数为1(含有10个节点)。
采用基于Sugeno模糊积分的多模型融合算法,利用模糊积分可以表达模型之间交互作用的优点[21],对模糊测度进行非线性积分运算来实现多个模型结果的融合[22]。将基于PRPD图谱的DRN识别结果、基于分形特征参数的BPNN识别结果进行融合,进而计算得到最终的识别结果,其流程如图 7所示。
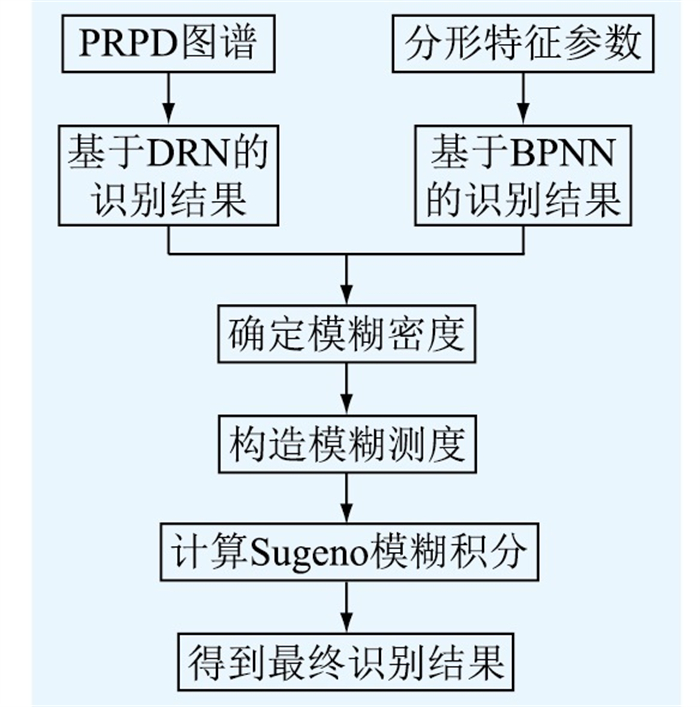
|
图 7 融合流程 Fig. 7 Flow chat of integration |
设C= C1, C2, C3, C4为4类局部放电缺陷组成的集合,Cj(j=1, 2, 3, 4)为第j类局部放电缺陷, 分别对应电晕放电、气隙放电、沿面放电与悬浮电位放电;X={x1, x2}为DRN和BPNN 2个模型集合,xi(i=1, 2)为第i个模型。如图 8所示,将样本s输入到对应的模型中进行决策,得到每类局部放电缺陷的概率分布。对于文中4类局部放电模式的识别问题,2个模型的输出结果可组成一个决策剖面(decision profile,DP)矩阵,其表达式如式(3)所示。
| $ \mathit{\boldsymbol{D}} = \left[ {\begin{array}{*{20}{l}} {{h_{11}}}&{{h_{12}}}&{{h_{13}}}&{{h_{14}}}\\ {{h_{21}}}&{{h_{22}}}&{{h_{23}}}&{{h_{24}}} \end{array}} \right] $ | (3) |

|
图 8 融合步骤 Fig. 8 Fusion steps |
DP矩阵每个行向量hi=(hi1, hi2, hi3, hi4)为模型xi对样本s的输出结果;每个列向量hj=(h1j, h2j)T为相对某个类别Cj,各个模型对于样本s的识别结果;hij为样本s被xi判别属于Cj的可能度。文中将xi对各类局部放电类型的识别准确率作为模糊密度gi, j。将可测函数h重新排列,使得满足h1j≤h2j,并将相应的模糊密度与X={x1, x2}中的元素进行重新排列,记作Si={x1, x2}。
模糊测度gj(Si)为样本s被分类器集Si识别为第j类的重要程度,可根据式(4)计算。
| $ \left\{ {\begin{array}{*{20}{l}} {{g_j}\left( {{S_1}} \right) = {g_j}\left( {\left\{ {{x_1}} \right\}} \right) = {g_{1, j}}}\\ {{g_j}\left( {{S_2}} \right) = {g_{2, j}} + {g_j}\left( {{S_1}} \right) + {\lambda _j}{g_{2, j}}{g_j}\left( {{S_1}} \right)} \end{array}\quad j = 1, 2, 3, 4} \right. $ | (4) |
式中:λj为λ律,由式(5)得出。
| $ {\lambda _j} + 1 = \prod\limits_{i = 1}^2 {\left( {1 + {\lambda _j}{g_{i, j}}} \right)} \quad j = 1, 2, 3, 4 $ | (5) |
此时定义可测函数h在集合X上关于模糊测度的Sugeno模糊积分为:
| $ {e_j} = \int {{h_j}} {\rm{d}}g = \mathop {\sup }\limits_{i = 1}^2 \left( {\min \left( {{h_{ij}}, {g_j}\left( {{S_i}} \right)} \right)} \right)\quad j = 1, 2, 3, 4 $ | (6) |
式中:sup(·)为取上限函数;ej为融合后样本s属于类别Cj的可能性。
综合ej可得各分类器对样本s的融合识别结果为:
| $ E = \left\{ {{e_1}, {e_2}, {e_3}, {e_4}} \right\} $ | (7) |
最大的ej对应的识别类型即为该样本在融合后的最终识别类型。
4 实验结果与分析基于TensorFlow深度学习框架搭建DRN模型,利用Python语言在PyCharm软件上进行模型的迁移和训练。每次迭代从训练集随机投入20张图谱,学习率设置为0.000 1,每经过20次迭代实时绘制测试集的识别准确率与损失值曲线,共循环5个周期。
4.1 有无迁移学习模型的训练过程对比绘制ResNet101与P-ResNet101(即迁移学习模型)的训练过程曲线,如图 9所示。P-ResNet101模型在180次训练时识别准确率就已趋于稳定,而ResNet101模型迭代250次后才趋于稳定。这是因为非迁移学习网络在训练时须对所有参数进行更新,识别准确率提升慢,而迁移学习无须针对新任务从头开始训练,有效提升了网络的训练效果。ResNet101在初始训练时刻由于网络参数随机出现了较大的训练误差,而P-ResNet101在网络初始训练阶段的训练误差较小,且其训练误差在小幅波动中减少并趋于稳定,说明P-ResNet101的固定参数部分具有提取公有特性的能力,加快了训练过程。

|
图 9 训练过程 Fig. 9 Training process |
DRN除去顶层的分类层后可作为输入图像的特征提取部分,据此,可将测试集图像送入各训练过的模型,得到全连接层计算后的特征值并保存,将其作为DRN对图像数据提取的特征量。将训练180次后的ResNet101与P-ResNet101提取的多维特征,采用t分布随机邻域嵌入(t-distribution stochastic neighbor embedding,t-SNE)算法[23]降至二维,进行可视化处理,可视化结果如图 10、图 11所示。各簇间距离越远表示对局部放电缺陷的区分度越好。由图 10、图 11可知,P-ResNet101全连接层提取的特征相比于ResNet101有更好的聚类结果,证明了迁移学习能有效提高网络训练效果,且具有更好的泛化能力。
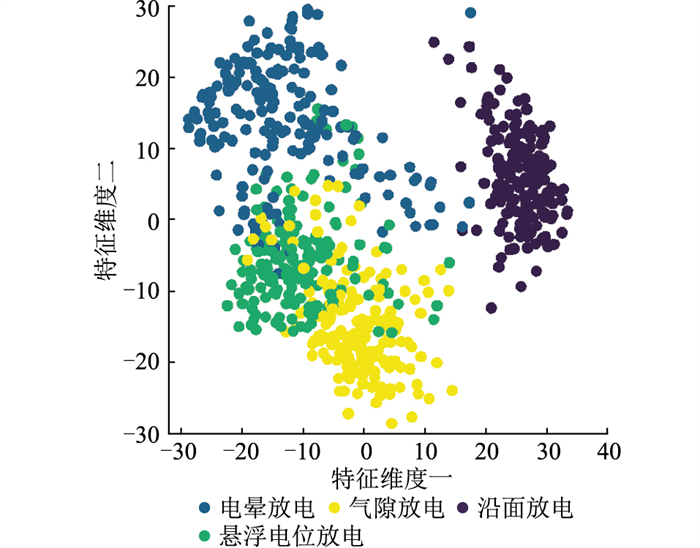
|
图 10 ResNet101特征聚类 Fig. 10 ResNet101 characteristic clustering |

|
图 11 P-ResNet101特征聚类 Fig. 11 P-ResNet101 characteristic clustering |
训练时间影响了识别模型的更新能力,当样本数量增加时,对局部放电模式识别模型进行及时更新,有利于进一步提升识别准确率,更好地满足电力设备局部放电缺陷识别的需求。训练过程中使用早停技术(在识别准确率不能得到明显提升时暂停模型训练),ResNet101和P-ResNet101模型的训练和测试时间如图 12所示。
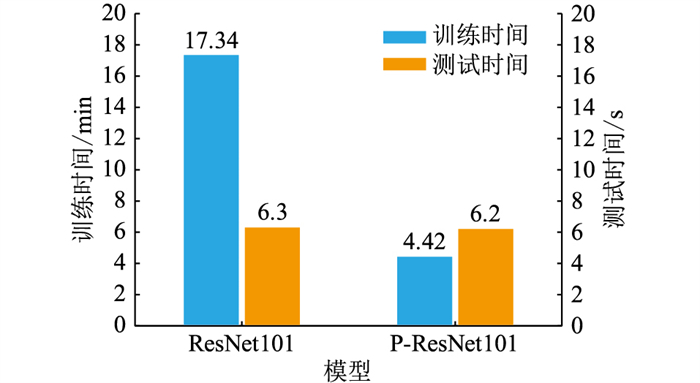
|
图 12 不同模型的训练与测试时间 Fig. 12 Training and testing time of different models |
由图 12可知, 2种模型的测试时间相差不大,而P-ResNet101模型的训练时间比ResNet101缩短了近3/4。可通过对比各模型须训练的参数量来分析训练速度提升的原因,ResNet101的参数量为44.707×106个,P-ResNet101的参数量为2.102×106个。经分析,P-ResNet101模型卷积层的42.605×106个训练参数由预训练模型提供,无须训练,只须对全连接层的2.102×106个参数进行训练,因此训练速度大大提升,节约了时间成本。
4.2 融合模型与单一模型对比根据DRN和BPNN对测试集的识别准确率绘制混淆矩阵作为模型识别能力的评价指标,如图 13、图 14所示。在混淆矩阵中,主对角线上的数字表示模型对该类局部放电缺陷的识别准确率;非主对角线上的数字表示模型将该局部放电缺陷分类为其他缺陷的误识别率。

|
图 13 DRN模型混淆矩阵 Fig. 13 Confusion matrix of DRN model |

|
图 14 BPNN模型混淆矩阵 Fig. 14 Confusion matrix of BPNN model |
由图 13、图 14可知,不同模型识别各类缺陷有着各自优势与不足:DRN模型对悬浮电位放电的识别率最高,为98.33%,对气隙放电的识别率较高,为96.67%,对沿面放电的识别率略低,为93.22%;BPNN模型对沿面放电的识别率最高,为96.97%,对气隙放电的识别率略低,为88.24%。
将融合模型对每类局部放电的识别结果与DRN和BPNN模型进行对比分析,如表 1所示。
|
|
表 1 识别准确率对比 Table 1 Comparison of recognition accuracy |
DRN和BPNN对局部放电缺陷的平均识别率分别为95.88%和91.60%,融合模型的平均识别准确率为97.85%,较BPNN模型提高了6.25%,较DRN提高了1.97%,相比于单一模型,识别率有了明显的提高。融合模型对沿面放电的识别率明显高于DRN模型,其他3类识别率均有一定程度的提高;融合模型对悬浮放电和气隙放电的识别率明显高于BPNN模型,对悬浮放电的识别率高达100%。整体说明融合模型在识别局部放电缺陷类型时优于单一模型,能够利用各个模型的特点并融合其优势,提高了分类识别的准确度。
5 结论(1) 将迁移学习的思想应用到局部放电模式识别领域,可以克服深度学习中训练样本数量和复杂度不足的问题,文中给出了一种小样本下仍可以充分利用深度学习特性的局部放电缺陷诊断方法。实验结果表明,与普通残差网络相比,迁移学习模型训练时间相比普通DRN缩短近3/4,且相同训练次数下提取特征的区分度也更为明显,验证了迁移学习模型具有更好的泛化性能与更新能力。
(2) 综合运用特高频信号的图像特征与分形特征,将深度学习与传统识别模型利用Sugeno模糊积分进行融合,能够解决单一识别模型对某些缺陷识别准确率低的问题。实验结果表明,融合模型的平均识别准确率相比基于分形特征参数的BPNN模型提高了6.25%,相比基于图像特征的DRN提高了1.97%,有效提高了局部放电缺陷诊断的准确性。
| [1] |
牛勃, 魏莹, 马飞越, 等. 电气设备长间歇性局部放电检测系统研究[J]. 电测与仪表, 2021, 58(7): 173-179. NIU Bo, WEI Ying, MA Feiyue, et al. Research on long-interval sparse partial discharge detection system for electrical equipment[J]. Electrical Measurement & Instrumentation, 2021, 58(7): 173-179. (  0) 0) |
| [2] |
徐卫东, 聂一雄, 周文文, 等. 固体绝缘开关柜局部放电模式识别优化算法[J]. 高压电器, 2019, 55(5): 100-107. XU Weidong, NIE Yixiong, ZHOU Wenwen, et al. Optimization algorithm for partial discharge pattern recognition of solid insulated switchgear[J]. High Voltage Apparatus, 2019, 55(5): 100-107. (  0) 0) |
| [3] |
潘志新, 刘利国, 钱程, 等. 基于融合极限学习机的局部放电模式识别[J]. 电力工程技术, 2019, 38(5): 42-48. PAN Zhixin, LIU Liguo, QIAN Cheng, et al. Pattern recognition of partial discharge based on fusion extreme learning machine[J]. Electric Power Engineering Technology, 2019, 38(5): 42-48. (  0) 0) |
| [4] |
周电波, 许本茂, 张劲, 等. GIS固体绝缘缺陷所激发特高频信号时频特征研究[J]. 高压电器, 2021, 57(2): 33-41. ZHOU Dianbo, XU Benmao, ZHANG Jin, et al. Study on time-frequency characteristics of UHF signals excited by solid insulation defects in GIS[J]. High Voltage Apparatus, 2021, 57(2): 33-41. (  0) 0) |
| [5] |
WANG Y X, YAN J L, YANG Z, et al. Partial discharge pattern recognition of gas-insulated switchgear via a light-scale convolutional neural network[J]. Energies, 2019, 12(24): 4674. DOI:10.3390/en12244674 (  0) 0) |
| [6] |
丁浩, 苏志雄, 王婷婷, 等. 基于脉冲电流和紫外测弧的开关柜局部放电缺陷识别方法[J]. 高电压技术, 2022, 48(11): 4527-4539. DING Hao, SU Zhixiong, WANG Tingting, et al. Partial discharge defect identification method of switch cabinet based on pulse current and ultraviolet arc measurement[J]. High Voltage Engineering, 2022, 48(11): 4527-4539. (  0) 0) |
| [7] |
饶章权, 郑书生, 王增彬, 等. 负极性OLIV下GIS局部放电UHF信号的相位特征[J]. 高电压技术, 2019, 45(12): 3924-3931. RAO Zhangquan, ZHENG Shusheng, WANG Zengbin, et al. Phase characteristics of UHF signals radiated by partial discharges in GIS under negative oscillating lightning impulse voltage[J]. High Voltage Engineering, 2019, 45(12): 3924-3931. (  0) 0) |
| [8] |
关少平, 韩肖清, 王佳莉, 等. 基于联合检测的环网柜局部放电方法研究[J]. 电测与仪表, 2020, 57(13): 126-129, 136. GUAN Shaoping, HAN Xiaoqing, WANG Jiali, et al. Research on partial discharge of ring network cabinet based on combined detection method[J]. Electrical Measurement & Instrumentation, 2020, 57(13): 126-129, 136. (  0) 0) |
| [9] |
司良奇, 钱勇, 白万建, 等. 基于支持向量机的GIS超高频局部放电模式识别[J]. 高压电器, 2014, 50(11): 1-6. SI Liangqi, QIAN Yong, BAI Wanjian, et al. Pattern recognition of UHF partial discharge for GIS with support vector machine[J]. High Voltage Apparatus, 2014, 50(11): 1-6. (  0) 0) |
| [10] |
孙才新, 许高峰, 唐炬, 等. 以盒维数和信息维数为识别特征量的GIS局部放电模式识别方法[J]. 中国电机工程学报, 2005, 25(3): 100-104. SUN Caixin, XU Gaofeng, TANG Ju, et al. PD pattern recognition method using box dimension and information dimension as discriminating features in GIS[J]. Proceedings of the CSEE, 2005, 25(3): 100-104. (  0) 0) |
| [11] |
杨眉. 基于统计和分形特征的油纸绝缘局部放电模式识别研究[D]. 重庆: 重庆大学, 2006. YANG Mei. Research on pattern recognition of PD inoil-paper insulation based on statistical and fractal feature[D]. Chongqing: Chongqing University, 2006. (  0) 0) |
| [12] |
李宏波, 朱永利, 王京保. 基于多层特征融合CNN的变压器PRPD图谱识别[J]. 电测与仪表, 2020, 57(18): 63-68. LI Hongbo, ZHU Yongli, WANG Jingbao. Transformer PRPD pattern recognition based on multi-layer feature fusion CNN[J]. Electrical Measurement & Instrumentation, 2020, 57(18): 63-68. (  0) 0) |
| [13] |
贾勇勇, 邓敏, 李玉杰, 等. 基于深度残差网络的GIS局部放电模式识别技术研究[J]. 高压电器, 2018, 54(11): 123-129. JIA Yongyong, DENG Min, LI Yujie, et al. Research on GIS partial discharge pattern recognition based on deep residual network[J]. High Voltage Apparatus, 2018, 54(11): 123-129. (  0) 0) |
| [14] |
曹智. 基于深度学习和多信息融合的GIS特高频局部放电类型识别研究[D]. 北京: 华北电力大学, 2021. CAO Zhi. Research on GIS UHF partial discharge pattern recognition based on deep learning and multi-information fusion[D]. Beijing: North China Electric Power University, 2021. (  0) 0) |
| [15] |
谢荣斌, 杨超, 申强, 等. TEV与HFCT法测量开关柜局部放电的特性对比[J]. 中国电力, 2022, 55(3): 37-47. XIE Rongbin, YANG Chao, SHEN Qiang, et al. Comparative study on the switchgear partial discharge characteristics based on transient earth voltage and pulse current detection methods[J]. Electric Power, 2022, 55(3): 37-47. (  0) 0) |
| [16] |
张聪聪, 王刚, 高栋, 等. 基于卷积网络的GIS局部放电缺陷诊断方法与应用[J]. 电工电能新技术, 2021, 40(3): 72-80. ZHANG Congcong, WANG Gang, GAO Dong, et al. Partial discharge pattern recognition based on convolutional neural network[J]. Advanced Technology of Electrical Engineering and Energy, 2021, 40(3): 72-80. (  0) 0) |
| [17] |
王彦彪, 陈振勇, 郭文萍, 等. 基于双注意力机制优化CNN架构的GIS局部放电模式识别[J]. 电力科学与技术学报, 2022, 37(2): 22-29. WANG Yanbiao, CHEN Zhenyong, GUO Wenping, et al. PD pattern recognition for GIS based on CNN architecture optimized by the double attention mechanism[J]. Journal of Electric Power Science and Technology, 2022, 37(2): 22-29. (  0) 0) |
| [18] |
唐志国, 曹智, 何宁辉. 卷积神经网络迁移学习在局部放电类型诊断中的应用[J]. 高压电器, 2022, 58(4): 158-164. TANG Zhiguo, CAO Zhi, HE Ninghui. Application of convolutional neural network transfer learning in partial discharge type diagnosis[J]. High Voltage Apparatus, 2022, 58(4): 158-164. (  0) 0) |
| [19] |
许辰航, 陈继明, 刘伟楠, 等. 基于深度残差网络的GIS局部放电PRPD谱图模式识别[J]. 高电压技术, 2022, 48(3): 1113-1123. XU Chenhang, CHEN Jiming, LIU Weinan, et al. Pattern re- cognition of partial discharge PRPD spectrum in GIS based on deep residual network[J]. High Voltage Engineering, 2022, 48(3): 1113-1123. (  0) 0) |
| [20] |
HE K M, ZHANG X Y, REN S Q, et al. Deep residual learning for image recognition[C]//2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Las Vegas, NV, USA. IEEE, 2016: 770-778.
(  0) 0) |
| [21] |
张秦梫. 基于声电融合的变压器局部放电智能诊断方法[D]. 上海: 上海交通大学, 2019. ZHANG Qinqin. Intelligent partial discharge diagnosis based on acoustic-electric fusion[D]. Shanghai: Shanghai Jiao Tong University, 2019. (  0) 0) |
| [22] |
赵辉, 单云霄, 姜欣格. γ-模糊算子的Sugeno概率积分研究[J]. 哈尔滨理工大学学报, 2020, 25(4): 151-156. ZHAO Hui, SHAN Yunxiao, JIANG Xinge. Study on Sugeno probability integral of γ-fuzzy operator[J]. Journal of Harbin University of Science and Technology, 2020, 25(4): 151-156. (  0) 0) |
| [23] |
MAATEN L V D, HINTON G. Visualizing data using t-SNE[J]. Journal of Machine Learning Research, 2008, 9(86): 2579-2605. (  0) 0) |
 2023, Vol. 42
2023, Vol. 42


 王婷婷(1996),女,硕士,研究方向为高电压试验技术、电力设备状态监测与故障诊断(E-mail:
王婷婷(1996),女,硕士,研究方向为高电压试验技术、电力设备状态监测与故障诊断(E-mail: