文章编号: 2096-3203(2023)03-0036-08 中图分类号: TM712
2. 国网浙江省电力有限公司杭州供电公司,浙江 杭州 310016;
3. 强磁场工程与新技术国家重点实验室(华中科技大学),湖北 武汉 430074
在交流配电网的基础上建设交直流混合配电网是未来配电网的发展趋势[1-2]。电力电子变压器(power electronic transformer,PET)因其交直流转换的灵活性,在交直流配电网中得到了广泛应用。因PET含有多个PET模块,其接入配电网势必会对配电网的稳定运行造成影响[3]。在某交直流混合配电网试验过程中,其直流侧出现了4 Hz左右低频振荡的现象,影响了该配电网的稳定运行,因此有必要深入研究该配电网的稳定性问题。
目前针对含PET的交直流配电网研究可概括为两方面:一是PET装备本身的拓扑和控制研究,二是含PET的交直流配电网研究。在PET的拓扑与控制方面,文献[4-9]介绍了PET的分类、拓扑、控制方式,并进行了各类PET的优缺点比较。由目前的研究可知,有关PET的拓扑及控制研究较为完善。在含PET的交直流配电网研究方面,文献[10]针对交直流配电网中的多端口PET,提出其稳态模型,重点研究以交直流系统节点电压偏移最小为目标的PET功率-电压协调控制方法。文献[11]在能效评估方面针对含PET的交直流混合电网建立了一种改进的综合能效评估模型。文献[12]基于含PET的交直流配电网故障穿越,提出一种改进的依据电压跌落深度分段不同特性调节无功电流给定的控制策略。文献[13]主要针对多端口PET交直流配电网建立了可靠性评估方法。文献[14]针对配电网进行了大扰动条件下的稳定性分析。上述文献对含有PET的交直流配电网在过电压[15]、潮流计算[16]、继电保护[17]、状态估计[18]等方面均进行了研究,但针对交直流配电网的小扰动稳定性研究以及对于系统直流侧出现低频振荡现象的介绍少有涉及。
为深入研究该低频振荡现象,文中从实际网架结构出发,对该交直流配电网系统进行了模型简化,分别介绍了系统中各个模块的主要结构及其作用,并最终在Matlab中建立了该系统的数学模型,还原了4 Hz的振荡波形,验证了数学建模的正确性并对影响振荡的因素做了定性分析。该数学模型的建立有助于认识交直流配电网的低频振荡现象,为后续系统小信号稳定性分析、振荡机理解释和优化控制奠定基础。
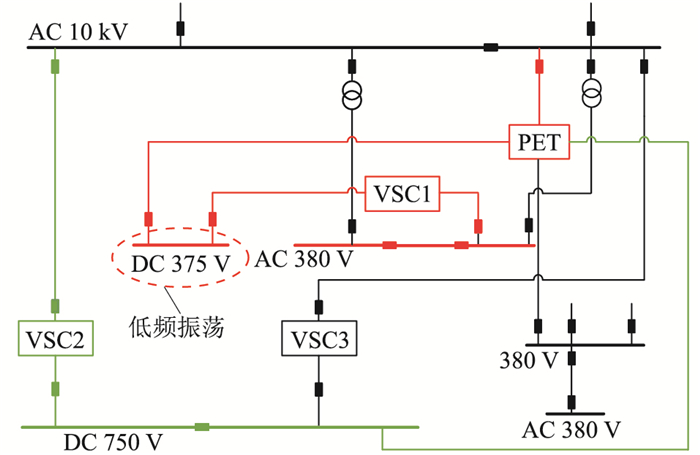
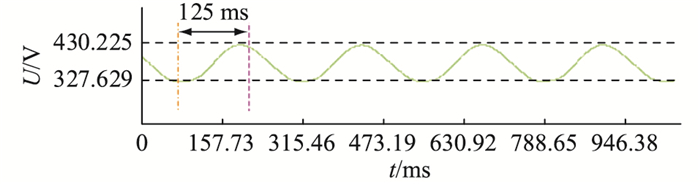
1 多端口交直流配电网场景概述在某交直流配电网的PET与电压源换流器(voltage-sourced converter,VSC)功率对拖试验过程中,运行方式如图 1所示。交直流配电网系统主要有2个闭合回路:一个是由VSC2和750 V直流母线构成的750 V闭合回路(用绿线表示);另一个是由VSC1和375 V直流母线构成的375 V闭合回路(用红线表示)。当PET的750 V端口连接到VSC2(传输功率为1 200 kW),375 V端口连接到VSC1,并经380 V端口连接到无穷大电网(传输功率为60 kW),此时将在375 V直流侧发生低频振荡。图 2给出了375 V直流母线电压的实际录波的振荡波形,其频率约为4 Hz。文中将研究这种低频振荡现象。
|
图 1 交直流配电网实际运行 Fig. 1 Actual operation of the AC/DC distribution network |
|
图 2 375 V直流侧实际振荡波形 Fig. 2 Actual oscillation waveform of the 375 V DC side |
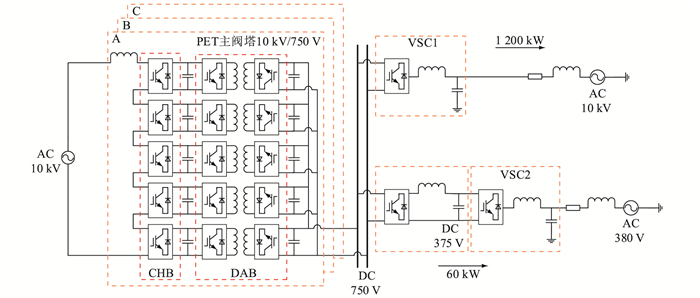
为了简化系统建模过程,基于一些合理假设,将图 1的实际物理运行系统简化为图 3所示的简化模型。图 3中,A、B、C号PET分别表示图 1中ABC三相PET的单体。简化模型假设如下:
|
图 3 交直流配电网系统的简化模型 Fig. 3 Simplified model of AC/DC distribution network system |
(1) 将图 1中的VSC2和VSC3合并成1台VSC连接750 V直流母线和10 kV交流母线(图 3中2个10 kV电源实为1条母线,为方便作图将二者分开,并非实际的电气隔离),因为系统的振荡主要发生在375 V直流侧,10 kV交流母线与750 V直流母线间连接的VSC2和VSC3对振荡的发生影响较小。
(2) 忽略配电变压器对系统的影响,等效到线路阻抗中。
(3) 忽略PET的380 V交流端口对系统的影响,因为振荡发生时380 V交流侧波形正常,故其对振荡的影响也可忽略。
该交直流配电网系统的简化模型共有4个端口,交流端口(AC 10 kV、AC 380 V)和直流端口(DC 750 V、DC 375 V)各2个。三相10 kV交流经过PET主阀塔变换成750 V直流供给直流公共母线,PET输入级和中间级采用多级H桥串联(cascaded H-bridge, CHB)和隔离型双向有源桥(dual active bridge, DAB)的拓扑结构,每相交流单独控制,经CHB整流后再经高频变压器输出。由于级联H桥拓扑高度模块化,易于扩展,当选择的级联数合适时,可以在较高的输入电压下使用较低电压等级的器件。对于H桥结构的控制相对成熟,无需额外的复杂算法,同时级联结构输出电平数多,谐波特性较好[9]。
2 各模块的拓扑及控制方式 2.1 PET主阀塔拓扑及控制方法PET主阀塔由CHB和DAB组成,下文将分别进行介绍。
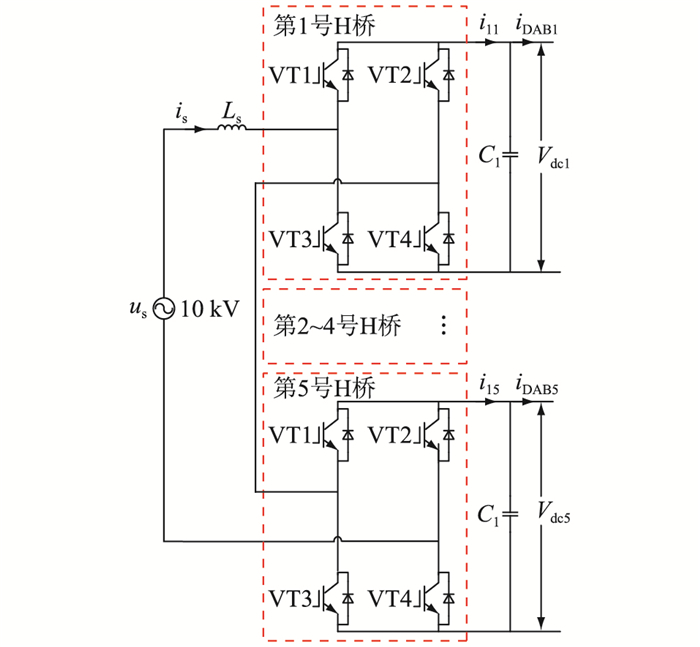
2.1.1 CHB拓扑和控制结构CHB为多级串联的H桥结构,H桥采用电压源型整流器,将5个H桥串联起来构成1个单相CHB,其拓扑如图 4所示。5级H桥的各个开关管、滤波电容参数一致,使得高压侧在各H桥上的分压一致,每个开关管承受较小的电压,这样可以选取耐受电压值较小的开关管,降低成本。
|
图 4 PET主阀塔中单相CHB拓扑 Fig. 4 Single phase CHB topology in PET main valve tower |
该CHB中电感和电容的表达式如式(1)所示。
| $ \left\{\begin{array}{l} L_{\mathrm{s}} \frac{\mathrm{d} i_{\mathrm{s}}}{\mathrm{d} t}=u_{\mathrm{s}}-5 v_{\mathrm{s}} \\ C_1 \frac{\mathrm{d} \boldsymbol{V}_{\mathrm{dc}}}{\mathrm{d} t}=\boldsymbol{i}_1-\boldsymbol{i}_{\mathrm{DAB}} \end{array}\right. $ | (1) |
式中:Ls为CHB的交流侧滤波电感;C1为H桥直流侧的滤波电容;is为流过电感的电流;us为单相交流源;vs为H桥的输入电压;i1为各级H桥输出电流矩阵,i1=[i11 i12 i13 i14 i15]T;Vdc为输出直流电压矩阵,Vdc=[Vdc1 Vdc2 Vdc3 Vdc4 Vdc5]T;iDAB为各级DAB的输入电流矩阵,iDAB=[iDAB1 iDAB2 iDAB3 iDAB4 iDAB5]T。
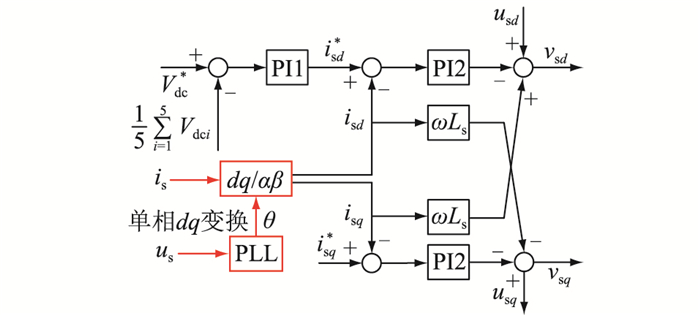
CHB常见的控制方式为直流电压外环和电流内环控制[19],如图 5所示。PI为比例积分控制器;PLL为锁相环;θ为锁相环输出角;dq/αβ为坐标变换;ω为工频角频率;usd、usq分别为us的d、q轴分量;vsd、vsq分别为vs的d、q轴分量;isd、isq分别为is的d、q轴分量。文中,x*为对应变量x的参考值,如Vdc*为Vdc的参考值。
|
图 5 CHB控制方式 Fig. 5 The control mode of CHB |
电压外环对输出直流电压控制,将实际电压值与参考值作差,电压误差经过PI控制器得到输入电流d轴分量的参考值,电流内环分别对d轴电流和q轴电流控制,从而可以调节整流器的有功和无功,调节功率因数。
理想情况下,CHB中5个H桥的各个参数应该完全相同,这样可以保证5个输出电压大小相同。但实际中,开关管以及电容参数不可能完全一致,因此须对各级H桥采取均压控制。具体方法是:将各级H桥输出电压与参考值比较,电压误差经过PI控制器得到整流桥输入电压d轴分量的误差Δvsd,将这部分误差加到控制器输出vsd上,以第一个H桥为例,说明均压控制方式,如图 6所示。

|
图 6 CHB均压控制方式 Fig. 6 The voltage balance control mode of CHB |
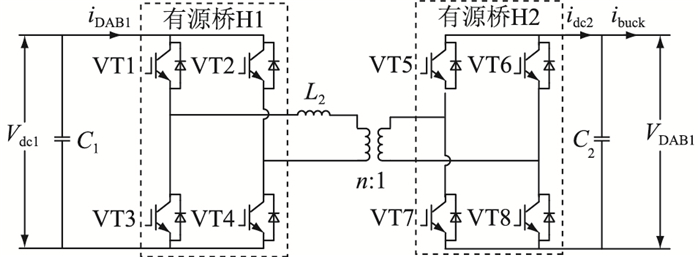
DAB为隔离型双有源桥结构,其拓扑如图 7所示。隔离级的原边和副边采用完全相同的全桥结构,即每个DAB单元都是由2个单相全桥与高频变压器组成。隔离级DAB采用双主动全桥移相控制方式,通过控制变压器两侧电压波形的相位关系来控制功率的大小和流向。
|
图 7 PET主阀塔中单相DAB拓扑 Fig. 7 Single phase DAB topology in PET main valve tower |
定义d=nVDAB1/Vdc1,其中,n为变压器变比;VDAB1为单级DAB输出电压。当d>1,即nVDAB1>Vdc1时,变换器工作于Boost模式; 当d < 1,即nVDAB1<Vdc1时,变换器工作于Buck模式。
文中,DAB工作在Buck模式。由文献[20]可知,单级DAB的传输功率为:
| $ P=\frac{n V_{\mathrm{dc1}} V_{\mathrm{DAB} 1}}{2 f_{\mathrm{s}} L_2} d_{\mathrm{DAB}}\left(1-d_{\mathrm{DAB}}\right) $ | (2) |
式中:fs为有源桥开关管开关频率;L2为变压器原边串联电感值;dDAB为移相控制中的移相占空比,即dDAB=φ/2π,φ为移相角。
单级DAB输出端电流为:
| $ i_{\mathrm{dc} 2}=\frac{P}{V_{\mathrm{DAB} 1}}=\frac{n V_{\mathrm{dc} 1}}{2 f_{\mathrm{s}} L_2} d_{\mathrm{DAB}}\left(1-d_{\mathrm{DAB}}\right) $ | (3) |
DAB采用单移相控制,控制器须要得到移相角,具体方法是:将模型中得到的DAB输出电压VDAB1与电压参考值VDAB1*作差,将误差经过PI控制器得到移相角φ,将该移相角除以2π即可得到式(2)中的移相占空比dDAB。控制器如图 8所示。

|
图 8 DAB控制方式 Fig. 8 The control mode of DAB |
三相Buck变换器经750 V直流母线连接输出375 V直流,其拓扑如图 9所示。

|
图 9 三相Buck变换器拓扑 Fig. 9 The topology of the three-phase Buck converter |
三相Buck DC/DC变换器采用3个单相Buck电路并联而成,开关管左侧为高压侧,右侧为低压侧,低压侧采用LC无源滤波。6个开关管分为2组,上半组和下半组。当电路为Buck模式时,下半组开关管恒关断;当电路为Boost模式时,上半组开关管恒关断。
在建立数学模型时忽略开关动作过程,各个器件均由数值代替,脉冲宽度调制(palse-width modulation, PWM)发生器也由占空比代替,故输出电压不存在纹波,其数学表达式为:
| $ \left\{\begin{array}{l} L_3 \frac{\mathrm{d} i_{\mathrm{L}}}{\mathrm{d} t}=d_{\text {buck }} V_{\mathrm{DAB}}-V_{\text {buck }} \\ C_3 \frac{\mathrm{d} V_{\text {buck }}}{\mathrm{d} t}=i_{\mathrm{L}}-i_{\mathrm{VSC}} \end{array}\right. $ | (4) |
式中:L3、C3分别为滤波电感和电容;iL为流过Buck变换器电感的电流;Vbuck为Buck变换器的输出电压;iVSC为流过后一级VSC的电流;dbuck为开关函数占空比。三相Buck变换器采用电压外环和电流内环控制,Buck变换器输出电压Vbuck与参考值比较,经过PI控制器得到电流参考值,再经过PI控制器的占空比,最终得到dbuck,控制方式见图 10。

|
图 10 三相Buck变换器控制 Fig. 10 The control of the three-phase Buck converter |
该交直流配电网中共有2台三相逆变器分别为经750 V直流母线变换成10 kV交流接无穷大电网和经三相Buck变换器输出的375 V直流变换成380 V接无穷大电网。此处只介绍第二种情况,第一种情况与其类似,其拓扑如图 11所示。其中,Lf、Cf分别为VSC出口的滤波电感和滤波电容;Rg、Lg分别为并网点无穷大电源内电阻和内电感;e为三相逆变器的内电势;if为流过滤波电感的电流;ut为三相逆变器输出端电压;ig为并网后流入无穷大电网的电流;ug为无穷大电网的电压。

|
图 11 三相逆变器接无穷大电网拓扑 Fig. 11 The topology of three-phase inverter connected to infinite power grid |
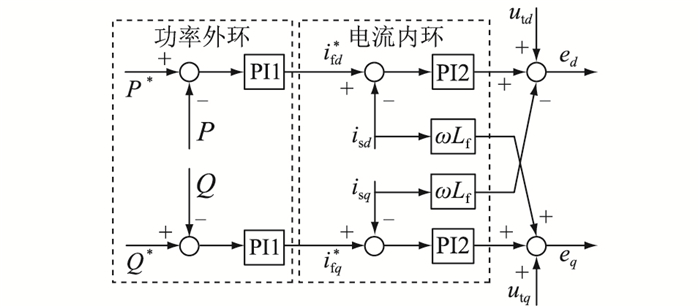
三相逆变器的输出端滤波电路为LC无源滤波,结合控制算法可对输出的波形进行调节,使其输出为工频、谐波含量较小的交流。三相逆变器控制方法如图 12所示。
|
图 12 三相逆变器控制方式 Fig. 12 The control block mode of the three-phase inverter |
图 12中,P、Q分别为三相逆变器输入有功和无功功率;ed、eq分别为e的d、q轴分量;utd、utq分别为ut的d、q轴分量;ifd、ifq分别为if的d、q轴分量。采用功率外环和电流内环控制。功率外环将有功和无功与指令值比较,经过PI控制器得到滤波电感电流的指令值,dq轴滤波电感电流除受控制量utd、utq的控制外,还受到电流交叉耦合项ωLfifd和ωLfifq的影响。为了消除电流耦合,电流内环采用输出滤波电感电压解耦控制,最终控制器输出内电势ed、eq作为电气部分的输入。
有功和无功的计算方法如下。
| $ \left\{\begin{array}{l} P=\frac{3}{2}\left(e_d i_{\mathrm{f} d}+e_q i_{\mathrm{f} q}\right) \\ Q=\frac{3}{2}\left(e_q i_{\mathrm{f} d}-e_d i_{\mathrm{f} q}\right) \end{array}\right. $ | (5) |
根据第2章关于系统拓扑和控制方式的分析,依照图 3所示的连接方式,在Matlab/Simulink中搭建该交直流配电网的仿真模型,并输出各个模块的波形。时域仿真系统主要参数的选取如表 1所示。
|
|
表 1 时域仿真系统主要参数的选取 Table 1 Selection of the main parameters of time-domain simulation system |
CHB交流输入侧为10 kV交流电压,由于其是由5个相同的H桥组成,故每级H桥分得2 kV交流电压,经整流得到2 200 V直流作为DAB的输入,仿真得到的CHB输出电压波形如图 13(a)所示。CHB的输出作为DAB的输入,经过DC/DC变换,输出750 V直流电压,仿真波形如图 13(b)所示。750 V直流母线接入三相Buck变换器输出375 V直流电压,仿真波形如图 13(c)所示。

|
图 13 各模块的输出电压波形 Fig. 13 The output voltage waveforms of each module |
为了验证CHB的均压控制策略的有效性,改变第5号H桥的参数使其与第1~4号H桥的参数不一致。仿真得到输出波形如图 13(d)所示,可知,当有均压控制时,即使是H桥参数不一致(体现在直流电压初始阶段的波形有偏差),输出直流电压的稳态值仍能保持一致。
由以上结果可知,该仿真模型符合预期要求,各个模块输出波形稳定,表明各模块拓扑和控制结构功能有效。
3.2 数学模型正确性验证在验证数学模型的正确性之前,首先应建立系统的时域开关模型。时域开关模型为系统的详细模型,考虑了开关管的动作过程,可以可靠地仿真实际试验过程,然而对于复杂的系统而言,时域开关模型运算时往往会占用计算机大量内存,从而导致运算速度缓慢。同时,时域开关模型因考虑了开关管的动作过程,对后续系统的线性化以及深入研究其机理造成不便。数学模型简化了时域开关模型中开关管的动作过程,将PWM波对开关管的作用以占空比代替,各个电路元件也同样用数值代替,极大缓解了计算机内存的占用率,提高了计算效率,同时也方便了后续对系统的小信号分析。时域开关模型是验证数学模型正确性的重要依据,对时域开关模型和数学模型同时施加一小扰动,若数学模型在小扰动下的响应与时域开关模型保持一致,则证明了数学模型的正确性。
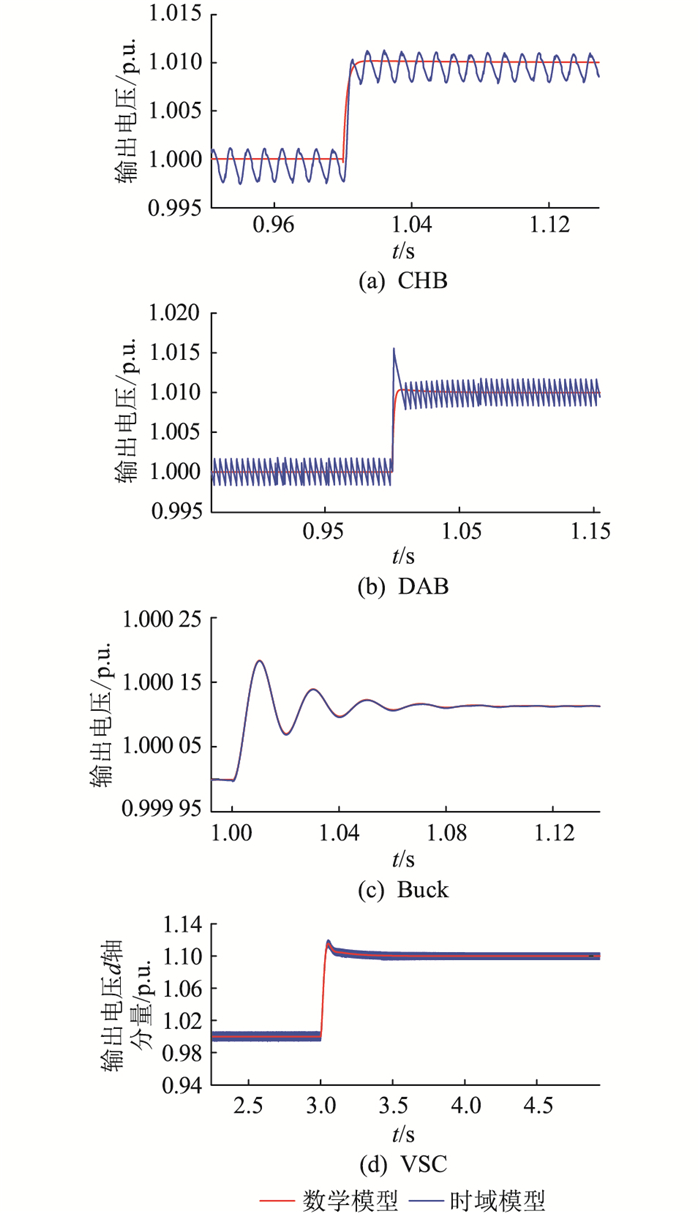
为了验证所建数学模型正确性,在Matlab/Simulink中搭建了详细的时域仿真模型进行对比验证。在系统进入稳态后,对系统中各个模块施加一小扰动,观察在扰动时数学模型与时域模型的响应是否一致,对比结果如图 14所示,分别为CHB输出电压、DAB输出电压、Buck变换器输出电压、VSC输出电压d轴分量的标幺值。
|
图 14 各模块数学模型与时域模型对比 Fig. 14 Comparison between mathematical model and time-domain model of each module |
由图 14对比结果可知,在扰动发生时,数学模型与时域模型的响应一致,验证了文中所建立的含PET交直流配电网数学模型的正确性。
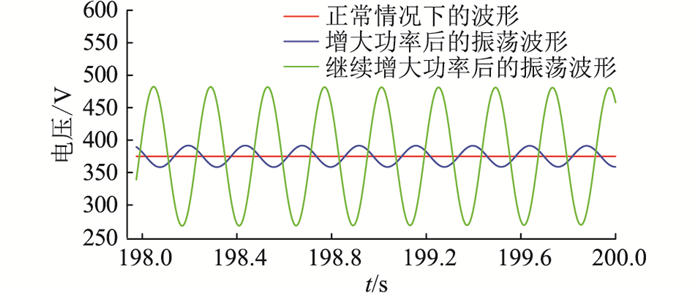
3.3 振荡波形的复现在375 V直流侧,逐渐增大该侧功率至约54 kW时,直流侧将会出现低频振荡现象,振荡频率约为4 Hz左右,如图 15所示。在第1章系统的介绍中,实际现场测试时,三相Buck变换器侧的功率达到60 kW时,低频振荡将会发生,在该简化的仿真模型中,三相Buck变换器侧的功率增大至约54 kW时,低频振荡同样会发生。在图 2的实际录波波形中,低频振荡频率约为4 Hz,在该简化的仿真模型中,振荡的频率同样为4 Hz。这说明所建立的含PET交直流配电网系统能够有效还原4 Hz低频振荡现象,为后续系统的稳定性分析、振荡机理解释和优化控制奠定基础。
|
图 15 不同功率下375 V直流侧电压波形 Fig. 15 The voltage waveforms of the 375 V DC side with different powers |
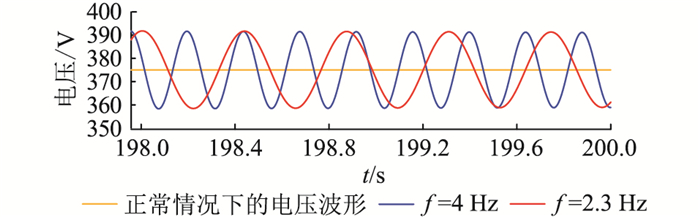
基于当前所建系统,通过参数调节可进行定性分析,发现该直流侧振荡的发生与多种关键因素有关。其中,系统的功率水平对振荡现象的发生起到重要影响。由图 15可知,当功率从14 kW(对应红色波形)增加到53.2 kW(对应蓝色波形)时,375 V直流侧将发生低频振荡,继续增加至53.6 kW(对应绿色波形)时,振荡幅度将增大,即375 V直流侧的功率越高,越容易出现振荡现象。三相Buck变换器的控制参数对直流侧振荡起到重要主导作用。三相Buck变换器的控制参数对直流侧振荡起到重要主导作用,如图 16所示。蓝色波形表示现有参数下的4 Hz振荡波形,当电压外环的比例系数由5增加到6且积分系数由30减小到12时,375 V直流侧波形将变成稳定的直流波形(对应黄色波形)。同时电流内环的积分系数还会影响振荡的频率,同样在现有参数下4 Hz振荡波形(对应蓝色波形)为例,当电流内环的积分系数由320减小到170时,振荡频率将变为2.3 Hz(对应红色波形),即电流内环的积分系数越小,振荡的频率越小。通过上述对一些关键影响因素的定性分析,可为后续系统的稳定性机理分析和稳定性定量分析提供的重要参考。
|
图 16 不同控制器参数下375 V直流侧电压波形 Fig. 16 The voltage waveforms of the 375 V DC side with different controller parameters |
文中依托某交直流配电网,基于实际电网测试中发生的直流低频振荡现象,建立了适用于分析该低频振荡现象的含PET交直流配电网系统的数学模型,主要结论如下:
(1) 基于实际现场的配电网结构,将该复杂的系统进行简化,该简化模型经过验证证实了其正确性,不仅能够还原实际振荡波形,还提高了计算机的计算效率,加强了对交直流配电网直流侧低频振荡现象的认识。
(2) 分别对该系统的PET部分、三相逆变器和三相Buck变换器做了梳理,描述了各个模块的拓扑结构以及控制方式,说明了其工作原理及在系统中的作用。
(3) 在Matlab平台上建立了其数学仿真模型,得到了各个部分的输出波形。在发生扰动情况下将数学模型的响应与时域模型对比,二者响应一致,从而验证了模型的正确性。
(4) 文中对影响因素进行了定性分析。Buck变换器功率越大越易发生振荡;Buck变换器电压外环比例系数增大、积分系数越小,系统越易稳定;Buck变换器电流内环积分系数越小,振荡频率越小。文中所建立的含PET交直流配电网系统能够有效还原4 Hz低频振荡现象,为后续对系统的进一步理论分析奠定了基础。
致谢
本文得到国网江苏省电力有限公司科技项目“多端口交直流混合配电网的系统稳定机理研究”(J2020078)资助,谨此致谢!
| [1] |
程亮, 黄河, 朱磊, 等. 交直流配电网的交换功率灵活性提升方法研究[J]. 电力工程技术, 2019, 38(4): 10-17. CHENG Liang, HUANG He, ZHU Lei, et al. Method of improving exchange power flexibility between AC/DC distribution network and transmission network[J]. Electric Power Engineering Technology, 2019, 38(4): 10-17. (  0) 0) |
| [2] |
陈庆, 范栋琛, 王晨清, 等. 交直流配电网小信号模型和直流侧低频振荡分析[J]. 电力工程技术, 2022, 41(1): 117-125, 200. CHENQING, FAN Dongchen, WANG Chenqing, et al. Small signal model and DC side low frequency oscillation analysis of AC/DC distribution network[J]. Electric Power Engineering Technology, 2022, 41(1): 117-125, 200. (  0) 0) |
| [3] |
WU H, WANG X F. A mode-adaptive power-angle control method for transient stability enhancement of virtual synchronous generators[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(2): 1034-1049. DOI:10.1109/JESTPE.2020.2976791 (  0) 0) |
| [4] |
司佳, 穆云飞, 肖迁, 等. 基于PET控制特性的交直流混合配电网状态估计[J]. 电力系统及其自动化学报, 2020, 32(12): 1-6, 25. SI Jia, MU Yunfei, XIAO Qian, et al. State estimation of AC/DC hybrid distribution network based on PET control characteristics[J]. Proceedings of the CSU-EPSA, 2020, 32(12): 1-6, 25. (  0) 0) |
| [5] |
WANG Z, SU J, CUI Y Y, et al. Research on the structures and application scenarios of medium voltage AC-DC hybrid distribution network[C]//2019 IEEE 3rd Information Technology, Networking, Electronic and Automation Control Conference (ITNEC). Chengdu, China. IEEE, 2019: 743-747.
(  0) 0) |
| [6] |
夏杨红, 孙勇, 韦巍. 光伏接入直流配电网时的功率振荡分析[J]. 中国电机工程学报, 2018, 38(23): 6814-6824, 7116. XIA Yanghong, SUN Yong, WEI Wei. Power oscillation analysis of PV generators connected to DC distribution network[J]. Proceedings of the CSEE, 2018, 38(23): 6814-6824, 7116. (  0) 0) |
| [7] |
李子欣, 高范强, 赵聪, 等. 电力电子变压器技术研究综述[J]. 中国电机工程学报, 2018, 38(5): 1274-1289. LI Zixin, GAO Fanqiang, ZHAO Cong, et al. Research review of power electronic transformer technologies[J]. Proceedings of the CSEE, 2018, 38(5): 1274-1289. (  0) 0) |
| [8] |
庞博, 侯丹, 李天瑞. 中压多端口电力电子变压器技术研究[J]. 高压电器, 2019, 55(9): 1-9. PANG Bo, HOU Dan, LI Tianrui. Analysis of medium voltage multi-port power electronic transformer technology[J]. High Voltage Apparatus, 2019, 55(9): 1-9. (  0) 0) |
| [9] |
王优, 郑泽东, 李永东. 中高压电力电子变压器拓扑与控制应用综述[J]. 电工电能新技术, 2017, 36(5): 1-10. WANG You, ZHENG Zedong, LI Yongdong. Review of topology and control application of medium and high voltage power electronic transformer[J]. Advanced Technology of Electrical Engineering and Energy, 2017, 36(5): 1-10. (  0) 0) |
| [10] |
刘向龙, 刘友波, 张宸宇, 等. 基于电力电子变压器的交直流混合配电网功率-电压协调控制[J]. 电工电能新技术, 2019, 38(2): 35-43. LIU Xianglong, LIU Youbo, ZHANG Chenyu, et al. Coordinating voltage regulation for AC-DC hybrid distribution network with multiple power electronic transformer[J]. Advanced Technology of Electrical Engineering and Energy, 2019, 38(2): 35-43. (  0) 0) |
| [11] |
洪澜, 彭勇刚, 李悦, 等. 计及电力电子变压器的交直流混合配电网能效评估[J]. 电工电能新技术, 2019, 38(2): 72-79. HONG Lan, PENG Yonggang, LI Yue, et al. Energy efficiency evaluation of AC/DC hybrid distribution network considering power electronic transformers[J]. Advanced Technology of Electrical Engineering and Energy, 2019, 38(2): 72-79. (  0) 0) |
| [12] |
张亮, 陆永灿, 周永荣, 等. 一种基于PET的交直流混合配网故障穿越控制策略[J]. 电力电子技术, 2019, 53(12): 81-83. ZHANG Liang, LU Yongcan, ZHOU Yongrong, et al. A control strategy of fault ride through for AC/DC hybrid distribution network based on PET[J]. Power Electronics, 2019, 53(12): 81-83. (  0) 0) |
| [13] |
LIU Y, LI H B, YU Z Q, et al. Reliability evaluation method for AC/DC hybrid distribution power network considering cascaded multiport power electronic transformer[J]. IET Generation, Transmission & Distribution, 2019, 13(23): 5357-5364. (  0) 0) |
| [14] |
ZHAO W Z, ZHENG J H, HAN Z H, et al. Large-disturbance stability analysis method based on mixed potential function for AC/DC hybrid distribution network with PET[J]. IET Generation, Transmission & Distribution, 2020, 14(18): 3802-3813. (  0) 0) |
| [15] |
YU Z Q, WANG X R, QU L, et al. DC side over-voltage characteristics analysis of AC/DC hybrid distribution power system[J]. IEEE Access, 2020, 8: 133248-133257. (  0) 0) |
| [16] |
刘朋, 贾燕冰, 韩肖清. 含双有源全桥变换器多电压等级直流配电网潮流分析与计算[J]. 电网技术, 2021, 45(2): 741-751. LIU Peng, JIA Yanbing, HAN Xiaoqing. DAB-based power flow analysis and calculation for multi-voltage grades DC distribution network[J]. Power System Technology, 2021, 45(2): 741-751. (  0) 0) |
| [17] |
王一, 侯成, 程旭, 等. 交直流混合配电网控制保护技术研究与应用[J]. 广东电力, 2020, 33(12): 90-101. WANG Yi, HOU Cheng, CHENG Xu, et al. Research and application of control and protection technology for AC-DC hybrid distribution network[J]. Guangdong Electric Power, 2020, 33(12): 90-101. (  0) 0) |
| [18] |
李光辉, 王伟胜, 郭剑波, 等. 风电场经MMC-HVDC送出系统宽频带振荡机理与分析方法[J]. 中国电机工程学报, 2019, 39(18): 5281-5297, 5575. LI Guanghui, WANG Weisheng, GUO Jianbo, et al. Broadband oscillation mechanism and analysis for wind farm integration through MMC-HVDC system[J]. Proceedings of the CSEE, 2019, 39(18): 5281-5297, 5575. (  0) 0) |
| [19] |
李小栋. H桥级联型电力电子变压器的控制系统研究[D]. 长沙: 湖南大学, 2015. LI Xiaodong. Research on control system of H-bridge cascaded power electronic transformer[D]. Changsha: Hunan University, 2015. (  0) 0) |
| [20] |
谷泓杰. 隔离型双向全桥DC-DC变换器研究[D]. 杭州: 浙江大学, 2016. GU Hongjie. Research on isolated bidirectional full-bridge DC-DC converter[D]. Hangzhou: Zhejiang University, 2016. (  0) 0) |
2. State Grid Zhejiang Electric Power Co., Ltd. Hangzhou Power Supply Company, Hangzhou 310016, China;
3. State Key Laboratory of Advanced Electromagnetic Engineering and Technology (Huazhong University of Science and Technology), Wuhan 430074, China
 2023, Vol. 42
2023, Vol. 42


 范栋琛(1993),男,硕士,工程师,从事电力系统交直流配网稳定性研究工作(E-mail:
范栋琛(1993),男,硕士,工程师,从事电力系统交直流配网稳定性研究工作(E-mail: