文章编号: 2096-3203(2023)02-0084-10 中图分类号: TM711
2. 梯级水电站运行与控制湖北省重点实验室(三峡大学), 湖北 宜昌 443002
近年来,随着新能源技术的发展,风电将会以更大规模并网[1]。由于双馈风电机组通过电力电子设备并网,转子转速与电网频率解耦,导致其等效惯量为零,高比例风电电力系统惯量水平减小,频率特性严重恶化[2-4]。为了解决该问题,虚拟惯性控制技术以及虚拟同步发电机(virtual synchronous generator,VSG)技术应运而生[5-6]。与此同时,电力系统惯量在形式和特点上也发生了改变,系统惯量由旋转惯量、新能源/储能提供的虚拟惯量等多种形式组成[7]。鉴于此,在线实时监测高渗透率风电电力系统等效惯量的动态变化,不仅利于合理安排风电并网计划,还能对频率危险事故作出判断,防止频率快速跌落[8]。
目前,电力系统惯量估计方法可归纳为基于大扰动事件评估、基于小扰动事件评估和基于准稳态运行评估3种[9]。同步相量测量单元(phasor measurement unit,PMU)装置的大量使用使得电网惯量精确评估成为现实。文献[10]对系统发生大扰动事件下的暂态频率进行多项式拟合,再根据发电机转子运动方程得出了较粗略的电网惯量。随着新能源并入电网,频率特性日益复杂,该方法已不适用。文献[11-12]提出一种基于大扰动转子运动方程对2个区域作差的系统惯量估计方法,但是该方法只适用于大扰动情况下,估计结果易受噪声数据影响,且对扰动发生时刻的判定较为困难。文献[13]提出一种基于惯量图心的新能源电力系统等效惯量评估方法,但是计算结果会随扰动选取时间的变化而变化,不能完全剔除一次调频的介入对估计结果的干扰。基于准稳态运行的惯量评估主要依据大量的历史数据以及电网运行状态,通过人工智能、概率预测和相关性分析等方法实现电网惯量趋势预测[14-15]。文献[16]采取系统总动能作为衡量系统惯量的指标,无须量测大量的有功-频率信息,仅根据新能源比例就能推断出系统惯量范围。但由于该方法要对整个宏观系统统计分析,须预先了解与确定虚拟惯量的来源及其大小,然而虚拟惯量大小本身就具有未知性,因此该工作开展具有一定难度。
综上所述,基于小扰动惯量估计成为目前的研究热点[17-18]。为了定量分析虚拟惯量对电网等效惯量的影响,文中提出一种含风电虚拟惯性响应的电力系统惯量估计方法。首先,对风电电力系统等效惯性时间常数的理论表达式进行梳理;然后基于有功-频率量测数据,详细介绍了含有遗忘因子的递推最小二乘(time-varying forgetting factor recursive least squares,TFF-RLS)算法的辨识思路;最后通过算例系统验证了文中所提新能源电力系统惯量估计方法的有效性与适用性。文中所提方法可以精确地获得不同风电渗透率的电网等效惯量,从而为调度中心提供实时的电网惯量数据,为评估系统频率动态稳定性提供理论基础。
1 电力系统惯量的理论表达式 1.1 电力系统惯性响应惯性是电力系统的固有属性,表现为阻碍系统频率变化的能力[5]。单台同步机的惯性时间常数H定义为额定转速ω下转子的旋转动能E与其额定容量SN的比值:
| $ H=E / S_{\mathrm{N}}=\frac{1}{2} J \omega^2 / S_{\mathrm{N}} $ | (1) |
式中:J为转子的转动惯量。
传统电力系统惯量主要由同步机组提供,即当系统功率平衡遭到破坏时,发电机转子释放/吸收能量,对外表现为电磁功率的增减,从而抵抗系统频率变化,这一物理现象就是发电机惯性响应过程。对于风电机组而言,由于电力电子设备的接入使得系统频率与风机转子转速完全解耦,当系统频率发生变化时,风电机组仍然运行在最大功率跟踪(maximum power point tracking,MPPT)模式,不主动响应系统频率变化,因此无法向系统提供惯量支撑功率。
风电机组转子转速的变化范围为0.7~1.2 p.u.,隐藏在转子中的动能不可忽视[19]。对风机施加虚拟惯性控制时,通过控制转子侧变流器改变风电机组输出的电磁功率的大小,实现对电网的动态有功功率输出,从而模拟同步机组的惯性响应过程[20]。
综上,不论是同步机组还是风电机组,其惯性响应都可以由转子运动方程来描述。若不考虑系统阻尼,那么系统不平衡功率ΔP、惯性时间常数H与系统频率变化率(rate of change of frequency,RoCoF)[21]dΔf/dt的关系为:
| $ \Delta P=2 H \frac{\mathrm{d} \Delta f}{\mathrm{~d} t} $ | (2) |
由式(2)可见,RoCoF与H成反比,即H越小,RoCoF的值就越大。
1.2 含风电虚拟惯性响应的电力系统等效惯量文中虚拟惯性控制采用微分反馈控制,利用锁相环实时检测频率并进行微分运算,附加在风机MPPT模式上。施加了典型微分惯性控制策略的风电机组的内部控制模型如图 1所示。
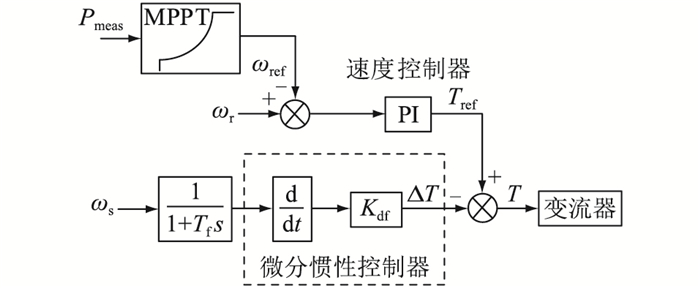
|
图 1 风电机组虚拟惯性控制模型 Fig. 1 Wind turbine model incorporating virtual inertial control |
图 1中,Pmeas为风机实时输出有功功率;ωr、ωref分别为风机实际转子转速和参考转速;Tref为参考转矩;ΔT为叠加转矩;T为给变流器的转矩信号;Kdf为微分惯性控制增益;Tf为频率测量滤波器参数;ωs为系统实测角速度。
当采取相同类型的双馈风电机组构成一个风电场时,风电机组具有相同的参数以及相同的虚拟惯性控制模型和控制参数[22],可将整个风电场等值为1台机组,表现出来的惯性响应强度用聚合等效虚拟惯性时间常数HeqWF表示,具体表达式以及推导过程见文献[23-24]。
因此,含有风电虚拟惯性响应的电力系统等效惯性时间常数HΣ为:
| $ H_{\Sigma}=\frac{\sum\limits_{i=1}^n H_{\mathrm{CON}, i} S_{\mathrm{CON}, i}+\sum\limits_{j=1}^m H_{\mathrm{eqWF}, j} S_{\mathrm{eqWF}, j}}{\sum\limits_{i=1}^n S_{\mathrm{CON}, i}+\sum\limits_{j=1}^m S_{\mathrm{eqWF}, j}}=H_0+\Delta H $ | (3) |
| $ H_0=\frac{\sum\limits_{i=1}^n H_{\mathrm{CON}, i} S_{\mathrm{CON}, i}}{\sum\limits_{i=1}^n S_{\mathrm{CON}, i}+\sum\limits_{j=1}^m S_{\mathrm{eqWF}, j}} $ | (4) |
| $ \Delta H=\frac{\sum\limits_{j=1}^m H_{\mathrm{eqWF}, j} S_{\mathrm{eqWF}, j}}{\sum\limits_{i=1}^n S_{\mathrm{CON}, i}+\sum\limits_{i=1}^m S_{\mathrm{eqWF}, j}} $ | (5) |
式中:HCON,i、SCON,i分别为第i个同步机的惯性时间常数、额定容量;HeqWF,j、SeqWF,j分别为第j个含虚拟惯性控制风电场的等效虚拟惯性时间常数、额定容量;n、m分别为同步机台数以及风电场数量;H0为风电场未施加虚拟惯性控制时的全网等效惯性时间常数;ΔH为施加了虚拟惯性控制的风电场所提供的等效虚拟惯性时间常数,即电网等效惯性时间常数的增量部分。
将第j个含有虚拟惯性控制的风电场风电渗透率定义为αj,结合式(5)得到式(6)[25-26]。
| $ \Delta H=H_{\mathrm{eqWF}, 1} \alpha_1+H_{\mathrm{eqWF}, 2} \alpha_2+\cdots+H_{\mathrm{eqWF}, j} \alpha_j $ | (6) |
从式(6)可以看出,ΔH的每部分值均与风电渗透率成正比。
2 含风电电力系统惯量评估基本原理只要发生功率扰动,惯性响应过程就会持续存在,系统频率也会发生变化。通过获取发电机有功功率和频率扰动数据就能辨识出单台发电机惯量值或系统等效惯量。下文对电网惯量辨识的基本原理进行详细叙述。
对于单台发电机而言,发电机等值转子运动方程小信号增量[27]形式为:
| $ 2 H_{\mathrm{eq}} \frac{\mathrm{d} \Delta f}{\mathrm{~d} t}=\Delta P_{\mathrm{m}}-\Delta P_{\mathrm{e}}-D_{\mathrm{eq}} \Delta f $ | (7) |
式中:ΔPm、ΔPe分别为发电机的机械功率增量和电磁功率增量;Δf为发电机的转子频率偏差;Heq为发电机的惯性时间常数;Deq为阻尼系数。除了Heq、Deq以外,其他参数均为标幺值。
2.1 基于类噪声小扰动的惯量估计适用性分析当系统发生基于类噪声扰动时,一次调频处于调频死区从而不动作,此时ΔPm=0,将式(7)时域形式转化为复频域,则蕴含有惯量特征的有功-频率动态模型为:
| $ G_1(s)=\frac{\Delta f(s)}{\Delta P_{\mathrm{e}}(s)}=-\frac{1 /\left(2 H_{\mathrm{eq}}\right)}{s+D_{\mathrm{eq}} /\left(2 H_{\mathrm{eq}}\right)} $ | (8) |
式中:Δf (s)为发电机转子频率增量的频域形式;ΔPe(s) 为发电机母线上功率增量频域形式;s为拉普拉斯算子。
将式(8)转换为时域形式有:
| $ g_1(t)=-\frac{1}{2 H_{\mathrm{eq}}} \times \exp \left(-\frac{D_{\mathrm{eq}}}{2 H_{\mathrm{eq}}} t\right) $ | (9) |
由式(9)可见,g1(t)按照指数函数衰减,其幅值为2倍惯量的负倒数。若能获取g1(t)的初始幅值,就可以估计出发电装置惯性常数。
2.2 大扰动过程的惯量估计适用性分析当系统发生大扰动时,一次调频作出响应减小频率偏差,将一次调频响应过程用传递函数hc(s)来表示,hc(s)为有理真分式。此时,基于频率响应模型的开环传递函数[28]为:
| $ \begin{gathered} G_2(s)=\frac{\Delta f(s)}{\Delta P_{\mathrm{e}}(s)}=-\frac{1 /\left(2 H_{\mathrm{eq}}+D_{\mathrm{eq}}\right)}{1+h_{\mathrm{c}}(s) /\left(2 H_{\mathrm{eq}} s+D_{\mathrm{eq}}\right)}= \\ -\frac{1}{2 H_{\mathrm{eq}} s+D_{\mathrm{eq}}+h_{\mathrm{c}}(s)} \end{gathered} $ | (10) |
系统中水电/火电机组调速器模型的传递函数为:
| $ h_{\mathrm{c}}(s)=-\frac{1}{R\left(T_1 s+1\right)\left(T_2 s+1\right)} $ | (11) |
式中:R为等值机组一次调频调差系数;T1、T2为原动机模型响应时间常数。
根据初值定理,当t趋近于0时,s趋近于无穷,传递函数G2(s)的冲激响应初始值可用式(12)进行表示。
| $ \left.s G_2(s)\right|_{s \rightarrow \infty}=-\frac{1}{2 H_{\mathrm{eq}}+D_{\mathrm{eq}} / s+h_{\mathrm{c}}(s) / s}=-\frac{1}{2 H_{\mathrm{eq}}} $ | (12) |
由式(12)可知,在将发电机惯性响应和一次调频响应同时考虑在内时,仍可通过求解系统有功-频率模型的冲激响应初始值来估计Heq,其数值等于-1/(2Heq)。由于含风电虚拟惯性响应的电力系统等效惯量具有时变性,因此亟须寻求适应的辨识方法。
3 电网惯量辨识过程 3.1 数据获取与处理通过使用PMU对各发电装置母线出口处的有功功率以及频率进行实时量测,然后将有功功率扰动作为辨识模型的输入,频率扰动作为模型的输出,即可对电网惯量进行进一步辨识。数据预处理的过程主要包括:
(1) 由于数据具有噪声,利用滑动窗口平均滤波算法对输入/输出数据进行处理,将数据噪声进行剔除;
(2) 把步骤(1)中处理好的数据转化成标幺值,即将发电机母线出口处有功功率和频率分别除以发电机额定容量和母线额定频率;
(3) 将步骤(2)中处理好的数据去均值处理,得出有功功率和频率扰动偏差值,将有功和频率偏差分别作为输入、输出数据。
3.2 系统参数辨识CAR模型的通用表达式为:
| $ y(t)=\frac{B(q)}{A(q)} u\left(t-n_{\mathrm{k}}\right)+e(t) $ | (13) |
式中:u(t)、y(t)、e(t)分别为系统输入、系统输出和零均值白噪声;nk为输入-输出延迟,通常取0或1;多项式A(q)、B(q)的表达式见式(14)。
| $ \left\{\begin{array}{l} A(q)=1+a_1 q^{-1}+\cdots+a_{n_{\mathrm{a}}} q^{-n_{\mathrm{a}}} \\ B(q)=b_1 q^{-1}+\cdots+b_{n_{\mathrm{b}}} q^{-n_{\mathrm{b}}} \end{array}\right. $ | (14) |
式中:na、nb分别为多项式A(q)、B(q)的阶次;q-1为单位后移算子,且有q-1y(t)=y(t-1)。
可将式(13)修改为最小二乘形式,如式(15)所示。
| $ y(t)=\boldsymbol{\varphi}^{\mathrm{T}}(t) \boldsymbol{\theta}+e(t) $ | (15) |
其中:
| $ \left\{\begin{array}{c} \boldsymbol{\varphi}^{\mathrm{T}}(t)=\left[\begin{array}{cccc} -y(t-1) & \cdots & -y\left(t-n_{\mathrm{a}}\right) \\ u(t-1) & \cdots & u\left(t-n_{\mathrm{b}}\right) \end{array}\right] \\ \boldsymbol{\theta}=\left[\begin{array}{lllll} a_1 a_2 \cdots & a_{n_{\mathrm{a}}} b_1 & b_2 & \cdots & b_{n_{\mathrm{b}}} \end{array}\right]^{\mathrm{T}} \end{array}\right. $ | (16) |
式中:φT(t)为包含了系统有功-频率量测数据的输入、输出信息向量;θ为待辨识的参数向量。
文中提出利用TFF-RLS算法对新能源系统进行参数辨识[29],该算法由传统的递推最小二乘(recursive least squares,RLS)算法衍生而来,不仅克服了“数据饱和”的缺陷,还解决了不能兼顾跟踪能力、收敛速度的问题。如能调节合适的遗忘因子,既能确保对时变参数的快速跟踪能力,还能减小参数估计误差。因此,该算法适用于风电场的时变惯量辨识,同时也适用于同步机组的时不变惯量辨识。若对自回归模型中的时变参数向量进行辨识,就能实时提取出时变惯性常数。该算法具体实现过程如下。
在此引入准则函数为:
| $ \begin{gathered} J(\boldsymbol{\theta})=\sum\limits_{k=1}^t \lambda^{t-k}(y(k)-\hat{y}(k \mid \boldsymbol{\theta}))^2= \\ \sum\limits_{k=1}^t \lambda^{t-k}\left(y(k)-\boldsymbol{\varphi}^{\mathrm{T}}(k) \boldsymbol{\theta}(k)\right)^2= \\ \quad\left(\boldsymbol{Y}_t-\boldsymbol{\psi}_t \boldsymbol{\theta}\right)^{\mathrm{T}} \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}\left(\boldsymbol{Y}_t-\boldsymbol{\psi}_t \boldsymbol{\theta}\right) \end{gathered} $ | (17) |
其中:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{Y}}_t} = {\left[ {\begin{array}{*{20}{l}} {y(1)}&{y(2)}& \cdots &{y(t)} \end{array}} \right]^{\rm{T}}}\\ {\mathit{\boldsymbol{\psi }}_t} = {\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{\varphi }}^{\rm{T}}}(1)}&{{\mathit{\boldsymbol{\varphi }}^{\rm{T}}}(2)}& \cdots &{{\mathit{\boldsymbol{\varphi }}^{\rm{T}}}(t)} \end{array}} \right]^{\rm{T}}}\\ \mathit{\boldsymbol{ \boldsymbol{\varLambda} }} = {\mathop{\rm diag}\nolimits} \left( {{\lambda ^{t - 1}}{\lambda ^{t - 2}} \cdots 1} \right) \end{array} \right. $ | (18) |
式中:J(θ)为累积平方误差;λ为遗忘因子,一般取值为0.92~0.99;y(k)为系统k时刻实际输出;
| $ \hat{\boldsymbol{\theta}}=\left(\boldsymbol{\psi}_t^{\mathrm{T}} \mathit{\boldsymbol{ \boldsymbol{\varLambda} }} \boldsymbol{\psi}_t\right)^{-1} \boldsymbol{\psi}_t^{\mathrm{T}} \mathit{\boldsymbol{ \boldsymbol{\varLambda} }} \boldsymbol{Y}_t $ | (19) |
TFF-RLS算法辨识过程有:
| $ \left\{\begin{array}{l} \hat{\boldsymbol{\theta}}(t)=\hat{\boldsymbol{\theta}}(t-1)+\boldsymbol{K}(t)\left(y(t)-\boldsymbol{\varphi}^{\mathrm{T}}(t) \hat{\boldsymbol{\theta}}(t-1)\right) \\ \boldsymbol{K}(t)=\frac{\boldsymbol{P}(t-1) \boldsymbol{\varphi}(t)}{\lambda+\boldsymbol{\varphi}^{\mathrm{T}}(t) \boldsymbol{P}(t-1) \boldsymbol{\varphi}(t)} \\ \boldsymbol{P}(t)=\frac{1}{\lambda}\left(\boldsymbol{I}-\boldsymbol{K}(t) \boldsymbol{\varphi}^{\mathrm{T}}(t)\right) \boldsymbol{P}(t-1) \end{array}\right. $ | (20) |
式中:K(t)为卡尔曼增益矢量;P(t)为协方差矩阵;I为单位矩阵。
设置初值为:
| $ \left\{\begin{array}{l} \hat{\boldsymbol{\theta}}(0)=\boldsymbol{\varepsilon} \\ \boldsymbol{P}(0)=c \boldsymbol{I} \end{array}\right. $ | (21) |
式中:ε为充分小的实向量;c为足够大的数(一般取值为105)。
3.3 节点惯量提取由于数据的复杂性以及辨识结果存在偶然误差,文中采用滑动数据窗法对一段采样时间内的有功-频率数据进行多次辨识。由于采样信息包含系统多种复杂的动态特性,辨识出来的有功-频率动态模型应由多阶传递函数表示:
| $ G(s)=\frac{k_0 s^{n-1}+k_1 s^{n-2}+\cdots+k_{n-1}}{s^n+l_0 s^{n-1}+l_1 s^{n-2}+\cdots+l_{n-1}} $ | (22) |
式中:k0、k1、…、kn-1为传递函数的分子系数;l0、l1、…、ln-1为传递函数的分母系数。对传递函数施加冲激响应,由初值定理可以得到:
| $ \left.g(t)\right|_{t=0}=\lim\limits _{s \rightarrow \infty} s G(s)=k_0 $ | (23) |
因此,结合式(12)和式(23)可得惯量估计值为:
| $ H_{\mathrm{eq}}=-\frac{1}{2 k_0} $ | (24) |
结合前述分析,可将文中所提方法的惯量辨识过程总结为如图 2所示的流程图。
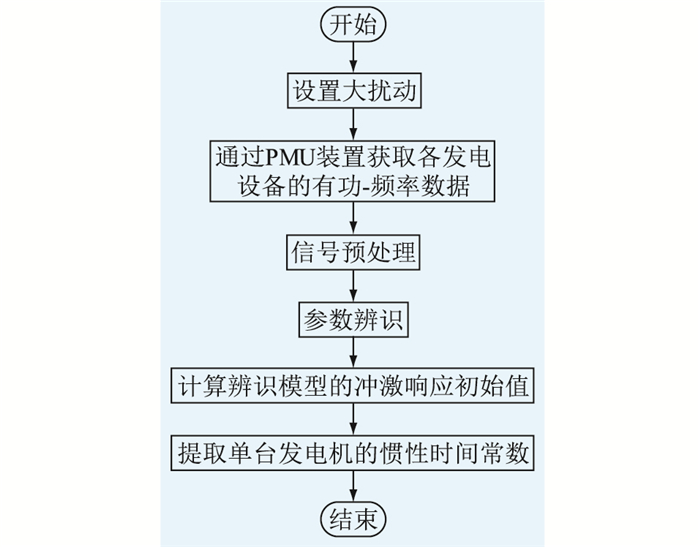
|
图 2 电网惯量辨识流程 Fig. 2 Flow chart of grid inertia identification |
将IEEE-10机39节点作为算例基础,在Matlab/Simulink中验证文中所提方法的可行性。仿真算例拓扑如图 3所示,其同步机参数如表 1所示,额定容量SN=1 000 MV ·A。
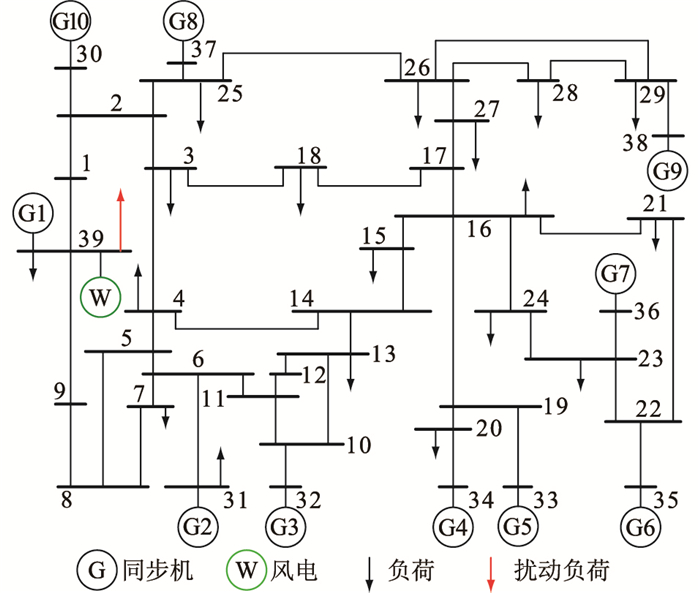
|
图 3 IEEE-10机39节点算例系统 Fig. 3 IEEE-10-machine 39-node test system |
|
|
表 1 IEEE-10机39节点同步机组惯量 Table 1 IEEE-10-machine 39-node system synchronous unit inertia |
在39节点处并入741台风电机组构成一个风电场,每台风电机组都施加虚拟惯性控制,风电场内双馈风机参数设置为:额定电压Vn为575 V;额定功率Pn为1.5 MW;定子电阻Rs为0.023 p.u.;定子电感Ls为0.18 p.u.;转子电阻Rr为0.016 p.u.; 转子电感Lr为0.16 p.u.;励磁电感Lm为2.90 p.u.;固有惯性时间常数HDFIG为5.04 s;微分惯性控制器滤波时间常数Tf为0.60 s;惯性控制增益Kdf为10.58;速度控制器比例和积分系数分别为KpT=3.0、KiT=0.6;额定角速度ωnom为157.08 rad/s;额定风速VWN为11.70 m/s;转速下垂控制增益Kpf为20.0;初始桨距角β为0。为了验证文中所提方法,作如下设置:
(1) 基于类噪声小扰动的随机负荷模拟。分别在节点15、节点23、节点25、节点26、节点28、节点31处加入变化幅值很小的扰动负荷。
(2) 大扰动频率响应暂态过程模拟。在t=150 s时对图 3中母线39处突增10%额定功率负荷,并在1 s内切除,系统频率在20 s内恢复正常。
4.1 估计模型精确性验证式(18)—式(21)惯量估计模型为惯量估计的基础,以发电机G10为例,通过PMU装置量测到母线出口处有功-频率扰动数据如图 4所示。数据预处理之后,将量测的发电机母线出口处的频率实测数据与有功功率输入到该模型输出的频率估计数据进行对比,验证模型的精确性与适用性,频率偏差实测值与估计值的对比结果如图 5所示。
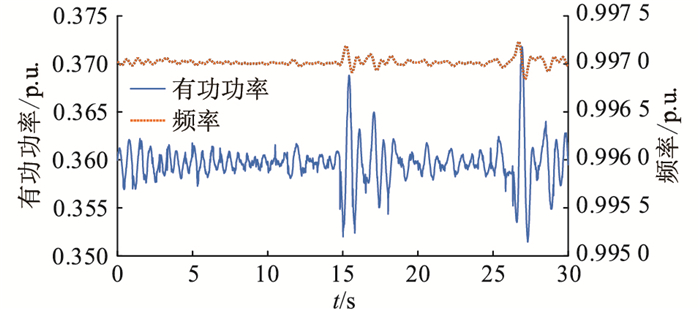
|
图 4 G10母线出口处有功-频率扰动数据 Fig. 4 Active power-frequency disturbance data at the exit of G10 bus |
|
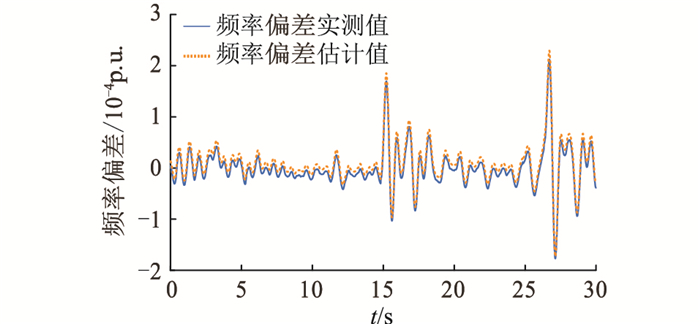
图 5 G10频率偏差实测值与偏差估计值对比 Fig. 5 Comparison between measured and estimated frequency deviation of G10 |
由图 5可以看出,频率偏差实测值与频率偏差估计值的最大偏差在10-4以内,拟合度较高,说明该模型能够可靠地拟合实际输出,可以作为系统惯量辨识模型。
4.2 惯量估计结果验证 4.2.1 同步机惯量辨识结果为验证文中所提方法对新能源电力系统惯量辨识的有效性,根据第3章,分别获取同步机G1—G10母线出口处的有功和频率变化数据,设置长度为30 s、间隔为5 s的移动数据窗进行多次辨识,可得大、小扰动下同步机惯量辨识结果,如表 2所示。
|
|
表 2 大、小扰动下同步机惯量估计结果 Table 2 Estimation results of synchronous machine inertia under small disturbance and large disturbance |
由表 2可以看出,不论是在小扰动下还是大扰动情况下,同步机组惯量估计误差都控制在2.64%以内,最小达到0.04%,可见该方法不仅能够很好地适用于小扰动惯量辨识,同样适用于大扰动下的惯量辨识,精确度高、跟踪能力强。
4.2.2 风电场等效惯量辨识结果当风电场施加虚拟惯性控制时,输出的功率增量与频率变化率成正比。因此,只有在频率处于动态变化时可用于辨识虚拟惯量,即风电场惯量辨识只适用于系统大扰动情况下。同理,可以获取风电场在发生大扰动时及扰动发生后的30 s内的有功功率变化和频率变化数据,见图 6。此时风电场表现出虚拟惯性响应来阻碍电网频率变化,有功功率在150 s处瞬时增大,同时释放出动能,转速下降。

|
图 6 大扰动下风电场母线出口处有功和频率变化 Fig. 6 Variation of active power and frequency at the bus exit of wind farm under large disturbance |
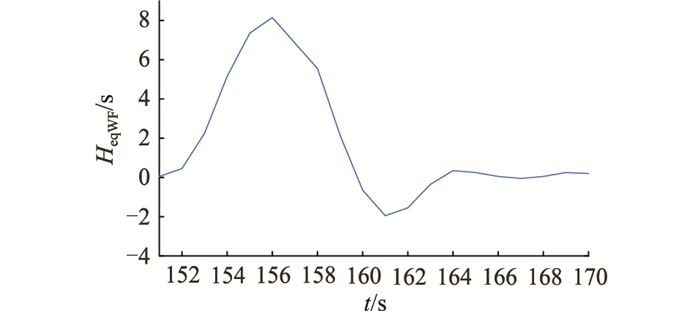
通过图 6采样得到的有功-频率数据可以辨识得到风电场在扰动发生后20 s之内的惯量动态变化曲线如图 7所示。
|
图 7 大扰动下风电场等效虚拟惯量辨识结果 Fig. 7 Real-time results of wind turbine under large disturbance |
由图 7可以看出,风电场等效惯量并不是一个定值,而是具有时变性的参数,在惯性响应初始阶段(150~156 s),风机虚拟惯性控制快速被激发,惯量持续增大,直至达到最大值;在156~164 s阶段,惯量逐渐减小;稳态时(164 s以后)由于频率变化率为零,因此虚拟惯性控制不作用,对外表现出的虚拟惯量为零。
4.2.3 大扰动下不同风电渗透率的全网等效惯量辨识结果针对全网等效惯量的估计,可将整个电力系统等效为1台等值同步发电机,通过辨识该等值同步发电机组的惯量即可得到全网等效惯量。此时,等值同步机组的有功功率输出ΔPsys为系统内各同步机组以及风电场有功功率输出ΔPl的总和,即:
| $ \Delta P_{\mathrm{sys}}=\sum\limits_{l=1}^N \Delta P_l $ | (25) |
式中:N为系统中发电装置的数量。
考虑到频率的时空分布特性,等值同步机组的连接母线频率Δfsys可由发电装置连接母线频率fl加权平均聚合得到:
| $ \Delta f_{\mathrm{sys}}=\Delta f_{\mathrm{COI}}=\frac{\sum\limits_{l=1}^N H_l S_l f_l}{\sum\limits_{l=1}^N H_l S_l} $ | (26) |
式中:ΔfCOI为系统等效中心频率偏差;Hl为各发电装置的惯性常数;Sl为各发电装置的额定容量。
通过改变风电场并网容量,设置风电渗透率分别为0、10%、30%的新能源电力系统作为算例场景。分别讨论含有风电虚拟惯性响应和不含风电虚拟惯性响应的系统等效惯量,并进行对比分析,不同场景下全网等效惯量辨识结果如图 8所示。

|
图 8 大扰动下不同风电渗透率的全网等效惯量辨识结果 Fig. 8 Identification results of equivalent inertia of the whole grid under large disturbance at different wind power penetration rates |
分析图 8(b)可知,当风电渗透率为0时,全网等效惯量只由10台同步发电机提供,计算可得,全网等效惯量为5.16 s。当风电渗透率增加为10%时,假设同步机容量不变,只改变风机机组容量,系统总容量增加,根据式(3)分析计算可得,同步机提供的等效惯量相应地减小,其值为4.64 s,与图 8(a)中未施加虚拟惯性控制时风电渗透率为10%的全网等效惯量相一致,而风电场虚拟惯量与风电渗透率成正比增大,在扰动发生后6 s时,全网等效惯量为5.40 s。当风电渗透率为30%时,风电虚拟惯性响应作用愈发显著,虚拟惯量对全网等效惯量的影响更加突出,全网等效惯量变化幅值较10%要大得多,全网等效惯量瞬时最大值达到6 s。
对比图 8(a)、(b)可以看出:(1) 全网等效惯性时间常数呈现时变性的特点,与图 7风电场等效虚拟惯性时间常数相对应,表现出三阶段时变特性,即150~156 s阶段(惯性响应初始阶段),全网等效惯量快速增大,此时风机虚拟惯性响应被激发;当频率下降到最低点时,风机虚拟惯性响应作用效果逐渐减弱;稳态时风机虚拟惯量为0,此时只有同步机提供惯量;(2) 相同风电渗透率下,含有虚拟惯性控制比不含虚拟惯性控制的全网等效惯量在惯性响应初始阶段要大得多,并且随着渗透率的增大,效果越突出,然而稳态值趋于一致;(3) 趋于稳态的电网等效惯量随着渗透率的增大而减小,且小于风电渗透率为0时的全网等效惯量值,与图 8(a)不含有虚拟惯性控制的全网等效惯量值相对应。
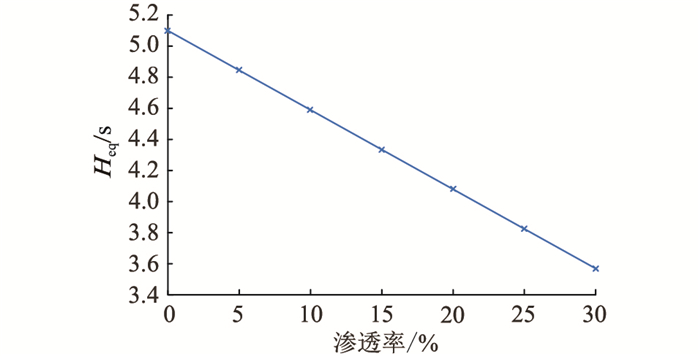
4.2.4 小扰动下不同风电渗透率的全网等效惯量辨识结果由于风机虚拟惯性控制只在大扰动时作用,小扰动情况下风机虚拟惯量近似为0,全网等效惯量只由同步机转动惯量提供,因此结合4.2.1节—4.2.3节分析可以得到不同风电渗透率全网等效惯量值,如图 9所示。
|
图 9 小扰动下不同风电渗透率的全网等效惯量辨识结果 Fig. 9 Identification results of equivalent inertia of the whole grid under small disturbance at different wind power penetration rates |
由图 9可以看出,小扰动时全网等效惯量值随着风电渗透率增大而呈线性规律减小。
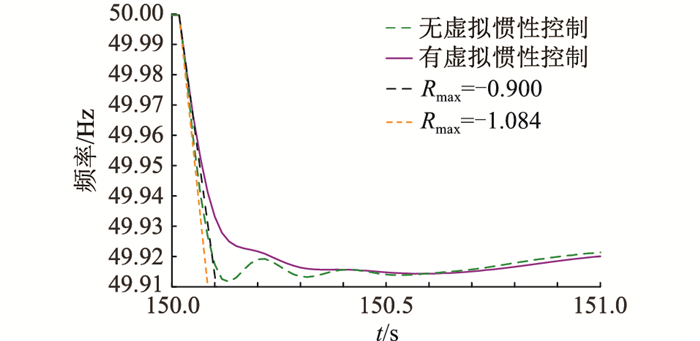
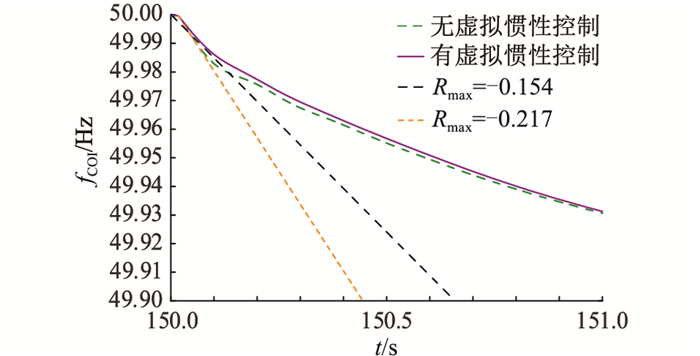
4.3 有/无虚拟惯性控制的系统频率特性分析对有/无风电虚拟惯性控制的系统频率特性进行分析,以验证文中所提方法对惯量估计的准确性。大扰动下风电渗透率为10%时的风电场、系统频率特性曲线分别如图 10、图 11所示。
|
图 10 大扰动下10%风电渗透率时风电场频率变化曲线 Fig. 10 Variation curve of wind farm frequency under large disturbance at 10% wind power penetration |
|
图 11 大扰动下10%风电渗透率时系统频率变化曲线 Fig. 11 Variation curve of system frequency under large disturbance at 10% wind power penetration |
由图 10可知,在施加相同负荷扰动时,有/无虚拟惯性控制的风电场出口初始频率变化率值(即频率变化率最大值,用Rmax表示)分别为-0.900 Hz/s、-1.084 Hz/s。可见含有虚拟惯性控制的系统频率特性明显得到改善,频率变化率绝对值减小,由于Rmax与惯量成反比,则含有虚拟惯性控制的系统等效惯量较没有虚拟惯性控制的系统等效惯量有所增加,与4.2.3节结论相符合,验证了惯量估计结果的有效性与准确性。
4.4 方法精确性比较文献[30]提出利用子空间辨识方法对同步机惯量进行辨识,也得到了较精确的结果。现将文中所提方法与子空间辨识方法在全网等效惯量估计结果的精确性方面进行对比。文献[30]辨识结果如表 3所示。根据表 3可知,虽然同步机惯量辨识结果较精确,最大误差为5.77%,但是对于风电场时变惯量跟踪能力差,辨识结果粗糙,不能很好地体现其时变特性,辨识误差高达27.30%。
|
|
表 3 大扰动下子空间辨识方法惯量评估结果 Table 3 Evaluation results of inertia of subspace identification method under large disturbance |
综上,与子空间辨识方法相比,文中所提的TFF-RLS算法对于风电电力系统惯量辨识具有更好的鲁棒性与适应性。TFF-RLS算法对新数据灵敏度高,不受历史坏数据的影响,对辨识结果反复递推迭代,从而得到新的结果。未来电网中风机、光伏等新能源比例逐年攀升,并且新能源具有随机性和间歇性的特点,电网惯量呈现出时变特征,文中所提方法能够很好地适用于新能源电网时变惯量辨识。
5 结论文中基于有功-频率扰动数据,利用TFF-RLS算法以及自回归模型对不同风电渗透率的新能源电力系统等效惯量进行辨识,得出如下结论:
(1) 在惯性响应初始阶段,风电机组虚拟惯性控制快速被激发,不同风电渗透率下的全网等效惯量迅速增大,且风电渗透率越大,风电机组虚拟惯量效果越显著。
(2) 大扰动情况下,含有风电虚拟惯性响应的全网等效惯量具有三阶段时变特性,与风电场时变惯量具有一致性;小扰动时,风电机组虚拟惯性控制不作用,全网等效惯量只由同步机组所提供,随着风电渗透率增大,全网等效惯量呈现出线性减小规律。
(3) 文中算例验证了TFF-RLS算法适用于新能源电力系统惯量辨识,有效量化了风电机组虚拟惯量对全网等效惯量的影响,可为高渗透率新能源电力系统频率安全稳定性分析提供参考。
| [1] |
文云峰, 杨伟峰, 汪荣华, 等. 构建100%可再生能源电力系统述评与展望[J]. 中国电机工程学报, 2020, 40(6): 1843-1856. WEN Yunfeng, YANG Weifeng, WANG Ronghua, et al. Review and prospect of toward 100% renewable energy power systems[J]. Proceedings of the CSEE, 2020, 40(6): 1843-1856. (  0) 0) |
| [2] |
肖友强, 林晓煌, 文云峰. 直流和新能源高渗透型电网惯性水平多维度评估[J]. 电力建设, 2020, 41(5): 19-27. XIAO Youqiang, LIN Xiaohuang, WEN Yunfeng. Multi-dimensional assessment of the inertia level of power systems with high penetration of HVDCs and renewables[J]. Electric Power Construction, 2020, 41(5): 19-27. (  0) 0) |
| [3] |
董昱, 梁志峰, 王上行, 等. 新型电力系统下推动储能与新能源协调有序发展的分析与思考[J]. 供用电, 2022, 39(10): 84-92. DONG Yu, LIANG Zhifeng, WANG Shangxing, et al. Analysis and thinking on promoting coordinated and orderly development of energy storage and new energy under new power system[J]. Distribution & Utilization, 2022, 39(10): 84-92. (  0) 0) |
| [4] |
杨运国, 侯健生, 边晓燕, 等. 面向高比例新能源配电网的灵活性资源综合评价[J]. 供用电, 2021, 38(11): 68-76. YANG Yunguo, HOU Jiansheng, BIAN Xiaoyan, et al. Comprehensive evaluation of flexible resources for high penetration of renewable energy sources integrated to the distribution network[J]. Distribution & Utilization, 2021, 38(11): 68-76. (  0) 0) |
| [5] |
刘中建, 周明, 李昭辉, 等. 高比例新能源电力系统的惯量控制技术与惯量需求评估综述[J]. 电力自动化设备, 2021, 41(12): 1-11, 53. LIU Zhongjian, ZHOU Ming, LI Zhaohui, et al. Review of inertia control technology and requirement evaluation in renewable-dominant power system[J]. Electric Power Automation Equipment, 2021, 41(12): 1-11, 53. (  0) 0) |
| [6] |
秦晓辉, 苏丽宁, 迟永宁, 等. 大电网中虚拟同步发电机惯量支撑与一次调频功能定位辨析[J]. 电力系统自动化, 2018, 42(9): 36-43. QIN Xiaohui, SU Lining, CHI Yongning, et al. Functional orientation discrimination of inertia support and primary frequency regulation of virtual synchronous generator in large power grid[J]. Automation of Electric Power Systems, 2018, 42(9): 36-43. (  0) 0) |
| [7] |
曾繁宏, 张俊勃. 电力系统惯性的时空特性及分析方法[J]. 中国电机工程学报, 2020, 40(1): 50-58, 373. ZENG Fanhong, ZHANG Junbo. Temporal and spatial characteristics of power system inertia and its analysis method[J]. Proceedings of the CSEE, 2020, 40(1): 50-58, 373. (  0) 0) |
| [8] |
王博, 杨德友, 蔡国伟. 高比例新能源接入下电力系统惯量相关问题研究综述[J]. 电网技术, 2020, 44(8): 2998-3007. WANG Bo, YANG Deyou, CAI Guowei. Review of research on power system inertia related issues in the context of high penetration of renewable power generation[J]. Power System Technology, 2020, 44(8): 2998-3007. (  0) 0) |
| [9] |
孙华东, 许涛, 郭强, 等. 英国"8·9"大停电事故分析及对中国电网的启示[J]. 中国电机工程学报, 2019, 39(21): 6183-6192. SUN Huadong, XU Tao, GUO Qiang, et al. Analysis on blackout ingreat Britain power grid on August 9th, 2019 and its enlightenment to power grid in China[J]. Proceedings of the CSEE, 2019, 39(21): 6183-6192. (  0) 0) |
| [10] |
INOUE T, TANIGUCHI H, IKEGUCHI Y, et al. Estimation of power system inertia constant and capacity of spinning-reserve support generators using measured frequency transients[J]. IEEE Transactions on Power Systems, 1997, 12(1): 136-143. (  0) 0) |
| [11] |
刘方蕾, 胥国毅, 王凡, 等. 基于差值计算法的系统分区惯量评估方法[J]. 电力系统自动化, 2020, 44(20): 46-53. LIU Fanglei, XU Guoyi, WANG Fan, et al. Assessment method of system partition inertia based on differential calculation method[J]. Automation of Electric Power Systems, 2020, 44(20): 46-53. (  0) 0) |
| [12] |
查雨欣, 林健, 王悦, 等. 基于广义下垂控制的光伏发电系统的惯量特性分析[J]. 智慧电力, 2021, 49(2): 54-59. ZHA Yuxin, LIN Jian, WANG Yue, et al. Analysis of inertia characteristics of photovoltaic power generation system based on generalized droop control[J]. Smart Power, 2021, 49(2): 54-59. (  0) 0) |
| [13] |
李东东, 张佳乐, 徐波, 等. 考虑频率分布特性的新能源电力系统等效惯量评估[J]. 电网技术, 2020, 44(8): 2913-2921. LI Dongdong, ZHANG Jiale, XU Bo, et al. Equivalent inertia assessment in renewable power system considering frequency distribution properties[J]. Power System Technology, 2020, 44(8): 2913-2921. (  0) 0) |
| [14] |
CAO X, STEPHEN B, ABDULHADI I F, et al. Switching Markov Gaussian models for dynamic power system inertia estimation[J]. IEEE Transactions on Power Systems, 2015, 31(5): 3394-3403. (  0) 0) |
| [15] |
张武其, 文云峰, 迟方德, 等. 电力系统惯量评估研究框架与展望[J]. 中国电机工程学报, 2021, 41(20): 6842-6856. ZHANG Wuqi, WEN Yunfeng, CHI Fangde, et al. Research framework and prospect on power system inertia estimation[J]. Proceedings of the CSEE, 2021, 41(20): 6842-6856. (  0) 0) |
| [16] |
任凯奇, 张东英, 黄越辉, 等. 基于新能源出力比例的大规模系统惯量估计[J]. 电网技术, 2022, 46(4): 1307-1315. REN Kaiqi, ZHANG Dongying, HUANG Yuehui, et al. Large-scale system inertia estimation based on new energy output ratio[J]. Power System Technology, 2022, 46(4): 1307-1315. (  0) 0) |
| [17] |
TUTTELBERG K, KILTER J, WILSON D, et al. Estimation of power system inertia from ambient wide area measurements[J]. IEEE Transactions on Power Systems, 2018, 33(6): 7249-7257. (  0) 0) |
| [18] |
黄思维, 张俊勃, 曾繁宏. 适用于电力系统惯性秒级追踪的高效在线算法[J]. 高电压技术, 2021, 47(10): 3519-3527. HUANG Siwei, ZHANG Junbo, ZENG Fanhong. Efficient online algorithm for fast inertia tracking of power system[J]. High Voltage Engineering, 2021, 47(10): 3519-3527. (  0) 0) |
| [19] |
孙华东, 王宝财, 李文锋, 等. 高比例电力电子电力系统频率响应的惯量体系研究[J]. 中国电机工程学报, 2020, 40(16): 5179-5192. SUN Huadong, WANG Baocai, LI Wenfeng, et al. Research on inertia system of frequency response for power system with high penetration electronics[J]. Proceedings of the CSEE, 2020, 40(16): 5179-5192. (  0) 0) |
| [20] |
徐波, 章林炜, 俞向栋, 等. 基于系统辨识的电力系统惯量在线评估改进方法[J]. 电力系统保护与控制, 2021, 49(18): 62-69. XU Bo, ZHANG Linwei, YU Xiangdong, et al. An improved method of power system inertia online estimation based on system identification[J]. Power System Protection and Control, 2021, 49(18): 62-69. (  0) 0) |
| [21] |
郭小龙, 刘方蕾, 胥国毅, 等. 风电机组参与调频的虚拟惯量控制与快速频率控制[J]. 智慧电力, 2020, 48(12): 1-7. GUO Xiaolong, LIU Fanglei, XU Guoyi, et al. Virtual inertia control and fast frequency control of wind turbine participating in frequency regulation[J]. Smart Power, 2020, 48(12): 1-7. (  0) 0) |
| [22] |
MILLER N W, SANCHEZ-GASCA J J, PRICE W W, et al. Dynamic modeling of GE 1.5 and 3.6 MW wind turbine-generators for stability simulations[C]//2003 IEEE Power Engineering Society General Meeting (IEEE Cat. No. 03CH37491). Toronto, ON, Canada. IEEE, 2004: 1977-1983.
(  0) 0) |
| [23] |
李世春, 邓长虹, 龙志君, 等. 风电场等效虚拟惯性时间常数计算[J]. 电力系统自动化, 2016, 40(7): 22-29. LI Shichun, DENG Changhong, LONG Zhijun, et al. Calculation of equivalent virtual inertial time constant of wind farm[J]. Automation of Electric Power Systems, 2016, 40(7): 22-29. (  0) 0) |
| [24] |
齐军, 陈磊, 闵勇, 等. 虚拟惯量控制响应延时对控制效果的影响分析[J]. 智慧电力, 2022, 50(6): 1-7. QI Jun, CHEN Lei, MIN Yong, et al. Influence of virtual inertia control response delay on control effect[J]. Smart Power, 2022, 50(6): 1-7. (  0) 0) |
| [25] |
李世春, 曹润杰, 雷小林, 等. 基于改进SFR模型的含风电虚拟惯性/一次调频电力系统频率响应特性[J]. 可再生能源, 2019, 37(5): 694-700. LI Shichun, CAO Runjie, LEI Xiaolin, et al. Frequency characteristics of power system involving virtual inertia and primary frequency regulation of wind power based on modified SFR model[J]. Renewable Energy Resources, 2019, 37(5): 694-700. (  0) 0) |
| [26] |
李东东, 孙雅茹, 徐波, 等. 考虑频率稳定的新能源高渗透率电力系统最小惯量与一次调频容量评估方法[J]. 电力系统保护与控制, 2021, 49(23): 54-61. LI Dongdong, SUN Yaru, XU Bo, et al. Minimum inertia and primary frequency capacity assessment for a new energy highpermeability power system considering frequency stability[J]. Power System Protection and Control, 2021, 49(23): 54-61. (  0) 0) |
| [27] |
KUNDUR P, BALU N J, LAUBY M G. Power system stability and control[M]. New York: McGraw-Hill, 1994.
(  0) 0) |
| [28] |
李世春, 夏智雄, 程绪长, 等. 基于类噪声扰动的电网惯量常态化连续估计方法[J]. 中国电机工程学报, 2020, 40(14): 4430-4439, 4723. LI Shichun, XIA Zhixiong, CHENG Xuchang, et al. Continuous estimation method of power system inertia based on ambient disturbance[J]. Proceedings of the CSEE, 2020, 40(14): 4430-4439, 4723. (  0) 0) |
| [29] |
ZENG F H, ZHANG J B, CHEN G, et al. Online estimation of power system inertia constant under normal operating conditions[J]. IEEE Access, 2020, 8: 101426-101436. (  0) 0) |
| [30] |
李浩然, 夏智雄, 李世春. 基于子空间法的电网暂态频率扰动惯量估计[J]. 电力建设, 2021, 42(2): 2-8. LI Haoran, XIA Zhixiong, LI Shichun. Power system inertia estimation based on subspace method under transient frequency disturbance[J]. Electric Power Construction, 2021, 42(2): 2-8. (  0) 0) |
2. Hubei Provincial Key Laboratory for Operation and Control of Cascade Hydropower Station (China Three Gorges University), Yichang 443002, China
 2023, Vol. 42
2023, Vol. 42


 李世春(1984), 男, 博士, 副教授, 研究方向为含新能源电力系统运行与控制(E-mail:
李世春(1984), 男, 博士, 副教授, 研究方向为含新能源电力系统运行与控制(E-mail: