文章编号: 2096-3203(2023)02-0180-08 中图分类号: TM93
为推动清洁能源利用发展,我国提出碳达峰、碳中和的低碳发展目标[1-4]。风电作为一种清洁无污染的可再生能源,近年来在电力系统中应用广泛,其渗透率不断提高[5-6],但其出力具有不稳定性与随机性,出力高峰还可能使系统出现双向潮流,影响系统电能质量与安全稳定运行[7]。储能系统(energy storage system,ESS)作为一种可双向调节且便于控制的灵活电源[8],能够在一定程度上平抑含风电配电网的电压与功率波动,减小负荷峰谷差,提升风电的消纳比例[9-10]。由于分布式ESS接入容量与安装位置对其平抑效果产生的影响非常大,合理且更优的储能配置方案对配电网电压质量与运行经济性具有显著的提升效果,因此,如何优化储能的配置成为了广受关注且亟须解决的问题。
为减小风电波动对配网系统的影响,国内外学者针对配网中分布式储能配置优化问题进行了研究。文献[11]采用小波包分解实现了储能的功率分配与容量配置,并实现了储能状态实时更新与控制策略长期运行,有效平抑了并网风功率的波动。文献[12-13]考虑风电输出功率的不确定性与储能维护运行成本,合理配置了储能容量以提高系统可靠性。以上研究均对储能平抑风电波动问题具有实际意义,且有效实现了ESS的容量配置,但未考虑优化ESS的接入节点位置。同时,含风电的ESS的优化配置为一个高维多目标优化问题,针对智能算法的改进与应用可用于优化储能配置。文献[14]为保证算法在求解储能配置问题中的准确与稳定,将改进k-means聚类算法应用于模型求解,以获得更高的计算效率与更优的储能配置方案。文献[15]对储能选址问题及容量配置进行了研究,采用贪婪算法求解多目标模型。文献[16-17]采用改进的群智能算法对分布式储能接入配网的多目标优化问题进行求解。上述文献多采用对某一种算法进行改进的求解方法,虽均一定程度提升了算法性能,但仍具有因算法本身寻优机制而存在的易陷入局部最优的问题。
文中以配网系统的节点电压偏差、日有功网损及储能配置容量为目标函数,建立了多目标储能选址定容问题的优化模型,针对传统多目标粒子群算法存在的缺点,提出一种基于天牛须搜索算法的改进多目标粒子群优化(beetle antennae search-im ̄prov ̄ed multi-objective particle swarm optimization,BAS-IMOPSO)算法对文中模型进行求解;为从最优解集中选取最佳接入方案,采用基于信息熵的逼近理想解排序法;最后,在IEEE 33节点系统中对模型进行仿真,验证文中所提出模型以及改进算法的有效性。
1 ESS优化配置模型 1.1 目标函数配电网中接入大量分布式风电后,风电自身随机波动出力的特点以及可能出现的双向潮流问题,会使配网系统产生电压波动等不利影响,导致电能质量无法满足系统安全稳定运行的需求。考虑储能接入对配网系统电压质量的改善作用与对有功网损的抑制效果,以系统电压偏差、日有功网损及ESS配置容量3个函数值作为文中储能优化配置模型的优化求解目标。
(1) 系统电压偏差。风电机组的出力波动会加剧配电网电压波动,电压偏差能有效反映ESS接入后对电压的补偿作用,将其设为目标函数f1。
| $ f_1=\left|\left(V_b-V_{\mathrm{N}}\right) / V_{\mathrm{N}}\right| $ | (1) |
式中:VN为线路末端电压额定值;Vb为支路b末端电压实际值。
(2) 日有功网损。降低系统网损是提高电力系统运行经济效益的一项重要任务。如风电机组的分布式电源接入配电网可能造成双向潮流问题,将储能接入含风电的配电网系统可改善网络功率潮流分布,从而平衡支路潮流,减小系统有功网损。储能灵活的双向调节作用可一定程度减小系统有功损耗。将配网系统的日有功网损作为模型优化的目标函数f2,其表达式为:
| $ f_2=\sum\limits_{t=1}^{24} \sum\limits_{b=1}^{n_{\mathrm{r}}}\left(\frac{P_{b, t}^2+Q_{b, t}^2}{V_{b, t}^2}\right) R_b $ | (2) |
式中:nr为支路数;Pb, t、Qb, t分别为t时刻支路b末端的有功负荷与无功负荷;Vb, t为t时刻支路b末端电压;Rb为支路b阻抗。
(3) ESS配置容量。在ESS的优化配置问题中,不仅要考虑储能接入对电压质量及系统网损的影响,还应考虑其经济性。将储能额定容量定为一个周期内储能的充/放电能量值极限,设ESS配置总容量为模型优化的目标函数f3,其表达式为:
| $ f_3=\sum\limits_{c=1}^{N_{\mathrm{ESS}} } \sum\limits_{t=t_0}^{t_0+n \Delta t}\left|P_c^{\mathrm{ESS}}(t)\right| \times \Delta t $ | (3) |
式中:NESS为该系统中ESS允许接入总数;t0为运行初始时刻;t0+nΔt为n个充放电时段总和;PcESS(t)为第c个ESS在t时刻的充/放电功率;Δt为储能充/放电持续时长。
综合考虑系统电压偏差、日有功网损和ESS配置容量,储能优化配置的多目标优化函数为:
| $ \min F=\left\{f_1, f_2, f_3\right\} $ | (4) |
(1) 系统功率平衡约束。
| $ \begin{gathered} P_{i, t}^{\mathrm{WT}}+P_{i, t}^{\mathrm{ESS}}-P_{i, t}^{\mathrm{Load}}= \\ U_{i, t} \sum\limits_{j=1}^{N_i} U_{j, t}\left(G_{i, j} \cos \delta_{i j, t}+B_{i, j} \sin \delta_{i j, t}\right) \end{gathered} $ | (5) |
| $ Q_{i, t}^{\mathrm{WT}}-Q_{i, t}^{\mathrm{Load}}=U_{i, t} \sum\limits_{j=1}^{N_i} U_{j, t}\left(G_{i, j} \sin \delta_{i j, t}-B_{i, j} \cos \delta_{i j, t}\right) $ | (6) |
式中:Pi, tWT、Qi, tWT分别为t时刻风电机组在节点i上输入的有功功率与无功功率;Pi, tLoad、Qi, tLoad分别为t时刻节点i的有功负荷与无功负荷;Ui, t、Uj, t分别为t时刻节点i、j的电压实际值;Gi, j、Bi, j分别为节点i、j之间互导纳的实部与虚部;δij, t为t时刻节点i、j的相角差;Ni为与节点i相连的节点个数。
(2) 节点电压约束。
| $ V_{\min } \leqslant V_{i t} \leqslant V_{\text {max }} $ | (7) |
式中:Vit为t时刻节点i的实际电压幅值;Vmin、Vmax分别为系统实际节点电压幅值的下限和上限。
(3) 储能运行约束。为使储能可靠、持续工作且始终保持在正常运行状态,储能的充/放电功率值应约束在一限定范围内,以避免充/放电功率过大或过小而损害储能电池寿命。与功率型储能不同,以蓄电池为典型的能量型储能的可循环充/放电次数较少[18]。为了防止ESS过充或过放而降低储能装置的循环使用寿命,对储能设置式(8)所示运行约束,包括储能容量约束、荷电状态(state of charge,SOC)约束及储能充/放电状态功率约束。
| $ \left\{\begin{array}{l} P_{c, \min }^{\mathrm{ESS}} \leqslant P_c^{\mathrm{ESS}}(t) \leqslant P_{c, \max }^{\mathrm{ESS}} \\ S_{c, \min }^{\mathrm{SOC}} \leqslant S_c^{\mathrm{SOC}}(t) \leqslant S_{c, \max }^{\mathrm{SOC}} \\ E_c^{\mathrm{ESS}}(t)=E_c^{\mathrm{ESS}}(t-1)+P_c^{\mathrm{ESS}}(t) \eta_{\mathrm{ch}} \Delta t \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;P_c^{\mathrm{ESS}}(t) \geqslant 0 \\ E_c^{\mathrm{ESS}}(t)=E_c^{\mathrm{ESS}}(t-1)+P_c^{\mathrm{ESS}}(t) \Delta t / \eta_{\mathrm{dis}} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;P_c^{\mathrm{ESS}}(t)<0 \end{array}\right. $ | (8) |
式中:PcESS(t)为第c个ESS在t时刻的充/放电功率;ScSOC(t)为第c个ESS在t时刻的SOC;EcESS(t)为第c个ESS在t时刻的剩余容量;Pc, maxESS、Pc, minESS为第c个ESS的充/放电功率上、下限;Sc, maxSOC、Sc, minSOC分别为第c个ESS的SOC上、下限;ηch、ηdis分别为ESS充/放电效率。
(4) 储能能量平衡约束。
| $ \sum\limits_{t=1}^{24} P_{i, t}^{\mathrm{ESS}} \Delta t=0 $ | (9) |
多目标粒子群优化(multi-objective particle swarm optimization,MOPSO)算法常用于求解多目标优化问题[19-22],其在优化多目标问题时给出的是一组Pareto全局最优解。为提高初始种群多样性与算法收敛性,文中首先利用Logistic混沌映射与动态非线性惯性权重策略对MOPSO算法进行改进,得到改进多目标粒子群优化(improved multi-objective particle swarm optimization,IMOPSO)算法。
Logistic混沌映射用于优化初始种群,使算法初始时粒子分布更均匀散布于求解域[23-24]。同时,参考文献[25]策略,引入动态非线性惯性权重取值策略,可令算法早期更注重全局寻优且后期更注重局部寻优,避免过早陷入小范围搜索而陷入早熟。
天牛须搜索(beetle antennae search,BAS)算法中[26],天牛通过比较两须目标函数适应度值的大小,不断向气味值大的方向前进实现觅食,具体算法流程见文献[27]。文中采用BAS-IMOPSO算法求解模型,该算法融合了BAS注重个体寻优及IMOPSO的群体寻优能力更强的特点,可在一定程度上有效避免算法收敛过早以及粒子陷入局部最优解的早熟问题,以得到更优的储能配置结果。
2.2 BAS-IMOPSO算法在储能优化配置中的应用文中所建立的分布式储能配置优化模型以ESS的安装节点位置与接入容量为决策变量,对应BAS-IMOPSO算法下天牛粒子在决策空间中所处的位置。优化进程中须对储能安装位置、容量以及充/放电功率进行编码,如式(10)所示。
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{x}} = \left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{X}}&\mathit{\boldsymbol{Z}}&{{\mathit{\boldsymbol{P}}_{{\rm{ESS}}}}} \end{array}} \right]}\\ {\mathit{\boldsymbol{X}} = \left[ {\begin{array}{*{20}{l}} {{x_1}}&{{x_2}}& \cdots &{{x_c}}& \cdots &{{x_{{N_{{\rm{ESS}}}}}}} \end{array}} \right]}\\ {\mathit{\boldsymbol{Z}} = \left[ {\begin{array}{*{20}{l}} {{z_1}}&{{z_2}}& \cdots &{{z_c}}& \cdots &{{z_{{N_{{\rm{ESS}}}}}}} \end{array}} \right]}\\ {{\mathit{\boldsymbol{P}}_{{\rm{ESS}}}} = \left[ {\begin{array}{*{20}{l}} {{p_{1, 1}}}&{{p_{1, 2}}}& \cdots &{{p_{c, k}} \cdots }&{{p_{{N_{{\rm{ESS}}}}, 24}}} \end{array}} \right]} \end{array}} \right. $ | (10) |
式中:x为粒子位置的编码;X为储能接入节点位置(须进行取整操作);xc为第c个ESS的接入节点位置编号;Z为ESS的配置容量;zc为第c个ESS的接入容量;PESS为ESS的充/放电功率;Pc, k为第c个ESS在k时刻的充放电功率。对粒子位置向量初始化即是对储能接入个数、接入节点及容量的初始化。
在模型寻优计算过程中,由ESS在相应时段的充/放电功率可计算得到配网中的储能配置容量,粒子在约束条件范围内逐步寻求可行域内的最佳储能配置方案。
文中基于BAS-IMOPSO算法求解配电网中储能的接入节点与安装容量的优化配置问题,基本流程如图 1所示。
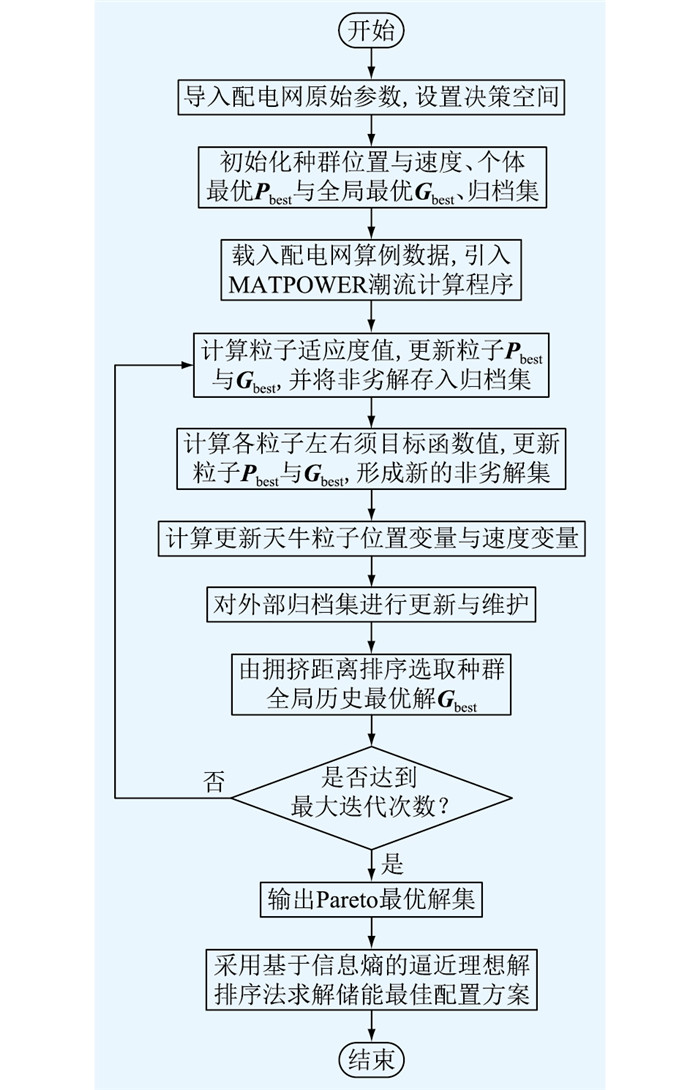
|
图 1 配电网储能优化配置流程 Fig. 1 Flow chart of energy storage allocation optimization for distribution network |
文中储能配置寻优模型的基本实现过程如下:
(1) 导入配电网原始参数,设置决策空间,初始化种群位置与速度,并进行粒子个体最优Pbest与全局最优Gbest初始化。
(2) 在模型迭代中,载入配电网算例数据,运用MATPOWER潮流计算程序对配电网电压偏差及日有功网损进行计算,并计算当前粒子适应度值。
(3) 基于BAS-IMOPSO算法搜索策略的粒子群不断更新自身位置以在决策空间寻得Pbest与Gbest,将非支配解加入到外部归档集中[28],并由拥挤距离排序选取前20%粒子作为最优粒子[29]。
(4) 迭代完成时输出一组Pareto最优解,代表算法迭代完成产生的一组储能最优配置方案。采用基于信息熵的逼近理想解排序法进行储能配置最优方案的选取[30-31],即是在多个储能配置方案的对比中产生一个最佳方案的过程。
3 算例分析 3.1 算例系统数据文中选取IEEE 33节点配电网系统作为算例,对不同算法下的储能优化配置模型仿真分析并进行结果比较,系统模型如图 2所示。系统额定电压为12.66 kV,标幺值取1.0 p.u.,初始未接入其他负荷时,有功负荷为3.715 MW,无功负荷为2.3 Mvar。
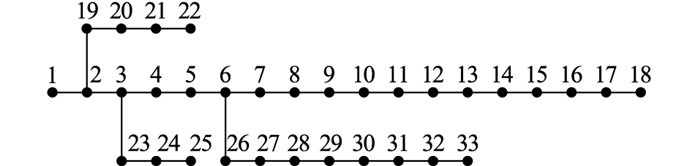
|
图 2 IEEE 33节点配电系统结构 Fig. 2 Structure of IEEE 33-node distribution network system |
仿真中将风电配置在节点20和节点25,图 3为风电与负荷的典型日特性曲线。储能装置最大可接入个数为2,可接入节点为2~33。风电输出上限为200 kW,故储能最大允许安装功率设置为200 kW。
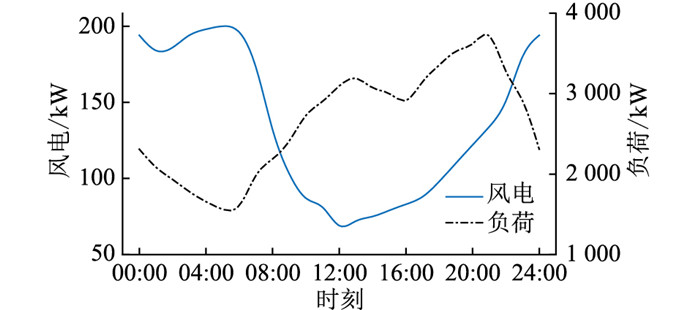
|
图 3 风电与负荷典型日特性曲线 Fig. 3 Typical daily characteristic curves of wind turbine and load |
文中设定3种不同场景仿真对比分析,以验证所提模型与算法的有效性:场景1为只接入风电而不接入储能;场景2为接入风电与储能,采用MOPSO算法;场景3为接入风电与储能,采用文中所提BAS-IMOPSO算法。仿真过程中参数设置如表 1所示。
|
|
表 1 仿真参数设置 Table 1 Values assigned to the simulation parameters |
对文中所设定3种场景下的模型分别进行仿真求解,仿真结果如表 2所示。由表 2可知,储能的接入一定程度上平抑了含风电的配电网系统的电压偏差,且电压偏差降幅达到31.47%,同时有效减小了系统的日有功网损,网损降幅达到了67.41%,表明ESS对配电网电能质量的提升效果明显。
|
|
表 2 不同场景优化结果 Table 2 Optimization results of different cases |
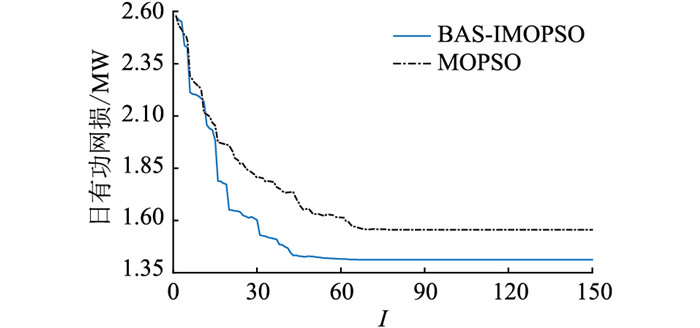
对比分析不同场景下优化结果,表 2中场景1下的系统电压偏差和日有功网损均较高。场景2和场景3所求得的最佳储能配置方案是分别从MOPSO算法与BAS-IMOPSO算法求解模型所获得的Pareto最优解中进行选取的。MOPSO算法下的储能配置方案在场景1的基础上将配电网系统节点电压偏差降低了0.010 1 p.u.,日有功网损降低了3.250 MW。BAS-IMOPSO算法下的储能配置方案在场景1的基础上将配电网系统电压偏差降低了0.014 6 p.u.,日有功网损降低了3.279 MW。对比可知,在多目标储能选址定容优化配置模型中,文中所提出的BAS-IMOPSO算法具有比MOPSO算法更强的寻得最优目标函数值的能力,从而可得到更优的储能配置结果,且优化结果更有利于配电网的安全稳定运行。为进一步体现BAS-IMOPSO算法较MOPSO算法的优越性,将场景2与场景3下的算法仿真模型各独立运行30次,所得电压偏差与有功网损的外部解[32]收敛曲线分别如图 4、图 5所示。结果表明BAS-IMOPSO算法的收敛性能显著优于MOPSO算法,更易寻得文中储能优化问题的全局最优解。
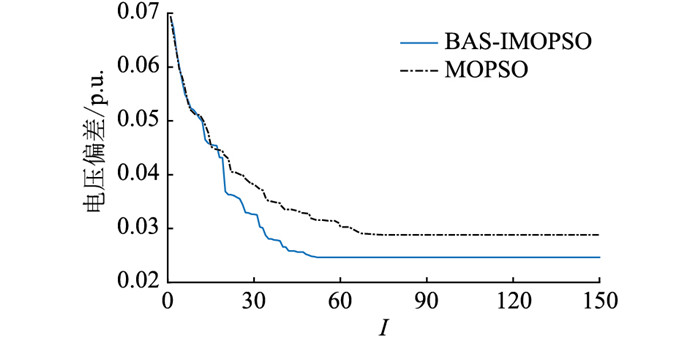
|
图 4 电压偏差外部解收敛曲线 Fig. 4 Convergence curves of outer solutions for voltage deviation |
|
图 5 日有功网损外部解收敛曲线 Fig. 5 Convergence curves of outer solutions for daily system loss |
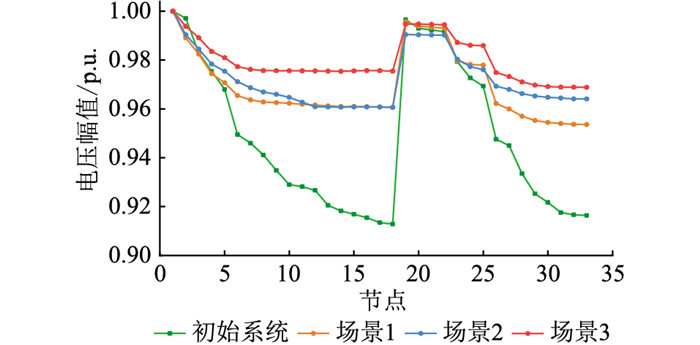
为进一步验证风电机组的接入与储能接入对原配电网系统的节点电压改善情况,现比较初始系统与3种场景下的节点电压幅值,如图 6所示。
|
图 6 不同场景下节点电压分布对比 Fig. 6 Comparison of node voltage distribution in different cases |
由图 6可知,在初始系统中,风电机组与ESS尚未配置,配电网系统各节点电压偏差较大,尤其在系统末端18节点与33节点附近电压均较大程度偏离允许范围,18节点处电压低至11.56 kV,约为0.91 p.u.,不符合国家标准节点电压允许范围;当在初始系统中配置风电后,如场景1,系统末端节点电压抬升至12.15 kV,约为0.96 p.u.,可见分布式风电的接入对系统整体电压水平有所提升。当在含风电的配电网系统中接入储能后,由场景2与场景3电压偏差情况分析及对比可得:储能配置使系统的整体电压水平进一步抬升,电压偏差进一步减小;BAS-IMOPSO算法优化下的系统末端节点电压最低为12.27 kV,较MOPSO算法优化下进一步抬升,且各节点电压偏差均在±3.5%以内,其平抑效果明显优于MOPSO算法,即在实际运行模型中验证了文中所提出的BAS-IMOPSO算法的有效性与其较MOPSO算法在储能优化配置问题上的优越性。由于ESS可向负荷提供一定功率支撑,且其在配电网中的配置可以改变网络的潮流分布与流向,故储能加入可有效平抑系统电压偏差。
文中优化模型下的ESS充/放电功率与对应时刻下储能的SOC曲线如图 7与图 8所示。
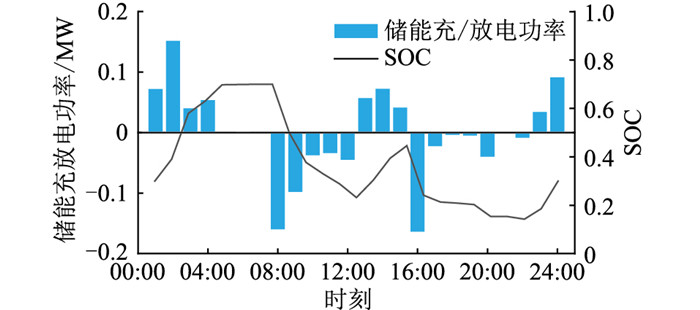
|
图 7 节点9的ESS系统充/放电功率及SOC曲线 Fig. 7 The ESS charging and discharging power and SOC curves of node 9 |

|
图 8 节点19的ESS系统充/放电功率及SOC曲线 Fig. 8 The ESS charging and discharging power and SOC curves of node 19 |
结合图 7、图 8和图 4中风电与负荷特性曲线可得,2个ESS的充放电情况及SOC变化情况大致相似,几乎全天始终保持正常运行状态,且系统中接入的2个储能装置的利用率均较高。
由ESS的24 h运行情况可知,00:00—07:00所带负荷较少,该时段储能充电,储能SOC增大,在风电高峰期将多余电能存储起来,减少了弃风量,提高了风电利用率。10:00—21:00为负荷高峰而风电低谷时段,该时段储能主要处于放电状态,储能将能量释放以给电网提供功率支撑,SOC逐渐减小。为保证储能的正常运行且在一定程度上延长储能装置的使用寿命,通常要控制储能合理的运行区间,将SOC值约束在合理范围内。文中设置SOC在0.1~0.9范围内,在保证一定调整裕度的同时避免储能过充电与过放电。
同时,由于风电出力特性具有与负荷相反的特点,即在一天初始时段储能应进行充电操作,储能SOC增大。为防止ESS持续运行于放电状态下导致SOC过低影响储能寿命,同时保证储能容量的充分利用,以及保持一定能量储备,将储能每天的初始SOC设置为30%。
在配电网系统中配置风电与ESS后,由于储能的双向功率调节能力,可在负荷低谷与风电出力高峰时期实现电能的存储,在负荷高峰与风电出力低谷时期实现电能的释放。加入储能前后负荷峰谷差对比如图 9所示。
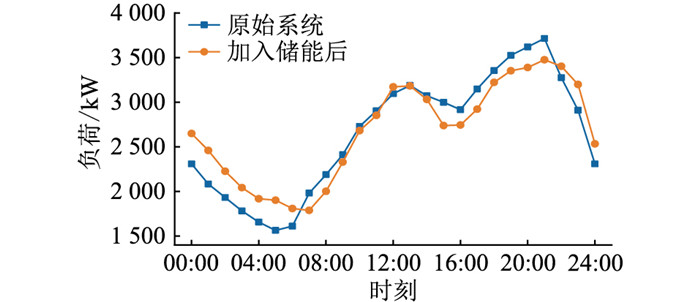
|
图 9 加入储能前后系统负荷曲线 Fig. 9 Load curves before and after adding energy storage |
可知,系统原始负荷峰谷差为2 151 kW,加入ESS之后系统峰谷差为1 766.52 kW,负荷峰谷差减小了384.48 kW。可见ESS的接入可有效减小系统负荷峰谷差,起到削峰填谷的作用。
4 结论为提高配电网系统运行的安全可靠性,文中针对储能在配电网系统中的接入位置与安装容量问题,建立了含风电的储能优化配置模型,提出用于求解该模型的BAS-IMOPSO算法。在IEEE 33节点配电网系统中利用BAS-IMOPSO算法进行求解验证,所得结论如下:
(1) 文中采取的分布式储能优化配置方法不仅改善了配电网系统的电压质量,有效降低了系统的电压偏差、系统日有功网损与储能配置容量,还提高了储能配置的经济性。ESS结合风电出力与系统运行状况,不断调整充放电功率,使ESS在保证其自身调整裕度的同时避免过充电与过放电,提高了风电利用率,减小了系统负荷峰谷差,具有削峰填谷的作用。
(2) 文中采用的BAS-IMOPSO算法较传统MOPSO算法具有更好的收敛性能,在相同迭代次数下,BAS-IMOPSO算法对于模型的寻优速度更快,更易寻得全局最优解。
| [1] |
李勇, 姚天宇, 乔学博, 等. 基于联合时序场景和源网荷协同的分布式光伏与储能优化配置[J]. 电工技术学报, 2022, 37(13): 3289-3303. LI Yong, YAO Tianyu, QIAO Xuebo, et al. Optimal configuration of distributed photovoltaic and energy storage system based on joint sequential scenario and source-network-load coordination[J]. Transactions of China Electrotechnical Society, 2022, 37(13): 3289-3303. (  0) 0) |
| [2] |
文福拴, 鲁刚, 黄杰. 面向碳达峰、碳中和的综合能源系统[J]. 全球能源互联网, 2022, 5(2): 116-117. WEN Fushuan, LU Gang, HUANG Jie. Integrated energy system towards carbon peak and neutrality targets[J]. Journal of Global Energy Interconnection, 2022, 5(2): 116-117. (  0) 0) |
| [3] |
王睿, 孙秋野, 胡伟, 等. 面向"碳达峰、碳中和"的新型电力系统的潮流计算[J]. 全球能源互联网, 2022, 5(5): 439-446. WANG Rui, SUN Qiuye, HU Wei, et al. Power flow calculation of new power system for carbon peaking and carbon neutralization[J]. Journal of Global Energy Interconnection, 2022, 5(5): 439-446. (  0) 0) |
| [4] |
李晖, 刘栋, 姚丹阳. 面向碳达峰碳中和目标的我国电力系统发展研判[J]. 中国电机工程学报, 2021, 41(18): 6245-6259. LI Hui, LIU Dong, YAO Danyang. Analysis and reflection on the development of power system towards the goal of carbon emission peak and carbon neutrality[J]. Proceedings of the CSEE, 2021, 41(18): 6245-6259. (  0) 0) |
| [5] |
陈伟伟, 张增强, 张高航, 等. 计及需求响应及抽水蓄能的含风电系统鲁棒机组组合[J]. 电力工程技术, 2022, 41(2): 75-82. CHEN Weiwei, ZHANG Zengqiang, ZHANG Gaohang, et al. Robust unit commitment of power systems integrated wind power considering demand response and pumped storage units[J]. Electric Power Engineering Technology, 2022, 41(2): 75-82. (  0) 0) |
| [6] |
齐晓光, 姚福星, 朱天曈, 等. 考虑大规模风电接入的电力系统混合储能容量优化配置[J]. 电力自动化设备, 2021, 41(10): 11-19. QI Xiaoguang, YAO Fuxing, ZHU Tiantong, et al. Capacity optimization configuration of hybrid energy storage in power system considering large-scale wind power integration[J]. Electric Power Automation Equipment, 2021, 41(10): 11-19. (  0) 0) |
| [7] |
BULATOV R V, BURMEYSTER M V, NASYROV R R, et al. Study of the influence of wind power station on the operating modes of the distribution electric network[C]//2020 International Youth Conference on Radio Electronics, Electrical and Power Engineering (REEPE). Moscow, Russia. IEEE, 2020: 1-5.
(  0) 0) |
| [8] |
李建林, 郭斌琪, 牛萌, 等. 风光储系统储能容量优化配置策略[J]. 电工技术学报, 2018, 33(6): 1189-1196. LI Jianlin, GUO Binqi, NIU Meng, et al. Optimal configuration strategy of energy storage capacity in wind/PV/storage hybrid system[J]. Transactions of China Electrotechnical Society, 2018, 33(6): 1189-1196. (  0) 0) |
| [9] |
蒋向兵, 汤波, 余光正, 等. 面向新能源就地消纳的园区储能与电价协调优化方法[J]. 电力系统自动化, 2022, 46(5): 51-64. JIANG Xiangbing, TANG Bo, YU Guangzheng, et al. Coordination and optimization method of park-level energy storage and electricity price for local accommodation of renewable energy[J]. Automation of Electric Power Systems, 2022, 46(5): 51-64. (  0) 0) |
| [10] |
陈泽西, 孙玉树, 张妍, 等. 考虑风光互补的储能优化配置研究[J]. 电工技术学报, 2021, 36(S1): 145-153. CHEN Zexi, SUN Yushu, ZHANG Yan, et al. Research on energy storage optimal allocation considering complementarity of wind power and PV[J]. Transactions of China Electrotechnical Society, 2021, 36(S1): 145-153. (  0) 0) |
| [11] |
张鹏, 张峰, 梁军, 等. 采用小波包分解和模糊控制的风电机组储能优化配置[J]. 高电压技术, 2019, 45(2): 609-617. ZHANG Peng, ZHANG Feng, LIANG Jun, et al. Capacity optimization of hybrid energy storage system for wind farm using wavelet packet decomposition and fuzzy control[J]. High Voltage Engineering, 2019, 45(2): 609-617. (  0) 0) |
| [12] |
ALHUMAID Y M, KHAN K A, KHALID M. Stochastic approach for optimal sizing and allocation of energy storage systems[C]//2021 IEEE Green Technologies Conference (GreenTech). Denver, CO, USA. IEEE, 2021: 569-573.
(  0) 0) |
| [13] |
AL-HUMAID Y M, KHAN K A, ABDULGALIL M A, et al. Two-stage stochastic optimization of sodium-sulfur energy storage technology in hybrid renewable power systems[J]. IEEE Access, 2021, 9: 162962-162972. (  0) 0) |
| [14] |
吴杰, 丁明, 张晶晶. 基于云模型和k-means聚类的风电场储能容量优化配置方法[J]. 电力系统自动化, 2018, 42(24): 67-73. WU Jie, DING Ming, ZHANG Jingjing. Capacity configuration method of energy storage system for wind farm based on cloud model and k-means clustering[J]. Automation of Electric Power Systems, 2018, 42(24): 67-73. (  0) 0) |
| [15] |
郭雨涵, 郁丹, 杨鹏, 等. 基于贪婪算法的分布式储能系统容量优化配置方法[J]. 储能科学与技术, 2022, 11(7): 2295-2304. GUO Yuhan, YU Dan, YANG Peng, et al. Optimal capacity allocation method of a distributed energy storage system based on greedy algorithm[J]. Energy Storage Science and Technology, 2022, 11(7): 2295-2304. (  0) 0) |
| [16] |
徐吉智, 张新燕, 常喜强, 等. 基于PV曲线和改进遗传算法储能选址定容研究[J]. 太阳能学报, 2022, 43(1): 263-268. XU Jizhi, ZHANG Xinyan, CHANG Xiqiang, et al. Research on energy storage location and capacity determination based on PV curve and improved genetic algorithm[J]. Acta Energiae Solaris Sinica, 2022, 43(1): 263-268. (  0) 0) |
| [17] |
林敏怡, 雷勇, 李宇泽, 等. 基于改进量子粒子群算法的储能容量优化配置[J]. 电源技术, 2021, 45(2): 203-207. LIN Minyi, LEI Yong, LI Yuze, et al. Capacity optimal research of hybrid energy based on optimized quantum particle swarm optimization[J]. Chinese Journal of Power Sources, 2021, 45(2): 203-207. (  0) 0) |
| [18] |
钱韦廷, 赵长飞, 万灿, 等. 基于概率预测的混合储能平抑风电波动随机优化调控方法[J]. 电力系统自动化, 2021, 45(18): 18-27. QIAN Weiting, ZHAO Changfei, WAN Can, et al. Probabilistic forecasting based stochastic optimal dispatch and control method of hybrid energy storage for smoothing wind power fluctuations[J]. Automation of Electric Power Systems, 2021, 45(18): 18-27. (  0) 0) |
| [19] |
张伟, 黄卫民. 基于种群分区的多策略自适应多目标粒子群算法[J]. 自动化学报, 2022, 48(10): 2585-2599. ZHANG Wei, HUANG Weimin. Multi-strategy adaptive multi-objective particle swarm optimization algorithm based on swarm partition[J]. Acta Automatica Sinica, 2022, 48(10): 2585-2599. (  0) 0) |
| [20] |
姚健, 刘爱军. 基于粒子群算法的区域综合能源优化调度方法[J]. 电力需求侧管理, 2022, 24(4): 67-72. YAO Jian, LIU Aijun. Optimal scheduling of regional integrated energy based on particle swarm optimization[J]. Power Demand Side Management, 2022, 24(4): 67-72. (  0) 0) |
| [21] |
陈若尘, 张英敏, 刘麒麟, 等. 基于粒子群算法的直流系统网架结构优化设计[J]. 电力系统保护与控制, 2021, 49(5): 165-172. CHEN Ruochen, ZHANG Yingmin, LIU Qilin, et al. Optimal design of grid structure in a DC system based on a PSO algorithm[J]. Power System Protection and Control, 2021, 49(5): 165-172. (  0) 0) |
| [22] |
闫群民, 董新洲, 穆佳豪, 等. 基于改进多目标粒子群算法的有源配电网储能优化配置[J]. 电力系统保护与控制, 2022, 50(10): 11-19. YAN Qunmin, DONG Xinzhou, MU Jiahao, et al. Optimal configuration of energy storage in an active distribution network based on improved multi-objective particle swarm optimization[J]. Power System Protection and Control, 2022, 50(10): 11-19. (  0) 0) |
| [23] |
王尔申, 贾超颖, 曲萍萍, 等. 基于混沌粒子群优化的北斗/GPS组合导航选星算法[J]. 北京航空航天大学学报, 2019, 45(2): 259-265. WANG Ershen, JIA Chaoying, QU Pingping, et al. BDS/GPS integrated navigation satellite selection algorithm based on chaos particle swarm optimization[J]. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(2): 259-265. (  0) 0) |
| [24] |
朱占龙, 刘永军. 融合混沌优化和改进模糊聚类的图像分割算法[J]. 电子学报, 2020, 48(5): 975-984. ZHU Zhanlong, LIU Yongjun. Anovel algorithm by incorporating chaos optimization and improved fuzzy C-means for image segmentation[J]. Acta Electronica Sinica, 2020, 48(5): 975-984. (  0) 0) |
| [25] |
张继荣, 张天. 基于改进粒子群算法的PID控制参数优化[J]. 计算机工程与设计, 2020, 41(4): 1035-1040. ZHANG Jirong, ZHANG Tian. Optimization of PID control parameters based on improved particle group algorithm[J]. Computer Engineering and Design, 2020, 41(4): 1035-1040. (  0) 0) |
| [26] |
JIANG X Y, LI S. BAS: beetle antennae search algorithm for optimization problems[J]. International Journal of Robotics and Control, 2018, 1(1): 1. (  0) 0) |
| [27] |
于嘉鹏, 袁鹤翔, 杨永华, 等. 基于自适应天牛须算法的航空发动机管路布局优化[J]. 机械工程学报, 2020, 56(20): 174-184. YU Jiapeng, YUAN Hexiang, YANG Yonghua, et al. Aero-engine pipe layout optimization based on adaptive beetle antennae search algorithm[J]. Journal of Mechanical Engineering, 2020, 56(20): 174-184. (  0) 0) |
| [28] |
王万良, 金雅文, 陈嘉诚, 等. 多角色多策略多目标粒子群优化算法[J]. 浙江大学学报(工学版), 2022, 56(3): 531-541. WANG Wanliang, JIN Yawen, CHEN Jiacheng, et al. Multi-objective particle swarm optimization algorithm with multi-role and multi-strategy[J]. Journal of Zhejiang University (Engineering Science), 2022, 56(3): 531-541. (  0) 0) |
| [29] |
顾春华, 刘鑫平, 罗飞, 等. 基于同步更新外部归档集的NSGA-Ⅱ改进算法[J]. 计算机工程与应用, 2018, 54(20): 28-34. GU Chunhua, LIU Xinping, LUO Fei, et al. Improved NSGA-Ⅱ algorithm based on synchronous update of external archive[J]. Computer Engineering and Applications, 2018, 54(20): 28-34. (  0) 0) |
| [30] |
李培强, 薛文琦, 唐学贤, 等. 一种基于TOPSIS法的光伏用户群内用户重要性评估方法[J]. 湖南大学学报(自然科学版), 2020, 47(12): 117-123. LI Peiqiang, XUE Wenqi, TANG Xuexian, et al. A method of user importance assessment in photovoltaic user group based on TOPSIS method[J]. Journal of Hunan University (Natural Sciences), 2020, 47(12): 117-123. (  0) 0) |
| [31] |
沈国辉, 陈光, 赵宇, 等. 基于双目标分层优化和TOPSIS排序的电动汽车有序充电策略[J]. 电力系统保护与控制, 2021, 49(11): 115-123. SHEN Guohui, CHEN Guang, ZHAO Yu, et al. Orderly char-ging optimization strategy of an electric vehicle based on double objective hierarchical optimization and TOPSIS ranking[J]. Power System Protection and Control, 2021, 49(11): 115-123. (  0) 0) |
| [32] |
曹裕捷, 张彬桥. 混合智能算法的多目标无功优化方法[J]. 三峡大学学报(自然科学版), 2019, 41(1): 81-86. CAO Yujie, ZHANG Binqiao. Hybrid intelligent algorithm for multipurpose reactive power optimization[J]. Journal of China Three Gorges University (Natural Sciences), 2019, 41(1): 81-86. (  0) 0) |
 2023, Vol. 42
2023, Vol. 42


 朱娟娟(1979), 女, 硕士, 实验师, 研究方向为电力系统运行与控制(E-mail:
朱娟娟(1979), 女, 硕士, 实验师, 研究方向为电力系统运行与控制(E-mail: