文章编号: 2096-3203(2023)02-0075-09 中图分类号: TM73
2. 中国电力科学研究院有限公司, 北京 100192
随着5G、云计算、人工智能等新一代信息技术的快速发展,信息技术与传统产业的融合加速,全球数据中心产业规模不断扩大[1-2],中国数据中心总能耗也将超过2 000亿千瓦时[3]。浙江省发展改革委发布的《浙江省关于建立健全高耗能行业阶梯电价和单位产品超能耗限额标准惩罚性电价的实施意见(征求意见稿)》中将数据中心列为高能耗行业。2021年10月24日,国务院下发《关于2030年前碳达峰行动方案的通知》,要求到2030年,非化石能源消费比重达到25%,风电、太阳能发电总装机容量超过12亿千瓦。因此,国家大力鼓励企业探索分布式光伏发电、燃气分布式供能等配套系统建设,引导新型数据中心向可再生能源发电侧方向发展,就地消纳可再生能源,优化用能结构[4-6]。数据中心亟须节能降耗,充分利用可再生能源,减少碳排放。
国内外众多学者针对数据中心使用可再生能源降低能耗进行了大量研究,主要思路是利用储能设备和不间断电源来解决可再生能源间歇性问题,通过与电网交互来解决能源供应不足或能源不能完全消纳的问题,从而提高数据中心可再生能源利用率并减少运行成本[7-9]。数据中心的负载具有很大的灵活性,部分文献重点研究负载分配策略,如文献[10-11]考虑了工作量分配的随机性特征,制定随机资源规划方案,从而优化数据中心的能源成本,减少碳排放。文献[12-14]以减少运行成本或提高可再生能源利用率为目的,将负载分配策略运用到数据中心可再生能源微电网中。围绕数据中心建立包括可再生能源和储能在内的微电网已成为一种趋势,上述研究侧重于数据中心如何利用可再生能源,减少可再生能源随机性的影响及负载分配策略,缺乏对数据中心可再生能源微电网前期容量规划的研究。
传统微电网中的负荷如电动汽车,工业生产负荷等可根据电价、可再生能源出力调整用电计划,提前进行后续计划的任务,实现负荷前移。但数据中心的任务来自互联网用户,在用户提交需求后数据中心才可进行任务,即数据中心不会和其他传统可调节负荷一样进行负荷的前移,只能在用户提交任务后在处理周期之内进行调节,具有单向转移的特征,且不同类型任务的处理周期也存在不同。如果按照传统工业生产负荷去配置,可能会导致配置容量不合理,不能实现可再生能源的充分利用和数据中心的经济运行。
因此,部分学者针对如何合理规划数据中心微电网,降低建设及运行成本展开了研究。文献[15]针对数据中心服务器的类型、数量及风光储供能系统进行了规划,但输入数据体量较大,计算复杂;文献[16]根据电网中各类资源之间的相互影响,提出一种针对数据中心及储能系统的容量规划方案,忽视了风光可再生能源的配置。文献[17]考虑电、热负荷之间的耦合关系,对数据中心综合能源系统进行了规划;文献[18]考虑了数据中心微电网建设和运行相关的总体规划成本,对分布式数据中心微电网的长期投资和短期运行进行了建模,但未考虑延时容忍型负载。
针对上述问题,文中在已有研究的基础上,构建计及负载特性的数据中心微电网双层容量优化模型。上层为多目标容量规划层,下层为运行优化层,并应用场景缩减法处理可再生能源的不确定性,降低计算复杂度。最后,使用带有精英策略的非支配排序遗传算法(non-dominated sorting genetic algorithm Ⅱ,NSGA-Ⅱ)与Gurobi完成求解。在求得的Pareto前沿面中利用模糊多属性决策方法获得折衷最优解。
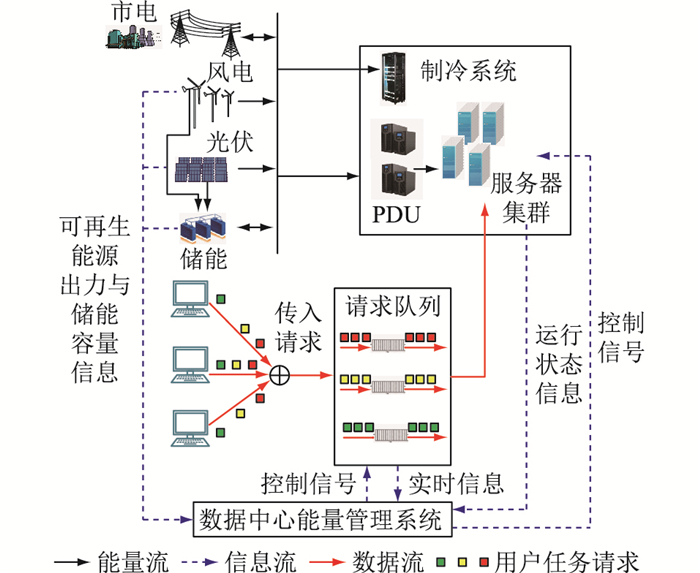
1 数据中心微电网模型如图 1所示,数据中心微电网主体包括风光储系统和数据中心。微电网可与大电网交互,出售和购买电能。数据中心内部包括服务器集群、冷却系统、电源分配单元(power distribution unit,PDU)以及能量管理系统等。在接收到用户任务请求,将其放入请求队列中后,管理系统会结合采集的可再生能源出力、储能容量、请求队列和服务器运行状态等信息在任务周期内把用户请求任务交给相应的服务器进行处理。
|
图 1 数据中心微电网架构 Fig. 1 Microgrid architecture of data center |
光伏发电系统的输出功率与辐照度和环境温度有关,具体关系[19]为:
| $ p_{t, i}^{\mathrm{PV}}=\frac{G_{t, i}^{\mathrm{s}}}{G_{\alpha_0}} P_0^{\mathrm{PV}}\left\{1+\psi\left[T_t^{\mathrm{s}}+\frac{\alpha G_{t, i}^{\mathrm{s}}\left(1-E^{\mathrm{ffc}}\right)}{h}-T_0\right]\right\} $ | (1) |
式中:pt,iPV为典型场景i下光伏发电系统t时刻的输出功率;Gt,is为典型场景i下t时刻的辐照度;Gα0为标准状态下的辐照度;P0PV为光伏发电系统的额定输出功率;ψ为功率温度因数;Tts为t时刻环境温度;α为辐照吸收系数;h为热交换系数;Effc为光伏组件的光电转换效率;T0为标准状态下的温度。
风力发电系统输出功率受风速变化的影响呈现波动性,其发电功率与风速的关系[20]为:
| $ p_{t, i}^{\mathrm{W}}=\left\{\begin{array}{l} 0 \quad v_{t, i}^{\mathrm{W}} <v^{\mathrm{W}, \text { in }} \\ P_0^{\mathrm{W}}\left(\frac{v_{t, i}^{\mathrm{W}}-v^{\mathrm{W}, \text { in }}}{v^{\mathrm{W}, \mathrm{ra}}-v^{\mathrm{W}, \text { in }}}\right)^3 \quad v^{\mathrm{W}, \text { in }} \leqslant v_{t, i}^{\mathrm{W}}<v^{\mathrm{W}, \mathrm{ra}} \\ P_0^{\mathrm{W}} \quad v^{\mathrm{W}, \text { ra }} \leqslant v_{t, i}^{\mathrm{W}}<v^{\mathrm{W}, \text { out }} \\ 0 \quad v^{\mathrm{W}, \text { out }} \leqslant v_{t, i}^{\mathrm{W}} \end{array}\right. $ | (2) |
式中:pt,iW、vt,iW分别为典型场景i下风机t时刻的输出功率与风速;vW,in、vW,out分别为切入、切出风速;P0W、vW,ra分别为风机额定功率和风机达到额定功率时的风速。
蓄电池作为微电网中的储能系统,能够实时充放电以满足电网负荷变化的需求,合理地充放电在一定程度上能解决可再生能源的间歇性问题,典型场景i下t时刻蓄电池电量Qt,iES的数学模型为:
| $ \left\{\begin{aligned} Q_{t, i}^{\mathrm{ES}} & =\left(1-L^{\mathrm{ES}}\right)\left[Q_{t-1, i}^{\mathrm{ES}}+\left(\eta_t^{\mathrm{ESC}} p_{t, i}^{\mathrm{ESC}}-\frac{p_{t, i}^{\mathrm{ESD}}}{\eta_t^{\mathrm{ESD}}}\right) \Delta t\right] \\ \text { s.t. } & 0 \leqslant p_{t, i}^{\mathrm{ESC}} \leqslant \omega_t^{\mathrm{ESC}} P_0^{\mathrm{ES}} \\ & 0 \leqslant p_{t, i}^{\mathrm{ESD}} \leqslant \omega_t^{\mathrm{ESD}} P_0^{\mathrm{ES}} \\ & \omega_t^{\mathrm{ESC}}+\omega_t^{\mathrm{ESD}} \leqslant 1 \end{aligned}\right. $ | (3) |
式中:LES为储能系统的自放电率;ηtESC、ηtESD分别为t时刻储能系统充电、放电效率;pt,iESC、pt,iESD分别为典型场景i下t时刻储能系统充电、放电功率;Δt为单位调度时长;P0ES为储能系统的额定充放电功率;ωtESC、ωtESD为0-1变量,ωtESC=1,储能系统处于充电状态,ωtESD=1,储能系统处于放电状态,并且充放电不能同时进行。
1.2 数据中心模型数据中心的功耗主要来源于服务器、冷却设备以及内部配电系统,用电设备的功耗与服务器处理的工作负载有直接关系。工作负载处理数量增加,服务器功耗增加,散发热量增加,制冷系统工作密度增加,数据中心整体能耗增加。数据中心须处理前端处理器所带来的工作负载,在场景i中,数据中心服务器t时刻的功率pt,iserver为:
| $ p_{t, i}^{\text {server }}=\frac{\left(p^{\text {peak }}-p^{\mathrm{idle}}\right) \lambda_{t, i}}{\mu}+p^{\mathrm{idle}} s_{t, i} $ | (4) |
式中:ppeak、pidle分别为数据中心单台服务器的峰值功率和闲时功率;μ为数据中心的服务速率,与CPU的运行频率有关;λt,i为场景i中数据中心t时刻要处理的延时容忍型工作负载量;st,i为场景i中t时刻前端处理器工作的数量。
在场景i中,数据中心制冷设备能耗[21]为:
| $ p_{t, i}^{\text {cool }}=\frac{p_{t, i}^{\text {server }}}{0.0068\left(T_{t, i}^{\text {sup }}\right)^2+0.0008 T_{t, i}^{\text {sup }}+0.458} $ | (5) |
式中:pt,icool为场景i中t时刻服务器对应制冷设备的能耗;Tt,isup为制冷设备的送风温度。
正常情况下,制冷设备的送风温度可用式(6)进行约束。
| $ T_{t, i}^{\text {in }}=T_{t, i}^{\text {sup }}+\frac{1}{\rho f \kappa}\left(\frac{p_{t, i}^{\text {server }}}{s_{t, i}}-\frac{1}{q-1}\right) \leqslant T^{\mathrm{red}} $ | (6) |
式中:Tt,iin为服务器的入口温度;ρ为数据中心内部空气密度,通常取1.19 kg/m3;f为制冷设备运行时的空气流速,取0.245 4 m3/s;κ为空气的比热容,通常取1 005 J/(kg ·℃);q为热分布系数,取值为0~1;Tred为设定温度,可取25 ℃。
数据中心需要相当大的基础设施来简单地分配不间断、稳定的电力。PDU将数据中心的高压电转换为适合服务器工作的电压,但会产生一定的功率损耗。在场景i中,PDU在t时刻的功率pt,iPDU为:
| $ p_{t, i}^{\mathrm{PDU}}=p_{t, i}^{\mathrm{PDU}, \mathrm{idle}}+\nu^{\mathrm{PDU}}\left(p_{t, i}^{\text {server }}\right)^2 $ | (7) |
式中:pt,iPDU,idle为场景i中PDU在t时刻的空闲功率;νPDU为能耗系数。
因此数据中心的总功耗pt,iDC为:
| $ p_{t, i}^{\mathrm{DC}}=p_{t, i}^{\text {server }}+p_{t, i}^{\text {cool }}+p_{t, i}^{\mathrm{PDU}} $ | (8) |
数据中心微电网可与大电网进行能量交互,从电网购电或售电来满足自身负荷的需求。数据中心与电网交互的功率pt,iG为:
| $ p_{t, i}^{\mathrm{G}}=p_{t, i}^{\mathrm{sup}}-p_{t, i}^{\mathrm{feed}} $ | (9) |
式中:pt,isup为场景i中t时刻电网向数据中心提供的功率;pt,ifeed为场景i中t时刻数据中心馈入电网的功率。
2 双层优化模型风机和光伏的输出功率具有间歇性和不可调度性,蓄电池能根据数据中心用能需求与出力之间的差额进行填补。通过联络线,数据中心微电网可与大电网进行能量交换,从而满足自身负荷需求。
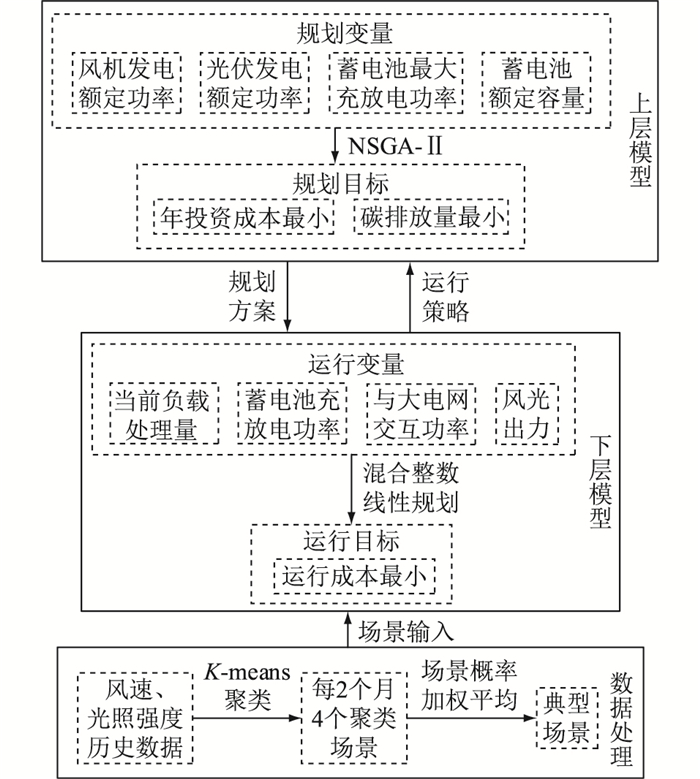
文中提出了双层优化配置策略,上层为数据中心微电网的风机、光伏和蓄电池容量规划,下层为数据中心微电网的运行策略,具体如图 2所示。
|
图 2 双层优化配置策略架构 Fig. 2 Architecture of bi-level optimal configuration strategy |
首先,每2个月的数据分为一组,使用K-means算法对风速、光照强度历史数据进行聚类,利用概率相加的方式对聚类场景进行加权,得到典型场景。
然后,构建双层优化配置模型。上层以数据中心微电网年投资成本与碳排放量最小为目标,对风光储进行规划;下层以各场景下运行成本最小为目标对各时间段负载处理量、风光储的出力情况和与电网交互情况进行优化。
双层模型的求解流程如下:首先,上层模型随机生成种群并将其传递给下层模型;其次,根据下层输入的设备容量数据和各典型场景下气象数据与负载需求,调用Gurobi求解器,求解最优运行方案,返回给上层模型;然后,上层模型根据下层模型返回的方案进行非支配排序和拥挤度计算,通过选择、交叉、变异生成新的种群;最后,将新种群传送到内部模型进行循环迭代计算,当迭代次数达到设定值时,停止循环并输出最后一代种群。
NSGA-Ⅱ求得的Pareto前沿面上各最优解的模糊隶属度函数取值为决策满意度,在所有Pareto最优解中取满意度最高的解作为多目标优化问题的最优折衷解。模糊隶属度函数如式(10)所示。
| $ \xi_{k, m}=\left\{\begin{array}{l} 1 \quad j_{k, m} \leqslant j_{k, m}^{\min } \\ \frac{j_{k, m}^{\max }-j_{k, m}}{j_{k, m}^{\max }-j_{k, m}^{\min }} \quad j_{k, m}^{\min } <j_{k, m}<j_{k, m}^{\max } \\ 0 \quad j_{k, m} \geqslant j_{k, m}^{\max } \end{array}\right. $ | (10) |
式中:ξk,m为标准化条件下第k个最优解的第m个目标函数的满意度;jk,m为第k个最优解的第m个目标函数值;jk,mmax、jk,mmin分别为第k个最优解的第m个目标函数的最大与最小值。
以满意度为评价指标,则标准化最优计算为:
| $ \xi_k=\frac{\sum\limits_{m=1}^M \xi_{k, m}}{\sum\limits_{k=1}^K \sum\limits_{m=1}^M \xi_{k, m}} $ | (11) |
式中:ξk为标准化条件下第k个最优解的满意度;M为目标函数数量;K为Pareto前沿面上最优解数量。
2.1 上层优化模型 2.1.1 目标函数上层优化模型以风电、光伏发电系统的额定装设容量、蓄电池的额定容量以及最大充放功率为规划变量。各目标及其函数表达式如下。
(1) 年折算投资成本与运行成本f1最小。
| $ \min f_1=\min \left(\left(C^{\mathrm{ini}}+C^{\text {rep }}+C^{\mathrm{aux}}\right) R+C^{\text {ope }}\right) $ | (12) |
式中:Cini为主要发电设备购置成本;Crep为蓄电池购换置成本;Caux为辅助设备购置成本;R为资金回收系数;Cope为数据中心运行成本。各参数计算见式(13)。
| $ \left\{\begin{array}{l} R=\frac{l(1+l)^y}{(1+l)^y-1} \\ C^{\mathrm{ini}}=P_0^{\mathrm{W}} c_0^{\mathrm{W}}+P_0^{\mathrm{PV}} c_0^{\mathrm{PV}} \\ C^{\mathrm{rep}}=\left(P_0^{\mathrm{ES}} c_0^{\mathrm{e}}+Q_0^{\mathrm{ES}} c_0^{\mathrm{Q}}\right) \frac{y}{y^{\mathrm{e}}} \\ C^{\mathrm{aux}}=k^{\mathrm{aux}}\left(C^{\mathrm{ini}}+\frac{y^{\mathrm{e}}}{y} C^{\mathrm{rep}}\right) \\ C^{\mathrm{ope}}=\frac{365}{N} \sum\limits_{i=1}^N C_i^{\mathrm{ope}} \end{array}\right. $ | (13) |
式中:l为折现率;y为规划使用年限;c0W、c0PV分别为风电、光伏发电系统的单位容量成本;Q0ES为蓄电池额定容量;c0e、c0Q分别为蓄电池的单位功率成本和单位容量成本;ye为蓄电池的使用年限;kaux为比例系数;Ciope为典型场景i中数据中心的运行成本;N为典型场景数量。
(2) 碳排放量f2最小。
| $ \min f_2=\min \left(\frac{365}{N} \sum\limits_{i=1}^N \sum\limits_{t=1}^T\left(p_{t, i}^{\text {sup }} \sum\limits_{k=1}^n e_k \vartheta_k\right)\right) $ | (14) |
式中:n为燃料类型总量;ek为第k种燃料在发电时的碳排放率;
在规划时考虑到场地、资金等实际情况,对数据中心微电网进行约束:
| $ \left\{\begin{array}{l} P_0^{\mathrm{W}, \text { min }} <P_0^{\mathrm{W}}<P_0^{\mathrm{W}, \text { max }} \\ P_0^{\mathrm{PV}, \text { min }}<P_0^{\mathrm{PV}}<P_0^{\mathrm{PV}, \text { max }} \\ P_0^{\mathrm{ES}, \text { min }}<P_0^{\mathrm{ES}}<P_0^{\mathrm{ES}, \text { max }} \\ Q_0^{\mathrm{ES}, \text { min }}<Q_0^{\mathrm{ES}}<Q_0^{\mathrm{ES}, \text { max }} \end{array}\right. $ | (15) |
式中:P0W,max、P0W,min分别为P0W的上下限;P0PV,max、P0PV,min分别为P0PV的上下限;P0ES,max、P0ES,min分别为P0ES的上下限;Q0ES,max、Q0ES,min分别为Q0ES的上下限。
2.2 下层优化模型 2.2.1 负载特性分析数据中心的业务负载类型通常可以分为2类:延时敏感型工作负载和延时容忍型工作负载[22]。延时敏感型工作负载如实时用户请求和Web服务,处理时间为秒级,基本上不具备调节能力。而延时容忍型工作负载,只要在指定时间内完成即可,其时间要求一般为小时级,在时间维度上具备较强的灵活性。可通过合理调节延时容忍型工作负载算力需求在时间上的分布,实现数据中心的经济运行[23-24]。由于可再生能源多分布在西部地区,数字产业多布局在东中部负荷中心,所以可将东中部的延时容忍型任务转移到西部进行,既平衡了负荷,又增加了当地可再生能源消纳。因此文中仅考虑延时容忍性工作负载。
文中使用队列模型对延时容忍型工作负载进行表述,如式(16)所示。
| $ L_{t, j, i}=L_{t-1, j, i}+\lambda_{t, j, i}-\lambda_{t, j, i}^{\text {allot }} $ | (16) |
式中:Lt,j,i为场景i中t时刻第j类延时容忍型工作负载的队列长度;λt,j,i、λt,j,iallot分别为t时刻数据中心到达与处理的第j类延时容忍型工作负载量。为保证在截止时间之前完成任务,须满足式(17)。
| $ \left\{\begin{array}{l} \lambda_{t, j, i}^{\text {allot }} \leqslant s_{t, j, i}^{\text {allot }} \mu \\ \sum\limits_j^B \sum\limits_t^\tau \lambda_{t, j, i}^{\text {allot }}=\sum\limits_t^\tau \lambda_{t, i} \\ \sum\limits_j^B s_{t, j, i}^{\text {allot }}=s_{t, i} \\ L_{\tau_j, j, i}=0 \end{array}\right. $ | (17) |
式中:st,j,iallot为场景i中t时刻安排处理第j类延时容忍型工作负载的前端服务器数量;B为批处理负载总类型数;τ为截止时刻;τj为第j类延时容忍型负载的处理截止时刻。
在数据中心中,服务器可以在活动状态或节能状态下工作[25-26]。节能状态下的功耗几乎为0,因此始终希望将尽可能多的负载任务分配给某些活动服务器,并将其余服务器保留为节能状态,以减少数据中心的能耗,但是服务器状态的频繁转换也会造成功耗[27]。服务器状态转化的功耗如式(18)所示,在服务器开启的整个时间内,电力消耗以峰值速率进行[27]。
| $ \left\{\begin{array}{l} p_{t, i}^{\text {trans }}=0 \quad t=1 \\ p_{t, i}^{\text {trans }}=p^{\text {peak }}\left[s_{t, i}-s_{t-1, i}\right]^{+} \Delta \tau \quad 2 \leqslant t \leqslant 24 \end{array}\right. $ | (18) |
式中:pt,itrans为场景i下t时刻服务器状态转化的功耗;[x]+=max(0, x);Δτ为服务器从休眠状态转为活跃状态的时间。
2.2.2 目标函数各场景以24 h为一个运行周期T,单位调度时长Δt为1 h,以各场景下运行周期内成本最小为目标,考虑在场景i中,可再生能源设备运维成本CiRES、储能系统充放电成本CiES、与电网功率交互的成本和收益CiGRID最小,即:
| $ \min C_i^{\mathrm{ope}}=\min \left(C_i^{\mathrm{RES}}+C_i^{\mathrm{ES}}+C_i^{\mathrm{GRID}}\right) $ | (19) |
其中:
| $ \left\{\begin{array}{l} C_i^{\mathrm{RES}}=\sum\limits_{t=1}^T\left(c^{\mathrm{W}} p_{t, i}^{\mathrm{W}}+c^{\mathrm{PV}} p_{t, i}^{\mathrm{PV}}\right) \Delta t \\ C_i^{\mathrm{ES}}=\sum\limits_{t=1}^T\left(c^{\mathrm{ESC}} p_{t, i}^{\mathrm{ESC}}+c^{\mathrm{ESD}} p_{t, i}^{\mathrm{ESD}}\right) \Delta t \\ C_i^{\mathrm{GRID}}=\sum\limits_{t=1}^T\left(c_t^{\mathrm{gt}} p_{t, i}^{\text {sup }}-s_t^{\mathrm{gt}} p_{t, i}^{\mathrm{feed}}\right) \Delta t \end{array}\right. $ | (20) |
式中:cW、cPV分别为风机与光伏发电系统的运维成本系数;cESC、cESD分别为储能系统充电与放电时的成本系数;ctgt、stgt分别为数据中心在t时刻的购电与售电电价。
2.2.3 约束条件(1) 功率平衡约束。
| $ p_{t, i}^{\mathrm{DC}}+p_{t, i}^{\text {trans }}=p_{t, i}^{\mathrm{W}}+p_{t, i}^{\mathrm{PV}}+p_{t, i}^{\mathrm{G}}+p_{t, i}^{\mathrm{ESD}}-p_{t, i}^{\mathrm{ESC}} $ | (21) |
(2) 储能系统容量约束。
| $ Q_0^{\min } \leqslant Q_{t, i}^{\mathrm{ES}} \leqslant Q_0^{\mathrm{ES}} $ | (22) |
式中:Q0min为储能系统的最小容量。
(3) 可靠性约束。通过储能系统满足故障时维持数据中心正常工作的可靠性要求[28]。
| $ Q_{t, i}^{\mathrm{ES}} \geqslant \sum\limits_{\theta=t}^{t+\tau^{\mathrm{es}}} P_{\theta, i}^{\mathrm{DC}} \Delta t $ | (23) |
式中:τes为出现供电故障时,储能系统能够维持数据中心正常工作的时长。
(4) 微电网峰谷差约束。为保障数据中心微电网平稳运行,对其峰谷差进行约束。
| $ p_{t, i}^{\mathrm{DC}, \max }-p_{t, i}^{\mathrm{DC}, \min } \leqslant \Delta p^{\mathrm{DC}} $ | (24) |
式中:pt,iDC,max、pt,iDC,min分别为数据中心微电网运行功率最大值和最小值;ΔpDC为数据中心微电网能容忍的最大峰谷差。
(5) 可再生能源出力约束。
| $ \left\{\begin{array}{l} 0 \leqslant p_{t, i}^{\mathrm{PV}} \leqslant P_0^{\mathrm{PV}} \\ 0 \leqslant p_{t, i}^{\mathrm{W}} \leqslant P_0^{\mathrm{W}} \end{array}\right. $ | (25) |
(6) 处理时延约束。考虑数据中心运营商和用户之间有着计算服务水平协议(service level agree ̄ment, SLA),假设SLA所允许的最大时延为D,则负载处理时延约束[29]为:
| $ \frac{1}{s_{t, i} \mu-\lambda_{t, i}}+d \leqslant D $ | (26) |
式中:d为传输时延。
(7) 并网功率容量约束[30]。
| $ \left|p_{t, i}^{\mathrm{G}}\right| \leqslant S_{\text {trans }} \cos \varphi $ | (27) |
式中:Strans为微电网配置的变压器容量;cos φ为变压器的功率因数。
3 算例分析 3.1 参数设置数据中心微电网相关参数设置见表 1,发电燃料的碳排放率与出力占比参照文献[8]。
|
|
表 1 系统主要参数设定 Table 1 Main parameter setting of system |
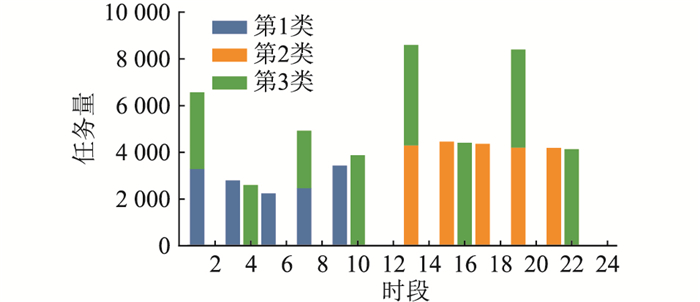
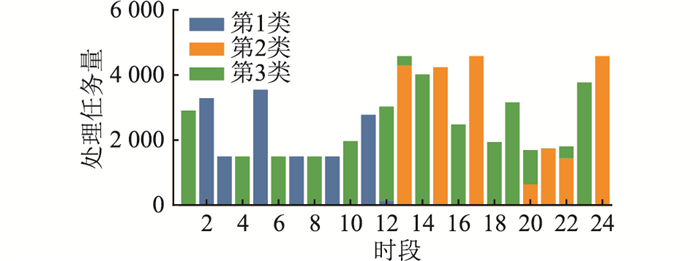
根据一年风速和辐照度的实测数据,利用K-means聚类算法,聚类成6个典型场景。数据中心每天的延时容忍型工作负载量波动不大,并且利用负载均衡技术可实现负载的稳定,因此文中假设各典型场景中须处理的负载量相同。各类型延时容忍型工作负载任务量如图 3所示。
|
图 3 各类延时容忍型工作负载任务量 Fig. 3 Number of various delay-tolerant work loads |
其中第1类延时容忍型工作负载处理截止时间为12:00,周期为12 h;第2类延时容忍型工作负载处理截止时间为24:00,周期为12 h;第3类延时容忍型工作负载截止时间为24:00,周期为24 h。
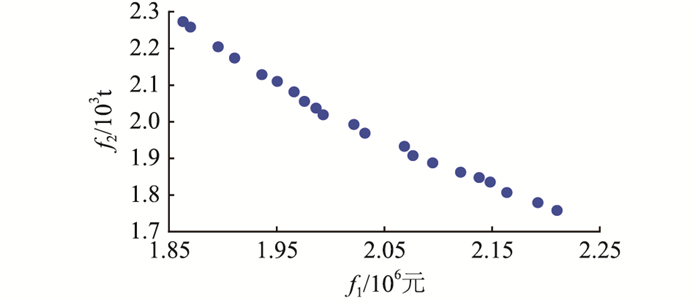
3.2 优化结果上层规划模型是一个多目标非线性模型,采用NSGA-Ⅱ进行求解,设置种群大小为30,迭代次数为100,交叉概率为0.8,变异概率为0.2,最优个体系数0.7;下层优化运行模型是一个单目标混合整数线性优化模型,在Matlab中调用Gurobi求解器求解。经求解可得图 4所示Pareto前沿面。
|
图 4 Pareto前沿面 Fig. 4 Pareto front |
由于种群大小为30,最优个体系数0.7。Pareto前沿面共21个点,每个点表示一种配置方案,具体包括了风电额定装设功率P0W、光伏额定装设功率P0PV、蓄电池额定装设容量Q0ES以及额定最大充放电功率P0ES。每个点的横纵坐标分别为此方案下微电网的年折算投资成本与运行成本f1和典型场景碳排放量f2。使用模糊多属性决策方法获得折衷最优解如表 2所示。
|
|
表 2 折衷最佳配置方案 Table 2 Compromise the best configuration |
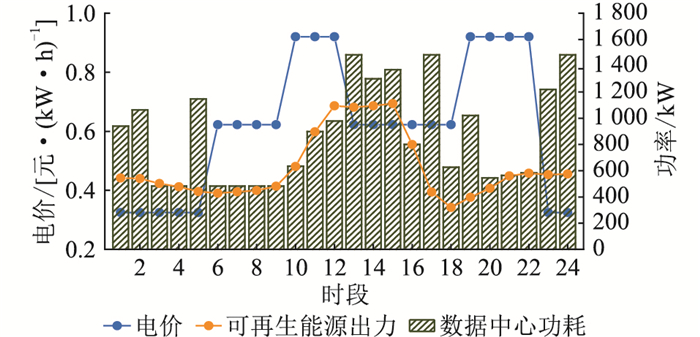
以场景一为例,分析负载分配情况。其数据中心功耗、分时电价和可再生能源出力如图 5所示,工作负载处理情况如图 6所示。
|
图 5 电价、可再生能源出力和数据中心功耗 Fig. 5 Electricity price, renewable energy output and data center energy consumption |
|
图 6 各类延时容忍型工作负载处理情况 Fig. 6 Handling of various delay-tolerant work loads |
结合图 5、图 6可知,延时容忍性工作负载在分配时,不仅考虑了分时电价还考虑了可再生能源出力,在各类延时容忍性工作负载的处理周期内,尽可能将负载分配在电价低、可再生能源出力大的时段。数据中心的功耗几乎与可再生能源出力相匹配,在时段12—时段15可再生能源出力较大,数据中心的功耗也相对增加。但是时段1和时段24的数据中心功耗相较于其他时间段有明显增加,主要是当数据中心功耗大于可再生能源出力时,对数据中心运行成本影响最大的是电价,所以选择电价最低的时间段。
以时段10为例,由图 3可知在时段10一共提交了3 877个任务量,但此时电价较高,可再生能源出力较低,因此对部分负载量进行转移。时段10共处理了1 958个任务量,其中包括时段7转移来的971个任务量,并向时段12转移了74.5%,使得时段10的任务量减少了49.4%,在一定程度上降低了数据中心运行成本,使得数据中心的功耗曲线与可再生能源的出力曲线更加贴合,减少碳排放。
3.3 对比分析为验证文中方法的有效性与优越性,设计如下案例进行对比分析:案例1中数据中心微电网的设备参数是给定的并且考虑负载分配策略;案例2为动态优化设备规划参数但不考虑负载分配;案例3为文中所提优化策略,即对数据中心微电网进行动态规划的同时考虑负载分配。
计算各案例的年折算投资与运行成本和年碳排放量,由于文中方法是在Pareto前沿面上求得的折衷解,并不是让每个目标函数都达到最优的解,所以又按照式(10)与式(11)计算3个案例的满意度,结果如表 3所示。
|
|
表 3 各案例结果对比 Table 3 Comparison of results of various cases |
由表 3可知,案例1为给定规划参数,没有进行合理的规划,满意度较低。案例3与案例2相比,风机、光伏、储能充放电功率以及储能容量分别增加0.05%、4.14%、-18.48%和-1.59%,风机与光伏的变化较小、储能系统变化较大。由于案例2不考虑负载分配,所以想要让数据中心功耗与可再生能源更好地匹配来减少年碳排放量,只能加强储能的建设,利用储能缓解可再生能源出力的间歇性,所以年折算投资与运行成本较案例1和案例3分别增加了36.13%和28.08%。而案例3考虑了负载分配,可根据可再生能源的出力合理分配负载,从而减少对储能系统的依赖,能够在保证较低的碳排放量的同时,减少年折算投资与运行成本,因此满意度较高。
4 结语文中针对数据中心可再生能源微电网容量规划提出一种计及负载特性的数据中心微电网双层优化模型。上层为数据中心微电网容量规划模型,下层为数据中心运行优化模型,采用NSGA-Ⅱ和Gurobi求解器进行迭代求解。为解决风电和光伏出力的不确定性、降低计算的复杂度,对输入的历史数据采用场景聚类的方法得到典型场景。同时考虑负载特性制定分配策略,让数据中心的功耗曲线更加贴合风光出力曲线,提高可再生能源的利用率、减少碳排放量。仿真结果表明文中提出的考虑负载分配的数据中心微电网双层优化模型极大地减少了年折算投资与运行成本和碳排放量,提高了运营商的满意度。
| [1] |
冯成, 王毅, 陈启鑫, 等. 能源互联网下的数据中心能量管理综述[J]. 电力自动化设备, 2020, 40(7): 1-9. FENG Cheng, WANG Yi, CHEN Qixin, et al. Review of energy management for data centers in energy Internet[J]. Electric Power Automation Equipment, 2020, 40(7): 1-9. DOI:10.16081/j.epae.202007003 (  0) 0) |
| [2] |
王圆圆, 韩丁, 白宏坤, 等. 能源大数据中心运营管理标准体系框架构建及实践路径[J]. 电力信息与通信技术, 2022, 20(3): 20-25. WANG Yuanyuan, HAN Ding, BAI Hongkun, et al. Construction and practice path of operation management standard system framework of energy big data center[J]. Electric Power Information and Communication Technology, 2022, 20(3): 20-25. DOI:10.16543/j.2095-641x.electric.power.ict.2022.03.003 (  0) 0) |
| [3] |
张文佺, 王晓烨, 乔军晶, 等. 点亮绿色云端: 中国数据中心能耗与可再生能源使用潜力研究[R]. 北京: 绿色和平, 华北电力大学, 2019. ZHANG Wenquan, WANG Xiaoye, QIAO Junjin, et al. Lighting up the green cloud: research on the energy consumption and renewable energy utilization potential of data centers in China[R]. Beijing: Greenpeace, North China Electric Power University, 2019. (  0) 0) |
| [4] |
工业信息化部. 新型数据中心发展三年行动计划(2021-2023年). (2021-07-14). https://www.miit.gov.cn/jgsj/txs/wjfb/art/2021/art_12cc04dc9daf4d57a7038811a57383b6.html. Ministry of Industry and Information Technology. Three year action plan for the development of new data center(2021-2023). (2021-07-14). https://www.miit.gov.cn/jgsj/txs/wjfb/art/2021/art_12cc04dc9daf4d57a7038811a57383b6.html. (  0) 0) |
| [5] |
王继业, 周春雷, 李洋, 等. 数据中心关键技术和发展趋势研究综述[J]. 电力信息与通信技术, 2022, 20(8): 1-21. WANG Jiye, ZHOU Chunlei, LI Yang, et al. Review of key technologies and development trend of data center construction[J]. Electric Power Information and Communication Technology, 2022, 20(8): 1-21. DOI:10.16543/j.2095-641x.electric.power.ict.2022.08.001 (  0) 0) |
| [6] |
余潇潇, 马玉草, 宋福龙, 等. 数据中心能耗建模及能量调节综述[J]. 电力信息与通信技术, 2022, 20(8): 38-49. YU Xiaoxiao, MA Yucao, SONG Fulong, et al. Overview of data center energy consumption modeling and demand response[J]. Electric Power Information and Communication Technology, 2022, 20(8): 38-49. (  0) 0) |
| [7] |
YU L, JIANG T, ZOU Y L. Real-time energy management for cloud data centers in smart microgrids[J]. IEEE Access, 2016, 4: 941-950. DOI:10.1109/ACCESS.2016.2539369 (  0) 0) |
| [8] |
李彬, 杜亚彬, 曹望璋, 等. 考虑风光储互补与工作负载分配的数据中心优化调度[J]. 现代电力, 2022, 39(3): 356-363. LI Bin, DU Yabin, CAO Wangzhang, et al. Optimal scheduling of data center considering wind-solar-storage complementary and workload distribution[J]. Modern Electric Power, 2022, 39(3): 356-363. DOI:10.19725/j.cnki.1007-2322.2021.0129 (  0) 0) |
| [9] |
吴云芸, 方家琨, 艾小猛, 等. 计及多种储能协调运行的数据中心实时能量管理[J]. 电力自动化设备, 2021, 41(10): 82-89. WU Yunyun, FANG Jiakun, AI Xiaomeng, et al. Real-time energy management of data center considering coordinated operation of multiple types of energy storage[J]. Electric Power Automation Equipment, 2021, 41(10): 82-89. (  0) 0) |
| [10] |
DING Z H, XIE L Y, LU Y, et al. Emission-aware stochastic resource planning scheme for data center microgrid considering batch workload scheduling and risk management[C]//IEEE/IAS 54th Industrial and Commercial Power Systems Technical Conference (I & CPS). Niagara Falls, ON, Canada. IEEE, 2018: 1-9.
(  0) 0) |
| [11] |
祁兵, 曹望璋, 李彬, 等. 考虑托管式数据中心负荷调节不确定性的区间优化模型[J]. 电网技术, 2022, 46(1): 39-49. QI Bing, CAO Wangzhang, LI Bin, et al. Interval optimization model considering uncertainty of load regulation for colocation data center[J]. Power System Technology, 2022, 46(1): 39-49. (  0) 0) |
| [12] |
NIU T, HU B, XIE K G, et al. Spacial coordination between data centers and power system considering uncertainties of both source and load sides[J]. International Journal of Electrical Power & Energy Systems, 2021, 124: 106358. (  0) 0) |
| [13] |
杨挺, 姜含, 侯昱丞, 等. 基于计算负荷时-空双维迁移的互联多数据中心碳中和调控方法研究[J]. 中国电机工程学报, 2022, 42(1): 164-177. YANG Ting, JIANG Han, HOU Yucheng, et al. Study on carbon neutrality regulation method of interconnected multi-datacenter based on spatio-temporal dual-dimensional computing load migration[J]. Proceedings of the CSEE, 2022, 42(1): 164-177. (  0) 0) |
| [14] |
兰洲, 蒋晨威, 谷纪亭, 等. 促进可再生能源发电消纳和碳减排的数据中心优化调度与需求响应策略[J]. 电力建设, 2022, 43(4): 1-9. LAN Zhou, JIANG Chenwei, GU Jiting, et al. Optimal dispatch and demand response strategies of data centers for promoting accommodation of renewable energy generation and reducing carbon emission[J]. Electric Power Construction, 2022, 43(4): 1-9. (  0) 0) |
| [15] |
HADDAD M, COSTA G D, NICOD J M, et al. Combined IT and power supply infrastructure sizing for standalone green data centers[J]. Sustainable Computing: Informatics and Systems, 2021, 30(7): 100505. (  0) 0) |
| [16] |
GUO C S, LUO F J, CAI Z X, et al. Integrated planning of Internet data centers and battery energy storage systems in smart grids[J]. Applied Energy, 2021, 281: 116093. (  0) 0) |
| [17] |
LYU J W, ZHANG S X, CHENG H Z, et al. Optimal sizing of energy station in the multienergy system integrated with data center[J]. IEEE Transactions on Industry Applications, 2021, 57(2): 1222-1234. (  0) 0) |
| [18] |
QI W B, LI J, LIU Y Q, et al. Planning of distributed Internet data center microgrids[J]. IEEE Transactions on Smart Grid, 2019, 10(1): 762-771. (  0) 0) |
| [19] |
张靠社, 冯培基, 张刚, 等. 考虑机会约束的多能源微电网双层优化配置[J]. 太阳能学报, 2021, 42(8): 41-48. ZHANG Kaoshe, FENG Peiji, ZHANG Gang, et al. Bi-level optimization configuration method for multienergy microgrid considering chance constraints[J]. Acta Energiae Solaris Sinica, 2021, 42(8): 41-48. (  0) 0) |
| [20] |
张长云, 黄景光, 李振兴, 等. 极地环境含风氢储混合微电网容量优化配置[J]. 电力工程技术, 2022, 41(1): 108-116. ZHANG Changyun, HUANG Jingguang, LI Zhenxing, et al. Optimal configuration of wind-hydrogen-storage hybrid microgrid capacity in polar environment[J]. Electric Power Engineering Technology, 2022, 41(1): 108-116. (  0) 0) |
| [21] |
高晋坤, 余娟, 刘珏麟, 等. 考虑多时段设备耦合的数据中心能效优化方法[J]. 电力系统自动化, 2022, 46(15): 153-161. GAO Jinkun, YU Juan, LIU Yulin, et al. Optimization method for energy efficiency of data center considering multi-period equipment coupling[J]. Automation of Electric Power Systems, 2022, 46(15): 153-161. (  0) 0) |
| [22] |
CHEN M, GAO C W, SHAHIDEHPOUR M, et al. Internet data center load modeling for demand response considering the coupling of multiple regulation methods[J]. IEEE Transactions on Smart Grid, 2021, 12(3): 2060-2076. (  0) 0) |
| [23] |
丁肇豪, 曹雨洁, 张素芳, 等. 能源互联网背景下数据中心与电力系统协同优化(一): 数据中心能耗模型[J]. 中国电机工程学报, 2022, 42(9): 3161-3177. DING Zhaohao, CAO Yujie, ZHANG Sufang, et al. Coordinated operation for data center and power system in the context of energy internet: energy demand management model of data center[J]. Proceedings of the CSEE, 2022, 42(9): 3161-3177. (  0) 0) |
| [24] |
高赐威, 吴刚, 陈宋宋. 考虑地理分散的数据中心服务器频率调节的电网降损模型[J]. 中国电机工程学报, 2019, 39(6): 1673-1681, 1863. GAO Ciwei, WU Gang, CHEN Songsong. A model aimed at reducing power net loss considering frequency scaling of servers in geo-distributed data centers[J]. Proceedings of the CSEE, 2019, 39(6): 1673-1681, 1863. (  0) 0) |
| [25] |
李凌, 张徐东, 钱声攀, 等. 数据中心能耗数据实时采集机制的研究与设计[J]. 电力信息与通信技术, 2021, 19(3): 26-33. LI Ling, ZHANG Xudong, QIAN Shengpan, et al. Research and design of real-time collection mechanism of energy consumption data in data center[J]. Electric Power Information and Communication Technology, 2021, 19(3): 26-33. (  0) 0) |
| [26] |
张林锋, 武彤, 沈庆飞, 等. 服务器实际运行功率测试方法研究及应用[J]. 电力信息与通信技术, 2021, 19(6): 64-69. ZHANG Linfeng, WU Tong, SHEN Qingfei, et al. Research and application of server actual operation power test method[J]. Electric Power Information and Communication Technology, 2021, 19(6): 64-69. (  0) 0) |
| [27] |
CHEN S M, IRVING S, PENG L. Operational cost optimization for cloud computing data centers using renewable energy[J]. IEEE Systems Journal, 2016, 10(4): 1447-1458. (  0) 0) |
| [28] |
王玚, 李鹏, 冀浩然, 等. 考虑多类型资源的数据中心园区供电协调规划[J]. 电力系统自动化, 2022, 46(14): 19-28. WANG Yang, LI Peng, JI Haoran, et al. Coordination planning of power supply in data center parks with multiple resources[J]. Automation of Electric Power Systems, 2022, 46(14): 19-28. (  0) 0) |
| [29] |
YUAN H T, BI J, ZHOU M C, et al. Biobjective task scheduling for distributed green data centers[J]. IEEE Transactions on Automation Science and Engineering, 2021, 18(2): 731-742. (  0) 0) |
| [30] |
王晓毅, 唐忠. 考虑供需自平衡和独立运行能力的并网型微电网容量优化配置[J]. 太阳能学报, 2021, 42(5): 74-82. WANG Xiaoyi, TANG Zhong. Capacity optimization of grid-connected microgrid considering self-balance and independent operation capability[J]. Acta Energiae Solaris Sinica, 2021, 42(5): 74-82. (  0) 0) |
2. China Electric Power Research Institute, Beijing 100192, China
 2023, Vol. 42
2023, Vol. 42


 李彬(1983), 男, 博士, 副教授, 研究方向为电力通信、电气信息(E-mail:
李彬(1983), 男, 博士, 副教授, 研究方向为电力通信、电气信息(E-mail: