文章编号: 2096-3203(2023)01-0011-08 中图分类号: TM41
随着电力电子变流技术的发展,直流配电技术快速兴起[1-4]。直流变压器(direct current transformer, DCT)是直流配电系统中的重要设备[5-6],是实现电压变换、潮流控制、故障保护等功能的关键,DCT的性能直接影响到整个系统的经济性与可靠性[7-8]。
双有源桥(dual active bridge,DAB)变换器可以实现可控的双向功率传输、电压调节等[9],被中压DCT广泛采用。除使用耐压更高的碳化硅(SiC)器件外[10],通过开关串联、多变换器模块串并联或采用模块化多电平结构也可以有效降低开关器件的电压应力,从而提高端口电压等级[11-14]。其中,应用最多的是输入串联输出并联型DAB变换器,凭借其软开关特性良好、冗余配置灵活等优势,已经在多个中压直流配电示范工程中得到应用[15-16]。开关串联在实际应用中无法做到各开关器件严格同步开关,从而产生分压不均衡问题,限制了其在实际应用中的推广[17]。
模块化多电平换流器(modular multilevel converter, MMC)是一项较为新兴的技术[18-20],基于MMC的DCT通过对子模块高频类方波调制,产生与DAB类似的波形,并通过移相控制实现可控的功率传输[21-22]。文献[23]提出一种基于模块化多电平和开关器件串联的直流变压器(modular multilevel with series-connected switches direct current transformer, M2S2DCT)。相较于传统DAB变换器,M2S2DCT将中压侧全桥的各开关管替换为串联开关模块,大幅提高电压等级。M2S2DCT引入了输入电感与阀串支路,阀串支路为模块化多电平结构,由多个半桥模块构成。通过阀串支路类方波调制,中压侧全桥的端口电压在一部分时间内下降为0,不仅实现了中压侧全桥的零电压开关,更解决了串联开关管的分压问题。通过调节类方波调制占空比随端口电压变化,拓展开关管零电压开关范围,提升DCT宽范围运行能力。
文献[23]针对M2S2DCT对于宽电压、功率范围的兼容性,提出阀串支路类方波调制占空比与低压、中压侧间移相联合调制的单移相(single phase shift, SPS)控制策略。该策略中,在中压侧全桥串联开关管换流点处,阀串支路电流存在尖峰,增大了器件的电流应力及损耗。针对这一现象,文中提出一种基于中压侧全桥换流移相的阀串支路电流优化控制策略。该策略通过改变M2S2DCT中压侧全桥换流移相角,减小电流尖峰,降低M2S2DCT部分器件的电流应力,优化运行状态。
1 中压侧全桥移相控制下M2S2DCT状态分析 1.1 M2S2DCT的工作原理图 1为M2S2DCT拓扑,包括高频隔离变压器Tr及其原副边绕组分别连接的中压侧和低压侧结构。低压侧结构含有由开关管Q1—Q4构成的全桥以及端口滤波电容CL。中压侧包含输入端口滤波电感Lf,由n个半桥子模块(SM1—SMn)串联构成的阀串支路,以及中压侧全桥。其中,中压侧全桥的直流端口与阀串支路端口并联,桥臂开关为由m个开关管串联构成的开关管组(SS1—SS4)组成。Lr与DAB变换器中的传输电感一致,表示Tr漏感与外接串联电感的集合。图 1中VMV为中压侧端口电压;VLV为低压侧端口电压;iM为中压侧输入电流;iL为低压侧输出电流;is为阀串支路电流;iF为中压侧全桥输入电流;ir为变压器中压侧绕组电流;vAB为阀串支路即中压侧全桥直流端口的电压;vCD为中压侧全桥交流端口的电压;vEF为低压侧全桥交流端口的电压。

|
图 1 M2S2DCT拓扑 Fig. 1 The topology of M2S2DCT |
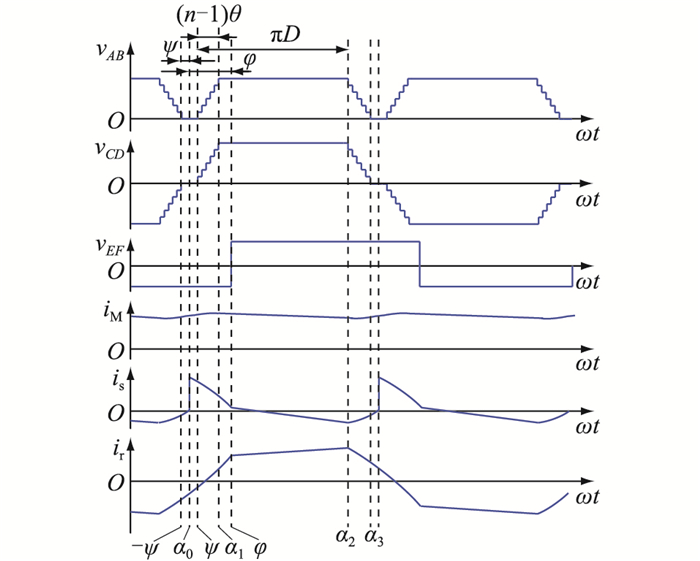
M2S2DCT的工作波形见图 2。仿照文献[23]对SPS控制模式的分析,选取SS1的开通时刻,即vAB零电平区间段中点作为电路状态分析的初始点α0,α0=0。记子模块上管S11—Sn1驱动信号占空比均为D,低压侧全桥驱动信号相对α0的移相角为φ,阀串支路相邻子模块驱动信号之间存在移相角θ。
|
图 2 M2S2DCT工作波形 Fig. 2 The working waveforms of M2S2DCT |
M2S2DCT的阀串支路采用类方波调制,占空比为D,其开关频率为中压侧全桥的2倍。在ψ~α1以及α2~α3区间内,各子模块依次间隔θ投入、切出,从而限制vAB的dv/dt。在-ψ~ψ区间内,vAB电压为0,中压侧全桥在该零电平区间内换流,实现了零电压开关。串联开关模块实现了零电压开关,因此不存在开关过程中的开关管均压问题。
1.2 M2S2DCT的单移相控制记M2S2DCT中压侧正常工作的最大电压为VABm,通过调节M2S2DCT类方波调制的占空比D,在VMV变化时维持vAB的峰值为VABm:
| D=VMVVABm | (1) |
根据M2S2DCT的功率特性,在-π/2<φ<π/2的区间内,M2S2DCT的传输功率随φ的增大单调增加,由负变正。故可选取φ作为唯一的功率控制变量,继而由φ产生各开关模块的驱动信号,对M2S2DCT的传输功率进行调节,可实现对电压或者传输功率的闭环控制[23]。由于该控制方式通过控制一个移相角进行调节,故被称为SPS控制。图 3为该控制方法的示意。图 3中Vref(Pref)为闭环控制的参考值;Vt(Pt)为采样反馈的电压(功率)值。在SPS控制中,中压侧全桥固定在α0处进行换流。

|
图 3 M2S2DCT的SPS控制 Fig. 3 SPS control of M2S2DCT |
开关周期内第一个导通的子模块驱动信号上升沿与α0之间的相位差为ψ,其表达式为:
| ψ=(1−D)π−(n−1)θ2 | (2) |
根据图 1,阀串支路的电流is可表示为:
| is=iM−iF=iM−sTir | (3) |
| sT={1SS1、SS4 导通 −1SS2、SS3 导通 | (4) |
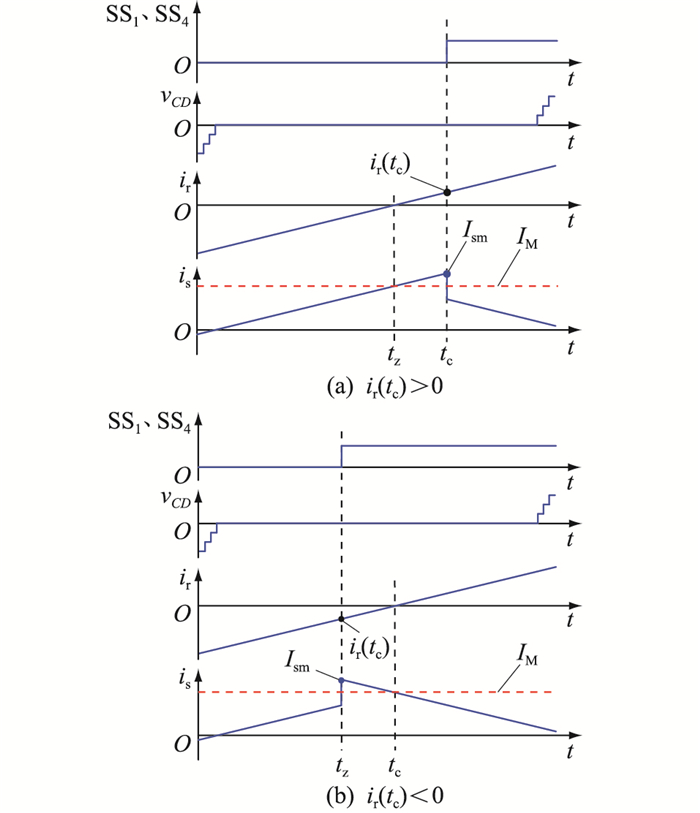
式中:sT为中压侧全桥开关函数。iM、iF、ir均为感性电流,因为iM为变换器中压端口的输入电流,所以中压侧电压和传输功率唯一确定,因此可基于ir及iF对阀串支路电流is进行分析。由于中压侧全桥在阶梯波电压vCD的零电平区间内进行换流,下文分析中将SPS控制下SS1、SS4驱动信号上升沿所在时刻记为tc,tc处的电感电流为ir(tc)。同时为方便分析,忽略iM纹波,记iM的平均值为IM。并假设SPS控制下的M2S2DCT工作在φ>ψ的模式,即低压侧全桥的换流点在vCD的零电平区间之外,此时ir在vCD为0的区间内保持单调增大,其他情况将在后续进一步讨论。当中压侧全桥换流点在vCD的零电平区间内变化时,不同情况下的电流波形如图 4所示。为便于观察,图 4中仅列举SS1、SS4驱动信号及vCD、ir、is在vCD的零电平区间附近波形。
|
图 4 换流点tc选取与Ism的关系示意 Fig. 4 Schematic diagram of the relationship between tc and Ism |
定义ir过零点的时间为tz,阀串支路电流is在分析区间内的最大值为Ism。根据传输电感Lr所在回路的电压电流关系,可以得到:
| Lrdirdt=vCD−nvEF | (5) |
根据变换器的工作状态可知在该区间内vCD=0,vEF=-VLV。由式(5)可以得出,在该区间内,电感电流ir保持单调增长。如图 2所示,根据式(3)、式(4)可知,is在SS1、SS4导通的区间内单调减小,在SS2、SS3导通的区间内单调增大。在中压侧全桥换流前后,is的最大值均出现在tc处,其值分别为Ism1=IM+ir(tc)以及Ism2=IM-ir(tc)。则在vCD为0的区间内,阀串支路电流的最大值为Ism1与Ism2中的较大值,即Ism=IM+ ir(tc)。
2 基于中压侧全桥换流点动态调节的M2S2DCT优化控制策略由上述分析可知,在阶梯波电压vCD为0的区间内,阀串支路电流is的最大值Ism出现在中压侧全桥串联开关管的换流时刻tc处。若此时ir(tc)=0,则Ism可以取得最小值IM,即中压侧端口输入电流。为此,提出一种中压侧全桥换流点动态控制策略,通过调节串联开关管SS1—SS4的驱动信号相对于阶梯波零电平中点的移相角,使tc尽可能靠近tz,则可以使ir(tc)尽可能接近0,从而减小is峰值和有效值。
稳态工作时,根据文献[23]的研究,α=α0时,ir的初值Ir0为:
| Ir0=(π−2φ)nVLV−πVMV4πfdLr | (6) |
在φ>ψ的工作模式下,根据式(6)可得-ψ<α<ψ时,ir为:
| ir(α)=Ir0+nVLV2πfdLr×α | (7) |
令ir(α)=0,可解出ir为0的时间点相对应的相位角δ:
| δ=φ−(1−VMVnVLV)×π2 | (8) |
而对于0<φ<ψ的情况,可以将Lr两端的电压vL作如下表示:
| vL={nVLVα∈(−ψ,φ)−nVLVα∈[φ,ψ) | (9) |
根据式(5)和式(9),可知ir先增大后减小,在(-ψ, ψ)内可能存在2个过零点δ1和δ2,与求解ψ<φ情况的方法相同,可得:
| {δ1=φ−(1−VMVnVLV)×π2δ2=φ+(1−VMVnVLV)×π2 | (10) |
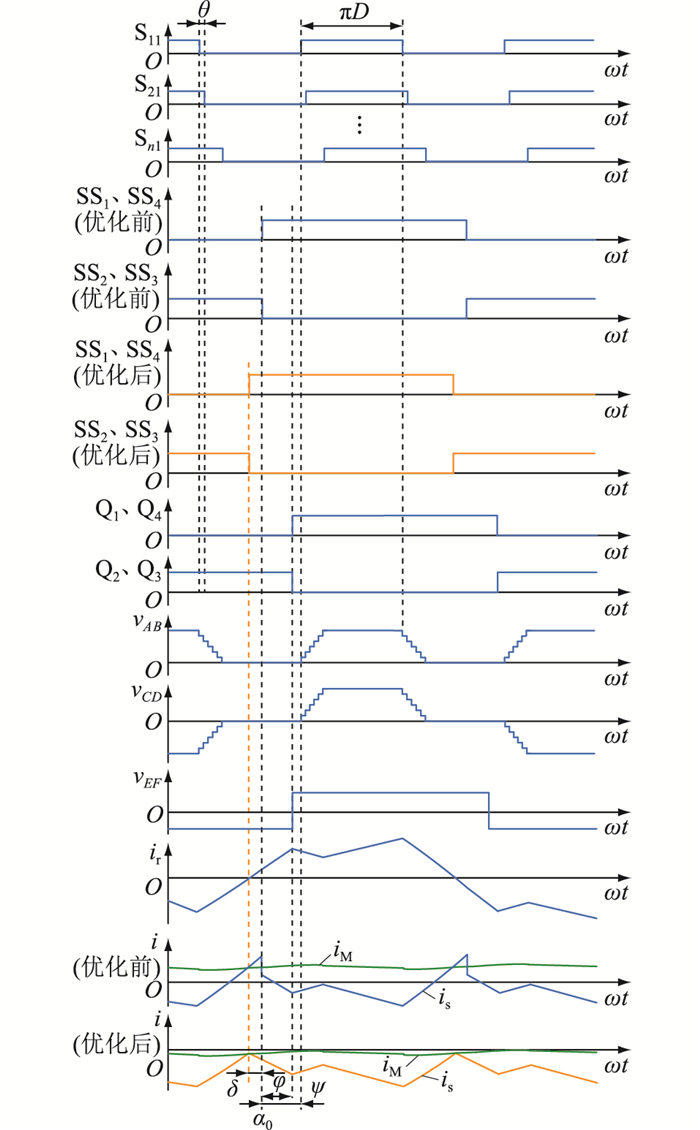
以0<φ<ψ情况为例,M2S2DCT中各开关管驱动信号及电压电流波形如图 5所示。
|
图 5 优化前后M2S2DCT的波形 Fig. 5 Waveforms of M2S2DCT with and without optimization |
为保证串联开关管的可靠换流,定义换流时刻tc与最近的非零阶梯波电压状态之间的时间长度为tcd,则tcd应不小于其允许的最小值tcdmin。一般情况下,tcdmin的取值可与中压侧各开关管驱动信号死区时间一致,或根据实际工作波形中零电平区间的稳定时间决定,旨在保证中压侧全桥零电压开关工作状态。在中压侧全桥换流移相角为δ的情况下,tcd可以表示为:
| tcd=ψ−|δ|2πfd>tcdmin | (11) |
由上式可知,基于tcdmin的限制,换流移相角δ应满足:
| |δ|<ψ−2πfdtcdmin | (12) |
根据式(10)与图 4,若上述2个过零点均满足式(12),则ir在δ1<α<δ2区间内始终大于0。此时若选取ωtc=δ1,则该区间内Ism=IM。若选取ωtc=δ2,由于is=IM+ir,该区间内Ism始终大于IM。因此,该种情况下串联开关管应在δ1处进行换流。若上述过零点均不存在,则说明ir在-ψ<α<ψ区间内恒小于0或恒大于0,此时ir在φ处达到最大值。另一方面,根据文献[23]中的软开关特性分析,当VMV>nVLV时,低压侧全桥开关管不能实现零电压开通,此时ir(φ)<0。由此推断,当满足VMV>nVLV且过零点不存在时,ir在-ψ<α<ψ区间内恒小于0。此时为了实现换流点tc处Ism最小的目标,应在φ处换流。综合上述分析,可以得到该模式下中压侧全桥换流点移相角δ的表达式如下:
| δ={φ−(1−VMVnVLV)×π21−VMVnVLV⩾ | (13) |
通过式(13)求得换流点移相角δ,进而根据式(12)进行限幅运算,在计算得到的δ超出M2S2DCT设计运行范围时将其限制在极限值,以保证中压侧全桥在零电压时换流,符合M2S2DCT的设计初衷。
须说明的是,该控制策略不改变SPS控制的D、φ、ψ、θ等参数,同时由于中压侧全桥始终在vAB零电压区间内进行换流,该调节过程不改变各支路端口的电压和变压器绕组与电感的电流,从而不会对变换器运行状态产生影响。因此该优化控制可以独立运行,不影响SPS控制下的M2S2DCT的功率调节。此外,优化控制策略应用前后is在vCD不为0的区间内没有发生变化,此时阀串支路各子模块的上管导通,因此流经子模块上管的电流将不受影响,差异主要体现在子模块下管导通区间is峰值和有效值的减小,从而实现电流应力和导通损耗优化。根据上述分析与推导,在图 3所示的SPS控制流程中,获得φ之后,通过式(13)的计算与式(12)的限幅,得到中压侧全桥的各开关模块的驱动信号。该优化控制策略示意如图 6所示。

|
图 6 优化控制策略示意 Fig. 6 Schematic diagram of optimized control strategy |
文中采用PLECS搭建仿真模型对上述理论分析进行验证。仿真中M2S2DCT的主要参数见表 1。
|
|
表 1 M2S2DCT仿真主要参数 Table 1 Simulation parameters of M2S2DCT |
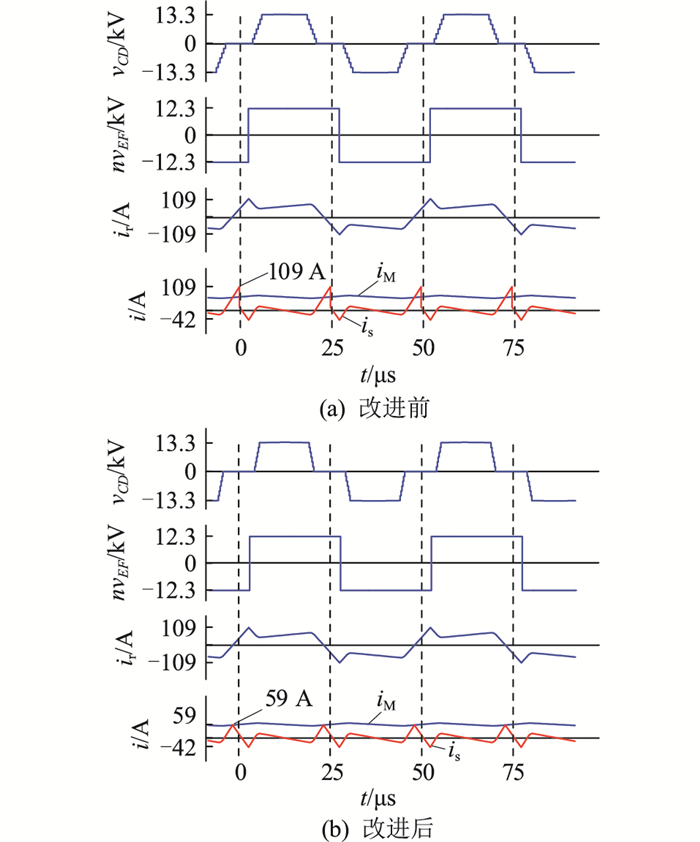
VMV为8 kV时,中压侧全桥移相控制应用前后,半载和满载情况下M2S2DCT的主要仿真波形如图 7、图 8所示。
|
图 7 半载时优化控制前后主要仿真波形 Fig. 7 Main simulation waveforms before and after optimized control at half load |
|
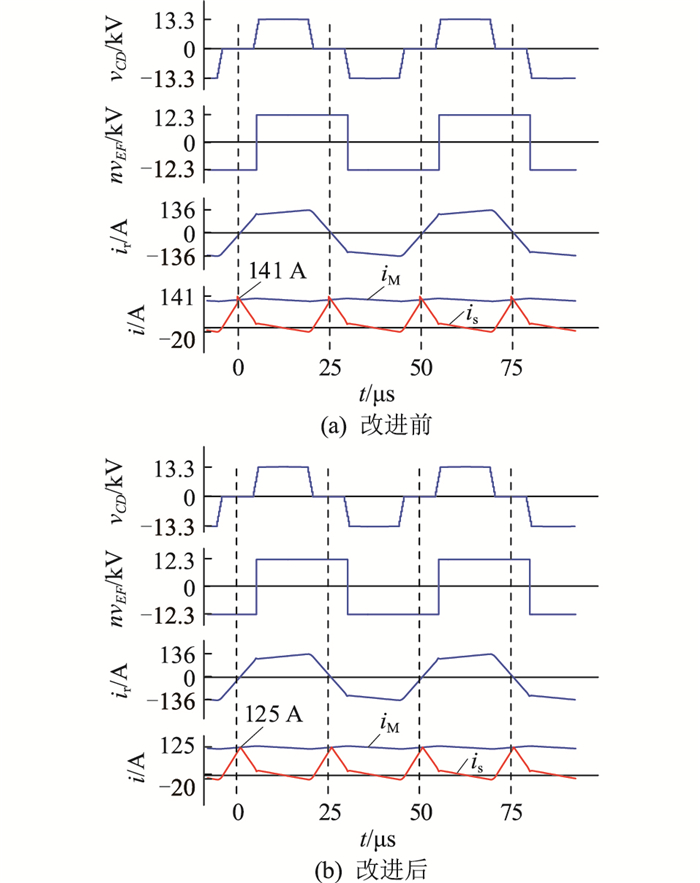
图 8 满载时优化控制前后主要仿真波形 Fig. 8 Main simulation waveforms before and after optimized control at full load |
图 7为半载情况,可以观察到优化方法应用前后vCD、vEF、ir和iM的波形均保持不变,该优化控制策略仅影响子模块下管导通区间内支路电流is的波形。改进前中压侧串联开关管在vCD零电平中点进行换流,换流时ir不为0导致is发生突变,产生较为明显的尖峰。此时is峰值为109 A,有效值为29 A,子模块下管电流有效值最大为45 A。相同的负载条件下采用优化控制后,换流移相角δ为-13.75°。此时is峰值减小为59 A,有效值减少为20 A,子模块下管电流最大有效值减少为28 A。该峰值与中压侧电流iM相同,证明换流点处ir=0。图 8为满载情况,中压侧全桥换流移相角δ为4.5°。改进后is峰值由141 A减小至125 A,有效值由50 A减小至47 A,下管电流有效值由76 A减小至71 A。上述结果体现了中压侧全桥换流移相角控制对is的优化效果,能够降低其峰值和有效值,尤其是子模块下管的损耗。同时可以观察到除中压侧全桥换流点附近以外的波形均未发生变化,证明了该方法不改变ir状态及功率特性,不影响SPS控制下M2S2DCT的功率调节。
4 实验验证为进一步验证上述优化控制效果,搭建样机平台并进行相关实验,主要参数如表 2所示。
|
|
表 2 M2S2DCT样机主要参数 Table 2 Parameters of the M2S2DCT prototype |
样机平台可分为功率部分及控制部分。其中,功率部分包括子模块串联支路、DAB变换结构、滤波电感Lf、传输电感Lr以及隔离变压器Tr;控制部分包含驱动电路、采样电路及DSP控制器。
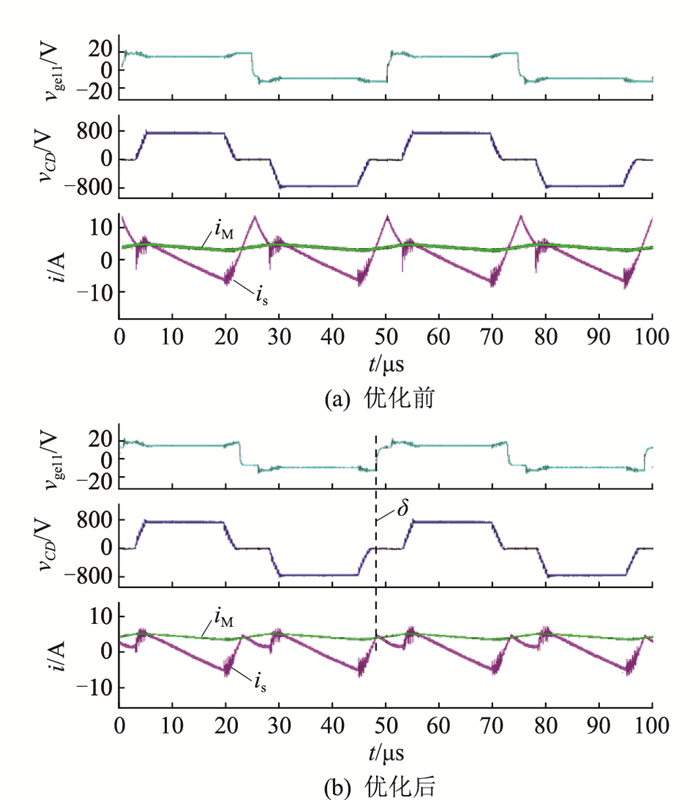
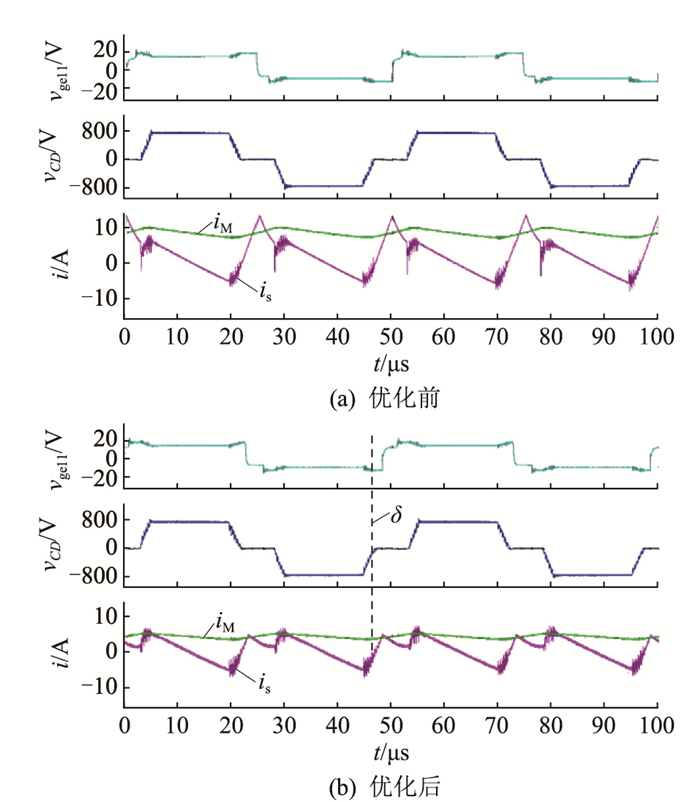
图 9、图 10为VMV=500 V时功率为半载和满载情况下实验样机的主要实验波形。可以看出,优化后中压侧串联开关管驱动信号vge11的上升沿和下降沿不再位于vCD零电平区间中点,而是随着运行状态进行调节,实现了对is峰值的抑制,vge11为串联开关模块SS1的第一个开关管T11的栅极-发射极电压。在半载情况下,优化移相角δ约为-15°,优化后is最大值和有效值分别为6.8 A和3.1 A,比优化前分别下降48%和36%。满载情况下,δ约为-7°,优化前后is峰值分别为13.6 A和8.8 A,有效值分别为5.1 A和3.9 A,优化幅度分别为35%和23%。上述结果体现了优化控制策略的有效性,能够优化子模块开关管运行状态,尤其是子模块下管,提升变换器效率和可靠性。阀串模块电流的优化除了能够提高变换器的效率,在采用相同器件的情况下,应用优化控制策略后阀串支路子模块下管需要承受的峰值电流明显降低,使变换器在运行时拥有更大的安全余量。另一方面,在进行变换器的设计时,阀串模块中绝缘栅双极型晶体管(insulated gate bipolar transistor,IGBT)的最大电流的取值有所降低,降低了器件选型的限制;IGBT的发热降低,在器件散热考虑上降低了设计要求。
|
图 9 2kW时优化控制前后主要工作波形 Fig. 9 Main working waveforms before and after optimized control at 2 kW |
|
图 10 4kW时优化控制前后主要工作波形 Fig. 10 Main working waveforms before and after optimized control at 4 kW |
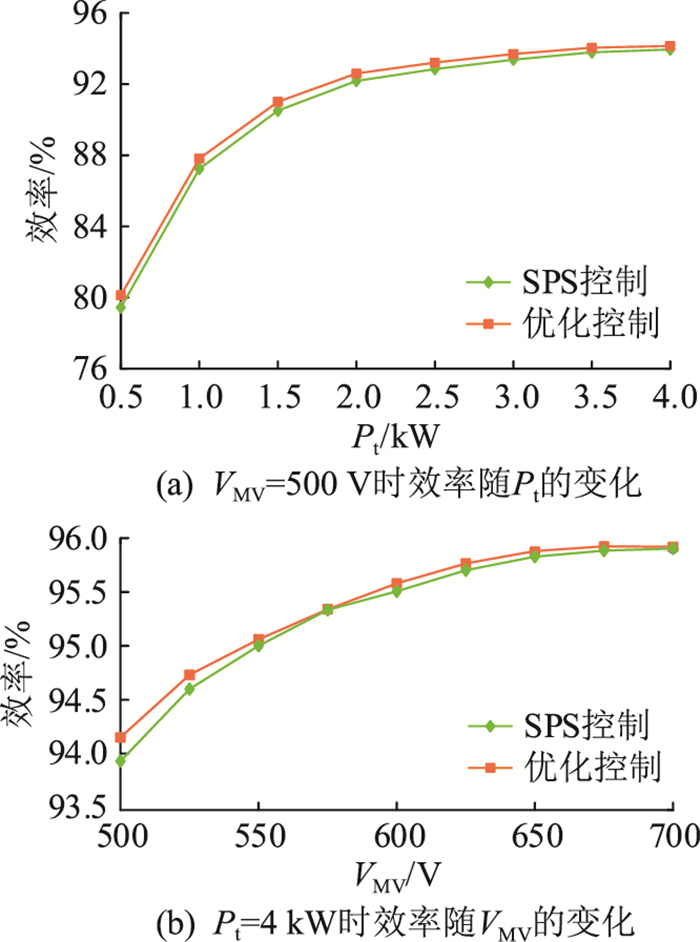
图 11(a)为VMV=500 V时应用优化控制前后实验样机的效率曲线。采用SPS控制且Pt=0.5 kW时,轻载下最低运行效率为79.45%,满载下最高运行效率为93.95%。在SPS控制的基础上对中压侧全桥移相优化后,通过降低子模块下管电流峰值及有效值,在整个功率区间内实现了效率提升。相较于SPS控制,串联开关换流移相控制在轻载情况下效果较为明显,Pt=0.5 kW时效率提升约0.7%,达到80.13%,满载情况下提升约0.2%,达到94.15%。
|
图 11 实验样机效率变化曲线 Fig. 11 Efficiency curves of the test prototype |
图 11(b)为功率满载状态时不同控制方式下实验样机效率关于VMV的变化曲线。仅采用SPS控制且VMV=500 V时最低效率为93.93%,VMV=700 V时达到最高效率95.90%。同时应用SPS控制和中压侧全桥移相控制时,相较于单独采用SPS控制,变换器传输效率得到进一步提升,VMV=500 V时的最低效率为94.15%,VMV=700 V时效率最高为95.92%。在VMV=575 V附近,由于传输电感电流ir过零点接近vAB零电平区间中点,中压侧全桥换流移相优化结果与基本控制相似;而当VM较高时,由于vAB零电平区间较短,换流移相角可调范围减小,因此两者效率接近。
综合上述数据,可知在SPS控制的基础上对中压侧全桥移相优化后,M2S2DCT样机的效率在整个功率、电压区间内均有一定的提升,体现了优化控制策略的有效性。
5 结语文中针对M2S2DCT在中压侧全桥换流时刻阀串支路电流出现尖峰的问题,提出一种基于中压侧全桥换流移相的阀串支路电流优化控制策略。通过调整中压侧全桥在尽可能接近零电流的时刻进行换流,减少了与其并联的阀串支路的电流突变,同时降低了阀串支路电流的峰值,降低了器件的电流应力及损耗。该策略使用基于中压侧电压和低压侧电压的计算方法,不依赖于功率控制环路,也不影响功率控制环路的运行。通过对中压侧全桥换流点的调整范围进行限制,保证了中压侧全桥的串联开关模块的零电压开关。该策略在M2S2DCT的多种运行状态下均能提升效率,且实现简单,对于设备安全运行和器件选型都有借鉴意义,具备进一步推广应用的潜力。
| [1] |
周孝信, 陈树勇, 鲁宗相, 等. 能源转型中我国新一代电力系统的技术特征[J]. 中国电机工程学报, 2018, 38(7): 1893-1904, 2205. ZHOU Xiaoxin, CHEN Shuyong, LU Zongxiang, et al. Technology features of the new generation power system in China[J]. Proceedings of the CSEE, 2018, 38(7): 1893-1904, 2205. (  1) 1) |
| [2] |
韩肖清, 李廷钧, 张东霞, 等. 双碳目标下的新型电力系统规划新问题及关键技术[J]. 高电压技术, 2021, 47(9): 3036-3046. HAN Xiaoqing, LI Tingjun, ZHANG Dongxia, et al. New issues and key technologies of new power system planning under double carbon goals[J]. High Voltage Engineering, 2021, 47(9): 3036-3046. (  0) 0) |
| [3] |
张勇军, 刘子文, 宋伟伟, 等. 直流配电系统的组网技术及其应用[J]. 电力系统自动化, 2019, 43(23): 39-49. ZHANG Yongjun, LIU Ziwen, SONG Weiwei, et al. Networking technology and its application of DC distribution system[J]. Automation of Electric Power Systems, 2019, 43(23): 39-49. (  0) 0) |
| [4] |
马钊, 焦在滨, 李蕊. 直流配电网络架构与关键技术[J]. 电网技术, 2017, 41(10): 3348-3357. MA Zhao, JIAO Zaibin, LI Rui. Network structures and key technologies of DC distribution systems[J]. Power System Technology, 2017, 41(10): 3348-3357. (  1) 1) |
| [5] |
孙贺, 张建成, 付超, 等. 直流固态变压器控制技术研究[J]. 电网技术, 2018, 42(1): 56-65. SUN He, ZHANG Jiancheng, FU Chao, et al. Research on control technology of DC solid state transformers[J]. Power System Technology, 2018, 42(1): 56-65. (  1) 1) |
| [6] |
李国胜, 向保林. 直流配网DC/DC变压器设计与调试[J]. 电气传动, 2021, 51(17): 28-33. LI Guosheng, XIANG Baolin. Design and test of DC/DC transformer in DC distribution network[J]. Electric Drive, 2021, 51(17): 28-33. (  1) 1) |
| [7] |
袁栋, 袁宇波, 贾勇勇, 等. 一种混合型输入串联输出并联直流变压器[J]. 电网技术, 2021, 45(1): 179-188. YUAN Dong, YUAN Yubo, JIA Yongyong, et al. An ISOP hybrid DC transformer[J]. Power System Technology, 2021, 45(1): 179-188. (  1) 1) |
| [8] |
PÁEZ J D, FREY D, MANEIRO J, et al. Overview of DC-DC converters dedicated to HVDC grids[J]. IEEE Transactions on Power Delivery, 2019, 34(1): 119-128. (  1) 1) |
| [9] |
涂春鸣, 管亮, 肖凡, 等. 双有源桥DC-DC变换器的模态分析方法[J]. 中国电机工程学报, 2019, 39(18): 5468-5479, 5595. TU Chunming, GUAN Liang, XIAO Fan, et al. Modal analysis method of dual active bridge DC-DC converter[J]. Proceedings of the CSEE, 2019, 39(18): 5468-5479, 5595. (  1) 1) |
| [10] |
WANG F F, ZHANG Z Y. Overview of silicon carbide technology: device, converter, system, and application[J]. CPSS Transactions on Power Electronics and Applications, 2016, 1(1): 13-32. (  1) 1) |
| [11] |
FLOURENTZOU N, AGELIDIS V G, DEMETRIADES G D. VSC-based HVDC power transmission systems: an overview[J]. IEEE Transactions on Power Electronics, 2009, 24(3): 592-602. (  1) 1) |
| [12] |
TRIPATHI A, MADHUSOODHANAN S, VECHALAPU K M K, et al. Enabling DC microgrids with direct MVDC interfacing dab converter based on 15 kV SiC IGBT and 15 kV SiC MOSFET[C]//IEEE Energy Conversion Congress and Exposition. Milwaukee, WI, USA. IEEE, 2016: 1-6.
(  0) 0) |
| [13] |
LU Z B, LI C M, ZHU A K, et al. Medium voltage soft-switching DC/DC converter with series-connected SiC MOSFETs[J]. IEEE Transactions on Power Electronics, 2021, 36(2): 1451-1462. (  0) 0) |
| [14] |
YAO J J, CHEN W, XUE C Y, et al. An ISOP hybrid DC transformer combining multiple SRCs and DAB converters to interconnect MVDC and LVDC distribution networks[J]. IEEE Transactions on Power Electronics, 2020, 35(11): 11442-11452. (  1) 1) |
| [15] |
苏麟, 朱鹏飞, 闫安心, 等. 苏州中压直流配电工程设计方案及仿真验证[J]. 中国电力, 2021, 54(1): 78-88. SU Lin, ZHU Pengfei, YAN Anxin, et al. Design scheme and simulation verification of Suzhou medium voltage DC distribution project[J]. Electric Power, 2021, 54(1): 78-88. (  1) 1) |
| [16] |
刘瑞煌, 杨景刚, 贾勇勇, 等. 中压直流配电网中直流变压器工程化应用[J]. 电力系统自动化, 2019, 43(23): 131-140. LIU Ruihuang, YANG Jinggang, JIA Yongyong, et al. Engineering applications of DC transformer in medium-voltage DC distribution network[J]. Automation of Electric Power Systems, 2019, 43(23): 131-140. (  1) 1) |
| [17] |
LIU J H, HUANG M, ZHANG X J, et al. Voltage balancing scheme based on active voltage cross control for series-connected IGBTs[C]//IEEE 9th International Power Electronics and Motion Control Conference. Nanjing, China. IEEE, 2020: 2588-2593.
(  1) 1) |
| [18] |
杨晓峰, 郑琼林, 薛尧, 等. 模块化多电平换流器的拓扑和工业应用综述[J]. 电网技术, 2016, 40(1): 1-10. YANG Xiaofeng, ZHENG Trillion Q, XUE Yao, et al. Review on topology and industry applications of modular multilevel converter[J]. Power System Technology, 2016, 40(1): 1-10. (  1) 1) |
| [19] |
随顺科, 任铁强, 邹强, 等. 连接风电系统的柔性直流电网MMC在线投入分析与验证[J]. 供用电, 2022, 39(11): 26-31. SUI Shunke, REN Tieqiang, ZOU Qiang, et al. Analysis and verification of MMC online entry into a flexible DC gridconnected to wind power system[J]. Distribution & Utilization, 2022, 39(11): 26-31. (  0) 0) |
| [20] |
熊盛涛, 刘振兴, 廖雪超. 基于电压电平的MMC直接功率预测控制策略[J]. 电力电容器与无功补偿, 2022, 43(4): 131-138. XIONG Shengtao, LIU Zhenxing, LIAO Xuechao. Direct power predictive control strategy of modular multilevel converter based on voltage level[J]. Power Capacitor & Reactive Power Compensation, 2022, 43(4): 131-138. (  1) 1) |
| [21] |
SHAO S, LI Y C, SHENG J, et al. A modular multilevel resonant DC-DC converter[J]. IEEE Transactions on Power Electronics, 2020, 35(8): 7921-7932. (  1) 1) |
| [22] |
KENZELMANN S, RUFER A, DUJIC D, et al. A versatile DC/DC converter based on modular multilevel converter for energy collection and distribution[C]//IET Conference on Renewable Power Generation (RPG 2011). Edinburgh, London. IET: 1-6.
(  1) 1) |
| [23] |
LI R G, CHEN W, SHAO S, et al. A novel hybrid DC transformer combining modular multilevel converter structure and series-connected semiconductor switches[J]. IEEE Transactions on Power Electronics, 2022, 37(5): 5699-5713. (  6) 6) |
 2023, Vol. 42
2023, Vol. 42



 朱旭豪(1998), 男, 硕士在读, 研究方向为直流变压器(E-mail:
朱旭豪(1998), 男, 硕士在读, 研究方向为直流变压器(E-mail: