文章编号: 2096-3203(2023)01-0143-11 中图分类号: TM715
当前电力系统正加快向清洁低碳转型[1],大量的风电和光伏等分布式电源(distributed generation, DG)接入配电网。风光出力由于受自然因素影响,具有波动性和不确定性,因此对配电网会产生功率供给不足[2]、消纳不完全[3]、网损增加[4]和电压越限[5]等问题。针对负荷需求及风光出力的波动性,进行配电网优化调度和灵活性资源调配方案研究,从而实现配电网运行经济性与灵活性,是当前亟须解决的问题。
随着电力电子技术的不断发展,具有配电网柔性互联功能的智能软开关(soft open point, SOP)[6-7]得到广泛关注。SOP可以实现线路间的柔性互联,灵活调节馈线间的有功功率。文献[8]在配电网分区边界引入SOP与直流充电装置结合的柔性互联装置,建立配电网多区域优化模型;文献[9]以最小化有源配电网运营成本为目标函数,建立多时间尺度的SOP及电动汽车联合优化调度模型。上述文献主要说明了在配电网中SOP实现经济调度的方法为提升SOP的利用率以及增强自身功能。文献[10]提出通过DC/DC换流器将储能系统连接至SOP直流环节的智能储能软开关(SOP integrated with energy storage system, ESOP)[11]拓扑,通过控制ESOP两端的换流器可以实现对储能系统充放电状态的控制。文献[12]将ESOP接入配电网以应对光伏发电的瞬态波动。文献[13]建立含ESOP的有源配电网时序优化模型,实现改善配电网电压水平及降低网损的功能。ESOP的投资建设成本较高,因此,在进行经济调度时要考虑ESOP的投资建设及运行成本。
随着配电网对灵活性需求的逐渐增加,针对配电网灵活性的研究正逐步开展,当前主要集中于对灵活性的定义及不同评价方法的指标选取[14-15];文献[16]从容量裕度和不可控DG适应率2个角度定义配电网灵活性指标体系,证明了储能及可中断负荷等灵活性资源对配电网灵活性提升的作用。但上述文献未研究配电网的灵活性资源如何参与优化调度,也未对灵活性资源规划建设与配电网运行的经济性进行平衡。
当前面向配电网的SOP规划已有较为广泛的研究。这些研究主要对配电网规划和配电网运行经济性进行综合考虑,文献[17]提出DG与SOP不平衡配电网协调优化规划方法;文献[18]考虑最优化ESOP的换流器与储能电池容量配置方案规划,以降低配电网的综合运行成本;文献[19]通过合理规划ESOP的建设容量有效减少网络损耗,提高配电网运行经济性。但随着配电网的灵活性需求不断增加,当前研究在进行含SOP的配电网规划时未考虑灵活性资源和运行灵活性。
针对上述问题,文中首先对ESOP的原理和数学模型进行了阐述。其次,对配电网灵活性和经济性进行分析,在考虑可控DG、储能系统、可控负荷和ESOP等灵活性资源的基础上,提出了配电网节点和网架灵活性评价指标;同时考虑配电网运行成本及ESOP规划建设成本,从而建立了以配电网运行经济性和灵活性为目标函数,以配电网潮流约束、灵活性资源调度和ESOP运行规划约束为约束条件的优化调度模型。最后,将模型转化为二阶锥规划模型进行求解,通过算例计算和对比验证了ESOP的规划建设方案及其对实现配电网经济灵活运行的有效性。
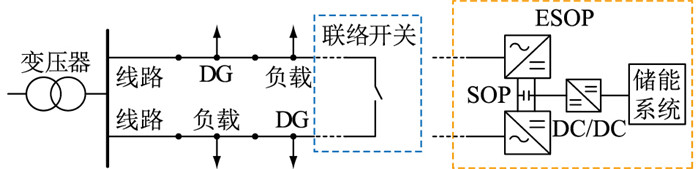
1 ESOP原理及模型 1.1 ESOP工作原理将ESOP代替线路间的联络开关接入配电网。ESOP在配电网正常运行时作为互联装置,故障时发挥联络开关的作用,其接入方式如图 1所示。
|
图 1 ESOP接入配电网示意 Fig. 1 Schematic diagram of ESOP access to distribution network |
图 1中的SOP是基于背靠背型电压源换流器(voltage source converter, VSC)的开关,因此SOP的控制模式主要由VSC的控制模式决定,在配电网中主要采用PQ-VQ下垂控制对配电网潮流进行控制。在进行配电网优化时,一般设定VSC直流端口电压为定值,因此将注入VSC端口的有功功率和无功功率作为优化变量,同时考虑有功功率在VSC中的功率损耗,采用损耗系数进行损耗计算。而2个VSC通过直流环节进行连接,因此在AC-DC-AC变换环节没有无功功率的损耗。
由于SOP内存在直流环节,因此储能系统通过DC/DC变换器即可与SOP相连。在SOP设备间增加储能系统后,可以控制储能单元处于充放电状态,将向储能单元充电和放电的有功功率作为优化变量,实现配电网的优化运行。
1.2 ESOP稳态数学模型 1.2.1 ESOP储能系统数学模型| $ s_{\mathrm{ESS}, n, t}^{\mathrm{e}}+s_{\mathrm{ESS}, n, t}^{\mathrm{d}} \leqslant 1 $ | (1) |
| $ \left\{\begin{array}{l} 0 \leqslant P_{\mathrm{ESS}, n, t}^{\mathrm{c}} \leqslant s_{\mathrm{ESS}, n, t}^{\mathrm{c}} S_{\mathrm{ESOP}, n, \mathrm{DCDC}} \\ 0 \leqslant P_{\mathrm{ESS}, n, t}^{\mathrm{d}} \leqslant s_{\mathrm{ESS}, n, t}^{\mathrm{d}} S_{\mathrm{ESOP}, n, \mathrm{DCDC}} \end{array}\right. $ | (2) |
| $ \begin{gathered} P_{\mathrm{ESS}, n, t}^{\mathrm{loss}}=P_{\mathrm{ESS}, n, t}^{\mathrm{c}}-A_{\mathrm{ESS}} P_{\mathrm{ESS}, n, t}^{\mathrm{c}}- \\ P_{\mathrm{ESS}, n, t}^{\mathrm{d}}+P_{\mathrm{ESS}, n, t}^{\mathrm{d}} / A_{\mathrm{ESS}} \end{gathered} $ | (3) |
| $ E_{\mathrm{ESS}, n, t+1}=E_{\mathrm{ESS}, n, t}+A_{\mathrm{ESS}} P_{\mathrm{ESS}, n, t}^{\mathrm{c}}-P_{\mathrm{ESS}, n, t}^{\mathrm{d}} / A_{\mathrm{ESS}} $ | (4) |
| $ 0 \leqslant E_{\mathrm{ESS}, n, t} \leqslant S_{\mathrm{ESOP}, n, \mathrm{ESS}} $ | (5) |
| $ E_{\mathrm{ESS}, n, t=1}=E_{\mathrm{ESS}, n, t=T} $ | (6) |
式中:
在上述模型中,式(1)表示储能系统在一个时段仅可以处于一个充放电状态;式(2)为储能系统通过DC/DC变换器向SOP输入和输出功率的容量约束;式(3)为储能系统有功功率损耗模型;式(4)为储能系统实时电荷量和储能充放电功率的关系;式(5)为储能系统电荷量上下限约束;式(6)为储能装置在一个调度周期内将能量释放完成的等式约束。
1.2.2 SOP数学模型| $ \begin{gathered} P_{\mathrm{SOP}, n, i, t}+P_{\mathrm{SOP}, n, j, t}+P_{\mathrm{SOP}, n, i, t}^{\mathrm{loss}}+ \\ P_{\mathrm{SOP}, n, j, t}^{\mathrm{loss}}=P_{\mathrm{ESS}, n, t}^{\mathrm{c}}-P_{\mathrm{ESS}, n, t}^{\mathrm{d}}-P_{\mathrm{ESS}, n, t}^{\mathrm{loss}} \end{gathered} $ | (7) |
| $ \left\{\begin{array}{l} P_{\mathrm{SOP}, n, i, t}^{\text {loss }}=A_{\mathrm{SOP}, i} \sqrt{P_{\mathrm{SOP}, n, i, t}^2+Q_{\mathrm{SOP}, n, i, t}^2} \\ P_{\mathrm{SOP}, n, j, t}^{\text {loss }}=A_{\mathrm{SOP}, j} \sqrt{P_{\mathrm{SOP}, n, j, t}^2+Q_{\mathrm{SOP}, n, j, t}^2} \end{array}\right. $ | (8) |
| $ \left\{\begin{array}{l} Q_{\mathrm{SOP}, i, \text { min }} \leqslant Q_{\mathrm{sop}, n, i, t} \leqslant Q_{\mathrm{sop}, i, \max } \\ Q_{\mathrm{SOP}, j, \text { min }} \leqslant Q_{\mathrm{SOP}, n, j, t} \leqslant Q_{\mathrm{SOP}, j, \text { max }} \end{array}\right. $ | (9) |
| $ \left\{\begin{array}{l} \sqrt{P_{\mathrm{SOP}, n, i, t}^2+Q_{\mathrm{SOP}, n, i, t}^2} \leqslant S_{\mathrm{SOP}, n, \mathrm{C}} \\ \sqrt{P_{\mathrm{SOP}, n, j, t}^2+Q_{\mathrm{SOP}, n, j, t}^2} \leqslant S_{\mathrm{SOP}, n, \mathrm{C}} \end{array}\right. $ | (10) |
| $ P_{\mathrm{ESOP}, n, t}^{\text {loss }}=P_{\mathrm{ESS}, n, t}^{\text {loss }}+P_{\mathrm{SOP}, n, i, t}^{\text {loss }}+P_{\mathrm{SOP}, n, j, t}^{\text {loss }} $ | (11) |
式中:
式(7)为ESOP的功率平衡约束,表示从换流器两侧节点流入的有功功率及线路上的损耗之和为流出储能装置的有功功率;式(8)为SOP的有功功率损耗计算公式;式(9)为SOP的无功出力上下限约束;式(10)为SOP的容量约束;式(11)为ESOP的总损耗。
2 配电网灵活性分析及评价指标建立配电网灵活性指在一定调度周期内,配电网通过调配灵活性资源以应对负荷波动和电源波动不确定性,实现配电网的功率平衡,并且要考虑灵活性资源调控的经济性,从而实现兼顾配电网灵活性与经济性的最优运行状态。
2.1 配电网灵活性资源配电网的灵活性资源可分为节点型和网架型。节点灵活性资源主要为连接在配电网节点处的可控DG、储能系统和可控负荷,通过发挥节点灵活性资源的功率调节能力,如功率调整裕度和爬坡功率等向配电网提供灵活性。网架灵活性资源主要包括配电网的网架结构及互联装置,传统的互联装置主要为隔离开关。
随着以SOP为代表的柔性互联装置的应用,配电网通过互联装置可实现传输功率的灵活调节以及形成优化网架结构的功率传输通道。因此,为满足配电网的灵活性需求,应充分发挥节点灵活性资源的功率调节能力,并与网架灵活性资源的功率传输能力相配合。
2.2 配电网灵活性评价指标文中针对不同类型灵活性资源的调节能力和手段,提出净负荷调节量和支路负荷裕度2个评价指标,以此对节点和网架灵活性资源共同配合、实现配电网灵活运行进行评价。
2.2.1 节点灵活性资源调节特性及评价节点灵活性资源中的可控DG通过增加或减少出力提供向上或向下灵活性调节能力,储能系统通过控制电池充放电量提供向上或向下灵活性调节能力,可控负荷通过增加或减少出力提供向上或向下灵活性调节能力。上述节点灵活性资源的调节能力量化计算如式(12)—式(14)所示。
| $ \left\{\begin{array}{l} F_{\mathrm{CDG}, i, t}^{\mathrm{up}}=\min \left\{P_{\mathrm{CDG}, i, \max }-P_{\mathrm{CDG}, i, t}, R_{\mathrm{CDG}, i}^{\mathrm{up}}\right\} \\ F_{\mathrm{CDG}, i, t}^{\mathrm{down}}=\min \left\{P_{\mathrm{CDG}, i, t}-P_{\mathrm{CDG}, i, \min }, R_{\mathrm{CDG}, i}^{\mathrm{down}}\right\} \end{array}\right. $ | (12) |
| $ \left\{\begin{array}{l} F_{\mathrm{ESS}, i, t}^{\mathrm{up}}=s_{\mathrm{ESS}, i, t}^{\mathrm{d}}\left(P_{\mathrm{ESS}, i, t, \text { max }}^{\mathrm{d}}-P_{\mathrm{ESS}, i, t}^{\mathrm{d}}\right) \\ F_{\mathrm{ESS}, i, t}^{\mathrm{down}}=s_{\mathrm{ESS}, i, t}^{\mathrm{c}}\left(P_{\mathrm{ESS}, i, t, \text { max }}^{\mathrm{c}}-P_{\mathrm{ESS}, i, t}^{\mathrm{c}}\right) \end{array}\right. $ | (13) |
| $ \left\{\begin{array}{l} F_{\mathrm{CL}, i, t}^{\mathrm{up}}=s_{\mathrm{CL}, i, t}^{\mathrm{up}}\left(P_{\mathrm{CL}, i, t, \max }^{\mathrm{up}}-P_{\mathrm{CL}, i, t}^{\mathrm{up}}\right) \\ F_{\mathrm{CL}, i, t}^{\text {down }}=s_{\mathrm{CL}, i, t}^{\text {down }}\left(P_{\mathrm{CL}, i, t, t, \max }^{\text {down }}-P_{\mathrm{CL}, i, t}^{\mathrm{down}}\right) \end{array}\right. $ | (14) |
式中:
配电网的节点灵活性资源主要用来应对净负荷功率波动的不确定性对配电网的影响。净负荷功率定义为配电网负荷功率减去不可控DG出力后的配电网实际功率需求。为展现灵活性资源对净负荷波动的调节能力,文中提出净负荷调节量指标,即为节点灵活性资源调节能力与净负荷波动量的比值,计算公式如下:
| $ F_{\mathrm{LA}}=\frac{1}{T} \sum\limits_{t=1}^T \frac{s_t F_t^{\mathrm{up}}-\left(1-s_t\right) F_t^{\mathrm{down}}}{P_{\mathrm{NL}, t+1}-P_{\mathrm{NL}, t}} $ | (15) |
| $ {P_{{\text{NL}}, t}} = \sum\limits_{i \in \mathit{\Omega }} {\left( {{P_{{\text{L}}, i, t}} - P_{{\text{PV}}, i, t}^{{\text{pre}}} - P_{{\text{WT}}, i, t}^{{\text{pre}}}} \right)} $ | (16) |
| $ \left\{ {\begin{array}{*{20}{l}} {F_t^{{\text{up}}} = \sum\limits_{i \in {\mathit{\Omega }_{{\text{CDG}}}}} {F_{{\text{CDG}}, i, t}^{{\text{up}}}} + \sum\limits_{i \in {\mathit{\Omega }_{{\text{ESS}}}}} {F_{{\text{ESS}}, i, t}^{{\text{up}}}} + \sum\limits_{i \in {\mathit{\Omega }_{{\text{CL}}}}} {F_{{\text{CL}}, i, t}^{{\text{up}}}} } \\ {F_t^{{\text{down}}} = \sum\limits_{i \in {\mathit{\Omega }_{{\text{CDG}}}}} {F_{{\text{CDG}}, i, t}^{{\text{down}}}} + \sum\limits_{i \in {\mathit{\Omega }_{{\text{ESS}}}}} {F_{{\text{ESS}}, i, t}^{{\text{down}}}} + \sum\limits_{i \in {\mathit{\Omega }_{{\text{CL}}}}} {F_{{\text{CL}}, i, t}^{{\text{down}}}} } \end{array}} \right. $ | (17) |
式中:FLA为净负荷调节量;st为净负荷功率增加标志,为0-1变量;
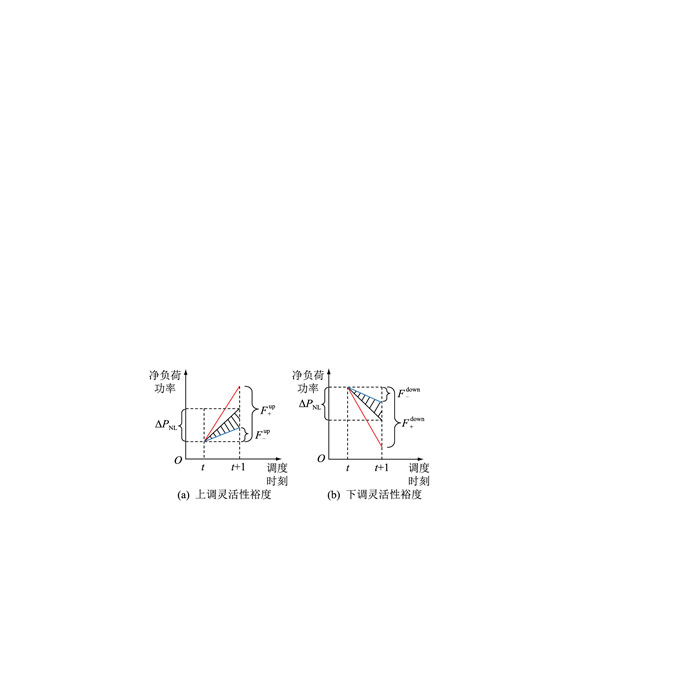
图 2为在一个调度时刻内净负荷功率曲线的变化,图 2(a)、图 2(b)分别展现净负荷功率增加和减少时节点灵活性资源的上调和下调灵活性能力。当节点灵活性资源充足时为红色实线,图中大括号所示的F+up和F+down为灵活性资源充足时的上调和下调灵活性裕度,其灵活性裕度足以应对净负荷功率变化;当节点灵活性资源不足时为蓝色实线,图中小括号所示的F-up和F-down为灵活性资源不足时的上调和下调灵活性裕度。此时阴影部分为灵活性裕度不足时产生的弃风弃光或负荷投切功率变化。净负荷调节量用以量化图中各调度时刻的上调和下调灵活性裕度与净负荷波动量ΔPNL的比值,以展现灵活性资源对净负荷波动的调节能力。
|
图 2 节点灵活性资源裕度分析 Fig. 2 Node flexibility resource margin analysis |
当前研究对于网架灵活性的评价主要定义为支路电流或功率与支路最大允许电流或功率的百分比[16],并采用平均值计算整个配电网的负荷裕度[20]。针对配电网线路网架结构及柔性互联装置2种网架灵活性资源,文中提出将支路负荷裕度分为普通支路的负荷裕度以及含SOP支路的负荷裕度,作为配电网网架灵活性的评价指标。定义普通支路的负荷裕度为支路最大允许通过电流与当前电流的差值除以前者,含SOP支路的负荷裕度为SOP允许传输的最大功率与当前端口传输功率的差值除以前者,这体现了输电线路及柔性互联装置传输功率的能力,计算公式如式(18)—式(20)所示。
| $ F_{\mathrm{LM}}=\frac{1}{T} \times \frac{1}{L+N} \sum\limits_{t=1}^T\left(F_{\mathrm{LM}, t}+F_{\mathrm{LMSOP}, t}\right) $ | (18) |
| $ F_{\mathrm{LM}, t}=\sum\limits_{i j \in L} \frac{I_{i j, \max }-I_{i j, t}}{I_{i j, \max }} $ | (19) |
| $ {F_{{\text{LMSOP}}, t}} = \sum\limits_{n \in {\mathit{\Omega }_{{\text{ESOP}}}}} {\frac{{2{P_{{\text{SOP}}, \max }} - {P_{{\text{SOP}}, n, i, t}} - {P_{{\text{SOP}}, n, j, t}}}}{{{P_{{\text{SOP}}, \max }}}}} $ | (20) |
式中:FLM为支路负荷裕度;L为配电网支路集合;N为SOP个数;
当普通支路负荷裕度
配电网灵活性资源参与调度优化运行,可以极大提升配电网运行的经济性与灵活性。基于2.2节提出的配电网节点和网架灵活性评价指标,文中结合配电网的运行经济性设计ESOP的投资建设规划,同时考虑灵活性资源以及ESOP对配电网运行灵活性的影响。由于所提节点和网架灵活性指标属于短时间尺度的运行指标,因此文中考虑了年规划问题中风光出力和负荷大小的季节性波动。通过选取风光和负荷出力的四季典型场景,并结合各场景出现的概率,转化为年时间尺度规划方案的灵活性资源裕度评价指标。文中构建了最小化配电网年运行经济性和最大化灵活性资源调节裕度的目标函数。
3.1 目标函数目标函数同时考虑配电网年运行经济性以及灵活性2个目标,因此针对多目标优化问题通过设置权重系数并将灵活性资源调节裕度转化为经济性收益,从而转化为单目标优化问题进行求解,计算公式如式(21)—式(24)所示。
| $ \min C=\lambda_1 C_{\text {eco }}-\lambda_2 C_{\text {fle }} $ | (21) |
| $ \begin{gathered} C_{\text {eco }}=\sum\limits_{h=1}^{N_h} D_h\left\{3 6 5 \sum\limits _ { t = 1 } ^ { T } \left[c_{\mathrm{p}, t} P_{\mathrm{g}, i, t}+\sum\limits_{i \in \mathit{\Omega}_{\mathrm{CDG}}} c_{\mathrm{CDG}} P_{\mathrm{CDG}, i, t}+\right.\right. \\ \left(\sum\limits_{i j \in L} r_{i j} I_{i j, t}^2+\sum\limits_{n \in \mathit{\Omega}_{\mathrm{FSOP}}} P_{\mathrm{ESOP}, n, t}^{\mathrm{loss}}\right) c_{\mathrm{p}, t}+\sum\limits_{i \in \mathit{\Omega}_{\mathrm{FSS}}} c_{\mathrm{ESS}} P_{\mathrm{ESS}, i, t}+ \\ \sum\limits_{i \in \mathit{\Omega}_{\mathrm{PV}}} c_{\mathrm{PV}}\left(P_{\mathrm{PV}, i, t}^{\mathrm{pre}}-P_{\mathrm{PV}, i, t}\right)+\sum\limits_{i \in \mathit{\Omega}_{\mathrm{WT}}} c_{\mathrm{WT}}\left(P_{\mathrm{WT}, i, t}^{\mathrm{pre}}-P_{\mathrm{WT}, i, t}\right)+ \\ \left.\left.\sum\limits_{i \in \mathit{\Omega}_{\mathrm{CL}}} c_{\mathrm{CL}} P_{\mathrm{CL}, i, t}\right]+C_{\mathrm{ESOP}}\right\} \end{gathered} $ | (22) |
| $ \begin{gathered} C_{\mathrm{ESOP}}=\left[\frac{d(1+d)^y}{(1+d)^y-1}+\eta_{\mathrm{ESOP}}\right] \times \\ \sum\limits_{i \in \Omega_{\mathrm{SOP}}}\left(2 c_{\mathrm{SOP}, \mathrm{C}} S_{\mathrm{SOP}, i, \mathrm{C}}+c_{\mathrm{SOP}, \mathrm{CELL}} S_{\mathrm{ESOP}, i, \mathrm{CELL}}+\right. \\ \left.c_{\mathrm{SOP}, \mathrm{DCDC}} S_{\mathrm{ESOP}, i, \mathrm{DCDC}}\right) \end{gathered} $ | (23) |
| $ C_{\mathrm{fle}}=365 \sum\limits_{h=1}^{N_h} D_h\left(F_{\mathrm{LA}}+F_{\mathrm{LM}}\right) c_{\mathrm{fle}} $ | (24) |
式中:C为目标函数年综合成本;λ1、λ2分别为经济性和灵活性权重系数;Ceco、Cfle分别为经济性和灵活性评价指标;Nh为场景个数;Dh为第h个场景发生概率;
配电网Distflow潮流约束的标准形式参见文献[21],由于其为非线性潮流约束,为快速求解,采用二阶锥松弛转化将支路电流和节点电压幅值的平方设为变量,则可将潮流约束线性化。转化后的有功功率平衡约束如式(25)和式(26)所示,无功功率平衡约束表示形式和有功功率相同,其余配电网潮流及安全约束参见文献[9]。
| $ P_{i j, t}-\tilde{I}_{i j, t}^2 r_{i j}-\sum\limits_{k \in \omega_j} P_{j k, t}=P_{i, t} $ | (25) |
| $ \begin{gathered} P_{i, t}=P_{\mathrm{g}, i, t}-P_{\mathrm{L}, i, t}+P_{\mathrm{PV}, i, t}+P_{\mathrm{WT}, i, t}+P_{\mathrm{CDG}, i, t}+ \\ P_{\mathrm{ESS}, i, t}^{\mathrm{d}}-P_{\mathrm{ESS}, i, t}^{\mathrm{c}}+P_{\mathrm{CL}, i, t}^{\mathrm{down}}-P_{\mathrm{CL}, i, t}^{\mathrm{up}}+P_{\mathrm{SOP}, n, i, t} \end{gathered} $ | (26) |
式中:Pij, t为t时刻ij支路上传输的有功功率;
风电和光伏出力不可控,因此无法作为灵活性资源,其出力约束为:
| $ \left\{\begin{array}{l} 0 \leqslant P_{\mathrm{PV}, i, t} \leqslant P_{\mathrm{PV}, i, t}^{\mathrm{pre}} \\ Q_{\mathrm{PV}, i, t}=P_{\mathrm{PV}, i, t} \tan \varphi_{\mathrm{PV}} \\ 0 \leqslant P_{\mathrm{WT}, i, t} \leqslant P_{\mathrm{WT}, i, t}^{\mathrm{pre}} \\ Q_{\mathrm{WT}, i, t}=P_{\mathrm{WT}, i, t} \tan \varphi_{\mathrm{WT}} \end{array}\right. $ | (27) |
式中:
(1) 可控DG。
| $ \left\{\begin{array}{l} -R_{\mathrm{CDG}, i}^{\mathrm{down}} \leqslant P_{\mathrm{CDG}, i, t}-P_{\mathrm{CDG}, i, t-1} \leqslant R_{\mathrm{CDG}, i}^{\mathrm{up}} \\ P_{\mathrm{CDG}, i, \min } \leqslant P_{\mathrm{CDG}, i, t} \leqslant P_{\mathrm{CDG}, i, \max } \\ Q_{\mathrm{CDG}, i, \min } \leqslant Q_{\mathrm{CDG}, i, t} \leqslant Q_{\mathrm{CDG}, i, \max } \end{array}\right. $ | (28) |
式中:
(2) 储能系统。
| $ \left\{\begin{array}{l} s_{\mathrm{ESS}, i, t}^{\mathrm{d}}+s_{\mathrm{ESS}, i, t}^{\mathrm{c}} \leqslant 1 \\ s_{\mathrm{ESS}, i, t}^{\mathrm{d}} P_{\mathrm{ESS}, i, t, \min }^{\mathrm{d}} \leqslant P_{\mathrm{ESS}, i, t}^{\mathrm{d}} \leqslant s_{\mathrm{ESS}, i, t}^{\mathrm{d}} P_{\mathrm{ESS}, i, t, \max }^{\mathrm{d}} \\ s_{\mathrm{ESS}, i, t}^{\mathrm{c}} P_{\mathrm{ESS}, i, t, \text { min }}^{\mathrm{c}} \leqslant P_{\mathrm{ESS}, i, t}^{\mathrm{c}} \leqslant s_{\mathrm{ESS}, i, t}^{\mathrm{c}} P_{\mathrm{ESS}, i, t, \max }^{\mathrm{c}} \\ P_{\mathrm{ESS}, i, t}=P_{\mathrm{ESS}, i, t}^{\mathrm{d}}+P_{\mathrm{ESS}, i, t}^{\mathrm{c}} \\ E_{\mathrm{ESS}, i, t+1}=E_{\mathrm{ESS}, i, t}+\eta_i^{\mathrm{c}} P_{\mathrm{ESS}, i, t}^{\mathrm{c}}-\eta_i^{\mathrm{d}} P_{\mathrm{ESS}, i, t}^{\mathrm{d}} \\ E_{\mathrm{ESS}, i, t, \min } \leqslant E_{\mathrm{ESS}, i, t} \leqslant E_{\mathrm{ESS}, i, t, \max } \end{array}\right. $ | (29) |
式中:
(3) 可控负荷。
| $ \left\{\begin{array}{l} s_{\mathrm{CL}, i, t}^{\text {up }}+s_{\mathrm{CL}, i, t}^{\text {down }} \leqslant 1 \\ s_{\mathrm{CL}, i, t}^{\text {up }} P_{\mathrm{CL}, i, t, \min }^{\text {up }} \leqslant P_{\mathrm{CL}, i, t}^{\text {up }} \leqslant s_{\mathrm{CL}, i, t}^{\text {up }} P_{\mathrm{CL}, i, t, \max }^{\text {up }} \\ s_{\mathrm{CL}, i, t}^{\text {down }} P_{\mathrm{CL}, i, t, \min }^{\text {down }} \leqslant P_{\mathrm{CL}, i, t}^{\text {down }} \leqslant s_{\mathrm{CL}, i, t}^{\text {down }} P_{\mathrm{CL}, i, t, \max }^{\text {down }} \\ P_{\mathrm{CL}, i, t}=P_{\mathrm{CL}, i, t}^{\text {up }}+P_{\mathrm{CL}, i, t}^{\text {down }} \\ Q_{\mathrm{CL}, i, t}=P_{\mathrm{CL}, i, t} Q_{\mathrm{L}, i, t} / P_{\mathrm{L}, i, t} \\ -S_{i, \max }^{\text {down }} \leqslant \sum\limits_{t=1}^T\left(P_{\mathrm{CL}, i, t}^{\text {up }}-P_{\mathrm{CL}, i, t}^{\text {down }}\right) \leqslant S_{i, \max }^{\text {up }} \end{array}\right. $ | (30) |
式中:
ESOP的约束包括背靠背型VSC和储能系统的运行约束条件,如式(1)—式(11)所示。式(8)和式(10)的二阶锥松弛形式为:
| $ \left\{\begin{array}{l} P_{\mathrm{SOP}, n, i, t}^2+Q_{\mathrm{SOP}, n, i, t}^2 \leqslant 2 \frac{P_{\mathrm{SoP}, n, i, t}^{\text {loss }}}{\sqrt{2} A_{\mathrm{SOP}, i}} \times \frac{P_{\mathrm{SOP}, n, i, t}^{\text {loss }}}{\sqrt{2} A_{\mathrm{SOP}, i}} \\ P_{\mathrm{SOP}, n, j, t}^2+Q_{\mathrm{SOP}, n, j, t}^2 \leqslant 2 \frac{P_{\mathrm{SOP}, n, j, t}^{\text {loss }}}{\sqrt{2} A_{\mathrm{SOP}, j}} \times \frac{P_{\mathrm{SOP}, n, j, t}^{\text {loss }}}{\sqrt{2} A_{\mathrm{SOP}, j}} \end{array}\right. $ | (31) |
| $ \left\{\begin{array}{l} P_{\mathrm{SOP}, n, i, t}^2+Q_{\mathrm{SOP}, n, i, t}^2 \leqslant 2 \frac{S_{\mathrm{SOP}, n, \mathrm{C}}}{\sqrt{2}} \times \frac{S_{\mathrm{SOP}, n, \mathrm{C}}}{\sqrt{2}} \\ P_{\mathrm{SOP}, n, j, t}^2+Q_{\mathrm{SOP}, n, j, t}^2 \leqslant 2 \frac{S_{\mathrm{SOP}, n, \mathrm{C}}}{\sqrt{2}} \times \frac{S_{\mathrm{SOP}, n, \mathrm{C}}}{\sqrt{2}} \end{array}\right. $ | (32) |
ESOP规划约束如式(33)所示。
| $ \left\{\begin{array}{l} S_{\mathrm{SOP}, n, \mathrm{C}}=m_{\mathrm{SOP}, n, \mathrm{C}} s_{\mathrm{SOP}, n, \mathrm{C}} \\ S_{\mathrm{ESOP}, n, \mathrm{DCDC}}=m_{\mathrm{ESOP}, n, \mathrm{DCDC}} s_{\mathrm{ESOP}, n, \mathrm{DCDC}} \\ S_{\mathrm{ESOP}, n, \mathrm{CELL}}=m_{\mathrm{ESOP}, n, \mathrm{CELL}} s_{\mathrm{ESOP}, n, \mathrm{CELL}} \end{array}\right. $ | (33) |
式中:
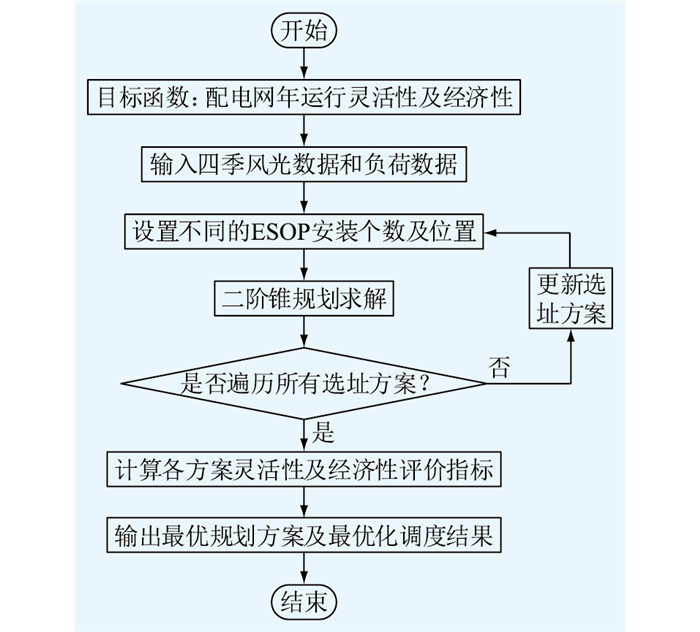
基于以上规划模型,文中提出的ESOP规划建设及运行方法的计算流程如图 3所示。以配电网年运行灵活经济性为目标函数,将年规划分为4个季度的日风光出力及负荷数据作为原始数据输入,并遍历不同ESOP安装个数下的选址方案,通过二阶锥规划方法求解各ESOP规划方案中的最优解,最后计算各方案灵活性及经济性评价指标,输出ESOP的最优规划方案及考虑配电网经济灵活运行的四季场景日内最优化调度结果。
|
图 3 算法流程 Fig. 3 Algorithm flow chart |
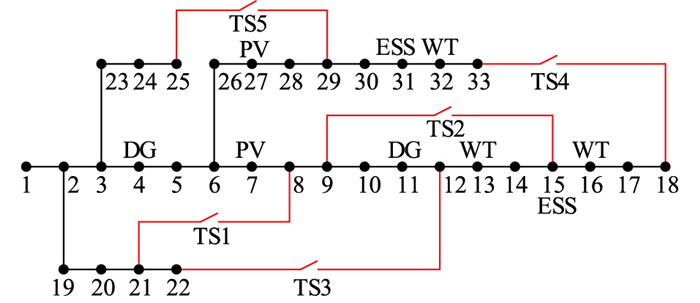
文中采用改进的IEEE 33节点配电网系统进行算例验证,系统拓扑如图 4所示,其中WT为风力发电机;PV为光伏电站;ESS为储能系统。配电网系统包含32条闭合支路以及5条联络开关(TS1—TS5)接入的常开支路,电压等级为12.66 kV,基准功率为100 MV ·A。系统有功功率负荷为3 715 kW,无功功率负荷为2 300 kvar,具体节点和支路数据参见文献[22]。为在保证配电网规划运行经济性的前提下合理考虑配电网灵活性,文中根据文献[17]的层次分析方法设置经济性和灵活性权重系数λ1和λ2分别为0.833和0.167。当配电网存在灵活性需求时,若灵活性资源有足够的调节裕度,则可向配电网出售,从而获得灵活性资源调节裕度收益,综合各灵活性资源的运行成本[23]。文中设置灵活性资源调节收益系数cfle为0.5元/(kW ·h),其余经济性成本系数参见文献[24],ESOP投资建设及维护成本参见文献[18],可控负荷分类及配置参见文献[20]。
|
图 4 改进的IEEE 33节点配电网拓扑 Fig. 4 Modified IEEE 33-bus distribution network topology |
为契合当前实际配电网的多DG接入的特点,在13、16、32节点接入风力发电机,在7、27节点接入光伏电站,在4、11节点接入可控DG,在15、31节点接入储能系统,其容量和配置如表 1所示,设定所有的DG均在额定功率因数0.9下运行。
|
|
表 1 DG及储能配置参数 Table 1 Configuration parameters of DG and energy storage |
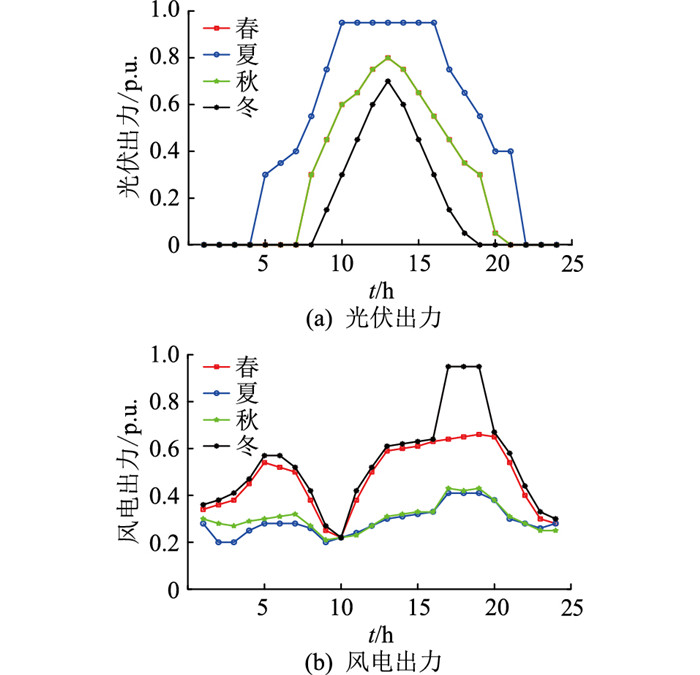
文中针对的是ESOP投资建设的规划问题,因此涉及ESOP的使用年限等问题。由于风光出力及负荷在年规划问题中有季节性的特性,文中选取场景个数为4,以此表示四季出力的不同场景,每个场景概率为0.25。文中在夏冬季节的负荷数据比春秋季节高10%,风光出力季节性波动曲线[25]如图 5所示。
|
图 5 风光四季出力曲线 Fig. 5 Wind and photovoltaic power output curves in four seasons |
考虑到将ESOP接入到配电网时,不能过多地影响配电网的正常运行,因此将5条联络开关支路作为ESOP的待选安装位置,并合理设计其安装容量。设置不同的ESOP个数选址方案,在年运行优化中考虑不同季节的风光出力及负荷功率波动,得到的优化结果如表 2所示。
|
|
表 2 不同ESOP个数规划结果 Table 2 Planning results with different number of ESOP |
由于ESOP的安装位置对配电网的运行灵活性和经济性有影响,而不同个数的ESOP有不同的安装组合,通过文中算法可以计算出在不同ESOP个数情况下最优的安装位置。由表 2可知,当安装3个ESOP时目标函数年综合成本最小,为962.44万元。其中ESOP安装个数为1~3时,配电网年灵活性资源调节裕度收益随之增加,在安装个数为3时达到最大。由于ESOP的年建设及维护成本的提高,使得在安装2个及以上ESOP时的配电网年运行成本相比于安装1个时的有所上升。安装个数为2~4时,配电网的年运行成本随着多ESOP发挥作用而降低。综上可得,最优规划方案为分别在TS2、TS4和TS5位置处安装ESOP。
4.2 配电网接入ESOP规划经济性及灵活性对比分析为对比文中所提ESOP接入配电网对提升配电网运行经济性和灵活性的有效性,采用上述含DG并网的IEEE 33节点配电网测试算例进行计算,并采用如下3种规划方案进行对比。
方案1:未考虑接入SOP,只对原有配电网进行运行优化;
方案2:采用普通型SOP进行选址定容规划及运行优化;
方案3:采用文中所提的ESOP进行选址定容规划及运行优化。
规划建设方案如表 3所示。
|
|
表 3 方案2和3规划结果 Table 3 Planning results in case 2 and 3 |
由表 3可知,方案2为安装普通型SOP的规划建设方案,主要在TS1、TS4和TS5处安装SOP,最佳安装个数为3个;方案3为安装ESOP的规划建设方案,在TS2、TS4和TS5处安装ESOP,其中SOP安装的容量应配合支路功率传输大小及通过DC/DC变换器向储能系统输出功率的大小。因此相较于安装普通型SOP,ESOP中的SOP的容量更大,要达到500 kV ·A。
表 4为3种方案的经济性对比结果。由表 4可知,方案2和方案3通过在配电网中安装SOP和ESOP,均降低了配电网的年运行成本。方案2的配电网年运行成本相较于原配电网减少了10.61万元,其中可控负荷成本降低了9.14万元,年网损成本降低了0.78万元,说明在安装SOP后能通过合理的功率传输有效减少对负荷用户的功率调节及远距离的功率传输;弃风和弃光成本分别降低了1.63万元和3.09万元,大幅降低了弃风和弃光量,提高了风光出力的消纳。比较方案1与方案3可知,安装ESOP后配电网年运行成本减少了95.75万元。其中ESOP通过优化功率传输路径及发挥自身储能系统的优势降低了储能系统运行成本和可控负荷成本,分别降低了35.87万元和76.46万元;同时也发挥了ESOP的降损能力及风光消纳能力,分别降低了2.68万元和4.53万元弃风、弃光惩罚成本,减少主网购电成本16.5万元,进而降低从主网输入的功率在配电网的损耗成本1.88万元。由上述方案对比可知,配电网安装ESOP相较于安装SOP有更好的经济性。方案2和3通过减少的运行成本即可达到SOP或ESOP年投资运行的成本边界,并能通过灵活性裕度实现收益。因此,当减少的配电网年运行成本和增加的灵活性裕度收益大于ESOP的年投资运行成本时,配电网安装ESOP具有更好的经济性。
|
|
表 4 经济性对比 Table 4 Economy comparison |
表 5为3种方案的灵活性对比结果。通过方案1和2的对比可知,当配电网接入SOP时,配电网的灵活性资源调节裕度收益提高了32.14万元,通过SOP的功率调度减少了配电网节点灵活性资源以及网架灵活性资源的使用,收益分别增加了31.73万元和0.41万元。而对比方案1和3,更凸显了ESOP对于配电网灵活性的提升,其灵活性资源调节裕度收益提高了121.13万元,节点和网架灵活性收益分别增加了120.45万元和0.68万元。ESOP不仅能发挥SOP对灵活性的提升作用,还能将内部的储能系统作为节点灵活性资源,增加配电网的灵活性资源调节裕度收益。
|
|
表 5 灵活性对比 Table 5 Flexibility comparison |
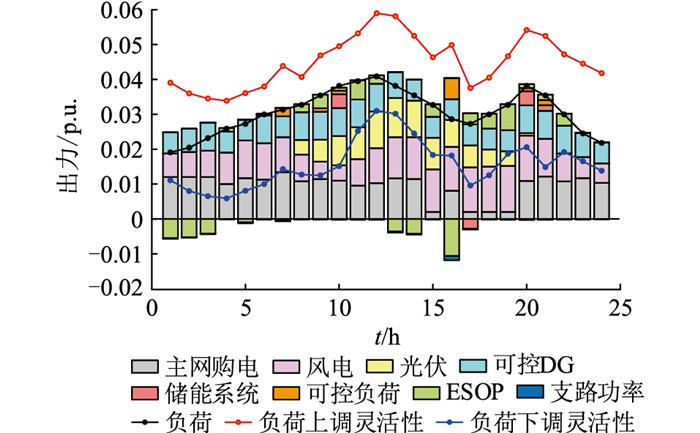
为体现ESOP接入配电网的日最优化调度运行结果及对配电网灵活性的作用,以春季日调度结果为例进行分析,结果如图 6和图 7所示。
|
图 6 优化调度结果 Fig. 6 Optimize scheduling results |
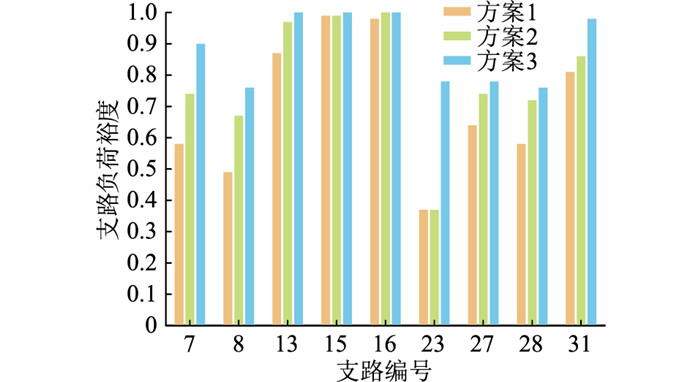
|
图 7 支路负荷裕度 Fig. 7 Branch load margin |
由图 6可知,主网输入、风光出力以及燃气机组对负荷进行大比例的功率供给。在晚间和正午时段,如1时—3时、13时—14时和16时,ESOP和储能系统出力为负,表示其对负荷无法消纳的风光出力进行储存;在负荷高峰期,如10时—12时和19时—21时输出储存电能,实现对风光资源的最大化利用。负荷曲线上下的2条折线分别表示负荷可以增加或减少的上下限,折线范围表示节点灵活性资源上调裕度和下调裕度,展现了配电网应对负荷波动从而调整节点灵活性资源向负荷供电或者吸收多余风光出力的能力。
图 7展现了网架灵活性资源裕度的情况,所选支路包含SOP所接入节点的相邻支路以及普通支路。通过对比3种方案在春季的最优化运行结果可知,SOP可以通过优化其有功功率的传输大小、方向和无功功率的支撑实现配电网的最优潮流分布,从而增大配电网整体的支路负荷裕度;而ESOP则结合了SOP和储能装置的优点,将其接入配电网对增大支路负荷裕度有更显著的效果,提高了配电网的网架灵活性。
4.3 有源配电网向上级电网反送功率算例分析当前有源配电网的新能源渗透率逐渐增加,配电网在功率充裕时可以向上级电网反送一定的功率,但反送功率受到变压器容量的限制[26],对此可修改第3章的优化规划模型,增加针对配电网向上级电网反送功率的约束条件,如式(34)所示。
| $ P_{\mathrm{g}, i, \min } \leqslant P_{\mathrm{g}, i, t} \leqslant P_{\mathrm{g}, i, \max } $ | (34) |
式中:
重新进行优化规划后的结果如表 6所示,其中差值为考虑上级电网功率反送的优化规划方案与原方案3的差值。当允许配电网向上级电网反送功率后,配电网整体年运行成本下降了11.2万元,其中可控DG成本以及主网购电成本的下降较多,分别减少了6.01万元和7.91万元;弃风弃光成本相较于自身有大比例的减少,但同时配电网的网损和可控负荷的成本有所上升,分别上升了3.28万元和4.24万元;而配电网的灵活性资源调节裕度收益有所下降,下降了10.67万元。其原因主要为有源配电网将自身无法消纳的风光出力向上级电网进行反送,增加了输电线路上的损耗成本,同时向功率反送路径上的负荷进行供给,减少了可控DG的成本;式(22)中将配电网反送功率的交易价格以分时电价进行交易,从而将获得的售电收益与主网购电成本相加,减少了主网购电成本;同时配电网利用自身的灵活性资源向上级电网进行功率反送,因此配电网的灵活性资源裕度收益有所下降。
|
|
表 6 计算结果对比 Table 6 Comparison of calculation results |
综合上述算例分析可知,当有源配电网允许向上级电网反送功率时,上级电网可以更好地实现对配电网内部风光出力的消纳以及负荷波动的供给,以实现对配电网的支撑。若上级电网功率出现波动并发出调度指令要求配电网提供反送功率,则配电网可以及时通过内部的储能系统和可控DG等灵活性资源进行功率反送以提供支撑,但这会减少配电网运行灵活性。因此,允许有源配电网和上级电网的功率双向输送有利于增加配电网风光出力的消纳、抑制功率波动以及保证上级电网的运行安全。
5 结论文中针对ESOP在有源配电网中的应用,以配电网运行经济性和灵活性为目标,提出了配电网节点和网架灵活性评价指标,对ESOP在配电网中的规划建设进行研究,并在优化配电网运行中发挥作用,构建了含ESOP规划与运行的有源配电网经济性与灵活性优化规划模型,通过算例验证得出了以下结论:
(1) ESOP在配电网中能够通过灵活的功率调节和无功补偿改变配电网的潮流分布,从而达到降低网损和提高风光出力消纳的作用。通过合理规划安装位置和容量,可以实现ESOP建设成本和配电网经济性的平衡。
(2) 文中分别将净负荷调节量和支路负荷裕度作为节点灵活性和网架灵活性的评价指标,以此来表征配电网的灵活性,通过对配电网灵活性资源的调配实现灵活性资源调节裕度收益。ESOP包含了SOP的网架灵活性资源和储能系统的节点灵活性资源,并参与有源配电网的运行优化调度,通过算例验证了含ESOP的配电网优化规划模型对配电网灵活经济运行的有效性,以及主配网功率交互对有源配电网风光出力消纳及功率波动抑制和上级电网运行安全的作用。
致谢
本文得到新能源电力系统国家重点实验室(华北电力大学)自主研究课题(LAPS202124)资助,谨此致谢!
| [1] |
谭显东, 刘俊, 徐志成, 等. "双碳"目标下"十四五"电力供需形势[J]. 中国电力, 2021, 54(5): 1-6. TAN Xiandong, LIU Jun, XU Zhicheng, et al. Power supply and demand balance during the 14th Five-year Plan period under the goal of carbon emission peak and carbon neutrality[J]. Electric Power, 2021, 54(5): 1-6. (  0) 0) |
| [2] |
卢佳. 计及功率平衡含风电的发电系统可靠性评估[J]. 中国电力, 2017, 50(6): 146-151, 184. LU Jia. Reliability evaluation of power generation system with wind power and reactive power balance[J]. Electric Power, 2017, 50(6): 146-151, 184. (  0) 0) |
| [3] |
董逸超, 王守相, 闫秉科. 配电网分布式电源接纳能力评估方法与提升技术研究综述[J]. 电网技术, 2019, 43(7): 2258-2266. DONG Yichao, WANG Shouxiang, YAN Bingke. Review on evaluation methods and improvement techniques of DG hosting capacity in distribution network[J]. Power System Technology, 2019, 43(7): 2258-2266. (  0) 0) |
| [4] |
何英静, 沈舒仪, 何东, 等. 兼顾网损优化效益与投资成本的SNOP容量规划方法[J]. 中国电力, 2020, 53(4): 32-40. HE Yingjing, SHEN Shuyi, HE Dong, et al. A SNOP capacity planning method considering network-loss optimization benefit and investment cost[J]. Electric Power, 2020, 53(4): 32-40. (  0) 0) |
| [5] |
罗旷, 王莉, 陈超, 等. 考虑电压稳定性与越限的配电网电压质量评估指标[J]. 南方电网技术, 2019, 13(4): 48-53, 72. LUO Kuang, WANG Li, CHEN Chao, et al. Voltage quality assessment index for distribution network considering voltage stability and over-limit[J]. Southern Power System Technology, 2019, 13(4): 48-53, 72. (  0) 0) |
| [6] |
CAO W Y, WU J Z, JENKINS N, et al. Operating principle of soft open points for electrical distribution network operation[J]. Applied Energy, 2016, 164: 245-257. DOI:10.1016/j.apenergy.2015.12.005 (  0) 0) |
| [7] |
叶宇鑫, 李更丰, 别朝红, 等. 考虑智能软开关的有源配电网恢复力评估与提升[J]. 全球能源互联网, 2022, 5(3): 203-212. YE Yuxin, LI Gengfeng, BIE Zhaohong, et al. Resilience assessment and improvement of active distribution networks considering soft open point[J]. Journal of Global Energy Interconnection, 2022, 5(3): 203-212. (  0) 0) |
| [8] |
贾善翔, 彭克, 李喜东, 等. 基于智能软开关的柔性互联交直流配电系统分布式优化[J]. 电力系统自动化, 2021, 45(8): 95-103. JIA Shanxiang, PENG Ke, LI Xidong, et al. Distributed optimization of flexible interconnected AC/DC distribution system based on soft open point[J]. Automation of Electric Power Systems, 2021, 45(8): 95-103. (  0) 0) |
| [9] |
YANG X D, XU C B, ZHANG Y B, et al. Real-time coordinated scheduling for ADNs with soft open points and charging stations[J]. IEEE Transactions on Power Systems, 2021, 36(6): 5486-5499. (  0) 0) |
| [10] |
王成山, 宋关羽, 李鹏, 等. 基于智能软开关的智能配电网柔性互联技术及展望[J]. 电力系统自动化, 2016, 40(22): 168-175. WANG Chengshan, SONG Guanyu, LI Peng, et al. Research and prospect for soft open point based flexible interconnection technology for smart distribution network[J]. Automation of Electric Power Systems, 2016, 40(22): 168-175. (  0) 0) |
| [11] |
YAO C. A sequential optimization method for soft open point integrated with energy storage in active distribution networks[J]. Energy Procedia, 2018, 145: 528-533. (  0) 0) |
| [12] |
BLOEMINK J M, GREEN T C. Increasing photovoltaic penetration with local energy storage and soft normally-open points[C]//2011 IEEE Power and Energy Society General Meeting. Detroit, MI, USA. IEEE, 2011: 1-8.
(  0) 0) |
| [13] |
熊正勇, 苗虹, 曾成碧. 基于智能软开关与储能系统联合的有源配电网运行优化[J]. 电测与仪表, 2020, 57(13): 33-39. XIONG Zhengyong, MIAO Hong, ZENG Chengbi. Operation optimization of active distribution network based on smart soft open point and energy storage system[J]. Electrical Measurement & Instrumentation, 2020, 57(13): 33-39. (  0) 0) |
| [14] |
陈垚煜, 江全元, 周自强, 等. 考虑典型场景的配电网调控方案灵活性评估方法[J]. 电力建设, 2019, 40(7): 34-40. CHEN Yaoyu, JIANG Quanyuan, ZHOU Ziqiang, et al. An evaluation method on the flexibility of regulation methods in distribution network considering typical scene sets[J]. Electric Power Construction, 2019, 40(7): 34-40. (  0) 0) |
| [15] |
MOHANDES B, MOURSI M S E, HATZIARGYRIOU N, et al. A review of power system flexibility with high penetration of renewables[J]. IEEE Transactions on Power Systems, 2019, 34(4): 3140-3155. (  0) 0) |
| [16] |
王洪坤, 王守相, 潘志新, 等. 含高渗透分布式电源配电网灵活性提升优化调度方法[J]. 电力系统自动化, 2018, 42(15): 86-93. WANG Hongkun, WANG Shouxiang, PAN Zhixin, et al. Optimized dispatching method for flexibility improvement of distribution network with high-penetration distributed generation[J]. Automation of Electric Power Systems, 2018, 42(15): 86-93. (  0) 0) |
| [17] |
WANG J, ZHOU N C, CHUNG C Y, et al. Coordinated planning of converter-based DG units and soft open points incorporating active management in unbalanced distribution networks[J]. IEEE Transactions on Sustainable Energy, 2020, 11(3): 2015-2027. (  0) 0) |
| [18] |
王俊丰, 孔令生, 范心明, 等. 面向有源配电网运行经济性的智能储能软开关规划[J]. 电力建设, 2020, 41(10): 63-70. WANG Junfeng, KONG Lingsheng, FAN Xinming, et al. Optimal planning for soft open point integrated with ESS to improve the economy of active distribution network[J]. Electric Power Construction, 2020, 41(10): 63-70. (  0) 0) |
| [19] |
DING Z J, WANG C Y, WANG F, et al. Planning of soft open point integrated with ESS in active distribution network[C]//2021 3rd Asia Energy and Electrical Engineering Symposium (AEEES). Chengdu, China. IEEE, 2021: 427-432.
(  0) 0) |
| [20] |
朱晓荣, 鹿国微, 谢婉莹. 考虑源网荷灵活性资源的配电网储能鲁棒规划[J]. 电力自动化设备, 2021, 41(8): 8-16, 40. ZHU Xiaorong, LU Guowei, XIE Wanying. Robust planning of energy storage in distribution network considering source-network-load flexible resources[J]. Electric Power Automation Equipment, 2021, 41(8): 8-16, 40. (  0) 0) |
| [21] |
BARAN M E, WU F F. Optimal capacitor placement on radial distribution systems[J]. IEEE Transactions on Power Delivery, 1989, 4(1): 725-734. (  0) 0) |
| [22] |
BARAN M E, WU F F. Network reconfiguration in distribution systems for loss reduction and load balancing[J]. IEEE Power Engineering Review, 1989, 9(4): 101-102. (  0) 0) |
| [23] |
姜云鹏, 任洲洋, 李秋燕, 等. 考虑多灵活性资源协调调度的配电网新能源消纳策略[J]. 电工技术学报, 2022, 37(7): 1820-1835. JIANG Yunpeng, REN Zhouyang, LI Qiuyan, et al. An accommodation strategy for renewable energy in distribution network considering coordinated dispatching of multi-flexible resources[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1820-1835. (  0) 0) |
| [24] |
吴红斌, 郭彩云. 计及电动汽车的分布式发电系统中储能单元的优化配置[J]. 中国电机工程学报, 2012, 32(S1): 15-21. WU Hongbin, GUO Caiyun. Capacity optimization of energy storage unit in distribution generation system considering electric vehicle[J]. Proceedings of the CSEE, 2012, 32(S1): 15-21. (  0) 0) |
| [25] |
李锰, 王利利, 陈鹏浩, 等. 一种直流配电网中换流站的选址定容方法[J]. 电力系统保护与控制, 2020, 48(21): 109-116. LI Meng, WANG Lili, CHEN Penghao, et al. Method for selecting and setting the capacity of a converter station in a DC distribution network[J]. Power System Protection and Control, 2020, 48(21): 109-116. (  0) 0) |
| [26] |
梁志峰, 夏俊荣, 孙檬檬, 等. 数据驱动的配电网分布式光伏承载力评估技术研究[J]. 电网技术, 2020, 44(7): 2430-2439. LIANG Zhifeng, XIA Junrong, SUN Mengmeng, et al. Data driven assessment of distributed photovoltaic hosting capacity in distribution network[J]. Power System Technology, 2020, 44(7): 2430-2439. (  0) 0) |
 2023, Vol. 42
2023, Vol. 42


 黄子桐(1998), 男, 硕士在读, 研究方向为配电网规划及运行优化(E-mail:
黄子桐(1998), 男, 硕士在读, 研究方向为配电网规划及运行优化(E-mail: