文章编号: 2096-3203(2023)01-0107-09 中图分类号: TM73
2. 新能源利用与节能安徽省重点实验室(合肥工业大学), 安徽 合肥 230009;
3. 国网山东省电力公司荣成市供电公司, 山东 荣成 264300
高比例接入电网的风电、光伏等新能源具有间歇性,使得电网传输功率波动频繁,容易造成线路过载运行。过载线路故障跳闸会使潮流转移到关联输电断面内其他线路上,造成输电断面发生潮流过载,引起过载保护装置动作,导致电网发生大规模连锁跳闸事故,严重威胁电力系统的安全稳定运行[1-4]。因此,当电网面临切除过载线路引发输电断面连锁过载的风险时,调度人员应快速制定有效的潮流控制策略,紧急消除线路过载,使电网恢复到安全运行状态[5-7]。目前消除线路过载的主要措施为紧急调整发电机组出力和切负荷操作。潮流控制策略主要包括灵敏度分析方法[8-13]和直接优化类方法[14-18]。
文献[8-9]提出的灵敏度分析方法无须迭代,不存在收敛性问题,可以快速得到潮流控制策略。但是该方法仅考虑过载线路与调度节点之间的灵敏度关系,而电网具有高度非线性特征,调度节点会对其他线路的潮流有不同程度的影响,可能会导致新的线路发生过载,须进行多次潮流校验。文献[10]基于交流潮流模型,得到支路有功潮流对节点有功注入的灵敏度,通过节点有功灵敏度和负载率等指标对输电断面潮流越限进行调度指导。但是该方法仅提供调度人员指导建议,没有给出消除输电断面潮流越限的实际调度方案。文献[11]充分考虑节点对过载及重载线路潮流的整体控制作用,将综合灵敏度定义为节点对过载及重载线路灵敏度的加权和。文献[12-13]提出基于综合灵敏度分析的潮流越限切负荷调度方案,但违背了机组出力调整的优先级高于切负荷操作的原则,会对供电可靠性产生不利影响,在实际电力系统调度中的应用合理性有待检验。由于电力系统的非线性因素,调整发电机组出力以降低某些线路载荷的同时会增加其他线路的载荷。如果不加筛选地利用综合灵敏度指标来控制线路潮流,可能出现某些机组节点对群体线路的整体作用与对局部线路的作用相反,部分控制节点被划分到出力调整效果加剧过载线路越限的节点集合中,导致优化算法需要更多的机组节点参与调度以平抑不同机组的相互反作用,不利于潮流策略的制定。
灵敏度分析方法将节点有功注入与线路有功潮流间的非线性关系简化为线性关系,当仅依靠灵敏度关系通过多个控制节点来调整线路潮流时误差较大,难以达到实际电网的潮流控制精度要求。在输电断面潮流控制策略中,文献[14]对比了灵敏度分析方法和粒子群优化算法,验证了基于粒子群算法的输电断面潮流越限控制方法可以消除因简化的灵敏度线性关系导致的潮流误差,并且调节效率高。直接优化类方法[15-18]直接利用潮流计算建立数学模型,充分考虑符合电力系统安全运行的各类要求,得到的潮流控制策略有较好的安全性和经济性。但随着系统规模的扩大,该类方法的控制变量逐步增加,会导致维数灾,计算时间过长,难以满足电网实时潮流控制的要求。
针对灵敏度分析方法精确度不高和直接优化类方法计算量过大的缺点,文中提出一种基于正负综合灵敏度的输电断面双层优化潮流控制策略。首先根据节点对过载及重载线路潮流的整体调节作用,提出节点的正负综合灵敏度指标,剔除对关键线路集潮流控制效果较差的节点。然后通过双层优化方法快速制定潮流控制策略,第一步构建第一层调度节点多目标筛选优化模型,根据模糊满意度优选评价方法,选择参与潮流控制的调度节点;第二步通过第二层潮流调控优化模型计算所选调度节点的精确出力调整量,快速制定潮流控制策略。文中制定的潮流控制策略首先确定参与潮流控制的调度节点,能极大降低优化搜索空间维度,再优化少量调度节点的出力调整量,满足输电断面潮流越限的在线调度要求。
1 节点对关键线路集的综合灵敏度计算 1.1 节点对线路的有功灵敏度计算系统运行中线路有功潮流不满足安全约束时,须适当调整节点有功出力使线路有功潮流恢复到正常运行状态。文中以直流潮流模型为基础,建立线路有功潮流对节点有功注入的灵敏度数学模型[19]:
| $ \left\{\begin{array}{l} \Delta \boldsymbol{P}=\boldsymbol{B} \cdot \Delta \boldsymbol{\theta} \\ \Delta P_a=\Delta \theta_a / x_a \\ S_{a, i}=\Delta P_a / \Delta P_i \end{array}\right. $ | (1) |
式中:ΔP为系统线路有功潮流变化量的列向量;B为系统电纳矩阵;Δθ为系统线路电压相角差的列向量;ΔPa为线路a的有功潮流变化量;Δθa为线路a首末两端节点的电压相位差;xa为线路a的电抗;ΔPi为节点i的有功注入变化量;Sa, i为线路a有功潮流对节点i有功注入的灵敏度。Sa, i的物理意义为:节点i增加单位有功功率,相应平衡机组减少单位有功功率时线路a的有功潮流变化量。
1.2 正负综合灵敏度指标为了使消除线路过载的调度节点出力调整量最少,应优先调度对过载线路有功灵敏度较大的节点。与此同时,在调度过程中应保证其他线路不出现过载情况,尤其是重载线路不过载。为此,考虑到对过载及重载线路潮流的整体控制作用,文献[11]提出综合灵敏度指标。但是不加筛选地利用综合灵敏度指标来消除潮流越限,可能导致更多机组节点参与消除输电断面内线路过载,甚至负荷节点被迫执行切负荷操作。针对上述问题,文中提出正负综合灵敏度指标,计算公式为:
| $ \begin{cases}S_{K, i}^{+}=\sum\limits_{l \in L} \alpha_l S_{l, i}+\sum\limits_{m \in M} \alpha_m S_{m, i} & S_{l, i}, S_{m, i} \geqslant 0 \\ S_{K, i}^{-}=\sum\limits_{l \in L} \alpha_l S_{l, i}+\sum\limits_{m \in M} \alpha_m S_{m, i} & S_{l, i}, S_{m, i}<0\end{cases} $ | (2) |
式中:SK, i+、SK, i-分别为节点i对关键线路集K的正、负综合灵敏度指标;L为过载线路集合;M为重载线路集合,文中将线路有功潮流大于其自身热稳定功率极限的90%的线路定义为重载线路;关键线路集K为过载线路l和重载线路m的集合;αl、αm分别为过载线路l和重载线路m对应的潮流权重;Sl, i、Sm, i分别为过载线路l和重载线路m对节点i有功注入的灵敏度。
消除线路过载是潮流控制策略的首要任务,过载线路越限量越大,电网消除线路过载的需求就越迫切,过载线路对应潮流权重就越大。与此同时,须重点关注重载线路的运行状况,重载线路负载率越高,在潮流控制过程中过载的概率就越大,其对应潮流权重就越大。潮流权重指的是电网某一运行方式下线路的负载率,其值由线路当前运行状态的有功潮流决定。文中将潮流权重作为比例系数计算节点的正负综合灵敏度指标,以此反映节点对关键线路集的综合调整效果。过载线路和重载线路对应的潮流权重定义如下:
| $ \left\{\begin{array}{l} \alpha_l=P_l / P_l^{\max } \\ \alpha_m=P_m / P_m^{\max } \end{array}\right. $ | (3) |
式中:Pl、Plmax分别为过载线路l当前有功潮流和热稳定功率极限;Pm、Pmmax分别为重载线路m当前有功潮流和热稳定功率极限。一般情况下,αl>1,0.9<αm<1。
得到节点的正负综合灵敏度指标后,根据灵敏度的绝对值,将每个节点的正负综合灵敏度指标按从大到小排序,构建基于正综合灵敏度指标的节点顺序集和基于负综合灵敏度指标的节点顺序集。
2 调度节点的确定 2.1 节点的初步筛选在实际电力系统中,参与消除线路过载的有效节点并不多。为了使控制方法更加高效,减少计算量,在基于正、负综合灵敏度指标的节点顺序集中分别剔除各自综合灵敏度较小的节点。剔除完成后,合并正、负综合灵敏度指标节点顺序集中剩余节点,得到对过载线路和重载线路具有良好潮流控制效果的节点集合N。
调度专家根据电网规模和过载线路越限量确定剔除节点比例β。当过载线路越限量较大时,需要更多的节点参与调整,剔除节点比例可以相应降低;当电网规模较大时,对过载线路潮流控制作用较小的节点较多,剔除节点比例可以相应提高。
2.2 第一层调度节点多目标筛选优化模型的构建通过初步筛选得到节点集合N后,利用双层优化方法快速制定潮流控制策略。首先构建第一层调度节点多目标筛选优化模型,该模型以筛选参与潮流控制的调度节点为目的,不进行耗时较大的潮流计算,可实现调度节点的快速筛选。
2.2.1 优化算法的数学模型为实现以少量调度节点消除线路过载,同时避免执行切负荷操作和减少平衡机组出力调整量的目标,文中构建调度节点多目标筛选优化数学模型。
(1) 目标函数。目标1:为保证尽快完成输电断面潮流控制策略的构建,避免过多的节点参与调度,参与调度的节点要最少,目标函数见式(4)。
| $ \min f_1=\sum\limits_{g=1}^{N_{\mathrm{G}}} u_g+\sum\limits_{k=1}^{N_{\text {load }}} u_k $ | (4) |
式中:NG、Nload分别为机组节点数和负荷节点数;ug、uk为0-1变量,分别表征机组节点g和负荷节点k参与调度情况,为1表示参与,为0表示不参与。
目标2:在潮流控制中,切负荷操作会切断部分用户的供电,影响供电可靠性。因此,要确保在调整机组出力无法消除线路过载时才执行切负荷操作。执行切负荷操作时,如果对供电等级较高的用户进行切除,会造成较大的影响,所以应不切或少切该类用户;对供电等级较低的用户进行切除,虽然不会造成较大的影响,但是该类负荷的过量切除同样不利于电力系统的稳定运行。综上所述,在避免执行切负荷操作的同时,应使切除负荷产生的影响降到最低,目标函数见式(5)。
| $ \min f_2=\sum\limits_{k=1}^{N_{\text {load }}} u_k \eta_k\left|\Delta P_k\right| $ | (5) |
式中:ηk为负荷节点k切除单位有功负荷的影响系数;ΔPk为负荷节点k执行切负荷操作的负荷调整量。
目标3:平衡机组在电网调度运行中主要承担二次调频工作,为减少平衡机组的出力调整量,调度节点的出力增加调整量与出力减少调整量之差应最小,目标函数见式(6)。
| $ \min f_3=\sum\limits_{g=1}^{N_{\mathrm{G}}} u_g \Delta P_g+\sum\limits_{k=1}^{N_{\text {load }}} u_k\left|\Delta P_k\right| $ | (6) |
式中:ΔPg为机组节点g的出力调整量。
(2) 约束条件。在消除线路l过载的同时须保证不导致新的线路过载,即满足式(7)、式(8);式(9)为机组节点g的出力调整量上下限约束;式(10)为负荷节点k执行切负荷操作的负荷调整量上下限约束。
| $ \sum\limits_{g=1}^{N_{\mathrm{G}}} S_{l, g} u_g \Delta P_g+\sum\limits_{k=1}^{N_{\text {load }}} S_{l, k} u_k\left|\Delta P_k\right|+P_l^0 \leqslant P_l^{\max } $ | (7) |
| $ \sum\limits_{g=1}^{N_{\mathrm{G}}} S_{m, g} u_g \Delta P_g+\sum\limits_{k=1}^{N_{\text {load }}} S_{m, k} u_k\left|\Delta P_k\right|+P_m^0 \leqslant P_m^{\max } $ | (8) |
| $ P_g^{\min } \leqslant \Delta P_g+P_g^0 \leqslant P_g^{\max } $ | (9) |
| $ 0 \leqslant\left|\Delta P_k\right| \leqslant P_k^0-P_k^{\min } $ | (10) |
式中:Pl0、Pm0分别为过载线路l和重载线路m的初始有功潮流;Sl, g、Sl, k分别为过载线路l对机组节点g和负荷节点k有功注入的灵敏度;Sm, g、Sm, k分别为重载线路m对机组节点g和负荷节点k有功注入的灵敏度;Pg0为机组节点g初始有功功率;Pgmin、Pgmax分别为机组节点g的有功下限和上限;Pk0为负荷节点k初始有功功率;Pkmin为负荷节点k参与潮流调整的有功下限。
2.2.2 基于NSGA-Ⅱ的控制模型求解带有精英策略的非支配排序遗传算法(non-dominated sorting genetic algorithm Ⅱ,NSGA-Ⅱ)在求解多目标优化问题上具有较强的处理能力[20-21]。该算法优势在于:通过快速非支配排序对个体进行分层化处理;引入拥挤度距离确保个体均匀分布在目标空间,保持种群多样性;通过精英策略将优秀个体保留到下一代,提高种群水平。文中基于NSGA-Ⅱ构建调度节点多目标筛选优化模型,优化求解得到帕累托(Pareto)前沿解集。
2.2.3 模糊满意度优选评价方法得到Pareto前沿解集后,采用模糊理论选择最优候选解。通过模糊隶属度函数表示Pareto前沿解中目标函数对应的模糊隶属度,具体见式(11)。
| $ R_{c, h}=\left\{\begin{array}{l} 1 \quad f_c \leqslant f_c^{\min } \\ \frac{f_c^{\max }-f_c}{f_c^{\max }-f_c^{\min }} \quad f_c^{\min }<f_c<f_c^{\max } \\ 0 \quad f_c \geqslant f_c^{\max } \end{array}\right. $ | (11) |
式中:Rc, h为非支配解h中第c个目标函数对应的模糊隶属度;fcmin、fcmax分别为非支配解集中目标函数fc的最小值和最大值。
对每一个非支配解h进行归一化处理,归一化后的隶属度函数Rh为:
| $ R_h=\sum\limits_{c=1}^{N_{\mathrm{obj}}} R_{c, h} / \sum\limits_{h=1}^H \sum\limits_{c=1}^{N_{\mathrm{obj}}} R_{c, h} $ | (12) |
式中:H、Nobj分别为非支配解集中解的数量和子目标函数的数量。
通过模糊满意度优选评价方法,在非支配解集中选择Rh值最大的解作为最优解,将最优解中的节点作为参与消除线路过载的调度节点。
3 最优出力调整量的确定 3.1 第二层潮流调控优化模型的构建确定参与消除线路过载的调度节点后,得到调度节点的精确出力调整量是制定输电断面潮流控制策略的关键。为减少对调度节点出力的调整,文中以调度节点的总出力调整量最少为优化目标,构建第二层潮流调控优化模型,计算出所选调度节点的精确出力调整量。该模型的目标函数为:
| $ \min f=\sum\limits_{i \in N^{\prime}}\left|\Delta P_i\right| $ | (13) |
式中:N′为参与潮流控制的调度节点集合;ΔPi为第i个调度节点的出力调整量。
等式约束条件为系统交流模型下的潮流方程:
| $ \left\{\begin{array}{l} P_{\mathrm{G} i}-P_{\mathrm{D} i}-U_i \sum\limits_{j \in N^{\prime}} U_j\left(G_{i j} \cos \delta_{i j}+B_{i j} \sin \delta_{i j}\right)=0 \\ Q_{\mathrm{G} i}-Q_{\mathrm{D} i}-U_i \sum\limits_{j \in N^{\prime}} U_j\left(G_{i j} \sin \delta_{i j}-B_{i j} \cos \delta_{i j}\right)=0 \end{array}\right. $ | (14) |
式中:PGi、QGi分别为节点i的有功出力和无功出力;PDi、QDi分别为节点i的有功负荷和无功负荷;Ui为节点i的电压幅值;Gij、Bij、δij分别为节点i、j之间的电导、电纳和相位差。
不等式约束条件分别为发电机有功出力约束、无功出力约束、节点电压幅值约束以及线路有功潮流约束,表达式为:
| $ \left\{\begin{array}{l} P_{\mathrm{G} i}^{\min }<P_{\mathrm{G} i}<P_{\mathrm{G} i}^{\max } \\ Q_{\mathrm{G} i}^{\min }<Q_{\mathrm{G} i}<Q_{\mathrm{G} i}^{\max } \\ U_i^{\min }<U_i<U_i^{\max } \\ \left|P_a\right|= \\ \left|U_i U_j\left(G_{i j} \sin \delta_{i j}-B_{i j} \cos \delta_{i j}\right)-U_i^2 G_{i j}\right| \leqslant P_a^{\max } \end{array}\right. $ | (15) |
式中:PGimax、PGimin分别为节点i可以参与潮流调整的有功出力上下限;QGimax、QGimin分别为节点i可以参与潮流调整的无功出力上下限;Uimax、Uimin分别为节点i的电压幅值上下限;Pa为线路a的有功潮流;Pamax为线路a的热稳定功率极限。
3.2 调度节点精确出力调整量的优化求解文中采用Cplex求解器进行电力系统最优潮流问题的求解[22]。Cplex是一种集成多种优化算法的求解器,具有编程易于实现、高性能、计算速度快等优点。针对潮流方程具有非凸性、难以获得全局最优解的问题,文中首先对潮流方程进行二阶锥松弛转化[23],然后通过Cplex求解器对第二层潮流调控优化模型进行优化求解,获得全局最优解,从而得到每个调度节点的精确出力调整量。
4 潮流控制策略总体流程基于正负综合灵敏度的输电断面潮流控制策略的具体步骤为:
(1) 获取电网当前运行方式下的状态数据以及输电断面信息,根据线路有功潮流大小确定过载线路l和重载线路m,并组成关键线路集K。
(2) 在系统中选取可以参与消除线路过载的机组节点和负荷节点,计算这些节点对关键线路集K的正负综合灵敏度指标,构建基于正负综合灵敏度指标的节点顺序集。
(3) 运行专家根据电网规模和过载线路越限量确定剔除节点比例β,剔除正、负综合灵敏度节点顺序集中灵敏度较小的节点,合并节点顺序集中剩余节点,得到初步筛选的节点集合N。
(4) 为快速得到参与潮流控制的调度节点,构建第一层调度节点多目标筛选优化模型,采用NSGA-Ⅱ算法进行优化求解,得到第一层优化模型的Pareto前沿解集。
(5) 得到Pareto前沿解集后,采用模糊满意度优选评价方法,计算非支配解的Rh值,选取Rh值最大的非支配解作为最优解,将最优解中的节点作为参与潮流控制的调度节点。
(6) 得到参与消除线路潮流过载的调度节点后,构建第二层潮流调控优化模型,通过Cplex求解器计算出所选调度节点的精确出力调整量。
(7) 根据上述优化结果,得到参与潮流控制的调度节点和对应出力调整量,从而快速制定潮流控制方案,实现输电断面潮流越限的精准调度。
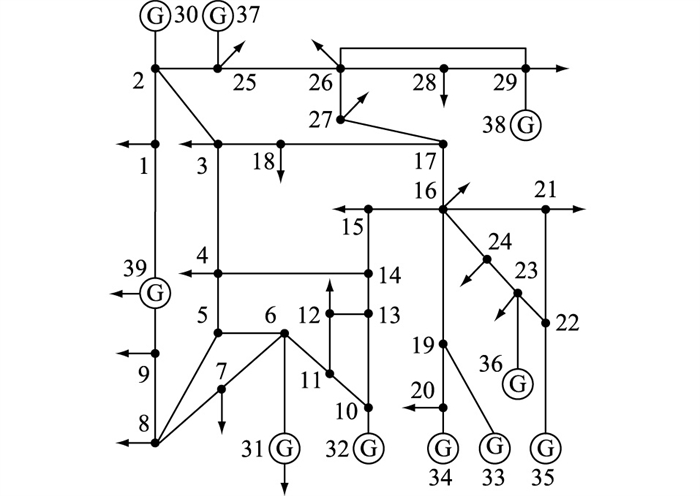
5 算例分析 5.1 IEEE 39节点系统潮流越限调整仿真分析为验证文中方法的有效性,采用某一运行方式下的IEEE 39节点系统作为算例进行仿真分析。IEEE 39节点系统拓扑如图 1所示。
|
图 1 IEEE 39节点系统拓扑 Fig. 1 The topology of IEEE 39-bus system |
为应对新能源出力的波动性,设置系统机组的备用容量,以满足高比例新能源电力系统的备用需求。在该运行方式下,对IEEE 39节点系统的机组有功出力限值进行修正,设置机组G30、G32、G33、G34、G35、G36、G37、G38、G39参与潮流控制的有功出力上限分别为290 MW、300 MW、220 MW、240 MW、300 MW、450 MW、450 MW、530 MW、1 100 MW。
采用文献[24-25]提出的基于拓扑聚合的输电断面搜索方法对当前运行方式下的IEEE 39节点系统进行关键输电断面辨识,确定当前存在内部线路过载的输电断面为线路l1—39、l2—3、l17—27的集合。该输电断面内的过载线路l以及重载线路m的潮流分布情况如表 1所示。从表 1可以看出,过载线路l1—39的潮流越限量为72.40 MW,潮流控制策略的目的是将过载线路l1—39的有功潮流控制在250 MW以下,同时系统中其他线路不产生新的潮流越限。
|
|
表 1 关键线路集的潮流运行情况 Table 1 Power flow operation of key line set |
选取可以参与消除输电断面潮流越限的机组节点(G30、G32、G33、G34、G35、G36、G37、G38、G39)和执行切负荷操作的负荷节点(D4、D7、D20、D21、D24、D27)。负荷节点分为3类,第1类为D7、D24,第2类为D21、D27,第3类为D4、D20,其对应的切负荷影响系数η分别为1、0.5、0.2。计算这些节点对关键线路集的正负综合灵敏度指标。
为降低后续优化算法的计算复杂度,根据电网规模和线路l1—39的越限量设置剔除节点比例β为40%。正综合灵敏度节点顺序集中灵敏度较小的节点依次为D20、D24、G36、D7、G32、D4,负综合灵敏度节点顺序集中灵敏度较小的节点依次为D4、G35、G33、G32、D7、G39,最终剔除对关键线路集潮流控制效果较差的节点G32、D4、D7,将剩余节点进行合并,得到初步筛选的节点集合N。
首先构建基于NSGA-Ⅱ算法的第一层调度节点多目标筛选优化模型,在节点集合N中得到Pareto前沿解集后,根据模糊满意度优选评价方法选择参与调整的调度节点,最终得到参与消除线路l1—39潮流越限的调度节点为G30、G34、G37、G39。可以看出,通过第一层调度节点多目标筛选优化模型得到的调度节点均为发电机组,符合电网实际潮流控制时机组出力调整的优先级高于切负荷操作的原则,保证了用户供电的可靠性。然后构建第二层潮流调控优化模型得到调度节点的精确出力调整量,快速制定消除线路过载的潮流控制策略,具体调整措施和调整结果见表 2和表 3。由表 2可以看出,通过文中方法得到的输电断面潮流控制策略需要4个机组节点进行调度控制,机组节点G30、G34、G37的出力增加调整量总和近似等于节点G39的出力减少调整量,总出力调整量为251.93 MW,平衡机组G31参与潮流控制的出力调整量很小。由表 3可以看出,过载线路l1—39的潮流越限量被消除,系统所有线路的有功潮流均在热稳定功率极限内。
|
|
表 2 调度节点的出力调整措施 Table 2 Output adjustment of scheduling nodes |
|
|
表 3 关键线路集调整结果 Table 3 The adjustment results of key line set |
为验证文中方法的优越性,将文中方法、文献[8]提出的灵敏度分析方法和直接优化类方法进行对比。3种方法制定的潮流控制策略的差异如表 4所示,其中直接优化类方法采用NSGA-Ⅱ进行优化,线路潮流越限误差计算见式(16)。
|
|
表 4 调整方法性能对比 Table 4 Performance comparison between adjustment methods |
| $ E_l=\left\{\begin{array}{l} \frac{P_{\mathrm{cor}, l}-P_{\lim , l}}{P_{\lim , l}} P_{\mathrm{cor}, l}>P_{\lim , l} \\ 0 \quad P_{\mathrm{cor}, l} \leqslant P_{\lim , l} \end{array}\right. $ | (16) |
式中:El为线路l潮流越限误差;Pcor, l为原过载线路l经过潮流控制后的有功潮流大小;Plim, l为过载线路l的热稳定功率极限。
由表 4可知,在制定潮流控制策略的过程中,文献[8]提出的基于反向等量配对原则的灵敏度分析方法虽然计算速度快,但是存在较大的潮流误差,调整后线路l1—39的有功潮流为257.25 MW,超过其热稳定功率极限,存在2.9%的潮流误差,线路仍处于潮流越限状态,因此须进行多次潮流校验。灵敏度分析方法出现潮流误差的主要原因为灵敏度计算过程中将节点出力与线路有功潮流间的非线性关系简化为线性关系。在消除线路l1—39潮流过载时,灵敏度分析方法因简化的线性关系无法得到各机组的精确出力调整量,造成过载线路l1—39在潮流调整后仍然越限,无法实现对输电断面潮流越限的精准调度。
采用文中方法进行潮流调整时,过载线路l1—39的有功潮流由过载时的322.40 MW调整为248.68 MW,低于其热稳定功率极限。文中方法不会产生潮流误差的原因在于:文中采用双层优化思想,首先构建第一层调度节点多目标筛选优化模型,确定参与潮流控制的调度节点,再通过第二层潮流调控优化模型计算所选调度节点的精确出力调整量,所得的调整方法能够保证过载线路l1—39在调整后有功潮流低于其热稳定功率极限,实现消除线路越限的精准调度。而且,文中方法仅调度4台机组,灵敏度分析方法则须调度5台机组,对发电厂的既定发电计划影响较大。
直接优化类方法制定的潮流控制策略能够保证过载线路l1—39的有功潮流由过载时的322.40 MW下降为248.23 MW,低于其热稳定功率极限,不会产生潮流误差。但是,该方法将节点是否参与调度的0-1变量以及对应的出力调整量作为控制变量,控制策略的制定变为复杂的非线性潮流规划,搜索空间过大,计算量激增,很有可能无法在过载线路热稳定功率极限的耐受时间内得到潮流控制策略,导致大规模连锁跳闸停电事故。
将文中方法与文献[11]提出的综合灵敏度分析方法进行比较。采用文献[11]的方法,计算机组节点G30、G33、G37、G38对过载及重载线路的综合灵敏度分别为0.501 1、0.055 3、0.361 6、0.292 9,与对应过载线路的灵敏度指标相反,这使得机组节点G30、G33、G37、G38被划分到出力减少节点集合,与节点实际情况相反,导致仅通过机组节点无法消除线路过载,负荷节点D4被迫执行切负荷操作。但实际上,通过文中方法得到的潮流控制策略只需机组节点G30、G34、G37、G39参与调度控制,验证了文献[11]提出的综合灵敏度分析方法有可能导致负荷节点被迫执行切负荷操作,降低供电可靠性。
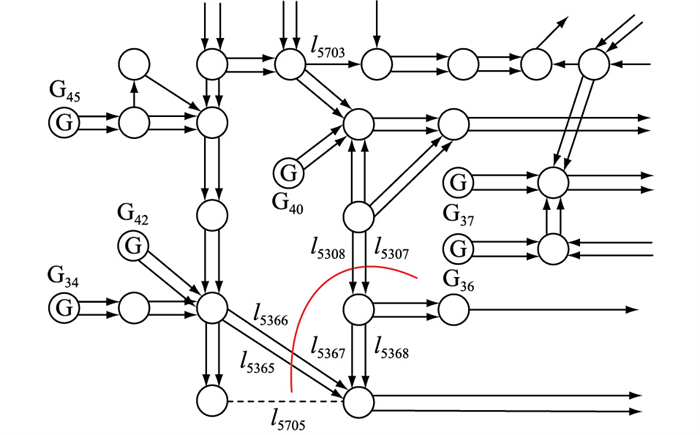
5.2 某省级电网潮流越限调整仿真分析为进一步验证文中方法制定的潮流控制策略的有效性,以某省级电网5月6号08:00—10:00时的潮流运行为例进行分析。如图 2所示,省级电网输电断面T1发生潮流越限,图中红色曲线途径的线路集合为发生潮流越限的输电断面T1,节点间的双线代表双回线路,箭头指向代表潮流方向。输电断面T1在5月6号08:00—10:00的有功潮流见图 3。
|
图 2 输电断面T1位置示意 Fig. 2 Schematic diagram of position of transmission section T1 |
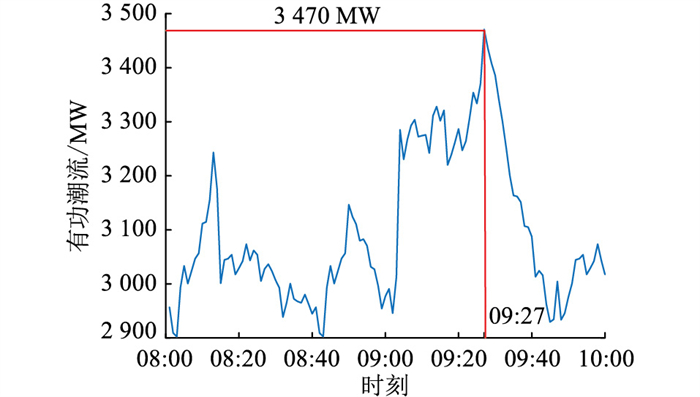
|
图 3 输电断面T1的有功潮流 Fig. 3 Active power flow of transmission section T1 |
根据电网日前检修计划安排,5月6号09:25,对电网线路l5705进行检修操作,开断线路l5705。通过实时潮流分析确定当前存在内部线路潮流过载的输电断面T1为线路l5308、l5307、l5366、l5365的集合,如图 2所示。对线路l5705进行检修操作后,输电断面T1内的线路l5307、l5308的有功潮流迅速增加,09:27,线路l5307、l5308的有功潮流增加到1 336 MW、1 337 MW,超过其线路自身的热稳定功率极限;与此同时,输电断面T1传输的有功潮流增加到3 470 MW,超过其自身的极限传输功率(3 400 MW),造成输电断面潮流越限,潮流越限量为70 MW。输电断面T1内过载线路以及重载线路的潮流分布情况见表 5。
|
|
表 5 实际电网中关键线路的潮流运行状态 Table 5 Power flow operation of key lines in the actual power grid |
切除过载线路会引发输电断面连锁过载,因此,采用文中方法对输电断面T1进行潮流越限调整,制定的潮流控制策略如表 6所示。
|
|
表 6 潮流控制方案 Table 6 Power flow control scheme |
由表 6可知,文中方法制定的潮流控制策略要调度的机组节点为G42、G34、G40,符合机组节点G42、G34、G40对关键线路潮流调整效果较好的实际情况。而且G42、G34的出力增加调整量近似等于G40的出力减少调整量,总出力调整量为793 MW,有效避免平衡机组过度参与潮流调整。通过制定的潮流控制策略对潮流越限的输电断面T1进行调整控制,得到的线路潮流调整结果如表 7所示。
|
|
表 7 实际电网中关键线路调整结果 Table 7 Adjustment results of key lines in the actual power grid |
由表 7可知,根据文中方法制定的潮流控制策略,在09:27开始对输电断面T1进行潮流调整。经过潮流调整后,输电断面T1内的过载线路l5307、l5308的有功潮流分别由越限时的1 336 MW、1 337 WM逐渐调整为1 249 MW、1 246 WM;09:30,输电断面T1的有功潮流调整为3 390 MW,低于其自身的极限传输功率,潮流越限量被消除;09:40左右,调度节点的潮流调整结束。通过潮流调整,输电断面T1在其极限传输功率的范围内安全运行,且所有线路的有功潮流均在热稳定功率极限内,可实现电网的安全稳定运行。
通过IEEE 39节点系统和某省级电网的输电断面潮流控制分析可以看出:文中提出的基于正负综合灵敏度的输电断面双层优化潮流控制方法能够快速制定出符合调度目标的潮流越限控制策略,完成对过载线路的有功安全校正,实现对输电断面潮流越限的精准调度。
6 结论针对灵敏度分析方法精确度不高以及直接优化类方法计算速度过慢等缺陷,文中提出一种基于正负综合灵敏度的输电断面双层优化潮流控制策略,该方法具有以下优点:
(1) 该方法充分考虑节点对过载及重载线路潮流的整体控制作用,提出节点的正负综合灵敏度指标。同时为减少计算量,剔除对关键线路集潮流控制效果较差的节点。
(2) 该方法采用双层优化思想,首先构建第一层调度节点多目标筛选优化模型,快速选择参与潮流控制的调度节点,有效避免搜索空间过大导致计算量激增的问题。然后构建第二层潮流调控优化模型,计算所选调度节点的精确出力调整量,实现对输电断面潮流越限的精准调度。
致谢
本文得到国网安徽省电力有限公司科技项目(B31200200005)资助,谨此致谢!
| [1] |
严道波, 文劲宇, 杜治, 等. 2021年得州大停电事故分析及其对电网规划管理的启示[J]. 电力系统保护与控制, 2021, 49(9): 121-128. YAN Daobo, WEN Jinyu, DU Zhi, et al. Analysis of Texas blackout in 2021 andits enlightenment to power system planning management[J]. Power System Protection and Control, 2021, 49(9): 121-128. (  0) 0) |
| [2] |
赵静波, 张思聪, 廖诗武. 美国加州2020年8月中旬停电事故分析及思考[J]. 电力工程技术, 2020, 39(6): 52-57. ZHAO Jingbo, ZHANG Sicong, LIAO Shiwu. Analysis and reflection for the rotating outages in mid-August 2020 in California[J]. Electric Power Engineering Technology, 2020, 39(6): 52-57. (  0) 0) |
| [3] |
孙华东, 许涛, 郭强, 等. 英国"8·9"大停电事故分析及对中国电网的启示[J]. 中国电机工程学报, 2019, 39(21): 6183-6192. SUN Huadong, XU Tao, GUO Qiang, et al. Analysis on blackout ingreat Britain power grid on August 9th, 2019 and its enlightenment to power grid in China[J]. Proceedings of the CSEE, 2019, 39(21): 6183-6192. (  0) 0) |
| [4] |
易俊, 卜广全, 郭强, 等. 巴西"3·21"大停电事故分析及对中国电网的启示[J]. 电力系统自动化, 2019, 43(2): 1-6. YI Jun, BU Guangquan, GUO Qiang, et al. Analysis on blackout in Brazilian power grid on March 21, 2018 and its enlightenment to power grid in China[J]. Automation of Electric Power Systems, 2019, 43(2): 1-6. (  0) 0) |
| [5] |
ZHAI C. A model predictive approach to protect power systems against cascading blackouts[J]. International Journal of Electrical Power & Energy Systems, 2019, 113: 310-321. (  0) 0) |
| [6] |
任建文, 魏俊姣, 谷雨峰. 基于多目标粒子群优化算法的连锁跳闸预防控制[J]. 电力自动化设备, 2016, 36(7): 53-59. REN Jianwen, WEI Junjiao, GU Yufeng. Preventive control based on multi-objective particle swarm optimization algorithm for cascading trips[J]. Electric Power Automation Equipment, 2016, 36(7): 53-59. (  0) 0) |
| [7] |
顾雪平, 张尚, 王涛, 等. 安全域视角下的有功安全校正优化控制方法[J]. 电力系统自动化, 2017, 41(18): 17-24. GU Xueping, ZHANG Shang, WANG Tao, et al. Optimization control strategy for active power correction from perspective of security region[J]. Automation of Electric Power Systems, 2017, 41(18): 17-24. (  0) 0) |
| [8] |
程临燕, 郝治国, 张保会, 等. 基于内点法消除输电断面过载的实时控制算法[J]. 电力系统自动化, 2011, 35(17): 51-55. CHENG Linyan, HAO Zhiguo, ZHANG Baohui, et al. Fast elimination of overload in transmission line section based on simplified primal-dual interior point method[J]. Automation of Electric Power Systems, 2011, 35(17): 51-55. (  0) 0) |
| [9] |
袁晓丹, 张会强. 多支路开断潮流转移识别及防连锁过载策略研究[J]. 现代电力, 2014, 31(5): 74-79. YUAN Xiaodan, ZHANG Huiqiang. Study on power flow transferring identification of multi-line tripping and the strategy to prevent cascading overload strategy[J]. Modern Electric Power, 2014, 31(5): 74-79. (  0) 0) |
| [10] |
甘德树, 冯伯庚, 蒋芳玉, 等. 基于功率灵敏度分析的断面潮流安全控制方法[J]. 陕西电力, 2017, 45(1): 82-85. GAN Deshu, FENG Bogeng, JIANG Fangyu, et al. Security control method for interface power flow based on power sensitivity analysis[J]. Shaanxi Electric Power, 2017, 45(1): 82-85. (  0) 0) |
| [11] |
徐岩, 郅静. 基于功率灵敏度的线路过载划区域紧急控制策略[J]. 电工技术学报, 2015, 30(15): 60-72. XU Yan, ZHI Jing. A zone-divided emergency control strategy for overload lines based on power sensitivity[J]. Transactions of China Electrotechnical Society, 2015, 30(15): 60-72. (  0) 0) |
| [12] |
徐伟, 李群, 杨君军, 等. 基于综合贡献度指标的紧急减负荷控制多目标优化方法[J]. 电力自动化设备, 2018, 38(8): 189-194. XU Wei, LI Qun, YANG Junjun, et al. Multi-objective optimization method for emergency load shedding based on comprehensive contribution index[J]. Electric Power Automation Equipment, 2018, 38(8): 189-194. (  0) 0) |
| [13] |
张丹丹, 张婉婕, 武乃虎, 等. 基于综合灵敏度分析的线路过载联切负荷优化决策方法[J]. 山东电力技术, 2018, 45(7): 20-24. ZHANG Dandan, ZHANG Wanjie, WU Naihu, et al. Load shedding strategy coordinate optimization based on sensitivity analysis[J]. Shandong Electric Power, 2018, 45(7): 20-24. (  0) 0) |
| [14] |
徐正清, 肖艳炜, 李群山, 等. 基于灵敏度及粒子群算法的输电断面功率越限控制方法对比研究[J]. 电力系统保护与控制, 2020, 48(15): 177-186. XU Zhengqing, XIAO Yanwei, LI Qunshan, et al. Comparative study based on sensitivity and particle swarm optimization algorithm for power flow over-limit control method of transmission section[J]. Power System Protection and Control, 2020, 48(15): 177-186. (  0) 0) |
| [15] |
徐岩, 郅静, 樊世通. 基于功率灵敏度和经济补偿最小化的线路过负荷紧急控制方法[J]. 电力自动化设备, 2017, 37(1): 118-123. XU Yan, ZHI Jing, FAN Shitong. Line overload emergency control based on power sensitivity and minimized economic compensation[J]. Electric Power Automation Equipment, 2017, 37(1): 118-123. (  0) 0) |
| [16] |
REDDY S S. Multi-objective based congestion management using generation rescheduling and load shedding[J]. IEEE Transactions on Power Systems, 2017, 32(2): 852-863. (  0) 0) |
| [17] |
王健, 李国平. 基于改进和声搜索算法线路过载控制策略研究[J]. 电气传动, 2021, 51(12): 23-27. WANG Jian, LI Guoping. Research on line overload control strategy based on improved harmony search algorithm[J]. Electric Drive, 2021, 51(12): 23-27. (  0) 0) |
| [18] |
孙淑琴, 颜文丽, 吴晨悦, 等. 基于原-对偶内点法的输电断面有功安全校正控制方法[J]. 电力系统保护与控制, 2021, 49(7): 75-85. SUN Shuqin, YAN Wenli, WU Chenyue, et al. Active power flow safety correction control method of transmission sections based on a primal-dual interior point method[J]. Power System Protection and Control, 2021, 49(7): 75-85. (  0) 0) |
| [19] |
夏成军, 华夏, 李清. 基于功率灵敏度的等值机出力定向调整策略[J]. 电力自动化设备, 2019, 39(2): 123-127, 134. XIA Chengjun, HUA Xia, LI Qing. Directional adjustment strategy for equivalent generator output based on power sensitivity[J]. Electric Power Automation Equipment, 2019, 39(2): 123-127, 134. (  0) 0) |
| [20] |
BATTAPOTHULA G, YAMMANI C, MAHESWARAPU S. Multi-objective simultaneous optimal planning of electrical vehicle fast charging stations and DGs in distribution system[J]. Journal of Modern Power Systems and Clean Energy, 2019, 7(4): 923-934. (  0) 0) |
| [21] |
张军, 王红敏, 刘廷章. 基于NSGA-Ⅱ的ICS算法微网多目标优化调度[J]. 电工电能新技术, 2019, 38(12): 19-27. ZHANG Jun, WANG Hongmin, LIU Tingzhang. Multi-objective optimization scheduling of microgrid based on improved cuckoo algorithm[J]. Advanced Technology of Electrical Engineering and Energy, 2019, 38(12): 19-27. (  0) 0) |
| [22] |
李超, 苗世洪, 盛万兴, 等. 考虑动态网络重构的主动配电网优化运行策略[J]. 电工技术学报, 2019, 34(18): 3909-3919. LI Chao, MIAO Shihong, SHENG Wanxing, et al. Optimization operation strategy of active distribution network considering dynamic network reconfiguration[J]. Transactions of China Ele-trotechnical Society, 2019, 34(18): 3909-3919. (  0) 0) |
| [23] |
杨智超, 孙磊, 丁明. 计及关键恢复路径的机组启动次序优化策略[J]. 电力建设, 2019, 40(10): 28-35. YANG Zhichao, SUN Lei, DING Ming. Optimization strategy for start-up sequence of generation units considering critical restoration paths[J]. Electric Power Construction, 2019, 40(10): 28-35. (  0) 0) |
| [24] |
ZHANG D B, WANG N J, YANG H J, et al. Fast search algorithm for key transmission sections based on topology converging adjacency matrix[J]. IEEE Access, 2020(8): 108235-108246. (  0) 0) |
| [25] |
张大波, 王博欣, 郭怀新, 等. 基于拓扑聚合的输电断面辨识方法与断面传输极限的研究[J]. 电力系统保护与控制, 2022, 50(5): 33-42. ZHANG Dabo, WANG Boxin, GUO Huaixin, et al. A method of identifying a transmission section based on topology aggregation and the transmission limit of the section[J]. Power System Protection and Control, 2022, 50(5): 33-42. (  0) 0) |
2. Anhui Province Key Laboratory of Renewable Energy Utilization and Energy Saving(Hefei University of Technology), Hefei 230009, China;
3. State Grid Rongcheng Power Supply Company of Shandong Electric Power Company, Rongcheng 264300, China
 2023, Vol. 42
2023, Vol. 42


 谢大为(1978), 男, 硕士, 高级工程师, 从事电力系统分析控制相关工作(E-mail:
谢大为(1978), 男, 硕士, 高级工程师, 从事电力系统分析控制相关工作(E-mail: