文章编号: 2096-3203(2023)01-0088-10 中图分类号: TM761
近年来我国电动汽车(electric vehicle, EV)保有量迅速增加,截至2022年底预计超过1 000万辆,大量EV接入使电网的负荷压力不断增大[1-2]。EV同时具备负荷和电源的双重性质,因此将其用作分布式储能的车网互动(vehicle-to-grid, V2G)技术得到快速发展[3-6]。利用V2G技术合理调配EV入网,不仅能减小EV带来的负荷压力,还可以为电网提供辅助服务,包括:调频、无功调压、调峰等[7-9],其中EV参与调频是目前研究最多,被认为最有价值和前景的方向[10]。
EV通过电力电子接口接入电网参与V2G调频,具有比传统机组更快的响应速度,但同时EV进行充/放电时缺乏惯性和阻尼,会影响电网的稳定性。虚拟同步机(virtual synchronous generator, VSG)技术通过模拟同步发电机的内在电磁暂态特性,可以使充电机的AC/DC变换器具备和同步发电机相似的运行特性和频率调节特性[11]。将VSG技术与V2G技术结合能够有效解决传统V2G调频的惯性和阻尼缺失问题,已成为目前的研究热点[12-15]。
EV参与调频时不能无控制地充放电,须兼顾对汽车电池、用户以及电网的影响,因此调频控制策略至关重要。现阶段的EV调频控制策略研究通过考虑EV的电池寿命[16-17]、用户期望电量[18]、电网频率[19]等因素来平衡EV、用户和电网三者的需求。特别地,为适应EV固有的交通工具属性,在参与调频时必须考虑用户的充电计划,即EV须在设定的时间内充电至期望的荷电状态(state of charge, SOC)。因此文献[11]将实时SOC(记为SSOC)作为控制量来调节EV的调频功率,保证满足用户出行需求,但SOC的期望值SSOC_e不可控。文献[13]根据SSOC、SSOC_e自适应改变频率下垂系数来调节一次调频功率,但并未考虑EV的充电时间,无法保证按时完成充电计划。文献[14]根据EV剩余充电时间和从当前SOC以额定功率充电至SSOC_e所需时间的关系,实时控制调频功率,可保证按时完成充电。但该策略仅考虑剩余充电时间的作用,而对SOC的情况考虑不足,导致EV的调频能力未被充分利用,还容易造成部分EV在调频时出现过充、过放的情况,损害电池寿命。
合理的EV调频策略须克服以上不足,还应使EV在充电完成后能维持SOC在期望值。基于此,文中首先定义了SOC偏离度Sx,并在文献[14]的基础上提出V2G剩余时间因子α,从SSOC和充电时间两方面监控EV的充电状态。然后针对一、二次调频分别设计T-S模糊控制器,使EV可以根据电网频率、剩余充电时间以及SOC情况智能调节充/放电功率,在保证调频出力的前提下,按时完成用户的充电计划,并规避过充、过放风险。最后,进行仿真对比,验证文中所提EV辅助调频策略在完成用户充电计划和维持电网频率稳定方面的有效性。
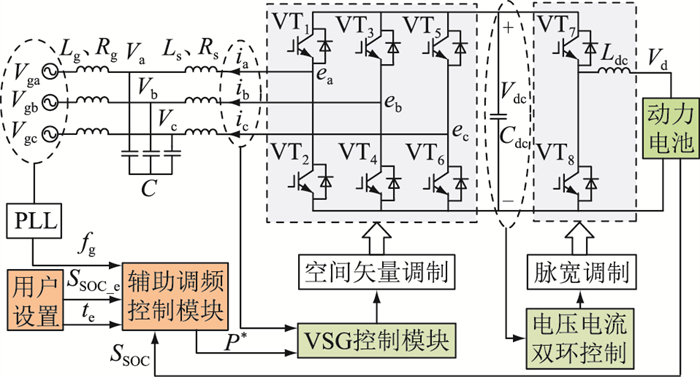
1 EV充放电电路拓扑及控制 1.1 基于VSG的EV充电机拓扑基于VSG的EV充电机拓扑见图 1。该充电机拓扑由两级电路组成,前级为包含LCL滤波器的三相全桥AC/DC变换器,后级为双向Buck/Boost变换器。图 1中,Vga、Vgb、Vgc分别为电网侧三相电压;Lg、Rg分别为电网侧电感和电阻,与逆变器侧电阻、电感、电容(Rs、Ls、C)构成LCL滤波器;ea、eb、ec分别为AC/DC变换器交流侧三相电动势;Va、Vb、Vc分别为滤波器电容端三相电压;ia、ib、ic分别为交流侧三相输出电流;Cdc为直流母线电容;Vdc为直流母线电压;Vd为DC/DC变换器低压侧电压;Ldc为电池侧电感;te为用户设定的期望充电时间;fg为锁相环(phase locked loop, PLL)测得的电网频率;P*为EV的充/放电功率信号;VT1—VT8为8个功率开关管。
|
图 1 充电机电路拓扑 Fig. 1 Circuit topology of charging machine |
如图 1所示,整体控制结构由上层辅助调频模块、AC/DC变换器VSG控制模块以及DC/DC电压电流双环控制模块3个部分组成。辅助调频控制模块根据用户设置的te和SSOC_e,结合实时检测到的电网频率和电池SOC,智能调节EV的充/放电功率信号P*;VSG控制模块响应该功率信号P*,并增加系统的惯量和阻尼;DC/DC电压电流双环控制通过维持直流侧电容电压恒定来响应系统的功率变化。
1.2 VSG控制模块三相全桥AC/DC变换器采用VSG控制,将图 1中Rs和Ls等效为同步发电机定子阻抗;ea、eb、ec等效为电机电动势;Va、Vb、Vc等效为电机定子三相端电压;ia、ib、ic等效为同步发电机的定子电流,从而将AC/DC变换器等效为同步发电机。两者具有相同的惯性、阻尼特性和频率/电压下垂特性[16]。VSG的基本方程由式(1)—式(6)给出:
| $ J \frac{\mathrm{d} \omega}{\mathrm{d} t}=T_{\mathrm{m}}-T_{\mathrm{e}}+D_{\mathrm{p}}\left(\omega_{\mathrm{n}}-\omega\right) $ | (1) |
| $ \boldsymbol{e}=M_{\mathrm{f}} i_{\mathrm{f}} \omega \boldsymbol{F} $ | (2) |
| $ T_{\mathrm{e}}=M_{\mathrm{f}} i_{\mathrm{f}}\langle\boldsymbol{i}, \boldsymbol{F}\rangle $ | (3) |
| $ Q=-M_{\mathrm{f}} i_{\mathrm{f}} \omega\langle\boldsymbol{i}, \boldsymbol{G}\rangle $ | (4) |
| $ \boldsymbol{F}=\left[\begin{array}{c} \sin \theta \\ \sin (\theta-2 \pi / 3) \\ \sin (\theta+2 \pi / 3) \end{array}\right] $ | (5) |
| $ \boldsymbol{G}=\left[\begin{array}{c} \cos \theta \\ \cos (\theta-2 \pi / 3) \\ \cos (\theta+2 \pi / 3) \end{array}\right] $ | (6) |
式中:〈〉表示点积运算;J为虚拟惯量;Te为电磁转矩;Tm为机械转矩;Dp为转子机械阻尼系数;ωn为电网的参考角频率;ω为VSG转子的角频率;e =[ea,eb,ec]T、i =[ia,ib,ic]T分别为三相电动势和三相电流构成的向量;Mf为VSG定、转子之间的互感;if为虚拟励磁电流;Q为VSG输出的无功功率;θ为转子电角度。
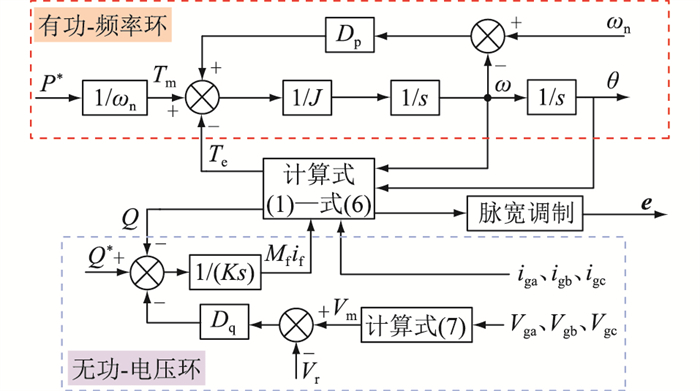
VSG控制模块的基本框图如图 2所示,整体上分为有功-频率环与无功-电压环。在有功-频率环中,P*为VSG有功功率参考值,即EV的充/放电功率信号;S为复频率。在无功-电压环中,Dq为电压下垂系数;Q*为VSG无功功率参考值;K为积分系数;iga、igb、igc分别为电网三相相电流;Vr为电网额定相电压有效值的幅值;Vm为相电压有效值的幅值, Vm由式(7)计算得出[11]。
| $ V_{\mathrm{ga}} V_{\mathrm{gb}}+V_{\mathrm{ga}} V_{\mathrm{gc}}+V_{\mathrm{gb}} V_{\mathrm{gc}}=-\frac{3}{4} V_{\mathrm{m}}^2 $ | (7) |
|
图 2 VSG控制结构 Fig. 2 Control structure of VSG |
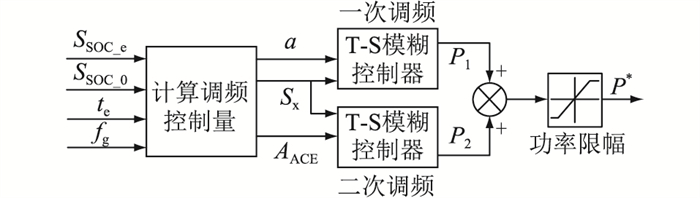
EV参与辅助调频时要平衡电网、用户与EV三方的需求,即在满足电网频率调节需求的前提下,还须保证在期望充电时间内将EV充电至SSOC_e,同时减少对电池寿命的损害。因此除了考虑电网频率偏差,还要在电池SOC、充电时间两方面设置控制参数。为此,文中定义SOC偏离度Sx与V2G剩余时间因子α,实时监控EV的充/放电状态。由T-S模糊控制器根据Sx、α以及区域控制偏差信号(area control area, ACE)等3个调频控制量来决定EV的一、二次调频功率P1、P2,如图 3所示。图 3中AACE为ACE的取值;SSOC_0为SOC的初始值;功率限幅模块将EV的总充/放电功率限制在最大充/放电功率Pcmax和Pdmax范围内。
|
图 3 辅助调频控制框图 Fig. 3 Control block diagram of frequency regulation |
(1) SOC偏离度Sx。Sx从SOC方面反映EV偏离充电计划的程度,其设计原则为:SSOC < SSOC_e表示EV处于欠电状态,SSOC越小则EV的充电功率应越大以防止过放;SSOC>SSOC_e表示EV的电量充足,SSOC越大,放电功率应越大以防止过充;SSOC=SSOC_e表示EV的电量已达到用户期望值,充/放电功率都应适中以维持SOC。通过式(8)计算Sx,该值越接近±1表示SSOC偏离SSOC_e的程度越大。根据Sx的大小状态来调整充/放电功率,便能防止过充、过放,起到维持SOC的作用,还可适应用户对不同SSOC_e的需求。考虑到实际情况中SOC接近0和1的极端情况,将Sx的值限制在[-1, 1]内。
| $ {S_{\rm{x}}} = \left\{ {\begin{array}{*{20}{l}} {\frac{{{S_{{\rm{SOC}}}} - {S_{{\rm{SO}}{{\rm{C}}_ - }{\rm{e}}}}}}{{{S_{{\rm{SO}}{{\rm{C}}_ - }{\rm{max}}}} - {S_{{\rm{SO}}{{\rm{C}}_ - }{\rm{e}}}}}}\quad {S_{{\rm{SOC}}}} > {S_{{\rm{SO}}{{\rm{C}}_ - }{\rm{e}}}}}\\ {0\quad {S_{{\rm{SOC}}}} = {S_{{\rm{SO}}{{\rm{C}}_ - }{\rm{e}}}}}\\ {\frac{{{S_{{\rm{SOC }}}} - {S_{{\rm{SO}}{{\rm{C}}_{\rm{e}}}}}}}{{{S_{{\rm{SO}}{{\rm{C}}_ -{\rm{e}}}}} - {S_{{\rm{SO}}{{\rm{C}}_{\rm{_ -}}}{\rm{min}}}}}}\quad {S_{{\rm{SOC }}}} < {S_{{\rm{SO}}{{\rm{C}}_ - {\rm{e}}}}}} \end{array}} \right. $ | (8) |
式中:SSOC_max、SSOC_min分别为EV电池SOC的最大和最小值。
(2) V2G剩余时间因子α。α从时间方面反映EV完成充电计划的紧迫程度,用以保证充电计划可以按时完成。其设计原则为:若EV在剩余入网时间内足够以额定功率充电至SSOC_e,则有多余的时间用来参与V2G;若剩余的入网时间小于以额定功率充电至SSOC_e的时间tn,则EV只能进行单向充电。文献[14]的调频策略设置α=te/(tnow+tn)-1,范围规定为[0, 1],其中tnow为已充电时间,tn的计算为:
| $ t_{\mathrm{n}}=\frac{\left(S_{\mathrm{SOC}_{-} \mathrm{e}}-S_{\mathrm{SOC}}\right) Q_{\mathrm{n}}}{P_{\mathrm{n}}} $ | (9) |
式中:Pn为EV的额定充电功率;Qn为EV电池的额定容量。文献[14]中α的计算方法虽能反映EV剩余入网时间的多少,但当用户将te设置得较大时,α很容易达到最大值,此时调频策略中放电调频下垂系数达到最大,限制了EV的充电调频能力,EV的SSOC极小时还会有过放风险。因此文中引入tf,直接表示EV可用于参与V2G的时间,te、tf、tnow、tn的关系见图 4,即tf=te-tnow-tn。由式(10)计算α,并将α限定在[0, 1]之内,只有在出现te=tf或te=tn的特殊情况时,α才会达到极值,更加合理。
| $ \alpha=t_{\mathrm{f}} / t_{\mathrm{e}} $ | (10) |

|
图 4 EV充电时间示意 Fig. 4 Schematic diagram for charging time of EV |
(3) 区域控制偏差信号AACE。AACE用于二次调频,反映区域内电网的频率偏差程度,其计算见式(11),其中B为区域频率偏差因子,Δf为电网频率偏差。
| $ A_{\mathrm{ACE}}=B \Delta f $ | (11) |
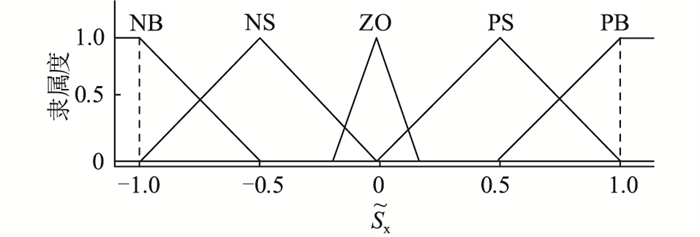
(1) Sx的模糊化。设
|
图 5 Sx的隶属度函数 Fig. 5 Membership function of Sx |
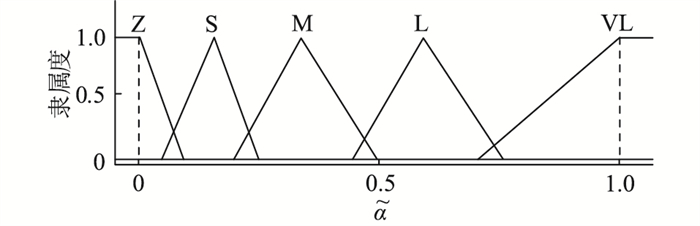
(2) α的模糊化。设
|
图 6 α的隶属度函数 Fig. 6 Membership function of α |
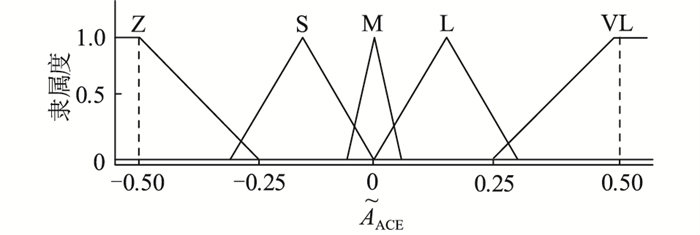
(3) AACE的模糊化。设
|
图 7 AACE的隶属度函数 Fig. 7 Membership function of AACE |
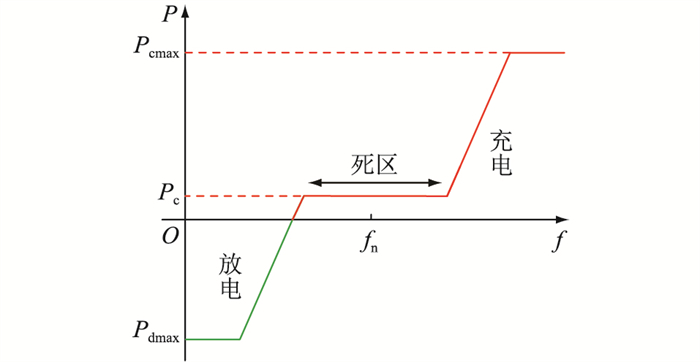
与传统下垂控制不同,EV参与一次调频时为保证充电需求,须设置基本充电功率Pc[20]。另外为防止EV频繁充放电,设置一次调频死区为[fn-0.03, fn+0.03],其中fn为额定电网频率,取fn=50 Hz。在死区内仅以Pc进行充电,当频率超出死区时,功率变化量为频率下垂系数与频率偏差之积[21]。EV参与一次调频的下垂特性如图 8所示,图中一次调频功率P1由式(12)计算得到,并被限制在[Pcmax, Pdmax]范围内,式中Kc、Kd分别为充、放电频率下垂系数。
|
图 8 EV参与一次调频的下垂特性曲线 Fig. 8 Droop characteristic curve of EV participating in primary frequency regulation |
| $ P_1=\left\{\begin{array}{l} P_{\mathrm{c}}+K_{\mathrm{c}}\left(f_{\mathrm{g}}-50.03\right) \quad f_{\mathrm{g}} \geqslant 50.03 \\ P_{\mathrm{c}} \quad 49.97<f_{\mathrm{g}}<50.03 \\ P_{\mathrm{c}}+K_{\mathrm{d}}\left(f_{\mathrm{g}}-49.97\right) \quad f_{\mathrm{g}} \leqslant 49.97 \end{array}\right. $ | (12) |
为保证按时完成用户的充电计划,Pc与下垂系数Kc、Kd应随EV的充电进程变化,为此文中设计了考虑用户充电计划的一次调频策略。
(1) 在Sx < 0时,设计其Pc为(1-α)Pn,能够随α减小而增大,直至以额定功率Pn进行充电,确保EV有基本的充电功率用以完成充电计划;Sx≥0时,EV无充电需求,则Pc=0。因此EV的基本充电功率Pc可表示如下:
| $ P_{\mathrm{c}}=\left\{\begin{array}{l} (1-\alpha) P_{\mathrm{n}} \quad S_{\mathrm{x}}<0 \\ 0 \quad S_{\mathrm{x}} \geqslant 0 \end{array}\right. $ | (13) |
(2) 设计下垂系数也随α变化,α越小则充电下垂系数越大,放电下垂系数越小,同时为防止调频时EV出现过充、过放,充/放电下垂系数还应受实时SOC的限制,三者之间存在复杂的非线性关系,因此采用模糊控制,根据α与Sx直接决定下垂系数的取值。基于以上分析,设最大下垂系数为Kmax,充电下垂系数Kc=Kmax-Kd,Kd由T-S模糊控制器得到。一次调频采用的模糊控制规则为:若模糊控制器的输入x1、x2分别属于模糊集合W1, i、W2, i,则第i条模糊控制规则的输出为:
| $ K_{\mathrm{d}, i}=f_i\left(x_1, x_2\right)=a_i x_1+b_i x_2+c \quad i=1, 2, \cdots, n $ | (14) |
式中:Kd, i为第i条模糊规则决定的放电下垂系数;ai、bi为输入系数;c为常数;n为模糊控制规则数。
文中取x1=α,x2=Sx,
| $ K_{\mathrm{d}, i}=f_i(\alpha)=a_i \alpha+c $ | (15) |
模糊控制规则的设计依据如下:
(1) SSOC>SSOC_e或接近SSOC_min时,为防止过充过放,下垂系数不由aiα项直接控制,此时ai=0,由c根据Sx和α进行调整,包括以下情况:① Sx接近-1,此时若α极小/较小,对应Pc较大,无过放风险,可设置较大的Kd;若α极大/较大,由于SSOC极小,且Pc较小,设置Kd较小以防止过放。② 0 < Sx < 1,c随α增大而逐渐减小。③ Sx接近1,无论α为何值,Kd应为最大,此时EV不进行充电,只参与放电调频。
(2) 当SSOC较小或接近SSOC_e时,EV处于充电过程的中后期阶段,无过充、过放问题,此时主要由aiα控制下垂系数,α取值越小,充电功率越大,同时放电功率越小。
根据以上分析,设计放电下垂系数模糊控制规则如表 1所示,其中C1、C2分别为0.9Kmax和Kmax,Ki=12 000i(i=1, 2, …, 5)。
|
|
表 1 放电下垂系数模糊控制规则 Table 1 Fuzzy control rules for droop coefficient of discharging |
当电网频率的波动幅度大、波动时间长时,需要EV在一次调频的基础上增加功率P2来参与二次调频[22-25],文中设置EV参与二次调频的动作阈值为Δf ≥0.1 Hz。二次调频控制策略仍采用T-S模糊控制器决定P2的取值,如图 9所示。

|
图 9 EV参与二次调频控制策略 Fig. 9 Control strategy of EV participating in secondary frequency regulation |
二次调频采用的模糊控制规则为:若模糊控制器的输入y1、y2分别属于模糊集合Z1, i、Z2, i,则第i条模糊控制规则的输出为:
| $ P_{2, i}=g_i\left(y_1, y_2\right)=p_i y_1+q_i y_2+d \quad i=1, 2, \cdots, n $ | (16) |
式中:P2, i为第i条模糊规则决定的二次调频功率;pi、qi为输入系数;d为常数。文中取y1= Sx,y2=AACE,Z1, i∈
| $ P_{2, i}=g_i\left(S_{\mathrm{x}}\right)=p_i\left|S_{\mathrm{x}}\right|+d $ | (17) |
当AACE < 0且Sx>0时,Sx越大则放电功率越大,AACE>0且Sx < 0时,Sx越小则充电功率越大,这2种情况下P2由pi Sx项决定。剩余情况由d根据AACE对充/放电功率进行精细控制:(1) AACE < 0且Sx < 0时,以小功率放电;(2) AACE>0且Sx>0时,以小功率充电;(3) 在Sx接近1或-1时,控制P2为0,防止过充、过放。根据以上分析,设计二次调频模糊控制规则如表 2所示,其中Hi=1 000i(i=1, 2, …, 5),单位为W,正值表示放电,负值表示充电;Z、S、M、L、VL为AACE的模糊语言。
|
|
表 2 二次调频模糊控制规则 Table 2 Fuzzy control rules for secondary frequency regulation |
为验证文中所提EV调频策略的有效性,并对比分析EV参与调频时,文献[14]中控制策略(以下称为策略1)与文中控制策略(以下称为策略2)在不同充电计划下的控制效果。使用Matlab R2020b/Simulink搭建电路模型进行仿真分析,仿真步长设置为1μs,充电机仿真模型的关键参数采用文献[11]中的参数,具体取值如表 3所示。模型中的EV电池类型设置为磷酸铁锂电池[26-29],额定电压为300 V。
|
|
表 3 充电机模型仿真参数 Table 3 Simulation parameters for the model of EV charging machine |
设计3组初始SOC(记为SSOC_0)分别为30%,50%,95%的6辆EV,每组中2辆EV的期望充电时间te分别设置为4 h和10 h,用以对比在不同电网频率、SOC和期望充电时间条件下,一次调频策略对充放/电功率的控制效果。一次调频仿真工况设置如表 4所示,6辆EV的具体参数如表 5所示,其中α0为策略2中EV的初始α。仿真结果见图 10。
|
|
表 4 一次调频工况 Table 4 Working condition of primary frequency control |
|
|
表 5 EV的仿真参数 Table 5 Simulation parameters of EV |
|
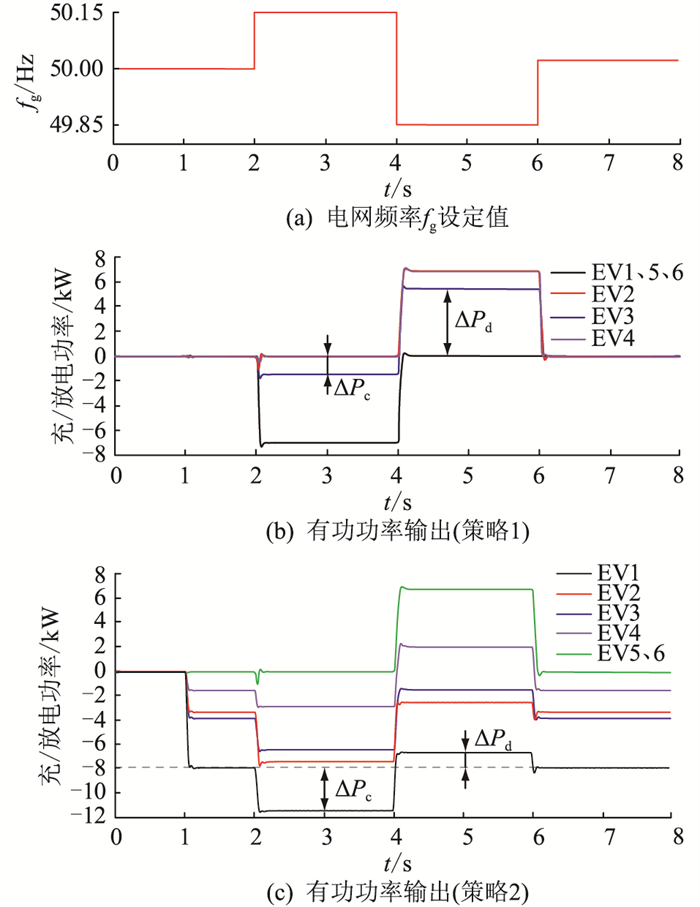
图 10 EV参与一次调频的仿真结果 Fig. 10 Simulative results of EV participating in primary frequency regulation |
(1) 工况1:EV未并网,且电网频率为50 Hz,由图 10可以看出2种策略控制下的EV无充/放电功率。
(2) 工况2:EV并网运行,电网频率为50 Hz,因此调频功率为0。①策略1未设置基本充电功率,当电网频率正常时EV不进行充电,会造成充电时间的浪费;②策略2中电动汽车以Pc功率充电,其中α越小的EV充电功率越大,以保证能够按时完成充电计划。
(3) 工况3:电网频率高于额定频率,EV应进行充电或减少放电功率,Sx和α越小的EV充电调频功率ΔPc越大。①策略1中,EV2的ΔPc为0,调频能力不足,并且未考虑SSOC>SSOC_e的情况,导致EV5、EV6的充电功率较大,有过充风险。②策略2中SSOC接近SSOC_min的EV1、EV2的ΔPc最大;EV3、EV4的SSOC适中,ΔPc较小并随α增大而减小;EV5、EV6的SSOC>SSOC_e且α0为1,充电功率为0。
(4) 工况4:电网频率低于额定频率,EV应进行放电或减小充电功率。①策略1中EV2在SSOC接近SSOC_min时仍承担较大的放电功率,有过放风险,并且由于未考虑SSOC>SSOC_e的情况,EV5、EV6并无放电功率,未充分利用其放电调频能力;②策略2中EV1、EV2的SSOC接近SSOC_min,其放电调频功率ΔPd最小;EV3、EV4的SSOC适中,其ΔPd较大且随α增大而增大;EV5、EV6的α最大,因此其ΔPd最大且基本充电功率为0。
(5) 工况5:电网频率未超越死区,故调频功率为0,与工况2结果相同。
由上述分析可以看出,策略1仅通过α决定一次调频功率,未考虑SOC的限制,无法充分发挥EV的调频潜力,同时还有过充、过放风险。而策略2的一次调频策略可以根据用户对充电时间和电量的需求以及EV的充电状态对充/放电功率进行智能调节。
3.2 二次调频充放电控制效果仿真验证二次调频选取表 5中SSOC_0不同的EV1、EV3、EV5,在一次调频同样的电网频率工况下进行仿真,仿真结果如图 11所示。由图 11可以看出:工况1,由于EV未并网,充/放电功率都为0;工况2,EV并网模式运行,电网频率设定为50 Hz,因此二次调频功率为0;工况3,电网频率高于额定频率,二次调频动作以增大EV的充电功率,Sx越小的EV充电功率越大,EV5的Sx为1,因此充电功率为0;工况4,电网频率低于额定频率,二次调频动作以增大EV的放电功率,其中EV1的Sx最小,因此放电功率最小;工况5,电网频率为50.02 Hz,未超越调频死区,因此EV的二次调频功率为0。
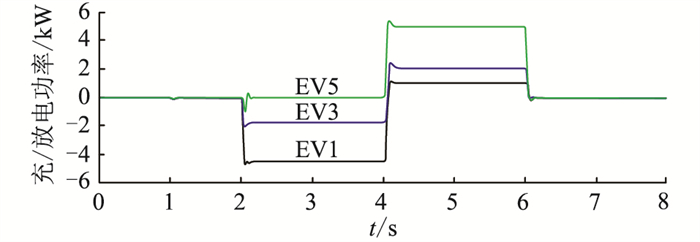
|
图 11 EV参与二次调频的仿真结果 Fig. 11 Simulative results of EV participating in secondary frequency regulation |
由上述分析可以看出,文中设计的二次调频策略根据EV的实时SOC和电网频率偏差对二次调频功率进行智能调节,提高EV的调频能力。
3.3 单区域多EV参与调频仿真算例分析 3.3.1 模型建立为研究采用文中所提充放电控制策略的EV接入电网时对系统频率的调节作用,采用图 12所示含EV的单区域电力系统模型[8, 30]进行仿真,设该系统基准功率为300 MW。图 12中re为调差系数;Tg、Tch分别为调速器时间常数和汽轮机时间常数;M为发电机惯性常数;D为负荷阻尼系数;kr为控制增益;ΔPEV、ΔPM、ΔPL分别为EV、发电机、负荷扰动的功率变化量。
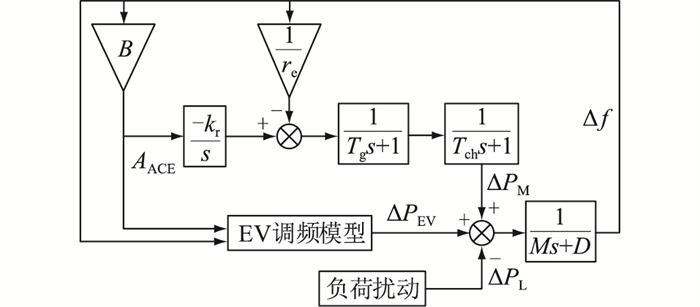
|
图 12 含EV的单区域电力系统模型 Fig. 12 Model of single area power system including EV |
图 12中的EV调频模型如图 13所示,根据充电机工作原理以及VSG模型,用二阶惯性响应函数G(s)模拟EV的VSG功率响应特性[17],其中TEV为VSG的固有时间常数;Jvr、Dvr分别为VSG的等效虚拟惯量、等效虚拟阻尼。

|
图 13 EV调频模型 Fig. 13 Model of EV participating in frequency regulation |
单区域电力系统仿真模型参数采用文献[31]中所用参数,具体数值如表 6所示。
|
|
表 6 单区域电力系统仿真参数 Table 6 Simulation parameters for the model of single area power system |
以图 12电力系统模型为基础,算例场景设置为3种不同的工况:工况Ⅰ为EV不参与电网调频;工况Ⅱ为EV采用策略1参与电网调频;工况Ⅲ为EV采用策略2参与电网调频。仿真中EV仍选取具有代表性的EV1—EV6,具体参数和参与数量如表 7所示。
|
|
表 7 多辆EV参与区域调频的仿真参数 Table 7 Simulation parameters of multiple EVs partici- pating in frequency regulation for single area |
以图 14(a)所示国内某地区电网某日4 h连续负荷扰动ΔPL为研究对象[32],仿真3种工况下的系统频率响应,以及长时间扰动下EV充/放电功率和SOC变化,结果如图 14(b)—图 14(d)所示。
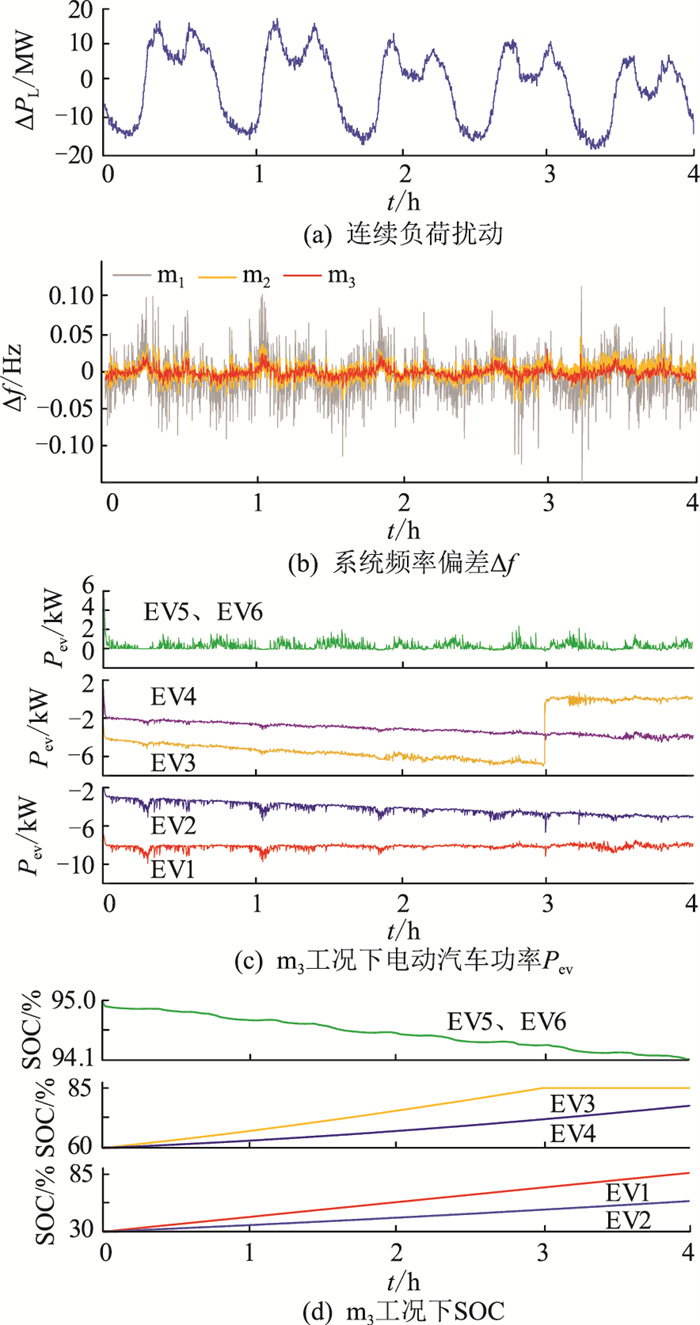
|
图 14 连续扰动仿真结果 Fig. 14 Simulation results of continuous disturbance |
图 14(b)中策略1由于SSOC>SSOC_e的EV未参与放电以及SSOC较小、α较大的EV充电调频能力不足,系统最大频率偏差达到0.048 Hz;而策略2最大频率偏差为0.03 Hz,相对于策略1减小了37%,系统更加稳定。
由图 14(c)可以看出工况Ⅲ中各EV的Pc随充电时间的减少在不断增大,EV的调频出力在Pc附近随频率波动发生如下变化:(1) EV1、EV2的SSOC_0最小,充电功率增加量多于减少量,以快速提升SOC。随着SOC的增加,充电功率减少量也逐渐增多。图 14(d)显示SSOC_0、α0最小的EV1在te时间内完成了充电计划;(2) EV3、EV4的SSOC_0适中,充电功率增加量与减少量相差较小,图 14(d)显示EV3在3 h完成充电计划,随即Pc减为0且充/放电功率的变化量趋于平衡以维持SOC;(3) EV5、EV6的SSOC_0接近SSOC_max,只有放电功率,但随着SOC减小,在负荷减小时也会有少量充电功率产生。
由以上分析可知,在长时间的负荷扰动中,相比于策略1,策略2由于能够在保证充电计划和防止过充、过放的基础上充分利用各EV的调频能力,因此有更好的调频效果,有利于维持系统稳定。并且在完成充电计划之后还能够有维持SOC的作用,做到电网、用户、EV三者需求的平衡协调。
4 结论EV可作为储能参与电网调频,但必须兼顾电网、用户、EV三者的需求。文中基于VSG和模糊控制技术,提出了考虑用户充电计划的EV辅助调频控制策略,并进行了仿真验证,所得结论如下:
(1) 文中定义了SOC偏离度Sx与V2G剩余时间因子α,两者从SOC和时间两方面监控EV的充电进程。
(2) 针对一、二次调频分别设计T-S型模糊控制器,根据α、Sx、AACE智能调节调频功率,EV可以按时完成充电计划,并且具有维持SOC和防止过充、过放的效果。仿真结果表明,相对于文献[13]的调频策略,以文中控制策略参与调频,电力系统最大频率偏差减小了37%。
文中调频控制策略能够有效、可靠地满足用户的充电计划,减小频率波动,为EV参与调频提供了一种新方案。
| [1] |
李丽, 来小康, 慈松, 等. 动力电池梯次利用与回收技术[M]. 北京: 科学出版社, 2020. LI Li, LAI Xiaokang, CI Song, et al. Reuse and recycling technology of power batteries[M]. Beijing: Science Press, 2020. (  0) 0) |
| [2] |
蔡黎, 张权文, 代妮娜, 等. 规模化电动汽车接入主动配电网研究进展综述[J]. 智慧电力, 2021, 49(6): 75-82. CAI Li, ZHANG Quanwen, DAI Nina, et al. Review on research progress of large-scale electric vehicle access to active distribution network[J]. Smart Power, 2021, 49(6): 75-82. (  0) 0) |
| [3] |
徐博文. 电动汽车V2G变换器及控制技术研究[D]. 济南: 山东大学, 2018. XU Bowen. Research on V2G converter for electric vehicles and its control strategy[D]. Jinan: Shandong University, 2018. (  0) 0) |
| [4] |
叶子欣, 刘金朋, 郭霞, 等. 基于用户响应画像的居民小区电动汽车充放电优化策略研究[J]. 智慧电力, 2022, 50(10): 87-94, 115. YE Zixin, LIU Jinpeng, GUO Xia, et al. Charging and discharging optimization strategy for electric vehicles in residential community based on user response portrait[J]. Smart Power, 2022, 50(10): 87-94, 115. (  0) 0) |
| [5] |
蔡黎, 葛棚丹, 代妮娜, 等. 电动汽车入网负荷预测及其与电网互动研究进展综述[J]. 智慧电力, 2022, 50(7): 96-103. CAI Li, GE Pengdan, DAI Nina, et al. Review of research progress on load prediction and grid interaction of electric vehicles[J]. Smart Power, 2022, 50(7): 96-103. (  0) 0) |
| [6] |
陈娜, 陈琛, 周强. 基于电动汽车V2G的柔性直流供电系统灵活资源调控策略研究[J]. 电力需求侧管理, 2022, 24(2): 41-47. CHEN Na, CHEN Chen, ZHOU Qiang. Research on flexible resource regulation strategy of flexible DC power supply system based on electric vehicle's V2G[J]. Power Demand Side Management, 2022, 24(2): 41-47. (  0) 0) |
| [7] |
李德胜, 李国策, 刘博. 基于虚拟同步发电机控制技术的V2G系统研究[J]. 电力系统保护与控制, 2021, 49(7): 127-133. LI Desheng, LI Guoce, LIU Bo. Research on V2G system based on virtual synchronous generator control technology[J]. Power System Protection and Control, 2021, 49(7): 127-133. (  0) 0) |
| [8] |
何晨颖, 耿天翔, 许晓慧, 等. 利用电动汽车可调度容量辅助电网调频研究[J]. 电力系统保护与控制, 2015, 43(22): 134-140. HE Chenying, GENG Tianxiang, XU Xiaohui, et al. Research on grid frequency regulation using schedulable capacity of electric vehicles[J]. Power System Protection and Control, 2015, 43(22): 134-140. (  0) 0) |
| [9] |
白泽洋, 巨健, 姜炎君, 等. 电动汽车参与电网调峰的关键技术研究综述[J]. 电力需求侧管理, 2022, 24(6): 25-31. BAI Zeyang, JU Jian, JIANG Yanjun, et al. Key technologies of electric vehicles participating in power grid peak shaving[J]. Power Demand Side Management, 2022, 24(6): 25-31. (  0) 0) |
| [10] |
李秉宇, 杜旭浩, 曾四鸣, 等. 电动汽车负荷虚拟同步机参与电网频率调节的充放电策略与实现[J]. 电工电能新技术, 2021, 40(6): 11-21. LI Bingyu, DU Xuhao, ZENG Siming, et al. Charge and discharge strategy based on load-side virtual synchronous machine for electric vehicles participating in grid frequency regulation and its realization[J]. Advanced Technology of Electrical Engineering and Energy, 2021, 40(6): 11-21. (  0) 0) |
| [11] |
刘东奇, 钟庆昌, 王耀南, 等. 基于同步逆变器的电动汽车V2G智能充放电控制技术[J]. 中国电机工程学报, 2017, 37(2): 544-557. LIU Dongqi, ZHONG Qingchang, WANG Yaonan, et al. A synchronverter-based V2G smart charging and discharging control strategy for electric vehicles[J]. Proceedings of the CSEE, 2017, 37(2): 544-557. (  0) 0) |
| [12] |
陈天锦, 牛高远, 甘江华, 等. 基于虚拟同步策略的电动汽车V2G充放电系统研究及样机实现[J]. 电力系统保护与控制, 2021, 49(3): 131-141. CHEN Tianjin, NIU Gaoyuan, GAN Jianghua, et al. Research and prototype manufacture on electric vehicle V2G systems based on virtual synchronous control strategy[J]. Power System Protection and Control, 2021, 49(3): 131-141. (  0) 0) |
| [13] |
JAN M U, XIN A, REHMAN H U, et al. Frequency regulation of an isolated microgrid with electric vehicles and energy storage system integration using adaptive and model predictive controllers[J]. IEEE Access, 2021, 9: 14958-14970. (  0) 0) |
| [14] |
苏粟, 李家浩, 李泽宁, 等. 考虑用户需求的电动汽车虚拟同步机辅助调频控制策略[J]. 电力自动化设备, 2021, 41(11): 1-8. SU Su, LI Jiahao, LI Zening, et al. Auxiliary frequency regulation control strategy based on virtual synchronous machine for electric vehicles considering user demand[J]. Electric Power Automation Equipment, 2021, 41(11): 1-8. (  0) 0) |
| [15] |
徐浩祥, 贾燕冰, 任春光, 等. 基于虚拟同步机的电动汽车双向变流器功率控制[J]. 电测与仪表, 2021, 58(12): 31-38. XU Haoxiang, JIA Yanbing, REN Chunguang, et al. Power control of electric vehicle bidirectional converter based on virtual synchronous machine[J]. Electrical Measurement & Instrumentation, 2021, 58(12): 31-38. (  0) 0) |
| [16] |
HERNÁNDEZ J C, SANCHEZ-SUTIL F, VIDAL P G, et al. Primary frequency control and dynamic grid support for vehicle-to-grid in transmission systems[J]. International Journal of Electrical Power & Energy Systems, 2018, 100: 152-166. (  0) 0) |
| [17] |
刘其辉, 逯胜建. 参与微电网调频的电动汽车虚拟同步机充放电控制策略[J]. 电力系统自动化, 2018, 42(9): 171-179. LIU Qihui, LU Shengjian. Charging and discharging control strategy based on virtual synchronous machine for electrical vehicles participating in frequency regulation of microgrid[J]. Automation of Electric Power Systems, 2018, 42(9): 171-179. (  0) 0) |
| [18] |
鲍谚, 贾利民, 姜久春, 等. 电动汽车移动储能辅助频率控制策略的研究[J]. 电工技术学报, 2015, 30(11): 115-126. BAO Yan, JIA Limin, JIANG Jiuchun, et al. Research on the control strategy of electric vehicle mobile energy storage in ancillary frequency regulation[J]. Transactions of China Electrotechnical Society, 2015, 30(11): 115-126. (  0) 0) |
| [19] |
FALAHATI S, TAHER S A, SHAHIDEHPOUR M. Grid secondary frequency control by optimized fuzzy control of electric vehicles[J]. IEEE Transactions on Smart Grid, 2018, 9(6): 5613-5621. (  0) 0) |
| [20] |
LIU S, XIE X, YANG L Y. Analysis, modeling and implementation of a switching bi-directional buck-boost converter based on electric vehicle hybrid energy storage for V2G system[J]. IEEE Access, 2020, 8(56): 65868-65879. (  0) 0) |
| [21] |
诸晓骏, 陈曦, 李妍, 等. 考虑电动汽车接入的主动配电网优化调度[J]. 电力工程技术, 2021, 40(3): 141-147. ZHU Xiaojun, CHEN Xi, LI Yan, et al. Optimal dispatching of active distribution network considering electric vehicle access[J]. Electric Power Engineering Technology, 2021, 40(3): 141-147. (  0) 0) |
| [22] |
LEHTOLA T A, ZAHEDI A. Electric vehicle battery cell cycle aging in vehicle to grid operations: a review[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(1): 423-437. (  0) 0) |
| [23] |
张谦, 邓小松, 岳焕展, 等. 计及电池寿命损耗的电动汽车参与能量-调频市场协同优化策略[J]. 电工技术学报, 2022, 37(1): 72-81. ZHANG Qian, DENG Xiaosong, YUE Huanzhan, et al. Coordinated optimization strategy of electric vehicle cluster participating in energy and frequency regulation markets considering battery lifetime degradation[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 72-81. (  0) 0) |
| [24] |
米阳, 伦雪莹, 孟凡斌, 等. 基于无模型算法和电动汽车辅助调节的新能源电力系统频率协调控制[J]. 电力系统保护与控制, 2021, 49(24): 13-20. MI Yang, LUN Xueying, MENG Fanbin, et al. Frequency coordinated control of a new energy power system based on a model-free algorithm and EV auxiliary regulation[J]. Power System Protection and Control, 2021, 49(24): 13-20. (  0) 0) |
| [25] |
赵竞智. 电动汽车参与电网辅助调频控制策略研究[D]. 哈尔滨: 哈尔滨工业大学, 2021. ZHAO Jingzhi. Research on control strategy of electric vehicle participating in grid frequency regulation[D]. Harbin: Harbin Institute of Technology, 2021. (  0) 0) |
| [26] |
QIN D H, SUN Q Y, WANG R, et al. Adaptive bidirectional droop control for electric vehicles parking lot with vehicle-to-grid service in microgrid[J]. CSEE Journal of Power and Energy Systems, 2020, 6(4): 793-805. (  0) 0) |
| [27] |
JAN M U, XIN A, ABDELKARIM ABDELBAKY M, et al. Adaptive and fuzzy PI controllers design for frequency regulation of isolated microgrid integrated with electric vehicles[J]. IEEE Access, 2020, 8: 87621-87632. (  0) 0) |
| [28] |
孟凡斌, 周静, 张霄, 等. 基于改进FPA-LHS算法的并网型微电网容量优化配置研究[J]. 智慧电力, 2021, 49(10): 45-51. MENG Fanbin, ZHOU Jing, ZHANG Xiao, et al. Optimal capacity configuration of grid-connected microgrid based on improved FPA-LHS algorithm[J]. Smart Power, 2021, 49(10): 45-51. (  0) 0) |
| [29] |
元佳宇. 纯电动汽车动力电池热管理系统结构设计与优化[D]. 青岛: 青岛理工大学, 2022. YUAN Jiayu. Structural design and optimization of thermal management system for pure electric vehicle power battery[D]. Qingdao: Qingdao Tehcnology University, 2022. (  0) 0) |
| [30] |
JAMPEETHONG P, KHOMFOI S. Coordinated control of electric vehicles and renewable energy sources for frequency regulation in microgrids[J]. IEEE Access, 2020, 8: 141967-141976. (  0) 0) |
| [31] |
逯胜建. 基于虚拟同步机的电动汽车充放电控制及辅助调频策略[D]. 北京: 华北电力大学, 2018. LU Shengjian. Charge/discharge and auxiliary frequency modulation control strategy of electric vehicle based on virltual synchronous machine[D]. Beijing: North China Electric Power University, 2018. (  0) 0) |
| [32] |
张沅霞. 辅助电网二次调频的混合储能控制策略研究[D]. 长沙: 湖南大学, 2019. ZHANG Yuanxia. Research on integrated control strategy considering battery energy storage system participate in secondary frequency regulation in power system[D]. Changsha: Hunan University, 2019. (  0) 0) |
 2023, Vol. 42
2023, Vol. 42


 裴振坤(1998), 男, 硕士在读, 研究方向为电动汽车与电网互动技术(E-mail:
裴振坤(1998), 男, 硕士在读, 研究方向为电动汽车与电网互动技术(E-mail: