文章编号: 2096-3203(2023)01-0124-10 中图分类号: TM73
在“碳达峰、碳中和”的国家重大战略[1]背景下,电力行业承载着最先实现碳中和的期望,电力系统中的发输变配等环节均面临一系列新挑战。配电方式中,直流配电以其供电容量大、供电半径长、运行效率高、可控性好和适应新能源接入等优越性[2-3]成为未来配电网研究和发展的重要方向。与单极性网络相比,真双极直流配电网可以提供2个电压等级,方便分布式电源和直流负荷[4-5]接入,供电可靠性高,传输容量大,一般通过DC/DC变换器(DC/DC transformer,DCT)实现直流网内的母线电压变换。这种技术正逐渐应用于数据中心[6]、电动汽车充电系统[7]及光储应用系统[8]等,目前应用较广的控制方法为可靠性、扩展性和模块性较好的下垂控制[9-10]。但由于配电网内线缆阻抗的差异,传统下垂控制在追求较小的电压偏差和较高的分流精度时,存在着固有矛盾[11]。当配网结构复杂且各类负荷投切频繁时,会造成负荷分配不合理,且正负极换流器出口处电压严重不平衡,影响系统的稳定性和运行的经济性。正负极电压不平衡将会导致额外损耗增加,电能质量下降,严重时可能造成系统不稳定[12]。
针对直流配电网负荷分配不合理问题,文献[13]增加三电平Buck-Boost变换器实现双极性网络负荷功率的精确分配,但考虑功率等级较低;文献[14]提出调控分布式电源的二次电压控制策略,可动态分配负荷,经济性好。上述方法虽然实现了负荷的合理分配,但对通信要求较高,会影响系统的可靠性。为了降低对通信的依赖性,一些控制算法得到发展和应用,也促进了下垂控制的进一步改进。文献[15-17]提出基于电压源换流器(voltage source converter,VSC)的自适应虚拟电阻的改进下垂控制策略,下垂系数能自适应调整,提高了分流精度;文献[18-20]应用储能等分布式电源,应用一致性算法改进下垂控制,实现负荷的合理分配。虽然上述文献不是基于DCT真双极直流配电网,但其方法值得借鉴。
针对正负极电压不平衡问题,文献[21]基于VSC提出交错并联Buck/Boost型电压平衡器,解决了不平衡负载接入问题;文献[22]提出一种基于下垂控制和干扰观测器相结合的多电压平衡器并联运行与协调控制方法,但电压平衡器的控制系统可能与正、负极间电压控制系统相互影响,且电压平衡器的调节能力有限,同时会带来附加成本;文献[23-24]基于多储能间协调控制,稳定两极母线电压及抑制正负极电压不平衡;文献[25]基于储能三电平变换器抑制直流母线不平衡电压,但未考虑负荷分配问题;文献[26]通过负荷开关灵活切换负荷极性,削弱上游节点的不平衡电流对下游节点的影响,从而减小本段线路中线电流以抑制两极电压不平衡。上述文献为了抑制正负极电压不平衡,均增加了调控设备,而未考虑充分利用真双极直流配电网原有的DCT进行协调控制。
综上,针对真双极直流配电网中存在的负荷分配不合理问题及正负极电压不平衡问题,文中提出一种基于DCT的电压-电流二级控制策略。该策略基于通信采集同极并联DCT的电流以及异极串联DCT的电压,采用一致性算法使电流与电压控制均达到收敛,从而实现负荷合理分配及正负极电压平衡的双重控制目标。在PSCAD/EMTDC平台中搭建了真双极直流配电网的模型,采用电流分配精度及电压不平衡度进行量化评价,同时分析了通信延时对该控制策略的影响,仿真和评价结果验证了所提控制策略的有效性、适应性及可靠性。
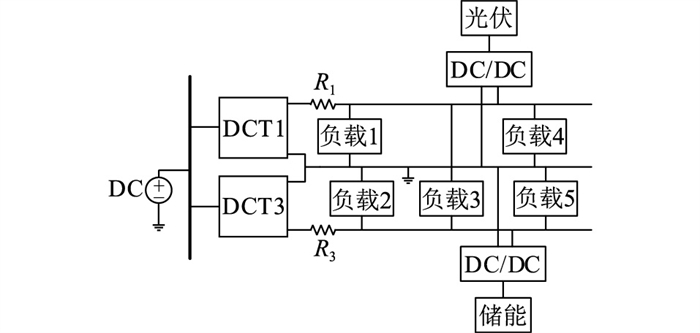
1 传统下垂控制在基于DCT的真双极直流配电网应用中存在的问题 1.1 真双极直流配电网拓扑以两端拓扑为例,真双极直流配电网如图 1所示,该配电网通过DCT与直流母线相连接,在配电网中含有单极性负载、双极性负载、光伏(工作于最大功率追踪模式)、储能及线缆等。正激、反激等电路具有变压器单向励磁、利用率低且难以达到较大功率等缺点,故文中选用适合大功率应用场景的全桥电路[27-28]作为4个DCT的拓扑。光伏单元选用Boost电路,储能单元选用双向Buck/Boost电路作为变换器的拓扑。

|
图 1 两端真双极直流配电网拓扑 Fig. 1 Topology of two-terminal true bipolar DC distribution network |
文中选用的4个DCT电路拓扑完全相同。图 2以DCT1为例展示了其电路结构。G1—G4为4个绝缘栅双极型晶体管;VD1—VD4为4个二极管;L1和C1组成LC滤波电路;Udc1、I1分别为DCT出口的电压和电流。

|
图 2 DCT的电路 Fig. 2 Circuit of DCT |
图 3给出了该直流配电网的传统下垂控制框图,其中Urefi为第i个DCT的参考电压值;Ui为第i个DCT出口侧的实际电压值;ki为下垂系数;Irefi为输出电流参考值;Ii为输出电流实际值;Kp、Ki分别为比例积分(proportional integral, PI)调节器的比例系数和积分系数;PWM为脉冲宽度调制。

|
图 3 传统下垂控制框图 Fig. 3 Traditional droop control block diagram |
由于线缆阻抗差异,采用下垂控制的真双极直流配电网无法在同极DCT上实现负荷的合理分配。由图 1可得同极性DCT并联运行电路,如图 4所示。图中,U1、U2分别为DCT1与DCT2出口的电压;I1、I2分别为DCT1与DCT2出口的电流;R1、R2分别为DCT1与DCT2出口的线缆电阻;Rload为负载等效电阻;Udc为负载等效电阻上的压降。

|
图 4 同极性DCT并联运行电路 Fig. 4 Circuit of DCT parallel operation with the same polarity |
由图 4可得:
| $ \left\{\begin{array}{l} U_{\mathrm{dc}}=U_1-I_1 R_1 \\ U_{\mathrm{dc}}=U_2-I_2 R_2 \end{array}\right. $ | (1) |
电压电流下垂控制为:
| $ U_i=U_{\text {ref}i}-k_i I_i $ | (2) |
将式(2)代入式(1)得:
| $ \frac{I_1}{I_2}=\frac{\left(U_{\text {ref1 }}-U_{\mathrm{dc}}\right)\left(k_2+R_2\right)}{\left(U_{\text {ref2 }}-U_{\mathrm{dc}}\right)\left(k_1+R_1\right)} $ | (3) |
当2个换流器出口处参考电压相同时,输出电流的比值为:
| $ \frac{I_1}{I_2}=\frac{k_2+R_2}{k_1+R_1} $ | (4) |
当换流器的下垂系数按额定电流设置时,有:
| $ k_1 I_{\mathrm{e} 1}=k_2 I_{\mathrm{e} 2} $ | (5) |
式中:Ie1、Ie2分别为DCT1、DCT2的额定电流。
将式(5)代入式(4)得:
| $ \frac{I_1}{I_2}=\frac{I_{\mathrm{e} 1} k_2+I_{\mathrm{e} 1} R_2}{I_{\mathrm{e} 2} k_2+I_{\mathrm{e} 1} R_1} $ | (6) |
由式(4)及式(6)可知,仅当忽略线路电阻时,才有:
| $ \frac{I_1}{I_2}=\frac{k_2}{k_1}=\frac{I_{\mathrm{e} 1}}{I_{\mathrm{e} 2}} $ | (7) |
由式(7)可知,此时负荷电流可实现按照额定电流进行分配。然而,在实际直流配电网中,线路电阻往往无法忽略。如式(6)所示,在下垂控制方式下,负荷无法在换流器间按照额定电流进行分配,这对各变换器的分流精度有较大影响。为此,有必要在传统下垂控制的基础上进行附加电流控制。
为了量化分流精度,考虑到实际直流配电网的建设工程中一般选择同型号同容量的DCT进行串并联,因此,文中选择按负荷均流的程度来量化,其定义如式(8)所示。
| $ \left\{\begin{array}{l} \Delta I_i=\frac{\left|I_i-I_{\text {ave }}\right|}{I_{\text {ave }}} \times 100 \% \\ I_{\text {ave }}=\frac{I_1+I_2+\cdots+I_{N-1}+I_N}{N} \end{array}\right. $ | (8) |
式中:ΔIi为电流分配精度;Ii为并联运行的DCT出口的电流;N为并联运行的DCT个数,在图 1所示配电网中,N=2。
1.3 正负极电压不平衡由于正负极线缆阻抗及所接负荷不同,采用下垂控制的真双极直流配电网可能在异极DCT上造成电压不平衡。由图 1可得异极性DCT串联运行电路图,如图 5所示。假设DCT1和DCT3出口侧的线缆电阻分别为R1和R3;中线电阻为R;U1、U3分别为DCT1、DCT3的输出电压;Rp、Rn分别为接在正负极母线上的负荷。

|
图 5 异极性DCT串联运行电路 Fig. 5 Circuit of DCT series operation with different polarity |
由图 5,根据电路的基尔霍夫定律,可知:
| $ \left\{\begin{array}{l} U_1=I_1\left(R_1+R_{\mathrm{p}}\right)-\left(I_1-I_3\right) R \\ U_3=I_3\left(R_3+R_{\mathrm{n}}\right)-\left(I_1-I_3\right) R \end{array}\right. $ | (9) |
将式(2)代入式(9),计算结果见附录A式(A1)。观察式(A1)可知,若要使正负极电压相等,需要两换流器电压参考值、下垂系数、正负极线缆阻抗及所接负荷同时满足式(A1),该条件极为苛刻,一般情况下很难实现。其原因是,一方面,当双极性直流配电网某一节点正极负荷Rp与负极负荷Rn不平衡时,不平衡电流流过中线,使正、负极电压产生偏移;另一方面,中线电阻R的存在使正、负极电压之间相互耦合,即正极电压变化时,负极电压同时也会变化。另直流负荷功率随机时变,具有一定的不确定性,其造成的不平衡同样值得关注。
在双极性网络中,正负极电压不平衡问题较为普遍,所以要改进算法附加控制对电压不平衡进行抑制。
量化直流电压不平衡的评估指标一般采用电压不平衡度[29],其定义如式(10)所示,限值取为3%[30]。
| $ \Delta U_{+-}=\frac{\left|U_{+}-U_{-}\right|}{\left(U_{+}+U_{-}\right) / 2} \times 100 \% $ | (10) |
式中:ΔU+-为电压不平衡度;U+、U-分别为正负极母线电压。
2 电压-电流二级控制策略上述传统下垂控制是面向各个DCT装置自身的控制,在文中将其称为一级控制。一级控制存在无法兼顾负荷分配及正负极电压平衡的固有矛盾,为此,引入二级控制。二级控制是指不同DCT之间的协调控制。二级控制要实现以下2个目标:(1) 同极并联的多个换流器实现电流的平均分配;(2) 同一节点的异极串联换流器实现两极电压的平衡。故在一级控制的基础上,图 1中同极的2个换流器(DCT1和DCT2、DCT3和DCT4)参与两端负荷分配的二级调控,同一节点的正负极换流器(DCT1和DCT3、DCT2和DCT4)参与两极电压平衡的二级调控。
信息采集是二级控制的基础,文中应用收敛条件简单且收敛速度较快的一致性算法[31]。其本质是每一个本地节点应得到同极节点的电流信息和同端异极节点的电压信息,更新本地节点的状态变量,使节点的状态变量收敛于稳定的共同值。在分布式控制中,根据相邻节点的状态变量调整各节点的状态变量,随着迭代次数的增加,节点的状态变量逐渐趋于相等,当所有节点的状态变量在一定精度范围内达到一致时系统稳定。根据一阶离散一致性算法,由当前时刻各单元的信息迭代得到相应单元下一时刻的状态信息。在各节点通信拓扑连通的情况下,令xi表示节点i 的状态,则一致性算法可以表达为:
| $ x_i(k+1)=\sum\limits_{j=1}^n d_{i j} x_j(k) $ | (11) |
其矩阵表示形式为:
| $ \boldsymbol{X}_{k+1}=\boldsymbol{D} \boldsymbol{X}_k $ | (12) |
式中:n为节点个数;D为状态转移矩阵;dij为状态转移矩阵系数,取决于网络的拓扑;k为迭代次数,当k足够大时,对于任意节点,有xi(k)=xj(k);X为状态向量。
| $ d_{i j}=\left\{\begin{array}{l} \frac{1}{1+a} \quad j \in N_i \\ 1-\sum\limits_{j \in N_i} \frac{1}{1+a} \quad i=j \\ 0 \text { 其他 } \end{array}\right. $ | (13) |
式中:a为该节点及相邻节点所含有的邻居节点数目的最大值;Ni为节点i所有的邻居节点。当网络拓扑改变时,按式(13)更新矩阵,迭代直至收敛。在一定的收敛精度范围内,当配电网中所有节点的状态值均相等时,认为该分布式系统一致收敛。
基于控制目标,以DCT1为例,其二级控制框图如图 6所示。文中采用的二级控制包括分流环节和调压环节。

|
图 6 二级控制框图 Fig. 6 Secondary control block diagram |
考虑多端情形,检测各同极并联DCT出口处的电流,若其为0,视为无效,从而得到同极有效并联DCT的平均电流,将其与自身采样电流进行比较得到电流偏差,然后通过PI环节对偏差进行校正,得到电压补偿值ΔUI。图 6是以两端为例,也就是当一端电流为0时,将电流二级控制闭锁,即其对应的电流补偿值ΔUI置0。
将异极串联DCT的平均电压与自身采样电压进行比较得到电压偏差,通过PI环节对偏差进行校正,得到电压补偿值ΔUU。若检测到其中某个DCT出口处的电压为0,视为其发生故障,从而将其对应的电压二级控制闭锁,即其对应的电压补偿值ΔUU置0。
然后将2个电压补偿值送入一级控制对电压参考值进行修正,从而实现双重控制目标。
在文中建立的真双极直流配电网模型中,将调控的各个DCT的输出电压和输出电流作为状态变量,应用电压电流一致性迭代算法。当同极DCT出口处的电流及异极同节点DCT出口处的电压均在一定精度范围内达到相等时,实现该直流配电网的一致收敛。
基于上述控制目标及算法,文中所提的二级控制策略的流程如图 7所示。图中,Ii, x中x取l或r,分别代表两端;Ui, m中m取p或n,分别代表正负极。
电流收敛判据为:
| $ \left|I_{\text {ave } i, x}[k+1]-I_{\text {ave } i, x}[k]\right|<\varepsilon_I $ | (14) |
其中,εI一般取10-2数量级。
电压平衡收敛判据为:
| $ \left|U_{\text {ave } i, m}[k+1]-U_{\text {ave } i, m}[k]\right|<\varepsilon_U $ | (15) |
其中,εU一般取10-2数量级。
由图 7可知,经过二级控制策略,以DCT1为例,新电压参考值被修正为:
| $ \begin{gathered} U_{\text {ref1} }^{\prime}=U_{\text {ref1 }}+\Delta U_I+\Delta U_U= \\ U_{\text {ref1}}+\left(\frac{I_1+I_2}{2}-I_1\right)\left(K_{\mathrm{p} i 1}+\frac{K_{\mathrm{i} i 1}}{s}\right)+ \\ \left(\frac{U_{\mathrm{dc} 1}+U_{\mathrm{dc} 3}}{2}-U_{\mathrm{dc} 1}\right)\left(K_{\mathrm{p} u 1}+\frac{K_{\mathrm{i} u 1}}{s}\right) \end{gathered} $ | (16) |

|
图 7 二级控制流程 Fig. 7 Flow chart of secondary control |
为验证文中所提基于一致性算法的二级控制策略的有效性和优越性,在PSCAD软件平台中搭建图 1所示直流配电网,进行仿真验证。变流器参数等按照某实验室多维灵活可控的综合能源系统物理实验平台来设置。真双极母线额定电压为±220 V,光伏额定功率为5 kW,储能额定功率5 kW。各负载均为直流负载,负载1和2为恒功率负载,功率分别为2 kW、8 kW;负载3—5均为恒电阻负载,阻值分别为14 Ω、10 Ω、10 Ω;线缆阻抗为R1—R4,其余参数详见表 1和表 2。
|
|
表 1 DCT一级系统参数 Table 1 Parameters of the DCT primary system |
|
|
表 2 二级控制参数 Table 2 Parameters of the secondary control |
由式(13),按控制目标将节点进行分类,可知该直流配电网的状态转移矩阵为:
| $ \boldsymbol{D}=\frac{1}{2}\left[\begin{array}{ll} 1 & 1 \\ 1 & 1 \end{array}\right] $ | (17) |
为验证控制策略的有效性,设计以下控制、光伏、储能及负荷的系列变化场景,观察各DCT的出口处电流和直流母线电压,并计算其评价指标。
初始时刻投入光伏不投入储能,仅投入负载1—3,应用一级控制;在2 s时,投入文中所提的二级控制;4 s时改变光伏光照强度,将其由600 W/m2增大至1 200 W/m2;5 s时在负极母线投入储能,其工作模式为电网向其充电;6 s时在正极母线接入负载4,同时在负极母线接入负载5;8 s时同时切除负载4和负载5。
仿真上述场景后,得到各DCT出口处的电流I1—I4、正零极以及零负极电压Udc1—Udc4的时域波形,分别如图 8及图 9所示。

|
图 8 各DCT输出电流波形(有二级控制) Fig. 8 Output current waveforms of four DCTs (with secondary control) |

|
图 9 各DCT输出电压波形(有二级控制) Fig. 9 Output voltage waveforms of four DCTs (with secondary control) |
仍然按上述场景,不施加二级控制时的各DCT出口处的电流、电压的时域波形分别如图 10及图 11所示。

|
图 10 各DCT输出电流波形(无二级控制) Fig. 10 Output current waveforms of four DCTs (without secondary control) |

|
图 11 各DCT输出电压波形(无二级控制) Fig. 11 Output voltage waveforms of four DCTs (without secondary control) |
同时计算有、无二级控制时各工况下的正负极电压不平衡度及分流精度,将数据列入表 3和表 4中。由式(8)可知,在两端拓扑下,ΔI1与ΔI2相等,ΔI3与ΔI4相等。
|
|
表 3 不平衡电压 Table 3 Unbalanced voltage |
|
|
表 4 分流精度 Table 4 Shunt accuracy |
由表 3和表 4可知,投入二级控制后,正负极电压不平衡度在0.09%~0.33%范围内,分流精度在0.18%~1.06%范围内。而同工况不投入二级控制时,正负极电压不平衡度在3.35%~5.29%范围内,均超过3%的限值;分流精度在2.85%~3.45%范围内,远大于投入二级控制时。说明在上述的各种工况下,二级控制均能有效减小正负极电压的不平衡且使负荷分配更加合理。
3.3 通信延时的影响前文的仿真分析都是在忽略通信延时的条件下进行的,而实际上通信延时是一个应考虑的随机变量。为进一步分析通信延时对文中所提的二级控制策略的影响,从仿真3 s时刻开始对相邻节点的电压信号和电流信号加入50 ms的通信延时[34],设置与3.2小节相同的工况进行仿真,其输出电流及输出电压分别如图 12、图 13所示。可以发现,其中8 s时在正、负极母线同时切除负载,有、无延时的输出差异最大。因此图 12、图 13中放大对比7.8 s—8.6 s间的仿真结果。图例中的I3delay、I4delay、Udc2delay、Udc4delay分别为各参量在通信延时下的波形。

|
图 12 负极母线DCT输出电流波形(考虑通信延时) Fig. 12 Output current waveforms of two negative DCTs (considering communication delay) |

|
图 13 右端DCT输出电压波形(考虑通信延时) Fig. 13 Output voltage waveforms of two right DCTs (considering communication delay) |
为进一步分析通信延时对系统动态性能的影响,采用最大超调量及调整时间[35]等指标对其量化,如表 5所示。其中,最大超调量指的是动态响应期间输出的瞬时最大偏差值与稳态值之比,一般用百分比表示。调整时间指的是系统响应到达并保持在终值5%上下内所需的最短时间,当最大超调量小于5%时调整时间取0。
|
|
表 5 动态性能比较 Table 5 Comparison of dynamic performance |
由图 12、图 13和表 5可以看出,通信延时的存在使得换流器出口处的电流与电压均出现波动且收敛速度变慢,动态性能有所下降。其中电压超调量最大,无延时最大为6.11%,有延时则最大为6.58%,均在10%的限值[36]范围内;Udc4的电压稳定在5%变化范围内的时间最长,无延时为8 ms,有延时为22 ms。总体而言,加入通信延时50 ms后,系统的动态性能受到了一定影响,但影响不大,而且系统的稳态性能没有受到影响,说明文中所提的二级控制策略能适用于存在一定通信延时的工况。然而,过长的通信延时可能会影响系统的稳定运行[37]。因而在实际工程应用中,应尽量减少通信延时以更好地改善系统性能。
3.4 考虑拓扑变化的适应性分析 3.4.1 连接成环网将DCT1和DCT2的正极母线经过线路阻抗R5连通,将DCT3和DCT4的负极母线经过线路阻抗R6连通,从而得两端网络变换为环状网络,如图 14所示。

|
图 14 环形真双极直流配电网拓扑 Fig. 14 Topology of annular true bipolar DC distribution network |
设置与3.2小节相同的场景,得到各DCT出口处电压及电流的时域波形,分别如图 15、图 16所示。

|
图 15 环网各DCT输出电流波形 Fig. 15 Output current waveforms of four DCTs in the annular network |

|
图 16 环网各DCT输出电压波形 Fig. 16 Output voltage waveforms of four DCTs in the annular network |
由图 15及图 16可知,当配电网拓扑由两端形改变为环形时,文中所提基于一致性算法的二级控制策略仍然能减小正负极电压的不平衡且使负荷分配更加合理,说明其适应性好。
3.4.2 断开成单端网络将图 1所示的两端网络从中部切断所有联络线,原网络就变为了2个真双极单端辐射状网络,以左端的部分为对象展开进一步研究,如图 17所示,此时对DCT1和DCT3来说没有同极有效并联DCT,故将二级控制中的电流控制闭锁,仅保留一级控制与二级控制中的电压控制。
|
图 17 单端真双极直流配电网拓扑 Fig. 17 Topology of single-terminal true bipolar DC distribution network |
设置与3.2小节相同的场景,得到各DCT出口处电压及电流的时域波形,分别如图 18、图 19所示。

|
图 18 单端网各DCT输出电流波形 Fig. 18 Output current waveforms of two DCTs in the single-terminal network |

|
图 19 单端网各DCT输出电压波形 Fig. 19 Output voltage waveforms of two DCTs in the single-terminal network |
由图 19可知,当原网络变为真双极单端辐射状拓扑时,通过采集另一极的电压信息进行本极电压的二级控制仍可以实现,但采集同一极的不同节点的电流信息就失去了意义,故文中所提的控制策略在单端网络中仍能实现抑制电压不平衡的目标。
3.5 可靠性分析为分析系统可靠性,一般根据N-1安全准则。为验证所提控制策略的可靠性,针对图 1的双端系统,仍设置与3.2节相同的场景,只是在5.5 s增加设置断开DCT1。仿真结果如图 20、图 21所示。

|
图 20 两端网各DCT输出电流波形 Fig. 20 Output current waveforms of four DCTs in the two-terminal network |

|
图 21 两端网各DCT输出电压波形 Fig. 21 Output voltage waveforms of four DCTs in the two-terminal network |
由图 20、图 21可以看出,在两端拓扑下,当正极母线上的DCT1切除后,DCT2增大出力来保证所有正极母线负荷的正常供电,说明当配电中任意一处出现故障时,各换流器仍能按既定控制策略实现负荷合理分配及正负极电压平衡的双重控制目标,故其可靠性好。
4 结论在双极性直流配电网中,传统的下垂控制存在负荷分配不合理及正负极电压不平衡等问题。文中提出一种适用于真双极直流配电网的基于DCT的电压-电流二级控制策略,主要通过一致性算法对各变换器进行分流及调压控制,以实现提高分流精度及抑制正负极电压不平衡的双重目标。仿真和评价结果说明了所提控制策略的有效性、适应性和可靠性。其主要结论如下:
(1) 文中所提二级控制能有效减小正负极电压的不平衡且使负荷分配更加合理;对两端、环状等不同的网络拓扑,均能较好地实现双重控制目标;当某个DCT因故障退出后,仍能实现既定控制目标。
(2) 该策略对通信延时适应性较好。其仅对系统的动态性能有较小程度的影响,对稳态性能基本没有影响。
附录A| $ \left\{\begin{array}{l} U_1=\frac{-k_1 R U_{\text {ref3 }}+k_3 R U_{\text {ref1 }}+k_3 R_1 U_{\text {ref1 }}+k_3 R_{\mathrm{p}} U_{\text {ref1 }}+R R_1 U_{\text {ref1 }}+R R_3 U_{\text {ref1 }}+R_1 R_3 U_{\text {ref1 }}+R R_{\mathrm{n}} U_{\text {ref1 }}+R_1 R_{\mathrm{n}} U_{\text {ref1 }}+R R_{\mathrm{p}} U_{\text {ref1 }}+R_3 R_{\mathrm{p}} U_{\text {ref1 }}+R_{\mathrm{n}} R_{\mathrm{p}} U_{\text {ref1 }}}{R R_1+R R_3+R_1 R_3+R R_{\mathrm{n}}+R_1 R_{\mathrm{n}}+R R_{\mathrm{p}}+R_3 R_{\mathrm{p}}+R_{\mathrm{n}} R_{\mathrm{p}}+k_1 k_3+k_1 R+k_3 R+k_1 R_3+k_3 R_1+k_1 R_{\mathrm{n}}+k_3 R_{\mathrm{p}}} \\ U_3=\frac{k_1 R U_{\text {ref3 }}-k_3 R U_{\text {ref1 }}+k_1 R_3 U_{\text {ref3 }}+k_1 R_{\mathrm{n}} U_{\text {ref3 }}+R R_1 U_{\text {ref3 }}+R R_3 U_{\text {ref3 }}+R_1 R_3 U_{\text {ref3 }}+R R_{\mathrm{n}} U_{\text {ref3 }}+R_1 R_{\mathrm{n}} U_{\text {ref3 }}+R R_{\mathrm{p}} U_{\text {ref }}+R_3 R_{\mathrm{p}} U_{\text {ref3 }}+R_{\mathrm{n}} R_{\mathrm{p}} U_{\text {ref3 }}}{R R_1+R R_3+R_1 R_3+R R_{\mathrm{n}}+R_1 R_{\mathrm{n}}+R R_{\mathrm{p}}+R_3 R_{\mathrm{p}}+R_{\mathrm{n}} R_{\mathrm{p}}+k_1 k_3+k_1 R+k_3 R+k_1 R_3+k_3 R_1+k_1 R_{\mathrm{n}}+k_3 R_{\mathrm{p}}} \end{array}\right. $ | (A1) |
| [1] |
李晖, 刘栋, 姚丹阳. 面向碳达峰碳中和目标的我国电力系统发展研判[J]. 中国电机工程学报, 2021, 41(18): 6245-6259. LI Hui, LIU Dong, YAO Danyang. Analysis andreflection on the development of power system towards the goal of carbon emission peak and carbon neutrality[J]. Proceedings of the CSEE, 2021, 41(18): 6245-6259. (  0) 0) |
| [2] |
杜翼, 江道灼, 尹瑞, 等. 直流配电网拓扑结构及控制策略[J]. 电力自动化设备, 2015, 35(1): 139-145. DU Yi, JIANG Daozhuo, YIN Rui, et al. Topological structure and control strategy of DC distribution network[J]. Electric Power Automation Equipment, 2015, 35(1): 139-145. (  0) 0) |
| [3] |
陈鹏伟, 肖湘宁, 陶顺. 直流微网电能质量问题探讨[J]. 电力系统自动化, 2016, 40(10): 148-158. CHEN Pengwei, XIAO Xiangning, TAO Shun. Discussion on power quality problems for DC microgrid[J]. Automation of Electric Power Systems, 2016, 40(10): 148-158. (  0) 0) |
| [4] |
吴在军, 谢兴峰, 杨景刚, 等. 直流配电网电压控制技术综述[J]. 电力工程技术, 2021, 40(2): 59-67. WU Zaijun, XIE Xingfeng, YANG Jinggang, et al. A review on voltage control strategies in DC distribution network[J]. Electric Power Engineering Technology, 2021, 40(2): 59-67. (  0) 0) |
| [5] |
杨美辉, 周念成, 王强钢, 等. 基于分布式协同的双极直流微电网不平衡电压控制策略[J]. 电工技术学报, 2021, 36(3): 634-645. YANG Meihui, ZHOU Niancheng, WANG Qianggang, et al. Unbalanced voltage control strategy of bipolar DC microgrid based on distributed cooperation[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 634-645. (  0) 0) |
| [6] |
梁会亭. 基于Boost升压电路的自适应MeterBus数据采集器的设计与实现[J]. 信息技术与信息化, 2020(1): 6-10. LIANG Huiting. Design and implementation of adaptive MeterBus data collector based on Boost circuit[J]. Information Technology and Informatization, 2020(1): 6-10. (  0) 0) |
| [7] |
张晓峰, 吕征宇. 混合动力车用全数字电流控制型双向DC/DC变换器[J]. 电工技术学报, 2009, 24(8): 84-89, 105. ZHANG Xiaofeng, LYU Zhengyu. Digital-current-controlled Bi-directional DC/DC converter in the hybrid electric vehicle[J]. Transactions of China Electrotechnical Society, 2009, 24(8): 84-89, 105. (  0) 0) |
| [8] |
梅杨, 李晓晴, 齐园园. 光储系统中双向DC/DC变换器预测电流控制[J]. 电力电子技术, 2016, 50(5): 28-30. MEI Yang, LI Xiaoqing, QI Yuanyuan. Current predictive control for Bi-directional DC/DC converter of photovoltaic energy storage system[J]. Power Electronics, 2016, 50(5): 28-30. (  0) 0) |
| [9] |
严铭, 蔡晖, 谢珍建, 等. 适用于多端柔性直流输电系统的分布式直流电压控制策略[J]. 电力自动化设备, 2020, 40(3): 134-140. YAN Ming, CAI Hui, XIE Zhenjian, et al. Distributed DC voltage control strategy for VSC-MTDC systems[J]. Electric Power Automation Equipment, 2020, 40(3): 134-140. (  0) 0) |
| [10] |
TEIXEIRA PINTO R, BAUER P, RODRIGUES S F, et al. A novel distributed direct-voltage control strategy for grid integration of offshore wind energy systems through MTDC network[J]. IEEE Transactions on Industrial Electronics, 2013, 60(6): 2429-2441. DOI:10.1109/TIE.2012.2216239 (  0) 0) |
| [11] |
朱珊珊, 汪飞, 郭慧, 等. 直流微电网下垂控制技术研究综述[J]. 中国电机工程学报, 2018, 38(1): 72-84, 344. ZHU Shanshan, WANG Fei, GUO Hui, et al. Overview of droop control in DC microgrid[J]. Proceedings of the CSEE, 2018, 38(1): 72-84, 344. (  0) 0) |
| [12] |
CHEN H C, CHENG P T. A DC bus voltage balancing technique for the cascaded H-bridge STATCOM with improved reliability under grid faults[J]. IEEE Transactions on Industry Applications, 2017, 53(2): 1263-1270. (  0) 0) |
| [13] |
王二永, 王帅. 基于自适应虚拟电阻的低压微电网下垂控制策略[J]. 电力系统保护与控制, 2020, 48(2): 144-149. WANG Eryong, WANG Shuai. Low voltage microgrid droop control strategy based on adaptive virtual resistance[J]. Power System Protection and Control, 2020, 48(2): 144-149. (  0) 0) |
| [14] |
喻思, 米阳, 马宇辰, 等. 自适应高通滤波下垂控制的孤岛直流微电网功率分配控制[J]. 电力系统保护与控制, 2020, 48(18): 19-26. YU Si, MI Yang, MA Yuchen, et al. Power distribution control of an island DC microgrid based on adaptive high-pass filter droop control[J]. Power System Protection and Control, 2020, 48(18): 19-26. (  0) 0) |
| [15] |
刘子文, 苗世洪, 范志华, 等. 基于自适应下垂特性的孤立直流微电网功率精确分配与电压无偏差控制策略[J]. 电工技术学报, 2019, 34(4): 795-806. LIU Ziwen, MIAO Shihong, FAN Zhihua, et al. Accurate power allocation and zero steady-state error voltage control of the islanding DC microgird based on adaptive droop characteristics[J]. Transactions of China Electrotechnical Society, 2019, 34(4): 795-806. (  0) 0) |
| [16] |
肖宏飞, 黄锦锋, 陈鑫, 等. 基于动态负荷分配的直流微电网电压控制策略[J]. 电力自动化设备, 2021, 41(8): 55-61. XIAO Hongfei, HUANG Jinfeng, CHEN Xin, et al. Voltage control strategy of DC microgrid based on dynamic load allocation[J]. Electric Power Automation Equipment, 2021, 41(8): 55-61. (  0) 0) |
| [17] |
江晨, 曾国宏, 吴学智, 等. 双极性直流微网的分层控制策略[J]. 电网技术, 2015, 39(8): 2217-2222. JIANG Chen, ZENG Guohong, WU Xuezhi, et al. Hierarchical control strategy of bipolar-type DC microgrid[J]. Power System Technology, 2015, 39(8): 2217-2222. (  0) 0) |
| [18] |
吕振宇, 吴在军, 窦晓波, 等. 基于离散一致性的孤立直流微网自适应下垂控制[J]. 中国电机工程学报, 2015, 35(17): 4397-4407. LYU Zhenyu, WU Zaijun, DOU Xiaobo, et al. An adaptive droop control for the islanded DC microgrid based on discrete consensus algorithm[J]. Proceedings of the CSEE, 2015, 35(17): 4397-4407. (  0) 0) |
| [19] |
周烨, 汪可友, 李国杰, 等. 基于多智能体一致性算法的微电网分布式分层控制策略[J]. 电力系统自动化, 2017, 41(11): 142-149. ZHOU Ye, WANG Keyou, LI Guojie, et al. Distributed hierarchical control for microgrid based on multi-agent consensus algorithm[J]. Automation of Electric Power Systems, 2017, 41(11): 142-149. (  0) 0) |
| [20] |
乐健, 周谦, 王曹, 等. 基于分布式协同的配电网电压和功率优化控制方法研究[J]. 中国电机工程学报, 2020, 40(4): 1249-1257, 1415. LE Jian, ZHOU Qian, WANG Cao, et al. Research on voltage and power optimal control strategy of distribution network based on distributed collaborative principle[J]. Proceedings of the CSEE, 2020, 40(4): 1249-1257, 1415. (  0) 0) |
| [21] |
汪飞, 雷志方, 徐新蔚. 面向直流微电网的电压平衡器拓扑结构研究[J]. 中国电机工程学报, 2016, 36(6): 1604-1612. WANG Fei, LEI Zhifang, XU Xinwei. Research on topologies of voltage balancers applied in DCmicro-grid[J]. Proceedings of the CSEE, 2016, 36(6): 1604-1612. (  0) 0) |
| [22] |
李霞林, 张雪松, 郭力, 等. 双极性直流微电网中多电压平衡器协调控制[J]. 电工技术学报, 2018, 33(4): 721-729. LI Xialin, ZHANG Xuesong, GUO Li, et al. Coordinated control of multiple voltage balancers in a bipolar DC microgrid[J]. Transactions of China Electrotechnical Society, 2018, 33(4): 721-729. (  0) 0) |
| [23] |
ZHANG C J, JIAO M, LIANG M N, et al. Power control of distributed energy storage system in bipolar DC microgrid[C]//2019 22nd International Conference on Electrical Machines and Systems (ICEMS). Harbin, China. IEEE, 2019: 1-6.
(  0) 0) |
| [24] |
ZHANG Z, SHI DH, JIN C, et al. Droop control of a bipolar dc microgrid for load sharing and voltage balancing[C]//2017 IEEE 3rd International Future Energy Electronics Conference and ECCE Asia (IFEEC 2017-ECCE Asia). Kaohsiung, Taiwan, China. IEEE, 2017: 795-799.
(  0) 0) |
| [25] |
RIVERA S, WU B. Electric vehicle charging station with an energy storage stage for split-DC bus voltage balancing[J]. IEEE Transactions on Power Electronics, 2017, 32(3): 2376-2386. (  0) 0) |
| [26] |
廖建权, 周念成, 王强钢. 辐射型双极直流配电网不平衡电压分析及抑制[J]. 中国电机工程学报, 2019, 39(18): 5380-5388, 5585. LIAO Jianquan, ZHOU Niancheng, WANG Qianggang. Analysis and suppression of unbalanced voltage in radiant bipolar DC distribution network[J]. Proceedings of the CSEE, 2019, 39(18): 5380-5388, 5585. (  0) 0) |
| [27] |
王育浦. 电动汽车双向全桥DC/DC转换器研究设计[D]. 北京: 北京理工大学, 2015. WANG Yupu. Research and design of bidirectional full bridge DC/DC converter on electric vehicle[D]. Beijing: Beijing Institute of Technology, 2015. (  0) 0) |
| [28] |
曾国辉, 廖鸿飞, 赵晋斌, 等. 直流微网双向DC/DC变换器虚拟惯量和阻尼系数自适应控制策略[J]. 电力系统保护与控制, 2022, 50(6): 65-73. ZENG Guohui, LIAO Hongfei, ZHAO Jinbin, et al. A self-adaptive control strategy of virtual inertia and a damping coefficient for bidirectional DC-DC converters in a DC microgrid[J]. Power System Protection and Control, 2022, 50(6): 65-73. (  0) 0) |
| [29] |
JUNG T H, GWON G H, KIM C H, et al. Voltage regulation method for voltage drop compensation and unbalance reduction in bipolar low-voltage DC distribution system[J]. IEEE Transactions on Power Delivery, 2018, 33(1): 141-149. (  0) 0) |
| [30] |
American national standard for electric power systems equipment—voltage ratings (60 H): ANSI C84.1-2020[S]. 2020.
(  0) 0) |
| [31] |
朱晓荣, 马英乔, 赵澄颢. 基于模型预测控制算法的多风储直流微电网分布式电压二次控制策略[J]. 电力自动化设备, 2021, 41(10): 184-191. ZHU Xiaorong, MA Yingqiao, ZHAO Chenghao. Distributed voltage secondary control strategy of multi wind-storage DC microgrid based on model predictive control algorithm[J]. E lectric Power Automation Equipment, 2021, 41(10): 184-191. (  0) 0) |
| [32] |
周敏, 吕振宇, 王琦, 等. 直流配电网换流站分布式有功-电压二级优化控制策略[J]. 中国电机工程学报, 2020, 40(24): 8002-8011, 8237. ZHOU Min, LYU Zhenyu, WANG Qi, et al. Distributed secondary power and voltage optimal control strategy for converter station in DC distribution network[J]. Proceedings of the CSEE, 2020, 40(24): 8002-8011, 8237. (  0) 0) |
| [33] |
陶顺, 马喜欢, 管尚书, 等. 真双极直流配电网有功-电压分布式二级控制策略[J]. 电力系统保护与控制, 2022, 50(8): 50-58. TAO Shun, MA Xihuan, GUAN Shangshu, et al. Distributed secondary power and voltage control strategy for a true bipolar DC distribution network[J]. Power System Protection and Control, 2022, 50(8): 50-58. (  0) 0) |
| [34] |
邓思成, 陈来军, 郑天文, 等. 考虑系统延时的微电网有功功率分布式控制策略[J]. 电网技术, 2019, 43(5): 1536-1542. DENG Sicheng, CHEN Laijun, ZHENG Tianwen, et al. Active power distributed control of microgrids considering system time delays[J]. Power System Technology, 2019, 43(5): 1536-1542. (  0) 0) |
| [35] |
吴忠强, 侯林成, 曹碧莲, 等. 输入受限情况下基于Hamilton系统的风力发电机组协同控制[J]. 中国电机工程学报, 2022, 42(13): 4884-4896. WU Zhongqiang, HOU Lincheng, CAO Bilian, et al. Cooperative control strategy for wind turbines based on Hamilton system under limited input[J]. Proceedings of the CSEE, 2022, 42(13): 4884-4896. (  0) 0) |
| [36] |
沈小军, 李梧桐, 乔冠伦, 等. 同步发电机励磁系统模型参数离线辨识自动寻优方法[J]. 电工技术学报, 2018, 33(18): 4257-4266. SHEN Xiaojun, LI Wutong, QIAO Guanlun, et al. Automatic optimization method for model parameters off-line identification of synchronous generator excitation system[J]. Transactions of China Electrotechnical Society, 2018, 33(18): 4257-4266. (  0) 0) |
| [37] |
WU X Y, XU Y, HE J H, et al. Delay-dependent small-signal stability analysis and compensation method for distributed secondary control of microgrids[J]. IEEE Access, 2019, 7: 170919-170935. (  0) 0) |
 2023, Vol. 42
2023, Vol. 42


 管尚书(1997), 男, 硕士在读, 研究方向为直流配电网运行控制(E-mail:
管尚书(1997), 男, 硕士在读, 研究方向为直流配电网运行控制(E-mail: