文章编号: 2096-3203(2023)01-0185-08 中图分类号: TM733
变电站作为电力传输的关键环节,其生产安全关系着整个电网的安全稳定运行[1]。研究面向变电站环境的高精度定位方法,能有效管控和监督现场作业,对智能电网环境下的电网安全稳定运行具有重要的作用[2]。
在室外开阔场景下,高精度位置服务主要由全球卫星导航系统(global navigation satellite system,GNSS)提供。因此,在电力安全巡检系统中,大多使用北斗卫星系统实现人员的实时定位[3]。然而, 变电站区域大型设备较多,经常存在卫星信号半遮挡现象,卫星信号衰减或可视卫星数量不足,须融合其他基站信号辅助定位。文献[4]结合地理信息系统和超宽带(ultra wide band,UWB)对巡检人员进行室内外跟踪定位;文献[5]结合全球定位系统(global positioning system,GPS)和高精度激光雷达,基于无迹卡尔曼滤波进行数据融合;文献[6]结合差分GPS和里程计,构建基于卡尔曼增量模型的数据融合方法。然而,这些融合定位技术没有考虑不同环境类型对基站信号质量的影响,在复杂环境下,往往由于无法选择适合当前环境类型的融合策略而造成定位误差[7]。
为匹配环境特征,已有学者通过引入地图约束和地图匹配,利用地理信息实现环境分类,自适应地调整定位策略,剔除异常量测值。文献[8]提出一种GPS与地图匹配组合的定位方法,解决了部分无卫星信号的复杂环境中的定位问题。文献[9]提出一种Wi-Fi、行人航迹追踪(pedestrian dead rec-koning,PDR)和地图信息融合的定位方法,采用虚拟轨迹和虚拟链接描述地图约束中的数据结构。文献[10]基于行人运动模型,采用自适应的无迹卡尔曼滤波来融合PDR、磁力计和地图投影的定位结果。但是地图信息的构建费时费力,往往需要使用激光雷达扫描仪、双目视觉摄像头等获得精确的三维环境信息。面对陌生变电站的半遮挡环境,在不知晓地图先验信息的情况下,巡检人员定位技术不能在线切换定位算法,造成了融合定位选择过程迟滞;同时,GNSS、UWB、电子罗盘等传感器受变电站电磁干扰严重,大大降低了其信号统计特征精度,造成环境信息误判。
为精确匹配变电站环境信息,鲁棒地选择多传感器融合定位方法,文中提出了一种基于传感器信号特征分类的融合定位方法,使用传感器信号的统计特征模型代替精确地图信息,实现环境分类,并根据分类结果自适应地切换不同的融合定位策略。该方法通过真实变电站环境的信号分析结果,选取大尺度空间下较为成熟的北斗卫星信号和受变电站干扰较小的近超声(17~23 kHz)信号来提取信号统计特征,针对信道分布统计模型采用t分布随机近邻嵌入(t-distributed stochastic neighbor embedding, t-SNE)算法进行数据降维,再根据降维结果选择无监督的密度峰值聚类(density peaks clustering, DPC)算法作可解释的聚类处理。为将信号特征的聚类结果映射至相应的卡尔曼滤波的多源融合定位模型中,文中通过误差反向传播(back propagation,BP)神经网络优化融合参数,实现了不同环境特征匹配下的最优多源信息位置估计。在江苏某220 kV变电站区域测试得到真实数据,可知该方法在变电站半遮挡环境下,可利用卫星和近超声信号特征实时、准确地进行环境特征分类,鲁棒地切换传感器融合策略。文中提出的方法在未知地图信息的情况下,相较传统的GNSS+地图定位、UWB+惯性传感器(inertial measurement unit,IMU)融合定位等手段,极大地提升了定位精度。
1 多传感器信息的特征提取及分类变电站环境复杂,存在变压器、高压断路器等大型电气设备以及防火墙壁的遮挡,信号直达成分少,非视距、多径成分多。在不同场景,如高低压配电室附近和空旷道路下,GNSS、近超声、Wi-Fi以及蓝牙等信号的传播特性和衰减程度差异较大,因此可提取这些信号的特征,如信号强度、信道时延、多径频率衰落等代替环境信息。通过分析特征参数在不同环境下的真实分布特性,识别环境类型以等效地图信息。
在变电站巡检人员管控中,GNSS技术是目前室外场景中最为通用的定位技术,在大尺度空间下有优越性能。而在卫星拒止环境下,近超声定位技术不仅不受变电站电磁干扰,还具有成本低、广兼容、无用户数量限制、可实现芯片完全自主化等优势[11],可以在小尺度空间实现高精度定位。因此,文中选择提取卫星信号和近超声信号的特征,结合其统计分布模型,选取t-SNE降维算法和DPC算法划分环境类型。
1.1 多传感器信息的特征提取 1.1.1 卫星信号特征提取通常,导航卫星与卫星导航接收机之间的数据传输遵循NMEA-0183协议。基于NMEA-0183协议,可获得信号强度、卫星几何精度因子(dilution of precision, DOP)值、可见卫星信息、定位信息、大地坐标信息、卫星星历信息等十余种数据观测值[12]。而在变电站半遮挡环境下,卫星信号观测值主要受周围建筑物遮挡程度的影响。在变电站大尺度范围内,若区域的遮挡物稠密,卫星信号在穿过金属或水泥时,信号强度呈现大尺度衰减。同时由于反射和散射路径增多,卫星信号的多径干扰较为严重,信号强度会在短时间内快速波动,呈现小尺度衰减。此外,若遮挡物过于高大,卫星直接不可见,可见卫星数量减少,DOP值会明显增大[13]。
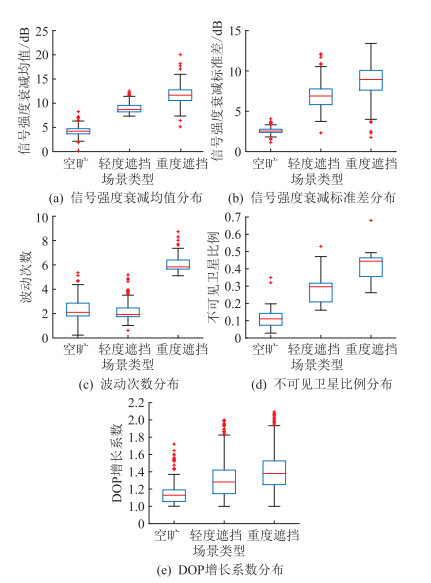
基于上述分析,文中提取信号强度特征、多径特征和卫星空间分布特征,不同遮挡程度下特征参数的统计分布如图 1所示。
|
图 1 各特征参数的统计分布 Fig. 1 Statistical distribution of characteristic each parameter |
(1) 信号强度特征。考虑到卫星信号强度受不同卫星位置影响,文中选择卫星信号衰减的均值μ和标准差σ作为信号强度特征。在重度遮挡区域,绝大多数衰减值处于18~23 dB之间;在轻度遮挡区域,大多数处于5~10 dB之间;而在空旷区域,卫星信号质量最高。
(2) 多径特征。信号强度在1 s内的波动次数β反映了多径干扰程度。由图 1(c)可知,随着遮挡程度增加,波动次数β随之增加,因为遮挡物增加了接收信号的多径成分。
(3) 卫星空间分布特征。不可见卫星比例ζ和DOP的增长系数λ反映了当前卫星空间几何分布特征。由图 1(d)、图 1(e)可知,ζ和λ的整体分布较为相似,在重度遮挡区域,空中可见卫星数减少,ζ、λ明显增大;另外,由于DOP值受卫星空间分布影响,λ的离散值更多。
1.1.2 近超声信号特征提取在变电站半遮挡场景下,非视距现象是影响近超声信号的主要因素[14]。在非视距场景下,声信号发送端与接收端之间的视距传播路径被障碍物遮挡,由于声信号的穿透能力弱,反射路径和散射路径的数量明显增加,如图 2所示。

|
图 2 视距与非视距场景描述 Fig. 2 Line of sight and none line of sight description |
因此,视距和非视距场景下的声信道相对增益-时延分布具有明显差异。在视距情况下,分布中的主成分较为集中,且主时延较小。而在非视距环境下的信道情况复杂,分布相对分散且主成分时延较大[15],如图 3所示。

|
图 3 相对增益-时延分布 Fig. 3 Relative gain-delay distribution |
针对声信道相对增益-时延分布图,文中分别提取以下特征:
(1) 时延特征。平均附加时延τmed、均方根时延τrmsd是典型的信道时延特征。在非视距情况下,τmed和τrmsd往往更大。因为遮挡物削弱了第一径成分信号的能量,能量较小的多径反射成分首先到达。此外,由于反射路径平均长度和散射面的增加,信号总能量下降,分布更加平均,主成分的时延增加。
(2) 波形特征。峰度κ、偏度s分别表示数据分布相对于正态分布的顶峰尖平程度和偏斜程度。在非视距情况下主成分右移,顶峰更平,接近于正态分布,κ和s更大。
(3) 多径特征。文中参考无线信道的多径衰落模型,选择Rician-K系数表示视距成分和非视距成分的比值。在非视距情况下,声信道衰落模型更接近瑞利衰落。
除了声信道的时域特征,信号在幅值上的特征也体现出信号在传播过程中受到环境影响,采用相对增益幅值进行表示。环境对相对增益的频数特征影响如图 4所示,相应地,提取平均附加增益gm、均方根时延grms、峰度kf和偏度ks等特征。

|
图 4 相对增益幅值的频数分布 Fig. 4 Frequency distribution of relative gain amplitude |
根据上述分析,文中共提取14种特征参数描述卫星信号、近超声信号与不同环境类型的影响。由于特征维度过高,在聚类之前需要作降维处理。
1.2.1 特征向量降维t-SNE是近年来较为流行的非线性数据降维方法,可以保留高维数据的局部特征,核心思想是使得高维空间与低维空间数据点的联合概率分布尽可能相似[16-17]。与主成分分析(principle component analysis, PCA)等主流降维方法不同的是,t-SNE在对数据特征进行降维时,保留了特征的分布特点,因此更适合描述传感器的特征。
设原始高维特征空间任意2个数据点为xi、xj,在低维空间的映射点为yi、yj。则联合分布概率函数pij为:
| $ p_{i j}=\frac{p_{i \mid j}+q_{i \mid j}}{2 n} $ | (1) |
| $ p_{i \mid j}=\frac{\exp \left(-\left\|\boldsymbol{x}_i-\boldsymbol{x}_j\right\|^2 /\left(2 \sigma_i^2\right)\right)}{\sum\limits_{u \neq i} \exp \left(-\left\|\boldsymbol{x}_u-\boldsymbol{x}_i\right\|^2 /\left(2 \sigma_i^2\right)\right)} $ | (2) |
| $ q_{i \mid j}=\frac{\exp \left(-\left\|\boldsymbol{y}_i-\boldsymbol{y}_j\right\|^2\right)}{\sum\limits_{u \neq i} \exp \left(-\left\|\boldsymbol{y}_i-\boldsymbol{y}_u\right\|^2\right)} $ | (3) |
式中:n为数据点个数;σi为标准差;xu为第u个高维空间数据点;u为数据点编号;yu为第u个低维空间映射点。
为保证数据局部特征尽量不变,t-SNE降维算法引入Kullback-Leibler(KL)散度衡量高维空间和低维空间的相似性,采用梯度下降法不断迭代,最小化KL散度C:
| $ C=D_{\mathrm{KL}}(P \| Q)=\sum\limits_i \sum\limits_j p_{i j} \lg \left(\frac{p_{i \mid j}}{q_{i \mid j}}\right) $ | (4) |
式中:DKL(P‖Q)为根据数据分布P与上近似分布Q计算出KL散度的表达式。迭代结束后可得特征参数的二维表征结果。
1.2.2 特征分类基于密度峰值的DPC算法可聚类任意形状数据,且参数唯一,可获取任意形状和任意数量的聚类结果[18-19],因此理论上降维之后的特征分布数据有更好的聚类性能。
对降维后任意数据点yi,采用DPC算法,并基于欧氏距离计算局部密度ρ和相对最小距离δ。
| $ \left\{\begin{array}{l} \rho_i=\sum\limits_{j \neq i} \chi\left(d_{i j}-d_{\mathrm{c}}\right) \\ \chi(x)= \begin{cases}1 & x<0 \\ 0 & x \geqslant 0\end{cases} \end{array}\right. $ | (5) |
式中:ρi为第i个数据点的局部密度;dij为原始数据点的欧氏距离;dc为聚类算法之后数据点的欧氏距离。
| $ \delta_i=\min\limits _{j: \rho_j>\rho_i} d_{i j} $ | (6) |
式中:ρj为第j个数据点的局部密度。另外,对于局部密度最大值的数据点yi,其相对最小距离δi定义为:
| $ \delta_i=\max d_{i j} $ | (7) |
将ρ和δ相对较高的数据点标记为聚类中心,ρ较低而δ较高的数据点标记为噪声点。最后按局部密度降序排列数据点,每个数据点归类到其最近邻且局部密度较大的数据点所在簇中。
2 基于多传感器信息分类的融合定位模型文中选择常用的卡尔曼滤波方法作为融合定位的基础框架,引入惯性测量单元用于状态预测,卫星与近超声的位置估计值用于状态更新。通过BP神经网络自适应修正在不同环境类型中的滤波参数。
2.1 基于卡尔曼滤波的融合定位算法卡尔曼滤波是一种常用的融合定位算法,基于隐马尔可夫模型(hidden Markov model, HMM)和贝叶斯框架,利用前一时刻的状态信息作为先验分布,利用状态转移方程和观测方程修正当前时刻的状态[20]。
算法主要分为两部分:状态预测和状态更新。在状态预测部分,文中使用IMU的测量值更新系统。通过IMU可以获取步长S和偏航角θ[21]。
| $ S=K\left(A_{z \max }-A_{z \min }\right)^{1 / 4} $ | (8) |
式中:K为步长计算常数;Azmax、Azmin分别为z轴最大垂直加速度和最小垂直加速度。
状态转换方程为:
| $ \boldsymbol{X}_{k \mid k-1}=\boldsymbol{F}_{k \mid k-1} \boldsymbol{X}_{k-1}+\boldsymbol{G}_{k \mid k-1} $ | (9) |
其中:
| $ \left\{\begin{array}{l} \boldsymbol{F}_{k \mid k-1}=\left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right] \\ \boldsymbol{G}_{k \mid k-1}=\left[\begin{array}{l} S_k \cos \theta_k \\ S_k \sin \theta_k \end{array}\right] \end{array}\right. $ | (10) |
式中:Xk|k-1为k-1时刻到k时刻的状态转移矩阵;Xk-1为k-1时刻系统的状态向量,即二维坐标系中的位置坐标;Sk、θk分别为k时刻的步长和偏航角。
系统的状态预测协方差矩阵为:
| $ \boldsymbol{P}_{k \mid k-1}=\boldsymbol{F}_{k \mid k-1} \boldsymbol{P}_{k-1} \boldsymbol{F}_{k \mid k-1}^{\mathrm{T}}+\boldsymbol{Q}_k $ | (11) |
式中:Pk|k-1为k-1时刻到k时刻的协方差转移矩阵;Pk-1为k-1时刻的协方差矩阵;Qk第k时刻系统的噪声。
在状态更新部分,使用卫星和近超声2个系统的位置估计值组成观测向量Zk,计算目标状态的后验均值和协方差。
| $ \boldsymbol{K}_k=\boldsymbol{P}_{k \mid k-1} \boldsymbol{C}\left(\boldsymbol{C} \boldsymbol{P}_{k \mid k-1} \boldsymbol{C}^{\mathrm{T}}+\boldsymbol{R}_k\right)^{-1} $ | (12) |
| $ \boldsymbol{X}_{k \mid k}=\boldsymbol{X}_{k \mid k-1}+\boldsymbol{K}_k\left(\boldsymbol{Z}_k-\boldsymbol{C} \boldsymbol{X}_{k \mid k-1}\right) $ | (13) |
| $ \boldsymbol{P}_{k \mid k}=\left(\boldsymbol{I}-\boldsymbol{K}_k \boldsymbol{C}\right) \boldsymbol{P}_{k \mid k-1} $ | (14) |
其中:
| $ \left\{\begin{array}{l} \boldsymbol{C}=\left[\begin{array}{llll} 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \end{array}\right]^{\mathrm{T}} \\ \boldsymbol{Z}_k=\left[\begin{array}{c} \boldsymbol{X}_{\text {BeiDou }, k} \\ \boldsymbol{X}_{\text {Sound }, k} \end{array}\right] \end{array}\right. $ | (15) |
式中:Kk为卡尔曼增益;Rk为测量误差的协方差矩阵;Xk|k为k时刻的状态矩阵;Pk|k为k时刻的协方差矩阵;I为单位矩阵;XBeiDou, k、XSound, k分别为北斗与声信号在k时刻的状态矩阵。可见,在卡尔曼滤波过程中,影响目标状态估计的3个主要参数为:卡尔曼增益Kk、观测向量与状态预测值的差值Zk-CXk|k-1及估计结果与状态预测值的差值Xk|k-Xk|k-1。
2.2 BP神经网络自适应修正卡尔曼滤波参数在不同环境类型下,影响卡尔曼滤波估计值的3个参数须自适应修正。因此,文中采用BP神经网络,依据环境类型构建输入层,提高卡尔曼滤波的定位精度,如图 5所示,其中T为多传感器融合系数矩阵;E为环境特征系数。

|
图 5 卡尔曼滤波参数自适应修正原理 Fig. 5 Principle of adaptive correction of Kalman filter parameters |
为简化网络结构,文中选择3层网络的BP神经网络模型。由于卡尔曼滤波是基于系统模型和噪声模型已知且不变,因此输入层由环境类型、Kk、Zk-CXk|k-1、Xk|k-Xk|k-1共同构成。
隐含层节点个数的确定选用经验公式[22]:
| $ l=\sqrt{m_{\mathrm{i}}+n_{\mathrm{o}}}+a $ | (16) |
式中:l、mi、no分别为隐含层、输入层、输出层的神经元个数;a为常数,保证隐含层节点个数大于输入层和输出层的节点个数。
输出层由定位结果真值和卡尔曼滤波器输出的估计值组成。最后将神经网络的输出值与未修正前的滤波估计值相加,即可得到自适应环境类型的估计值。
3 实例分析 3.1 实验场地文中选择江苏某220 kV变电站区域作为实验场地。基于地图和建筑结构信息,预先对实验场地进行网格划分,保证同一网格内卫星信号和近超声信号质量相似,如图 6所示,共标记了13类区域(空旷区域标注为1)作为后续聚类实验的真值标签。根据网格内最大建筑物的高度与宽度进行环境预分类,如图 7所示。

|
图 6 网格划分示意 Fig. 6 Schematic diagram of meshing |

|
图 7 不同环境类型的实地采集图 Fig. 7 Field acquisition map of different environmental types |
依次在网格内,使用U-blox ZED-F9 GNSS接收机收集卫星信号,上位机使用千寻位置提供的FindCM Pro差分服务分析卫星信号,接收机数据刷新率可达5 Hz。采集完所有网格内的卫星信号后,可获取卫星信号衰减的均值μ和方差σ、不可见卫星比例ζ等参数,构建卫星信号指纹库;同时,在网格内使用采样率为48 kHz的麦克风收集近超声信号。基于原始音频文件计算平均附加时延τmed、均方根时延τrmsd等参数,以图 6划分网格为单位构建近超声信号指纹库。
3.2 卫星-近超声特征分类结果在完成指纹库构建后,采用t-SNE降维算法对特征数据进行分析。文中分别采用t-SNE、PCA降维算法对特征数据进行分析,信号特征降维结果如图 8所示。结果表明,保留特征分布的二维t-SNE降维算法展现出了更为明显的分簇特性,且计算量更小;而PCA作为线性降维方法,得到的结果趋于随机,因此不利于进一步的特征解释及聚类中心提取。

|
图 8 降维算法对比 Fig. 8 Comparison between dimensionality reduction algorithms |
为使得降维得到的特征组合更具区分度,实验采用DPC算法进行聚类处理。以局部密度ρ为横轴,以相对最小距离δ为纵轴,绘制决策图,如图 9所示。ρ和δ相对较高的数据点共有3个,将其标记为聚类中心,这也符合基于地图信息的预分类情况。将所有数据点按局部密度降序排列,按照一步簇分配策略分配。其中,在决策图中靠近纵轴的数据点被视为噪声点。

|
图 9 DPC决策 Fig. 9 DPC decision |
为比较DPC算法的准确率,文中采用传统的K-means聚类算法进行比较,算法基于平台Matlab 2020a实现,聚类结果如图 10所示。K-means聚类算法选择cosine距离计算质心簇,使用新初始簇质心位置重复聚类的次数为3。由图 10可知,传统的K-means聚类算法严重依赖初始聚类中心,由于初始簇中心相距过近,导致重度遮挡和轻度遮挡的数据点有部分重叠;而DPC算法通过决策图选取聚类中心,排除了噪声点对聚类结果的污染。

|
图 10 2种算法的聚类结果 Fig. 10 Clustering results of two algorithms |
最后将基于地图信息的预分类结果作为真值,分析在不同环境类型下不同算法的环境识别准确率,如表 1所示。由表 1可知,在不同环境类型下,DPC算法的环境识别准确率均在90%以上。
|
|
表 1 2种算法的环境识别准确率比较 Table 1 Environment recognition accuracy comparison of two algorithms |
取DPC算法的聚类结果、Kk、Zk-CXk|k-1以及Xk|k-Xk|k-1构成BP神经网络的输入层。实验设置隐含层神经元个数为8,迭代次数为5 000,期望误差为0.01,训练集与测试集的比例为4 ∶1。
训练完成后,将神经网络的输出结果与卡尔曼滤波的估计值相加,获取修正后的位置估计。另外,文中选取了基于地图信息分类的卡尔曼滤波方法(方法1)、未考虑环境分类的标准卡尔曼滤波方法(方法2),与文中提出的卫星-近超声特征融合方法进行比较,如图 11、图 12所示。

|
图 11 3种方法的定位误差 Fig. 11 Positioning error of three methods |

|
图 12 3种方法的定位误差累积分布 Fig. 12 Cumulative distribution of positioning error of three methods |
对比图 11、图 12中的定位结果可得,文中所提方法较传统融合定位方法,平均精度提升了50%。由于变电站环境类型复杂,卡尔曼滤波的参数不适用于所有区域,仅在第60步后的区域定位误差稳定在0.6 m以内。
基于多传感器信息分类的融合定位方法与基于地图信息分类的融合定位方法基本类似。2种算法都通过环境分类结果修正了卡尔曼滤波参数,有效降低了定位误差。相比较而言,基于地图信息进行场景分类的定位方法要根据历史位置信息判断,在历史位置判断时可能出现波动及误差,使得基于位置判断的融合策略要大量预处理,因此文中所提方法更具优越性。另外,在一部分轻度遮挡区域,其卫星信号与近超声信号质量与空旷区域基本类似,在这些区域,基于多传感器信息分类的融合定位方法泛化能力更强,定位误差更低。
4 结论针对变电站的复杂环境,文中建立了一种基于多传感器信息特征分类的融合定位方法,主要结论如下:
(1) 在地图信息未知的条件下,文中基于卫星与近超声信号提取一种14维特征向量用于环境分类,样本数据分析表明各特征参数在不同场景下的统计分布特性具有明显差异。
(2) 基于特征向量构成指纹库,文中采用t-SNE降维算法与DPC算法处理数据,且能有效识别空旷、轻度遮挡、重度遮挡等3类环境类型,在特征聚类与降维中体现了一定的鲁棒性。
(3) 在变电站不同环境类型下,通过自适应优化卡尔曼滤波参数,有效降低了融合定位误差,提升了传统融合方法的效率。
| [1] |
衡思坤, 张自伟, 周光宇, 等. 变电站作业安全管控系统研究[J]. 江苏电机工程, 2016, 35(2): 31-33, 38. HENG Sikun, ZHANG Ziwei, ZHOU Guangyu, et al. Research on the safety management and control system for substation operation[J]. Jiangsu Electrical Engineering, 2016, 35(2): 31-33, 38. (  0) 0) |
| [2] |
刘故帅, 王世坤, 孙磊, 等. 基于电力物联网的变电站多维度场景管控系统[J]. 供用电, 2021, 38(3): 45-51. LIU Gushuai, WANG Shikun, SUN Lei, et al. Multi-dimensional scenario management and control system for substations based on electric Internet of Things[J]. Distribution & Utilization, 2021, 38(3): 45-51. (  0) 0) |
| [3] |
蒋晨, 郑立, 潘捷凯, 等. 基于北斗定位的变电站作业人员行为安全管控系统[J]. 电力信息与通信技术, 2022, 20(2): 76-81. JIANG Chen, ZHENG Li, PAN Jiekai, et al. Substation operator behavior safety control system based on Beidou positioning[J]. Electric Power Information and Communication Technology, 2022, 20(2): 76-81. (  0) 0) |
| [4] |
魏永, 范海波, 贾曲, 等. 基于UWB和GIS的变电站智能巡检系统的设计与实现[J]. 地理信息世界, 2018, 25(4): 100-104. WEI Yong, FAN Haibo, JIA Qu, et al. Design and implementation of power substation inspection system based on UWB and GIS[J]. Geomatics World, 2018, 25(4): 100-104. (  0) 0) |
| [5] |
ZHU J L, YAO J F, ZHU X S, et al. Research on substation safety monitoring system based on UWB positioning technology[C]//IEEE 3rd International Conference on Information Systems and Computer Aided Education. Dalian, China. IEEE, 2020: 332-334.
(  0) 0) |
| [6] |
魏苇. 基于差分GPS的变电站巡检机器人定位导航系统的研究[D]. 哈尔滨: 哈尔滨工业大学, 2015. WEI Wei. The location and navigation system of substation inspecting robot based on RTK GPS[D]. Harbin: Harbin Institute of Technology, 2015. (  0) 0) |
| [7] |
常强. 面向复杂环境的自适应定位关键技术研究[D]. 长沙: 国防科学技术大学, 2016. CHANG Qiang. Research on adaptable positioning in complicated environment[D]. Changsha: National University of Defense Technology, 2016. (  0) 0) |
| [8] |
高扬, 夏洪垚, 许豪, 等. 基于GPS与地图匹配的移动机器人定位方法[J]. 机床与液压, 2021, 49(3): 1-5. GAO Yang, XIA Hongyao, XU Hao, et al. Mobile robot localization method based on GPS and map matching[J]. Machine Tool & Hydraulics, 2021, 49(3): 1-5. (  0) 0) |
| [9] |
LEE M S, JU H, PARK C G. Map assisted PDR/Wi-Fi fusion for indoor positioning using smartphone[J]. International Journal of Control, Automation and Systems, 2017, 15(2): 627-639. (  0) 0) |
| [10] |
WANG J, HU A D, LI X, et al. An improved PDR/magnetometer/floor map integration algorithm for ubiquitous positioning using the adaptive unscented Kalman filter[J]. ISPRS International Journal of Geo-Information, 2015, 4(4): 2638-2659. (  0) 0) |
| [11] |
曹帅. 面向智能移动终端的音频室内定位关键技术研究[D]. 合肥: 中国科学技术大学, 2020. CAO Shuai. Research on key technologies of acoustic indoor positioning for smart mobile devices[D]. Hefei: University of Science and Technology of China, 2020. (  0) 0) |
| [12] |
DRAWIL N M, AMAR H M, BASIR O A. GPS localization accuracy classification: a context-based approach[J]. IEEE Transactions on Intelligent Transportation Systems, 2013, 14(1): 262-273. (  0) 0) |
| [13] |
王玉泽. 面向复杂城市环境的卫星导航信号特征统计分析研究[D]. 上海: 上海交通大学, 2019. WANG Yuze. Statistical anlysis of GNSS signal characteristics for complex urban environment[D]. Shanghai: Shanghai Jiao Tong University, 2019. (  0) 0) |
| [14] |
KUTTRUFF H. Room acoustics[M]. 6th ed. USA: CRC Press, 2016.
(  0) 0) |
| [15] |
张磊. 基于声音的智能移动终端室内定位关键技术研究[D]. 杭州: 浙江大学, 2019. ZHANG Lei. Key technologies of acoustic indoor localization systems for smart mobiles[D]. Hangzhou: Zhejiang University, 2019. (  0) 0) |
| [16] |
WATTENBERG M, VIÉGAS F, JOHNSON I. How to use t-SNE effectively[J]. Distill, 2016, 1(10): e2. (  0) 0) |
| [17] |
史东宇, 胡文强, 李刚, 等. 基于t-SNE的电力系统电气距离可视化方法研究[J]. 电力工程技术, 2018, 37(2): 78-82. SHI Dongyu, HU Wenqiang, LI Gang, et al. Study on visualization method of electrical distance in power system using t-SNE[J]. Electric Power Engineering Technology, 2018, 37(2): 78-82. (  0) 0) |
| [18] |
陆春光, 叶方彬, 赵羚, 等. 基于密度峰值聚类的电力大数据异常值检测算法[J]. 科学技术与工程, 2020, 20(2): 654-658. LU Chunguang, YE Fangbin, ZHAO Ling, et al. Abnormal value detection of large power data based on density peak clustering[J]. Science Technology and Engineering, 2020, 20(2): 654-658. (  0) 0) |
| [19] |
姚黄金, 雷霞, 付鑫权, 等. 基于改进自适应密度峰值算法的日负荷曲线聚类分析[J]. 电力系统保护与控制, 2022, 50(3): 121-130. YAO Huangjin, LEI Xia, FU Xinquan, et al. Cluster analysis of daily load curves based on an improved self-adaptive density peak clustering algorithm[J]. Power System Protection and Control, 2022, 50(3): 121-130. (  0) 0) |
| [20] |
BAZZI A, MASINI B M, ZANELLA A, et al. On the performance of IEEE 802.11p and LTE-V2V for the cooperative awareness of connected vehicles[J]. IEEE Transactions on Vehicular Technology, 2017, 66(11): 10419-10432. (  0) 0) |
| [21] |
周军, 魏国亮, 田昕, 等. 融合UWB和IMU数据的新型室内定位算法[J]. 小型微型计算机系统, 2021, 42(8): 1741-1746. ZHOU Jun, WEI Guoliang, TIAN Xin, et al. Novel indoor positioning algorithm by fusing data of UWB and IMU[J]. Journal of Chinese Computer Systems, 2021, 42(8): 1741-1746. (  0) 0) |
| [22] |
张鹏, 吴通, 李中, 等. BP神经网络法预测顺北超深碳酸盐岩储层应力敏感程度[J]. 石油钻采工艺, 2020, 42(5): 622-626. ZHANG Peng, WU Tong, LI Zhong, et al. Application of BP neural network method to predict the stress sensitivity of ultra deep carbonate reservoir in Shunbei oilfield[J]. Oil Drilling & Production Technology, 2020, 42(5): 622-626. (  0) 0) |
 2023, Vol. 42
2023, Vol. 42


 薛灿(1996), 男, 博士在读, 研究方向为声信号处理、定位导航(E-mail:
薛灿(1996), 男, 博士在读, 研究方向为声信号处理、定位导航(E-mail: