文章编号: 2096-3203(2023)01-0116-08 中图分类号: TM46
模块化多电平换流器(modular multilevel converter, MMC)具有输出谐波含量小、开关频率低、操作灵活等优点[1-5],被广泛应用于高压大功率场合[6-9]。MMC由大量子模块(submodule, SM)级联而成[10],内部包含大量开关器件,一旦SM开关器件发生故障将会危害系统的稳定运行和设备安全[11-12]。其中SM开关器件的短路故障特征明显,已有成熟的工业解决方案,在驱动电路配置过流保护即可快速闭锁出现短路故障的SM[13]。而开路故障往往不易及时检测,威胁系统正常运行,因此须对SM开路故障定位展开研究。
目前关于SM开路故障的定位方法大致可分为3类[14]。第一类是基于额外传感器的故障定位方法,文献[15]通过冗余的监控传感器实现SM的故障定位,但增加了硬件成本。第二类是基于人工智能算法的故障定位方法,通过分析一组相关变量,将其与正常条件下的值或轨迹进行比较来定位故障SM。如文献[16]利用大量原始电压和电流数据构建一维卷积神经网络进行SM故障定位。文献[17]基于聚类算法通过识别SM特征变量的二维轨迹模式来定位发生开路故障的SM。基于人工智能的方法需要对故障特征变量进行复杂计算来定位故障SM,算法计算量相对较大。第三类是基于数学模型的故障定位方法,通常采用构建MMC数学模型,比较故障特征变量的估计值与测量值的方式来定位故障。文献[18]基于滑模观测器估计桥臂电流、文献[19]基于卡尔曼滤波器估计环流、文献[20]通过状态观测器估计交流侧电流和环流来实现SM开路故障定位。基于数学模型的方法不仅要对MMC建立精确的数学模型,还要手动设置经验阈值,而MMC是高阶时变非线性系统,因此算法较为复杂。
文中提出了基于拉依达准则的SM开路故障定位方法。该方法根据桥臂内SM电容电压的平均值和标准偏差构建置信区间,通过检测SM电容电压数据异常来定位故障SM。最后通过仿真和实验验证该方法的有效性,并与其他方法进行性能对比。相比第一类基于传感器的方法,文中方法不用引入额外的传感器;相比第二类基于人工智能的方法,文中方法不用进行大量数据处理;相比第三类基于数学模型的方法,文中方法不用建立精确的数学模型,更不用手动设置经验阈值。基于拉依达准则的SM开路故障定位方法算法简单、计算量小,可有效定位SM开路故障,适用于含SM较多的MMC应用场景。
1 MMC拓扑和工作原理图 1(a)为三相MMC拓扑。该模型一共有3个相单元,每相包含上下2个桥臂,每个桥臂由N个相同的SM和1个桥臂电感Ls构成。从上、下桥臂连接点处引出三相交流电作为输入或输出,三相桥臂共用一条直流母线,可实现能量在交流和直流间双向流动。图 1(b)为A相上桥臂SM拓扑,由2个开关器件T1、T2,2个反并联二极管D1、D2和1个电容C构成。图 1中,idc、Udc分别为直流电流和直流电压;uua、ula分别为A相上、下桥臂电压;iua、ila分别为A相上、下桥臂电流;ia为A相电流;usm为SM输出电压;uc为电容电压。

|
图 1 三相MMC拓扑和SM拓扑 Fig. 1 Topologies of three-phase MMC and SM |
SM有投入和切除2种工作状态,可用开关函数S来控制SM的工作状态:
| $ S= \begin{cases}1 & \mathrm{~T}_1 \text { 导通 }, \mathrm{T}_2 \text { 关断 } \\ 0 & \mathrm{~T}_1 \text { 关断, } \mathrm{T}_2 \text { 导通 }\end{cases} $ | (1) |
S=1时,SM为投入状态,T1导通,T2关断,SM输出电压usm为电容电压。S=0时,SM为切除状态,T1关断,T2导通,SM输出电压usm为0。
当开关函数S确定时,由于桥臂电流方向不同,对应的SM电流通路不同,电容的充放电特性也不同。SM的4种工作模式总结如表 1所示。以A相上桥臂SM为例,规定电流iua的正方向如图 1(b)所示。S=1时,SM为投入状态,当桥臂电流iua>0时,电容处于充电状态,电容电压uc增大;当iua < 0时,电容处于放电状态,电容电压uc减小。S=0时,SM为切除状态,电容被旁路,此时无论桥臂电流方向如何,电容电压都不会改变。
|
|
表 1 SM工作模式 Table 1 Operation modes of SM |
SM的开关器件通常采用绝缘栅双极型晶体管(insulated gate bipolar transistor, IGBT),相比二极管,IGBT耐过压、过流能力低,易发生故障。IGBT的故障类型包括开路故障和短路故障,其中短路故障易引发过电流,故障特征明显,易于解决,在驱动电路配置过流保护即可快速闭锁出现短路故障的SM[13]。而开路故障往往具有一定潜伏性[21],不易及时定位。因此须分析IGBT的开路故障特性,找出故障特征变量,进而以此为依据进行故障定位。
2.1 T1开路故障特性分析SM正常运行过程中,当S=1且iua < 0时,电流经过T1流通,电容处于放电状态,其电压减小。若此时T1发生开路故障,如图 2所示,则iua将被迫流过D2,而不是C和T1,电容处于旁路状态,电容电压不变,此时本应减小的电容电压因T1开路故障而异常不变。SM其他3种工作模式则不受T1开路故障影响。表 2总结了T1故障下SM 4种工作模式,可知T1开路故障会导致SM电容电压出现异常,检测SM电容电压可定位出发生T1开路故障的SM。

|
图 2 T1开路故障 Fig. 2 T1 open-circuit fault |
|
|
表 2 T1开路故障时SM工作模式 Table 2 Operation modes of SM under T1 open-circuit fault |
SM正常运行过程中,当S=0且iua>0时,电流经过T2流通,电容处于旁路状态,其电压不变。若此时T2发生开路故障,见图 3,则iua将被迫流过D1和C,而不是T2,电容处于充电状态,电容电压增大,此时本应保持不变的电容电压因T2开路故障而异常增大。SM其他3种工作模式则不受T2开路故障的影响。表 3总结了T2故障下SM 4种工作模式,可见T2开路故障会导致SM电容电压出现异常,检测SM电容电压可定位出发生T2开路故障的SM。

|
图 3 T2开路故障 Fig. 3 T2 open-circuit fault |
|
|
表 3 开路故障时SM工作模式 Table 3 Operation modes of SM under T2 open-circuit fault |
由前文分析可知,当某个SM发生开路故障时,该SM的电容电压会出现异常变化,相对于其他SM的电容电压为异常数据。因此,可采用拉依达准则检测出桥臂SM电容电压中的异常数据,进而定位出发生开路故障的SM。
3.1 拉依达准则原理拉依达准则又称3σ准则,是基于概率论原理的一种异常数据判别原则,可有效检测出一组样本数据中的异常值,被广泛运用于金融、科研、工程等领域的数据处理中[22-23]。
拉依达准则判别异常值的原则是:首先假设一组测量数据只含随机误差,计算样本数据的均值μ和标准偏差σ。然后按照一定的概率确定一个置信区间,区间通常取μ±3σ,对应置信概率为99.7%。则数据集中在置信区间(μ-3σ, μ+3σ)内的概率超过99.7%,而超出这个范围的概率极小,所以可以认为超过这个置信区间的误差属于粗大误差,即异常数据[24]。因此,设一组正态分布数据为xi(i=1, 2, 3, …, n),其平均值为:
| $ \bar{x}=\frac{1}{n} \sum\limits_{i=1}^n x_i $ | (2) |
数据与均值之差的绝对值为:
| $ \left|v_i\right|=\left|x_i-\bar{x}\right| $ | (3) |
其标准偏差σ为:
| $ \sigma=\sqrt{\left(\sum\limits_{i=1}^n v_i^2\right) / n} $ | (4) |
由于正常样本点与均值之差超过3倍标准偏差的概率很小,可以忽略不计,因此当样本与均值之差的绝对值大于3倍标准偏差时,可认为该样本点为异常数据点。即当样本数据超出置信区间,满足式(5)或式(6)时,可认为该样本点为异常数据点。
| $ x_i>\bar{x}+3 \sigma $ | (5) |
| $ x_i<\bar{x}-3 \sigma $ | (6) |
拉依达准则通常适用于样本数量较大的场合,而MMC内部包含大量的SM,SM的数量可达几十、上百个,因此拉依达准则可用于检测SM电容电压中的异常数据。当SM发生开路故障后,该SM的电容电压出现异常变化,逐渐超出置信区间,可据此定位出发生开路故障的SM。为防止系统误判断,可设置一段判定时间,使其具有较好的可行性。基于拉依达准则的SM开路故障定位流程如图 4所示。

|
图 4 基于拉依达准则的故障定位流程 Fig. 4 Flow chart of fault localization based on Pauta criterion |
首先获取当前采样时刻同桥臂内SM电容电压数据ui (i=1, 2, 3, …,n),然后根据式(2)—式(4)计算电容电压均值u 和标准偏差σ,得到置信区间(u-3σ, u+3σ)。判断SM电容电压是否超出该区间,若某SM电容电压超出置信区间且至少持续时间Δt,则认为该SM出现故障,控制器发出信号迅速闭锁并替换掉该SM;否则,判定该桥臂正常运行,此定位算法继续执行。
3.3 基于拉依达准则的故障定位法性能分析 3.3.1 基于拉依达准则的故障定位方法执行时间假设桥臂内有n个SM,每个故障定位周期须对n个SM进行一次平均值和标准偏差计算,获取左右置信区间端点后进行2n次比较,则一共需要加法2n-1次,减法n+1次,乘法n+1次,除法2次,开方1次,比较2n次。以文献[25]中的数字信号处理器为例,其主频为150 MHz,则执行一次故障定位用时约(16n+536)/150 μs。
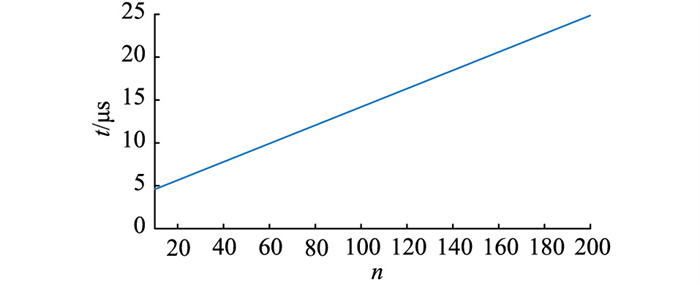
图 5为桥臂SM个数n与文中故障定位方法用时t之间的关系。可以看到,随着SM数量的增加,故障定位用时也增加。SM数量达到200个时,用时不超过25 μs。
|
图 5 执行时间与SM数量的关系 Fig. 5 Relationship between operation time and SM quantity |
表 4为文中方法与其他故障定位方法[14-20, 26]的对比。
|
|
表 4 SM故障定位方法对比 Table 4 Comparison of SM fault localization methods |
由表 4可知,基于额外传感器的方法[15]会增加额外的硬件成本。基于人工智能算法的方法[14, 16-17]要对SM开路故障特征变量进行大量数据分析和样本训练,计算过程相对复杂,计算量较大。聚类算法[17]和基于数学模型的方法[18-20, 26]应对MMC建立精确的数学模型,但MMC具有高阶时变非线性特点,因此算法相对复杂,且要手动设置经验阈值,而阈值会随着MMC实际运行工况的变化而改变,因此阈值难以确定。文中方法不用引入额外的传感器,不用建立精确的数学模型,也不用手动设置阈值,只要计算桥臂电容电压的均值和3倍标准偏差,计算量较小。此外,由于MMC正常运行时要测量电容电压数据来进行电容电压平衡控制,因此文中方法也不增加额外的测量负担,且文中方法所需时间短,仅约20 ms。
4 仿真验证为验证基于拉依达准则的SM开路故障定位方法的准确性,在PSCAD/EMTDC中搭建图 1(a)所示三相MMC并网系统模型进行仿真验证,系统参数见表 5。
|
|
表 5 MMC仿真系统参数 Table 5 Parameters of MMC simulation system |
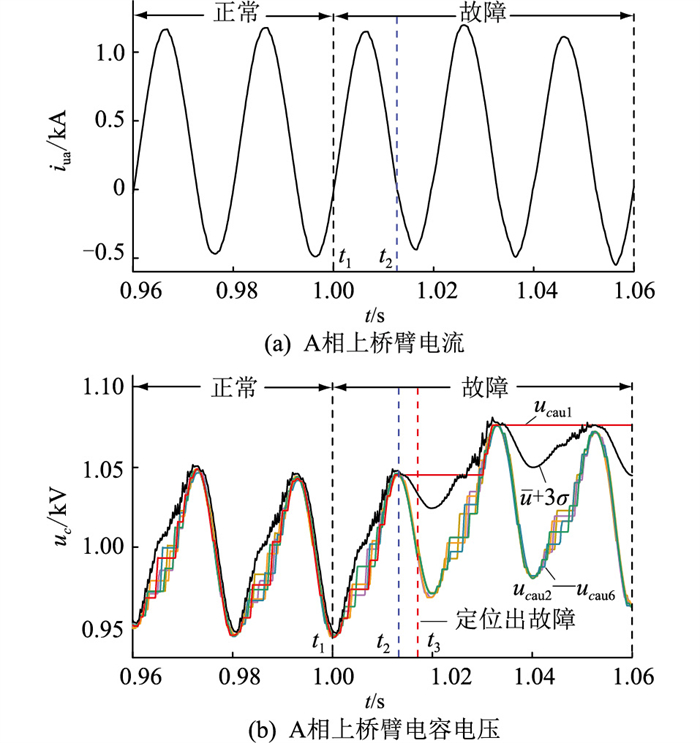
考虑MMC的A相上桥臂SM1发生T1开路故障,图 6为此时A相上桥臂电流和上桥臂SM电容电压波形。
|
图 6 T1开路故障时的仿真波形 Fig. 6 Simulation waveforms under T1 open-circuit fault |
图 6(a)为A相上桥臂电流iua波形,t1=1 s时SM1发生T1开路故障,由于桥臂电流iua>0,SM1仍能保持正常运行。直到t2=1.012 s时桥臂电流iua < 0,由于T1开路故障,SM1会进入异常运行状态,桥臂电流开始出现畸变。
图 6(b)为SM电容电压uc波形,由于SM数量较多,图中只给出了前6个SM的电容电压。其中红色曲线为SM1的电容电压ucau1,黑色曲线为置信区间的上限即u+3σ。由于故障SM电压只超过了区间一条边界,因此图中省略了置信区间下限,下文同理。t2=1.012 s后,由于T1开路故障,SM1电容电压异常不变,因此SM1的电容电压相对于其他SM为异常数据,t3=1.017 s时,基于拉依达准则的SM开路故障定位方法定位出SM1发生故障。从发生故障到定位出故障所需时间为17 ms,其中从SM1表现出故障特征到定位出故障SM所需时间为5 ms。
4.2 T2开路故障定位的仿真结果考虑MMC的A相上桥臂SM1发生T2开路故障,图 7为此时A相上桥臂电流和上桥臂SM电容电压波形。

|
图 7 T2开路故障时的仿真波形 Fig. 7 Simulation waveforms under T2 open-circuit fault |
图 7(a)为上桥臂电流iua波形,t1=1 s时SM1发生T2开路故障,此时桥臂电流iua>0,由于T2开路故障,SM1会进入异常运行状态,桥臂电流开始出现畸变。
图 7(b)为SM电容电压uc波形,由于SM数量较多,图中只给出了前6个SM的电容电压。T2开路故障,SM1电容电压异常增大,因此SM1电容电压相对于其他SM为异常数据。t3=1.006 s时,基于拉依达准则的SM开路故障定位方法定位出SM1发生故障。从发生故障到定位出故障所需时间为6 ms。
5 实验验证为验证基于拉依达准则的SM开路故障定位方法的准确性,在实验室搭建单相MMC平台进行验证,平台实物图如图 8所示,系统参数见表 6。直流电源用于支撑MMC直流侧电压,MMC交流侧接阻感负载。控制器的驱动信号通过光纤传输到各个SM的驱动板上。由于桥臂SM数量较多,而示波器通道有限,实验中通过控制器采集并记录桥臂中所有SM电容电压和桥臂电流。

|
图 8 MMC故障模拟平台 Fig. 8 MMC fault simulation platform |
|
|
表 6 MMC实验系统参数 Table 6 Parameters of MMC experimental system |
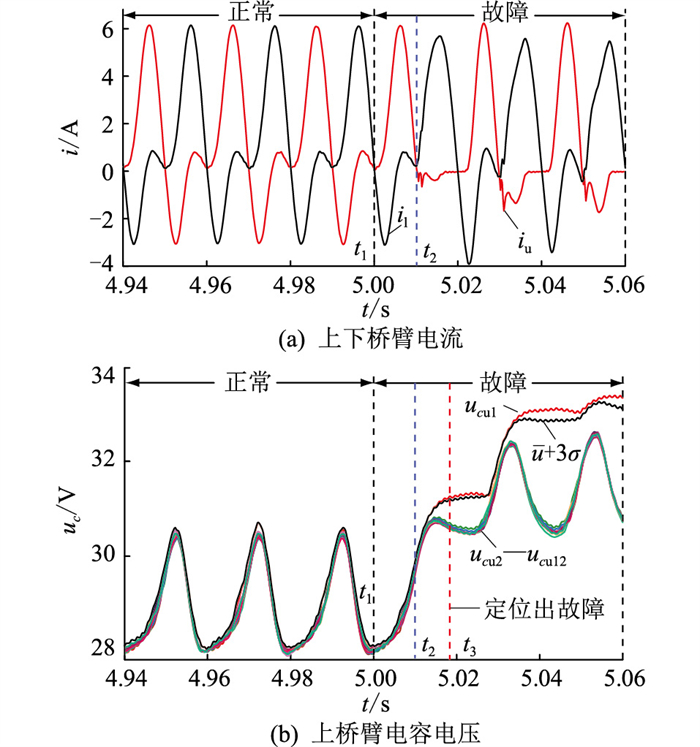
考虑MMC上桥臂SM1发生T1开路故障,图 9为此时MMC上下桥臂电流和上桥臂电容电压波形。
|
图 9 T1开路故障时的实验波形 Fig. 9 Experiment waveforms under T1 open-circuit fault |
图 9(a)为上桥臂电流iu和下桥臂电流il波形,t1=5 s时SM1发生T1开路故障,由于桥臂电流iu>0,SM1仍能保持正常运行。直到t2=5.01 s时桥臂电流iu<0,由于T1开路故障,SM1进入异常工作状态,桥臂电流开始出现畸变。
图 9(b)为上桥臂电容电压uc波形,t2=5.01 s后,SM1电容电压开始逐渐出现异常,t3=5.018 s时,基于拉依达准则的SM开路故障定位方法定位出SM1发生故障。从发生故障到定位出故障所需时间为18 ms,其中从SM1表现出故障特征到定位出故障SM所需时间为8 ms。
5.2 T2开路故障定位的实验结果考虑MMC上桥臂SM1发生T2开路故障,图 10为此时MMC上下桥臂电流和上桥臂电容电压。图 10(a)为上桥臂电流iu和下桥臂电流il波形,t1=5 s时SM1发生T1开路故障,此时桥臂电流iu>0,由于T2开路故障,SM1会进入异常工作状态,桥臂电流出现畸变。图 10(b)为SM电容电压波形,由于T2开路故障,SM1电容电压逐渐异常增大,相对于其他SM为异常数据。t3 =5.011 s时,基于拉依达准则的SM开路故障定位方法定位出SM1发生故障。从发生故障到定位出故障所需时间为11 ms。

|
图 10 T2开路故障时的实验波形 Fig. 10 Experiment waveforms under T2 open-circuit fault |
为实现MMC的SM开路故障定位,文中首先分析了SM中IGBT的开路故障特性,发现IGBT的开路故障会引起SM电容电压的异常变化,该异常变化可通过拉依达准则进行判别定位。据此,文中提出基于拉依达准则的SM开路故障定位方法,通过判断SM电容电压是否超出均值与3倍标准差构成的置信区间且持续一段时间来定位SM开路故障。将文中方法和其他常用故障定位方法进行对比,可以看出文中方法不用引入额外的传感器,不用建立精确的数学模型,也不用手动设置阈值,算法相对简单、计算量较小。最后通过仿真和实验证明,文中所提基于拉依达准则的SM开路故障定位方法可以有效定位SM开路故障。
| [1] |
PEREZ M A, BERNET S, RODRIGUEZ J, et al. Circuit topologies, modeling, control schemes, and applications of modular multilevel converters[J]. IEEE Transactions on Power Electronics, 2015, 30(1): 4-17. DOI:10.1109/TPEL.2014.2310127 (  0) 0) |
| [2] |
RAJU M N, SREEDEVI J, P MANDI R, et al. Modular multilevel converters technology: a comprehensive study on its topologies, modelling, control and applications[J]. IET Power Electronics, 2019, 12(2): 149-169. DOI:10.1049/iet-pel.2018.5734 (  0) 0) |
| [3] |
ZHANG L, ZOU Y T, YU J C, et al. Modeling, control, and protection of modular multilevel converter-based multi-terminal HVDC systems: a review[J]. CSEE Journal of Power and Energy Systems, 2017, 3(4): 340-352. DOI:10.17775/CSEEJPES.2017.00440 (  0) 0) |
| [4] |
王雪姣. 模块化多电平换流器子模块拓扑设计及其控制[D]. 淄博: 山东理工大学, 2021. WANG Xuejiao. Design of sub module topologies and their control for modular multilevel converter[D]. Zibo: Shandong University of Technology, 2021. (  0) 0) |
| [5] |
江畅. 基于模块化多电平换流器的统一电能质量调节器研究[D]. 上海: 上海电力大学, 2021. JIANG Chang. Research on unified power quality conditioner based on modular multilevel converter[D]. Shanghai: Shanghai University of Electric Power, 2021. (  0) 0) |
| [6] |
胡宏, 陈浩, 丁浩寅, 等. 特高压混合级联多端直流输电系统的协调控制策略研究[J]. 电力工程技术, 2021, 40(4): 42-51. HU Hong, CHEN Hao, DING Haoyin, et al. Coordinated control strategy for hybrid cascaded UHVDC system[J]. Electric Power Engineering Technology, 2021, 40(4): 42-51. (  0) 0) |
| [7] |
XIANG W, YANG S Z, ADAM G P, et al. DC fault protection algorithms of MMC-HVDC grids: fault analysis, methodologies, experimental validations, and future trends[J]. IEEE Transactions on Power Electronics, 2021, 36(10): 11245-11264. DOI:10.1109/TPEL.2021.3071184 (  0) 0) |
| [8] |
DU S X, WU B, ZARGARI N R, et al. A flying-capacitor modular multilevel converter for medium-voltage motor drive[J]. IEEE Transactions on Power Electronics, 2017, 32(3): 2081-2089. DOI:10.1109/TPEL.2016.2565510 (  0) 0) |
| [9] |
OKAZAKI Y, KAWAMURA W, HAGIWARA M, et al. Experimental comparisons between modular multilevel DSCC inverters and TSBC converters for medium-voltage motor drives[J]. IEEE Transactions on Power Electronics, 2017, 32(3): 1805-1817. DOI:10.1109/TPEL.2016.2562103 (  0) 0) |
| [10] |
ALI S, LING Z B, TIAN K, et al. Recent advancements in submodule topologies and applications of MMC[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(3): 3407-3435. DOI:10.1109/JESTPE.2020.2990689 (  0) 0) |
| [11] |
DENG F J, LYU Y, LIU C K, et al. Overview on submodule topologies, modeling, modulation, control schemes, fault diagnosis, and tolerant control strategies of modular multilevel converters[J]. Chinese Journal of Electrical Engineering, 2020, 6(1): 1-21. (  0) 0) |
| [12] |
CHEN X X, LIU J J, DENG Z F, et al. A diagnosis strategy for multiple IGBT open-circuit faults of modular multilevel converters[J]. IEEE Transactions on Power Electronics, 2021, 36(1): 191-203. DOI:10.1109/TPEL.2020.2997963 (  0) 0) |
| [13] |
GENG Z, HAN M X, KHAN Z W, et al. Detection and localization strategy for switch open-circuit fault in modular multilevel converters[J]. IEEE Transactions on Power Delivery, 2020, 35(6): 2630-2640. (  0) 0) |
| [14] |
DENG F J, JIN M, LIU C K, et al. Switch open-circuit fault localization strategy for MMCs using sliding-time window based features extraction algorithm[J]. IEEE Transactions on Industrial Electronics, 2021, 68(10): 10193-10206. DOI:10.1109/TIE.2020.3028808 (  0) 0) |
| [15] |
PICAS R, ZARAGOZA J, POU J, et al. Reliable modular multilevel converter fault detection with redundant voltage sensor[J]. IEEE Transactions on Power Electronics, 2017, 32(1): 39-51. DOI:10.1109/TPEL.2016.2526684 (  0) 0) |
| [16] |
KIRANYAZ S, GASTLI A, BEN-BRAHIM L, et al. Real-time fault detection and identification for MMC using 1-D convolutional neural networks[J]. IEEE Transactions on Industrial Electronics, 2019, 66(11): 8760-8771. DOI:10.1109/TIE.2018.2833045 (  0) 0) |
| [17] |
YANG Q C, QIN J C, SAEEDIFARD M. Analysis, detection, and location of open-switch submodule failures in a modular multilevel converter[J]. IEEE Transactions on Power Delivery, 2016, 31(1): 155-164. DOI:10.1109/TPWRD.2015.2477476 (  0) 0) |
| [18] |
SHAO S, WATSON A J, CLARE J C, et al. Robustness analysis and experimental validation of a fault detection and isolation method for the modular multilevel converter[J]. IEEE Transactions on Power Electronics, 2016, 31(5): 3794-3805. DOI:10.1109/TPEL.2015.2462717 (  0) 0) |
| [19] |
DENG F J, CHEN Z, KHAN M R, et al. Fault detection and localization method for modular multilevel converters[J]. IEEE Transactions on Power Electronics, 2015, 30(5): 2721-2732. DOI:10.1109/TPEL.2014.2348194 (  0) 0) |
| [20] |
LI B B, SHI S L, WANG B, et al. Fault diagnosis and tolerant control of single IGBT open-circuit failure in modular multilevel converters[J]. IEEE Transactions on Power Electronics, 2016, 31(4): 3165-3176. DOI:10.1109/TPEL.2015.2454534 (  0) 0) |
| [21] |
李豪, 赵孟, 董志文, 等. VSC-MTDC系统中IGBT开路检测方法研究[J]. 可再生能源, 2019, 37(12): 1802-1808. LI Hao, ZHAO Meng, DONG Zhiwen, et al. Fault detection of IGBT open-circuit for VSC-MTDC system[J]. Renewable Energy Resources, 2019, 37(12): 1802-1808. (  0) 0) |
| [22] |
林静, 唐国强, 覃良文. 基于3σ准则的分段拟合及其GARCH修正模型[J]. 经济数学, 2016, 33(3): 26-32. LIN Jing, TANG Guoqiang, QIN Liangwen. Piecewise Fitting based on 3σ guidelines and its GARCH remaining modified model[J]. Journal of Quantitative Economics, 2016, 33(3): 26-32. (  0) 0) |
| [23] |
徐琛辉, 马明辉. 基于拉依达准则的交通数据粗大误差处理优化方法[J]. 上海工程技术大学学报, 2018, 32(1): 64-67. XU Chenhui, MA Minghui. Optimization method for gross error processing of traffic data based on pauta criterion[J]. Journal of Shanghai University of Engineering Science, 2018, 32(1): 64-67. (  0) 0) |
| [24] |
杨婧, 辛明勇, 欧家祥, 等. 基于拉依达准则的计量自动化系统数据准确性判断方法[J]. 电力大数据, 2017, 20(11): 74-78. YANG Jing, XIN Mingyong, OU Jiaxiang, et al. Data accuracy judgment method of metrology automation system based on Pauta criterion[J]. Power Systems and Big Data, 2017, 20(11): 74-78. (  0) 0) |
| [25] |
DENG F J, HENG Q, LIU C K, et al. Capacitor ESR and C monitoring in modular multilevel converters[J]. IEEE Transactions on Power Electronics, 2020, 35(4): 4063-4075. (  0) 0) |
| [26] |
ZHOU W H, SHENG J, LUO H Z, et al. Detection and localization of submodule open-circuit failures for modular multilevel converters with single ring theorem[J]. IEEE Transactions on Power Electronics, 2019, 34(4): 3729-3739. (  0) 0) |
 2023, Vol. 42
2023, Vol. 42


 王宝安(1978), 男, 博士, 副教授, 研究方向为电能质量、电力电子技术(E-mail:
王宝安(1978), 男, 博士, 副教授, 研究方向为电能质量、电力电子技术(E-mail: